Low-Complexity Spectrum-efficiency Optimization Algorithm for Cell-Free Massive MIMO-NOMA Systems
-
摘要: 针对传统无蜂窝大规模多输入多输出(MIMO)非正交多址接入(NOMA)系统频谱效率优化算法复杂度高的问题,该文提出一种低复杂度的用户分簇与功率分配联合优化算法。首先构建下行链路总频谱效率最大化模型,将其分解为用户分簇与功率分配子问题;然后提出基于簇首选择与信道差异最大化的用户分簇算法,通过优化簇首选择降低配对搜索复杂度。基于分簇结果,引入用户最小速率增强约束机制,结合逐次凸逼近(SCA)方法将非凸功率分配问题转化为凸优化形式。通过理论分析与仿真验证,对比了不同用户分簇算法和功率分配方案下系统的频谱效率以及计算复杂度。结果表明:所提分簇算法在不同接入点部署和天线配置下能显著提升系统性能,且复杂度较统计学分簇方法降低47.5%;联合功率分配方案较全功率控制方案在频谱效率与用户公平性方面均展现出显著优势,验证了所提方案的高效性与实用性。Abstract:
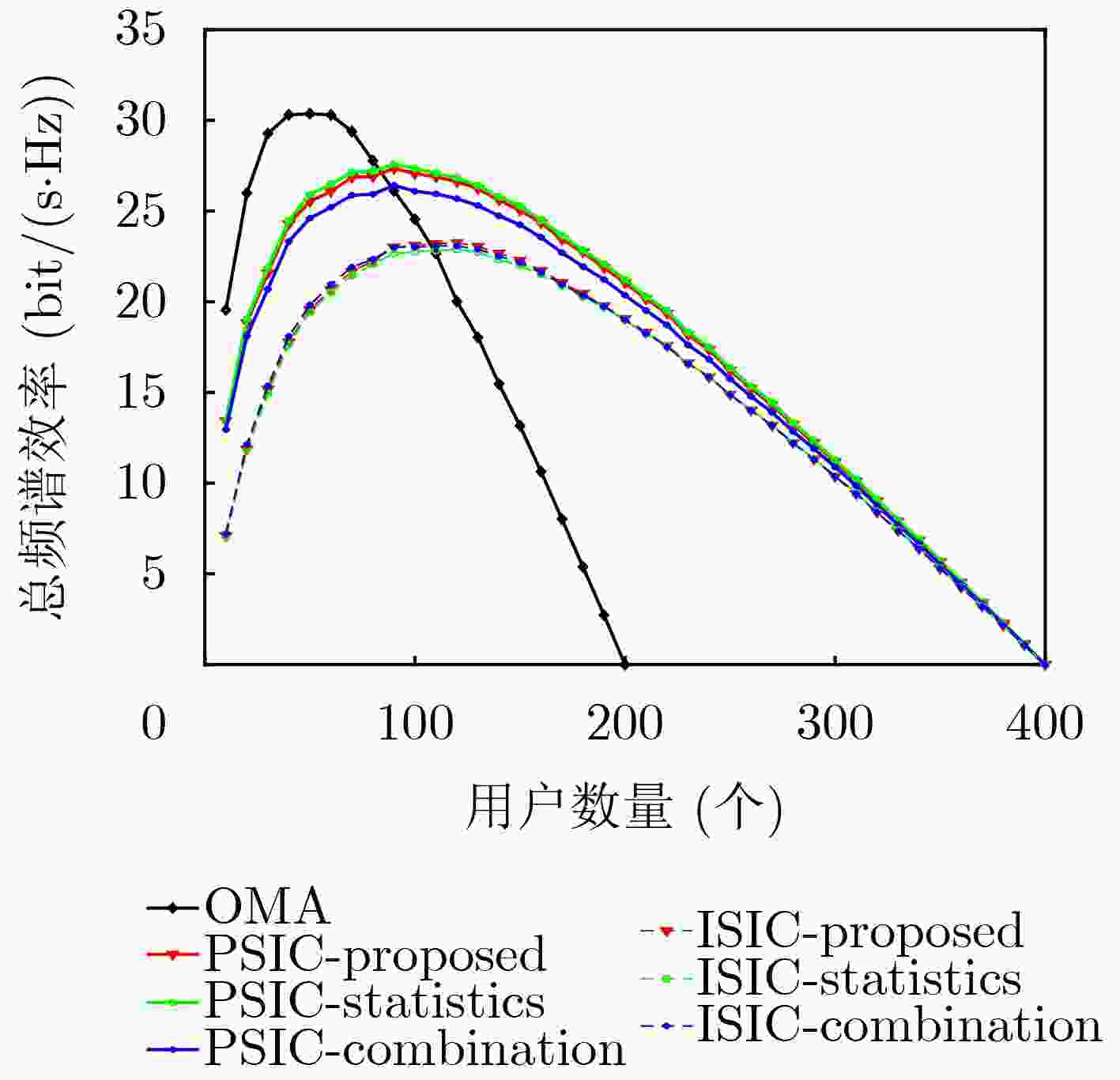
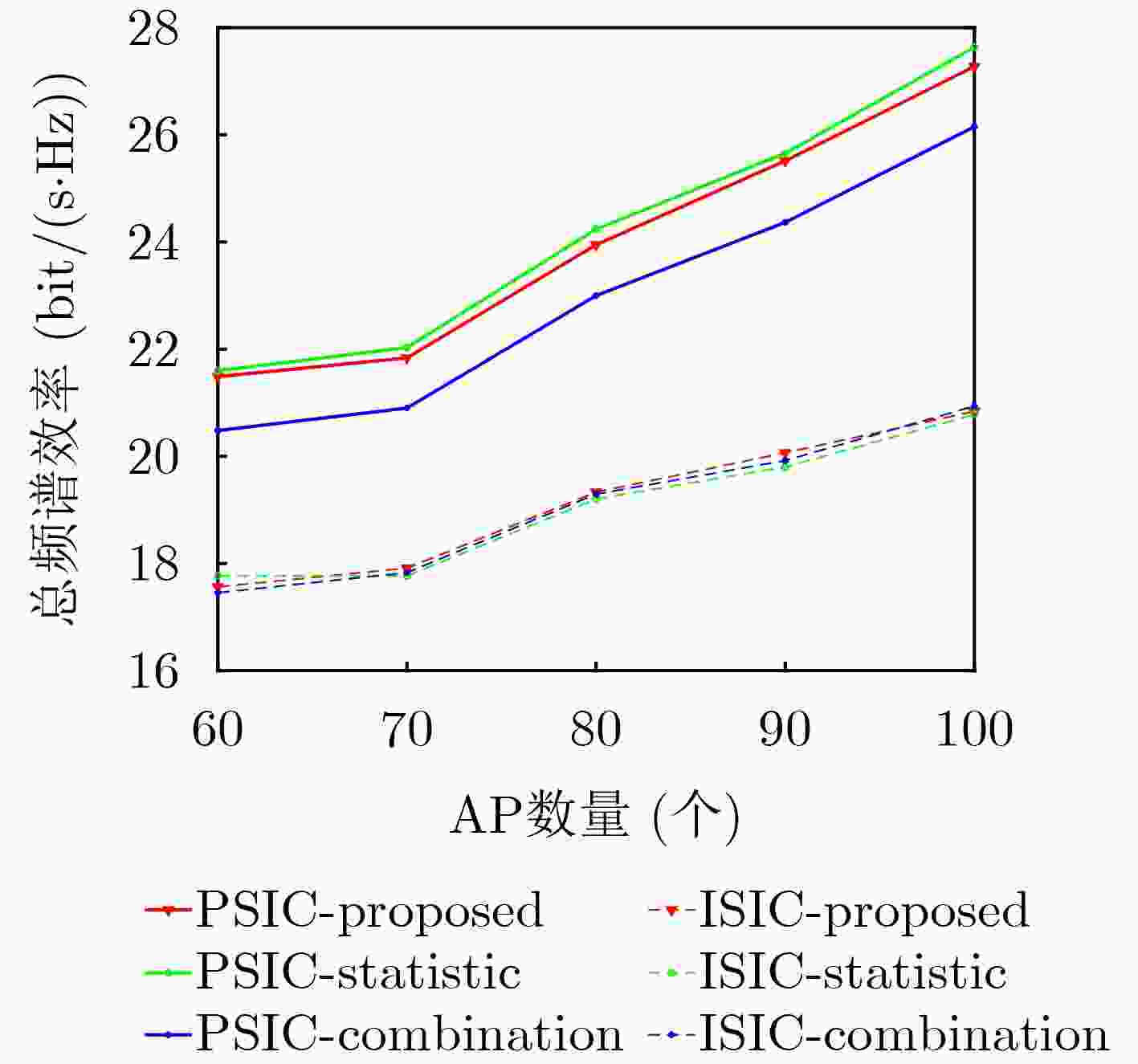
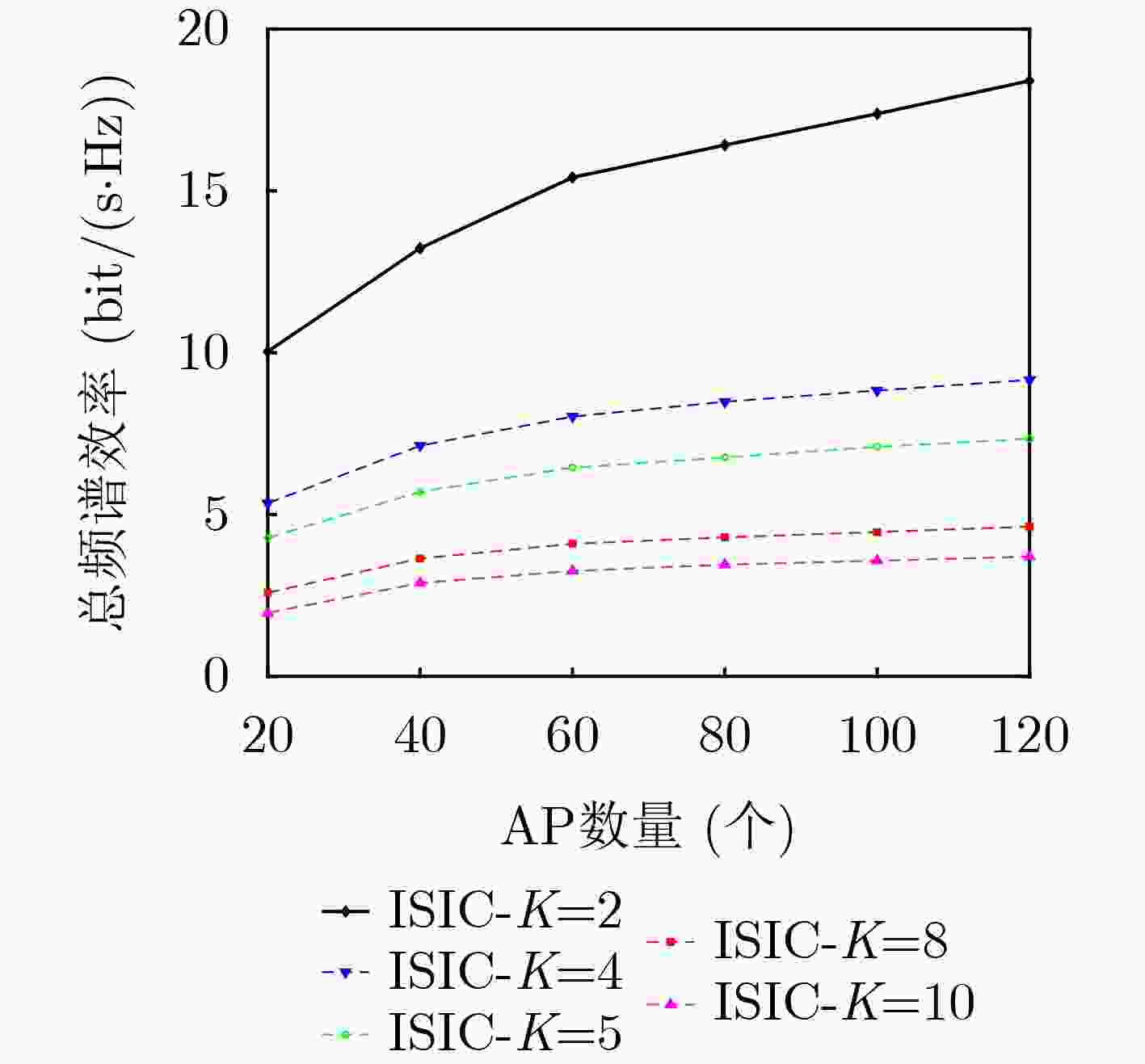
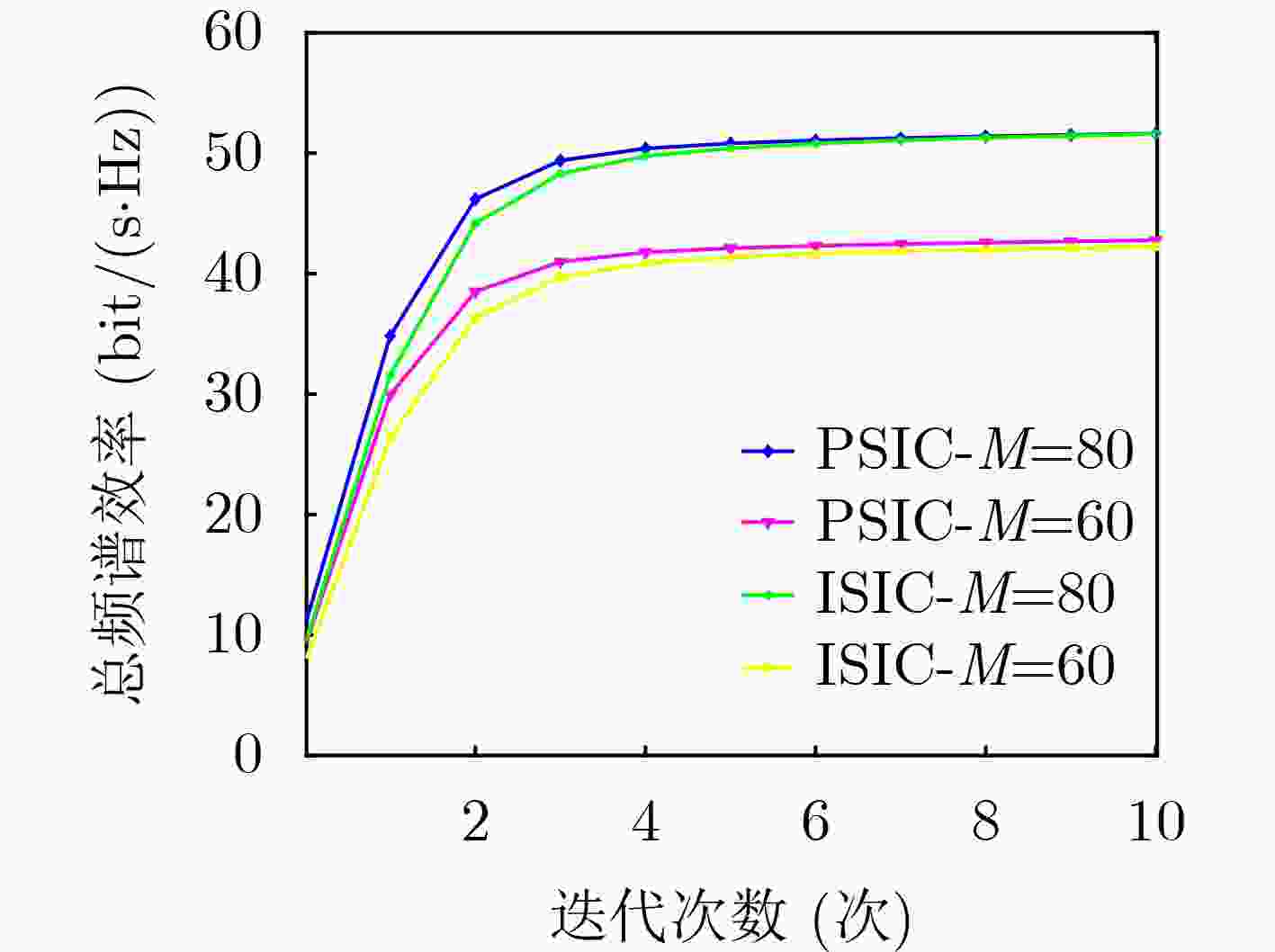
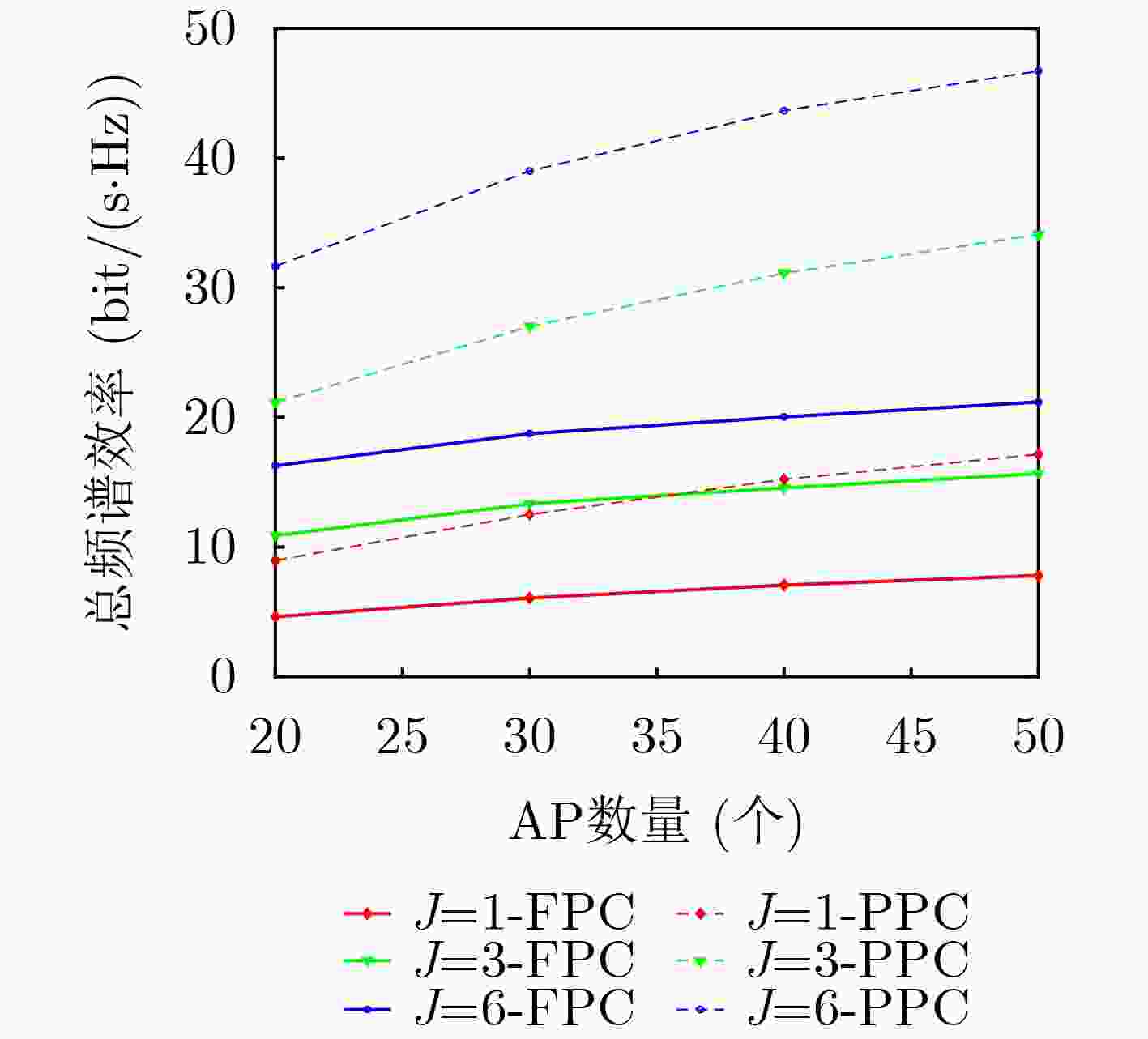
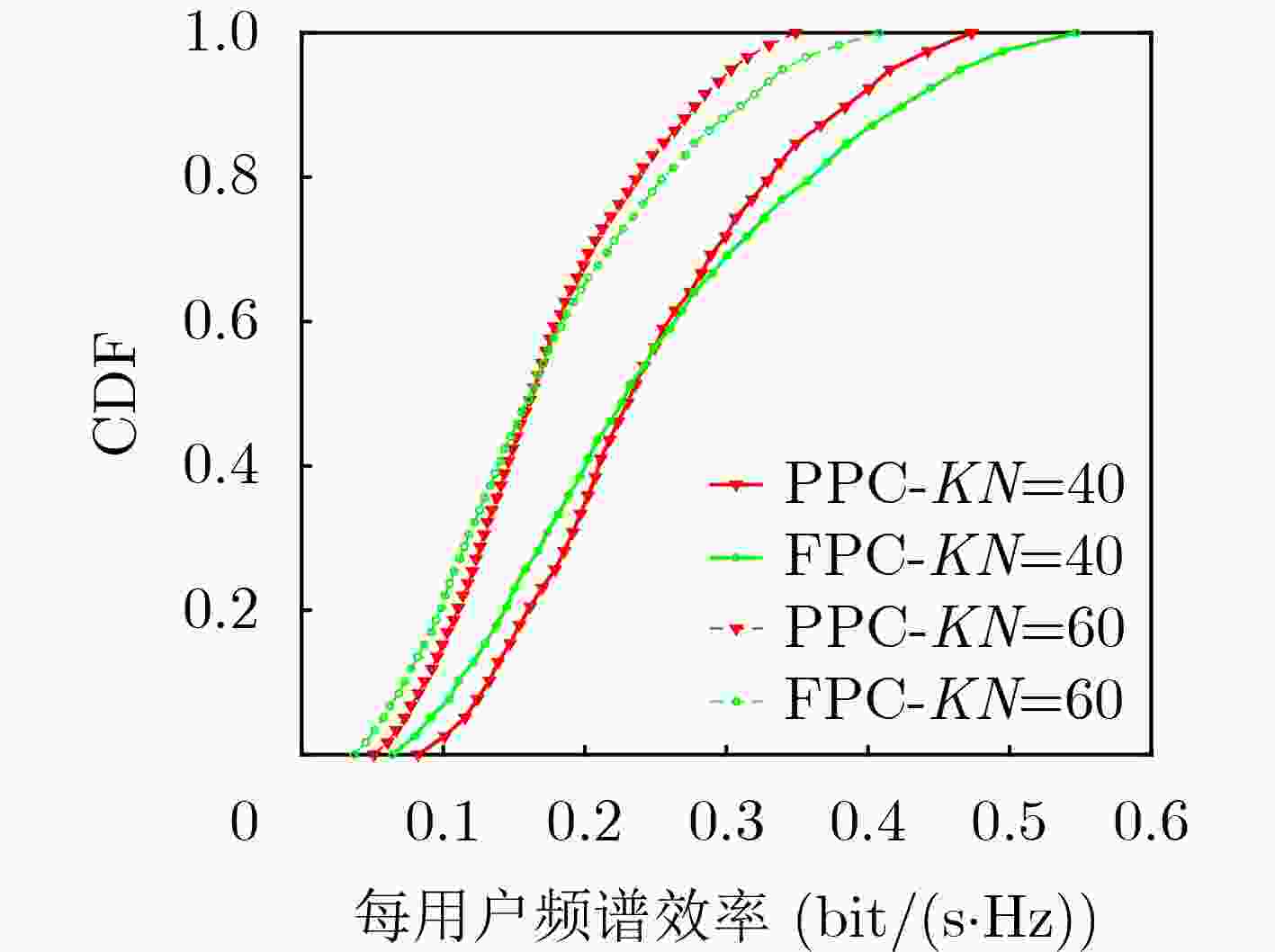
Objective With the evolution of wireless communication toward ultra-dense networks, optimizing spectrum efficiency in cell-free massive Multiple-Input Multiple-Output (MIMO) Non-Orthogonal Multiple Access (NOMA) systems faces the challenge of balancing algorithmic complexity and performance. Traditional user clustering methods, such as random clustering, exhibit high randomness and easily converge to suboptimal solutions, whereas exhaustive search is computationally prohibitive. Similarly, power allocation schemes with rigid fixed thresholds often fail to accommodate dynamic user demands, resulting in imbalanced resource utilization and reduced fairness. To address these limitations, this study proposes a low-complexity joint optimization algorithm. By collaboratively designing user clustering and power allocation, the algorithm maximizes the system’s sum spectrum efficiency while guaranteeing the quality of service for low-rate users, thereby offering an efficient resource allocation strategy for cell-free massive MIMO-NOMA systems. Methods A downlink sum spectrum efficiency maximization model is first constructed and decomposed into two sub-problems: user clustering and power allocation. A clustering algorithm based on cluster head selection and channel difference maximization is then proposed, which reduces the complexity of pairing searches by optimizing the selection of cluster heads. Based on the clustering results, a minimum-rate enhancement constraint mechanism is incorporated. The resulting non-convex power allocation problem is subsequently transformed into a convex optimization form using the Successive Convex Approximation (SCA) method. Results and Discussions The relationship between sum spectrum efficiency and the number of users under different clustering algorithms is shown in ( Fig. 2 ). Under perfect Successive Interference Cancellation (SIC) conditions, the proposed algorithm achieves performance comparable to that of the statistical clustering algorithm, whereas the combined clustering algorithm yields the lowest efficiency. Under imperfect SIC, the proposed algorithm maintains the highest spectrum efficiency, while the performance of the statistical algorithm decreases. The sum spectrum efficiency is markedly reduced by imperfect SIC, particularly when the number of users is small. This reduction arises from insufficient elimination of intra-cluster interference, leading to increased residual interference. Notably, the NOMA system supports twice the user capacity of Orthogonal Multiple Access (OMA), confirming its superior spectrum resource utilization. The relationship between sum spectrum efficiency and the number of Access Points (APs) is shown in (Fig. 3 ). Spectrum efficiency improves substantially as the number of APs increases, owing to enhanced channel hardening and interference suppression. Under perfect SIC, both the proposed algorithm and the statistical clustering algorithm achieve similar performance, exceeding the combined algorithm. The advantage of the proposed algorithm is further demonstrated under imperfect SIC. Increasing the number of deployed APs strengthens anti-interference capability and expands user capacity, verifying the efficiency and robustness of the proposed clustering algorithm under both perfect and imperfect SIC conditions. The effect of intra-cluster user numbers on spectrum efficiency is evaluated in (Fig. 4 ). Spectrum efficiency increases with the number of APs, largely due to improved coverage and channel estimation accuracy. However, efficiency decreases significantly as intra-cluster user numbers increase, which is attributed to aggravated intra-cluster interference and constraints on power resource allocation. The convergence of the proposed algorithm is demonstrated in (Fig. 5 ), where the optimal solution is reached within approximately seven iterations. After power allocation optimization, the efficiency gap between imperfect and perfect SIC remains below 0.2 bit/(s·Hz). Compared with Full Power Control (FPC), the Proposed Power Control (PPC) scheme effectively mitigates residual interference and achieves performance close to perfect SIC under practical conditions. The relationship between sum spectrum efficiency and AP numbers with different antenna configurations is presented in (Fig. 6 ). Efficiency continuously improves with increasing AP numbers and per-AP antenna numbers, owing to stronger channel hardening effects. Across all AP configurations, the PPC scheme demonstrates clear advantages over FPC, with the benefits becoming more pronounced in densely deployed networks. Power allocation optimization further enhances efficiency as antenna numbers increase. Finally, the cumulative distribution of per-user spectrum efficiency under different power control schemes is illustrated in (Fig. 7 ). The PPC scheme substantially reduces the proportion of inefficient users (0~0.2 bit/(s·Hz)), thereby improving system fairness. By contrast, the FPC scheme performs slightly better in the high-efficiency region, but this advantage comes at the expense of user fairness. In user-intensive scenarios, the PPC scheme effectively balances system stability and fairness by ensuring minimum rates for weak users.Conclusions A low-complexity joint optimization algorithm is presented to address the challenge of spectrum efficiency optimization in cell-free massive MIMO-NOMA systems. Through theoretical analysis and simulation, the spectrum efficiency and computational complexity of the system are compared under different user clustering algorithms and power allocation schemes. The results show that the proposed clustering algorithm significantly enhances system performance across various AP deployments and antenna configurations, while reducing computational complexity by 47.5% compared with the statistical clustering algorithm. Furthermore, the joint power allocation scheme demonstrates clear advantages over FPC in terms of spectrum efficiency and user fairness, verifying the effectiveness and practicality of the proposed algorithm. -
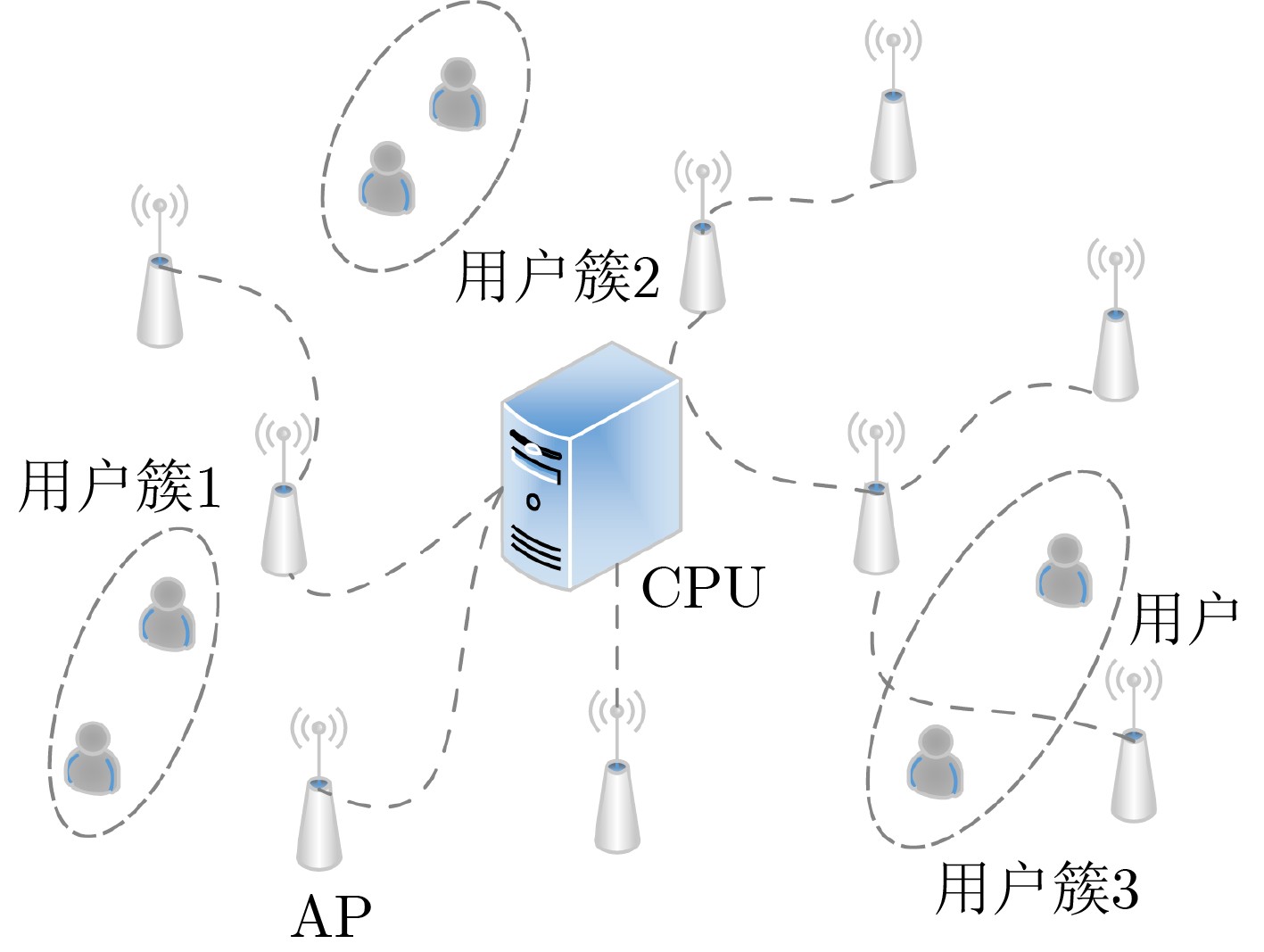
1 基于簇首选择与信道特性的用户分簇算法
(1)初始化:未分簇用户集合$\mathcal{U}$,分簇结果集合$ G = \varnothing $; (2)选择用户构造簇首候选集合$\mathcal{C}$,更新$\mathcal{U} = \mathcal{U}\backslash \mathcal{C}$; (3)在$\mathcal{C}$中,按从第N~1个簇首的逆序依次选择簇首用户${u_n}$; (4)对簇首用户${u_n}$,计算其与未分簇用户的评价指标$\hat {\boldsymbol{D}}$; (5) 按$\hat {\boldsymbol{D}}$降序选取前(K–1)个用户,与${u_n}$组成当前簇${G_n}$; (6)将${G_n}$加入$G$,更新$\mathcal{U} = \mathcal{U}\backslash {G_n}$; (7)重复步骤(3)~步骤(6),直至$\mathcal{U} = \varnothing $; (8)返回:分簇集合$G = \{ {G_1},{G_2}, \cdots ,{G_N}\} $。 表 1 复杂度对比
2 基于梯度下降的用户最小频谱效率增强方案
(1)初始化:功率分配系数$ {{\boldsymbol{\gamma}} ^{(0)}} $,学习率b,最大迭代次数L; (2)根据初始频谱效率,获得$\min {\text{S}}{{\text{E}}_{nk}}$; (3)梯度更新:$ \gamma _{mnk}^{(l + 1)} = \gamma _{mnk}^{(l)} + b \cdot \nabla {\text{S}}{{\text{E}}_{nk}} $; (4)更新用户最小频谱效率; (5)检查收敛条件:目标函数收敛或达到最大迭代次数,停止迭代;否则返回步骤3; (6)输出:所有用户频谱效率,优化后的功率分配系数。 表 2 系统参数
参数 值 接收端噪声方差$ \sigma _n^2 $ $290 \times k \times B \times {\text{NF}}$ 玻尔兹曼常数$k $ $1.381 \times {10^{ - 23}}$ J/K 带宽B 20 MHz 接收端噪声系数NF 9 dB 相干时间${\tau _{\text{c}}}$ 200 ms 导频长度${\tau _{\text{p}}}$ NOMA(N), OMA(KN) 学习率b 0.01 最大迭代次数L 50 导频发射功率${p_{\text{p}}}$ 0.1 W 信号发射功率${p_{\text{d}}}$ 0.2 W 阴影衰落方差${\sigma _{{\text{sh}}}}$ 8 dB 相关系数${\rho _{nk'}}$ 0.1 -
[1] APIYO A and IZYDORCZYK J. A survey of NOMA-aided cell-free massive MIMO systems[J]. Electronics, 2024, 13(1): 231. doi: 10.3390/electronics13010231. [2] NGO H Q, INTERDONATO G, LARSSON E G, et al. Ultradense cell-free massive MIMO for 6G: Technical overview and open questions[J]. Proceedings of the IEEE, 2024, 112(7): 805–831. doi: 10.1109/JPROC.2024.3393514. [3] JADIDI M, KHOUEINI A M, MOHAMMADI A, et al. Performance analysis and power allocation for uplink cell-free massive MIMO system with nonlinear power amplifier[J]. IEEE Transactions on Communications, 2024, 72(9): 5473–5485. doi: 10.1109/TCOMM.2024.3387854. [4] NGUYEN L D, TUAN H D, DUONG T Q, et al. Energy-efficient multi-cell massive MIMO subject to minimum user-rate constraints[J]. IEEE Transactions on Communications, 2021, 69(2): 914–928. doi: 10.1109/TCOMM.2020.3030780. [5] ZHANG Ruichen, XIONG Ke, LU Yang, et al. SWIPT-enabled cell-free massive MIMO-NOMA networks: A machine learning-based approach[J]. IEEE Transactions on Wireless Communications, 2024, 23(7): 6701–6718. doi: 10.1109/TWC.2023.3327596. [6] MOUSAVI S A, MONEMI M, and MOHSENI R. Leveraging common user clustering for improved performance in cell-free NOMA networks[J]. Wireless Networks, 2025, 31(3): 2573–2589. doi: 10.1007/s11276-025-03897-4. [7] WANG Jie, LI Jiamin, ZHU Pengcheng, et al. Spatial-separable NOMA-based intelligent hierarchical fast uplink grant for mURLLC over cell-free networks[J]. IEEE Internet of Things Journal, 2024, 11(19): 31974–31987. doi: 10.1109/JIOT.2024.3426048. [8] QIN Wen, MENG Yue, and ZHANG Zhi. Cost-aware resource allocation for hybrid multiple access in cell-free MIMO system[J]. IEEE Communications Letters, 2024, 28(4): 852–856. doi: 10.1109/LCOMM.2024.3356585. [9] LI Siyi, FANG Xiaojie, DONG Heng, et al. Cell-free massive MIMO-NOMA systems with nonreciprocal channels: Performance analysis and calibration method design[J]. IEEE Systems Journal, 2024, 18(3): 1729–1740. doi: 10.1109/JSYST.2024.3437769. [10] LI Yikai and BADUGE G A A. NOMA-aided cell-free massive MIMO systems[J]. IEEE Wireless Communications Letters, 2018, 7(6): 950–953. doi: 10.1109/LWC.2018.2841375. [11] REZAEI F, HEIDARPOUR A R, TELLAMBURA C, et al. Underlaid spectrum sharing for cell-free massive MIMO-NOMA[J]. IEEE Communications Letters, 2020, 24(4): 907–911. doi: 10.1109/LCOMM.2020.2966195. [12] LE Q N, NGUYEN V D, DOBRE O A, et al. Learning-assisted user clustering in cell-free massive MIMO-NOMA networks[J]. IEEE Transactions on Vehicular Technology, 2021, 70(12): 12872–12887. doi: 10.1109/TVT.2021.3121217. [13] DANG X T, LE M T P, NGUYEN H V, et al. Optimal user pairing approach for NOMA-based cell-free massive MIMO systems[J]. IEEE Transactions on Vehicular Technology, 2023, 72(4): 4751–4765. doi: 10.1109/TVT.2022.3225835. [14] ASHIKHMIN A, LI Liangbin, and MARZETTA T L. Interference reduction in multi-cell massive MIMO systems with large-scale fading precoding[J]. IEEE Transactions on Information Theory, 2018, 64(9): 6340–6361. doi: 10.1109/TIT.2018.2853733. [15] CHENG H V, BJÖRNSON E, and LARSSON E G. Performance analysis of NOMA in training-based multiuser MIMO systems[J]. IEEE Transactions on Wireless Communications, 2018, 17(1): 372–385. doi: 10.1109/TWC.2017.2767030. [16] LI Xiao, LI Na, LI Xiyue, et al. Joint AP selection and power control optimization for uplink user-centric cell-free massive MIMO[C]. 2024 IEEE 29th Asia Pacific Conference on Communications, BALI, Indonesia, 2024: 530–535. doi: 10.1109/APCC62576.2024.10767902. [17] ALI S, TABASSUM H, and HOSSAIN E. Dynamic user clustering and power allocation for uplink and downlink non-orthogonal multiple access (NOMA) systems[J]. IEEE Access, 2016, 4: 6325–6343. doi: 10.1109/ACCESS.2016.2604821. [18] ZHANG Jiayi, FAN Jingyi, AI Bo, et al. NOMA-based cell-free massive MIMO over spatially correlated Rician fading channels[C]. 2020 IEEE International Conference on Communications, Dublin, Ireland, 2020: 1–6. doi: 10.1109/ICC40277.2020.9148861. [19] 丁青锋, 李怡浩, 徐梦引. 去蜂窝大规模 MIMO-NOMA 系统能效优化算法[J]. 电子学报, 2023, 51(8): 2020–2029. doi: 10.12263/DZXB.20211351.DING Qingfeng, LI Yihao, and XU Mengyin. Energy efficiency optimization algorithm for cell-free massive MIMO-NOMA systems[J]. Acta Electronica Sinica, 2023, 51(8): 2020–2029. doi: 10.12263/DZXB.20211351. [20] ZHANG Yao, CAO Haotong, ZHOU Meng, et al. Non-orthogonal multiple access in cell-free massive MIMO networks[J]. China Communications, 2020, 17(8): 81–94. doi: 10.23919/JCC.2020.08.007. [21] NGO H Q, ASHIKHMIN A, YANG Hong, et al. Cell-free massive MIMO versus small cells[J]. IEEE Transactions on Wireless Communications, 2017, 16(3): 1834–1850. doi: 10.1109/TWC.2017.2655515. -





 下载:
下载:


 下载:
下载:
