OTFS通信链路构建及其三维星座加密设计

马英杰; 刘岳恒; 赵耿; 赵明晶; 王丹

doi:10.11999/JEIT250181

OTFS通信链路构建及其三维星座加密设计

doi: 10.11999/JEIT250181 cstr: 32379.14.JEIT250181

1.
北京电子科技学院电子与通信工程系北京 100070
2.
北京电子科技学院网络空间安全系北京 100070

基金项目: 国家自然科学基金(62441208)，中央高校基本科研业务费资金资助(3282024060, 3282025011)

详细信息

作者简介:
马英杰：女，副教授，研究方向为混沌保密通信、混沌密码

刘岳恒：男，硕士生，研究方向为混沌保密通信

赵耿：男，教授，研究方向为混沌保密通信、混沌密码

赵明晶：女，讲师，研究方向为信息安全

王丹：女，硕士生，研究方向为混沌保密通信

通讯作者:
刘岳恒　2397856865@qq.com

中图分类号: TN918.1
计量
- 文章访问数: 153
- HTML全文浏览量: 62
- PDF下载量: 26
- 被引次数: 0
出版历程
- 收稿日期: 2025-03-19
- 修回日期: 2025-07-10
- 网络出版日期: 2025-07-26

OTFS Communication Link Construction and Three-Dimensional Constellation Encryption Design

1.
Department of Electronic and Communication Engineering, Beijing Electronic Science and Technology Institute, Beijing 100070, China
2.
Department of Cyberspace Security, Beijing Electronic Science and Technology Institute, Beijing 100070, China

Funds: The National Natural Science Foundation of China (62441208), The Fundamental Research for the Central Universities (3282024060, 3282025011)

摘要

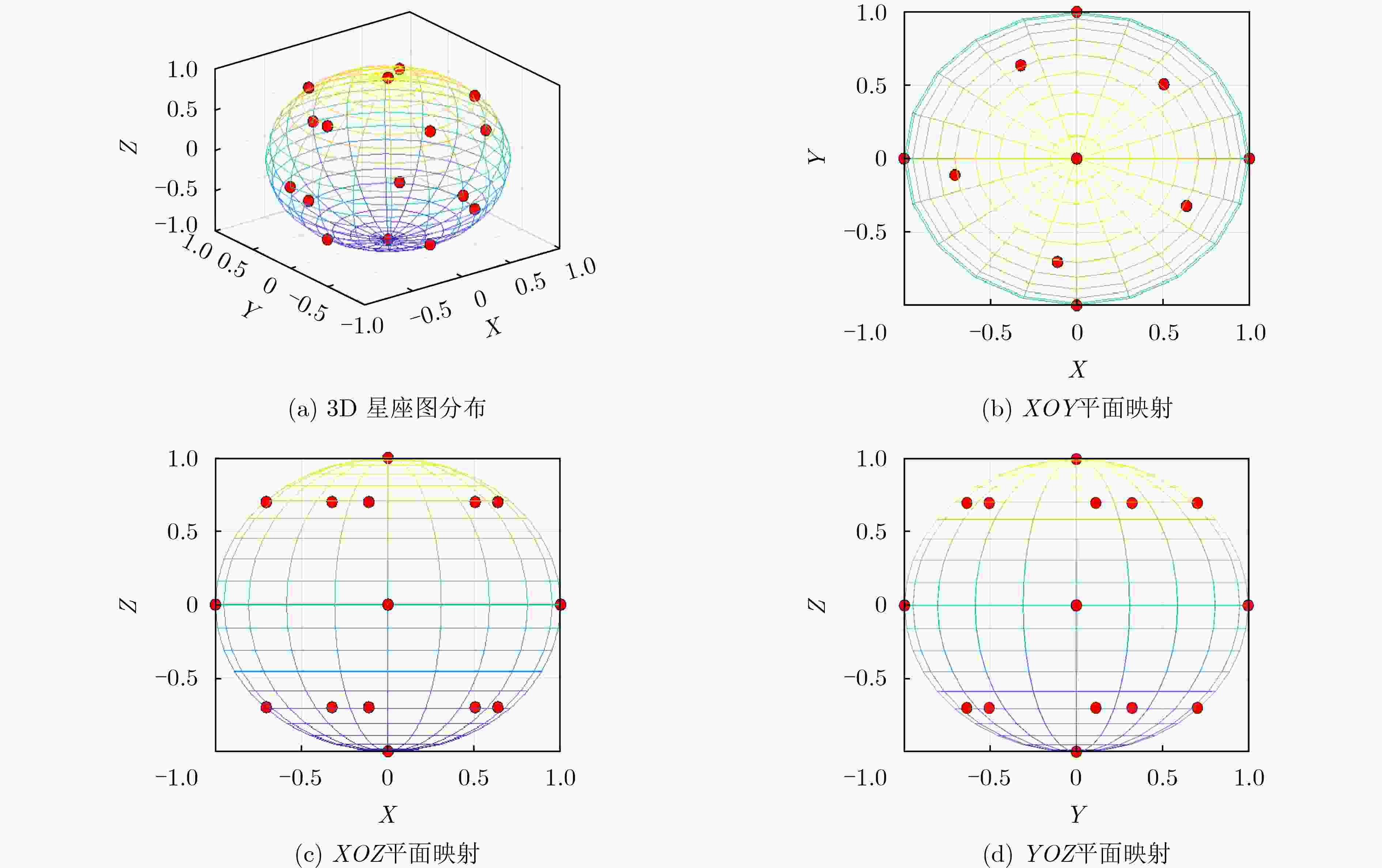
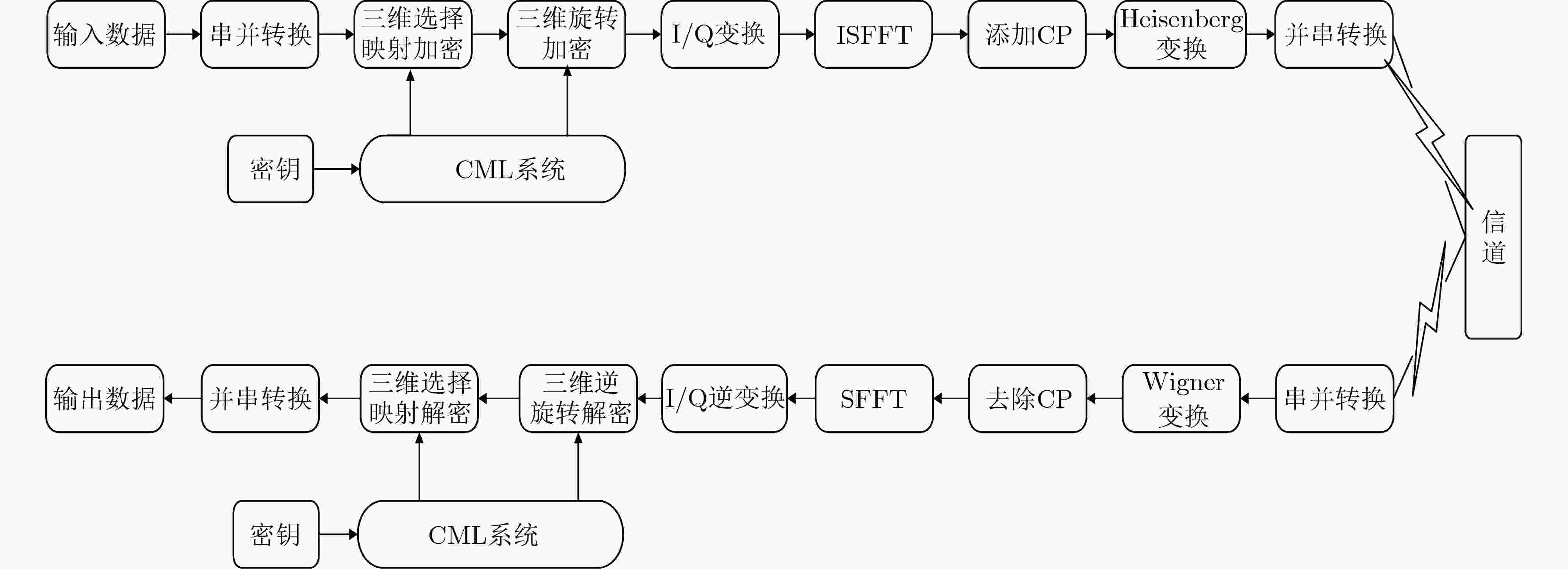
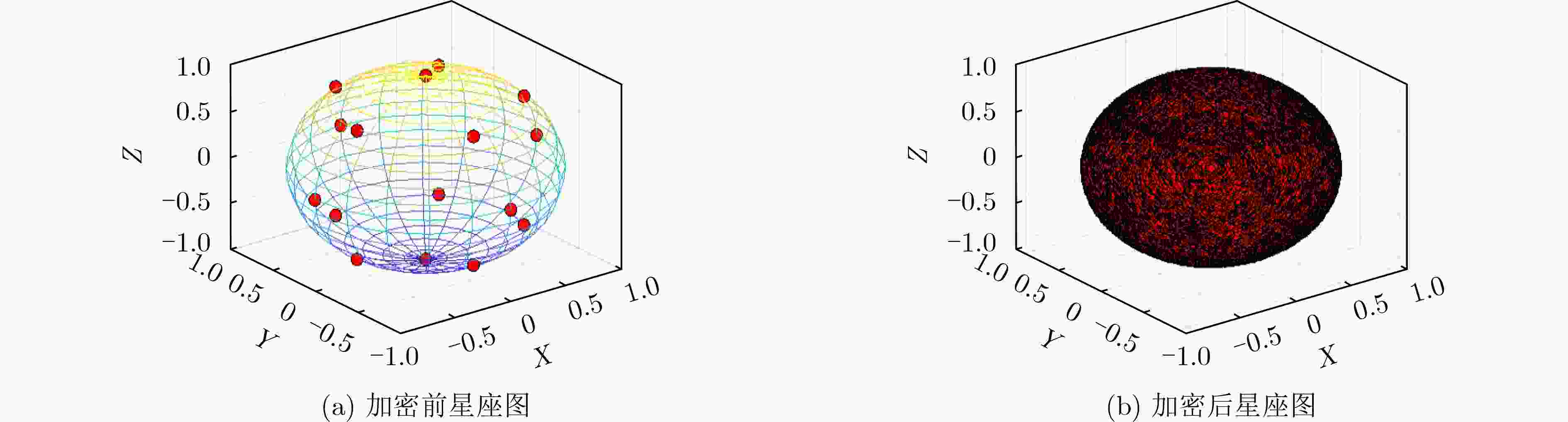
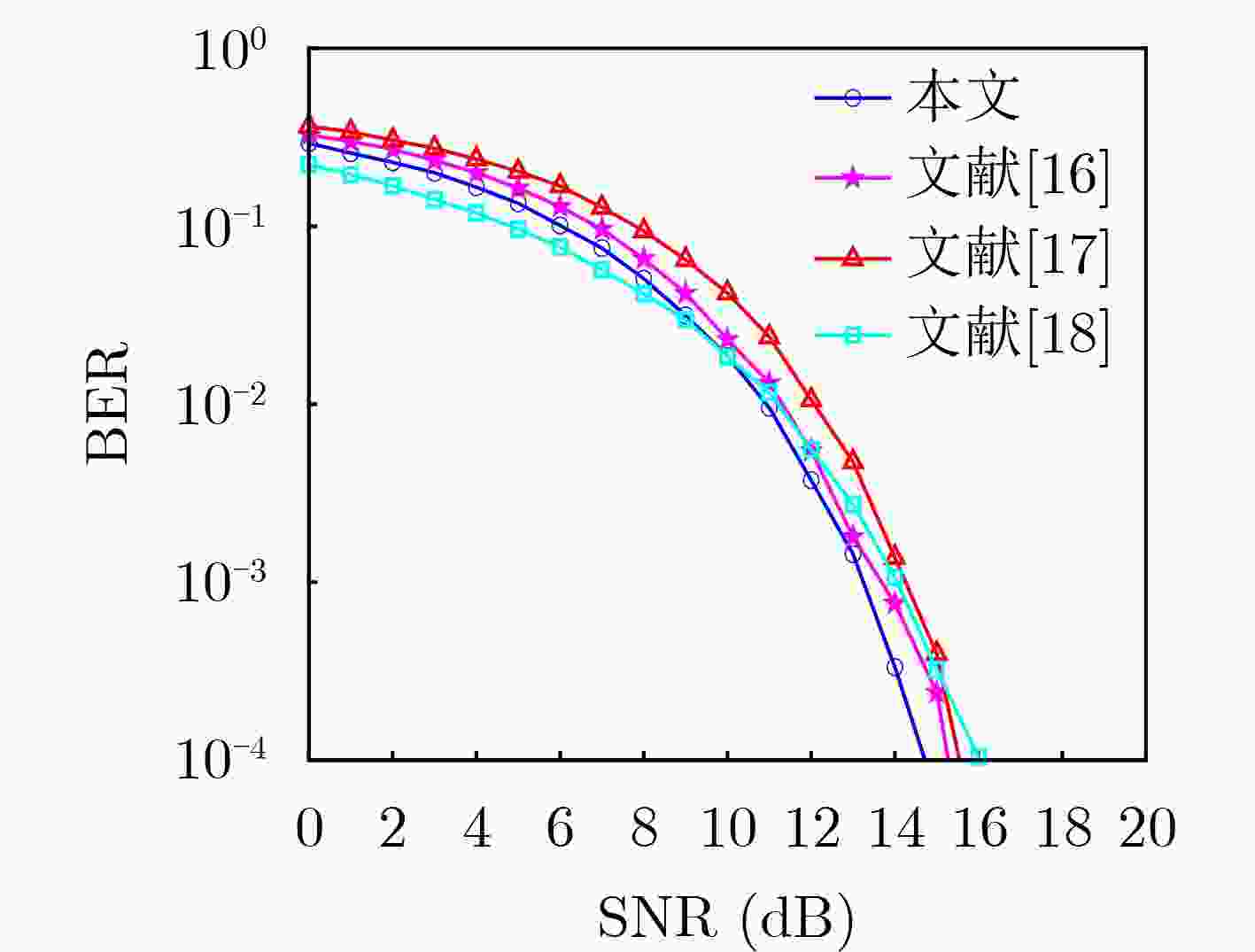
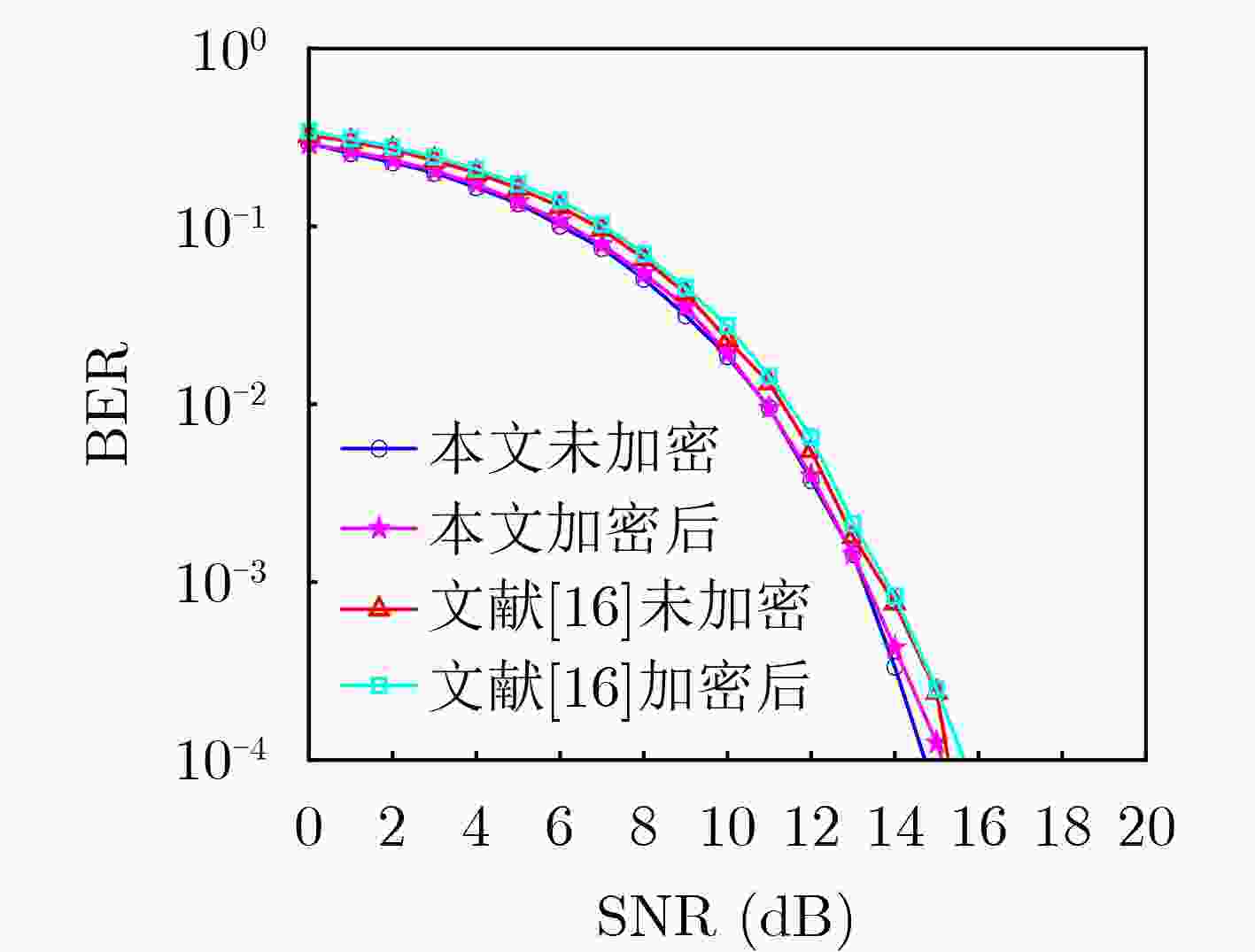
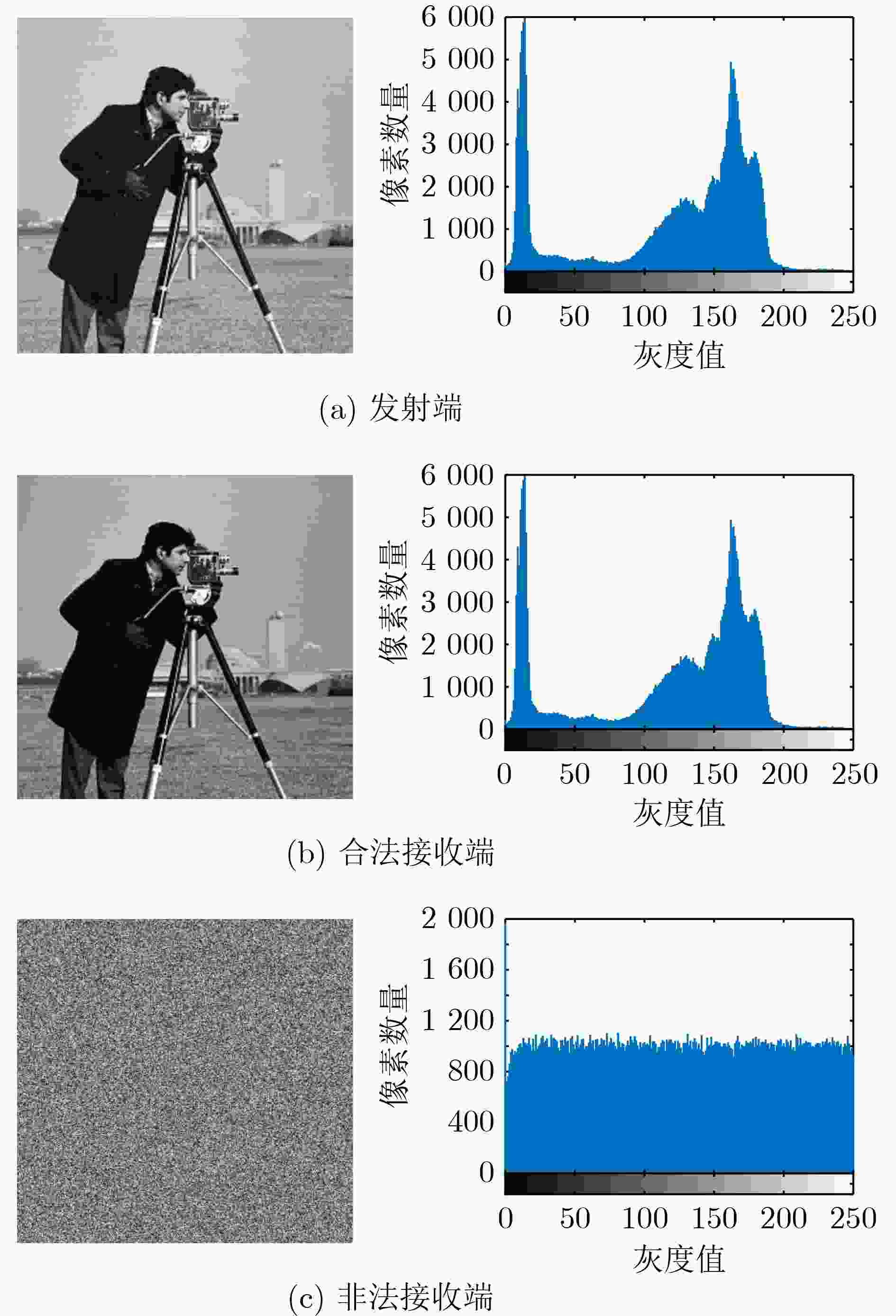
摘要: 为满足第6代移动通信(6G)在高速移动场景下高可靠、安全传输需求，针对正交时频空(OTFS)调制的通信链路，该文设计一种新的三维星座加密方案，充分发挥了OTFS与三维星座的性能优势。首先，设计了一种新型三维星座分布图，16个星座点分布在以原点为中心的球体表面，由球面与坐标轴的6个交点及两个平行于XOY平面的正五边形顶点构成，优化后星座点间最小欧氏距离提升5%，平均功率降低11%，星座图性能指数提升10%，改善了误码率性能。此外，提出了一种三维星座映射与旋转加密方案，通过16位量化混沌序列动态选择映射方式，并结合两次星座点旋转操作，实现了三维星座的高效加密。仿真结果表明，相较于现有方案，所提出的方案在确保通信性能的同时，安全性能有较好提升，误码率性能提升约0.6 dB，且密钥空间达10¹²⁰，能够有效抵抗暴力破解，加密后图像直方图分布均匀，相关系数趋近于0，具有强抗统计攻击能力，且密钥敏感性和鲁棒性测试进一步验证了其安全性能。
- 正交时频空间 /
- 三维星座映射 /
- 星座加密 /
- 物理层安全
Abstract: Objective With the advancement of Sixth-Generation (6G) communication technologies, the demand for highly reliable and secure transmission in high-speed mobile scenarios has grown significantly. Orthogonal Time Frequency Space (OTFS) modulation has emerged as a promising solution due to its superior transmission reliability in high-mobility environments. However, research on the security aspects of OTFS systems remains limited. To address this challenge, this study proposes a Three-Dimensional (3D) constellation encryption scheme for OTFS communication links. The objective is to enhance the security of OTFS systems while preserving communication performance by designing a novel 3D constellation structure and implementing physical-layer dynamic encryption based on a Coupled Map Lattice (CML) spatiotemporal chaotic system. This research provides a secure and efficient transmission strategy for future wireless communication systems. Methods The integration of 3D constellation encryption with OTFS modulation enhances the security of OTFS systems. First, a novel 3D constellation is designed, where 16 constellation points are uniformly distributed on the surface of a sphere centered at the origin. By optimizing the spatial distribution of constellation points, the minimum Euclidean Distance (MED) is increased and the average transmission power is reduced, thereby improving Bit Error Rate (BER) performance. Second, a dynamic encryption scheme for the 3D constellation over the OTFS link is proposed. In this scheme, pseudo-random sequences are generated using the CML system, quantized into 16-bit binary sequences, and employed to control both the selection of mapping rules and the rotational encryption of the 3D constellation. The encryption process operates as follows: first, the mapping rules are dynamically selected based on the quantized chaotic sequences; second, the rotation angles of the constellation points around the X, Y, and Z axes are determined by the same chaotic sequences. This dual encryption mechanism enhances the system’s security while maintaining reliable communication performance. Results and Discussions The performance of the proposed scheme is evaluated through extensive simulations. The results show that the optimized 3D constellation achieves a 22% improvement in MED compared with traditional 2D 16-quadrature amplitude modulation (16QAM). Compared with existing 3D constellations, the proposed design increases the MED by 5%, reduces average transmission power by 11%, and improves the Constellation Figure of Merit (CMF) by 10% (Table 2, Table 3). Superior communication performance is also demonstrated, with a BER improvement of approximately 0.6 dB over existing methods (Fig. 5, Fig. 6). In terms of security, the encryption scheme provides a key space of 10¹²⁰, effectively resisting brute-force attacks. Key sensitivity tests confirm that even minor changes to the initial key result in completely different decrypted images (Fig. 7), verifying the robustness of the encryption mechanism. The encrypted images exhibit uniform histogram distributions (Fig. 8) and correlation coefficients near zero (Table 6), indicating strong resistance to statistical attacks. Additionally, the scheme maintains reliable performance under noisy conditions, with decrypted images preserving high quality even at low Signal-to-Noise Ratios (SNR) (Fig. 9). Conclusions This study combines OTFS communication links with 3D constellation encryption to realize physical-layer security for OTFS systems, enhancing both communication performance and transmission security. The proposed 3D constellation improves the MED by 5%, reduces average power by 11%, and increases the CMF by 10%, thereby enhancing BER performance. The dual dynamic encryption mechanism based on a CML system offers strong security. Simulation results show that the proposed scheme achieves a favorable balance between communication performance and security. BER performance improves by approximately 0.6 dB, while the large key space, high key sensitivity, strong resistance to statistical attacks, and good robustness collectively ensure enhanced security. The combination of OTFS modulation and 3D constellation encryption not only improves spectrum resource utilization but also strengthens channel confidentiality, enhancing resilience to interference and potential attacks. This scheme improves transmission security without compromising communication performance, offering broad application prospects in fields such as the Internet of Things, unmanned aerial vehicles, satellite communication, and ocean communication. The proposed approach is expected to provide more secure and reliable transmission solutions for future wireless communication systems.
- Orthogonal Time Frequency Space (OTFS) /
- Three-dimensional constellation mapping /
- Constellation encryption /
- Physical-layer security

HTML全文

图 1 3D 16-ary星座图

下载: 全尺寸图片幻灯片

图 2 加密方案系统模型

下载: 全尺寸图片幻灯片

图 3 加密规则

下载: 全尺寸图片幻灯片

图 4 加密前后星座图对比

下载: 全尺寸图片幻灯片

图 5 加密前误码率对比

下载: 全尺寸图片幻灯片

图 6 加密前后误码率对比

下载: 全尺寸图片幻灯片

图 7 不同密钥解密结果

下载: 全尺寸图片幻灯片

图 8 图像及分布直方图

下载: 全尺寸图片幻灯片

图 9 鲁棒性对比

下载: 全尺寸图片幻灯片

表 1 3D 16-ary星座图坐标

	X轴坐标	Y轴坐标	Z轴坐标
A₁	1	0	0
A₂	–1	0	0
A₃	0	1	0
A₄	0	–1	0
A₅	0	0	1
A₆	0	0	–1
A₇	0.5050	0.5050	0.7000
A₈	–0.3242	0.6363	0.7000
A₉	–0.7054	–0.1117	0.7000
A₁₀	–0.1117	–0.7054	0.7000
A₁₁	0.6363	–0.3242	0.7000
A₁₂	0.5050	0.5050	–0.7000
A₁₃	–0.3242	0.6363	–0.7000
A₁₄	–0.7054	–0.1117	–0.7000
A₁₅	–0.1117	–0.7054	–0.7000
A₁₆	0.6363	–0.3242	–0.7000

下载: 导出CSV

表 2 MED对比

星座图	MED
2D 16QAM	0.6325
文献[16]	0.7654
文献[17]	0.7302
文献[18]	0.6874
本文方案	0.7677

下载: 导出CSV

表 3 不同星座性能对比

星座图	平均功率	峰值功率	CFM
2D 16QAM	9.930	18.000	0.4028
文献[16]	6.828	6.828	0.5858
文献[17]	7.500	13.503	0.5333
文献[18]	8.400	12.220	0.4762
本文方案	6.787	6.787	0.5894

下载: 导出CSV

表 4 选择映射规则

Y₁Y₂Y₃Y₄	A₁A₂$ \cdots $A₁₆
0000	9;0;15;6;3;5;10;14;1;2;11;12;13;8;7;4;
0001	2;1;4;11;8;14;7;5;0;9;6;13;12;3;10;15;
0010	7;2;13;8;1;11;4;12;3;0;5;14;15;6;9;10;
0011	0;3;10;5;6;12;9;11;2;7;8;15;141;4;13;
0100	13;4;11;2;7;1;14;10;5;6;15;8;9;12;3;0;
0101	6;5;0;15;12;10;3;1;4;13;2;9;8;7;14;11;
0110	3;6;9;12;5;15;0;8;7;4;1;10;11;2;13;14;
0111	4;7;14;1;2;8;1315;6;3;12;11;10;5;0;9;
1000	1;8;7;14;11;13;2;6;9;10;3;4;5;0;15;12;
1001	10;9;12;3;0;6;15;13;8;1;14;5;4;11;2;7;
1010	15;10;5;0;9;3;12;4;11;8;13;6;7;14;1;2;
1011	8;11;2;13;14;4;1;3;10;15;0;7;6;9;12;5;
1100	5;12;3;10;15;9;6;2;13;14;7;0;1;4;11;8;
1101	14;13;8;7;4;2;11;9;12;5;10;1;0;15;6;3;
1110	11;14;1;4;13;7;8;0;15;12;9;2;3;10;5;6;
1111	12;15;6;9;10;0;5;7;14;11;4;3;2;13;8;1;

下载: 导出CSV

表 5 三维星座旋转加密规则

Y₅Y₆Y₇/Y₈Y₉Y₁₀	旋转规则
000	不旋转
001	绕Z轴旋转
010	绕Y轴旋转
011	分别绕Y轴、Z轴旋转
100	绕X轴旋转
101	分别绕X轴、Z轴旋转
110	分别绕X轴、Y轴旋转
111	分别绕X轴、Y轴、Z轴旋转

下载: 导出CSV

表 6 复杂度对比

	星座调制/解调	OTFS调制/解调	信号检测算法
传统2维OTFS	O(L)	O(MNlogMN)	O(M²N²)
文献[16]	O(L+T+Q)	O(MNlogMN)	O(M³N³)
文献[18]	O(L)	O(MNlogMN)	O(M³N³)
本文方案	O(L+Q)	O(MNlogMN)	O(M³N³)

下载: 导出CSV

表 7 相关系数对比

图像名称/编号		水平方向	垂直方向	对角方向
Cameraman (512×512)	原始图像	0.9820	0.9882	0.9731
	本文加密	–0.0025	–0.0009	–0.0388
	文献[16]	–0.0100	–0.0087	0.0131
	文献[17]	0.0103	–0.0035	0.0597
7.1.09 (512×512)	原始图像	0.8691	0.9276	0.8915
7.1.09 (512×512)	本文加密	0.0016	–0.0023	0.0046
5.1.09 (256×256)	原始图像	0.8501	0.8716	0.8723
5.1.09 (256×256)	本文加密	–0.0023	–0.0083	–0.0097
5.1.10 (256×256)	原始图像	0.8067	0.8552	0.8950
5.1.10 (256×256)	本文加密	–0.0162	–0.0056	0.0011

下载: 导出CSV

表 8 PSNR对比

图像名称/编号		SNR=10	SNR=12	SNR=14
Cameraman (512×512)	本文加密	23.2124	29.9727	39.5546
	文献[16]	21.2720	27.7008	36.4857
	文献[17]	19.0376	24.4215	33.0136
7.1.09 (512×512)	本文加密	24.6201	30.6419	36.5844
	文献[16]	22.8693	28.9984	35.5868
	文献[17]	20.536	25.8338	33.5381
5.1.09 (256×256)	本文加密	24.5723	30.5089	36.7201
	文献[16]	23.1655	29.2437	35.8463
	文献[17]	20.7219	25.8530	33.3320
5.1.10 (256×256)	本文加密	24.1365	29.8549	35.8519
	文献[16]	22.2935	28.3417	35.9071
	文献[17]	19.9616	25.3111	32.1762

下载: 导出CSV

表 9 MSE对比

图像名称/编号		SNR=10	SNR=12	SNR=14
Cameraman (512×512)	本文加密	310.3394	65.4357	7.2048
	文献[16]	485.1497	110.4092	14.6053
	文献[17]	811.5578	234.9259	32.4877
7.1.09 (512×512)	本文加密	224.4243	56.0901	14.2770
	文献[16]	335.8523	81.8917	17.9639
	文献[17]	574.7482	169.7079	28.7921
5.1.09 (256×256)	本文加密	226.9086	57.8356	13.8380
	文献[16]	313.7177	77.3940	16.9219
	文献[17]	550.6714	168.9599	30.1913
5.1.10 (256×256)	本文加密	250.8602	57.2348	16.9002
	文献[16]	383.4729	95.2605	16.6867
	文献[17]	656.0297	191.4116	39.3964

下载: 导出CSV

参考文献(24)

[1]	YLI-KAAKINEN J, LOULOU A, LEVANEN T, et al. Frequency-domain signal processing for spectrally-enhanced CP-OFDM waveforms in 5G new radio[J]. IEEE Transactions on Wireless Communications, 2021, 20(10): 6867–6883. doi: 10.1109/TWC.2021.3077762.
[2]	SIRIWANITPONG A, SANADA K, HATANO H, et al. Deep learning-based channel estimation with 1D CNN for OFDM systems under high-speed railway environments[J]. IEEE Access, 2025, 13: 13128–13142. doi: 10.1109/ACCESS.2025.3531009.
[3]	WANG Xueyang, SHEN Wenqian, XING Chengwen, et al. Joint Bayesian channel estimation and data detection for OTFS systems in LEO satellite communications[J]. IEEE Transactions on Communications, 2022, 70(7): 4386–4399. doi: 10.1109/TCOMM.2022.3179389.
[4]	LI Bei, XIAO Tian, ZHOU Kai, et al. Research on OTFS Systems for 6G[C]. 2022 IEEE International Conference on Trust, Security and Privacy in Computing and Communications, Wuhan, China, 2022: 1498–1503. doi: 10.1109/TrustCom56396.2022.00213.
[5]	MIAO Qilong, LIANG Jing, ZHANG Ge, et al. A target parameters estimation method for CP-OTFS-based terrestrial radar system[J]. IEEE Wireless Communications Letters, 2025, 14(1): 233–237. doi: 10.1109/LWC.2024.3497959.
[6]	HADANI R, RAKIB S, TSATSANIS M, et al. Orthogonal time frequency space modulation[C]. 2017 IEEE Wireless Communications and Networking Conference, San Francisco, USA, 2017: 1–6. doi: 10.1109/WCNC.2017.7925924.
[7]	SHAFIE A, YUAN Jinhong, FITZPATRICK P, et al. On the coexistence of OTFS modulation with OFDM-based communication systems[J]. IEEE Transactions on Communications, 2024, 72(11): 6822–6838. doi: 10.1109/TCOMM.2024.3412776.
[8]	ALDABABSA M, ÖZYURT S, KURT G K, et al. A survey on orthogonal time frequency space modulation[J]. IEEE Open Journal of the Communications Society, 2024, 5: 4483–4518. doi: 10.1109/OJCOMS.2024.3422801.
[9]	MA Kejia, GAO Zhenzhen, WANG Jinchi, et al. Physical layer security design for FDD IM-OTFS transmissions based on secure mapping[J]. IEEE Access, 2023, 11: 98293–98304. doi: 10.1109/ACCESS.2023.3312580.
[10]	GUO Zhiruo, LIU Bo, REN Jianxin, et al. Doppler delay-time frequency cross-domain joint high security transmission scheme based on orthogonal time frequency space[J]. IEEE Photonics Journal, 2023, 15(5): 7202007. doi: 10.1109/JPHOT.2023.3307548.
[11]	CUI Jie, LIU Bo, REN Jianxin, et al. High-security three-dimensional optical transmission mechanism utilizing time-frequency-space interleaving disruption[J]. Optics Express, 2023, 31(23): 38640–38652. doi: 10.1364/OE.504520.
[12]	赵耿, 马英杰, 董有恒. 混沌密码理论研究与应用新进展[J]. 信息网络安全, 2024, 24(2): 203–216. doi: 10.3969/j.issn.1671-1122.2024.02.004. ZHAO Geng, MA Yingjie, and DONG Youheng. New progress in research and application of chaotic cryptography theory[J]. Netinfo Security, 2024, 24(2): 203–216. doi: 10.3969/j.issn.1671-1122.2024.02.004.
[13]	TAN Yanhua, TAO Yiwei, FANG Yi, et al. Three-dimensional constellation-assisted DCSK system: A new design for high-rate chaotic communication[J]. IEEE Transactions on Communications, 2024, 72(6): 3199–3210. doi: 10.1109/TCOMM.2024.3357611.
[14]	REN Jianxin, XIA Wenchao, LIU Bo, et al. Performance and security improvement of three-dimensional orthogonal chirp division multiplexing system with 2D-IDFnT[J]. Journal of Lightwave Technology, 2024, 42(16): 5544–5551. doi: 10.1109/JLT.2024.3398993.
[15]	CHEN Shuaidong, REN Jianxin, LIU Bo, et al. Performance improvement of non-orthogonal multiple access with a 3D constellation and a 2D IFFT modulator[J]. Optics Express, 2023, 31(5): 7425–7439. doi: 10.1364/OE.483799.
[16]	吴锐. 基于混沌系统的OFDM安全传输方案研究[D]. [硕士论文], 西安电子科技大学, 2023. doi: 10.27389/d.cnki.gxadu.2023.000510. WU Rui. Research on OFDM secure transmission scheme based on chaotic system[D]. [Master dissertation], Xidian University, 2023. doi: 10.27389/d.cnki.gxadu.2023.000510.
[17]	CHEN Gengyin, LIU Bo, REN Jianxin, et al. Three-dimensional non-orthogonal multiple access high-security seven-core transmission system based on constellation chaotic selection mapping[J]. Journal of Lightwave Technology, 2024, 42(17): 5910–5917. doi: 10.1109/JLT.2024.3406722.
[18]	CHEN Yuhua, ZHAO Lei, JIANG Yuan, et al. OTFS waveform based on 3-D signal constellation for time-variant channels[J]. IEEE Communications Letters, 2023, 27(8): 1999–2003. doi: 10.1109/LCOMM.2023.3286413.
[19]	REN Jianxin, LIU Bo, WU Xiangyu, et al. Three-dimensional probabilistically shaped CAP modulation based on constellation design using regular tetrahedron cells[J]. Journal of Lightwave Technology, 2020, 38(7): 1728–1734. doi: 10.1109/JLT.2019.2955728.
[20]	ZHANG Yiqun, JIANG Ning, ZHAO Anke, et al. Security enhancement in coherent OFDM optical transmission with chaotic three-dimensional constellation scrambling[J]. Journal of Lightwave Technology, 2022, 40(12): 3749–3760. doi: 10.1109/JLT.2022.3154091.
[21]	CAI Xiangming, YUEN C, HUANG Chongwen, et al. Toward chaotic secure communications: An RIS enabled M-Ary differential chaos shift keying system with block interleaving[J]. IEEE Transactions on Communications, 2023, 71(6): 3541–3558. doi: 10.1109/TCOMM.2023.3262834.
[22]	BAO Han, WANG Zhuowu, HUA Zhongyun, et al. Initial-offset-control coexisting hyperchaos in two-dimensional discrete neuron model[J]. IEEE Transactions on Industrial Informatics, 2024, 20(3): 4784–4794. doi: 10.1109/TII.2023.3327566.
[23]	KANEKO K. Spatiotemporal intermittency in coupled map lattices[J]. Progress of Theoretical Physics, 1985, 74(5): 1033–1044. doi: 10.1143/PTP.74.1033.
[24]	WEBER A. The USC-SIPI image database[EB/OL]. https://sipi.usc.edu/database/, 1977.