无人机平台单天线合成孔径全球导航卫星系统干扰源定位方法

王璐; 王轩; 吴仁彪

doi:10.11999/JEIT250169

无人机平台单天线合成孔径全球导航卫星系统干扰源定位方法

doi: 10.11999/JEIT250169 cstr: 32379.14.JEIT250169

中国民航大学天津市智能信号与图像处理重点实验室天津 300300

基金项目: 国家自然科学基金(U213320021)

详细信息

作者简介:
王璐：女，讲师，研究方向为卫星导航抗干扰、阵列信号处理

王轩：男，硕士生，研究方向为阵列信号处理

吴仁彪：男，教授，研究方向为自适应阵列信号处理、民航无线电干扰检测与自适应抑制、高分辨率雷达成像与自动目标识别等

通讯作者:
吴仁彪　rbwu@cauc.edu.cn

中图分类号: TN973
计量
- 文章访问数: 128
- HTML全文浏览量: 36
- PDF下载量: 18
- 被引次数: 0
出版历程
- 收稿日期: 2025-03-18
- 修回日期: 2025-08-07
- 网络出版日期: 2025-08-11

Global Navigation Satellite System Interference Source Localization Algorithm via Single-antenna Synthetic Aperture on the Unmanned Aerial Vehicle Platform

Tianjin Key Laboratory for Advanced Signal Processing, Civil Aviation University of China, Tianjin 300300, China

Funds: The National Natural Science Foundation of China (U213320021)

摘要

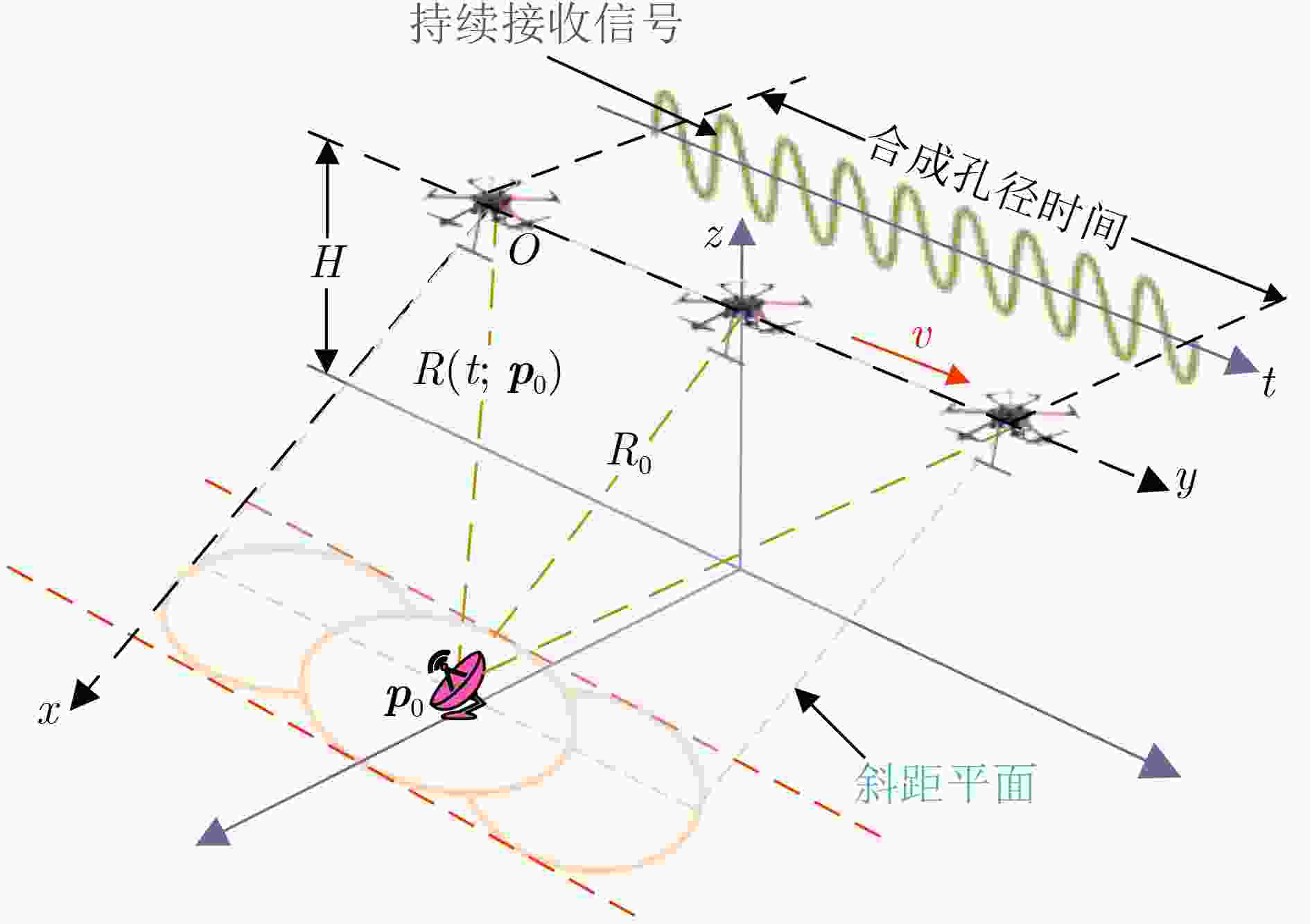
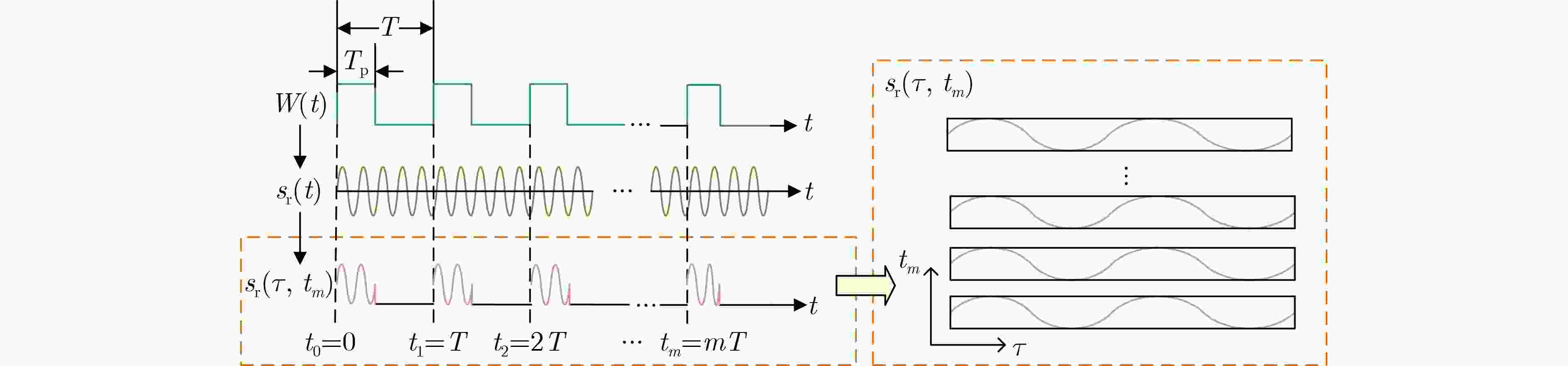
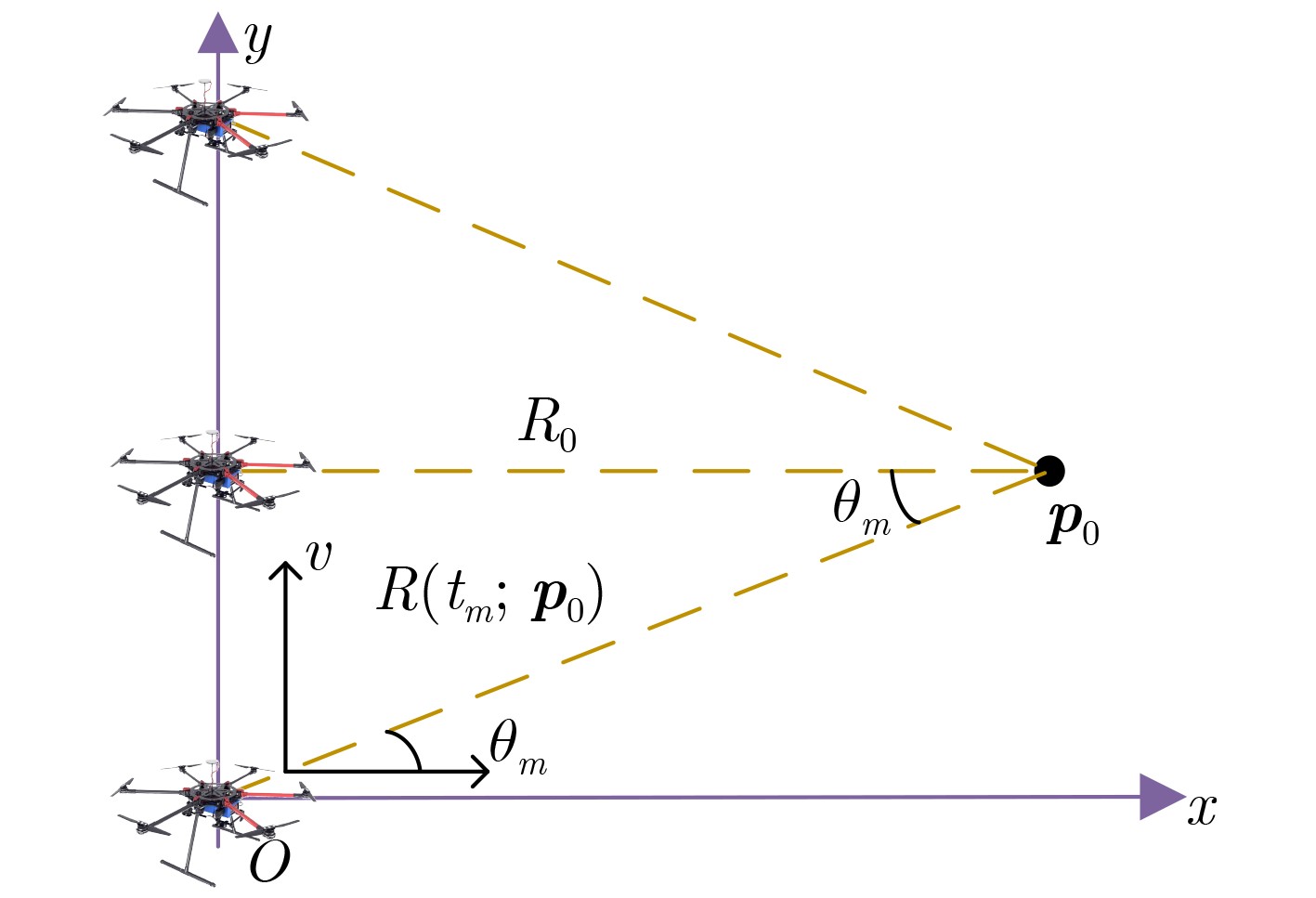
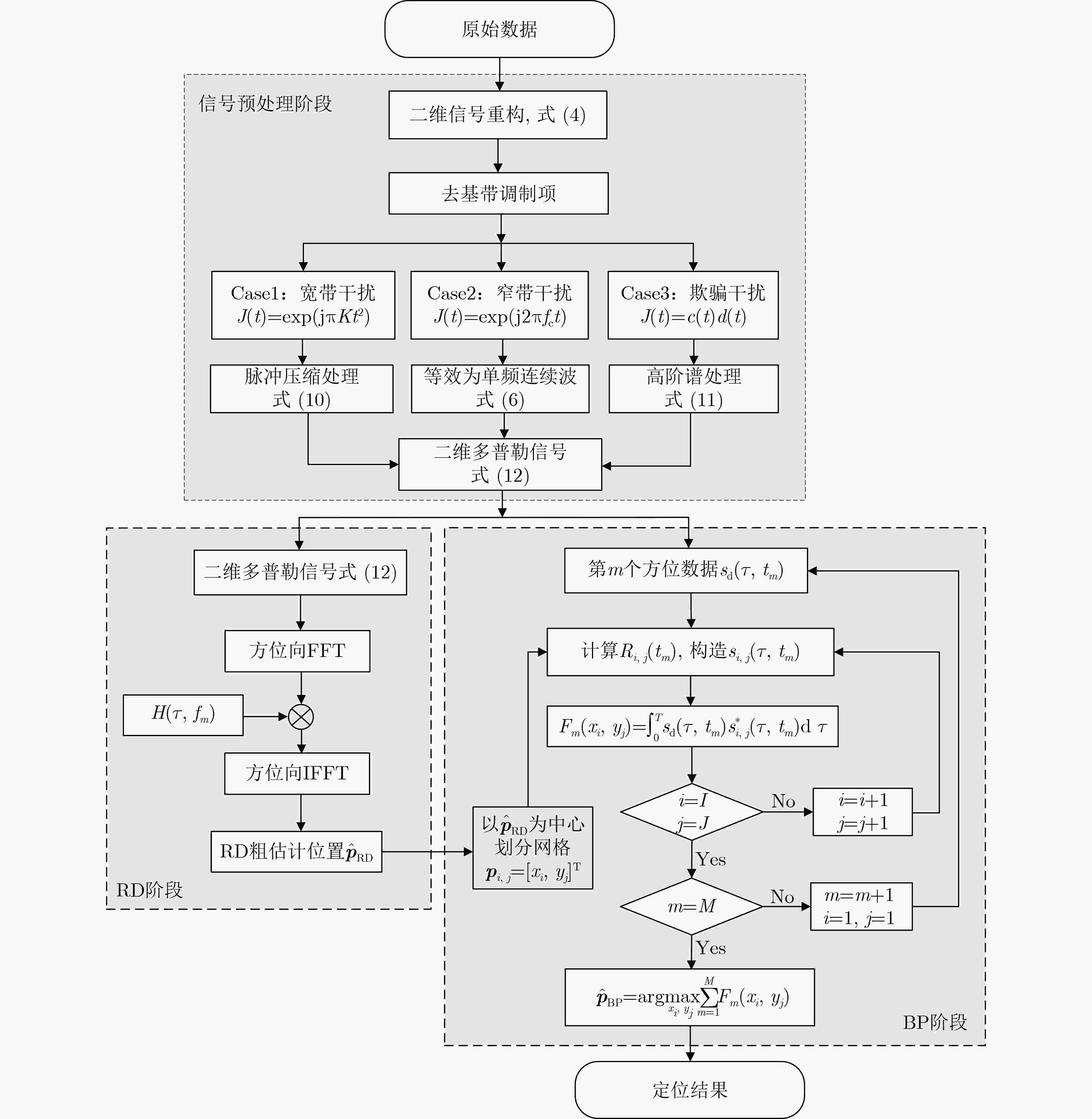
摘要: 被动合成孔径(PSA)技术在干扰源定位中具有广泛应用前景。针对低空低速无人机平台下全球导航卫星系统(GNSS)干扰源定位问题，该文提出一种基于无人机平台单天线合成孔径的GNSS干扰源定位方法。首先将不同类型干扰去基带调制，得到统一的信号表示；其次基于斜距精确表示的距离多普勒(RD)算法实现距离搜索与方位聚焦，获取粗定位结果；然后基于该结果构建高分辨率网格并运用后向投影(BP)算法得到代价函数；最后对代价函数进行峰值搜索，得到最终定位结果。仿真实验表明，所提算法能够实现高精度定位且性能稳定。
- 干扰源定位 /
- 被动合成孔径 /
- 距离多普勒算法 /
- 后向投影算法
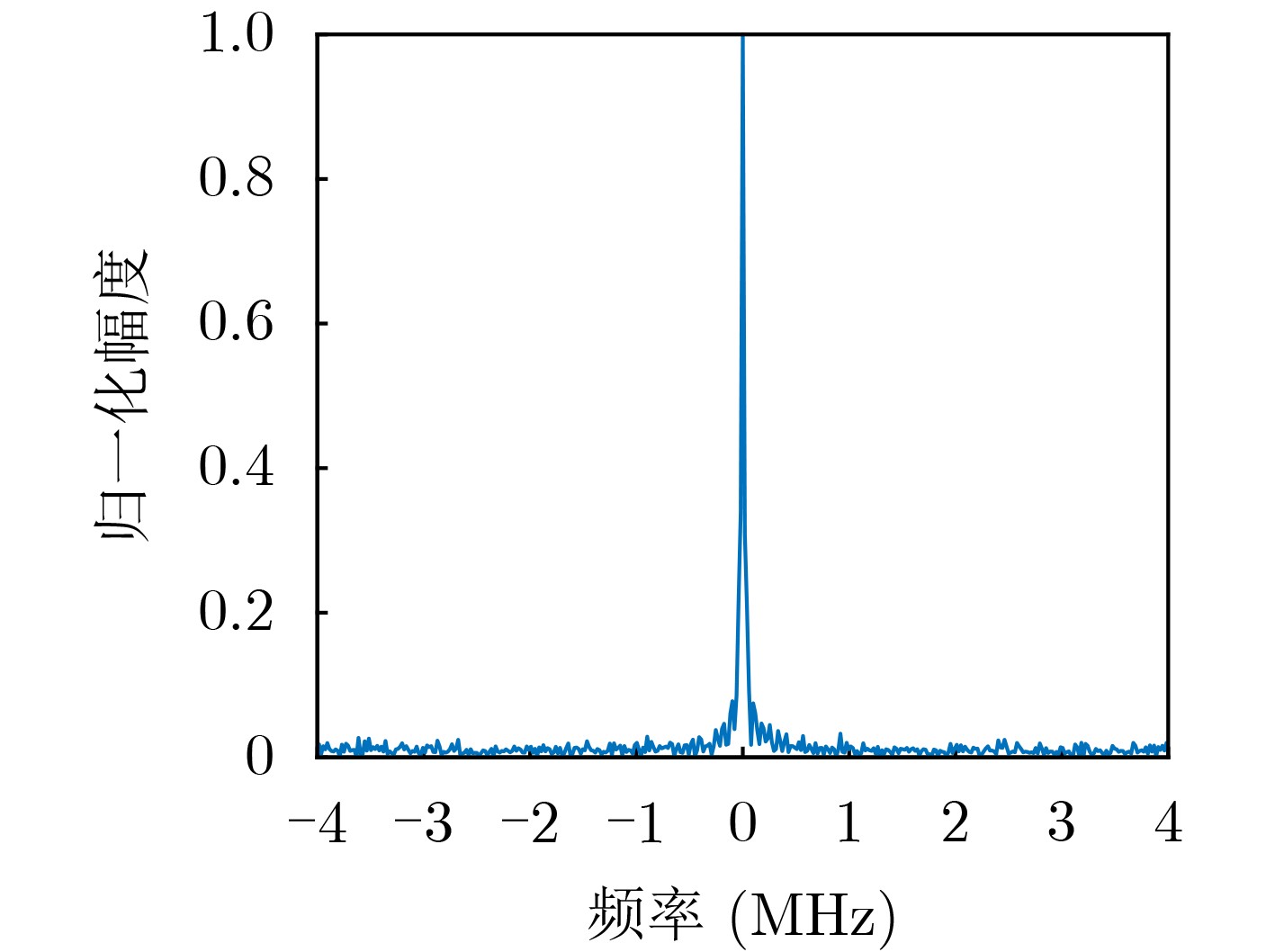
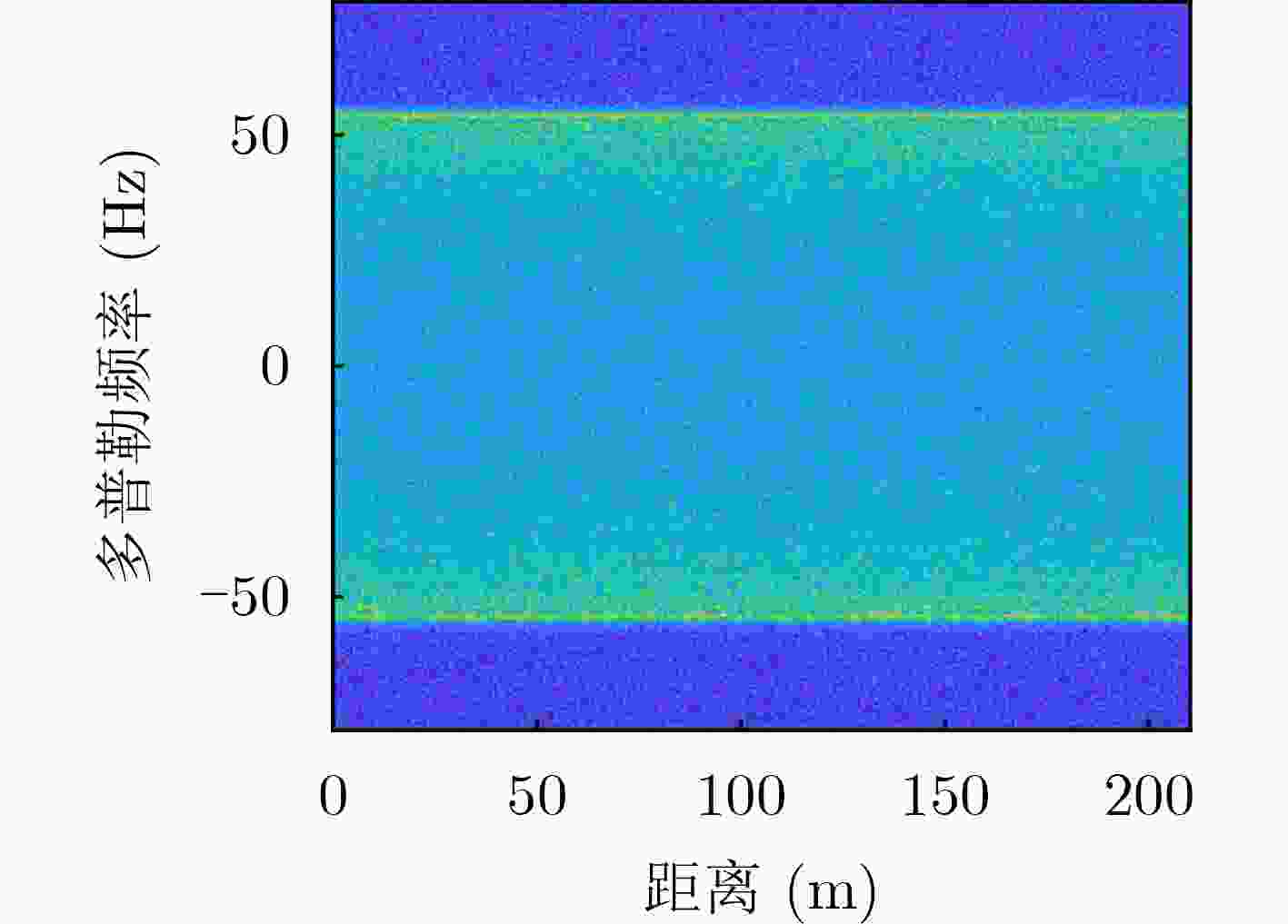
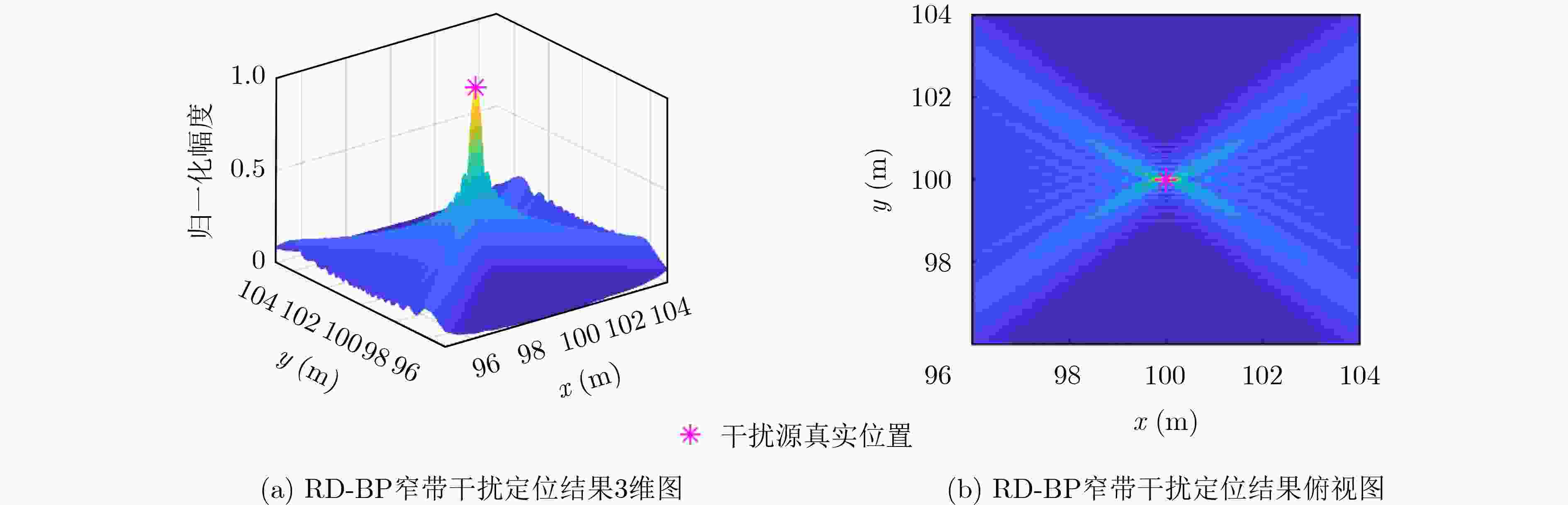
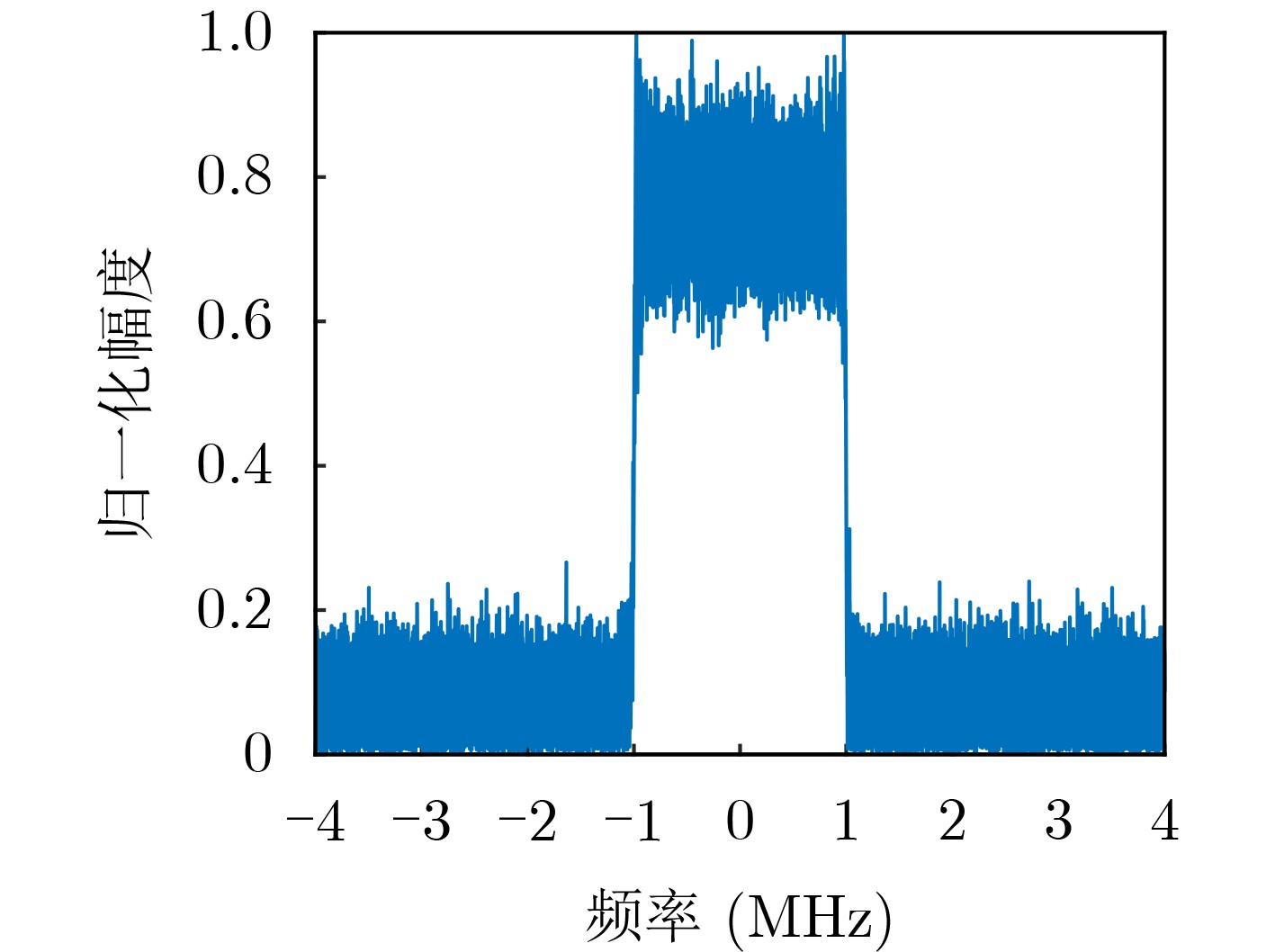
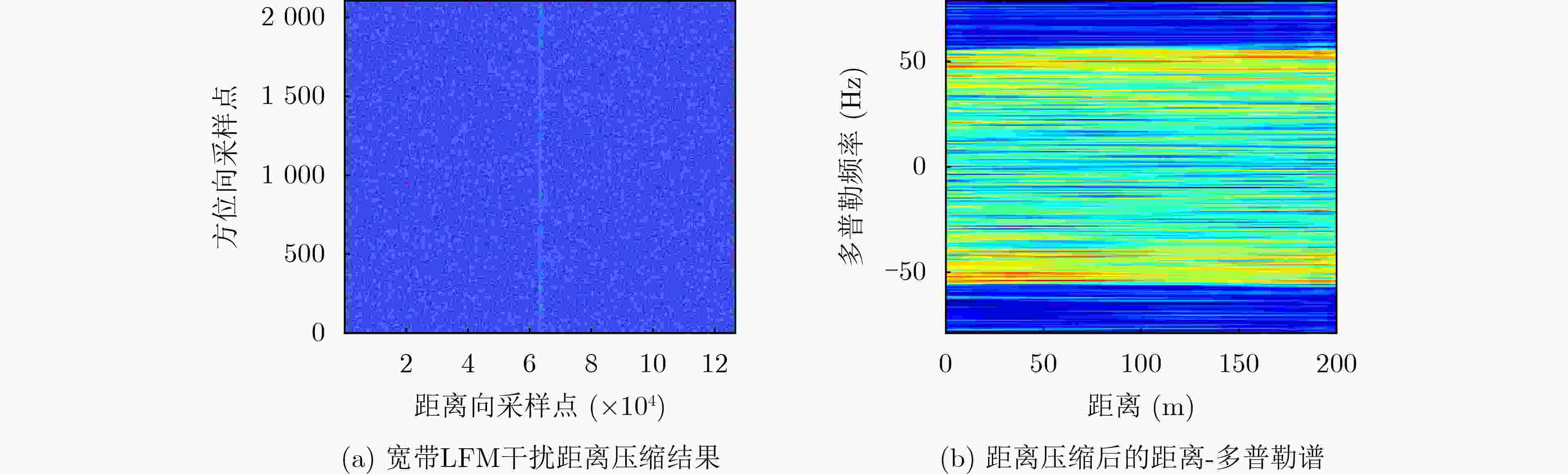
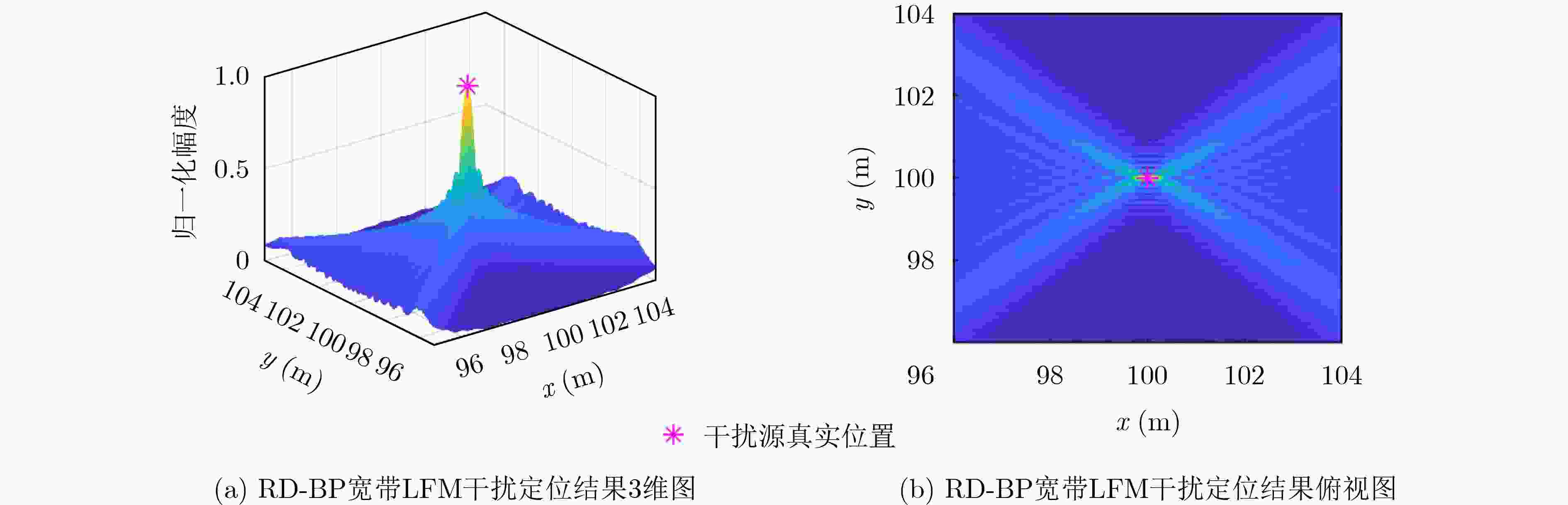
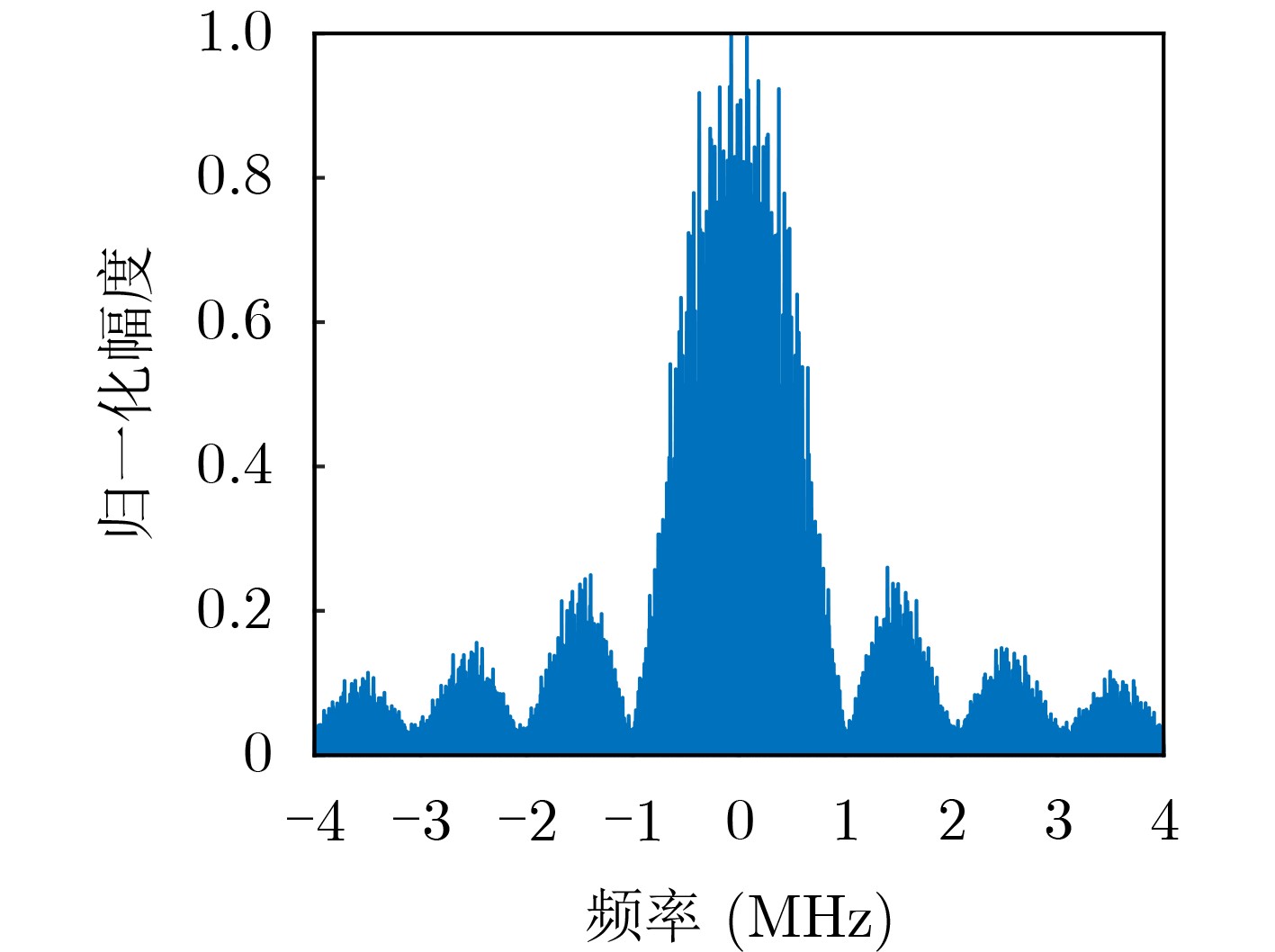
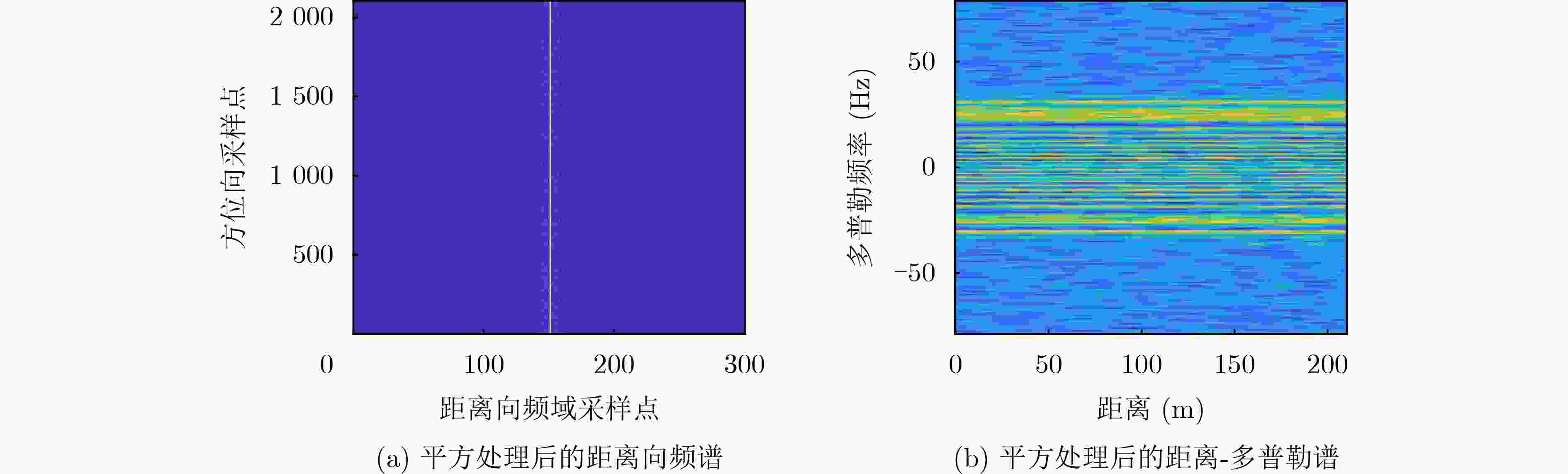
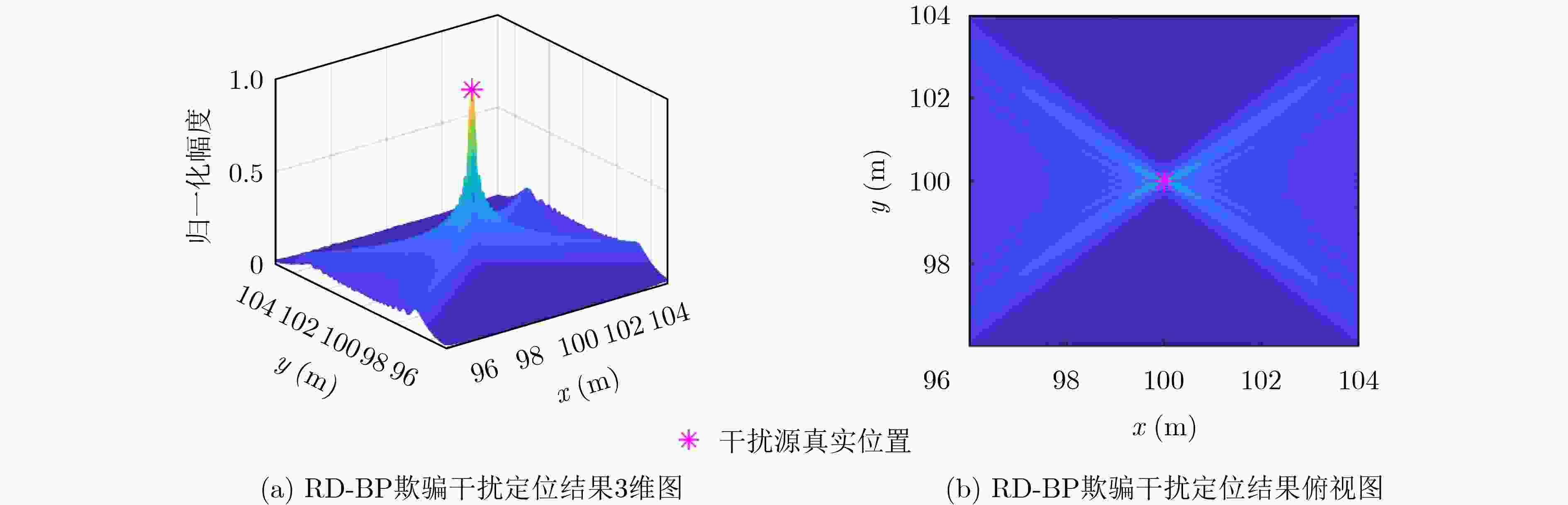
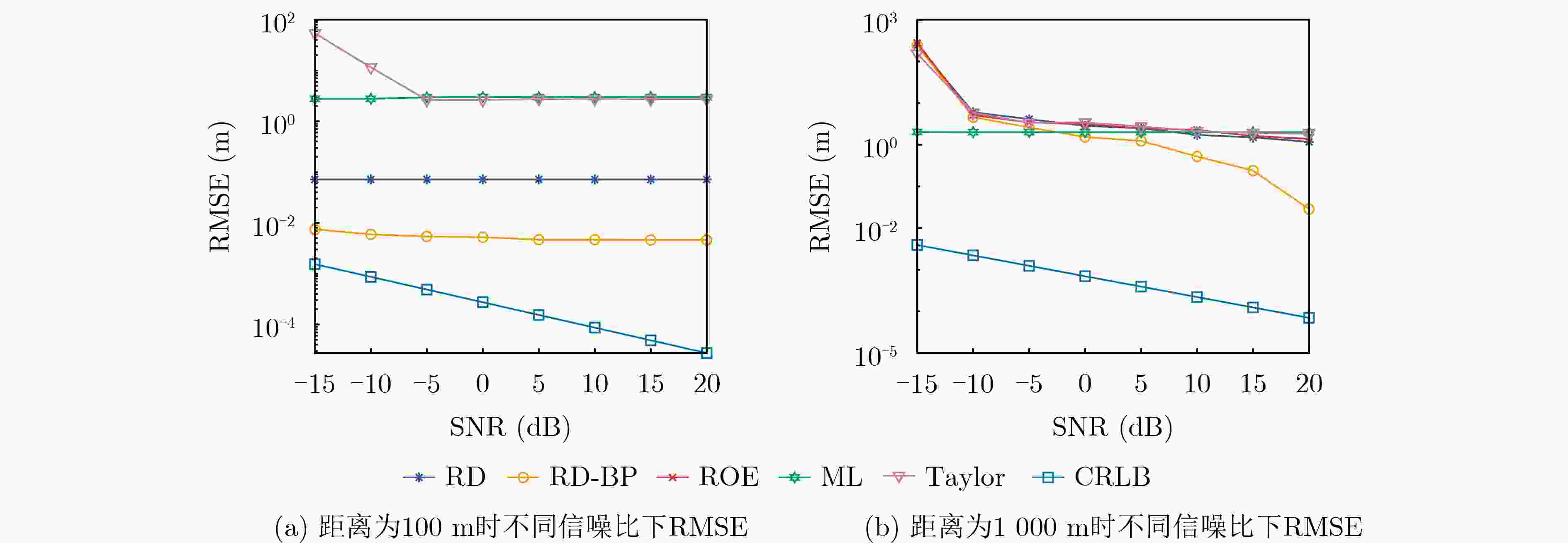
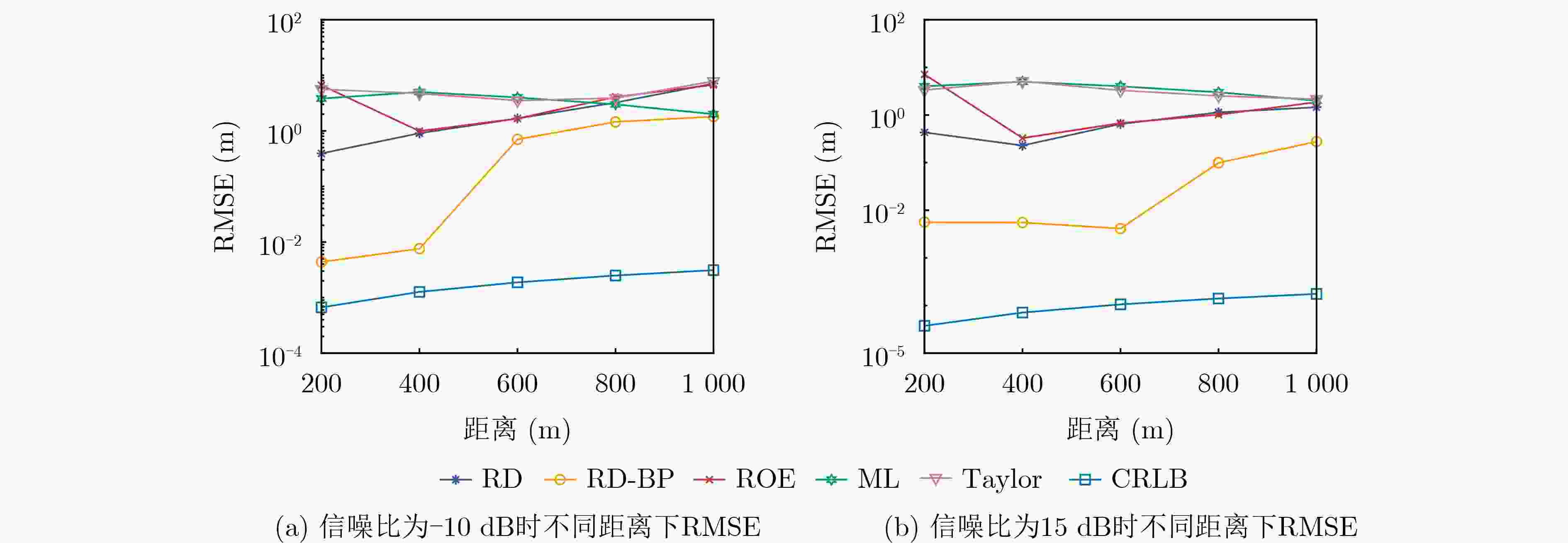
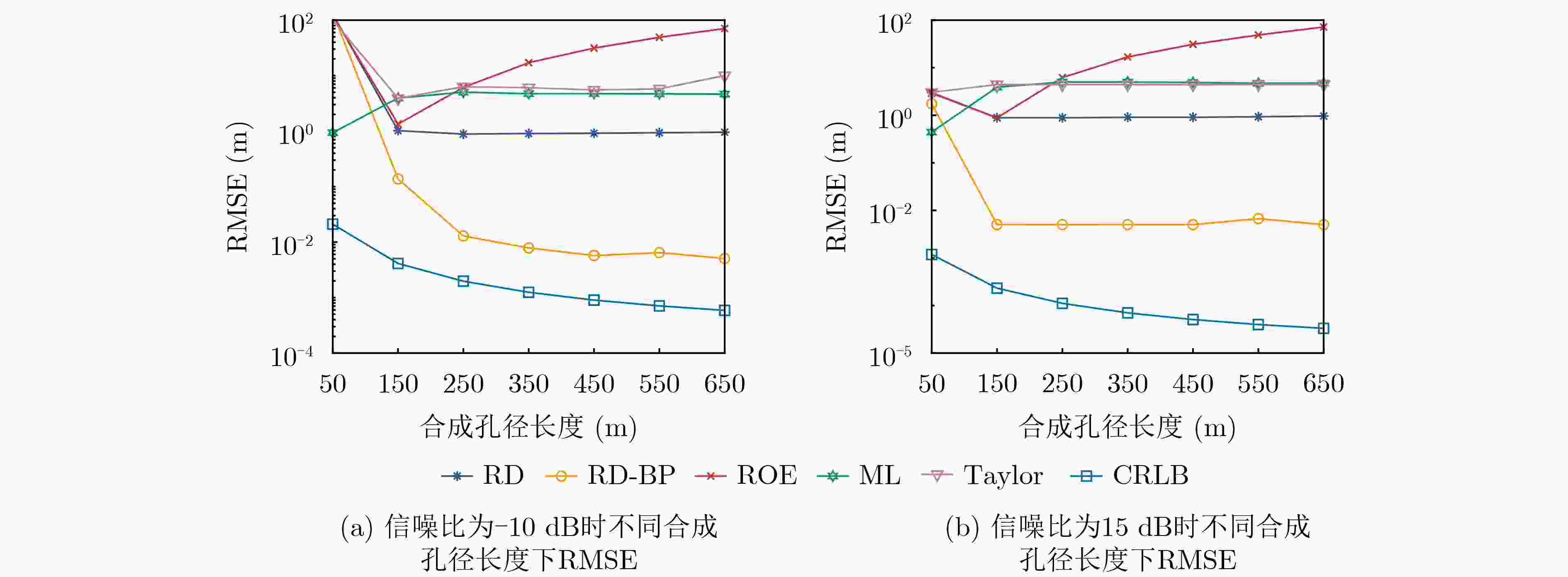
Abstract: Objective As Radio Frequency (RF) spectrum congestion intensifies and electromagnetic interference incidents occur more frequently, the reliable operation of the Global Navigation Satellite System (GNSS) is increasingly threatened. To ensure GNSS functionality, interference sources must be accurately monitored and localized. Conventional localization methods are constrained by the limited aperture of physical antenna arrays and often incur high deployment costs. With the gradual opening of low-altitude airspace, small Unmanned Aerial Vehicles (UAVs) are increasingly used as platforms for remote sensing, electronic reconnaissance, and communication tasks, offering a practical alternative for GNSS interference localization. Passive Synthetic Aperture (PSA) techniques have emerged as a solution to overcome the aperture limitations of physical arrays and are well suited for integration with UAV platforms. In this study, PSA technology is combined with a UAV-based system to locate GNSS interference sources. A unified signal model is established to describe various interference types. Based on this model, a slant-range-accurate Range-Doppler (RD) algorithm is derived and further integrated with the Back Projection (BP) algorithm to perform joint localization. This combined RD–BP approach enhances positioning accuracy while reducing computational complexity, demonstrating the feasibility and efficiency of the proposed UAV-based PSA localization framework. Methods This approach integrates a RD positioning algorithm based on a precise slant range expression with a BP algorithm. First, an accurate slant range expression is derived using the interference source direction and Doppler frequency. Applying this expression and the principle of stationary phase, the signal is transformed into the RD domain. Multiple matched filters are then constructed in the Doppler domain using the range gate. The outputs of these filters are converted into the range-azimuth domain for peak detection, yielding a coarse estimate of the interference source location. However, this initial estimate is susceptible to errors due to factors such as platform sampling rate and azimuth sampling interval. To refine the estimate, the BP algorithm is employed for fine positioning. A grid is defined around the coarse estimate, and each grid point is used to compute the projected signal. These projected signals are coherently accumulated with the received signals and integrated along the azimuth direction. Peak searching is then performed on the accumulated results to obtain the final, high-precision localization result. Results and Discussions Simulation results validate the effectiveness and excellent performance of the proposed RD-BP algorithm. As shown in (Fig. 7), (Fig. 10), and (Fig. 13), the algorithm successfully localizes interference sources after preprocessing for narrowband interference, Linear Frequency Modulated (LFM) interference, and spoofing interference. These results indicate the algorithm’s broad applicability across various interference types. (Fig. 14) illustrates the Root Mean Square Error (RMSE) under two scenarios in which the interference source is either close or distant. In both cases, RMSE decreases as the Signal-to-Noise Ratio (SNR) increases. When the source is nearby, RMSE changes slowly, indicating stable performance. When the source is distant, the algorithm maintains strong performance at higher SNRs. (Fig. 15) shows that under SNR conditions of –10 dB and 15 dB, RMSE increases with target distance. However, the RD-BP algorithm consistently outperforms other methods in accuracy, demonstrating its robustness and adaptability across varying distances. (Fig. 16) further confirms that RMSE stabilizes as the synthetic aperture length increases under both –10 dB and 15 dB SNR conditions. When the aperture length exceeds 100 m, the RD-BP algorithm achieves superior performance relative to other methods and approaches the Cramér–Rao Lower Bound (CRLB), indicating near-optimal estimation accuracy. (Table 1) compares the computational and localization performance of the proposed algorithm with that of the RD algorithm alone. While the RD algorithm is sensitive to platform sampling frequency, flight velocity, and other operational parameters, the RD-BP algorithm mitigates these limitations. It improves localization accuracy while maintaining manageable computational complexity, offering an effective trade-off between precision and efficiency. Conclusions This study addresses the problem of locating GNSS interference sources using low-altitude, low-speed UAV platforms. A localization method based on single-antenna synthetic aperture technology is proposed. The study begins by categorizing different types of GNSS interference and their respective preprocessing strategies. An RD algorithm is then derived based on the precise slant range representation, leveraging the relative direction of the interference source with respect to the UAV to achieve coarse localization. To address the accuracy limitations inherent in the RD algorithm due to initial condition constraints, an improved approach is proposed by incorporating the BP algorithm. This enhancement enables refined localization within a narrowed search region. Simulation results confirm that the proposed algorithm can reliably localize common GNSS interference sources under various interference conditions. Compared to conventional methods such as array antenna direction finding, the proposed technique requires only a single antenna mounted on the UAV platform, thereby increasing system flexibility and reducing both cost and design complexity. This demonstrates the feasibility of the method for rapid and efficient localization of GNSS interference sources.
- Interference source location /
- Passive Synthetic Aperture (PSA) /
- Range-Doppler(RD) algorithm /
- Back Project(BP) algorithm

HTML全文

图 1 被动合成孔径定位的几何场景

下载: 全尺寸图片幻灯片

图 2 二维信号重构示意图

下载: 全尺寸图片幻灯片

图 3 斜距平面运动情况示意图

下载: 全尺寸图片幻灯片

图 4 RD-BP联合定位算法流程图

下载: 全尺寸图片幻灯片

图 5 去载频后的窄带干扰频谱

下载: 全尺寸图片幻灯片

图 6 距离-多普勒谱

下载: 全尺寸图片幻灯片

图 7 窄带干扰定位结果

下载: 全尺寸图片幻灯片

图 8 去载频后的宽带LFM干扰频谱

下载: 全尺寸图片幻灯片

图 9 宽带LFM干扰预处理后结果

下载: 全尺寸图片幻灯片

图 10 宽带LFM干扰定位结果

下载: 全尺寸图片幻灯片

图 11 去载频后的欺骗干扰频谱

下载: 全尺寸图片幻灯片

图 12 欺骗干扰预处理后结果

下载: 全尺寸图片幻灯片

图 13 欺骗干扰定位结果

下载: 全尺寸图片幻灯片

图 14 与无人机轨迹距离100 m和1 000 m时RMSE随信噪比变化关系图

下载: 全尺寸图片幻灯片

图 15 信噪比为–10 dB和15 dB时RMSE随距离变化关系图

下载: 全尺寸图片幻灯片

图 16 信噪比为–10 dB和15 dB时RMSE随合成孔径长度变化关系图

下载: 全尺寸图片幻灯片

表 1 算法总计算量

算法	复数乘	复数加
RD	$ mn({\log _2}m + 1) $	$ 2mn\log _2^{}m $
ML	$ mnJ $	$ m(n - 1)J $
ROE	$ mn(\log _2^{}m + 1) $	$ 2mn\log _2^{}m $
Taylor	$ mn(\log _2^{}m + 1) $	$ 2mn\log _2^{}m $
RD-BP	$ mn(\log _2^{}m + 1 + I) $	$ m(n(2\log _2^{}m + I) - I) $

下载: 导出CSV

参考文献(24)

[1]	WU Renbiao, WANG Wenyi, LU Dan, et al. Adaptive Interference Mitigation in GNSS[M]. Singapore: Springer, 2018. doi: 10.1007/978-981-10-5571-3.
[2]	BAR-SHALOM O and WEISS A J. Emitter geolocation using single moving receiver[J]. Signal Processing, 2014, 105: 70–83. doi: 10.1016/j.sigpro.2014.05.006.
[3]	NYANTAKYI I O, WAN Qun, NI Lihua, et al. ACGA: Adaptive Conjugate Gradient Algorithm for non-line-of-sight hybrid TDOA-AOA localization[J]. Measurement, 2024, 224: 113820. doi: 10.1016/j.measurement.2023.113820.
[4]	YANG Yang, ZHENG Jibin, LIU Hongwei, et al. Optimal sensor placement and velocity configuration for TDOA-FDOA localization and tracking of a moving source[J]. IEEE Transactions on Aerospace and Electronic Systems, 2024, 60(6): 8255–8272. doi: 10.1109/TAES.2024.3430238.
[5]	LIU Yapeng, GAO Hongyuan, DU Yanan, et al. DOA estimation for mixed circular and noncircular coherently distributed sources under impulsive noise[J]. IEEE Transactions on Aerospace and Electronic Systems, 2024, 60(5): 6622–6637. doi: 10.1109/TAES.2024.3405450.
[6]	WEISS A J. Direct position determination of narrowband radio frequency transmitters[J]. IEEE Signal Processing Letters, 2004, 11(5): 513–516. doi: 10.1109/LSP.2004.826501.
[7]	ZHANG Yuan, WU Guizhou, LI Xi, et al. Direct position determination based on passive synthetic aperture for coherent receivers[J]. IEEE Sensors Journal, 2024, 24(11): 17917–17925. doi: 10.1109/JSEN.2024.3386869.
[8]	WU Guizhou, ZHANG Min, and GUO Fucheng. High-resolution direct position determination based on eigenspace using a single moving ULA[J]. Signal, Image and Video Processing, 2019, 13(5): 887–894. doi: 10.1007/s11760-019-01425-4.
[9]	吴癸周, 张源, 张文俊, 等. 基于互质阵列的运动单站信号直接定位方法[J]. 雷达学报, 2022, 11(4): 692–704. doi: 10.12000/JR22056. WU Guizhou, ZHANG Yuan, ZHANG Wenjun, et al. Coprime array based direct position determination of signals with single moving observation[J]. Journal of Radars, 2022, 11(4): 692–704. doi: 10.12000/JR22056.
[10]	TIRER T and WEISS A J. High resolution direct position determination of radio frequency sources[J]. IEEE Signal Processing Letters, 2016, 23(2): 192–196. doi: 10.1109/LSP.2015.2503921.
[11]	吴癸周, 郭福成, 张敏. 信号直接定位技术综述[J]. 雷达学报, 2020, 9(6): 998–1013. doi: 10.12000/JR20040. WU Guizhou, GUO Fucheng, and ZHANG Min. Direct position determination: An overview[J]. Journal of Radars, 2020, 9(6): 998–1013. doi: 10.12000/JR20040.
[12]	WANG Yuqi, SUN Guangcai, WANG Yong, et al. A high-resolution and high-precision passive positioning system based on synthetic aperture technique[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5230613. doi: 10.1109/TGRS.2022.3186767.
[13]	王裕旗, 孙光才, 邢孟道, 等. 合成孔径无源定位性能分析与参数设计[J]. 电子与信息学报, 2022, 44(9): 3155–3162. doi: 10.11999/JEIT210524. WANG Yuqi, SUN Guangcai, XING Mengdao, et al. Performance analysis and parameter design of synthetic aperture passive positioning[J]. Journal of Electronics & Information Technology, 2022, 44(9): 3155–3162. doi: 10.11999/JEIT210524.
[14]	DONG Wenlong, WANG Yuqi, SUN Guangcai, et al. Passive localization for frequency hopping signal emitter based on synthetic aperture principle[J]. IEEE Journal on Miniaturization for Air and Space Systems, 2023, 4(1): 33–40. doi: 10.1109/JMASS.2022.3218578.
[15]	WANG Yuqi, HAN Liang, ZHANG Xu, et al. A passive signal focusing algorithm based on synthetic aperture technique for multiple radiation source localization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 5206516. doi: 10.1109/TGRS.2024.3370390.
[16]	ZHANG Liting, HUAN Hao, TAO Ran, et al. Emitter localization algorithm based on passive synthetic aperture[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(4): 2687–2701. doi: 10.1109/TAES.2021.3137090.
[17]	HE Xinsheng, DENG Ming, CHAI Bingjie, et al. Synthetic aperture passive localization method based on slant range orthogonal expansion[J]. IEEE Journal on Miniaturization for Air and Space Systems, 2023, 4(3): 305–310. doi: 10.1109/JMASS.2023.3286271.
[18]	YANG Junhua, HUAN Hao, and TAO Ran. Multisubaperture backward projection positioning algorithm for radiation sources by single satellite[J]. IEEE Transactions on Aerospace and Electronic Systems, 2025, 61(2): 1267–1282. doi: 10.1109/TAES.2024.3453780.
[19]	DEBNATH D, VANEGAS F, SANDINO J, et al. A review of UAV path-planning algorithms and obstacle avoidance methods for remote sensing applications[J]. Remote Sensing, 2024, 16(21): 4019. doi: 10.3390/rs16214019.
[20]	ZHAO Li, XU Hongbo, QU Shaocheng, et al. Joint trajectory and communication design for UAV-assisted symbiotic radio networks[J]. IEEE Transactions on Vehicular Technology, 2024, 73(6): 8367–8378. doi: 10.1109/TVT.2024.3356587.
[21]	SUN Guangcai, WU Yuan, YANG Jun, et al. Full-aperture focusing of very high resolution spaceborne-squinted sliding spotlight SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(6): 3309–3321. doi: 10.1109/TGRS.2017.2669205.
[22]	王裕旗, 孙光才, 杨军, 等. 基于长合成孔径的辐射源成像定位算法[J]. 雷达学报, 2020, 9(1): 185–194. doi: 10.12000/JR19080. WANG Yuqi, SUN Guangcai, YANG Jun, et al. Passive localization algorithm for radiation source based on long synthetic aperture[J]. Journal of Radars, 2020, 9(1): 185–194. doi: 10.12000/JR19080.
[23]	WANG Yuqi, SUN Guangcai, XIANG Jixiang, et al. A imaging passive localization method for wideband signal based on SAR[C]. 2019 6th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Xiamen, China, 2019: 1–4. doi: 10.1109/APSAR46974.2019.9048398.
[24]	LI Ang, HUAN Hao, TAO Ran, et al. Passive synthetic aperture high-precision radiation source location by single satellite[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4010105. doi: 10.1109/LGRS.2021.3057902.