利用频谱衰减增强深度神经网络对抗迁移攻击

钱亚冠; 孔亚鑫; 陈科成; 沈云开; 鲍琦琦; 纪守领

doi:10.11999/JEIT250157

利用频谱衰减增强深度神经网络对抗迁移攻击

doi: 10.11999/JEIT250157 cstr: 32379.14.JEIT250157

1.
浙江科技大学人工智能与信息工程学院杭州 310023
2.
浙江大学计算机科学与技术学院杭州 310058

基金项目: 浙江科技大学基本科研业务费专项资金资助(2025QN060)，国家重点研发计划(2022YFB3102100)，国家自然科学基金(62476250)，浙江省自然科学基金重点项目(LZ22F020007, LQN25F010018)

详细信息

作者简介:
钱亚冠：男，教授，博士，研究方向为人工智能安全、机器学习、模式识别和机器视觉

孔亚鑫：女，硕士生，研究方向为计算机视觉、机器学习、深度学习

陈科成：男，硕士生，研究方向为深度学习、机器学习、计算机视觉

沈云开：男，硕士生，研究方向为机器学习、深度学习、计算机视觉

鲍琦琦：女，讲师，博士，研究方向为人工智能安全和计算机视觉

纪守领：男，教授，博士，研究方向为人工智能安全

通讯作者:
鲍琦琦　nora919530829@163.com

中图分类号: TN911.73; TP393
计量
- 文章访问数: 116
- HTML全文浏览量: 76
- PDF下载量: 9
- 被引次数: 0
出版历程
- 收稿日期: 2025-03-12
- 修回日期: 2025-07-16
- 网络出版日期: 2025-07-25

Adversarial Transferability Attack on Deep Neural Networks Through Spectral Coefficient Decay

1.
Zhejiang University of Science and Technology, School of Artificial Intelligence and Information Engineering, HangZhou 310023, China
2.
Zhejiang University, School of Computer Science and Technology, HangZhou 310058, China

Funds: The Special Fund for Basic Scientific Research of Zhejiang University of Science and Technology (2025QN060), The National Key Research and Development Program of China (2022YFB3102100), The National Natural Science Foundation of China (62476250), Zhejiang Provincial Natural Science Foundation Key Project (LZ22F020007, LQN25F010018)

摘要

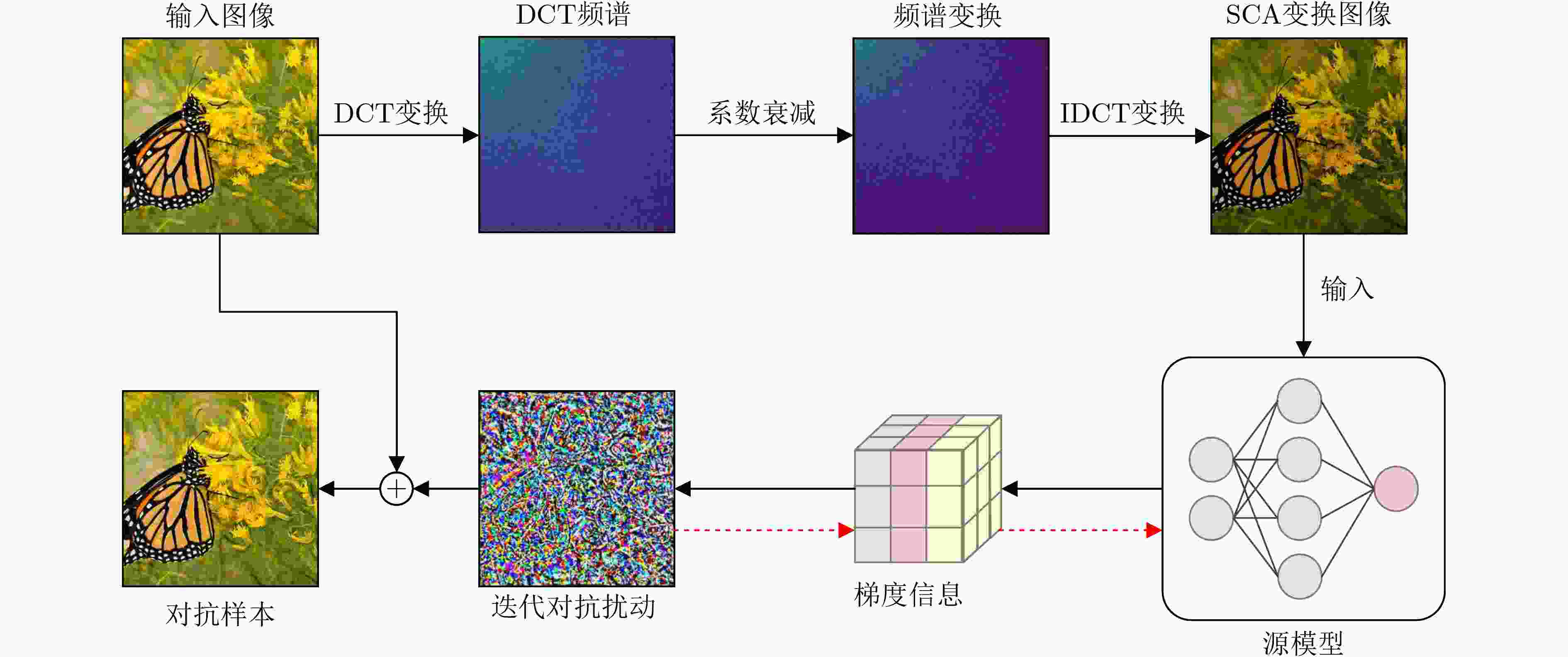
摘要: 在人工智能对抗攻击领域中，传统的白盒梯度攻击方法在生成对抗样本的迭代过程中，往往会因替代模型的局部最优解而陷入停滞，难以实现跨模型的泛化效果。当前研究普遍认为，这种现象的主要原因在于对抗样本生成过程中输入特征的多样性不足，致使生成的样本过度拟合于替代模型。针对这一问题，该文提出提升模型泛化能力的数据增强技术。与以往的研究在图像的空间域上进行诸如旋转、裁剪等变换不同，该文从频域视角入手，提出一种基于频谱系数衰减的输入变换方法。通过在输入图像的频域中衰减各频率分量的幅度信息，提高迭代中输入的多样性，有效降低对源模型特定的依赖，减小过拟合风险。在ImageNet验证集上的测试表明，该方法及两种优化方法在基于卷积和Transformer架构的模型上均能有效提升无目标对抗样本的迁移能力。
- 黑盒攻击 /
- 对抗样本迁移性 /
- 频域分析 /
- 深度学习
Abstract: Objective The rapid advancement of machine learning has accelerated the development of artificial intelligence applications based on big data. Deep Neural Networks (DNNs) are now widely used in real-world systems, including autonomous driving and facial recognition. Despite their advantages, DNNs remain vulnerable to adversarial attacks, particularly in image recognition, which exposes significant security risks. Attackers can generate carefully crafted adversarial examples that appear visually indistinguishable from benign inputs but cause incorrect model predictions. In critical applications, such attacks may lead to system failures. Studying adversarial attack strategies is crucial for designing effective defenses and improving model robustness in practical deployments. Methods This paper proposes a black-box adversarial attack method termed Spectral Coefficient Attenuation (SCA), based on Spectral Coefficient Decay (SCD). SCA perturbs spectral coefficients during the iterative generation of adversarial examples by attenuating the amplitude of each frequency component. This attenuation introduces diverse perturbation patterns and reduces the dependency of adversarial examples on the source model, thereby improving their transferability across models. Results and Discussions This study generated adversarial examples using three naturally trained deep models based on Convolutional Neural Network (CNN) architectures and evaluated their attack success rates against several widely used convolutional image recognition models. Compared with MI-FGSM, the proposed method achieved average increases in attack success rates of 4.7%, 4.1%, and 4.9%, respectively. To further assess the effectiveness of the SCA algorithm, additional experiments were conducted on vision models based on Transformer architectures. In these settings, the SCA method yielded average success rate improvements of 4.6%, 4.5%, and 3.7% compared with MI-FGSM. Conclusions The proposed method attenuates the energy of individual spectral components during the iterative generation of adversarial examples in the frequency domain. This reduces reliance on specific features of the source model, mitigates the risk of overfitting, and enhances black-box transferability across models with different architectures. Extensive experiments on the ImageNet validation set confirm the effectiveness of the SCA method. Whether targeting CNN-based or Transformer-based models, the SCA algorithm consistently achieves high transferability and robust attack performance.
- Black-box attack /
- Adversarial example transferability /
- Frequency domain analysis /
- Deep learning

HTML全文

图 1 图像的数据增强

下载: 全尺寸图片幻灯片

图 2 频谱系数衰减(SCA)攻击流程图

下载: 全尺寸图片幻灯片

图 3 在不同频谱衰减系数$\psi $下，SCA攻击在ResNet-18上生成的对抗样本对所选模型的攻击成功率

下载: 全尺寸图片幻灯片

图 4 在不同频谱衰减系数$\psi $下，SCA攻击在DenseNet-121上生成的对抗样本对所选模型的攻击成功率

下载: 全尺寸图片幻灯片

图 5 在不同频谱衰减系数$\psi $下，SCA攻击在VGG-19上生成的对抗样本对所选模型的攻击成功率

下载: 全尺寸图片幻灯片

图 6 改进的SCA方法在不同频谱衰减强度p下攻击基于 CNN架构模型的攻击成功率

下载: 全尺寸图片幻灯片

图 7 改进的SCA方法在不同频谱衰减强度p下攻击基Transformer 架构模型的攻成功率

下载: 全尺寸图片幻灯片

1 频谱系数衰减攻击算法

输入：真实标签为y的干净图像x，分类模型$ f $(x$ ;\theta ) $，损失函数　$ \mathcal{J}(x,y;\theta $)，最大扰动预算$ \mathrm{\varepsilon } $，
迭代次数T，动量衰减因子$ \mu $，衰减系数$ \psi ； $
输出：一个对抗样本$ {{\boldsymbol{x}}}^{\mathrm{a}\mathrm{d}\mathrm{v}} $
(1) $ \alpha =\varepsilon $/T; $ {\mathcal{G}}_{0} $= 0; $ {{\boldsymbol{x}}}_{0}^{\mathrm{a}\mathrm{d}\mathrm{v}}={\boldsymbol{x}} $;
(2) for t = 0 to T – 1 do
(3) 利用式(1)得到频谱系数衰减后的重建图像T (x)；
(4) 利用式(2)得到频域输入变换的图像的梯度　$ {{\text{∇}}}_{{{\boldsymbol{x}}}_{t}^{\mathrm{a}\mathrm{d}\mathrm{v}}}\left(T\left({\boldsymbol{x}}\right),y;\theta \right)； $
(5) 累计历史动量来更新梯度$ {\mathcal{G}}_{t+1}： $
$ {\mathcal{G}}_{t+1}\leftarrow {\mu \cdot \mathcal{G}}_{t} $+ $ \dfrac{{{\text{∇}}}_{{{\boldsymbol{x}}}_{t}^{\mathrm{a}\mathrm{d}\mathrm{v}}}\left(\mathcal{J}\left({\mathcal{F}}_{\mathcal{L}}\left(\psi \cdot \mathcal{F}\left({{\boldsymbol{x}}}_{t}^{\mathrm{a}\mathrm{d}\mathrm{v}}\right)\right),y;\theta \right)\right)}{\\|{{\text{∇}}}_{{{\boldsymbol{x}}}_{t}^{\mathrm{a}\mathrm{d}\mathrm{v}}}\left(\mathcal{J}\left({\mathcal{F}}_{\mathcal{L}}\left(\psi \cdot \mathcal{F}\left({{\boldsymbol{x}}}_{t}^{\mathrm{a}\mathrm{d}\mathrm{v}}\right)\right),y;\theta \right)\right)\\|} $
(6)通过应用梯度符号攻击更新对抗样本$ {{\boldsymbol{x}}}_{t+1}^{\mathrm{a}\mathrm{d}\mathrm{v}}： $
$ {{\boldsymbol{x}}}_{t+1}^{\mathrm{a}\mathrm{d}\mathrm{v}}\leftarrow {\mathrm{C}\mathrm{l}\mathrm{i}\mathrm{p}}_{{\boldsymbol{x}}}^{\varepsilon }\left\{{{\boldsymbol{x}}}_{t}^{\mathrm{a}\mathrm{d}\mathrm{v}}\right.+\alpha \cdot \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left.\left({\mathcal{G}}_{t+1}\right)\right\} $
(7) end for
(8)返回$ {{\boldsymbol{x}}}^{\mathrm{a}\mathrm{d}\mathrm{v}}\leftarrow {{\boldsymbol{x}}}_{T}^{\mathrm{a}\mathrm{d}\mathrm{v}} $

下载: 导出CSV

表 1 SCA攻击在7个基于CNN架构模型上的攻击成功率(%)

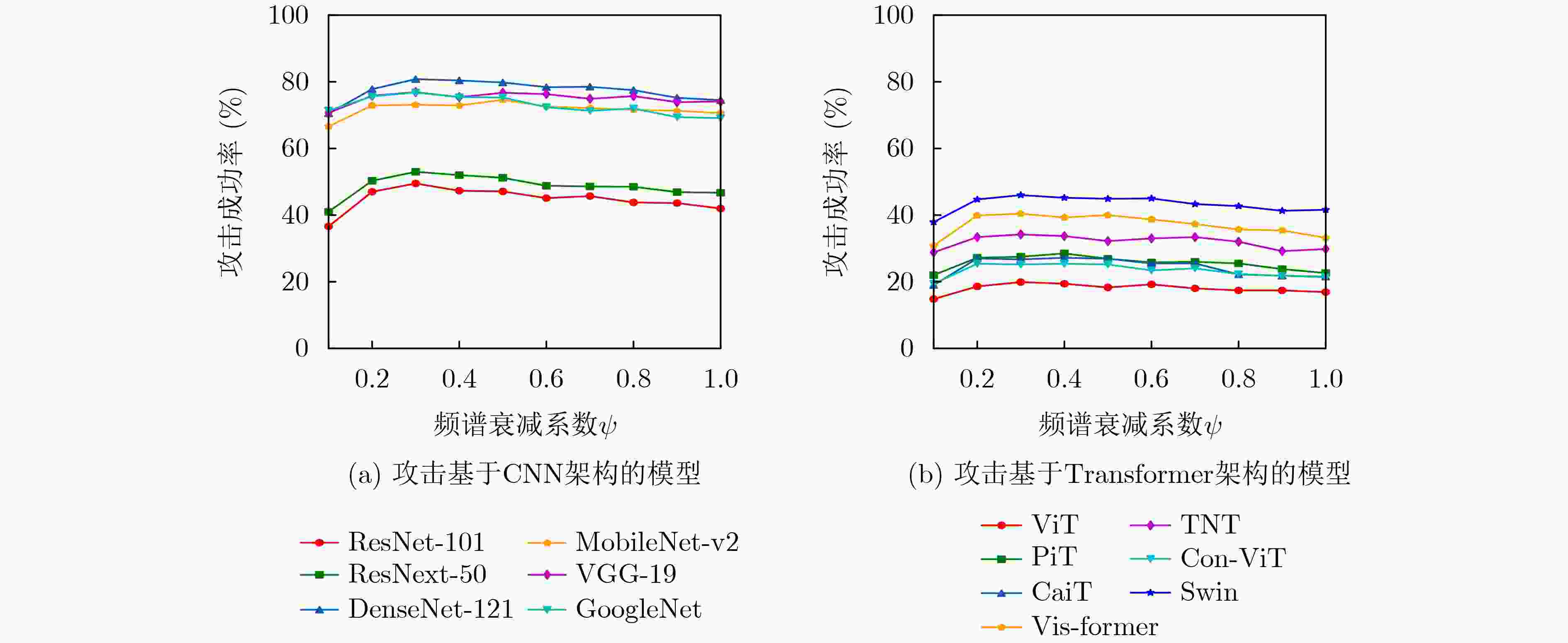
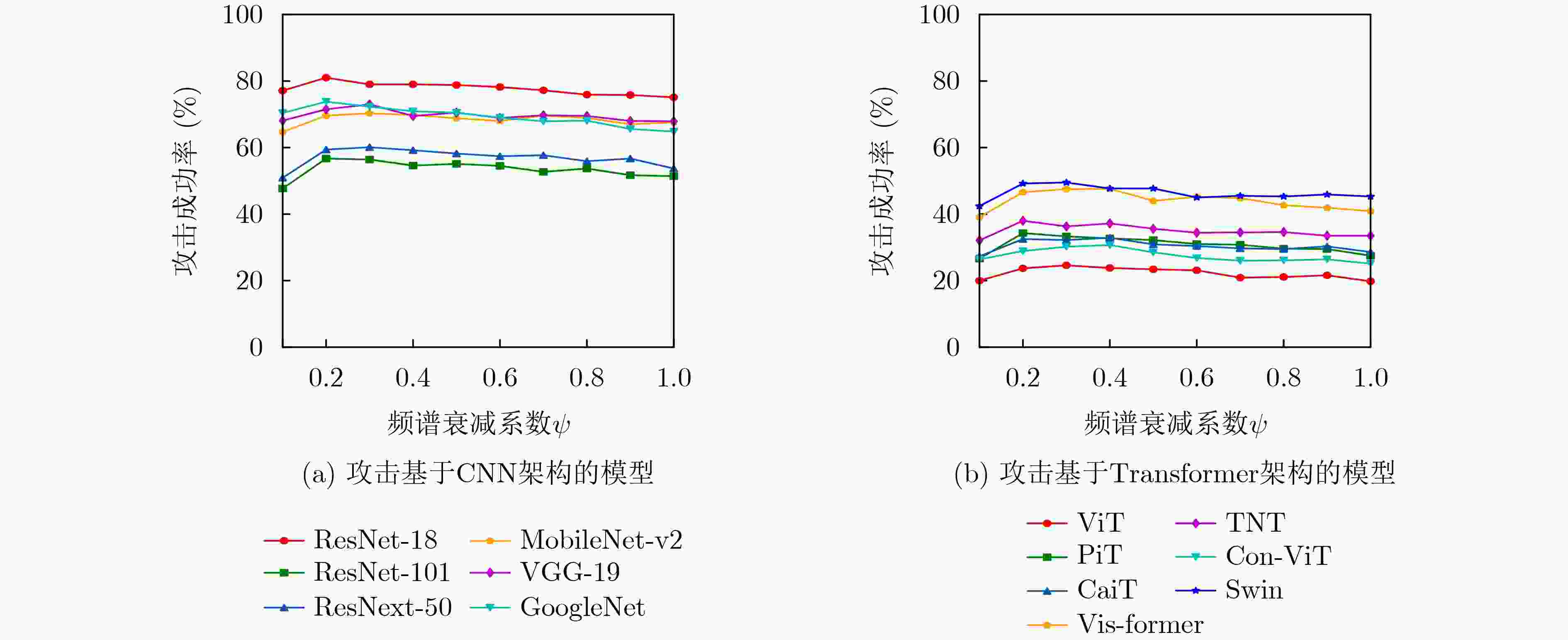
目标模型	ResNet-18		DenseNet-121		VGG-19
目标模型	MI-FGSM	SCA(本文)	MI-FGSM	SCA(本文)	MI-FGSM	SCA(本文)
ResNet-18	100.0*	100.0*	75.2	79.0	64.8	70.3
ResNet-101	42.2	49.5	50.5	56.4	33.2	37.4
ResNet-50	45.9	53.0	54.1	60.1	39.7	43.4
DenseNet-121	74.5	80.8	99.9*	99.9*	59.6	66.3
MobileNet-v2	71.6	73.1	67.1	70.3	64.9	69.1
VGG-19	73.8	76.9	69.4	73.0	99.3	99.9*
GoogleNet	69.5	76.8	66.4	72.3	55.1	64.1
Avg.ASR	68.2	72.9	68.9	73.0	59.5	64.4

下载: 导出CSV

表 2 SCA攻击在基于Transformer架构模型上的攻击成功率(%)

目标模型	ResNet-18		DenseNet-121		VGG-19
目标模型	MI-FGSM	SCA(本文)	MI-FGSM	SCA(本文)	MI-FGSM	SCA(本文)
ViT	16.7	19.9	20.5	24.6	13.3	15.9
PiT	22.3	27.5	28.0	33.3	20.5	23.3
CaiT	22.1	26.7	28.2	32.2	18.7	20.3
Vis-former	33.6	40.4	41.7	47.5	29.0	35.8
TNT	30.3	34.2	32.6	36.3	25.7	30.4
Con-ViT	21.9	25.2	26.5	30.2	15.3	18.8
Swin	41.0	46.0	44.5	49.5	35.0	38.9
Avg.ASR	26.8	31.4	31.7	36.2	22.5	26.2

下载: 导出CSV

表 3 改进的SCA攻击在7个基于CNN架构的自然训练模型上的攻击成功率

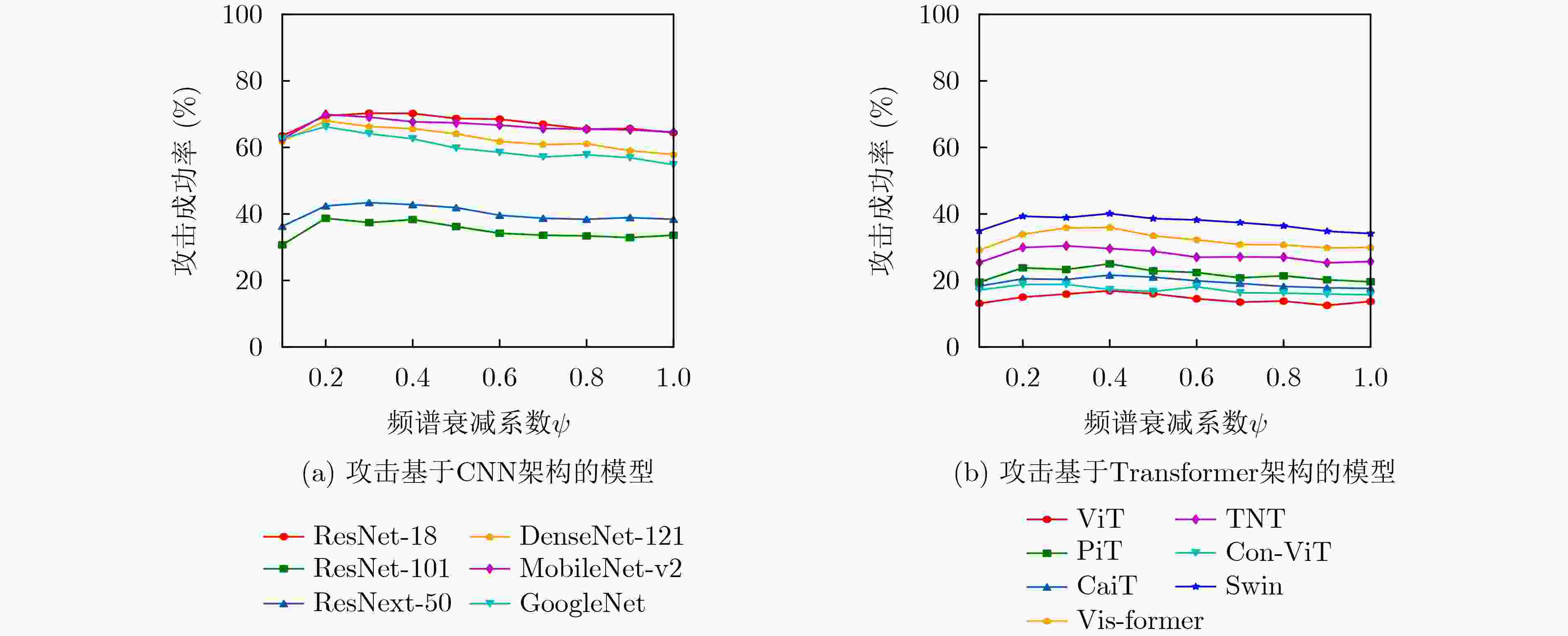
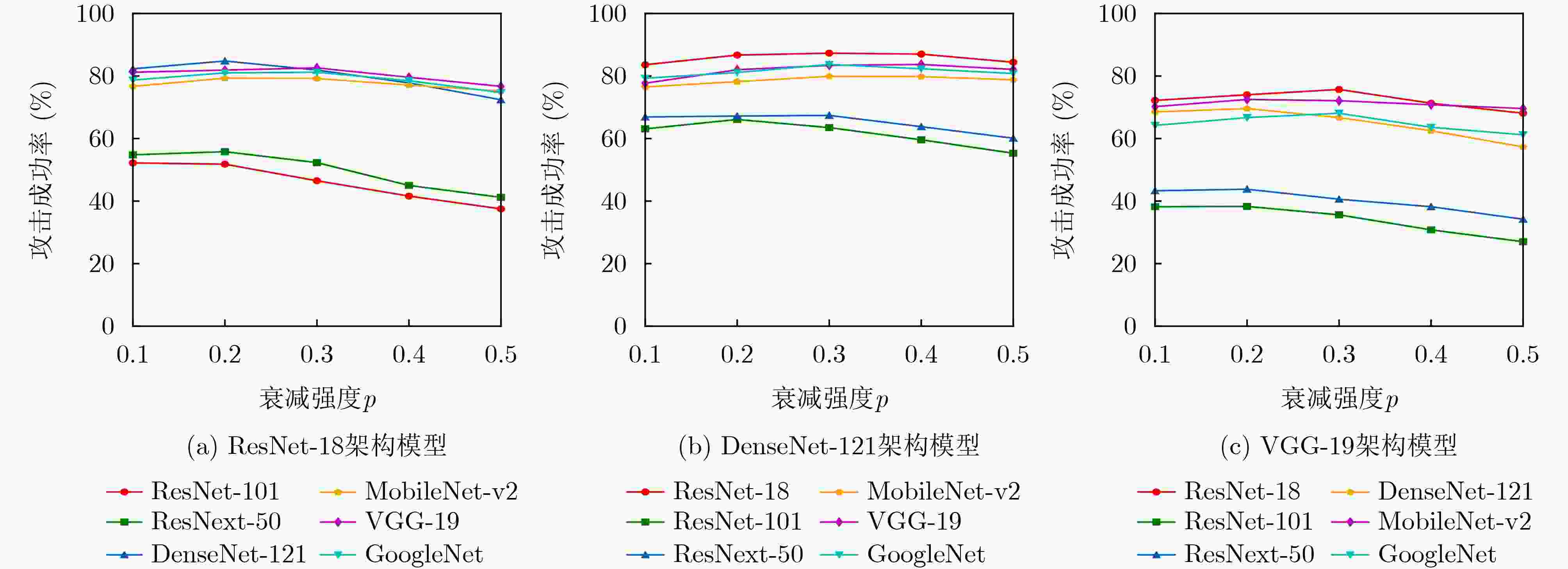
目标模型	替代模型
目标模型	ResNet-18	DenseNet-121	VGG-19
ResNet-18	100.0($ \uparrow $0.0)	84.5($ \uparrow $5.5)	73.6($ \uparrow $3.3)
ResNet-101	53.8($ \uparrow $4.3)	63.1($ \uparrow $6.7)	41.5($ \uparrow $4.1)
ResNet-50	57.9($ \uparrow $4.9)	65.4($ \uparrow $5.3)	45.8($ \uparrow $2.4)
DenseNet-121	84.8($ \uparrow $4.0)	99.9($ \uparrow $0.0)	70.0($ \uparrow $3.7)
MobileNet-v2	78.7($ \uparrow $5.6)	76.1($ \uparrow $5.8)	72.9($ \uparrow $3.8)
VGG-19	82.1($ \uparrow $5.2)	78.1($ \uparrow $5.1)	99.7($ \uparrow $0.2)
GoogleNet	80.4($ \uparrow $3.6)	77.0($ \uparrow $4.7)	67.8($ \uparrow $3.7)
Avg.ASR	76.8($ \uparrow $3.9)	77.7($ \uparrow $4.7)	67.3($ \uparrow $2.9)

下载: 导出CSV

表 4 改进的SCA攻击在7个基于Transformer架构的自然训练模型上的攻击成功率

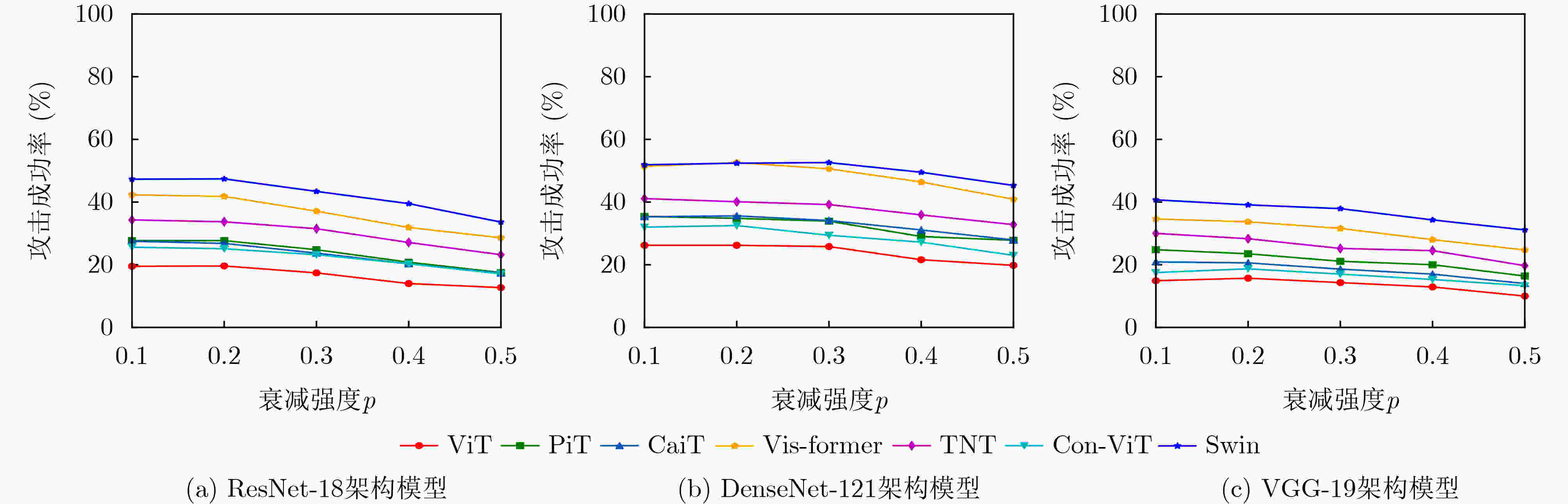
目标模型	替代模型
目标模型	ResNet-18	DenseNet-121	VGG-19
ViT	21.7($ \uparrow $1.8)	28.0($ \uparrow $3.4)	16.6($ \uparrow $0.7)
PiT	28.5($ \uparrow $1.0)	37.8($ \uparrow $4.5)	26.2($ \uparrow $2.9)
CaiT	28.5($ \uparrow $1.8)	36.9($ \uparrow $4.7)	22.7($ \uparrow $2.4)
Vis-former	43.2($ \uparrow $2.8)	53.1($ \uparrow $5.6)	37.8($ \uparrow $2.0)
TNT	36.8($ \uparrow $2.6)	39.8($ \uparrow $3.5)	31.4($ \uparrow $1.0)
Con-ViT	26.8($ \uparrow $1.6)	33.6($ \uparrow $3.4)	20.7($ \uparrow $1.9)
Swin	49.7($ \uparrow $3.7)	52.6($ \uparrow $3.1)	42.2($ \uparrow $3.3)
Avg.ASR	33.6($ \uparrow $2.2)	40.3($ \uparrow $4.1)	28.2($ \uparrow $2.0)

下载: 导出CSV

参考文献(37)

[1]	TSUZUKU Y and SATO I. On the structural sensitivity of deep convolutional networks to the directions of Fourier basis functions[C]. IEEE/CVF Conference on Computer Vision and Pattern Recognition, Beach, USA, 2019: 51–60. doi: 10.1109/CVPR.2019.00014.
[2]	YIN Dong, LOPES R G, SHLENS J, et al. A Fourier perspective on model robustness in computer vision[C]. The 33rd International Conference on Neural Information Processing Systems, Vancouver, Canada, 2019: 1189.
[3]	PANNU A and STUDENT M T. Artificial intelligence and its application in different areas[J]. International Journal of Engineering and Innovative Technology, 2015, 4(10): 79–84.
[4]	WANG Haohan, WU Xindi, HUANG Zeyi, et al. High-frequency component helps explain the generalization of convolutional neural networks[C]. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, USA, 2020: 8681–8691. doi: 10.1109/CVPR42600.2020.00871.
[5]	GOODFELLOW I J, SHLENS J, and SZEGEDY C. Explaining and harnessing adversarial examples[C]. 3rd International Conference on Learning Representations, San Diego, USA, 2015: 278293.
[6]	ZHANG Jiaming, YI Qi, and SANG Jitao. Towards adversarial attack on vision-language pre-training models[C]. The 30th ACM International Conference on Multimedia, Lisboa, Portugal, 2022: 5005–5013. doi: 10.1145/3503161.3547801.
[7]	LIU Yanpei, CHEN Xinyun, LIU Chang, et al. Delving into transferable adversarial examples and black-box attacks[C]. 5th International Conference on Learning Representations, Toulon, France, 2017.
[8]	GAO Sensen, JIA Xiaojun, REN Xuhong, et al. Boosting transferability in vision-language attacks via diversification along the intersection region of adversarial trajectory[C]. 18th European Conference on Computer Vision, Milan, Italy, 2024: 442–460. doi: 10.1007/978-3-031-72998-0_25.
[9]	BRUNA J, SZEGEDY C, SUTSKEVER I, et al. Intriguing properties of neural networks[C]. International Conference on Learning Representations, Banff, Canada, 2014.
[10]	KURAKIN A, GOODFELLOW I J, and BENGIO S. Adversarial examples in the physical world[C]. 5th International Conference on Learning Representations, Toulon, France, 2017.
[11]	DONG Yinpeng, LIAO Fangzhou, PANG Tianyu, et al. Boosting adversarial attacks with momentum[C]. IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, USA, 2018: 9185–9193. doi: 10.1109/CVPR.2018.00957.
[12]	MADRY A, MAKELOV A, SCHMIDT L, et al. Towards deep learning models resistant to adversarial attacks[C]. 6th International Conference on Learning Representations, Vancouver, Canada, 2018.
[13]	CARLINI N and WAGNER D. Towards evaluating the robustness of neural networks[C]. 2017 IEEE Symposium on Security and Privacy, San Jose, USA, 2017: 39–57. doi: 10.1109/SP.2017.49.
[14]	MOOSAVI-DEZFOOLI S M, FAWZI A, and FROSSARD P. DeepFool: A simple and accurate method to fool deep neural networks[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 2574–2582. doi: 10.1109/CVPR.2016.282.
[15]	ZHAO Yunqing, PANG Tianyu, DU Chao, et al. On evaluating adversarial robustness of large vision-language models[C]. The 37th International Conference on Neural Information Processing Systems, New Orleans, USA, 2023: 2355.
[16]	QIAN Yaguan, HE Shuke, ZHAO Chenyu, et al. LEA²: A lightweight ensemble adversarial attack via non-overlapping vulnerable frequency regions[C]. The IEEE/CVF International Conference on Computer Vision, Paris, France, 2023: 4487–4498. doi: 10.1109/ICCV51070.2023.00416.
[17]	QIAN Yaguan, CHEN Kecheng, WANG Bin, et al. Enhancing transferability of adversarial examples through mixed-frequency inputs[J]. IEEE Transactions on Information Forensics and Security, 2024, 19: 7633–7645. doi: 10.1109/TIFS.2024.3430508.
[18]	LIN Jiadong, SONG Chuanbiao, HE Kun, et al. Nesterov accelerated gradient and scale invariance for adversarial attacks[C]. International Conference on Learning Representations, Addis Ababa, Ethiopia, 2020.
[19]	WANG Xiaosen and HE Kun. Enhancing the transferability of adversarial attacks through variance tuning[C]. IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, USA, 2021: 1924–1933. doi: 10.1109/CVPR46437.2021.00196.
[20]	ZHU Hegui, REN Yuchen, SUI Xiaoyan, et al. Boosting adversarial transferability via gradient relevance attack[C]. 2023 IEEE/CVF International Conference on Computer Vision, Paris, France, 2023: 4718–4727. doi: 10.1109/ICCV51070.2023.00437.
[21]	XIE Cihang, ZHANG Zhishuai, ZHOU Yuyin, et al. Improving transferability of adversarial examples with input diversity[C]. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, USA, 2019: 2725–2734. doi: 10.1109/CVPR.2019.00284.
[22]	LONG Yuyang, ZHANG Qilong, ZENG Boheng, et al. Frequency domain model augmentation for adversarial attack[C]. 17th European Conference on Computer Vision, Tel Aviv, Israel, 2022: 549–566. doi: 10.1007/978-3-031-19772-7_32.
[23]	WANG Xiaosen, ZHANG Zeliang, and ZHANG Jianping. Structure invariant transformation for better adversarial transferability[C]. 2023 IEEE/CVF International Conference on Computer Vision, Paris, France, 2023: 4584–4596. doi: 10.1109/ICCV51070.2023.00425.
[24]	ZHANG Jianping, HUANG J T, WANG Wenxuan, et al. Improving the transferability of adversarial samples by path-augmented method[C]. 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, Canada, 2023: 8173–8182. doi: 10.1109/CVPR52729.2023.00790.
[25]	ZHAO Hongzhi, HAO Lingguang, HAO Kuangrong, et al. Remix: Towards the transferability of adversarial examples[J]. Neural Networks, 2023, 163: 367–378. doi: 10.1016/j.neunet.2023.04.012.
[26]	XU Yonghao and GHAMISI P. Universal adversarial examples in remote sensing: Methodology and benchmark[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5619815. doi: 10.1109/TGRS.2022.3156392.
[27]	XIAO Jun, LYU Zihang, ZHANG Cong, et al. Towards progressive multi-frequency representation for image warping[C]. The IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, USA, 2024: 2995–3004. doi: 10.1109/CVPR52733.2024.00289.
[28]	LIN Xinmiao, LI Yikang, HSIAO J, et al. Catch missing details: Image reconstruction with frequency augmented variational autoencoder[C]. The IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, Canada, 2023: 1736–1745. doi: 10.1109/CVPR52729.2023.00173.
[29]	RAO K R and YIP P. Discrete Cosine Transform: Algorithms, Advantages, Applications[M]. San Diego, USA: Academic Press Professional, Inc. , 1990.
[30]	HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]. IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 770–778. doi: 10.1109/CVPR.2016.90.
[31]	HUANG Gao, LIU Zhuang, VAN DER MAATEN L, et al. Densely connected convolutional networks[C]. IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, USA, 2017: 2261–2269. doi: 10.1109/CVPR.2017.243.
[32]	SIMONYAN K and ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[C]. 3rd International Conference on Learning Representations, San Diego, USA, 2015.
[33]	DOSOVITSKIY A, BEYER L, KOLESNIKOV A, et al. An image is worth 16x16 words: Transformers for image recognition at scale[C]. International Conference on Learning Representations, Vienna, Austria, 2021.
[34]	TOUVRON H, CORD M, SABLAYROLLES A, et al. Going deeper with image transformers[C]. 2021 IEEE/CVF International Conference on Computer Vision, Montreal, Canada, 2021: 32–42. doi: 10.1109/ICCV48922.2021.00010.
[35]	CHEN Zhengsu, XIE Lingxi, NIU Jianwei, et al. Visformer: The vision-friendly transformer[C]. 2021 IEEE/CVF International Conference on Computer Vision, Montreal, Canada, 2021: 569–578. doi: 10.1109/ICCV48922.2021.00063.
[36]	D’ASCOLI S, TOUVRON H, LEAVITT M L, et al. ConViT: Improving vision transformers with soft convolutional inductive biases[C]. The 38th International Conference on Machine Learning, 2021: 2286–2296.
[37]	LIU Ze, LIN Yutong, CAO Yue, et al. Swin transformer: Hierarchical vision transformer using shifted windows[C]. 2021 IEEE/CVF International Conference on Computer Vision, Montreal, Canada, 2021: 9992–10002. doi: 10.1109/ICCV48922.2021.00986.