面向多组群目标跟踪的多维资源管理优化策略

林木深; 曹丙霞; 闫锋刚; 孟祥天; 沙明辉; 李占国; 金铭

doi:10.11999/JEIT250152

面向多组群目标跟踪的多维资源管理优化策略

doi: 10.11999/JEIT250152 cstr: 32379.14.JEIT250152

1.
哈尔滨工业大学(威海)信息科学与工程学院威海 264209
2.
北京无线电测量研究所北京 100854

基金项目: 国家自然科学基金(62171150)，泰山学者工程专项经费资助(tsqn202211087)，山东省自然科学基金(ZR2023MF091, ZR2024MF071, ZR2024QF068)，航空科学基金(2023Z037077002)

详细信息

作者简介:
林木深：男，硕士生，研究方向为多目标跟踪、雷达资源管理

曹丙霞：女，副教授，研究方向为阵列信号处理、极化雷达技术

闫锋刚：男，教授，研究方向为雷达信号处理，反辐射制导

孟祥天：男，讲师，研究方向为阵列信号处理、反辐射制导

沙明辉：男，研究员，研究方向为雷达系统设计、雷达抗干扰技术

李占国：男，高级工程师，研究方向为电子对抗、技术侦察

金铭：男，教授，研究方向为雷达系统设计、阵列信号处理

通讯作者:
孟祥天　mxtian@hit.edu.cn

中图分类号: TN958
计量
- 文章访问数: 86
- HTML全文浏览量: 36
- PDF下载量: 18
- 被引次数: 0
出版历程
- 收稿日期: 2025-03-12
- 修回日期: 2025-06-03
- 网络出版日期: 2025-06-18

Multi-Dimensional Resource Management Optimization Strategy for Multi-Group Target Tracking

1.
School of Information Science and Engineering, Harbin Institute of Technology (Weihai), Weihai 264209, China
2.
Beijing Institute of Radio Measurement, Beijing 100854, China

Funds: The National Natural Science Foundation of China (62171150), Taishan Scholar Special Funding Project of Shandong Province (tsqn202211087), Shandong Provincial Natural Science Foundation (ZR2023MF091, ZR2024MF071, ZR2024QF068), The Aeronautical Science Foundation of China (2023Z037077002)

摘要

摘要: 针对现有网络化雷达难以实现群目标的高分辨率多目标跟踪问题，该文提出一种用于网络化雷达系统的波束选择与多维资源管理(BSMRM)策略，以提高目标分辨能力和多目标跟踪(MTT)精度。首先推导了概率数据关联(PDA)融合规则和交互多模型-扩展卡尔曼滤波器(IMM-EKF)下的贝叶斯克拉美-罗下限(BCRLB)，以此作为跟踪精度的性能指标，并通过归一化波束内观测目标与非观测目标的模糊函数幅值，量化了系统的分辨性能。随后构建基于对数障碍法的效用函数用于全局性能量化，将多维资源管理建模为优化问题，其目标函数为全局性能最优化，约束条件为给定的系统资源限制。最后采用基于网格搜索法和梯度下降算法的3阶段快速算法进行求解。仿真结果表明，与现有算法相比，该文所提方法能够在减少频谱占用和功率消耗的情况下，实现相当的目标分辨能力和多目标跟踪精度。
- 资源管理 /
- 网络化雷达 /
- 多目标跟踪
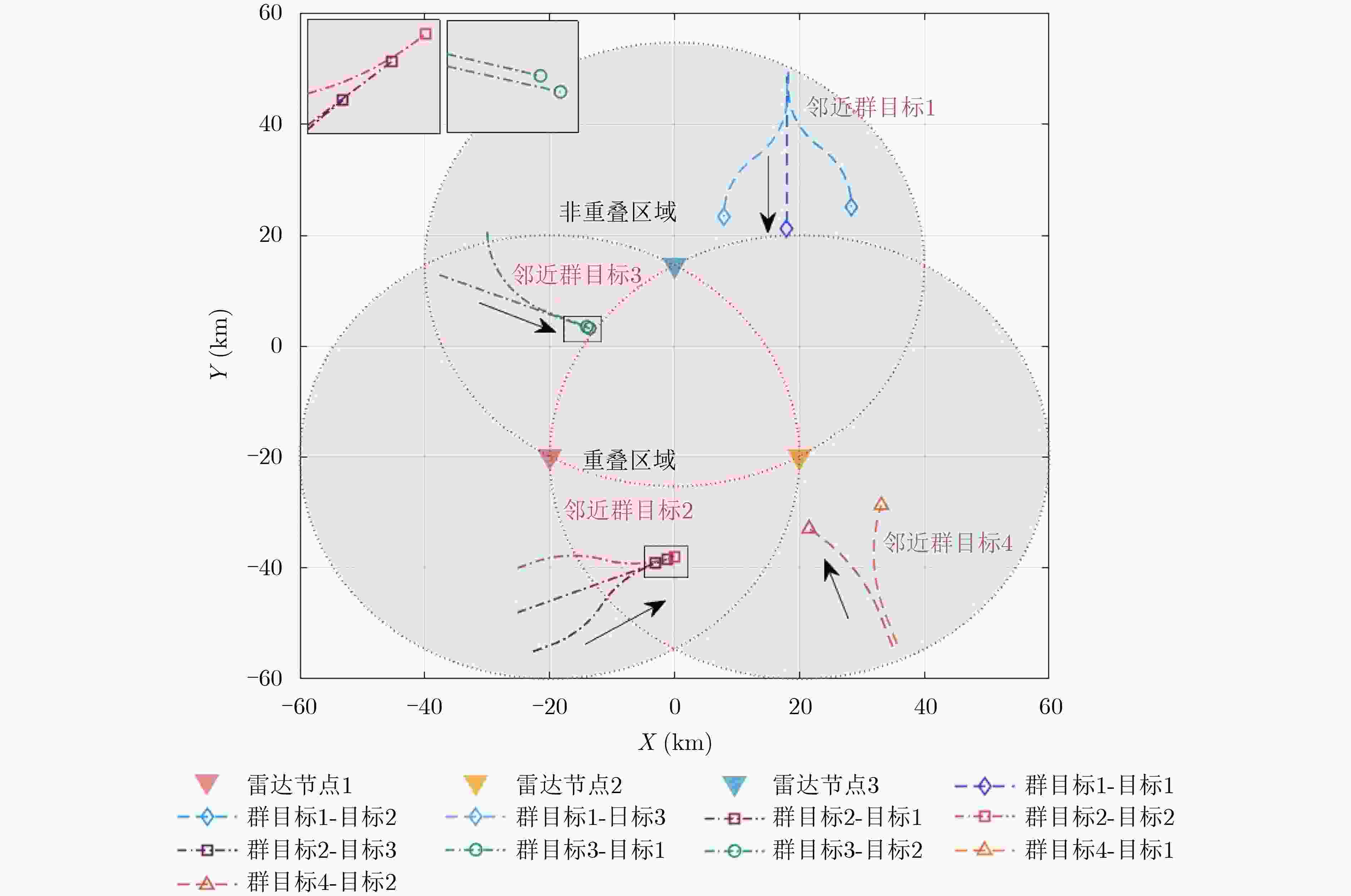
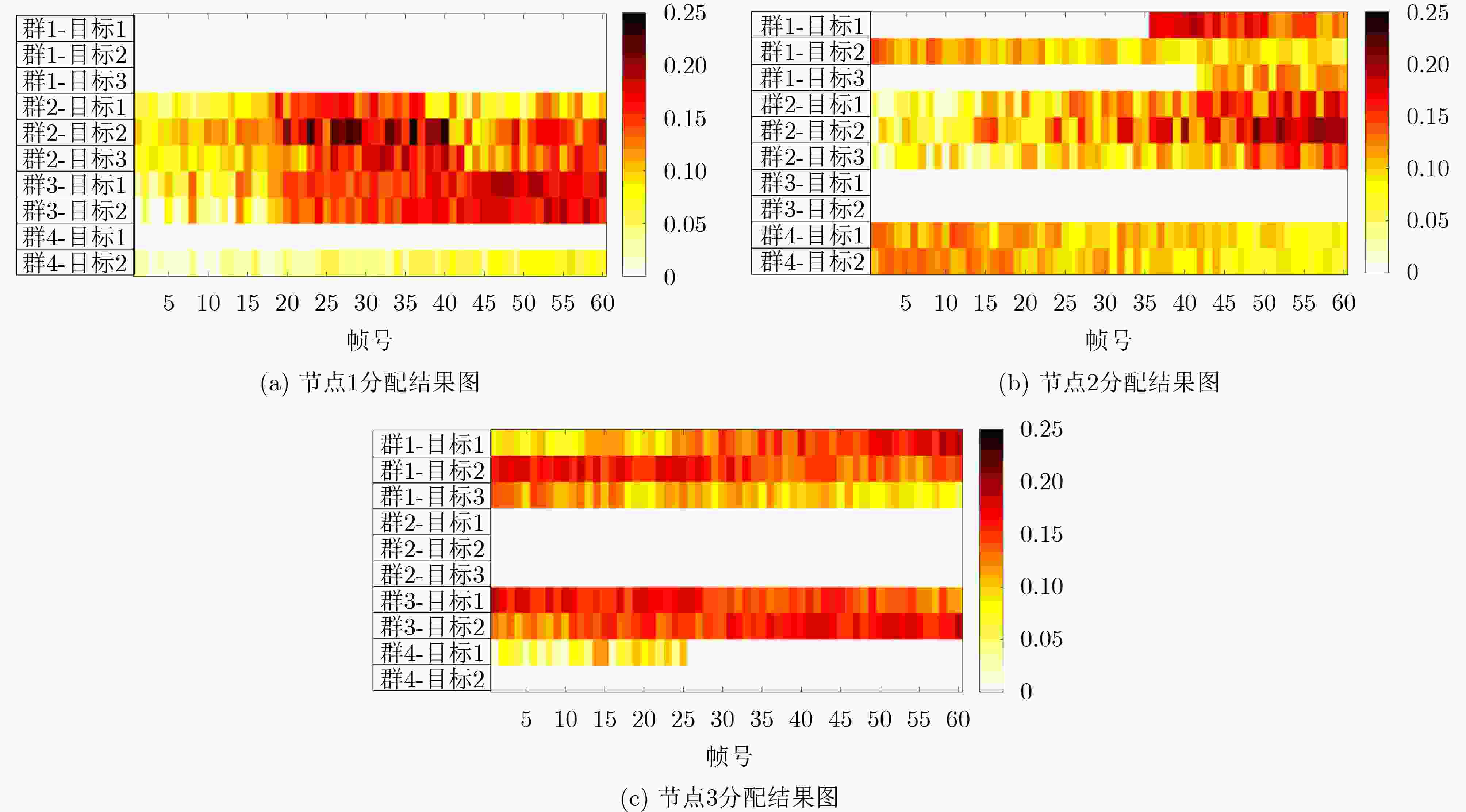
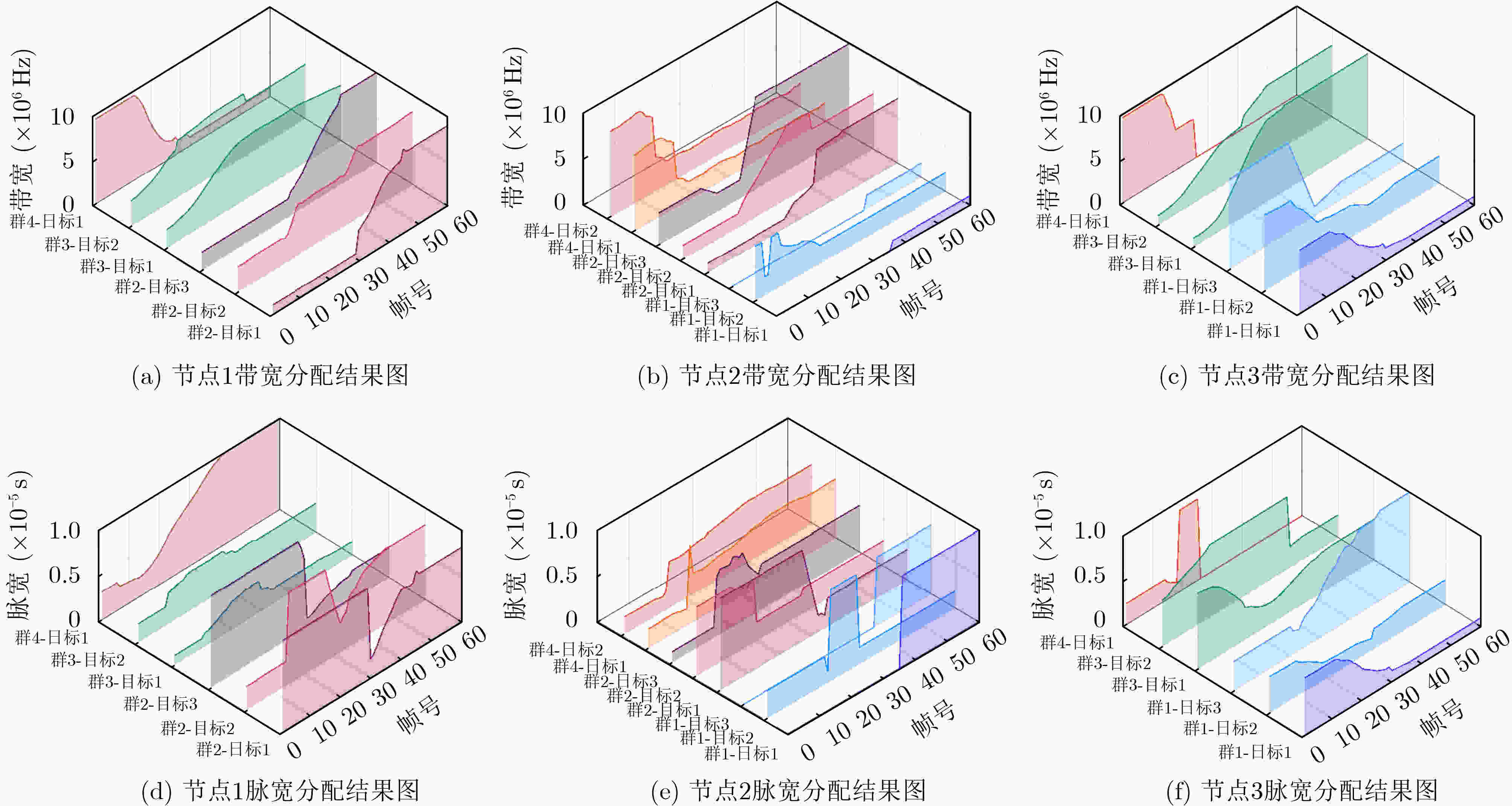
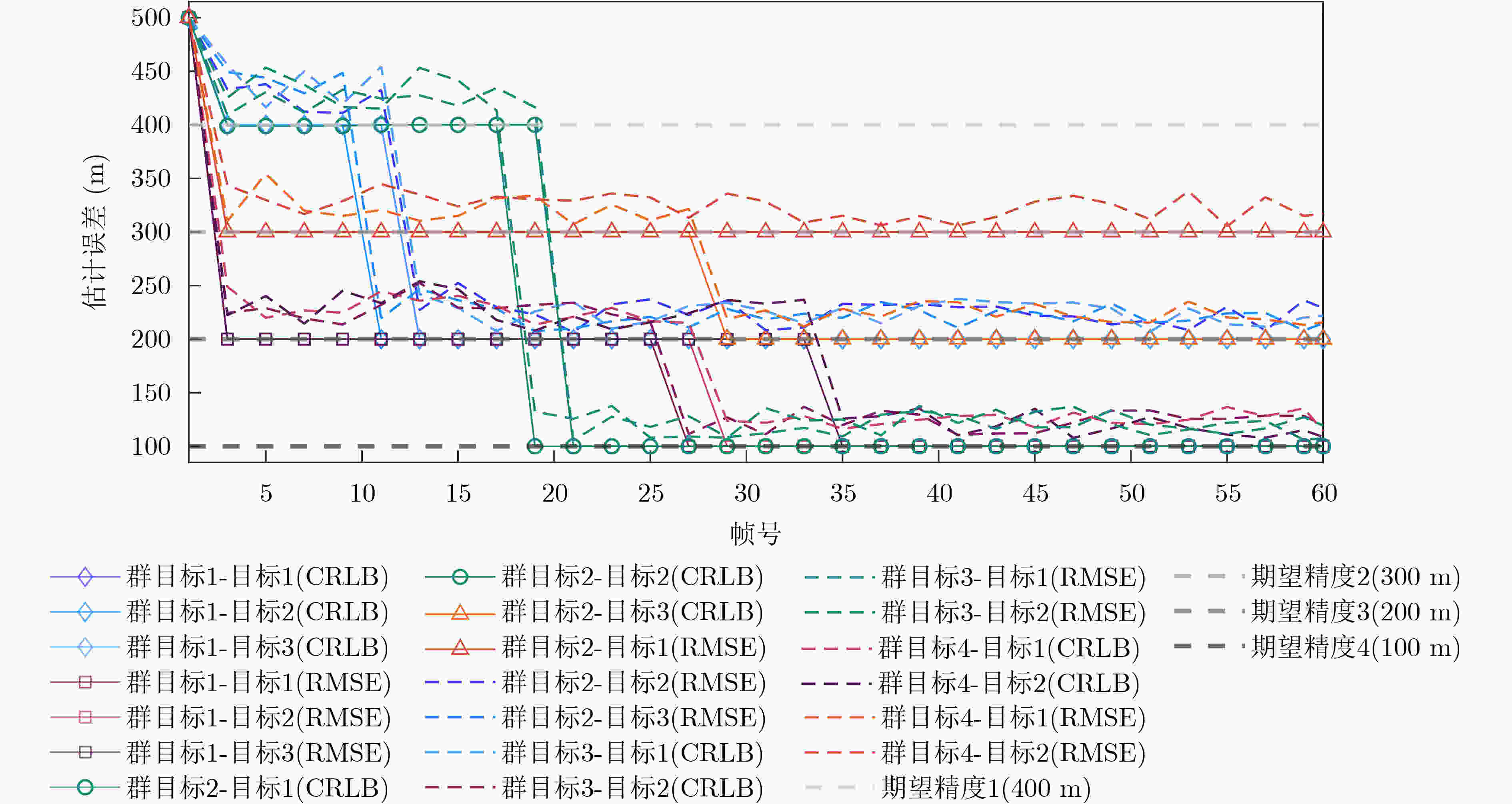
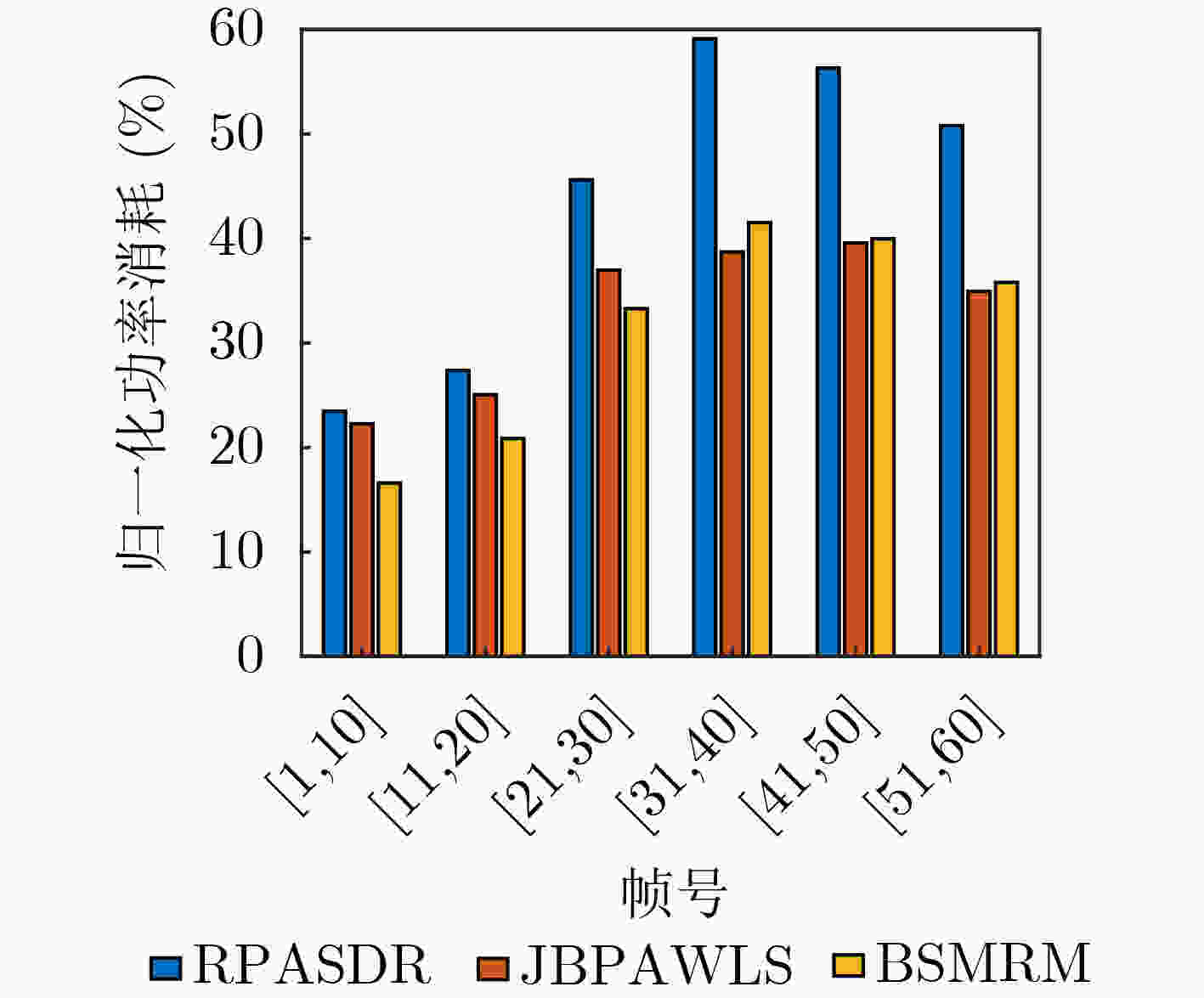
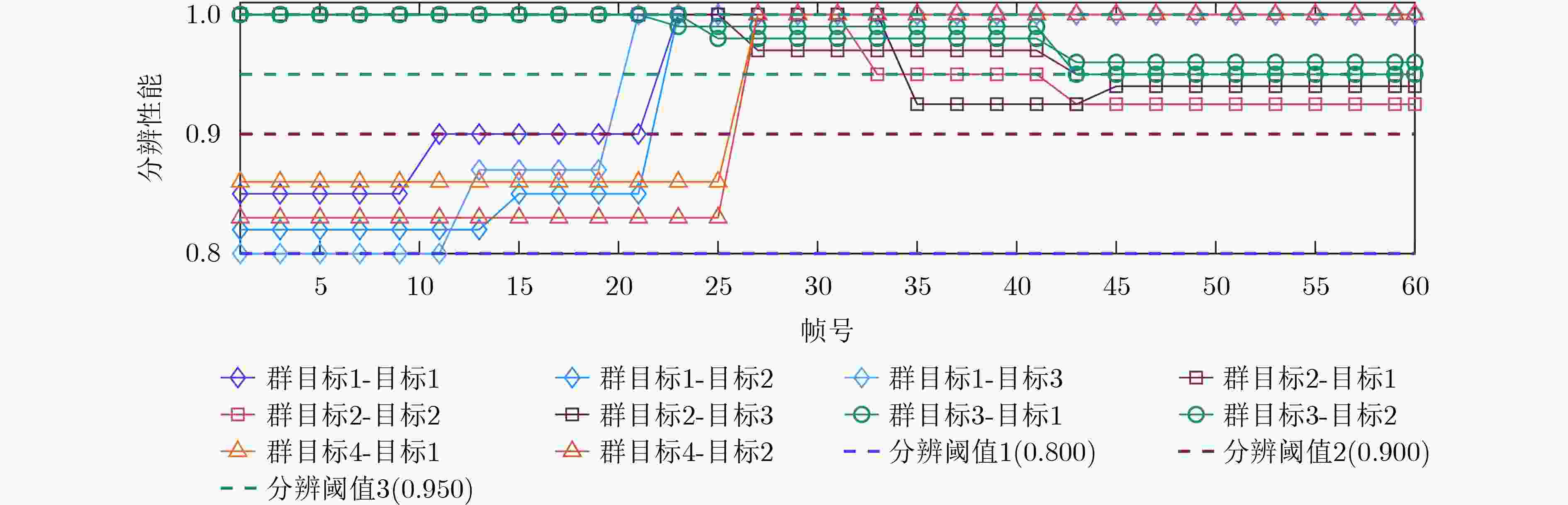
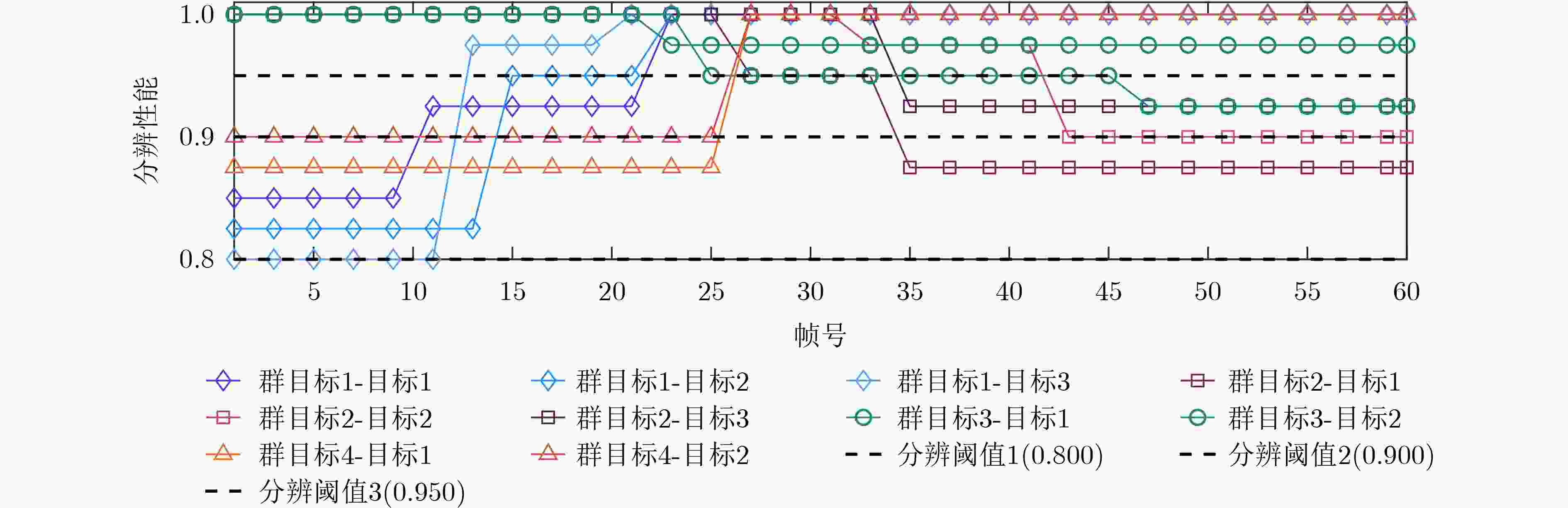
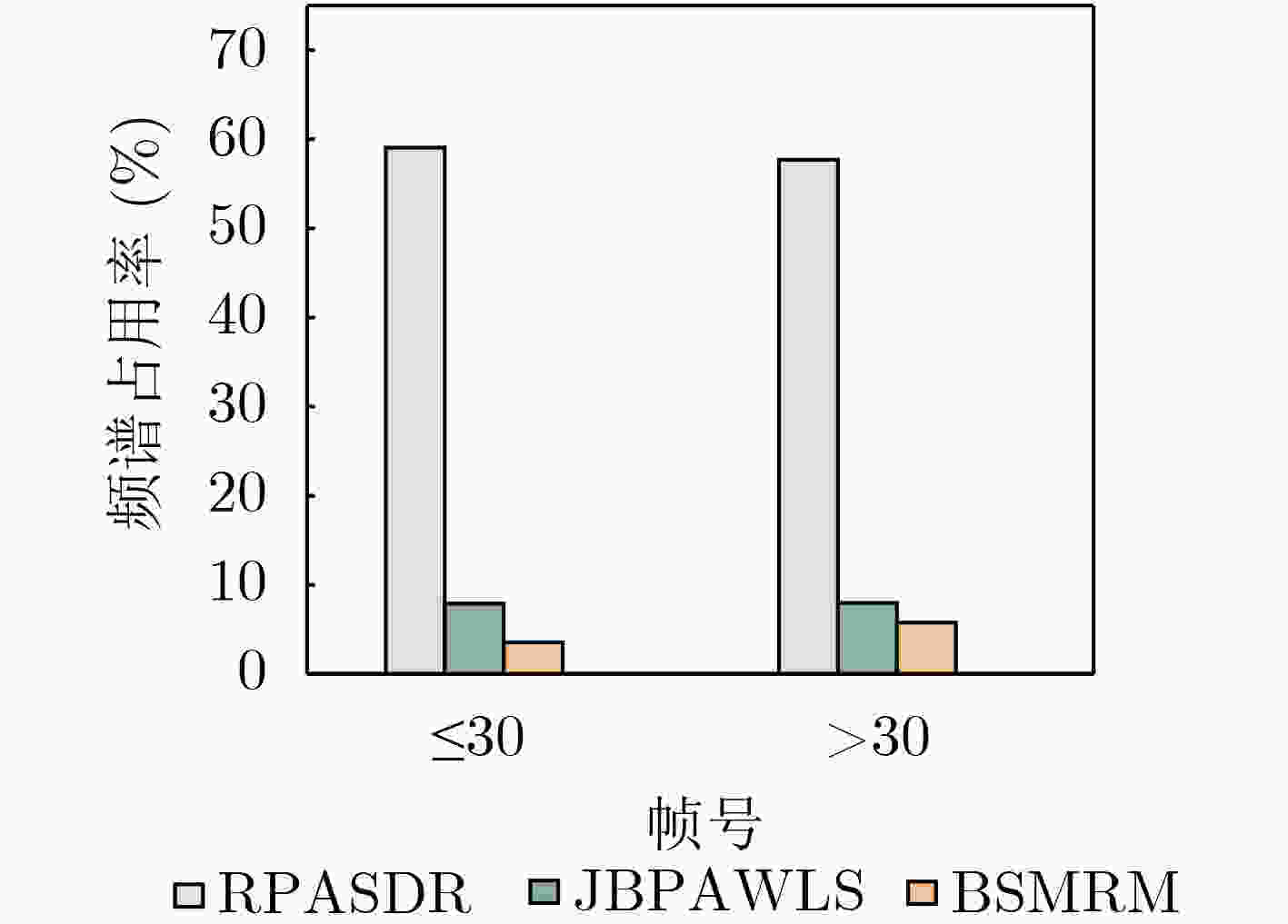
Abstract: Objective Although existing resource management strategies can improve the performance of Multiple Target Tracking (MTT), they generally assume that targets are well separated. With the development of swarm intelligence, multiple maneuvering targets can adopt group merging and splitting tactics to enhance task efficiency. This often results in the presence of several closely spaced targets within a single tracking beam, making them difficult to distinguish. In such cases, networked radars must coordinate the allocation of signal bandwidth and pulse width to increase both the resolution of adjacent targets and overall MTT performance. However, previous studies have not accounted for the effect of signal resolution capability on MTT performance. When adjacent targets emerge in the surveillance region, resource allocation schemes derived from existing methods become insufficient. To address this limitation, this study proposes a joint Beam Selection and Multi-dimensional Resource Management (BSMRM) strategy. By jointly optimizing the transmit beam, power, signal bandwidth, and pulse width, the proposed approach markedly improves MTT performance for multiple groups of clustered maneuvering targets and enhances the resolution of adjacent targets within the surveillance area. Methods This study proposes a BSMRM strategy for netted radar systems to improve target resolution capability and MTT accuracy. First, the Bayesian Cramér-Rao Lower Bound (BCRLB) is derived under the Probabilistic Data Association (PDA) fusion rule and the Interacting Multiple Model-Extended Kalman Filter (IMM-EKF) framework. Resolution performance is quantified using the normalized magnitude of the ambiguity function for both observed and unobserved targets located within the beam. A utility function is then formulated using the logarithmic barrier method to quantify global performance. Multi-dimensional resource management is modeled as a constrained optimization problem, with the objective of maximizing global performance under system resource constraints. A three-stage solver is developed to address the optimization problem. Simulation results show that the proposed BSMRM strategy achieves comparable target resolution and MTT accuracy to state-of-the-art algorithms, while demonstrating superior efficiency in spectrum usage and power allocation. Results and Discussions As shown in (Table 1) and (Fig. 1), this study evaluates the effectiveness and robustness of the proposed BSMRM strategy in a complex scenario where four groups of swarm targets maneuver within the surveillance region of three radar nodes. The performance of the BSMRM strategy is assessed through four simulation experiments. Experiment 1 presents the allocation of transmission resources, including beam selection and power distribution. The results are shown in (Fig. 2), where color-coded regions represent normalized transmit power levels determined by the BSMRM strategy. Experiment 2 reports the allocation of waveform resources—specifically, signal bandwidth and pulse width. In this experiment, resolution thresholds corresponding to various target states are first established. The BSMRM strategy is then used to adjust the signal bandwidth and pulse width of each transmit beam to enable effective discrimination of swarm targets. Experiment 3 analyzes tracking performance through numerical simulations, comparing the proposed strategy with benchmark algorithms. A sequence of 60 tracking frames with a time interval of T = 2.5 s is simulated, with 300 Monte Carlo runs. Root Mean Square Error (RMSE) is used as the evaluation metric. (Fig. 4) displays the BCRLB and RMSE curves for each target group under the BSMRM strategy. The RMSE converges toward the corresponding BCRLBs, indicating that the proposed method meets tracking accuracy requirements across all target groups. When sufficient transmit power is available, the BSMRM strategy drives the accuracy to the desired thresholds, thereby maximizing utility. (Fig. 5) compares the normalized average power consumption of three strategies. (Figs. 6 and 7) show resolution performance curves for the BSMRM and JBPAWLS strategies, respectively. (Fig. 8) compares spectrum occupancy across two operational phases to assess spectral efficiency under resolution constraints. Experiment 4 evaluates the computational complexity of the BSMRM strategy. Results show that, with parallel computing, the strategy satisfies the real-time requirements of resource scheduling. Conclusions This study proposes a BSMRM strategy for MTT in a C-MIMO radar network. The strategy jointly optimizes beam selection, transmit power, signal bandwidth, and pulse length to improve both target resolvability and tracking accuracy. An efficient three-stage solver is developed to address the resulting optimization problem. Simulation results show that the proposed strategy achieves high-resolution MTT while reducing spectral occupancy. Under sufficient power conditions, tracking accuracy is comparable to that of state-of-the-art algorithms. In the same simulation environment, the average CPU runtime per frame is 2.8617 s, which is reduced to 0.3573 s with GPU-based parallel processing—meeting the real-time requirements for resource allocation. Moreover, the BSMRM strategy demonstrates flexibility and robustness under limited power constraints.
- Resource management /
- Radar network /
- Multi-Target Tracking (MTT)

HTML全文

图 1 群目标和网络化雷达部署示意图

下载: 全尺寸图片幻灯片

图 2 采用BSMRM策略的波束选择和功率分配结果

下载: 全尺寸图片幻灯片

图 3 采用BSMRM策略的带宽和脉宽分配结果

下载: 全尺寸图片幻灯片

图 4 采用BSMRM策略的多目标跟踪误差结果

下载: 全尺寸图片幻灯片

图 5 不同资源管理算法的功率消耗对比

下载: 全尺寸图片幻灯片

图 6 采用BSMRM策略的群目标分辨率性能

下载: 全尺寸图片幻灯片

图 7 采用JBPAWLS策略的群目标分辨率性能

下载: 全尺寸图片幻灯片

图 8 不同资源管理算法的频谱占用率对比

下载: 全尺寸图片幻灯片

表 1 各组群目标的初始运动参数

	坐标 (km)	速度 (m/s)	目标间距离范围 (km)	群体行为	运动属性
群目标1	(18,48)	(0,–205)	[0.03,20]	分散行为	迎面目标
群目标2	(–25,–50)	(165,95)	[0.05,10]	聚集行为	迎面目标
群目标3	(–37,15)	(155,–105)	[0.05,10]	分散行为	迎面目标
群目标4	(37,–57)	(–100,155)	[0.03,10]	聚集行为	非迎面目标

下载: 导出CSV

参考文献(16)

[1]	HAIMOVICH A M, BLUM R S, and CIMINI L J. MIMO radar with widely separated antennas[J]. IEEE Signal Processing Magazine, 2008, 25(1): 116–129. doi: 10.1109/MSP.2008.4408448.
[2]	LI Jian and STOICA P. MIMO radar with colocated antennas[J]. IEEE Signal Processing Magazine, 2007, 24(5): 106–114. doi: 10.1109/MSP.2007.904812.
[3]	STOICA P, LI Jian, and XIE Yao. On probing signal design for MIMO radar[J]. IEEE Transactions on Signal Processing, 2007, 55(8): 4151–4161. doi: 10.1109/TSP.2007.894398.
[4]	GORJI A A, THARMARASA R, BLAIR W D, et al. Multiple unresolved target localization and tracking using colocated MIMO radars[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(3): 2498–2517. doi: 10.1109/TAES.2012.6237605.
[5]	GRECO M S, GINI F, STINCO P, et al. Cognitive radars: On the road to reality: Progress thus far and possibilities for the future[J]. IEEE Signal Processing Magazine, 2018, 35(4): 112–125. doi: 10.1109/MSP.2018.2822847.
[6]	STINCO P, GRECO M S, GINI F, et al. ComRadE: Cognitive passive tracking in symbiotic IEEE 802.22 systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(2): 1023–1034. doi: 10.1109/TAES.2017.2667498.
[7]	SU Yang, CHENG Ting, and HE Zishu. LPI-constrained collaborative transmit beampattern optimization and resource allocation for maneuvering targets tracking in colocated MIMO radar network[J]. Signal Processing, 2023, 207: 108935. doi: 10.1016/j.sigpro.2023.108935.
[8]	YAN Junkun, JIU Bo, LIU Hongwei, et al. Prior knowledge-based simultaneous multibeam power allocation algorithm for cognitive multiple targets tracking in clutter[J]. IEEE Transactions on Signal Processing, 2015, 63(2): 512–527. doi: 10.1109/TSP.2014.2371774.
[9]	YUAN Ye, YI Wei, HOSEINNEZHAD R, et al. Robust power allocation for resource-aware multi-target tracking with colocated MIMO radars[J]. IEEE Transactions on Signal Processing, 2021, 69: 443–458. doi: 10.1109/TSP.2020.3047519.
[10]	SHI Chenguang, WANG Yijie, SALOUS S, et al. Joint transmit resource management and waveform selection strategy for target tracking in distributed phased array radar network[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(4): 2762–2778. doi: 10.1109/TAES.2021.3138869.
[11]	ZHANG Peng, YAN Junkun, PU Wenqiang, et al. Multi-dimensional resource management scheme for multiple target tracking under dynamic electromagnetic environment[J]. IEEE Transactions on Signal Processing, 2024, 72: 2377–2393. doi: 10.1109/TSP.2024.3390119.
[12]	ZHANG Haowei, YAN Junkun, LIU Weijian, et al. Array scheduling with power and bandwidth allocation for simultaneous multibeam tracking low-angle targets in a VHF-MIMO radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(5): 5714–5730. doi: 10.1109/TAES.2023.3265950.
[13]	WU Linlong, MISHRA K V, SHANKAR M R B, et al. Resource allocation in heterogeneously-distributed joint radar-communications under asynchronous Bayesian tracking framework[J]. IEEE Journal on Selected Areas in Communications, 2022, 40(7): 2026–2042. doi: 10.1109/JSAC.2022.3157371.
[14]	SUN Jun, YUAN Ye, GRECO M S, et al. Coordinated deception jamming power scheduling for multijammer systems against distributed radar systems[J]. IEEE Transactions on Radar Systems, 2024, 2: 1076–1088. doi: 10.1109/TRS.2024.3484632.
[15]	SUN Jun, YUAN Ye, GRECO M S, et al. Robust resource allocation for multitarget tracking in multiradar systems with parameter estimation uncertainty[J]. IEEE Transactions on Aerospace and Electronic Systems, 2024, 60(5): 5823–5841. doi: 10.1109/TAES.2024.3397631.
[16]	MOROVATI V and POURKARIMI L. Extension of Zoutendijk method for solving constrained multiobjective optimization problems[J]. European Journal of Operational Research, 2019, 273(1): 44–57. doi: 10.1016/j.ejor.2018.08.018.