Hyperspectral Image Denoising Algorithm via Joint Low-Rank Tensor Decomposition and Product Graph Modeling
-
摘要: 针对高光谱图像(HSI)由于受采集、传输等过程的客观因素影响而存在各种噪声的问题,该文提出一种基于低秩张量分解与克罗内克积乘积图拉普拉斯正则化(LRTDKGLR)的HSI去噪算法。首先,该算法基于HSI的空间和光谱特性,利用图信号处理(GSP)理论分别构建空间图和光谱图,并通过克罗内克积将二者结合为乘积图,用于刻画HSI数据的空间-光谱联合关联特性。随后,通过Tucker分解提取空间和光谱维度的联合低维表示,进一步挖掘HSI图像的结构特征。此外,采用乘积图模型对HSI数据在空间和光谱维度上的分段平滑特性进行建模,从而增强空间-光谱维度间的关联性。随后,将HSI去噪问题转化为一个包含低秩张量分解和克罗内克积的图拉普拉斯正则化(KGLR)的优化问题,并通过增广拉格朗日乘子法(ALM)高效求解。模拟数据和真实数据实验结果表明,该文所提出的LRTDKGLR方法在去噪性能上优于现有方法,验证了其在HSI去噪中的有效性。Abstract:
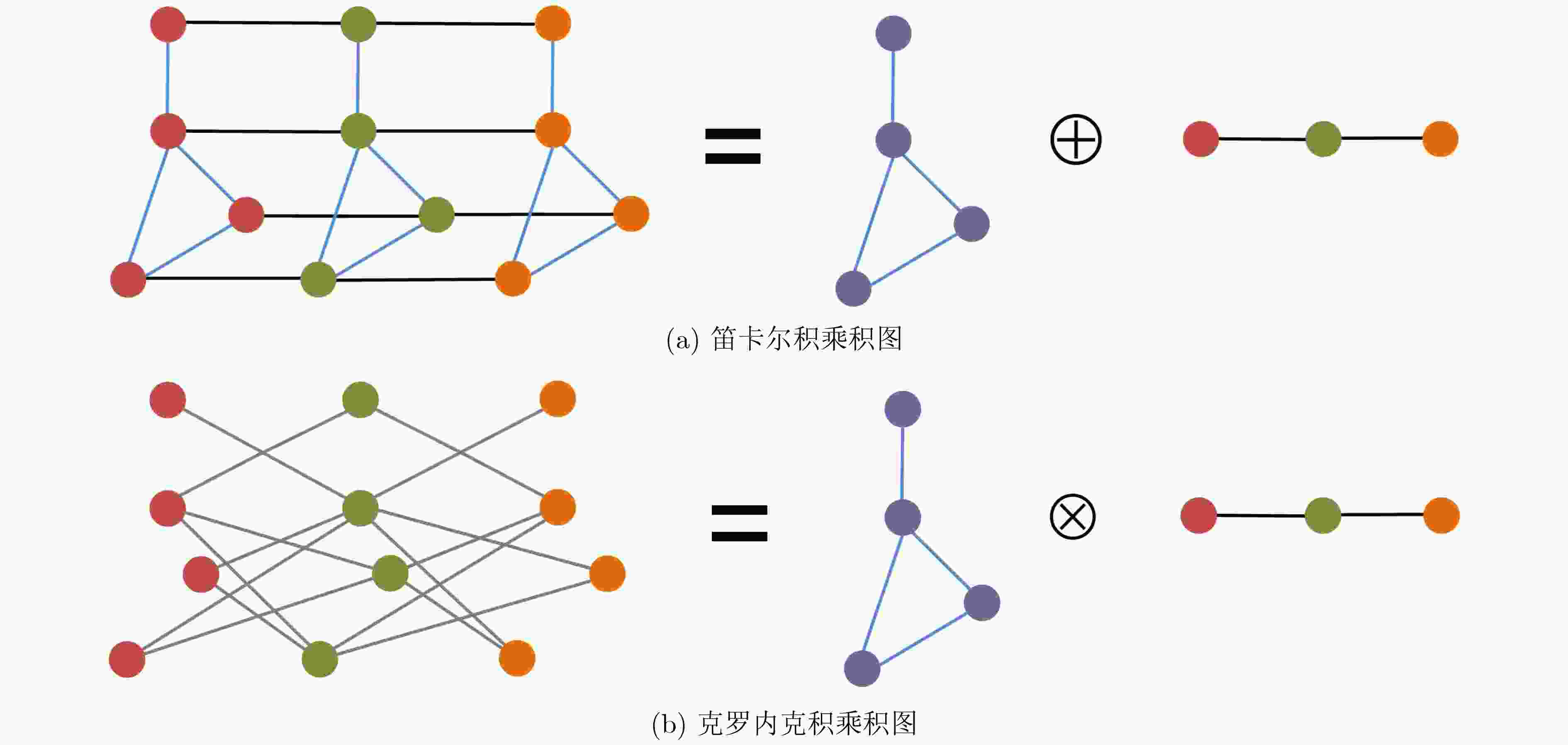
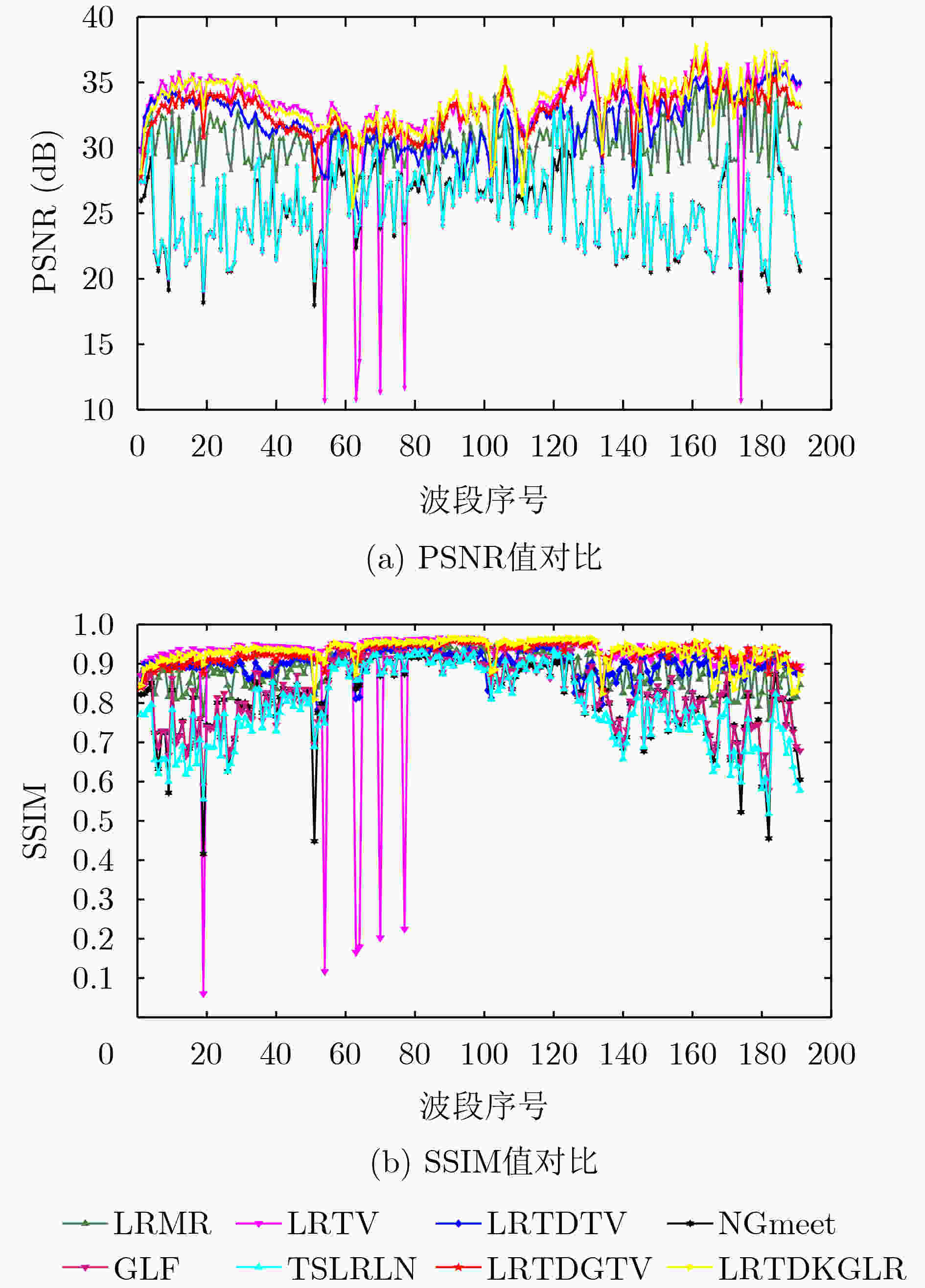
Various types of noise in HyperSpectral Images (HSI) can severely degrade subsequent analysis. To address this problem, this study proposes a denoising framework based on Low-Rank Tensor Decomposition and Kronecker product Graph Laplacian Regularization (LRTDKGLR). Spatial and spectral graphs are constructed using Graph Signal Processing (GSP) and fused into a joint spatial-spectral product graph through the Kronecker product. Tucker decomposition is applied to this product graph to extract a unified low-dimensional representation, capturing the global spatial and spectral structures. A Kronecker Graph Laplacian Regularization (KGLR) term is introduced to enforce piecewise smoothness across both spatial and spectral dimensions, enhancing inter-band coherence. The denoising problem is formulated as an optimization task that integrates low-rank decomposition and graph-based regularization, solved efficiently using an Augmented Lagrangian Multiplier (ALM) approach. Experimental results on simulated and real HSI datasets demonstrate that LRTDKGLR achieves superior performance in edge preservation and noise suppression compared with existing HSI denoising methods. Objective Traditional denoising approaches often fail to simultaneously preserve spatial details and spectral fidelity due to the high dimensionality and complex spectral characteristics of HSI data. This study aims to develop a method that effectively suppresses mixed noise, such as Gaussian and stripe noise, while preserving critical spatial features and edge structures. The proposed approach leverages LRTDKGLR to enhance inter-dimensional correlations between spatial and spectral domains, ensuring improved noise reduction and detail preservation. Additionally, this research investigates an efficient ALM-based optimization strategy to address the HSI denoising problem, providing a more robust solution for noise reduction in high-dimensional, contaminated environments. Methods The proposed LRTDKGLR algorithm performs HSI denoising by effectively modeling spatial-spectral correlations. Separate spatial and spectral graphs are constructed and integrated through the Kronecker product to form a unified product graph representation. This joint graph considers both pixel intensity and the values of neighboring pixels across spatial and spectral dimensions, enabling enhanced denoising through spatial-spectral correlation modeling. Tucker decomposition is applied to extract a low-rank representation that captures global spatial-spectral relationships within the data. This decomposition facilitates effective modeling of the inherent structure of HSI while supporting the denoising process. The KGLR term models smoothness across both spatial and spectral domains, preserving essential spatial details and spectral continuity. The denoising task is formulated as an optimization problem that integrates low-rank tensor decomposition and KGLR. This problem is efficiently solved using the ALM method. The proposed approach achieves a balance between noise suppression and detail preservation, providing an effective solution for HSI denoising in high-dimensional, noisy conditions. Results and Discussions The proposed LRTDKGLR algorithm effectively exploits the inherent spatial and spectral correlations in HSI data. By incorporating a low-rank constraint and leveraging the similarity between adjacent spectral bands, the model enhances its capacity to capture inter-band spectral dependencies. Fig. 2 illustrates the denoising performance of various algorithms under Scenario 3, which combines Gaussian and impulse noise, applied to the 106th band of the Washington DC Mall dataset. A magnified view of a local region is also provided. The LRTV, LRTDTV, and LRTDGTV algorithms remove most of the noise but introduce over-smoothing, resulting in the loss of important edge structures. The NGmeet algorithm performs less effectively due to insufficient utilization of spatial neighborhood relationships. Although the LRMR, GLF, and TSLRLN algorithms reduce part of the noise, residual artifacts persist and over-smoothing remains evident. In contrast, the proposed LRTDKGLR algorithm demonstrates substantially improved denoising performance, supported by both visual comparisons and quantitative metrics.Fig. 3 presents the PSNR and SSIM values across multiple spectral bands under Scenario 3. The proposed method achieves higher performance in both metrics across most bands, indicating enhanced noise suppression and improved preservation of structural details. Numerical results summarized inTable 2 further confirm the effectiveness of the proposed approach, which consistently outperforms competing algorithms under identical conditions, providing superior denoising performance. Additionally,Table 3 shows that LRTDKGLR exceeds two representative deep learning-based methods, HSID-CNN and HSI-SDeCNN, across different noise levels. These findings demonstrate the robustness of the proposed method in the presence of Gaussian noise. Compared with deep learning-based approaches, LRTDKGLR offers practical advantages, including no requirement for pre-training, ease of deployment, and higher computational efficiency, which collectively improve its applicability to real-world HSI denoising tasks.Conclusions This study proposes an HSI denoising algorithm, LRTDKGLR, which integrates low-rank prior knowledge with a product graph model. The algorithm models HSI data as a product graph using GSP theory and applies Tucker decomposition to extract a core tensor and factor matrices, effectively capturing global spatial and spectral correlations. Simultaneously, KGLR is employed to model piecewise smoothness in both spatial and spectral dimensions, enhancing the representation of inter-dimensional relationships within the data. The denoising task is formulated as an optimization problem that combines low-rank tensor decomposition with KGLR constraints and is efficiently solved using the ALM method. Experimental results on simulated and real-world datasets demonstrate that the proposed LRTDKGLR algorithm achieves superior noise suppression while preserving structural details, validating its effectiveness for HSI denoising. -
1 LRTDKGLR算法
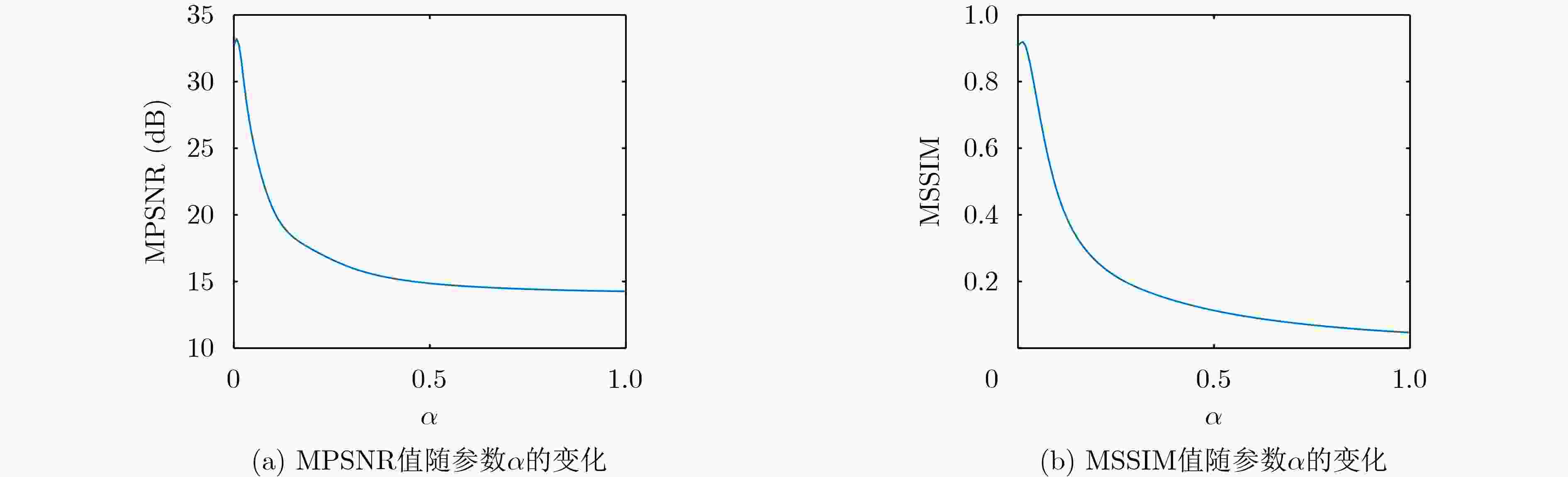
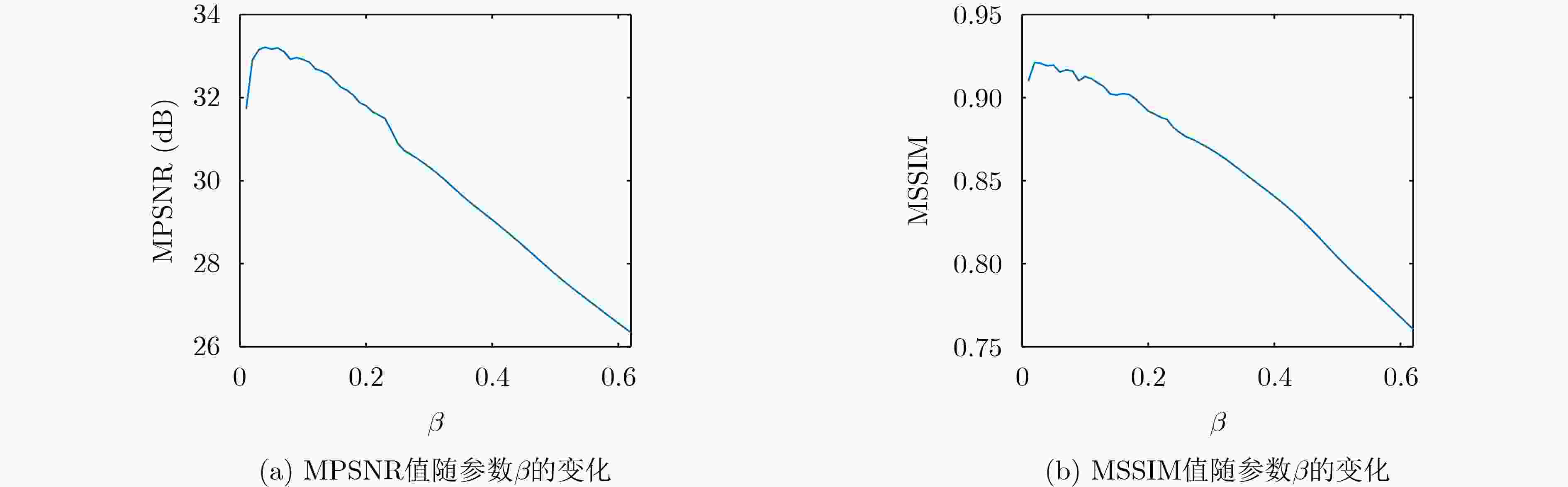
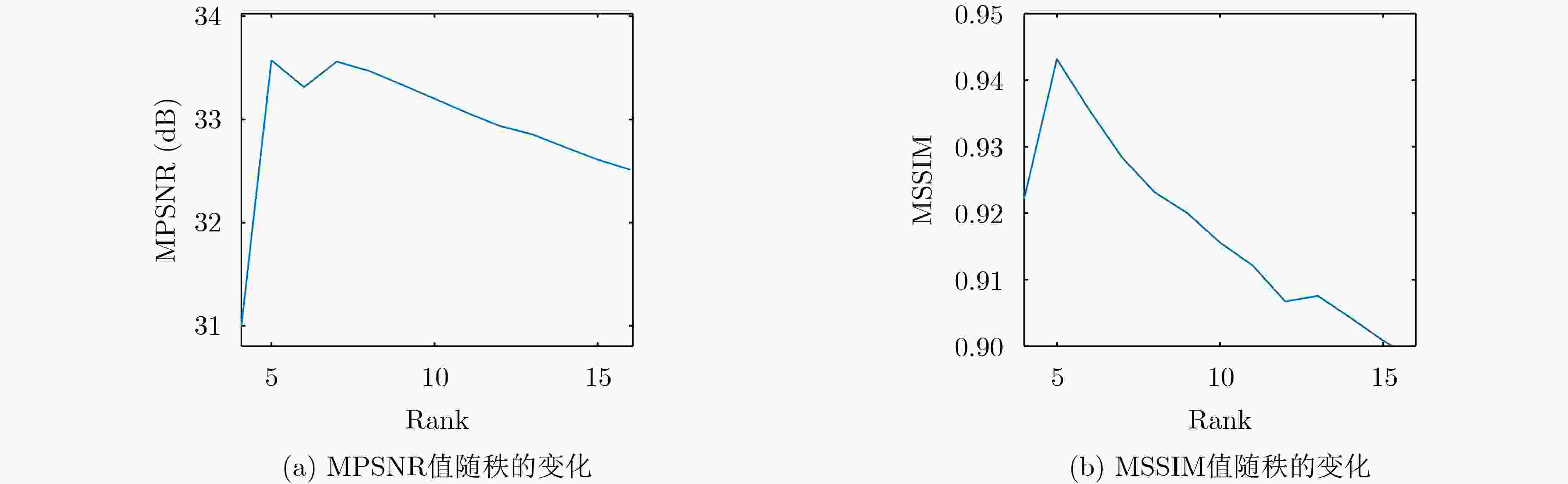
输入:含噪声的HSI数据$ \mathcal{Y} $,秩$ {\text{Rank}} = 5 $, $ \alpha = 0.007 $, $ \beta = 0.13 $。 输出:干净的HSI数据$ {\mathcal{H}^{(k + 1)}} $。 初始化:$ \mathcal{H} = \mathcal{X} = \mathcal{S} = \mathcal{N} = 0 $,$ {\mathcal{C}_1} = {\mathcal{C}_2} = 0 $,克罗内克积乘积图拉普拉斯矩阵${{\boldsymbol{L}}_{\text{K}}}$,惩罚参数$ \rho = {10^{ - 2}} $及其最大值$ {\rho _{\max }} = {10^6} $,惩罚参数
的增长系数$ \gamma = 1.5 $,迭代次数$ k = 0 $,误差因子$ {\varepsilon _1} = {e^{ - 6}},{\varepsilon _2} = {e^{ - 6}} $。迭代: 步骤1 提取HSI频带,构造乘积图,得到图拉普拉斯矩阵; 步骤2 通过式(11)更新$ {\mathcal{H}^{(k + 1)}} $、式(17)更新$ {{\boldsymbol{X}}^{(k + 1)}} $并重构$ {\mathcal{X}^{(k + 1)}} $、式(20)更新$ {\mathcal{S}^{(k + 1)}} $、式(21)更新$ {\mathcal{N}^{(k + 1)}} $、式(23)更新$ {\mathcal{C}}_{_1}^{(k + 1)} $、
式(24)更新$ {\mathcal{C}}_2^{(k + 1)} $;步骤3 更新惩罚参数$ \rho = \min (\gamma \rho ,{\rho _{\max }}) $; 步骤4 检查收敛条件:若满足$ {{\left\| {\mathcal{Y} - {\mathcal{H}^{(k + 1)}} - {\mathcal{S}^{(k + 1)}} - \mathcal{N}} \right\|_{\text{F}}^2} / {\left\| \mathcal{Y} \right\|_{\text{F}}^2}} \le {\varepsilon _1} $且$ \left\| {{\mathcal{X}^{(k + 1)}} - {\mathcal{H}^{(k + 1)}}} \right\|_{\text{F}}^2 \le {\varepsilon _2} $,则结束迭代,否则重复步
骤2。表 1 不同算法在不同情况下对模拟Washington DC Mall数据集的去噪效果对比
指标 LR
MRLR
TVLRT
DTVGLF TSL
RLNNG
meetLRTD
GTVLRTD
KGLR情况1:G=0.075, P=0.15 MPSNR (dB) 32.65 34.23 33.39 23.93 24.02 24.00 34.62 35.01 MSSIM 0.924 4 0.930 7 0.924 9 0.794 4 0.763 7 0.794 7 0.944 3 0.948 1 ERGAS 96.69 128.29 87.30 281.08 281.70 284.09 78.00 97.28 情况2:G=0.1, P=0.2 MPSNR (dB) 30.32 31.84 31.60 21.44 21.52 21.48 32.49 33.44 MSSIM 0.885 5 0.900 6 0.891 4 0.719 8 0.686 8 0.709 7 0.915 0 0.927 4 ERGAS 126.81 164.82 107.31 378.00 378.35 383.59 99.06 111.74 情况3:高斯噪声+脉冲噪声 MPSNR (dB) 30.69 33.04 32.03 25.50 25.49 25.07 32.93 33.89 MSSIM 0.889 4 0.911 3 0.899 1 0.823 4 0.792 2 0.810 8 0.928 1 0.936 0 ERGAS 126.77 189.94 103.64 267.37 268.55 274.91 94.52 84.94 情况4:高斯噪声+脉冲噪声+死线噪声 MPSNR (dB) 30.54 32.95 31.97 25.48 25.51 25.09 32.88 33.83 MSSIM 0.888 2 0.911 3 0.898 3 0.821 2 0.790 8 0.807 3 0.926 2 0.936 0 ERGAS 128.03 195.97 104.40 267.58 268.31 274.78 95.09 85.07 表 2 算法运行时间对比(s)
算法 LR
MRLR
TVLRT
DTVGLF TSL
RLNNG
meetLRTD
GTVLRTD
KGLR运行时间 31.9 142.6 154.6 448.2 24.6 47.2 278.5 69.1 表 3 在Washington DC Mall数据集上,对两种最新深度学习方法进行了定量对比分析
噪声水平
(方差)指标 HSID-CNN[5] HSI-SDeCNN[20] LRTDKGLR $ {\sigma _n} = 25 $ PSNR 33.050 33.444 34.170 (dB) SSIM 0.981 3 0.982 2 0.985 1 (dB) $ {\sigma _n} = 50 $ PSNR 28.968 29.612 31.351 (dB) SSIM 0.953 2 0.960 8 0.972 6 (dB) $ {\sigma _n} = 75 $ PSNR 26.753 27.351 29.187 (dB) SSIM 0.927 3 0.937 1 0.960 2 (dB) $ {\sigma _n} = 100 $ PSNR 25.296 25.753 27.982 (dB) SSIM 0.901 4 0.912 1 0.952 6 (dB) -
[1] WU Yongjun, GAO Guangjun, and CUI Can. Improved wavelet denoising by non-convex sparse regularization under double wavelet domains[J]. IEEE Access, 2019, 7: 30659–30671. doi: 10.1109/access.2019.2903125. [2] YUAN Qiangqiang, ZHANG Liangpei, and SHEN Huanfeng. Hyperspectral image denoising employing a spectral–spatial adaptive total variation model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(10): 3660–3677. doi: 10.1109/tgrs.2012.2185054. [3] HE Wei, ZHANG Hongyan, ZHANG Liangpei, et al. Hyperspectral image denoising via noise-adjusted iterative low-rank matrix approximation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(6): 3050–3061. doi: 10.1109/jstars.2015.2398433. [4] WANG Mengdi, YU Jing, XUE Jinghao, et al. Denoising of hyperspectral images using group low-rank representation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(9): 4420–4427. doi: 10.1109/JSTARS.2016.2531178. [5] YUAN Qiangqiang, ZHANG Qiang, LI Jie, et al. Hyperspectral image denoising employing a spatial–spectral deep residual convolutional neural network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(2): 1205–1218. doi: 10.1109/TGRS.2018.2865197. [6] TIAN Xin, XIE Kun, and ZHANG Hanling. Hyperspectral image denoising via $ {L_0} $ regularized low-rank tucker decomposition[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2024, 17: 3297–3313. doi: 10.1109/jstars.2023.3342408. [7] ZHOU Fang, JIANG Junzheng, and TAY D B. Distributed reconstruction of time-varying graph signals via a modified Newton’s method[J]. Journal of the Franklin Institute, 2022, 359(16): 9401–9421. doi: 10.1016/j.jfranklin.2022.08.059. [8] HU Wei, PANG Jiahao, LIU Xianming, et al. Graph signal processing for geometric data and beyond: Theory and applications[J]. IEEE Transactions on Multimedia, 2022, 24: 3961–3977. doi: 10.1109/tmm.2021.3111440. [9] LEUS G, MARQUES A G, MOURA J M F, et al. Graph signal processing: History, development, impact, and outlook[J]. IEEE Signal Processing Magazine, 2023, 40(4): 49–60. doi: 10.1109/msp.2023.3262906. [10] 潘奕洁. 基于超像素分割与低秩张量近似的高光谱图像去噪算法研究[D]. [硕士论文], 电子科技大学, 2024. doi: 10.27005/d.cnki.gdzku.2024.003710.PAN Yijie. Hyperspectral image denoising based on superpixel segmentation and low-rank tensor approximation[D]. [Master dissertation], University of Electronic Science and Technology of China, 2024. doi: 10.27005/d.cnki.gdzku.2024.003710. [11] XIAO Chuanfu and YANG Chao. RA-HOOI: Rank-adaptive higher-order orthogonal iteration for the fixed-accuracy low multilinear-rank approximation of tensors[J]. Applied Numerical Mathematics, 2024, 201: 290–300. doi: 10.1016/j.apnum.2024.03.004. [12] WRIGHT S J, NOWAK R D, and FIGUEIREDO M A T. Sparse reconstruction by separable approximation[J]. IEEE Transactions on Signal Processing, 2009, 57(7): 2479–2493. doi: 10.1109/tsp.2009.2016892. [13] HE Wei, ZHANG Hongyan, ZHANG Liangpei, et al. Total-variation-regularized low-rank matrix factorization for hyperspectral image restoration[J]. IEEE Transactions on Geoscience Remote Sensing, 2016, 54(1): 178–188. doi: 10.1109/tgrs.2015.2452812. [14] WANG Yao, PENG Jiangjun, ZHAO Qian, et al. Hyperspectral image restoration via total variation regularized low-rank tensor decomposition[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(4): 1227–1243. doi: 10.1109/jstars.2017.2779539. [15] ZHUANG Lina, FU Xiyou, NG M K, et al. Hyperspectral image denoising based on global and nonlocal low-rank factorizations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(12): 10438–10454. doi: 10.1109/tgrs.2020.3046038. [16] HE Chengxun, SUN Le, HUANG Wei, et al. TSLRLN: Tensor subspace low-rank learning with non-local prior for hyperspectral image mixed denoising[J]. Signal Processing, 2021, 184: 108060. doi: 10.1016/j.sigpro.2021.108060. [17] HE Wei, YAO Quanming, LI Chao, et al. Non-local meets global: An iterative paradigm for hyperspectral image restoration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 44(4): 2089–2107. doi: 10.1109/tpami.2020.3027563. [18] 蔡明娇, 蒋俊正, 蔡万源, 等. 张量分解和自适应图全变分的高光谱图像去噪[J]. 西安电子科技大学学报, 2024, 51(2): 157–169. doi: 10.19665/j.issn1001-2400.20230412.CAI Mingjiao, JIANG Junzheng, CAI Wanyuan, et al. Hyperspectral image denoising based on tensor decomposition and adaptive weight graph total variation[J]. Journal of Xidian University, 2024, 51(2): 157–169. doi: 10.19665/j.issn1001-2400.20230412. [19] ZHANG Hongyan, HE Wei, ZHANG Liangpei, et al. Hyperspectral image restoration using low-rank matrix recovery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(8): 4729–4743. doi: 10.1109/tgrs.2013.2284280. [20] MAFFEI A, HAUT J M, PAOLETTI M E, et al. A single model CNN for hyperspectral image denoising[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(4): 2516–2529. doi: 10.1109/TGRS.2019.2952062. [21] HYDICE Urban Dataset[EB/OL]. https://rslab.ut.ac.ir/data, 2024. [22] RASTI B, ULFARSSON M O, and SVEINSSON J R. Hyperspectral subspace identification using SURE[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(12): 2481–2485. doi: 10.1109/lgrs.2015.2485999. -





 下载:
下载:





 下载:
下载:
