多尺度特征注意力网络下的卫星信号识别研究

李云; 杨松林; 邢智童; 吴广富; 马豪

doi:10.11999/JEIT250126

多尺度特征注意力网络下的卫星信号识别研究

doi: 10.11999/JEIT250126 cstr: 32379.14.JEIT250126

李云^{1, 2},
杨松林³,
邢智童^2, ,,
吴广富¹,
马豪¹

1.
重庆邮电大学计算机科学与技术学院重庆 400065
2.
重庆邮电大学通信与信息工程学院重庆 400065
3.
重庆邮电大学人工智能学院重庆 400065

基金项目: 国家自然科学基金 (62301100)，重庆市教委科学研究计划青年项目 (KJQN202200606)，重庆市自然科学基金创新发展联合基金(CSTB2022NSCQ-LZX0055)，重庆市自然科学基金面上项目(CSTB2024NSCQ-MSX0210)

详细信息

作者简介:
李云：男，教授，研究方向为5G/6G移动通信技术、无人机自组网、卫星移动通信、移动边缘计算、人工智能使能的移动通信技术等

杨松林：男，硕士生，研究方向为卫星移动通信、信号调制识别等

邢智童：男，讲师，研究方向为TCP性能分析与改进、无线局域网自组织网络、无线Mesh 网络等

吴广富：男，高级工程师，研究方向为未来移动通信基带算法、多址接入算法、图像智能处理算法等

马豪：男，硕士生，研究方向为卫星移动通信、信号调制识别等

通讯作者:
邢智童　xingzhitong@cqupt.edu.cn

中图分类号: TN911.7
计量
- 文章访问数: 260
- HTML全文浏览量: 114
- PDF下载量: 64
- 被引次数: 0
出版历程
- 收稿日期: 2025-03-04
- 修回日期: 2025-05-30
- 网络出版日期: 2025-06-18
- 刊出日期: 2025-06-30

Study on Satellite Signal Recognition with Multi-scale Feature Attention Network

LI Yun^{1, 2},
YANG Songlin³,
XING Zhitong^{2
, ,},
WU Guangfu¹,
MA Hao¹

1.
School of Computer Science and Technology, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
2.
School of Communication and Information Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
3.
School of Artificial intelligence, Chongqing University of Posts and Telecommunications, Chongqing 400065, China

Funds: The National Natural Science Foundation of China (62301100), Chongqing Municipal Education Commission’s Youth Project for Scientific Research (KJQN202200606), Chongqing Natural Science Foundation for Innovative Development Joint Fund (CSTB2022NSCQ-LZX0055), Chongqing Natural Science Foundation General Program (CSTB2024NSCQ-MSX0210)

摘要

摘要: 针对卫星通信信号调制识别难题以及忽略不同频率和时间尺度特征的融合问题，该文提出多尺度特征注意力网络模型。该模型融合去噪卷积模块和多尺度全局感知模块，利用多尺度膨胀卷积和空间金字塔池化，结合高效通道注意力机制，有效捕捉不同频率和时间尺度特征。实验表明，在典型莱斯信道及数字视频广播卫星第2代标准信号制式下，该模型在[0, 5] dB区间内，对QPSK等卫星典型调制信号的类间识别率达到96.8%，性能优于传统模型的同时，参数量以及单周期训练时间显著减少，并且在低信噪比下仍保持高识别精度，充分验证了模型算法的有效性。
- 卫星通信 /
- 信号识别 /
- 多尺度特征 /
- 通道注意力机制 /
- 深度学习
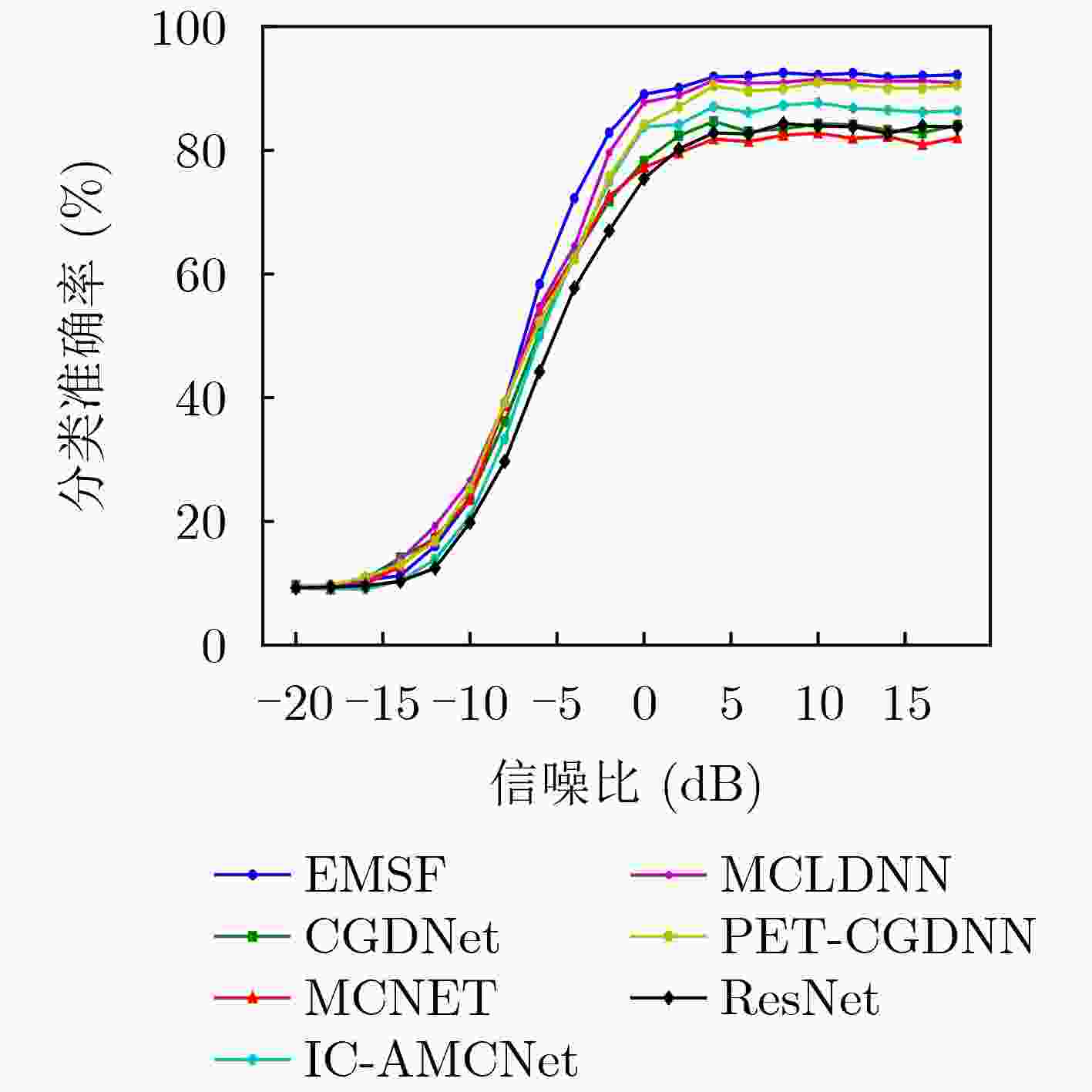
Abstract: Objective Automatic modulation recognition of satellite communication signals is essential for communication security, signal monitoring, and efficient spectrum management. Traditional methods face limitations in handling non-stationary signals, require substantial prior knowledge, and often incur high computational costs. To address these issues, this study proposes an Enhanced Multi-Scale Feature Attention Network (EMSF) for satellite signal recognition. EMSF is designed to deliver high recognition accuracy, robustness under noisy conditions, and computational efficiency, making it suitable for deployment on resource-constrained platforms. This model contributes to satellite communication, signal processing, and deep learning by improving the reliability and efficiency of automatic signal recognition. Methods The EMSF integrates four key components to effectively capture and classify satellite signals: Data Augmentation (DA), a denoising convolution module, a multi-scale global perception module, and an Efficient Channel Attention (ECA) mechanism. DA expands the training dataset via rotational transformations to improve generalization and robustness. A deep residual network with soft thresholding selectively suppresses noise while preserving key signal features, enhancing performance under low Signal-to-Noise Ratio (SNR) conditions. The multi-scale global perception module combines dilated convolutions with Spatial Pyramid Pooling (SPP) to extract both global and local contextual information across frequency and time scales, enabling the model to detect subtle signal variations. The ECA module learns channel-wise dependencies to emphasize informative features and suppress irrelevant ones, improving classification accuracy. The model is trained using the Adam optimizer with an adaptive learning rate and a cross-entropy loss function. Custom callbacks monitor validation loss and dynamically adjust the learning rate during training. Results and Discussions Extensive experiments were conducted using simulated satellite signals across various modulation types and SNR levels. The EMSF model consistently outperforms state-of-the-art models—including MCLDNN, MCNet, CGDNet, IC-AMCNet, PET-CGDNN, and ResNet—in terms of classification accuracy, parameter efficiency, and computational cost. Model accuracy improves with increasing SNR, maintaining strong performance even under low SNR conditions (Fig. 3). Notably, EMSF achieves nearly 90% accuracy for QAM16 and QAM64 at 0 dB SNR, demonstrating its ability to detect subtle signal variations. Compared with other models, EMSF achieves higher accuracy using significantly fewer parameters and shorter training time (Table 1; Fig. 5). Ablation experiments further verify the contribution of each component, with the denoising convolution module, SPP layer, and data augmentation strategy each yielding measurable performance gains (Table 2; Fig. 6). Conclusions The proposed EMSF demonstrates high accuracy, robustness under noisy conditions, and computational efficiency in satellite signal recognition. Its suitability for deployment in resource-constrained devices highlights its practical applicability. The EMSF model contributes to the advancement of satellite communication and offers a foundation for further research in signal processing and deep learning.
- Satellite communication /
- Signal recognition /
- Multi-scale feature /
- Channel attention mechanism /
- Deep learning

HTML全文

图 1 典型卫星信号传输链路示例流程图

下载: 全尺寸图片幻灯片

图 2 网络模型结构

下载: 全尺寸图片幻灯片

图 3 识别准确率

下载: 全尺寸图片幻灯片

图 4 混淆矩阵

下载: 全尺寸图片幻灯片

图 5 准确率曲线

下载: 全尺寸图片幻灯片

图 6 消融实验

下载: 全尺寸图片幻灯片

表 1 模型性能对比

模型名称	参数量	总训练时间(s)	单周期训练时间(s)	测试集损失值	测试集准确率(%)	最高准确率(%)
EMSF	17319	1682.65	10.83	1.08	59.89	91.66
CGDNet	124676	828.68	5.26	1.10	56.27	82.25
MCNet	121611	2597.63	23.78	1.14	55.92	81.86
IC-AMCNet	1264011	865.56	5.72	1.14	58.65	84.92
MCLDNN	406199	1410.47	13.78	1.09	59.32	91.36
PET-CGDNN	71487	552.11	4.79	1.11	57.27	90.12
ResNet	3098283	2348.81	17.44	1.21	53.98	82.78

下载: 导出CSV

表 2 消融实验

去除模块	准确率(%)
ECA	59.12
金字塔池化层	57.04
多尺度全局感知模块	58.78
数据增强	55.25
去噪卷积模块	51.42

下载: 导出CSV

参考文献(21)

[1]	SMITH A, EVANS M, and DOWNEY J. Modulation classification of satellite communication signals using cumulants and neural networks[C]. 2017 Cognitive Communications for Aerospace Applications Workshop (CCAA), Cleveland, USA, 2017: 1–8. doi: 10.1109/CCAAW.2017.8001878.
[2]	冯晓东, 曾军. 基于决策论的数字调制信号识别方法[J]. 电子科技, 2015, 28(4): 124–127. doi: 10.16180/j.cnki.issn1007-7820.2015.04.033. FENG Xiaodong and ZENG Jun. A method for digital modulation recognition based on decision theory[J]. Electronic Science and Technology, 2015, 28(4): 124–127. doi: 10.16180/j.cnki.issn1007-7820.2015.04.033.
[3]	HAZZA A, SHOAIB M, ALSHEBEILI S A, et al. An overview of feature-based methods for digital modulation classification[C]. 2013 1st International Conference on Communications, Signal Processing, and Their Applications (ICCSPA), Sharjah, United Arab Emirates, 2013: 1–6. doi: 10.1109/ICCSPA.2013.6487244.
[4]	闫文康, 闫毅, 范亚楠, 等. 基于小波变换熵值及高阶累积量联合的卫星信号调制识别算法[J]. 空间科学学报, 2021, 41(6): 968–975. doi: 10.11728/cjss2021.06.968. YAN Wenkang, YAN Yi, FAN Yanan, et al. A modulation recognition algorithm based on wavelet transform entropy and high-order cumulant for satellite signal modulation[J]. Chinese Journal of Space Science, 2021, 41(6): 968–975. doi: 10.11728/cjss2021.06.968.
[5]	杨洪娟, 时统志, 李博, 等. 基于联合特征参数的卫星单-混信号调制识别研究[J]. 电子与信息学报, 2022, 44(10): 3499–3506. doi: 10.11999/JEIT210768. YANG Hongjuan, SHI Tongzhi, LI Bo, et al. Research on satellite single-mixed signal modulation recognition based on joint feature parameters[J]. Journal of Electronics & Information Technology, 2022, 44(10): 3499–3506. doi: 10.11999/JEIT210768.
[6]	ZHANG Xueqin, LUO Zhongqiang, XIAO Wenshi, et al. Deep learning-based modulation recognition for MIMO systems: Fundamental, methods, challenges[J]. IEEE Access, 2024, 12: 112558–112575. doi: 10.1109/ACCESS.2024.3440350.
[7]	袁德品, 赵亮, 葛宪生. 基于复数深度神经网络的电磁信号调制识别[J]. 电子科技, 2025, 38(3): 1–6. doi: 10.16180/j.cnki.issn1007-7820.2025.03.001. YUAN Depin, ZHAO Liang, and GE Xiansheng. Electromagnetic signal modulation recognition based on complex-valued deep neural network[J]. Electronic Science and Technology, 2025, 38(3): 1–6. doi: 10.16180/j.cnki.issn1007-7820.2025.03.001.
[8]	ELSAGHEER M M and RAMZY S M. A hybrid model for automatic modulation classification based on residual neural networks and long short term memory[J]. Alexandria Engineering Journal, 2023, 67: 117–128. doi: 10.1016/j.aej.2022.08.019.
[9]	O’SHEA T J, ROY T, and CLANCY T C. Over-the-air deep learning based radio signal classification[J]. IEEE Journal of Selected Topics in Signal Processing, 2018, 12(1): 168–179. doi: 10.1109/JSTSP.2018.2797022.
[10]	LOTFY M, ESSAI M, and ATALLAH H. Automatic modulation classification: Convolutional deep learning neural networks approaches[J]. SVU-International Journal of Engineering Sciences and Applications, 2023, 4(1): 48–54. doi: 10.21608/svusrc.2022.162662.1076.
[11]	XU Jialang, LUO Chunbo, PARR G, et al. A spatiotemporal multi-channel learning framework for automatic modulation recognition[J]. IEEE Wireless Communications Letters, 2020, 9(10): 1629–1632. doi: 10.1109/LWC.2020.2999453.
[12]	HUYNH-THE T, HUA C H, PHAM Q V, et al. MCNet: An efficient CNN architecture for robust automatic modulation classification[J]. IEEE Communications Letters, 2020, 24(4): 811–815. doi: 10.1109/LCOMM.2020.2968030.
[13]	张承畅, 李晓梦, 李吉利, 等. 基于 JDA-BP 网络的 MQAM 信号调制识别[J]. 实验技术与管理, 2024, 41(5): 31–37. doi: 10.16791/j.cnki.sjg.2024.05.005. ZHANG Chengchang, LI Xiaomeng, LI Jili, et al. Recognition method for multiple quadrature amplitude modulation signals based on the JDA-BP network[J]. Experimental Technology and Management, 2024, 41(5): 31–37. doi: 10.16791/j.cnki.sjg.2024.05.005.
[14]	PACAL I, CELIK O, BAYRAM B, et al. Enhancing EfficientNetv2 with global and efficient channel attention mechanisms for accurate MRI-Based brain tumor classification[J]. Cluster Computing, 2024, 27(8): 11187–11212. doi: 10.1007/s10586-024-04532-1.
[15]	ZHAO Minghang, ZHONG Shisheng, FU Xuyun, et al. Deep residual shrinkage networks for fault diagnosis[J]. IEEE Transactions on Industrial Informatics, 2020, 16(7): 4681–4690. doi: 10.1109/TII.2019.2943898.
[16]	YU F and KOLTUN V. Multi-scale context aggregation by dilated convolutions[C]. The 4th International Conference on Learning Representations, San Juan, Puerto Rico, 2015.
[17]	HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Spatial pyramid pooling in deep convolutional networks for visual recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1904–1916. doi: 10.1109/TPAMI.2015.2389824.
[18]	NJOKU J N, MOROCHO-CAYAMCELA M E, and LIM W. CGDNet: Efficient hybrid deep learning model for robust automatic modulation recognition[J]. IEEE Networking Letters, 2021, 3(2): 47–51. doi: 10.1109/LNET.2021.3057637.
[19]	HERMAWAN A P, GINANJAR R R, KIM D S, et al. CNN-based automatic modulation classification for beyond 5G communications[J]. IEEE Communications Letters, 2020, 24(5): 1038–1041. doi: 10.1109/LCOMM.2020.2970922.
[20]	ZHANG Fuxin, LUO Chunbo, XU Jialang, et al. An efficient deep learning model for automatic modulation recognition based on parameter estimation and transformation[J]. IEEE Communications Letters, 2021, 25(10): 3287–3290. doi: 10.1109/LCOMM.2021.3102656.
[21]	LIU Xiaoyu, YANG Diyu, and EL GAMAL A. Deep neural network architectures for modulation classification[C]. 2017 51st Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, USA, 2017: 915–919. doi: 10.1109/ACSSC.2017.8335483.