Federated Deep Reinforcement Learning-based Intelligent Routing Design for LEO Satellite Networks
-
摘要: 低轨卫星通信网络拓扑结构动态变化,传统地面网络路由方法难以直接适用,同时由于卫星星载资源受限,基于人工智能的路由方法通常学习效率较低,而协同训练需要数据共享和传输,难度大且存在数据安全风险。为此,针对上述挑战,该文提出一种基于卫星分簇的多智能体联邦深度强化学习路由方法。首先,设计了结合网络拓扑、通信和能耗的低轨卫星通信网络路由模型;然后,基于每颗卫星的平均连接度将星座节点划分为多个簇,在簇内采用联邦深度强化学习框架,通过簇内卫星协同共享模型参数,共同训练对应簇内的全局模型,以最大化网络能量效率。最后,仿真结果表明,该文所设计方法对比Sarsa、MAD2QN和REINFORCE 3种基准方法,网络平均吞吐量分别提高83.7%, 19.8%和14.1%;数据包平均跳数分别减少25.0%, 18.9%和9.1%;网络能量效率分别提升55.6%, 42.9%和45.8%。Abstract:
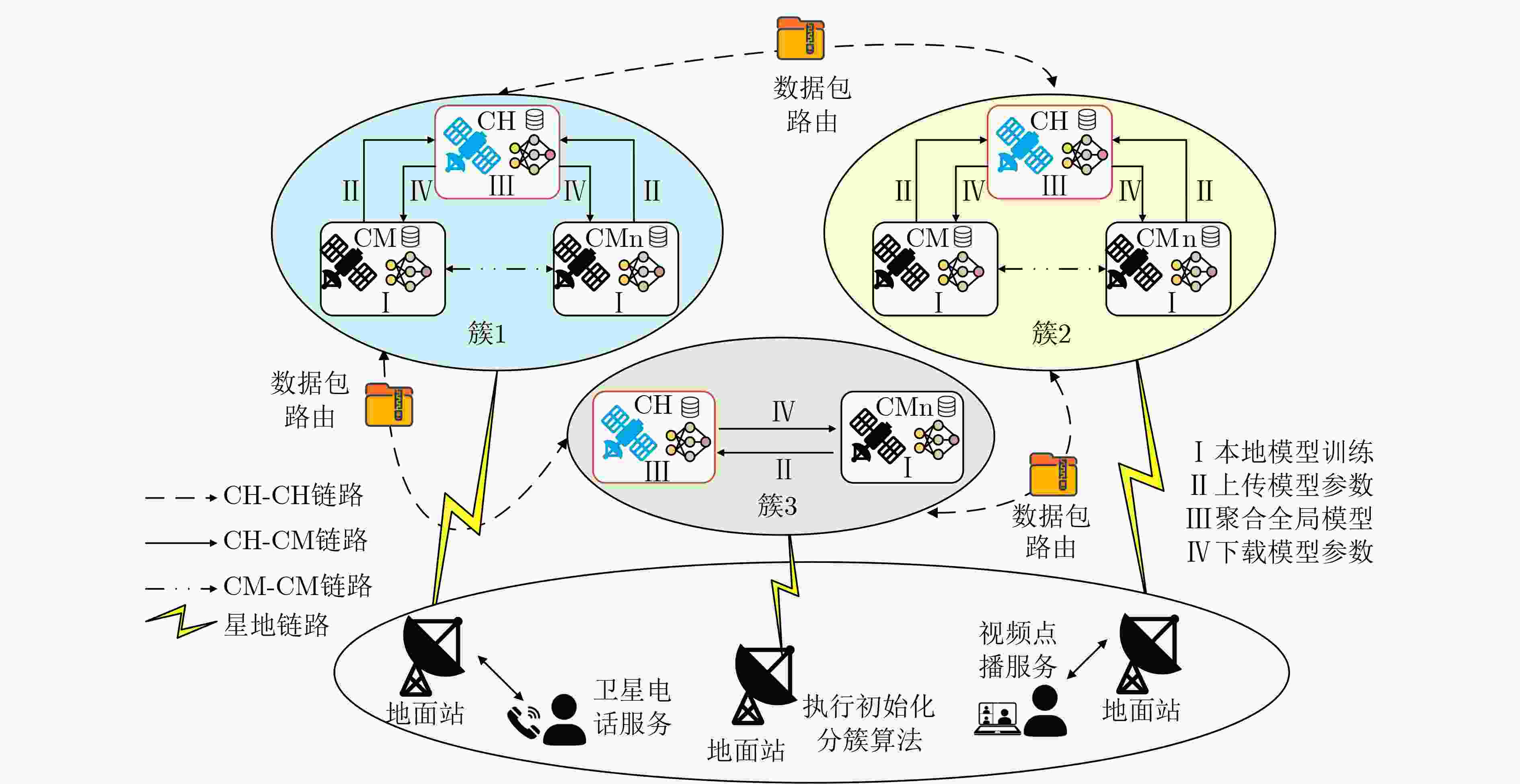
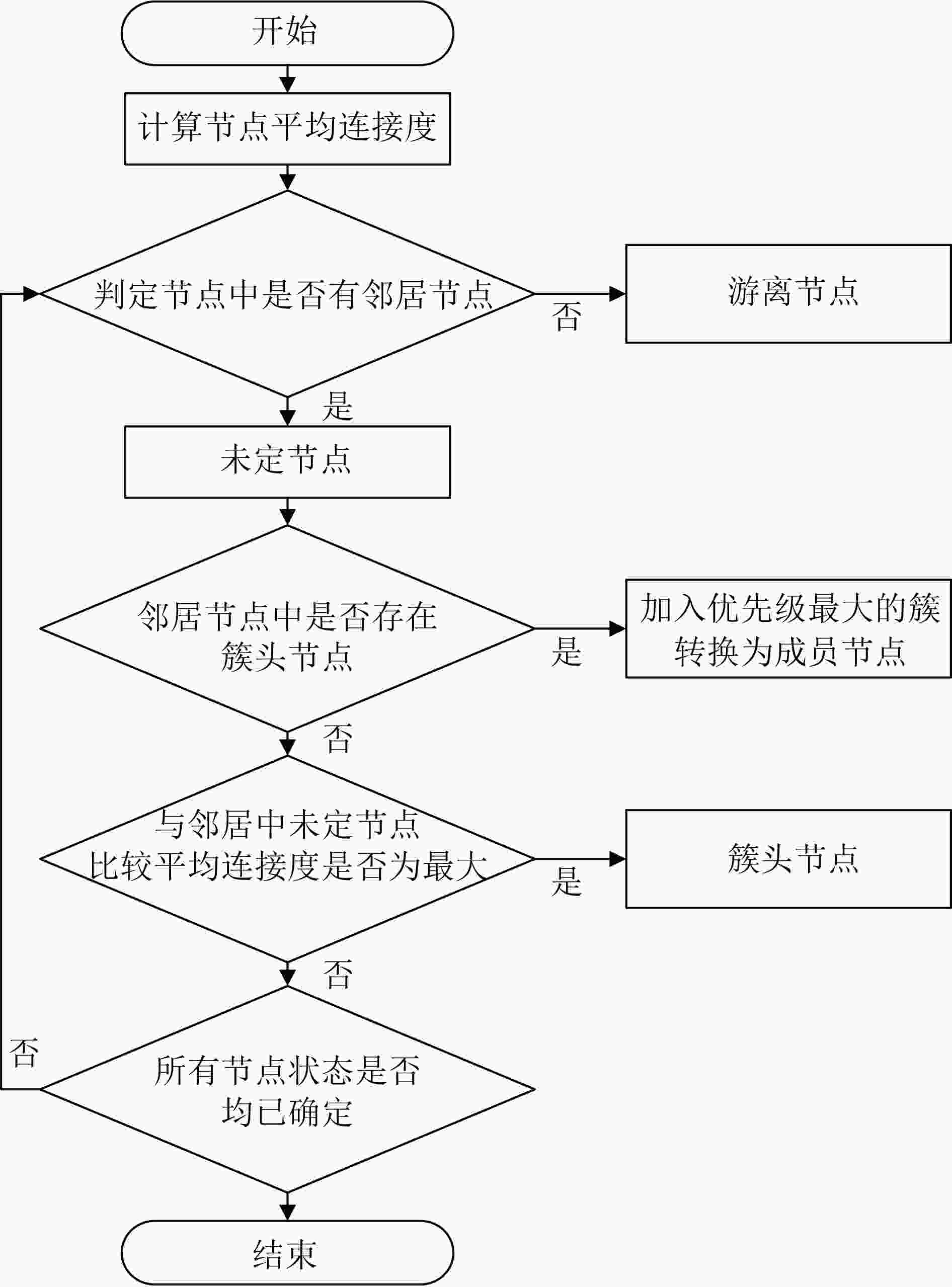
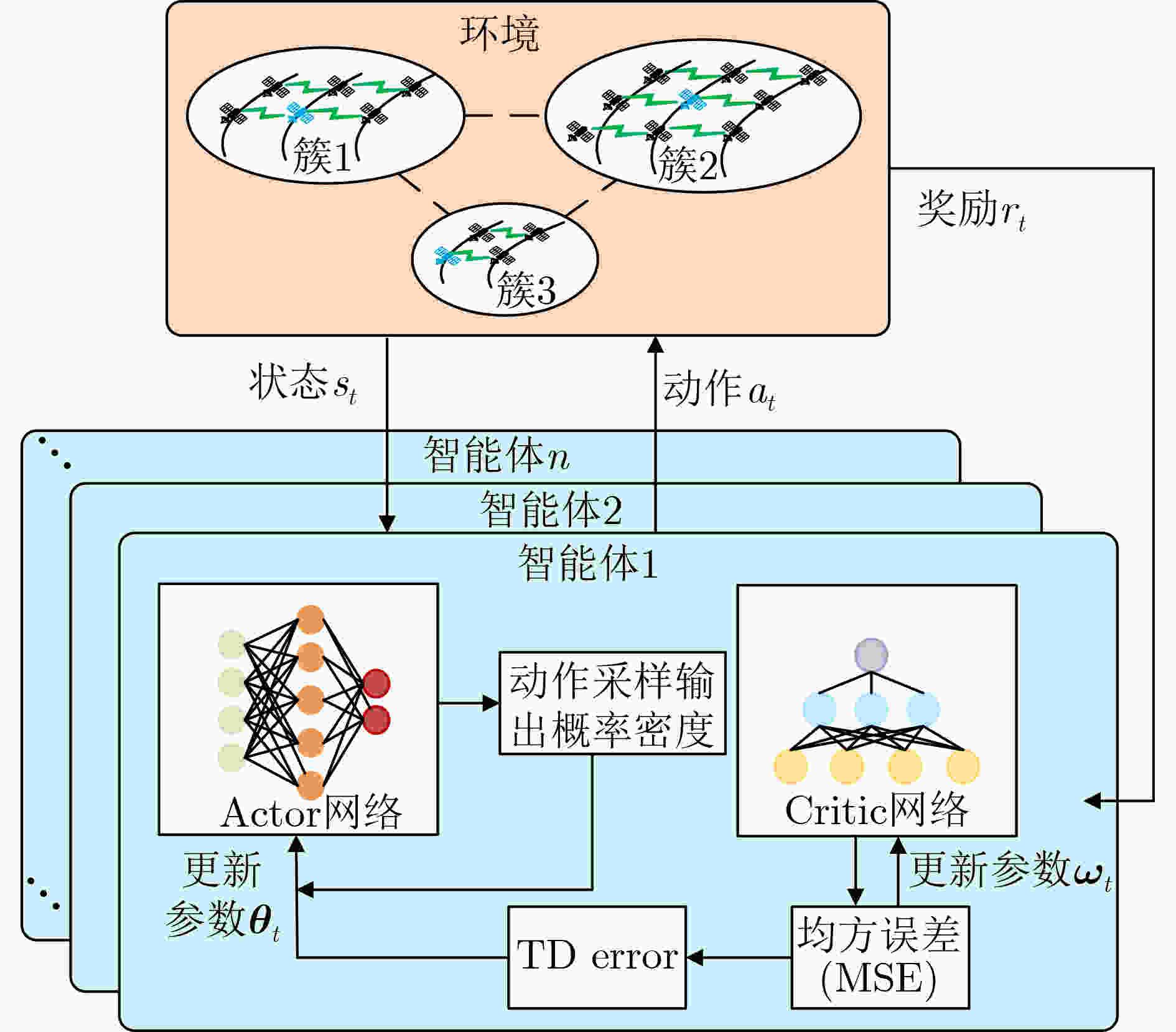
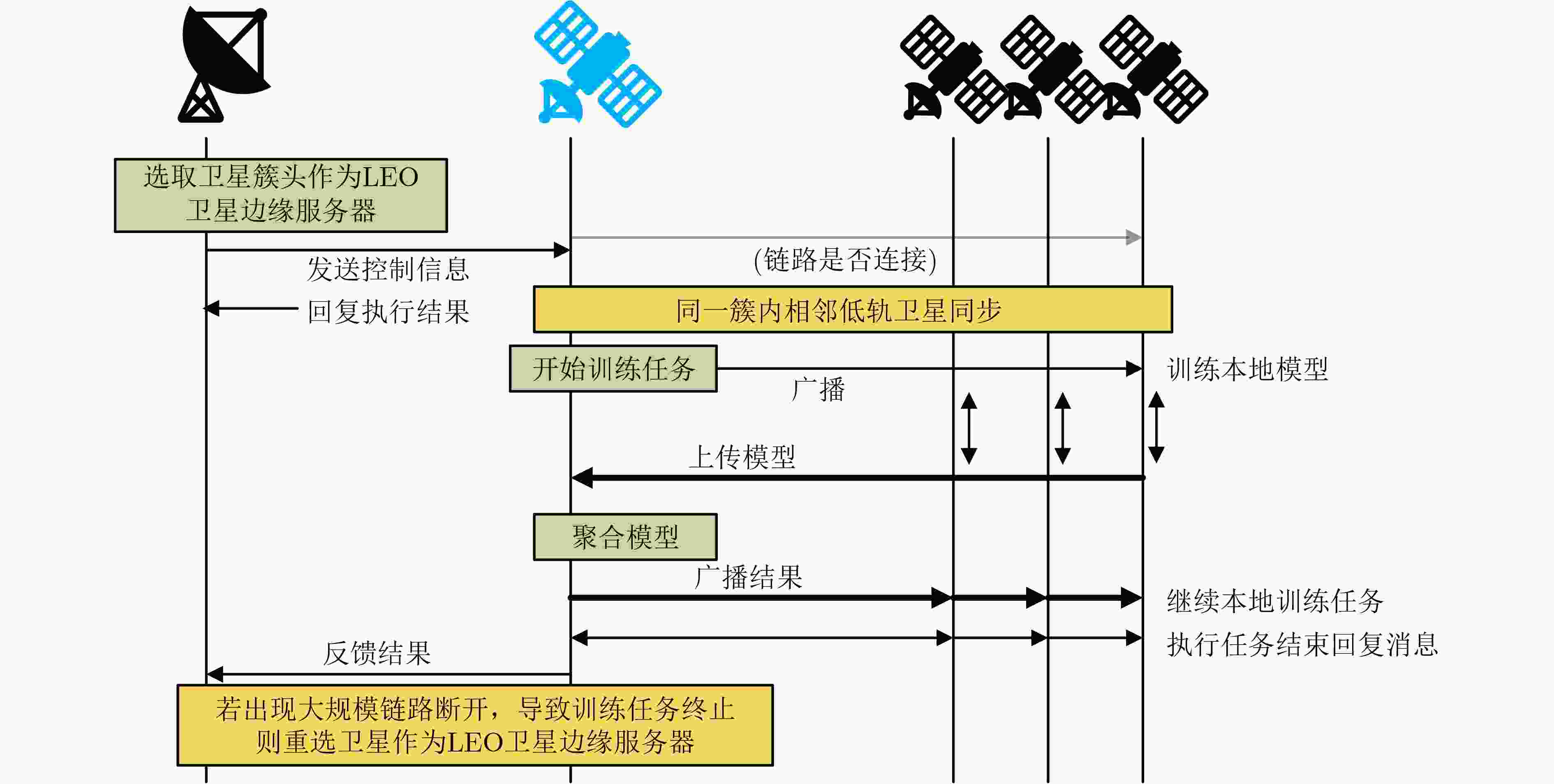
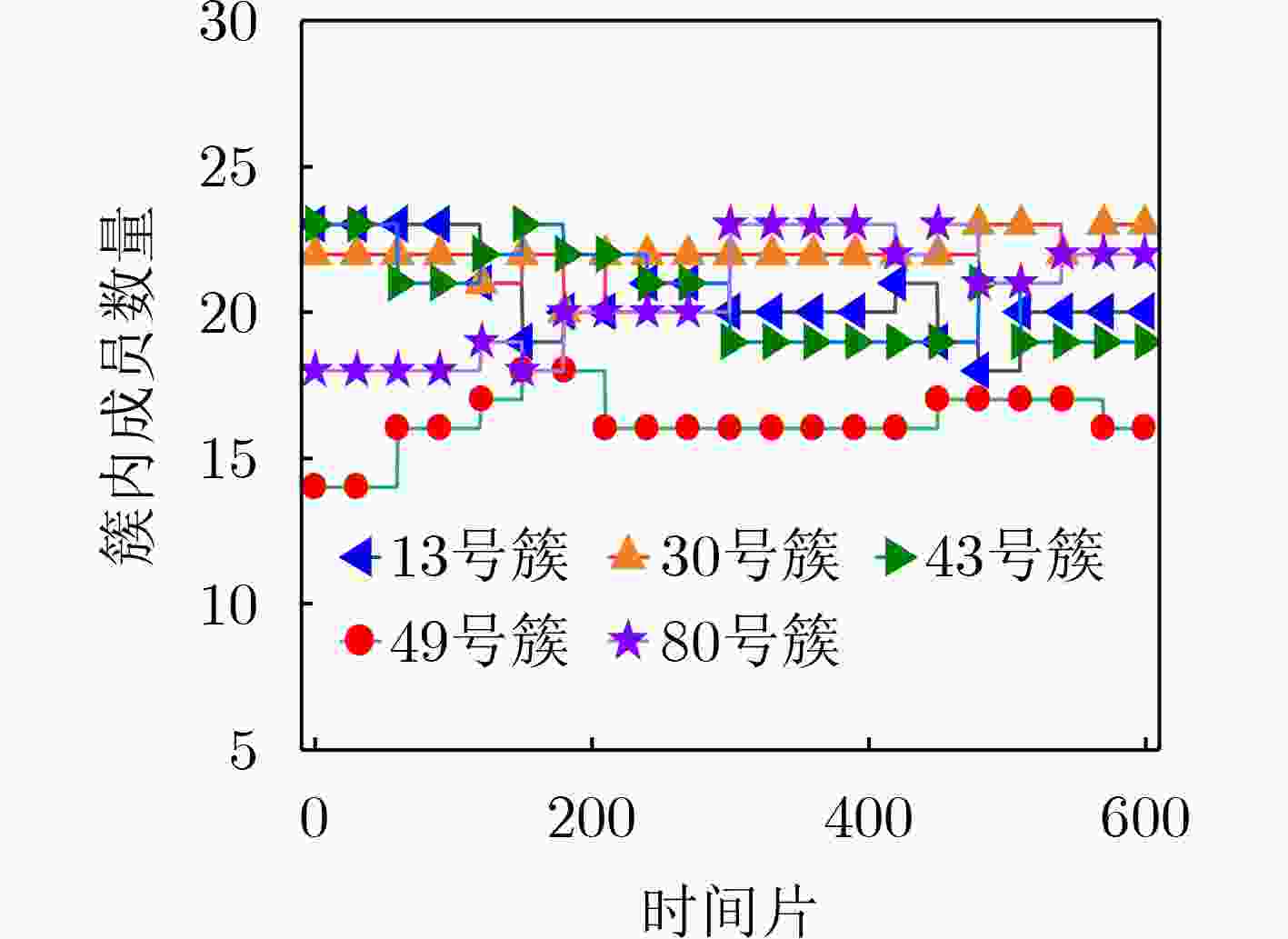
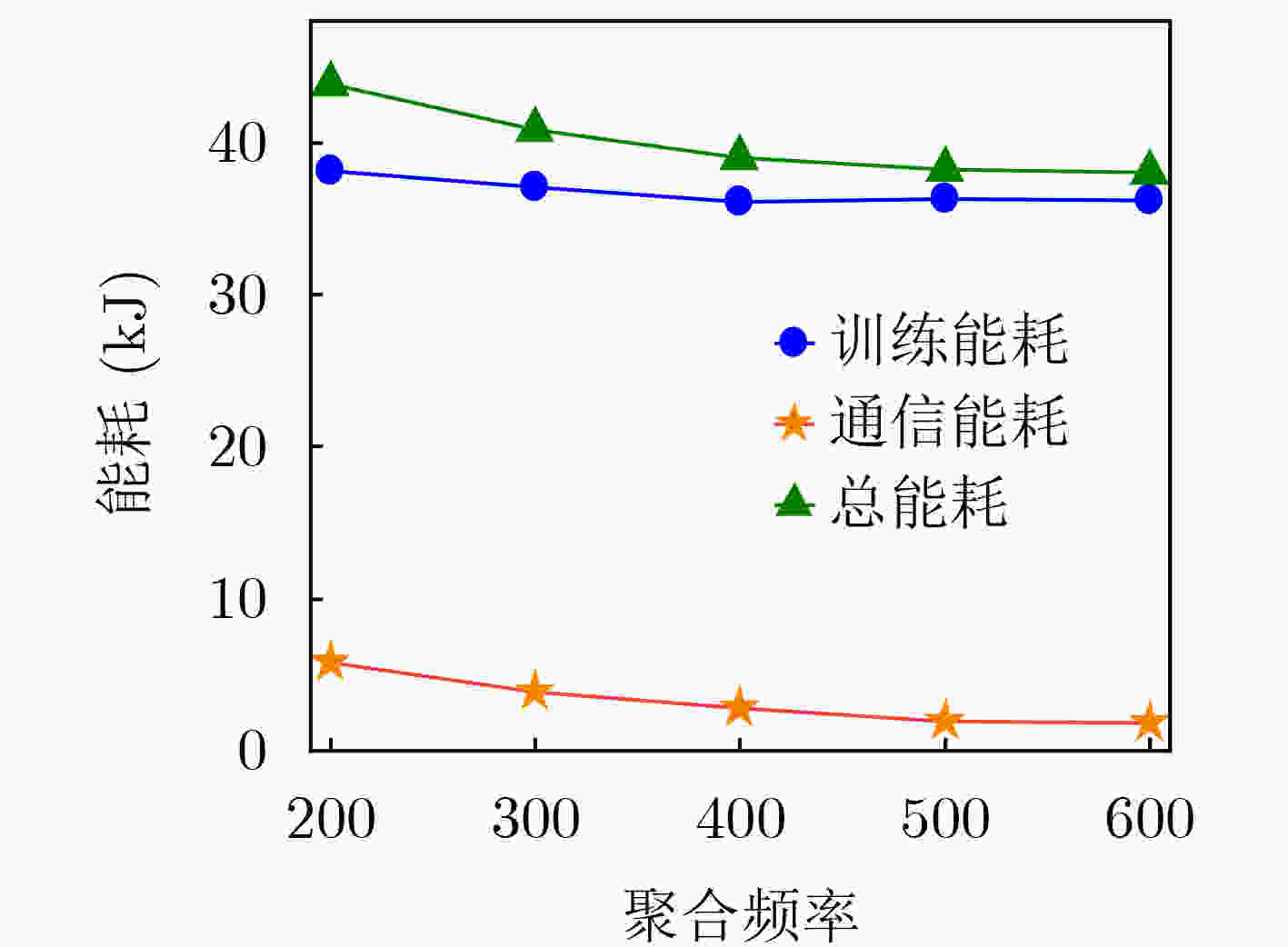
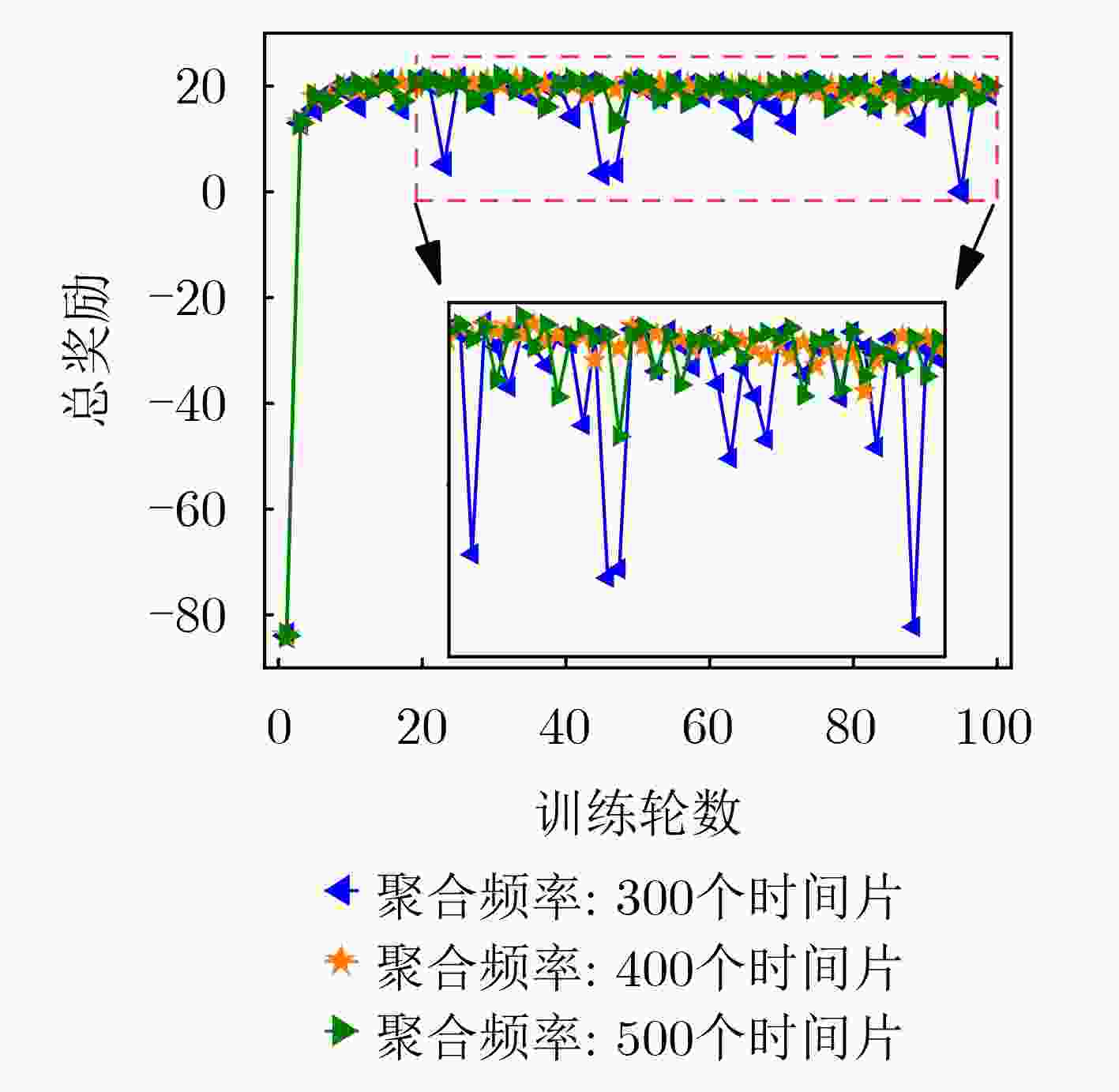
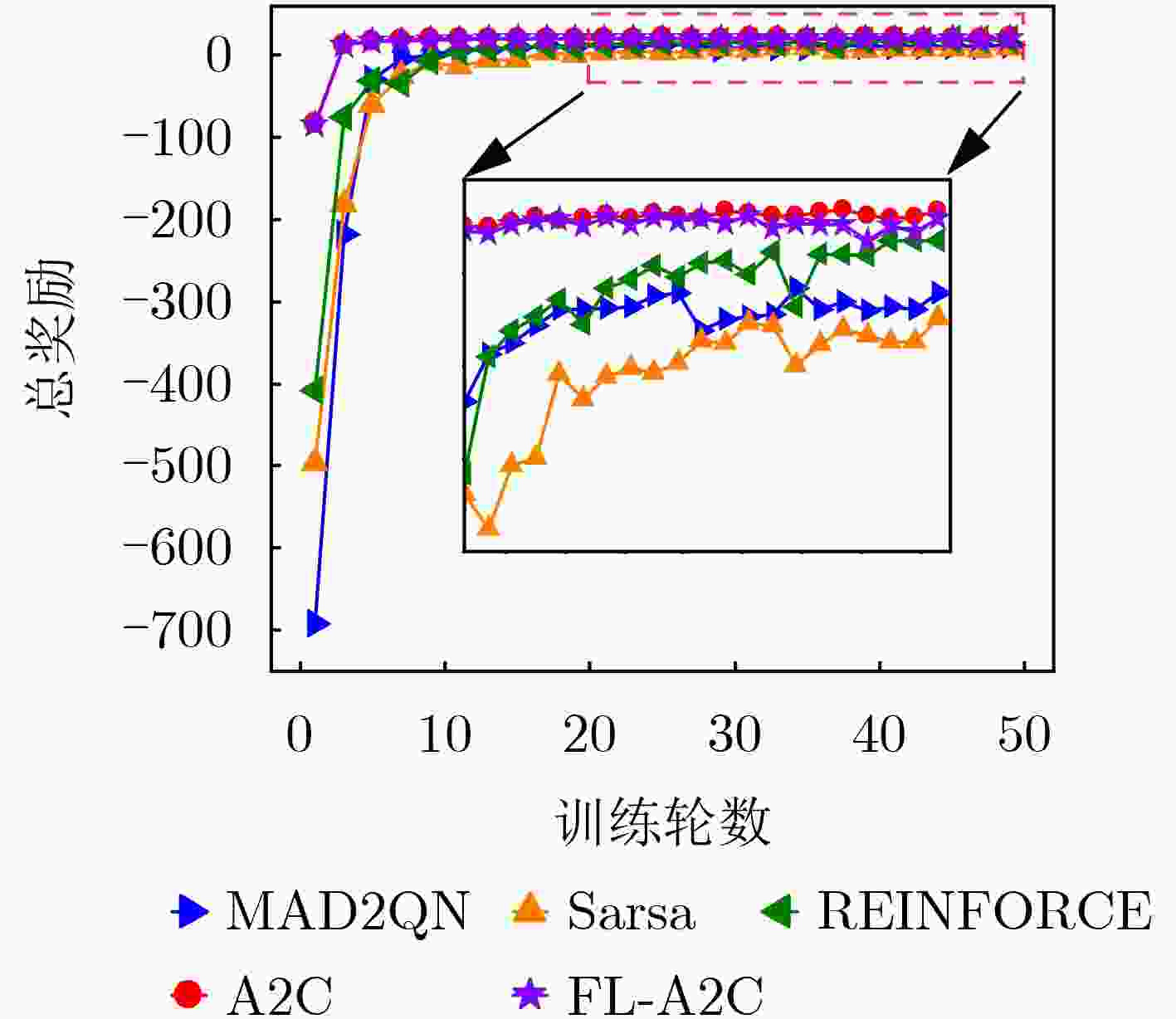
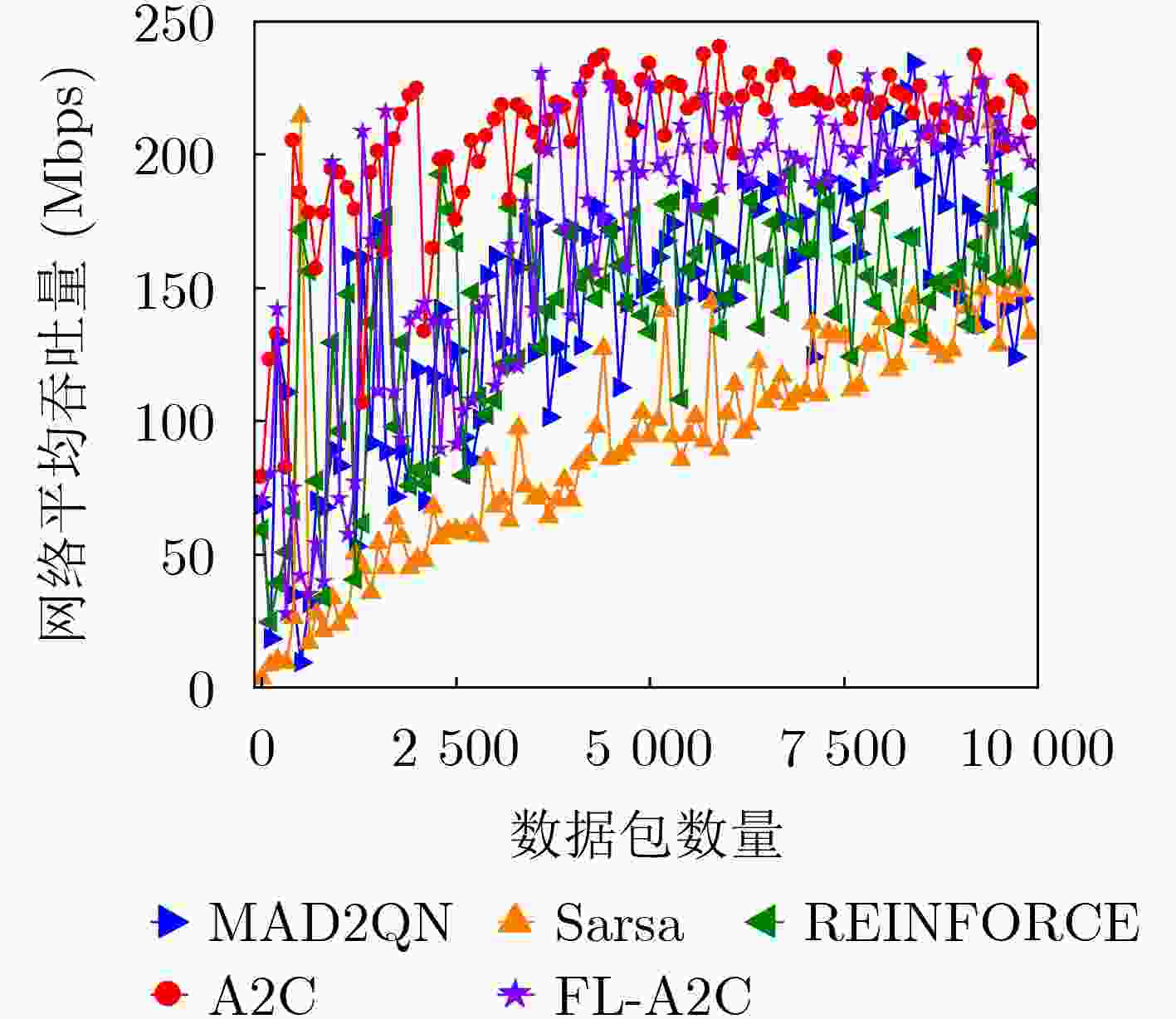
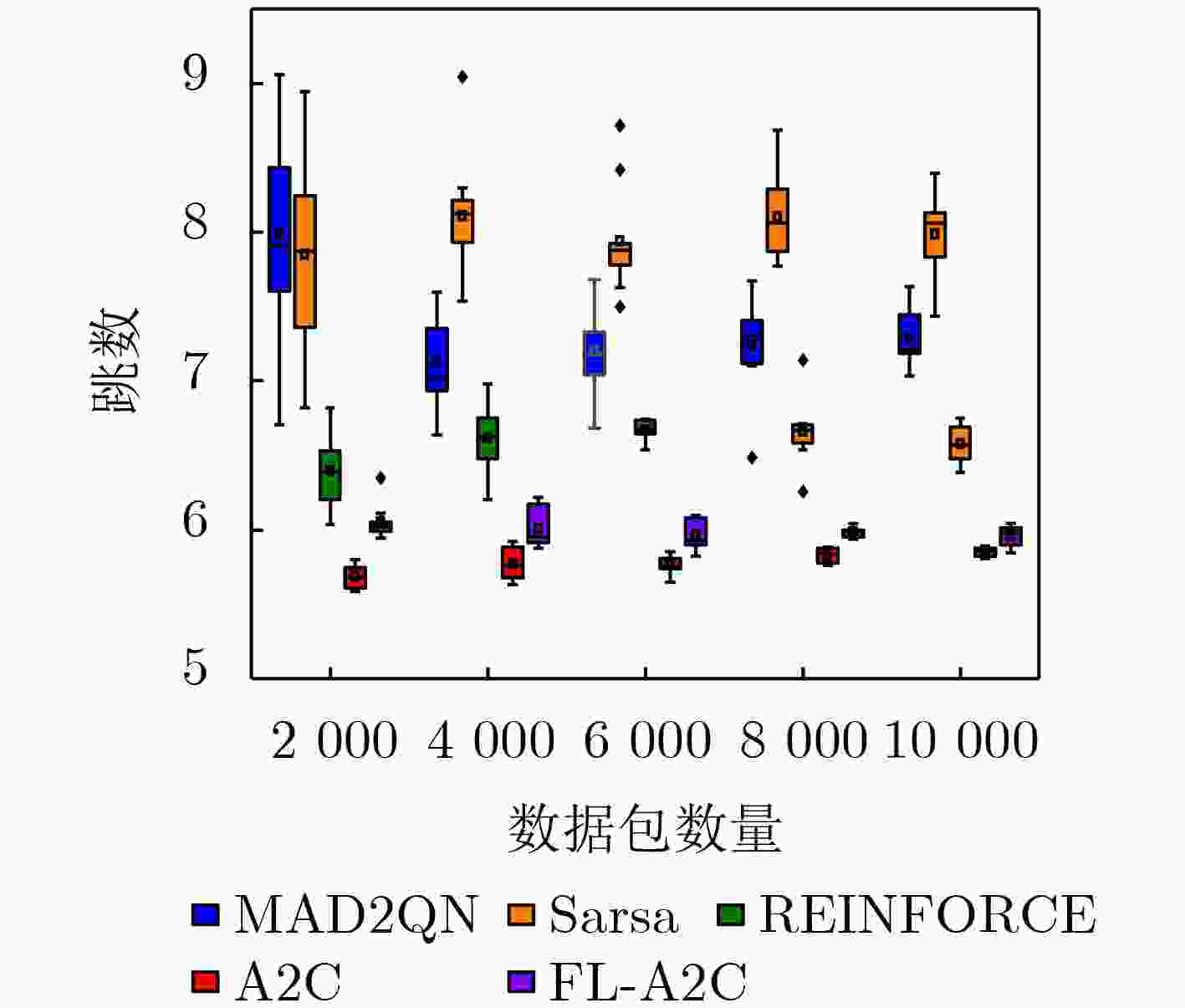
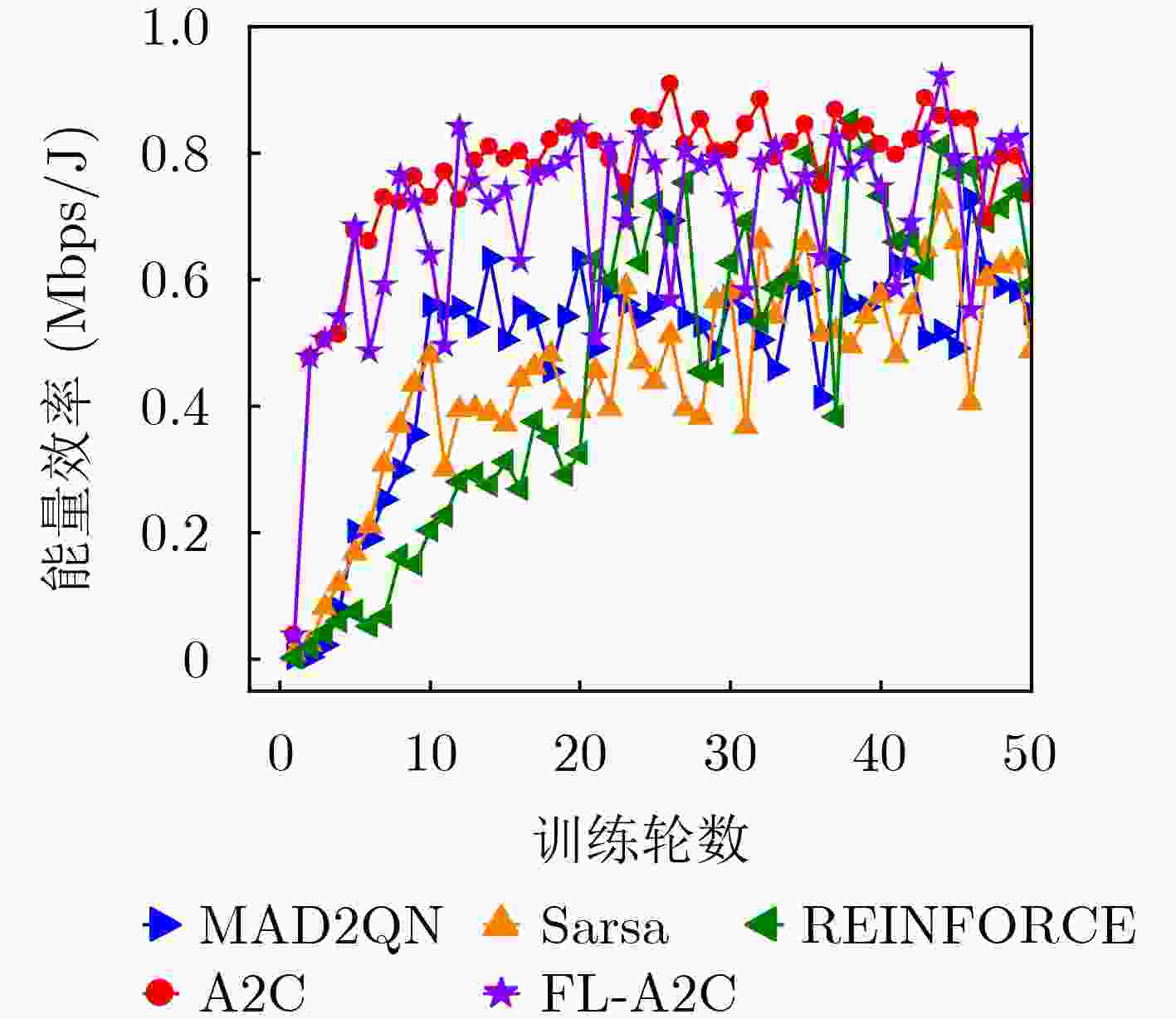
Objective The topology of Low Earth Orbit (LEO) satellite communication networks is highly dynamic, rendering traditional terrestrial routing methods unsuitable for direct application. Additionally, due to the limited onboard resources of satellites, Artificial Intelligence (AI)-based routing methods often experience low learning efficiency. Collaborative training requires data sharing and transmission, which poses significant challenges and data security risks. To address these issues, this research introduces Federated Deep Reinforcement Learning (FDRL) into LEO satellite communication networks. By leveraging FDRL’s capabilities in distributed perception, decision-making, and training, it facilitates the efficient learning of global routing strategies. Through local model aggregation and global model sharing among satellite nodes, FDRL dynamically adapts to topology changes while ensuring data privacy, thereby generating optimal routing decisions and enhancing the overall routing performance of LEO satellite networks. Furthermore, integrating Federated Learning (FL) into the LEO satellite network enables autonomous constellation training within regions, eliminating the need to transmit raw data to Ground Stations (GS), thus reducing reliance on GS and minimizing communication overhead during collaborative training. Methods A novel FDRL-based intelligent routing method for LEO satellite communication networks is proposed. This method develops a routing model that integrates network, communication, and computational energy consumption, with the optimization objective focused on maximizing the energy efficiency of the LEO satellite network. Utilizing a satellite clustering algorithm, the entire LEO satellite network is partitioned into multiple clusters. Within each cluster, the FDRL framework is implemented, where each LEO satellite uses the Advantage Actor-Critic (A2C) algorithm for local reinforcement learning. The policy network generates efficient routing actions, while the value network dynamically evaluates state values to reduce variance in policy updates. After a specified number of training rounds, the Federated Proximal Algorithm (FedProx) is applied at the cluster head satellite to conduct federated aggregation within the cluster. By collaboratively sharing model parameters among satellites, a global model is jointly trained, enhancing the generalization capability to optimize the network's energy efficiency. Results and Discussions To validate the effectiveness of the proposed method, the LEO satellite constellation is first clustered using the suggested clustering algorithm. The number of Cluster Member (CM) nodes within each cluster ranges from 6 to 8 ( Fig. 5 ), with the variation in the CM node count not exceeding 5, indicating relatively stable clustering. FDRL training is then conducted within each cluster. Simulation results show that when the aggregation frequency is set to 400 (i.e., aggregation occurs every 400 time slots), training energy consumption is minimized (Fig. 6 ), and the reward is most stable (Fig. 7 ) compared to other aggregation frequencies. Next, the performance of the designed FL-A2C algorithm is compared to other baseline algorithms. The results demonstrate that the FL-A2C algorithm exhibits better convergence and higher total reward values than the benchmarks, namely Sarsa, MAD2QN, and REINFORCE (Fig. 8 ), although its total reward is slightly lower than that of A2C. Compared to Sarsa, REINFORCE, and MAD2QN, the designed method improves average network throughput by 83.7%, 19.8%, and 14.1%, respectively (Fig. 9 ); reduces average hop count by 25.0%, 18.9%, and 9.1%, respectively (Fig. 10 ); and enhances energy efficiency by 55.6%, 42.9%, and 45.8%, respectively (Fig. 11 ).Conclusions To address the challenges posed by the highly dynamic network topology of LEO satellite networks and the limitations of traditional terrestrial routing methods, this research presents a multi-agent FDRL routing method combined with satellite clustering. Comprehensive simulations are conducted to evaluate the intelligent routing method, and the results demonstrate that: (1) The designed FL-A2C algorithm achieves better convergence and enhances the energy efficiency of LEO satellite networks; (2) The stability of LEO satellite clustering is ensured by the proposed scheme; (3) The intelligent routing method outperforms benchmark schemes (Sarsa, REINFORCE, MAD2QN) with triple advantages, achieving 83.7%/19.8%/14.1% higher network throughput, 25.0%/18.9%/9.1% lower hop counts, and 55.6%/42.9%/45.8% better energy efficiency, respectively. -
1 基于FL-A2C的智能路由算法(FL-A2C算法)
初始化:$ E $为训练轮数, $ T $为时间片数量,$ {\mathcal{K}_t} $为卫星分簇,$ \chi $为
卫星节点队列大小,$ {N_{{\text{packet}}}} $为数据包数量,$ {T_{{\text{agg}}}} $为聚合频率;1: 簇头初始化全局模型并将网络参数分发至各个簇中的成员卫
星节点2: for episodes = 1 to $ E $ do 3: 清空卫星队列生成$ {N_{{\text{packet}}}} $个数据包发送至各个卫星节点 4: for step = 1 to $ T $ do 5: for $ |{\kappa _t}| $ = 1 to $| {\mathcal{K}_t}| $ do 6: for agent = 1 to $ {\kappa _t} $ do 7: if agent 的发送队列$ Q_{{v_i}}^{{\text{send}}} $容量 < $ \chi $ and 接收队列
$ Q_{{v_i}}^{{\text{recv}}} $容量!=0 then8: 接收队列$ Q_{{v_i}}^{{\text{recv}}} $中的数据包进入发送队列$ Q_{{v_i}}^{{\text{send}}} $ 9: end if 10: for p = 1 to
$ Q_{{v_i}}^{{\text{send}}} $ do11: agent从队列中取出单个数据包并获取当前状态
$ s_t^{{v_i},p} $12: 将状态$ s_t^{{v_i},p} $输入至Actor网络依据策略
$ \pi \left( {{a_t}|{s_t},{{\boldsymbol{\theta}} _t}} \right) $进行采样获取动作$ a_t^{{v_i},p} $13: if 下一跳节点接收队列容量$ Q_{{v_i}}^{{\text{recv}}} $< $ \chi $ then 14: 执行动作$ a_t^{{v_i},p} $并获得奖励$ r_t^{{v_i},p} $,下一状态
$ s_{t + 1}^{{v_i},p} $以及结束二元变量done15: 记录历史动作信息,另$ a_{t - 1}^{{v_i},p} = a_t^{{v_i},p} $ 16: else 17: 将数据包p置入接收队列队尾 18: end if 19: 将当前状态$ s_t^{{v_i},p} $、下一状态$ s_{t + 1}^{{v_i},p} $、奖励$ r_t^{{v_i},p} $以
及动作概率密度输入至Critic网络20: 根据式(19)计算TD Error,并依据损失函数式(26)
做梯度下降更新Critic网络参数21: 根据TD Error得到优势函数,并根据损失函数
式(25)做梯度下降更新Actor网络参数22: end for 23: end for 24: end for 25: end for 26: 记录系统时间,另$ {t_{{\text{total}}}} = {t_{{\text{total}}}} + T $ 27: if $ {t_{{\text{total}}}} $ % $ {T_{{\text{agg}}}} $ == 0 then 28: 随机选取两个簇根据式(27)和式(28)在簇头做联邦聚合,并
将全局模型参数下发至各客户端29: end if 30: end for 表 1 星座及路由参数
星座及路由参数 数值 轨道高度$ H $, 倾角$ \beta $ 550 km, 53° 星座参数$ M $, $ N $ 10 个, 10颗 簇内最大跳数$ h $ 3 跳 最大容忍时延$ {\delta _s} $ 1000 ms单个数据包大小$ {l_s} $ 1024 Byte队列缓冲大小$ \chi $ 1 Mb CPU参数$ f $, $ {C_k} $ 3 GHz, 1 kcycle/bit 发射功率$ P $, 带宽$ B $ 5 kW, 100 Mbps 表 2 深度神经网络模型参数
模型参数 数值 损失函数 均方误差(MSE) 优化器 Adam 激活函数 ReLU, Softmax Actor网络, Critic网络 2个128个单元的隐藏层 折扣因子$ \gamma $ 0.99 学习率$ {\alpha _{\boldsymbol{\theta}} } $, $ {\alpha _{\boldsymbol{\omega}} } $ 0.0003 ,0.0005 联邦聚合频率$ {T_{{\text{agg}}}} $ 每400个时间片聚合1次 -
[1] SUN Yaohua, PENG Mugen, ZHANG Shijie, et al. Integrated satellite-terrestrial networks: Architectures, key techniques, and experimental progress[J]. IEEE Network, 2022, 36(6): 191–198. doi: 10.1109/MNET.106.2100622. [2] 孙耀华, 彭木根. 面向手机直连的低轨卫星通信: 关键技术、发展现状与未来展望[J]. 电信科学, 2023, 39(2): 25–36. doi: 10.11959/j.issn.1000–0801.2023031.SUN Yaohua and PENG Mugen. Low earth orbit satellite communication supporting direct connection with mobile phones: Key technologies, recent progress and future directions[J]. Telecommunications Science, 2023, 39(2): 25–36. doi: 10.11959/j.issn.1000–0801.2023031. [3] ZHU Xiangming and JIANG Chunxiao. Integrated satellite-terrestrial networks toward 6G: Architectures, applications, and challenges[J]. IEEE Internet of Things Journal, 2022, 9(1): 437–461. doi: 10.1109/JIOT.2021.3126825. [4] WANG Cheng, WANG Huawen, and WANG Weidong. A two-hops state-aware routing strategy based on deep reinforcement learning for LEO satellite networks[J]. Electronics, 2019, 8(9): 920. doi: 10.3390/electronics8090920. [5] XU Guoliang, ZHAO Yanyun, RAN Yongyi, et al. Spatial location aided fully-distributed dynamic routing for large-scale LEO satellite networks[J]. IEEE Communications Letters, 2022, 26(12): 3034–3038. doi: 10.1109/LCOMM.2022.3205300. [6] LIAO Hailong, ZHANG Xian, ZHOU Jiaen, et al. Real-time routing design for LEO satellite networks: An enhanced multi-agent DRL approach[C]. 2024 IEEE/CIC International Conference on Communications in China (ICCC Workshops), Hangzhou, China, 2024: 547–552. doi: 10.1109/ICCCWorkshops62562.2024.10693714. [7] MATTHIESEN B, RAZMI N, LEYVA-MAYORGA I, et al. Federated learning in satellite constellations[J]. IEEE Network, 2024, 38(2): 232–239. doi: 10.1109/MNET.132.2200504. [8] ELMAHALLAWY M and LUO Tie. Optimizing federated learning in LEO satellite constellations via intra-plane model propagation and sink satellite scheduling[C]. ICC 2023 - IEEE International Conference on Communications, Rome, Italy, 2023: 3444–3449. doi: 10.1109/ICC45041.2023.10279316. [9] SO J, HSIEH K, ARZANI B, et al. FedSpace: An efficient federated learning framework at satellites and ground stations[J]. arXiv: 2202.01267, 2022. [10] FADLULLAH Z M and KATO N. On smart IoT remote sensing over integrated terrestrial-aerial-space networks: An asynchronous federated learning approach[J]. IEEE Network, 2021, 35(5): 129–135. doi: 10.1109/MNET.101.2100125. [11] ZHAO Ming, CHEN Chen, LIU Lei, et al. Orbital collaborative learning in 6G space-air-ground integrated networks[J]. Neurocomputing, 2022, 497: 94–109. doi: 10.1016/j.neucom.2022.04.098. [12] SINGH J, DHURANDHER S K, and WOUNGANG I. Federated learning empowered routing for opportunistic network environments[C]. 2024 IEEE International Conference on Communications Workshops (ICC Workshops), Denver, USA, 2024: 1998–2004. doi: 10.1109/ICCWorkshops59551.2024.10615288. [13] WANG Xiaoding, HU Jia, LIN Hui, et al. QoS and privacy-aware routing for 5G-enabled industrial Internet of Things: A federated reinforcement learning approach[J]. IEEE Transactions on Industrial Informatics, 2022, 18(6): 4189–4197. doi: 10.1109/TII.2021.3124848. [14] FENG Xinao, SUN Yaohua, and PENG Mugen. Distributed satellite-terrestrial cooperative routing strategy based on minimum hop-count analysis in mega LEO satellite constellation[J]. IEEE Transactions on Mobile Computing, 2024, 23(11): 10678–10693. doi: 10.1109/TMC.2024.3380891. [15] 张朝辉, 周嘉琦. 基于半固定分簇的无线传感器网络节能分簇路由算法[J]. 通信学报, 2024, 45(4): 160–170. doi: 10.11959/j.issn.1000-436x.2024080.ZHANG Zhaohui and ZHOU Jiaqi. Energy-saving clustering routing algorithm based on semi-fixed cluster for wireless sensor networks[J]. Journal on Communications, 2024, 45(4): 160–170. doi: 10.11959/j.issn.1000-436x.2024080. [16] ZHANG Hong, TIAN Hao, DONG Mianxiong, et al. FedPCC: Parallelism of communication and computation for federated learning in wireless networks[J]. IEEE Transactions on Emerging Topics in Computational Intelligence, 2022, 6(6): 1368–1377. doi: 10.1109/TETCI.2022.3170471. [17] ZHANG Hangyu, LIU Rongke, KAUSHIK A, et al. Satellite edge computing with collaborative computation offloading: An intelligent deep deterministic policy gradient approach[J]. IEEE Internet of Things Journal, 2023, 10(10): 9092–9107. doi: 10.1109/JIOT.2022.3233383. [18] 陈宇, 张勇, 陈实. 大规模卫星集群网络自适应加权分簇算法[J]. 北京理工大学学报, 2021, 41(11): 1188–1192. doi: 10.15918/j.tbit1001-0645.2021.072.CHEN Yu, ZHANG Yong, and CHEN Shi. Adaptive weighted clustering algorithm for large-scale satellite cluster network[J]. Transactions of Beijing Institute of Technology, 2021, 41(11): 1188–1192. doi: 10.15918/j.tbit1001-0645.2021.072. [19] 王瑞峰, 张明, 黄子恒, 等. 利用A2C-ac的城轨车车通信资源分配算法[J]. 电子与信息学报, 2024, 46(4): 1306–1313. doi: 10.11999/JEIT230623.WANG Ruifeng, ZHANG Ming, HUANG Ziheng, et al. Resource allocation algorithm of urban rail train-to-train communication with A2C-ac[J]. Journal of Electronics & Information Technology, 2024, 46(4): 1306–1313. doi: 10.11999/JEIT230623. [20] LI Tian, SAHU A K, ZAHEER M, et al. Federated optimization in heterogeneous networks[C]. The 3rd Conference on Machine Learning and Systems (MLSys 2020), Austin, USA, 2020: 303–313. -





 下载:
下载:


 下载:
下载:
