基于信号间交叉项的非正交椭圆球面波信号检测方法

陆发平; 毛忠阳; 许志超; 舒轶昊; 康家方; 王峰; 王甍娇

doi:10.11999/JEIT250052

基于信号间交叉项的非正交椭圆球面波信号检测方法

doi: 10.11999/JEIT250052

陆发平^{1, 2},
毛忠阳^{1, 2},
许志超^{1, 2, 3},
舒轶昊⁴,
康家方^{1, 2, ,},
王峰³,
王甍娇^{1, 2}

1.
中国人民解放军海军航空大学烟台 264001
2.
山东省海空信息感知与处理技术重点实验室烟台 264001
3.
北京航空航天大学电子信息工程学院北京 100191
4.
中国人民解放军91001部队北京 100038

基金项目: 博士后创新人才支持计划(BX20200039)，山东省自然科学基金(ZR2023MD045)

详细信息

作者简介:
陆发平：男，讲师，研究方向为现代通信理论与应用、测控与通信信号波形设计、非正弦通信

毛忠阳：男，教授，研究方向为现代通信理论与应用、激光通信、无线通信组网技术

许志超：男，讲师，研究方向为卫星导航及其应用、无线通信网络与数据传输、非正弦通信

舒轶昊：男，高级工程师，研究方向为现代通信理论与应用、导航技术

康家方：男，副教授，研究方向为现代通信理论与应用、扩频调制技术、非正弦通信

王峰：男，副教授，研究方向为卫星导航及其应用、感知信号波形设计

王甍娇：女，助理讲师，研究方向为现代通信理论与应用、无线组网技术

通讯作者:
康家方　kangjiafang01@163.com

中图分类号: TN911.3
计量
- 文章访问数: 101
- HTML全文浏览量: 26
- PDF下载量: 22
- 被引次数: 0
出版历程
- 收稿日期: 2025-01-22
- 修回日期: 2025-04-22
- 网络出版日期: 2025-05-10

Non-orthogonal Prolate Spheroidal Wave Functions Signal Detection Method with Cross-terms

LU Faping^{1, 2},
MAO Zhongyang^{1, 2},
XU Zhichao^{1, 2, 3},
SHU Yihao⁴,
KANG Jiafang^{1, 2
, ,},
WANG Feng³,
WANG Mengjiao^{1, 2}

1.
Naval Aviation University, Yantai 264001, China
2.
Key Laboratory of Sea-Air Information Perception and Processing Technology of Shandong Province, Yantai 264001, China
3.
School of Electronic Information Engineering, Beihang University, Beijing 100191, China
4.
Unit 91001 of PLA, Beijing 100038, China

Funds: China National Postdoctoral Program for Innovative Talents (BX20200039), The National Natural Science Foundation of Shandong Province (ZR2023MD045)

摘要

摘要: 针对非正交椭圆球面波(PSWFs)信号因相互干扰导致信号检测性能低的难题，该文将信号时频域特性引入信号检测，提出了基于信号间交叉项的非正交PSWFs信号检测方法，将信号检测由“时域/频域1维能量域”拓展到“时频2维能量域”，并利用时频域局部区域能量进行信号检测，有效降低了非正交PSWFs信号间干扰、提升了非正交PSWFs信号检测性能。理论与仿真分析表明，相对于相干检测，所提方法具有更优的信号检测性能，当误比特率为4×10^–5时，系统误码性能提升约1 dB。
- 椭圆球面波函数 /
- 非正交 /
- 信号检测 /
- 时频域 /
- 交叉项
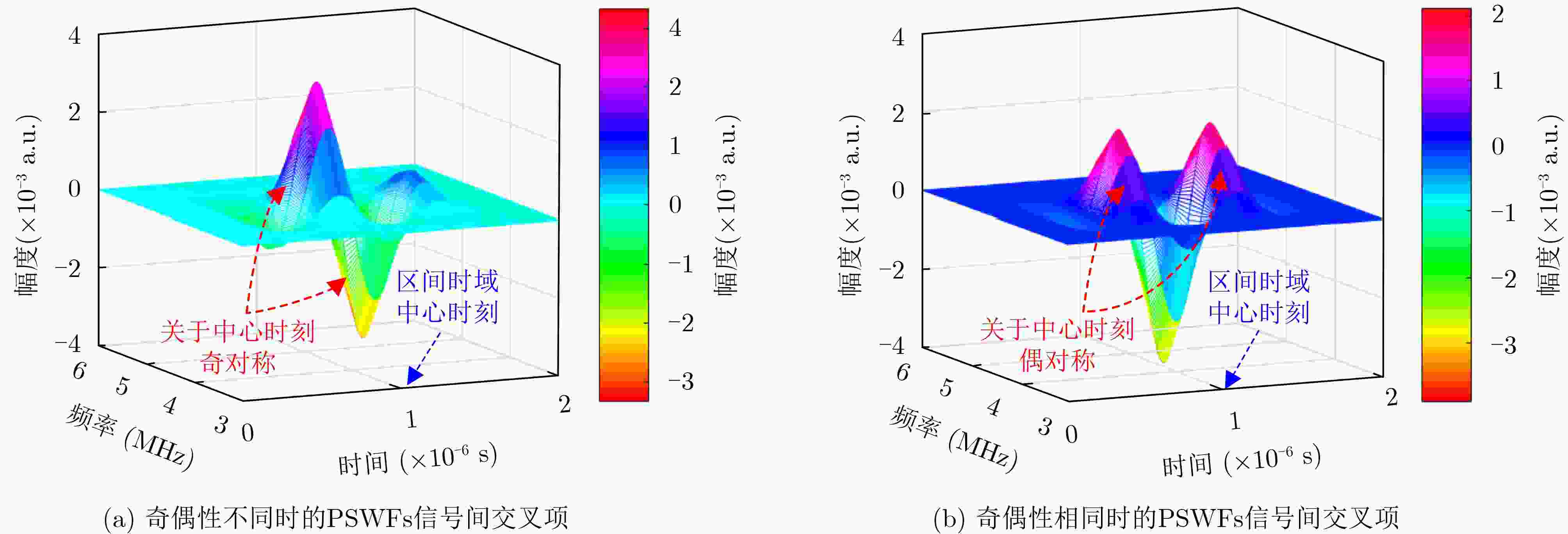
Abstract: Objective Non-orthogonal Shape Modulation based on Prolate Spheroidal Wave Functions (NSM-PSWFs) utilizes PSWFs with high time-frequency energy concentration as basis waveforms. This structure enables high spectral efficiency and time-frequency energy aggregation, making it a promising candidate for B5G/6G waveform design. However, due to the non-orthogonality of the PSWFs used for information transmission in NSM-PSWFs, mutual interference between non-orthogonal signals and poor bit error performance in coherent detection systems significantly limit their practical deployment. This issue is a common challenge in non-orthogonal modulation and access technologies. To address the problem of low detection performance resulting from mutual interference among non-orthogonal PSWFs, this study incorporates time-frequency domain characteristics into signal detection. A novel detection mechanism for non-orthogonal PSWFs in the time-frequency domain is proposed, with the aim of reducing interference between non-orthogonal PSWFs and enhancing detection performance. Methods Given the different time-frequency domain energy distribution characteristics of PSWF signals at various stages—particularly the "local" energy concentration in different regions—this study introduces cross-terms between signals. Based on an analysis of non-orthogonal signal time-frequency characteristics, with a focus on innovating detection mechanisms, a combined approach of theoretical modeling and numerical simulation is employed to explore novel methods for detecting non-orthogonal PSWF signals via cross-terms. Specifically: (1) The impact of interference between PSWF signals and Gaussian white noise on the time-frequency distribution of cross-terms is analyzed, demonstrating the feasibility of detecting PSWF signals in the time-frequency domain. (2) Building on this analysis, time-frequency characteristics are integrated into the detection process. A novel method for detecting non-orthogonal PSWFs based on cross-terms is proposed, accompanied by a strategy for selecting time-frequency feature parameters. The "integral value of cross-terms over symmetric time intervals at the frequency corresponding to the peak energy density of cross-terms" is chosen as the feature parameter. This shifts signal detection from the "one-dimensional energy domain (time or frequency)" to the "two-dimensional time-frequency energy domain," enabling detection by exploiting localized energy regions while simultaneously mitigating interference during statistical acquisition. Results and Discussions This study demonstrates the feasibility of detecting signals in the two-dimensional time-frequency domain and analyzes the impact of different PSWFs and AWGN on the distribution characteristics of cross-terms. Notably, AWGN interference can be regarded as a special form of "interference between PSWFs" exhibiting a linear superposition with PSWF-induced interference. The interference from PSWFs with time-domain parity opposite to that of the template signal can be eliminated through "symmetric time-interval integration" (Fig. 1, Table 1, Table 2). This establishes a theoretical foundation for the novel detection mechanism based on cross-terms and provides a reference for incorporating other two-dimensional distribution characteristics into signal detection. Additionally, a novel detection mechanism for non-orthogonal PSWFs based on cross-terms is proposed, utilizing time-frequency distribution characteristics for signal detection. This method effectively reduces interference between non-orthogonal PSWFs, thereby enhancing detection performance. It also offers valuable insights for exploring detection mechanisms based on other two-dimensional distribution characteristics. For example, compared to conventional coherent detection, the proposed method achieves a superior performance with approximately 1 dB improvement in bit error rate at 4 × 10^–5 (Fig. 4). Conclusions This paper demonstrates the feasibility of detecting PSWFs in the two-dimensional time-frequency domain and proposes a novel detection method for non-orthogonal PSWFs based on cross-terms. The proposed method transforms traditional coherent detection from “global energy in the time/frequency domain” to “local energy in the time-frequency domain” significantly reducing interference between non-orthogonal signals and enhancing detection performance. This approach not only provides a new perspective for developing efficient detection methods for non-orthogonal signals but also serves as a valuable reference for investigating novel signal detection mechanisms in two-dimensional domains.
- Prolate Spheroidal Wave Functions (PSWFs) /
- Non-orthogonal /
- Signal detection /
- Time-frequency domain /
- Cross-term

HTML全文

图 1 不同PSWFs信号间交叉项时频分布图

下载: 全尺寸图片幻灯片

图 2 基于信号间交叉项的PSWFs信号检测系统模型

下载: 全尺寸图片幻灯片

图 3 PSWFs信号频谱关系及信号时域波形

下载: 全尺寸图片幻灯片

图 4 系统误码性能

下载: 全尺寸图片幻灯片

表 1 模板信号为X31时，所提方法检测统计量(无滤波处理)

PSWFs 频率(MHz)	X31	X32	X11	X12	X21
PSWFs 频率(MHz)	奇函数	偶函数	奇函数	偶函数	偶函数
4.5	0.523 457	1.39E–15	0.037 742	3.74E–16	–1.42E–14
5.0	0.897 867	–1.29E–16	–0.002 974	–7.03E–16	4.02E–15
5.5	0.460 107	–1.55E–15	–0.027 583	–2.76E–16	2.69E–15
PSWFs 频率(MHz)	X22	X41	X42	X51	X52
PSWFs 频率(MHz)	奇函数	偶函数	奇函数	奇函数	偶函数
4.5	–0.192 651	8.26E–15	0.023 615	–0.020 002	1.04E–14
5.0	0.054 759	1.41E–14	0.040 326	0.014 6355	–7.69E–15
5.5	0.035 189	–4.97E–14	–0.144 358	0.024 962	–1.29E–14

下载: 导出CSV

表 2 模板信号为X31时，所提方法检测统计量(滤波处理)

PSWFs 频率 (MHz)	X31	X32	X11	X21
PSWFs 频率 (MHz)	奇函数	偶函数	奇函数	偶函数
4.5	0.537 571	–3.3E–14	–0.032 469	3.6E–14
5.0	0.999 995	–2.7E–15	–0.003 176	7.5E–16
5.5	0.460 898	3.1E–14	0.027 288	–3.4E–16
PSWFs 频率 (MHz)	X22	X41	X42	X52
PSWFs 频率 (MHz)	奇函数	偶函数	奇函数	偶函数
4.5	–0.779 201	3.1E–15	0.017 417	1.1E–14
5.0	–0.044 233	–6.4E–15	–0.041 200	–9.4E–15
5.5	0.019 324	–9.2E–14	–0.680 800	–3.3E–15

下载: 导出CSV

参考文献(20)

[1]	HOFFMANN M, KUNZMANN G, DUDDA T, et al. A secure and resilient 6G architecture vision of the German flagship project 6G-ANNA[J]. IEEE Access, 2023, 11: 102643–102660. doi: 10.1109/ACCESS.2023.3313505.
[2]	ABD ELAZIZ M, AL‐QANESS M A A, DAHOU A, et al. Evolution toward intelligent communications: Impact of deep learning applications on the future of 6G technology[J]. WIREs Data Mining and Knowledge Discovery, 2024, 14(1): e1521. doi: 10.1002/widm.1521.
[3]	ZAWISH M, DHAREJO F A, KHOWAJA S A, et al. AI and 6G into the Metaverse: Fundamentals, challenges and future research trends[J]. IEEE Open Journal of the Communications Society, 2024, 5: 730–778. doi: 10.1109/OJCOMS.2024.3349465.
[4]	FU Yu, WANG Chengxiang, MAO Xichen, et al. Spectrum-energy-economy efficiency analysis of B5G wireless communication systems with separated indoor/outdoor scenarios[J]. IEEE Transactions on Wireless Communications, 2023, 22(12): 9718–9731. doi: 10.1109/TWC.2023.3273261.
[5]	YI Xingrui, LI Jianqiang, LIU Yutong, et al. ArguteDUB: Deep learning based distributed uplink beamforming in 6G-based IoV[J]. IEEE Transactions on Mobile Computing, 2024, 23(4): 2551–2565. doi: 10.1109/TMC.2023.3262320.
[6]	WANG Wenjing, YU Tongzhou, LI Shuangyang, et al. A simple phase rotation based PAPR reduction method for multicarrier faster-than-Nyquist signaling[C]. 2023 IEEE 98th Vehicular Technology Conference (VTC2023-Fall), Hong Kong, China, 2023: 1–6. doi: 10.1109/VTC2023-Fall60731.2023.10333687.
[7]	MA Yunsi, WU Nan, WU Kai, et al. VAMP-based iterative equalization for index-modulated multicarrier FTN signaling[J]. IEEE Transactions on Communications, 2023, 71(4): 2304–2316. doi: 10.1109/TCOMM.2023.3240689.
[8]	ISHIHARA T and SUGIURA S. Differential multi-carrier faster-than-Nyquist signaling in doubly selective fading channel[J]. IEEE Transactions on Vehicular Technology, 2024, 73(1): 1424–1429. doi: 10.1109/TVT.2023.3305731.
[9]	陈昭男, 刘锡国, 王红星, 等. 基于PSWF框架的非正交脉冲波形调制方法[J]. 电子学报, 2016, 44(3): 620–626. doi: 10.3969/j.issn.0372-2112.2016.03.019. CHEN Zhaonan, LIU Xiguo, WANG Hongxing, et al. Nonorthogonal pulse shape modulation based on PSWF frames[J]. Acta Electronica Sinica, 2016, 44(3): 620–626. doi: 10.3969/j.issn.0372-2112.2016.03.019.
[10]	陆发平, 王红星, 刘传辉, 等. 基于功率复用的椭圆球面波函数非正交调制方法[J]. 航空学报, 2019, 40(9): 323102. doi: 10.7527/S1000-6893.2019.23102. LU Faping, WANG Hongxing, LIU Chuanhui, et al. Power domain non-orthogonal pulse modulation based on prolate spheroidal wave function[J]. Acta Aeronauticaet Astronautica Sinica, 2019, 40(9): 323102. doi: 10.7527/S1000-6893.2019.23102.
[11]	王骥, 李子龙, 肖健, 等. 基于低复杂度加法网络的非正交多址接入短报文多用户检测算法研究[J]. 电子与信息学报, 2024, 46(6): 2409–2417. doi: 10.11999/JEIT231186. WANG Ji, LI Zilong, XIAO Jian, et al. Research on multi-user detection algorithm for non-orthogonal multiple access short message based on low complexity adder network[J]. Journal of Electronics & Information Technology, 2024, 46(6): 2409–2417. doi: 10.11999/JEIT231186.
[12]	TONG Wen and ZHU Peiying. 6G: The Next Horizon: From Connected People and Things to Connected Intelligence[M]. Cambridge: Cambridge University Press, 2021: 271–285. doi: 10.1017/9781108989817.
[13]	张磊, 刘传辉, 王红星, 等. 基于白化变换的非正弦时域正交调制系统解调[J]. 吉林大学学报: 工学版, 2013, 43(3): 819–823. doi: 10.7964/jdxbgxb201303043. ZHANG Lei, LIU Chuanhui, WANG Hongxing, et al. Demodulation method of non-sinusoidal orthogonal modulation system based on whiting transformation[J]. Journal of Jilin University: Engineering and Technology Edition, 2013, 43(3): 819–823. doi: 10.7964/jdxbgxb201303043.
[14]	张磊, 陈昭男, 王红星, 等. 基于串行干扰消除的非正弦系统解调方法[J]. 电波科学学报, 2013, 28(5): 934–940. doi: 10.13443/j.cjors.2013.05.025. ZHANG Lei, CHEN Zhaonan, WANG Hongxing, et al. Demodulation method for non-sinusoidal orthogonal modulation system based on SIC[J]. Chinese Journal of Radio Science, 2013, 28(5): 934–940. doi: 10.13443/j.cjors.2013.05.025.
[15]	王红星, 陆发平, 刘传辉, 等. 椭圆球面波信号间交叉项时频分布特性研究[J]. 电子与信息学报, 2017, 39(6): 1319–1325. doi: 10.11999/JEIT160877. WANG Hongxing, LU Faping, LIU Chuanhui, et al. Study on time-frequency characteristics of cross-terms between Prolate Spheroidal Wave Function signal[J]. Journal of Electronics & Information Technology, 2017, 39(6): 1319–1325. doi: 10.11999/JEIT160877.
[16]	王红星, 赵乐源, 陆发平, 等. 椭圆球面波信号Wigner-Ville分布显式渐近求解方法[J]. 电子与信息学报, 2022, 44(10): 3574–3582. doi: 10.11999/JEIT210820. WANG Hongxing, ZHAO Leyuan, LU Faping, et al. Explicit and progressive solution method for Wigner-Ville distribution of prolate spheroidal wave functions signal[J]. Journal of Electronics & Information Technology, 2022, 44(10): 3574–3582. doi: 10.11999/JEIT210820.
[17]	PETTIT R H. Signal representation by prolate spheroidal wave functions[J]. IEEE Transactions on Aerospace and Electronic Systems, 1965, AES-1(1): 39–42. doi: 10.1109/TAES.1965.4501650.
[18]	王媛媛, 毛忠阳, 陆发平. 一种新的椭圆球面波信号时频域滤波方法[J]. 海军航空大学学报, 2023, 38(2): 173–178. doi: 10.7682/j.issn.2097-1427.2023.02.002. WANG Yuanyuan, MAO Zhongyang, and LU Faping. A novel time-frequency filter method for Prolate Spheroidal Wave Function signal[J]. Journal of Naval Aviation University, 2023, 38(2): 173–178. doi: 10.7682/j.issn.2097-1427.2023.02.002.
[19]	GUO Lanqing, HUANG Siyu, LIU Haosen, et al. Toward robust image denoising via flow-based joint image and noise model[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2024, 34(7): 6105–6115. doi: 10.1109/TCSVT.2023.3345667.
[20]	WU Yinhu, ZHANG Junping, and LIU Dongyang. A remote sensing hyperspectral image noise removal method based on multipriors guidance[J]. IEEE Geoscience and Remote Sensing Letters, 2024, 21: 1–5. doi: 10.1109/LGRS.2024.3357833.