Real-time Adaptive Suppression of Broadband Noise in General Sensing Signals
-
摘要: 自适应滤波是滤除传感输出中宽带噪声的常用方法。自适应过程跟随传感信号统计特征的变化进行调整,收敛时自适应滤波器输出为传感信号的最优估计,而收敛前的调整过程中输出并非最优,且会产生畸变引入额外噪声。该文根据噪声标准差$\sigma $对传感输出进行实时量化变换,变换结果基本保持平稳,且保留传感信号和噪声信息。以变换结果为待滤波信号,自适应滤波器一旦收敛就始终处于收敛状态。对实际传感输出的处理表明,该方法适用于各类传感输出的宽带噪声实时抑制,输出不会产生畸变引入额外噪声。Abstract:
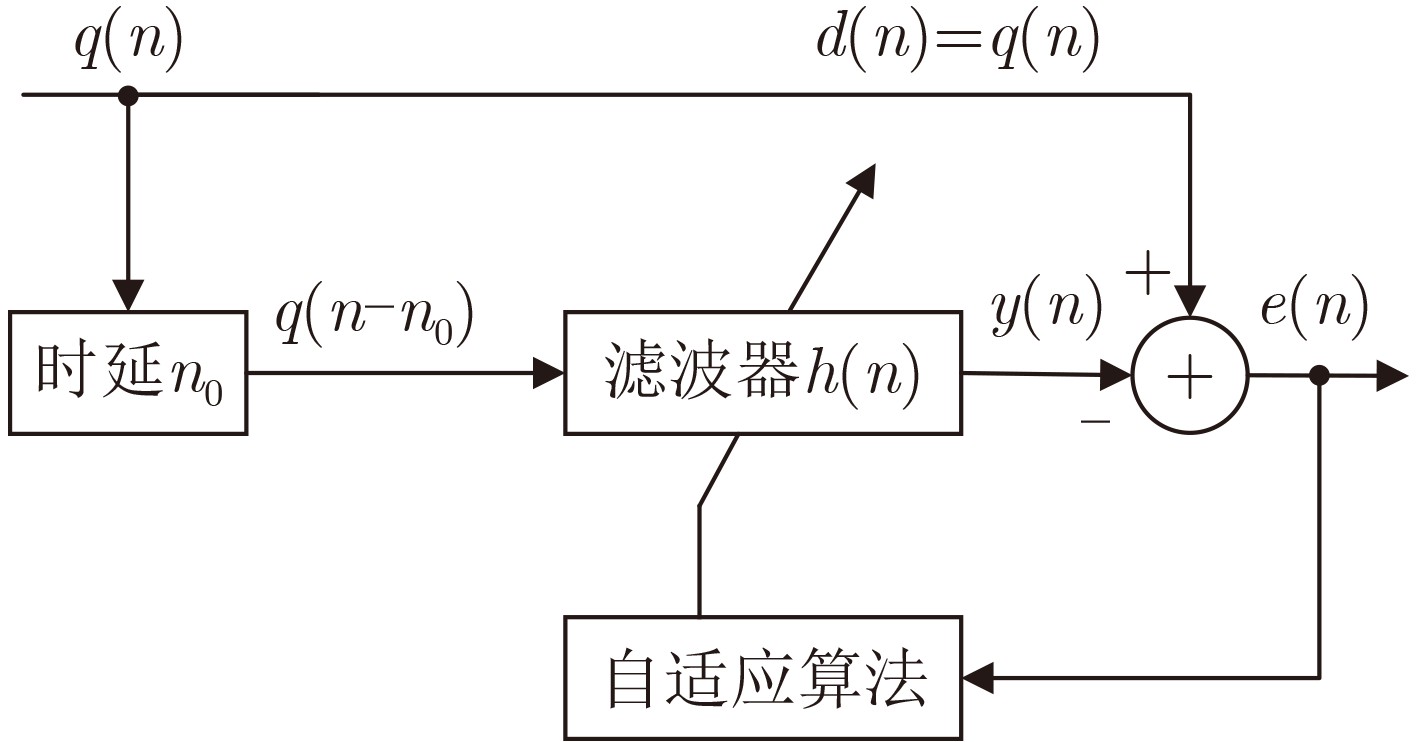
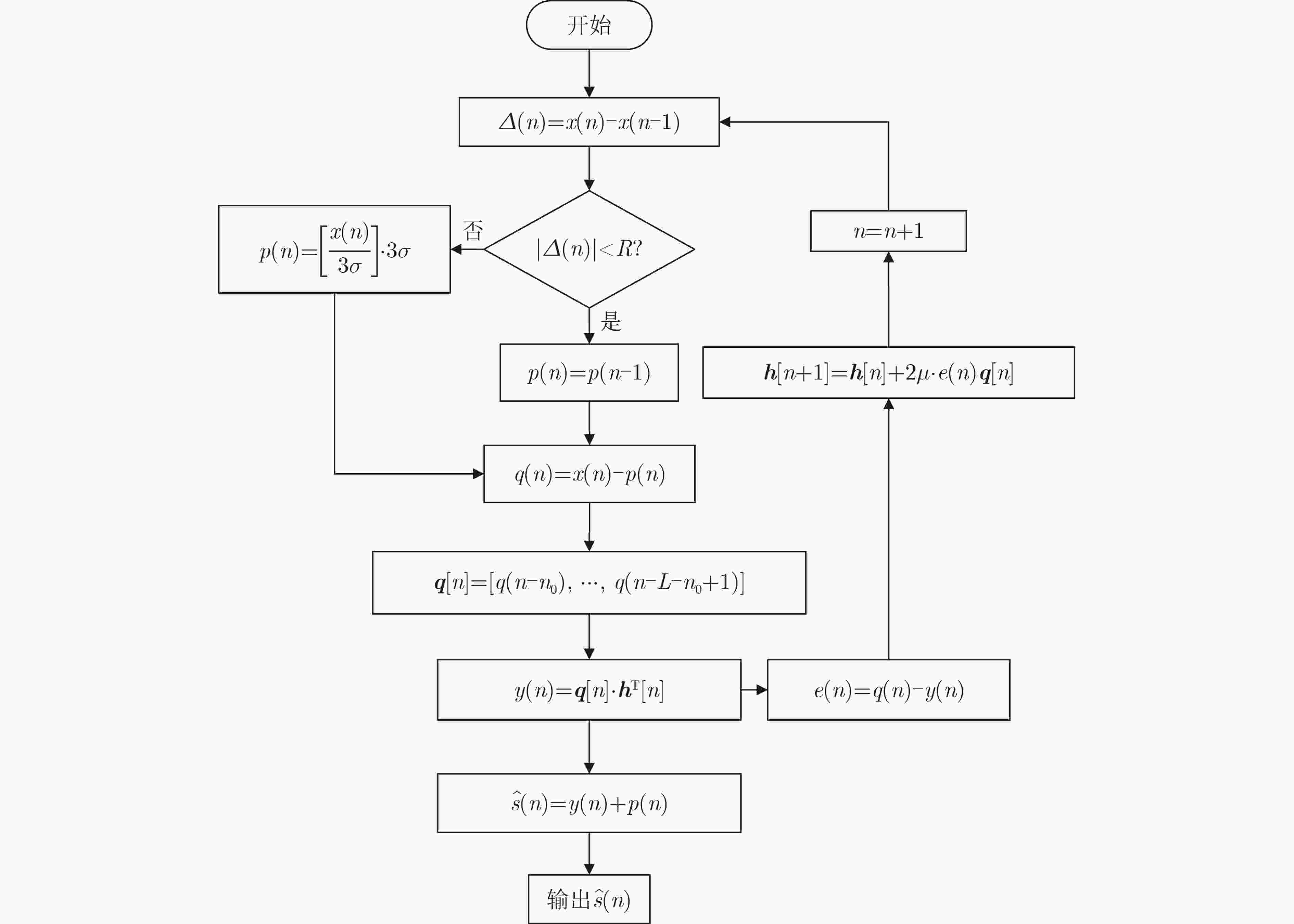
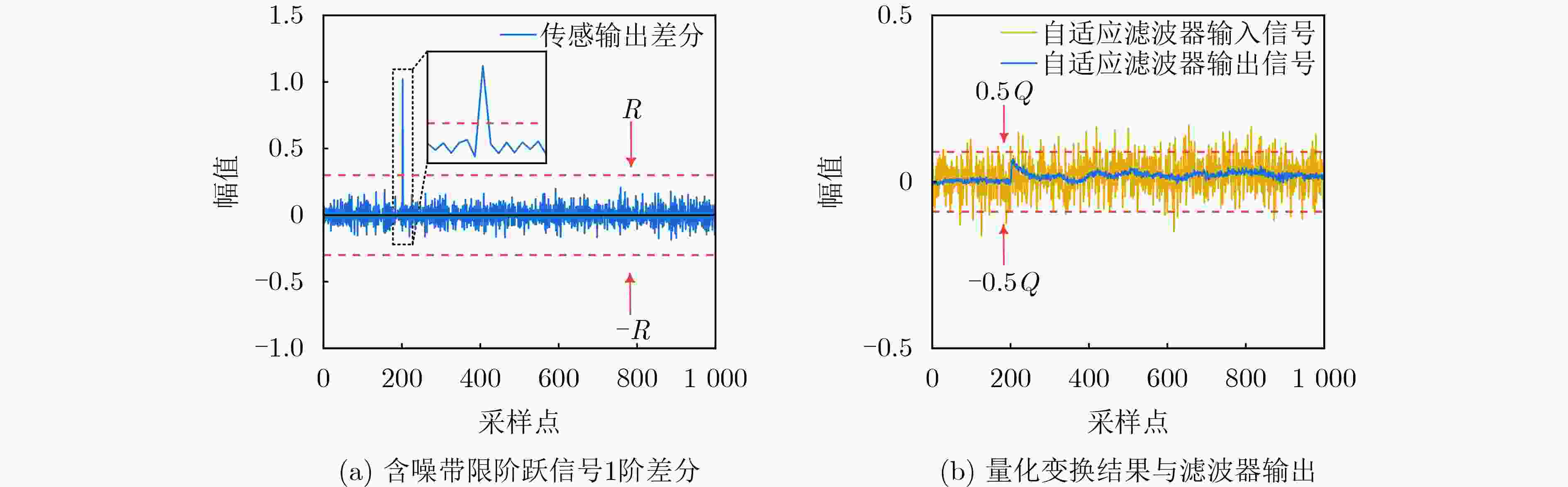
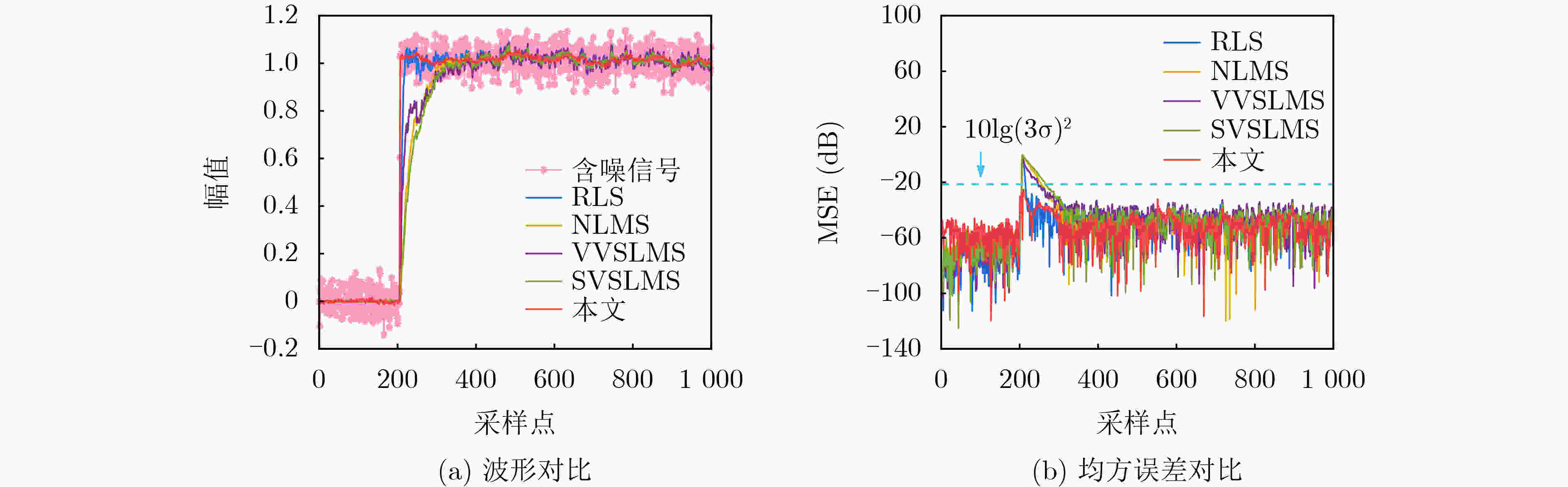
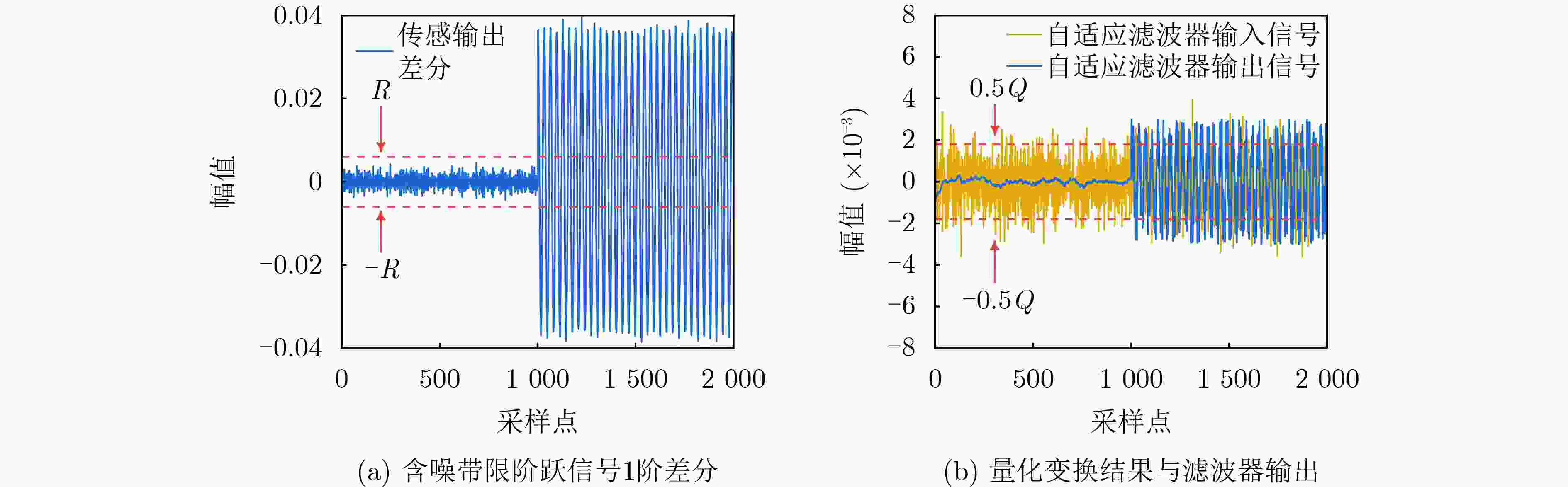
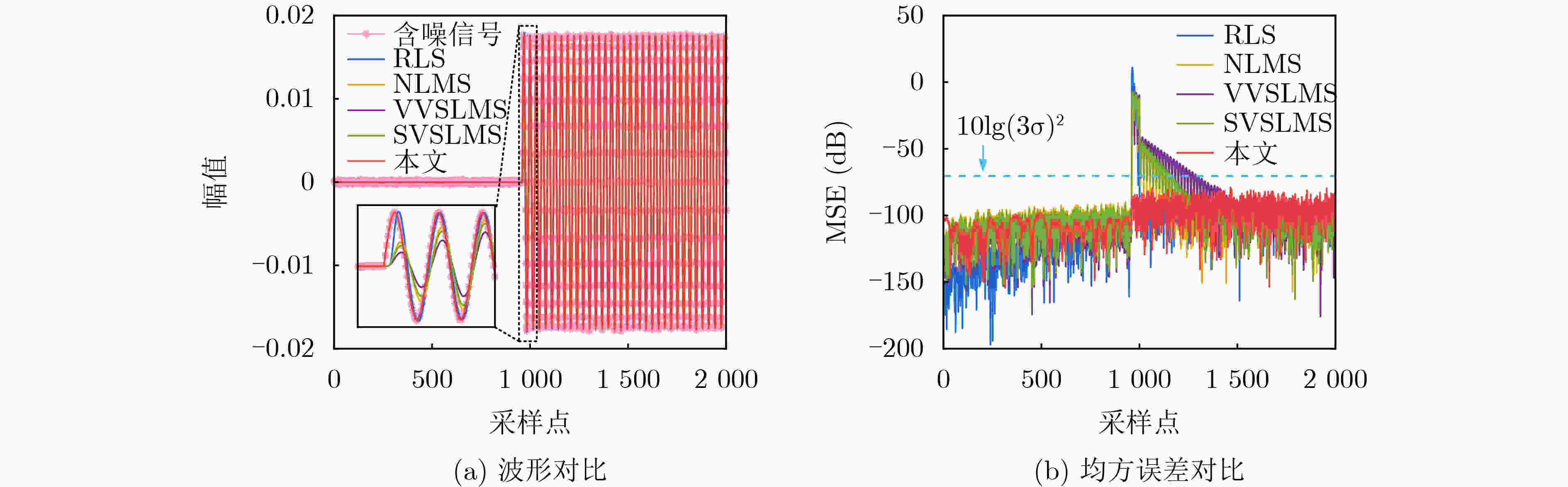
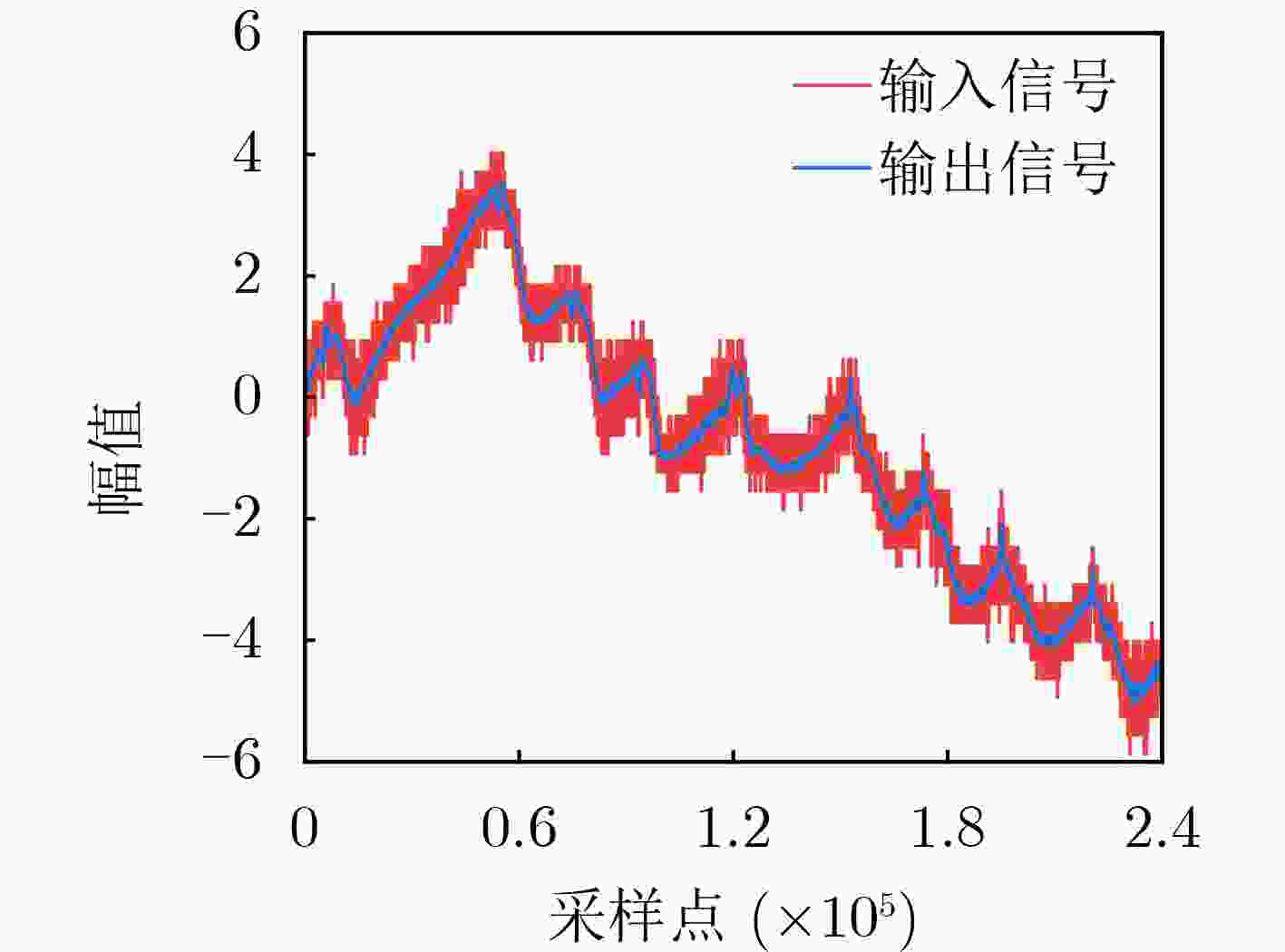
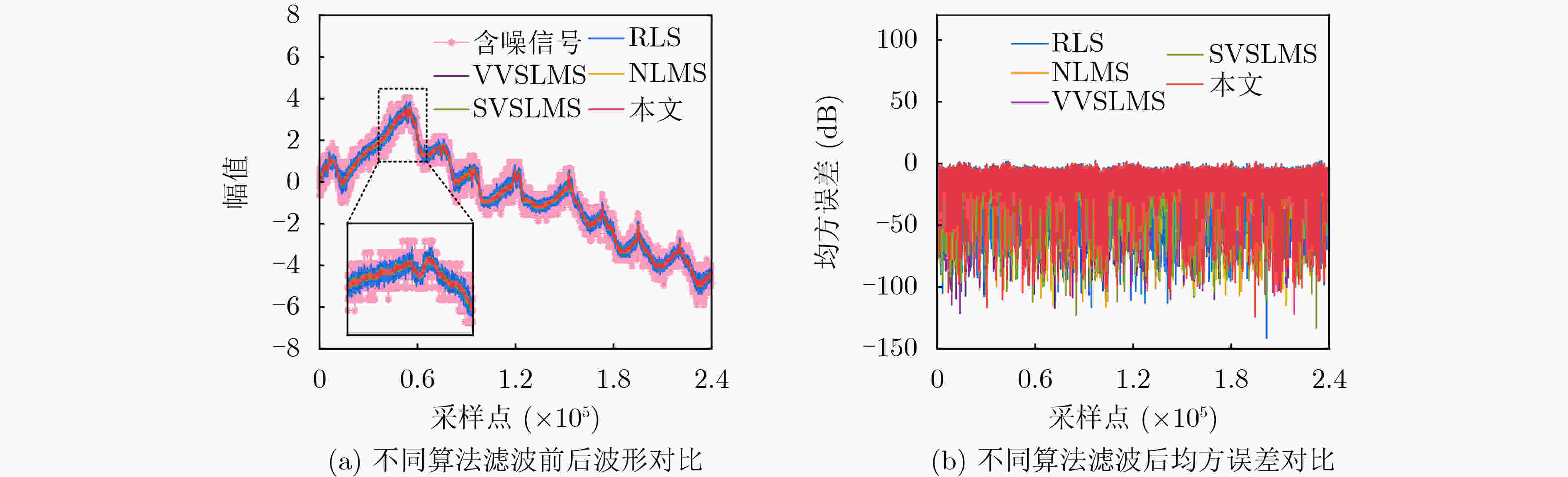
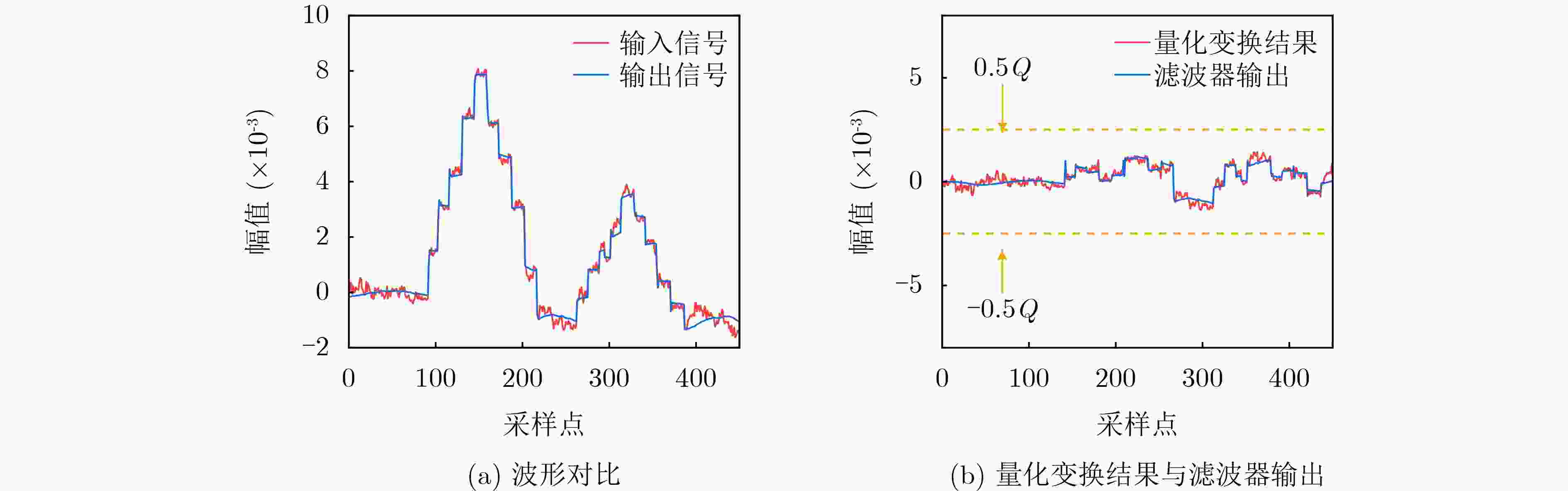
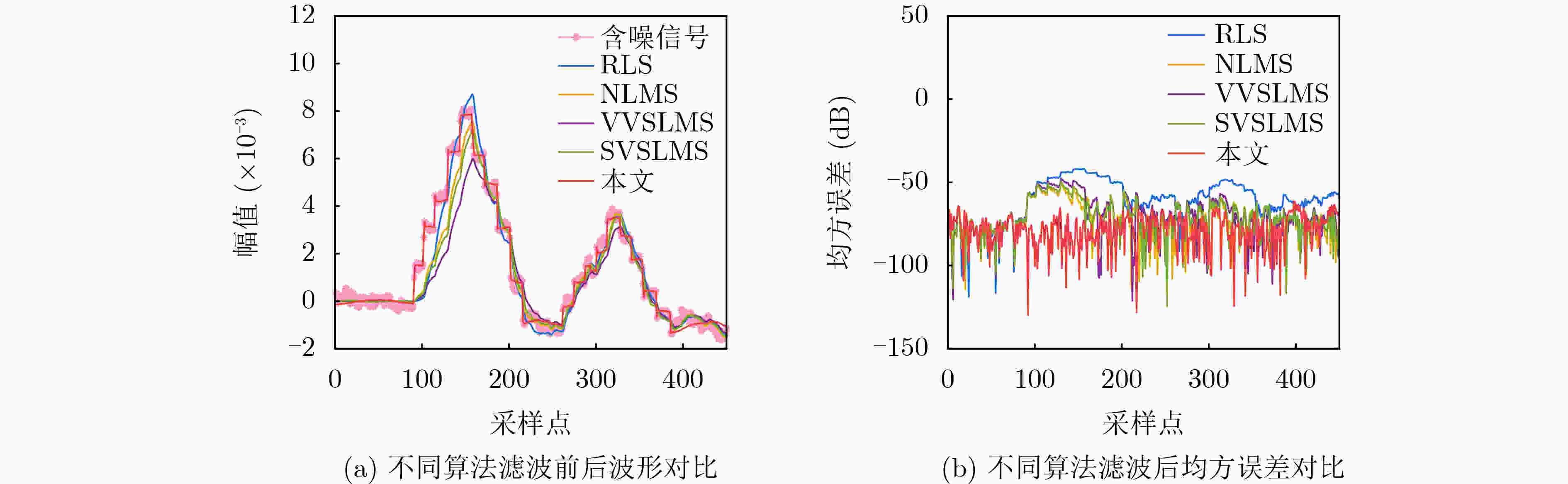
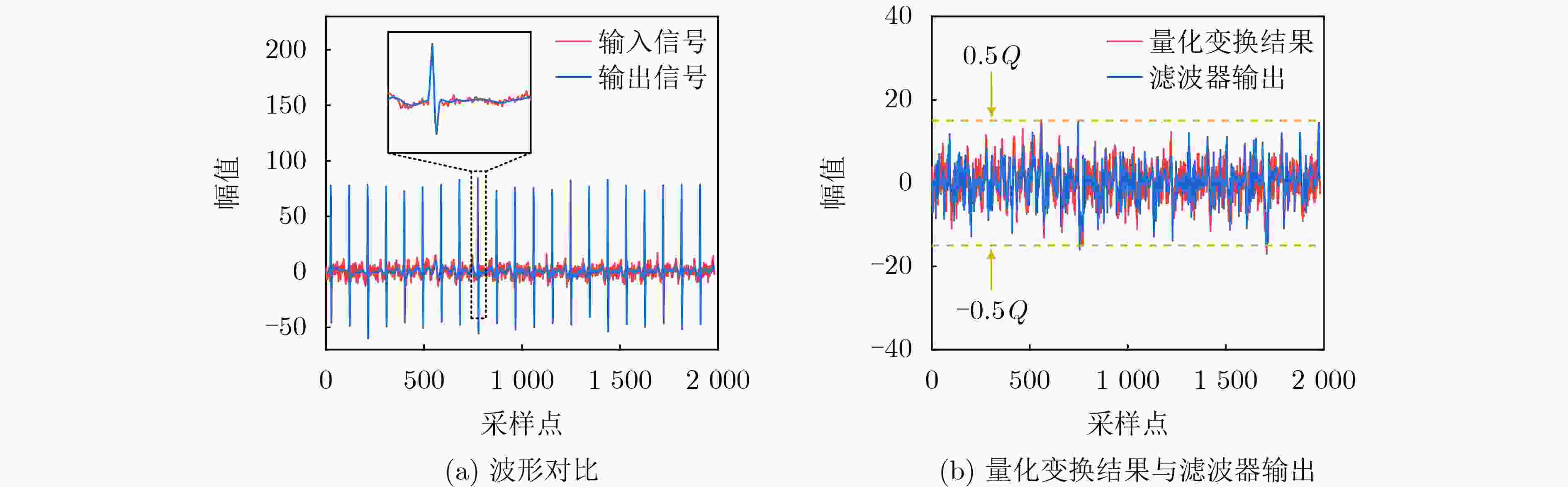
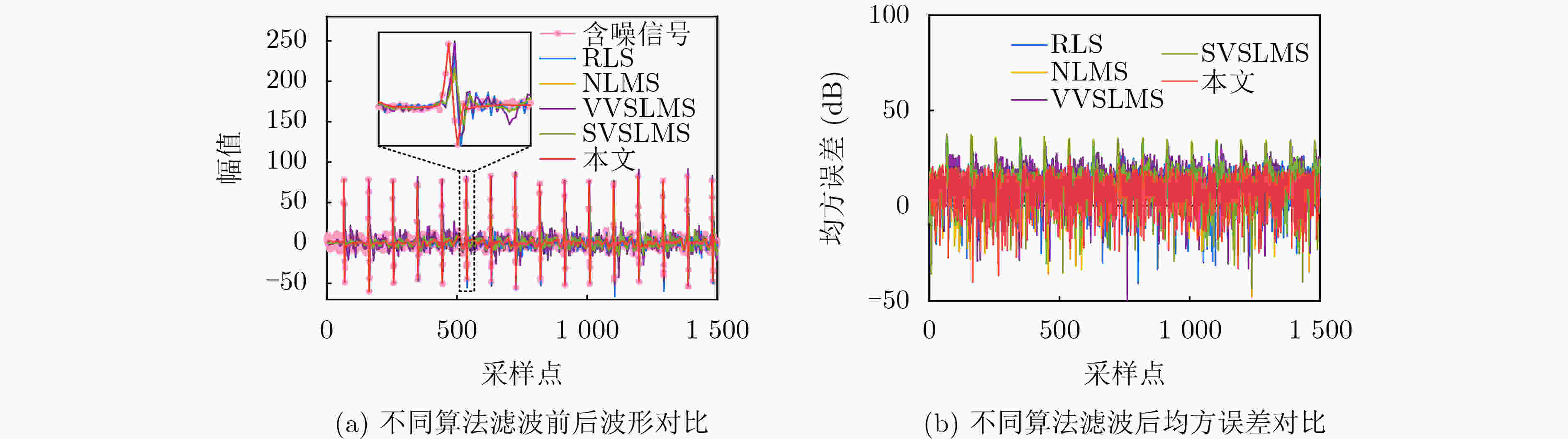
Objective Broadband noise is inevitable in sensing outputs due to thermal noise from the sensing system and various uncorrelated environmental disturbances. Adaptive filtering is a common method for removing such noise. At convergence, the adaptive filter output provides the optimal estimate of the sensing signal. However, during actual sensing, changes in the sensing signal lead to alterations in the statistical characteristics of the output. Therefore, the adaptive process must be re-adjusted to converge to a new steady state. The filter output during this adjustment is not the optimal estimate and introduces distortion, thereby adding extra noise. Fast-converging adaptive algorithms are typically employed to improve the filter’s response speed to such changes. Despite the speed of convergence and the methods used to update filter coefficients, the adjustment process remains unavoidable, during which the filter output is distorted, and additional noise is introduced. To ensure the filter remains at steady state without being influenced by changes in the sensing signal, a new adaptive filtering method is proposed. This method ensures that the input to the adaptive filter remains stationary, thereby preventing output distortion and the introduction of extra noise. Methods First, a threshold $ R $ and quantization scale $ Q $ are defined in terms of the noise standard deviation, $ \sigma $, where $ R = 3\sqrt 2 \sigma $ and $ Q = 3\sigma $. A quantization transformation is applied to the sensing output $ x(n) $ in real time, with the transformation result $ q(n) $ used as the new sequence to be filtered. When the absolute value of the first-order difference of $ x(n) $ is no less than $ R $, the sensing signal $ s(n) $ is considered to have changed, and $ p(n) $ is set as the quantization value of $ x(n) $ according to $ Q $. When the absolute value of the first-order difference of $ x(n) $ is less than $ R $, $ s(n) $ is considered unchanged, and $ p(n) $ is equal to the previous value, i.e., $ p(n) = p(n - 1) $. Let $ q(n) = x(n) - p(n) $, $ q(n) $ contains both the information of the sensing signal and the noise. Although its variance may change slightly, the mean of $ q(n) $ remains 0, ensuring that $ q(n) $ stays relatively stationary. Next, $ q(n - {n_0}) $ is used as the input to the adaptive filter, with $ q(n) $ serving as the reference for the adaptive filter. Here, $ q(n - {n_0}) $ represents the time delay of $ q(n) $ and $ {n_0} $ denotes the length of the time delay. This method performs adaptive linear prediction of $ q(n) $ and filters out broadband noise. Finally, the output of the adaptive filter, $ y(n) $, is compensated with $ p(n) $ to obtain an estimation of the sensing signal $ s(n) $ by removing noise. Results and Discussions The maximum mean square errors produced by the proposed method and conventional adaptive algorithms are compared using computer-simulated noisy band-limited step signals and noisy one-sided sinusoidal signals. Additionally, Signal-to-Noise Ratio (SNR) improvements obtained during filtering are also evaluated concurrently. For the noisy band-limited step signal ( Table 1 ), the maximum mean square error of the proposed method is only 0.18% of that produced by the Recursive Least Squares (RLS) algorithm and 0.15%~0.19% of those generated by the Least Mean Square (LMS) algorithms. Correspondingly, the SNR improvement is 25.88 dB higher than the RLS algorithm and between 28.65 dB and 32.35 dB greater than the LMS algorithms. In processing a noisy one-sided sinusoidal signal (Table 2 ), the maximum mean square error generated by the proposed method is 0.3% of that generated by the RLS algorithm and 0.06%~0.08% of that generated by the compared LMS algorithms. The SNR improvement is 10.25 dB higher than that of the RLS algorithm and 26.53 dB~29.61 dB higher than that of the compared LMS algorithms.Figures 3 and5 illustrate the quantization transformation outcomes for both the noisy band-limited step signal and noisy sinusoidal signal, demonstrating stability and consistency with theoretical expectations. Real sensing outputs primarily cover static or quasi-static signals (Figures 7 and8 ); step or step-like signals (Figures 9 and10 ), and periodic or quasi-periodic signals (Figures 11 and12 ). Comparative analysis of the proposed method against common adaptive algorithms on varied real sensing outputs consistently shows superior filtering performance by the proposed method, with minimal distortion and no additional noise introduction, regardless of whether the sensing signals undergo changes.Conclusions A new adaptive filtering method is proposed in this paper. The proposed method ensures that the adaptive filter always operates at a steady state, avoiding the introduction of additional noise caused by distortion during the adjustment to the new steady state. The results from computer simulations and actual signal processing demonstrate that the proposed method provides effective filtering for both dynamic and static sensing signals, indicating that it outperforms commonly used adaptive algorithms. -
Key words:
- Broadband noise /
- Noise suppression /
- Quantization /
- Real-time filtering /
- Adaptive algorithm
-
表 1 传感信号为带限阶跃信号时不同方法滤波效果对比(dB)
自适应算法 信噪比提升量 最大均方误差 本文 10.591 8 –27.716 5 RLS –15.286 7 –0.330 0 NLMS –20.883 2 –0.467 5 SVSLMS –21.761 1 0.503 4 VVSLMS –18.064 8 –0.429 7 表 2 传感信号为单边正弦信号时不同方法滤波效果对比(dB)
自适应算法 信噪比提升量 最大均方误差 本文 5.660 8 –48.215 0 RLS –4.586 1 –23,253 4 NLMS –20.866 3 –17.253 6 SVSLMS –22.038 0 –16.816 6 VVSLMS –23.950 7 –16.269 8 -
[1] LENSCHOW D H, WULFMEYER V, and SENFF C. Measuring second-through fourth-order moments in noisy data[J]. Journal of Atmospheric and Oceanic Technology, 2000, 17(10): 1330–1347. doi: 10.1175/1520-0426(2000)017<1330:Mstfom>2.0.Co;2. [2] 文玉梅, 谢仁峰, 杨进, 等. 管道泄漏检测中的噪声自适应抑制[J]. 仪器仪表学报, 2012, 33(10): 2228–2233. doi: 10.3969/j.issn.0254-3087.2012.10.011.WEN Yumei, XIE Renfeng, YANG Jin, et al. Adaptive noise suppression in pipeline leak detection[J]. Chinese Journal of Scientific Instrument, 2012, 33(10): 2228–2233. doi: 10.3969/j.issn.0254-3087.2012.10.011. [3] AKHTAR M T and MITSUHASHI W. Improving performance of hybrid active noise control systems for uncorrelated narrowband disturbances[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2011, 19(7): 2058–2066. doi: 10.1109/tasl.2011.2112349. [4] SUN Xun and KUO S M. Active narrowband noise control systems using cascading adaptive filters[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2007, 15(2): 586–592. doi: 10.1109/tasl.2006.881680. [5] WANG Ran, YU Longjing, WEI Chunhua, et al. Aerodynamic noise separation of helicopter main and tail rotors using a cascade filter with Vold-Kalman filter and cyclic wiener filter[J]. Applied Acoustics, 2022, 192: 108751. doi: 10.1016/j.apacoust.2022.108751. [6] VERED Y and ELLIOTT S. A parallel analog and digital adaptive feedforward controller for active noise control[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2024, 32: 1100–1108. doi: 10.1109/taslp.2024.3350882. [7] 陈建春, 耿富录, 徐少莹. 基于自适应线性预测滤波的反辐射导弹检测技术[J]. 电子学报, 2001, 29(6): 755–757. doi: 10.3321/j.issn:0372-2112.2001.06.009.CHEN Jianchun, GENG Fulu, and XU Shaoying. ARM detection technique based on adaptive linear prediction error filtering[J]. Acta Electronica Sinica, 2001, 29(6): 755–757. doi: 10.3321/j.issn:0372-2112.2001.06.009. [8] MA Yaping, XIAO Yegui, HUANG Boyan, et al. A robust feedback active noise control system with online secondary-path modeling[J]. IEEE Signal Processing Letters, 2022, 29: 1042–1046. doi: 10.1109/lsp.2022.3166396. [9] 高鹰, 谢胜利. 一种变步长LMS自适应滤波算法及分析[J]. 电子学报, 2001, 29(8): 1094–1097. doi: 10.3321/j.issn:0372-2112.2001.08.023.GAO Ying and XIE Shengli. A variable step size LMS adaptive filtering algorithm and its analysis[J]. Acta Electronica Sinica, 2001, 29(8): 1094–1097. doi: 10.3321/j.issn:0372-2112.2001.08.023. [10] 米建伟, 方晓莉, 仇原鹰. 非平稳背景噪声下声音信号增强技术[J]. 仪器仪表学报, 2017, 38(1): 17–22. doi: 10.3969/j.issn.0254-3087.2017.01.003.MI Jianwei, FANG Xiaoli, and QIU Yuanying. Enhancement technology for the audio signal with nonstationary background noise[J]. Chinese Journal of Scientific Instrument, 2017, 38(1): 17–22. doi: 10.3969/j.issn.0254-3087.2017.01.003. [11] LUO Zhengding, SHI Dongyuan, SHEN Xiaoyi, et al. GFANC-Kalman: Generative fixed-filter active noise control with CNN-Kalman filtering[J]. IEEE Signal Processing Letters, 2024, 31: 276–280. doi: 10.1109/lsp.2023.3334695. [12] SHI Jiaming and ZHU Huangqiu. Control study for compensating rotor vibration of four-DOF six-pole hybrid magnetic bearings based on variable step size LMS algorithm[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023, 11(2): 1616–1626. doi: 10.1109/jestpe.2022.3222656. [13] 火元莲, 龙小强, 连培君, 等. 一种类箕舌线函数的变步长归一化自适应滤波算法[J]. 电子与信息学报, 2021, 43(2): 335–340. doi: 10.11999/JEIT191003.HUO Yuanlian, LONG Xiaoqiang, LIAN Peijun, et al. A kind of versoria function normalized adaptive filtering algorithm[J]. Journal of Electronics & Information Technology, 2021, 43(2): 335–340. doi: 10.11999/JEIT191003. [14] TIGLEA D G, CANDIDO R, and SILVA M T M. A variable step size adaptive algorithm with simple parameter selection[J]. IEEE Signal Processing Letters, 2022, 29: 1774–1778. doi: 10.1109/lsp.2022.3195662. [15] PATEL V, BHATTACHARJEE S S, and CHRISTENSEN M G. Generalized soft-root-sign based robust sparsity-aware adaptive filters[J]. IEEE Signal Processing Letters, 2023, 30: 200–204. doi: 10.1109/lsp.2023.3252412. [16] KUMAR K, KARTHIK M L N S, and GEORGE N V. A novel family of sparsity-aware robust adaptive filters based on a logistic distance metric[J]. IEEE Transactions on Signal Processing, 2022, 70: 6128–6141. doi: 10.1109/tsp.2022.3233528. [17] JALAL B, YANG Xiaopeng, LIU Quanhua, et al. Fast and robust variable-step-size LMS algorithm for adaptive beamforming[J]. IEEE Antennas and Wireless Propagation Letters, 2020, 19(7): 1206–1210. doi: 10.1109/lawp.2020.2995244. [18] ELEFTHERIOU E and FALCONER D. Tracking properties and steady-state performance of RLS adaptive filter algorithms[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1986, 34(5): 1097–1110. doi: 10.1109/tassp.1986.1164950. [19] GODARA L C. Application of antenna arrays to mobile communications. II. Beam-forming and direction-of-arrival considerations[J]. Proceedings of the IEEE, 1997, 85(8): 1195–1245. doi: 10.1109/5.622504. [20] WANG Shengyu, JI Bowen, SHAO Dian, et al. A methodology for enhancing SSVEP features using adaptive filtering based on the spatial distribution of EEG signals[J]. Micromachines, 2023, 14(5): 976. doi: 10.3390/mi14050976. [21] 邓洪高, 余润华, 纪元法, 等. 偏差未补偿自适应边缘化容积卡尔曼滤波跟踪方法[J]. 电子与信息学报, 2025, 47(1): 156–166. doi: 10.11999/JEIT240469.DENG Honggao, YU Runhua, JI Yuanfa, et al. An adaptive target tracking method utilizing marginalized cubature Kalman filter with uncompensated biases[J]. Journal of Electronics & Information Technology, 2025, 47(1): 156–166. doi: 10.11999/JEIT240469. [22] VINOKUR M. Amplitude-quantised sample of unknown signal plus noise[J]. Proceedings of the Institution of Electrical Engineers, 1971, 118(3/4): 622–625. doi: 10.1049/piee.1971.0109. -





 下载:
下载:


 下载:
下载:
