融合兴趣点和联合损失函数的长时航迹预测模型

周传鑫; 简刚; 李凌书; 杨壹; 胡宇; 刘正铭; 张伟; 饶真珍; 李云霄; 吴超

doi:10.11999/JEIT250011

融合兴趣点和联合损失函数的长时航迹预测模型

doi: 10.11999/JEIT250011 cstr: 32379.14.JEIT250011

西南电子电信所成都 610000

详细信息

作者简介:
周传鑫：男，硕士，助理工程师，研究方向为人工智能、大数据分析

简刚：男，硕士，助理研究员，研究方向为大数据分析、大模型

李凌书：男，博士，助理研究员，研究方向为人工智能、大模型

杨壹：男，硕士，助理工程师，研究方向为人工智能、大模型

胡宇：男，硕士，助理研究员，研究方向为数据分析、人工智能

刘正铭：男，硕士，助理研究员，研究方向为数据分析、深度学习

张伟：男，硕士，副研究员，研究方向为数据分析、人工智能

饶真珍：女，硕士，助理研究员，研究方向为数据分析、深度学习

李云霄：男，硕士，助理研究员，研究方向为数据分析、人工智能

吴超：男，硕士，助理研究员，研究方向为数据分析、深度学习

通讯作者:
简刚　lyonardo@163.com

中图分类号: TN919.81; TP391.41
计量
- 文章访问数: 136
- HTML全文浏览量: 67
- PDF下载量: 17
- 被引次数: 0
出版历程
- 收稿日期: 2025-01-07
- 修回日期: 2025-07-10
- 网络出版日期: 2025-07-17
- 刊出日期: 2025-08-27

Long-Term Trajectory Prediction Model Based on Points of Interest and Joint Loss Function

Southwest Electronics and Telecommunications Institute, Chengdu 610000, China

摘要

摘要: 航迹预测在飞机舰船交通管理、路径规划和安全监测等领域具有重要意义。针对现有Transformer模型在航迹预测任务中存在的训练收敛速度慢、模型过拟合、长时误差大等问题，该文提出一种融合兴趣点和联合损失函数的长时航迹预测模型(PL-Transformer)。首先，通过专家经验定义预测范围内兴趣点的位置，引入航迹范围内待预测轨迹点与兴趣点间的关联特征，联合已有特征并转化为数据特征的稀疏表示，增强模型对运动航迹的全局特征捕捉能力，解决Transformer模型仅关注航迹自身局部特征变化的问题；其次，通过优化损失函数，将模型经纬度特征与兴趣点特征损失相关联，挖掘不同特征间的内涵损失，从而提高对航迹的长时预测精度。实验结果表明，PL-Transformer模型在较长时间尺度的航迹预测任务中，相较于基准长时模型预测误差平均降低了约10%，验证了该模型在航迹预测中的有效性与可靠性。
- 航迹预测 /
- Transformer /
- 兴趣点 /
- 损失函数优化
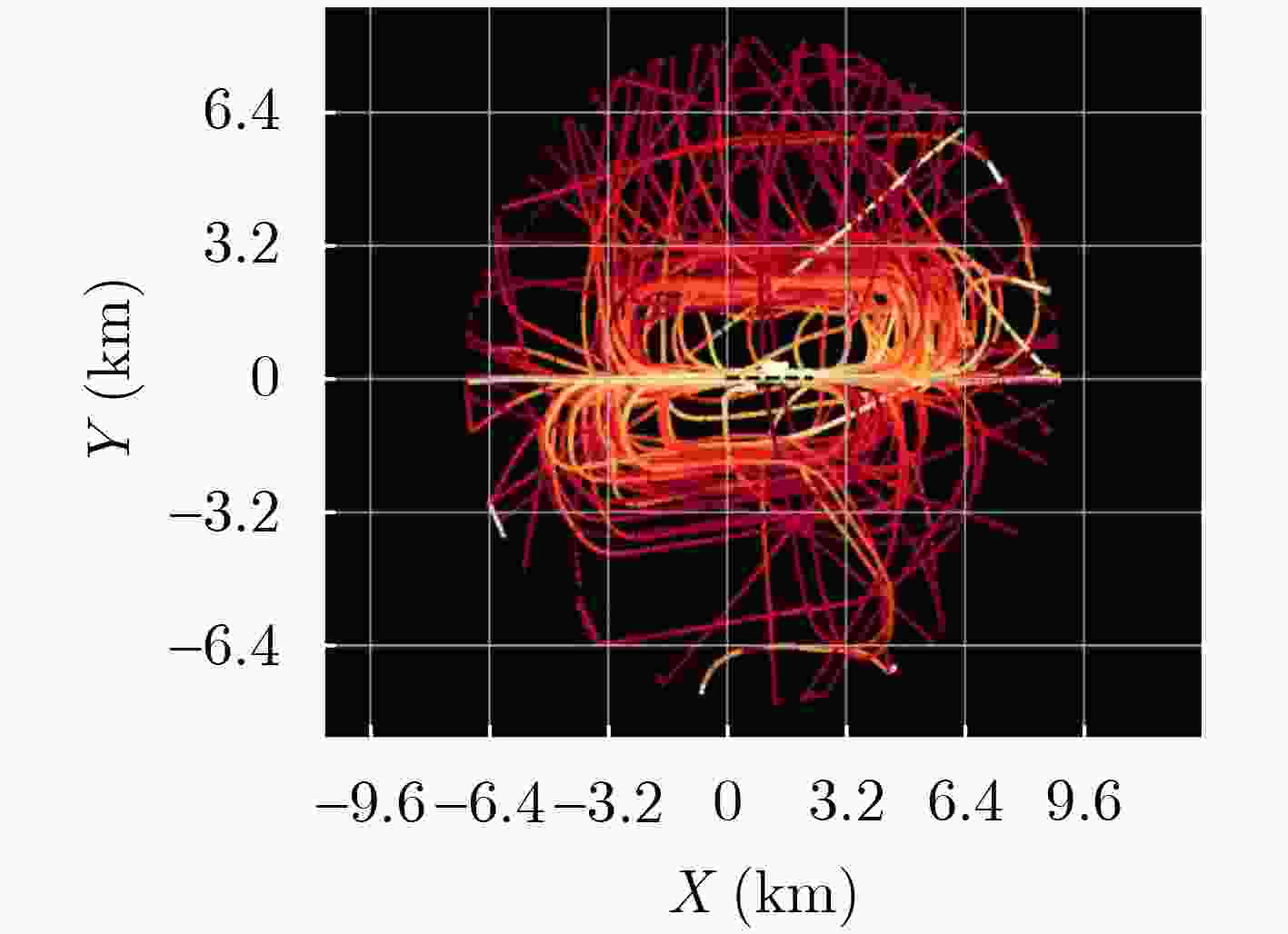
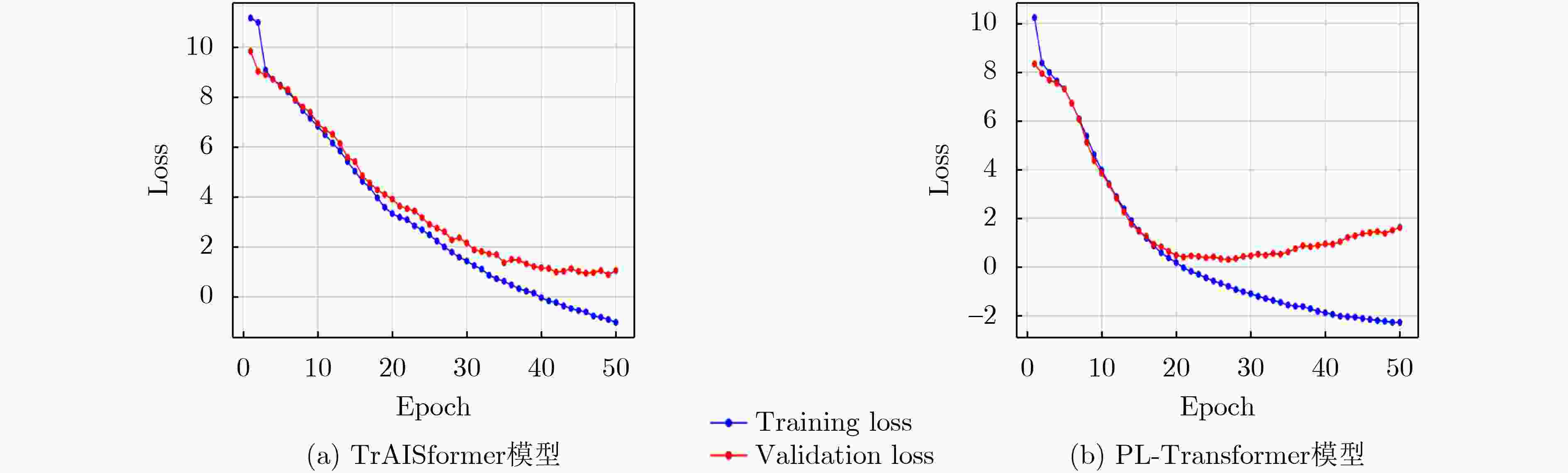
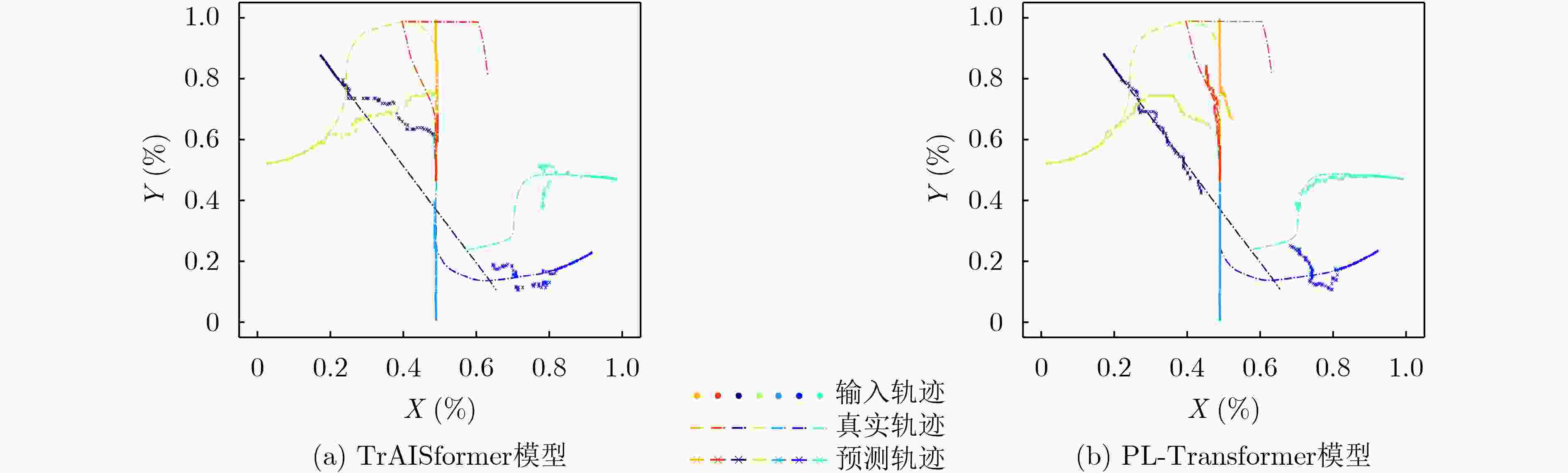
Abstract: Objective With the rapid development of modern maritime and aerospace sectors, trajectory prediction plays an increasingly critical role in applications such as ship scheduling, aviation, and security. Growing demand for higher prediction accuracy exposes limitations in traditional methods, such as Kalman filtering and Markov chains, which struggle with complex, nonlinear trajectory patterns and fail to meet practical needs. In recent years, deep learning techniques, including LSTM, GRU, CNN, and TCN models, have demonstrated notable advantages in trajectory prediction by effectively capturing time series features. However, these models still face challenges in representing the heterogeneity and diversity of trajectory data, with limited capacity to extract features from multidimensional inputs. To address these gaps, this study proposes a long-term trajectory prediction model, PL-Transformer, based on points of interest and a joint loss function. Methods Building on the TrAISformer framework, the proposed PL-Transformer incorporates points of interest and a joint loss function to enhance long-term trajectory prediction. The model defines the positions of points of interest within the prediction range using expert knowledge and introduces correlation features between trajectory points and points of interest. These features are integrated into a sparse data representation that improves the model’s ability to capture global trajectory patterns, addressing the limitation of conventional Transformer models, which primarily focus on local feature changes. Additionally, the model employs a joint loss function that links latitude and longitude predictions with feature losses associated with points of interest. This approach leverages inter-feature loss relationships to enhance the model’s capability for accurate long-term trajectory prediction. Results and Discussions The convergence performance of the PL-Transformer model is evaluated by analyzing the variation in training and validation losses and comparing them with those of the TrAISformer model. The corresponding loss curves are presented in (Fig. 5). The PL-Transformer model exhibits faster convergence and improved training stability on both datasets. These results indicate that the introduction of the joint loss function enhances convergence efficiency and training stability, yielding performance superior to the TrAISformer model. In terms of short-term prediction accuracy, the results in Table 1 show that the PL-Transformer model achieves comparable overall prediction accuracy to the TrAISformer model. The PL-Transformer model performs better in terms of the Mean Absolute Percentage Error (MAPE) metric, while it shows slightly higher errors than the TrAISformer model for Mean Absolute Error (MAE), median Absolute Error (MdAE), and coefficient of determination (R²). For the widely used Mean Squared Error (MSE) metric, both models perform similarly. These results indicate that after incorporating points of interest and optimizing the loss function, the PL-Transformer model retains competitive performance in relative error control and fitting accuracy, while preserving the stability and robustness of the TrAISformer model in complex trajectory prediction tasks. For long-term prediction visualization, Table 2 presents the loss values for both models across medium to long-term prediction horizons (1 to 3 h). The PL-Transformer model achieves better long-term prediction accuracy than the TrAISformer model. Specifically, the loss for the PL-Transformer model increases from 2.058 (1 h) to 5.561 (3 h), whereas the TrAISformer model’s loss rises from 2.160 to 6.145 over the same period. In terms of time complexity analysis, although the PL-Transformer model incorporates additional feature engineering and joint loss computation steps, these enhancements do not substantially increase the overall time complexity. The total computational complexity of the PL-Transformer model remains consistent with that of the TrAISformer model. Conclusions This study proposes the PL-Transformer model, which incorporates points of interest and an optimized loss function to address the challenges posed by complex dynamic features and heterogeneity in trajectory prediction tasks. By introducing distance and bearing angle through feature engineering and designing a joint loss function, the model effectively learns and captures spatial and motion characteristics within trajectory data. Experimental results demonstrate that the PL-Transformer model achieves higher prediction accuracy, faster convergence, and greater robustness than the TrAISformer model and other widely used baseline models, particularly in long-term and complex dynamic trajectory prediction scenarios. Despite the strong performance of the PL-Transformer model in experimental settings, trajectory prediction tasks in real-world applications remain affected by various challenges, including data noise, high-frequency trajectory fluctuations, and the influence of external environmental factors. Future research will focus on improving the model’s adaptability to multimodal trajectory data, integrating multi-source information to enhance generalization capability, and incorporating additional feature engineering and optimization strategies to address more complex prediction tasks. In summary, the proposed PL-Transformer model provides an effective advancement for Transformer-based trajectory prediction frameworks and offers valuable reference for practical applications in trajectory forecasting and related fields.
- Trajectory prediction /
- Transformer /
- Points of interest /
- Loss function optimization

HTML全文

图 1 PL-Transformer模型预测过程

下载: 全尺寸图片幻灯片

图 2 数据特征稀疏表示

下载: 全尺寸图片幻灯片

图 3 航迹预测空间中的兴趣点

下载: 全尺寸图片幻灯片

图 4 TrajAir数据集可视化展示

下载: 全尺寸图片幻灯片

图 5 模型训练过程loss曲线图

下载: 全尺寸图片幻灯片

图 6 航迹预测可视化

下载: 全尺寸图片幻灯片

1 PL-Transformer模型算法

输入：训练集$ \{ {{\boldsymbol{x}}_{0:L}}\} $，训练模型参数$ \theta $，学习率$ \eta $，分类区域　R，速度sog，方向角cog。
输出：模型训练参数$ \theta $。
for $ {{\boldsymbol{x}}_{0:L}} $ in $ \{ {{\boldsymbol{x}}_{0:L}}\} $ do
// 根据经纬度，计算与兴趣点A的距离和方向角
$ d_i^{{{\mathrm{A}}}},\theta _i^{{{\mathrm{A}}}} = {R_{{\mathrm{lat}}}},{R_{{\mathrm{lon}}}} $
for t in 0: L do
// 对每个时刻向量进行one-hot编码
$ {{\boldsymbol{h}}_t} = {\mathrm{onehot}}({R_{{\mathrm{lat}}}},{R_{{\mathrm{lon}}}},{\mathrm{cog}},{\mathrm{sog}},d_i^{{{\mathrm{A}}}},\theta _i^{{{\mathrm{A}}}}) $
end
// embedding编码和transformer模型
$ {{\boldsymbol{e}}_t} = {\mathrm{embedding}}({{\boldsymbol{h}}_t}) $
$ {{\boldsymbol{p}}_t} = {\mathrm{transformer}}({{\boldsymbol{e}}_t}) $
// 损失计算
$ {\mathrm{loss}} = 0 $
for l in 1: L do
$ {\mathrm{loss}} = {\mathrm{loss}} + \ell ({{\boldsymbol{h}}_t},{{\boldsymbol{p}}_t}) $
end
// 优化函数
$ \theta = {\mathrm{AdamW}}({\mathrm{loss}},\theta ,{{\boldsymbol{x}}_{0:L}}) $
end
Return: $ \theta $

下载: 导出CSV

表 1 不同算法的评价指标值情况(×10^–3)

指标	MSE	MAE	MdAE	R²	MAPE
GRU	0.187	6.484	4.874	994.974	19.214
LSTM	0.255	12.695	10.663	996.164	54.235
TrAISformer	0.122	3.130	1.889	996.628	17.817
PL-Transformer	0.122	3.172	1.904	996.426	15.317

下载: 导出CSV

表 2 长期预测性能(km)

模型	1 h	2 h	3 h
TrAISformer	2.160	4.195	6.145
PL-Transformer	2.058	3.815	5.561

下载: 导出CSV

参考文献(14)

[1]	SHUKLA P, SHUKLA S, and SINGH A K. Trajectory-prediction techniques for unmanned aerial vehicles (UAVs): A comprehensive survey[J]. IEEE Communications Surveys & Tutorials, 2025, 27(3): 1867–1910. doi: 10.1109/COMST.2024.3471671.
[2]	LIU Mengmeng, CHENG Hao, CHEN Lin, et al. LAformer: Trajectory prediction for autonomous driving with lane-aware scene constraints[C]. The 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, USA, 2024: 2039–2049. doi: 10.1109/cvprw63382.2024.00209.
[3]	CONG Peichao, DENG Murong, XIAO Yixuan, et al. Trajectory prediction based on the dynamic characteristics and coupling relationships among vehicles in highway scenarios[J]. Engineering Applications of Artificial Intelligence, 2025, 140: 109718. doi: 10.1016/j.engappai.2024.109718.
[4]	SHIN G H and YANG H. Vessel trajectory prediction in harbors: A deep learning approach with maritime-based data preprocessing and Berthing Side Integration[J]. Ocean Engineering, 2025, 316: 119908. doi: 10.1016/j.oceaneng.2024.119908.
[5]	张鹏, 杨涛, 刘亚楠, 等. 基于CNN-LSTM的QAR数据特征提取与预测[J]. 计算机应用研究, 2019, 36(10): 2958–2961. doi: 10.19734/j.issn.1001-3695.2018.04.0214. ZHANG Peng, YANG Tao, LIU Yanan, et al. Feature extraction and prediction of QAR data based on CNN-LSTM[J]. Application Research of Computers, 2019, 36(10): 2958–2961. doi: 10.19734/j.issn.1001-3695.2018.04.0214.
[6]	XIE Guo, SHANG Gnqi, FEI Rong, et al. Motion trajectory prediction based on a CNN-LSTM sequential model[J]. Science China Information Sciences, 2020, 63(11): 212207. doi: 10.1007/s11432-019-2761-y.
[7]	NAN Tian, CAO Wengeng, WANG Zhe, et al. Evaluation of shallow groundwater dynamics after water supplement in North China Plain based on attention-GRU model[J]. Journal of Hydrology, 2023, 625: 130085. doi: 10.1016/j.jhydrol.2023.130085.
[8]	AMIN F, GHARAMI K, and SEN B. TrajectoFormer: Transformer-based trajectory prediction of autonomous vehicles with spatio-temporal neighborhood considerations[J]. International Journal of Computational Intelligence Systems, 2024, 17(1): 87. doi: 10.1007/s44196-024-00410-1.
[9]	VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need[C]. The 31st International Conference on Neural Information Processing Systems, Long Beach, USA, 2017: 6000–6010.
[10]	唐光旭. 基于Transformer和Bi-LSTM模型的船舶轨迹预测[J]. 珠江水运, 2024(17): 109–111. doi: 10.14125/j.cnki.zjsy.2024.17.024. TANG Guangxu. Ship trajectory prediction based on Transformer and Bi-LSTM model[J]. Pearl River Water Transport, 2024(17): 109–111. doi: 10.14125/j.cnki.zjsy.2024.17.024.
[11]	SHAFIENYA H and REGAN A C. 4D flight trajectory prediction using a hybrid deep learning prediction method based on ADS-B technology: A case study of Hartsfield–Jackson Atlanta international airport (ATL)[J]. Transportation Research Part C: Emerging Technologies, 2022, 144: 103878. doi: 10.1016/j.trc.2022.103878.
[12]	NGUYEN D and FABLET R. A transformer network with sparse augmented data representation and cross entropy loss for AIS-based vessel trajectory prediction[J]. IEEE Access, 2024, 12: 21596–21609. doi: 10.1109/ACCESS.2024.3349957.
[13]	PATRIKAR J, MOON B, OH J, et al. Predicting like a pilot: Dataset and method to predict socially-aware aircraft trajectories in non-towered terminal airspace[C]. 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, USA, 2022: 2525–2531. doi: 10.1109/ICRA46639.2022.9811972.
[14]	NGUYEN D, VADAINE R, HAJDUCH G, et al. GeoTrackNet—a maritime anomaly detector using probabilistic neural network representation of AIS tracks and a contrario detection[J]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(6): 5655–5667. doi: 10.1109/TITS.2021.3055614.