一种改进的交互多模型算法在机场运动目标跟踪中的应用

鲁其兴; 汤新民; 齐鸣; 管祥民

doi:10.11999/JEIT241150

一种改进的交互多模型算法在机场运动目标跟踪中的应用

doi: 10.11999/JEIT241150

1.
南京航空航天大学民航学院南京 211106
2.
中国民航大学天津市城市空中交通系统技术与装备重点实验室天津 300300
3.
中国民用航空局运行监控中心北京 100010
4.
中国民航管理干部学院民航通用航空运行重点实验室北京 100102

基金项目: 国家重点研发计划(2021YFB1600500)，国家自然科学基金(52072174)，中国民航管理干部学院民航通用航空运行重点实验室开放基金(CAMICKFJJ-2019-04)

详细信息

作者简介:
鲁其兴：男，博士生，研究方向为机场场面引导、跟踪预测、冲突避障、优化及控制

汤新民：男，教授，博士生导师，研究方向为智能网联交通控制工程

齐鸣：女，教授级高级工程师，研究方向为空管新技术研究及应用

管祥民：男：副教授，研究方向为无人机自主感知与避让

通讯作者:
汤新民　tangxinmin@nuaa.edu.cn

中图分类号: TN96; V19
计量
- 文章访问数: 32
- HTML全文浏览量: 13
- PDF下载量: 4
- 被引次数: 0
出版历程
- 收稿日期: 2024-12-30
- 修回日期: 2025-03-17
- 网络出版日期: 2025-03-27

An improved Interacting Multiple Model Algorithm and Its Application in Airport Moving Target Tracking

1.
College of Civil Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China
2.
Key Laboratory of Technology and Equipment of Tianjin Urban Air Transportation System, Civil Aviation University of China, Tianjin 300300, China
3.
Operation Monitoring Center, Civil Aviation Administration of China, Beijing 100010, China
4.
Key Laboratory of Civil Aviation General Aviation Operation, Civil Aviation Management Institute of China, Beijing 100102, China

Funds: The National Key Research and Development Program of China (2021YFB1600500), The National Natural Science Foundation of China (52072174), Open Fund for the Key Laboratory of Civil Aviation General Aviation Operations of China Civil Aviation Management Cadre College (CAMICKFJJ-2019-04)

摘要

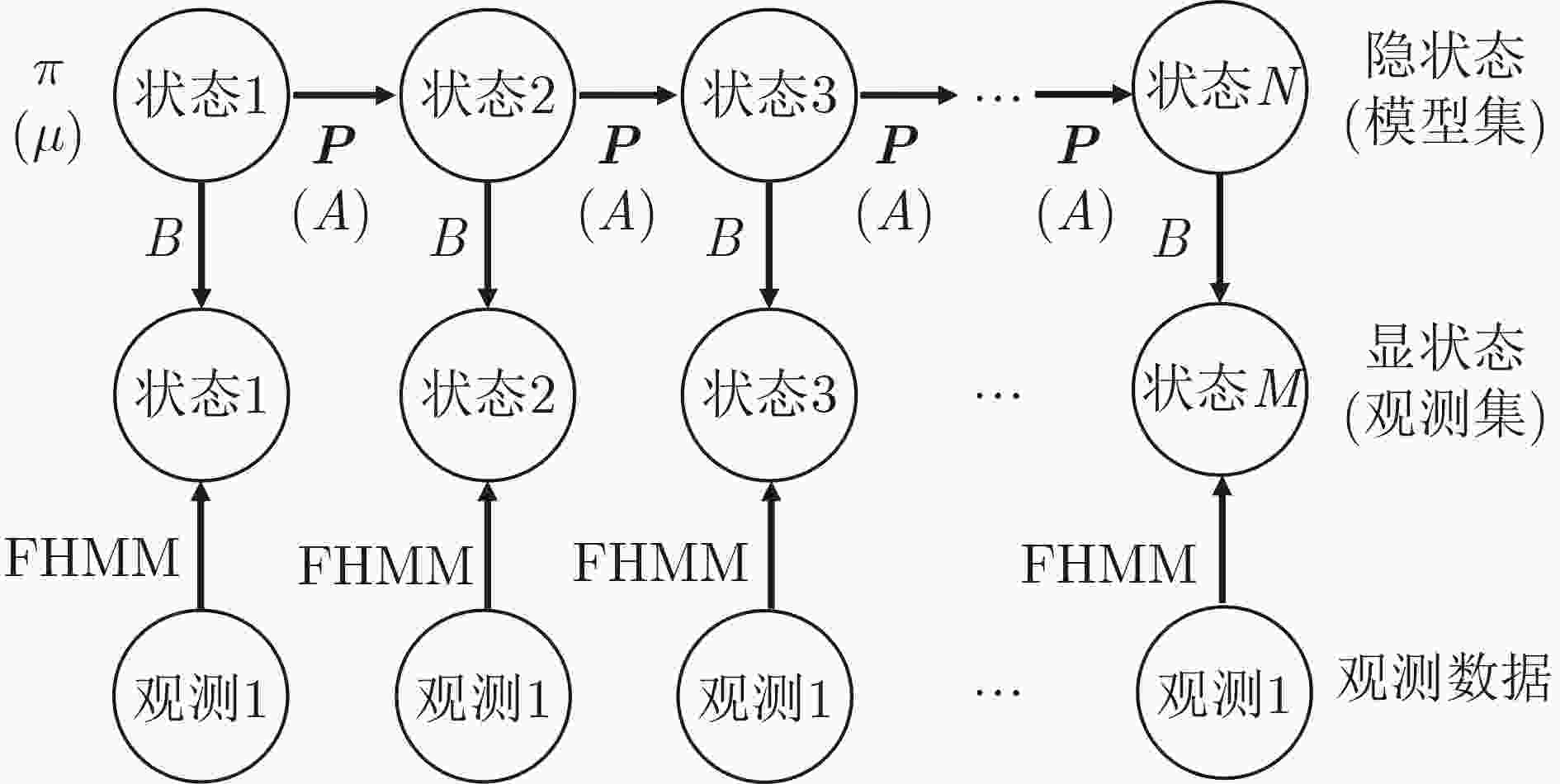
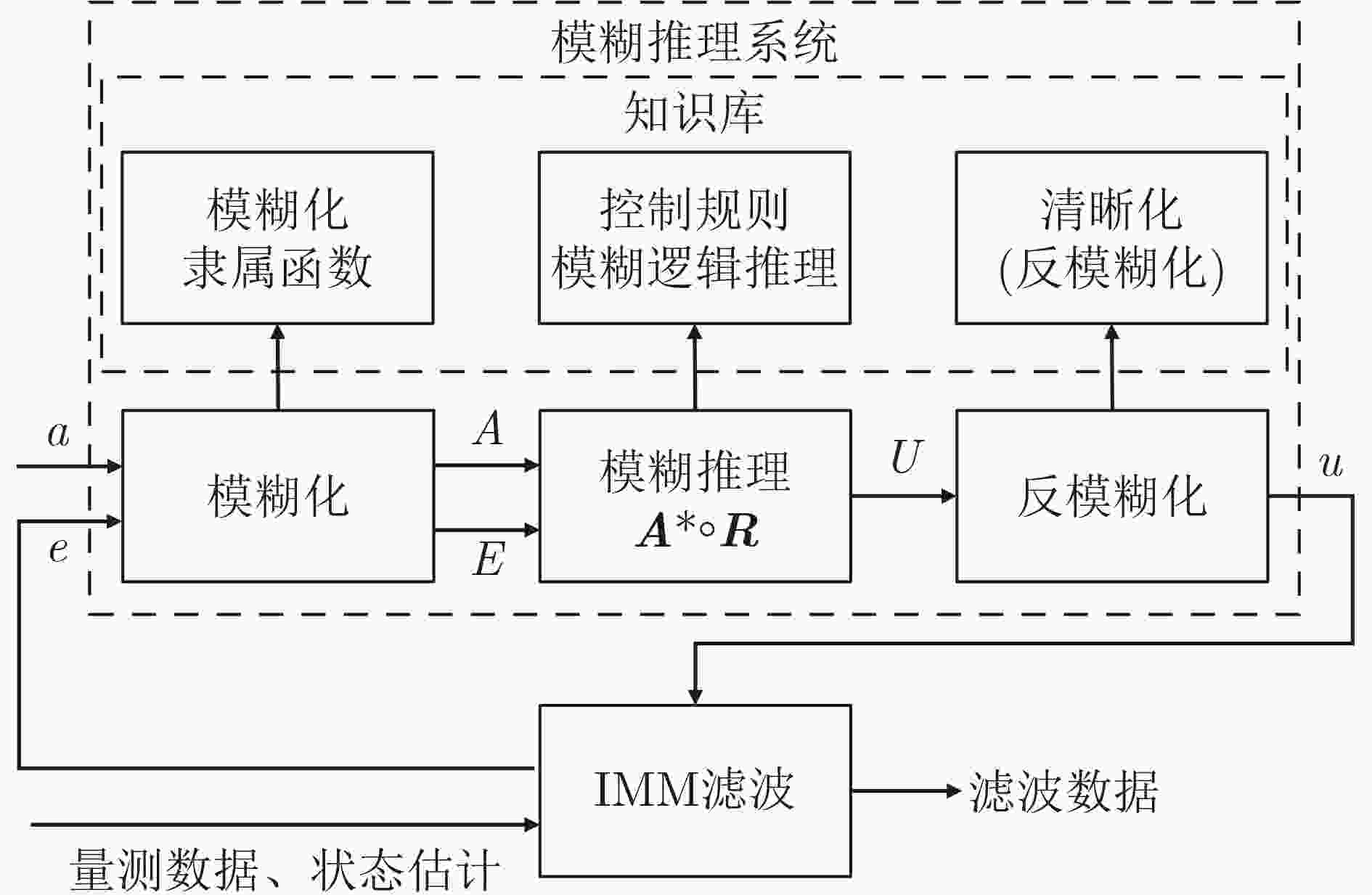
摘要: 为了提高场面监视效率，实现场面运动目标精准跟踪，考虑到传统交互多模型由于固定马尔可夫转移概率矩阵导致模型跟踪精度降低，该文提出一种转移概率自适应改进的交互多模型滤波算法。该算法利用观测数据和滤波残差数据，结合模糊推理算法，构建机动强弱模糊推理系统，推理出观测数据与隐马尔可夫显状态集合的映射关系，得到显状态集下的状态序列；根据隐马尔可夫模型中的Baum-Welch算法实时求解状态转移矩阵和更新观测概率矩阵，优化状态转移概率矩阵自适应更新策略；将机动强弱模糊推理系统和隐马尔可夫模型融入交互多模型算法中，构成机动目标实时估计的模糊隐马尔可夫-交互多模型算法，以提高跟踪精度；最后，基于实际场面ADS-B轨迹数据进行了验证，验证结果显示，改进后的交互多模型能够在非等间隔预测条件下实现参数的自适应调整，且在双维度4项统计指标中，位置跟踪精度方面分别提高了63.5%, 54.3%, 40.3%, 22.7%，速度和加速度的轨迹拟合精度均得到了提高，验证了改进算法的优越性。
- 目标跟踪 /
- 交互多模型 /
- ADS-B /
- 转移概率矩阵 /
- 跟踪误差
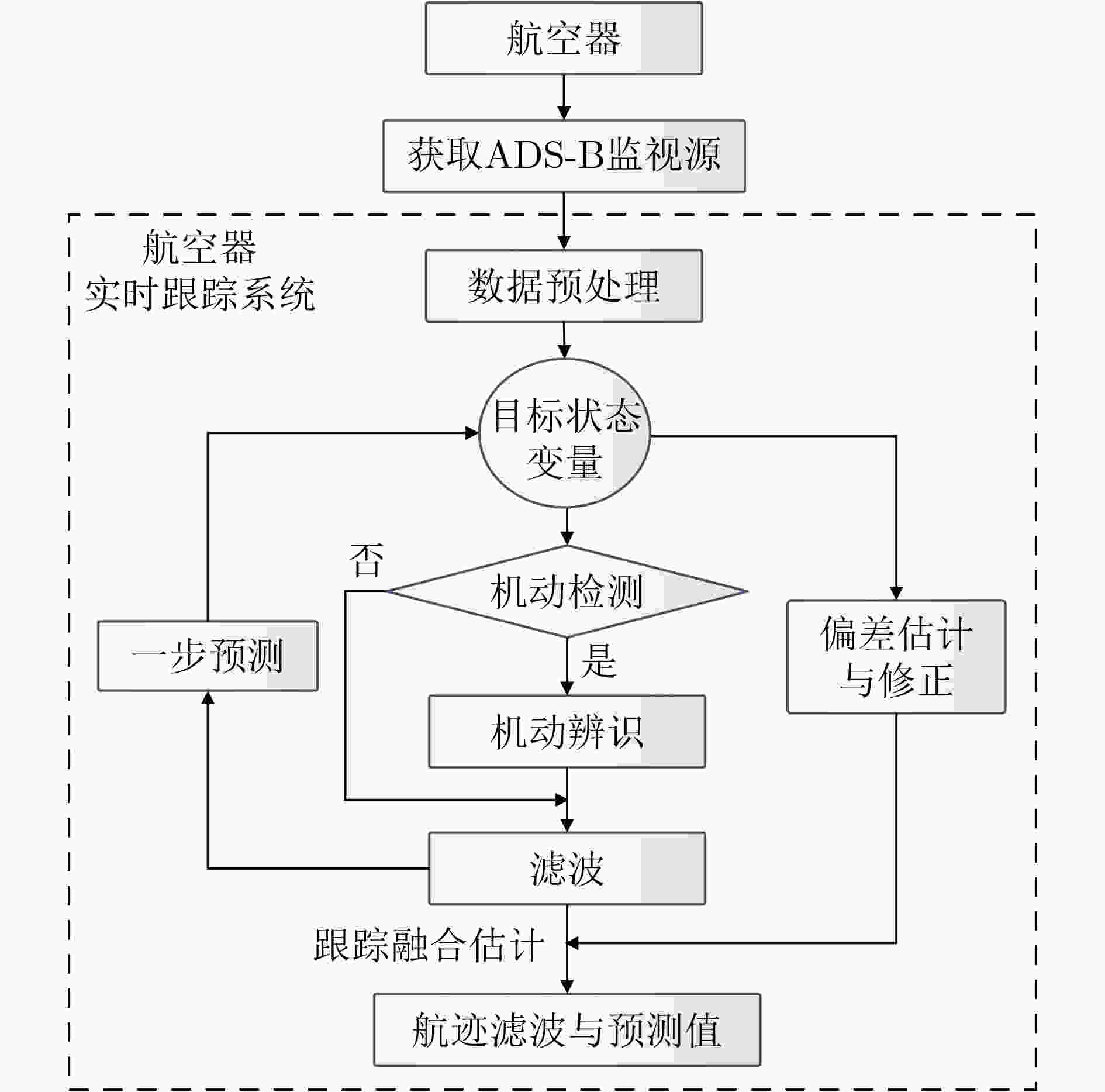
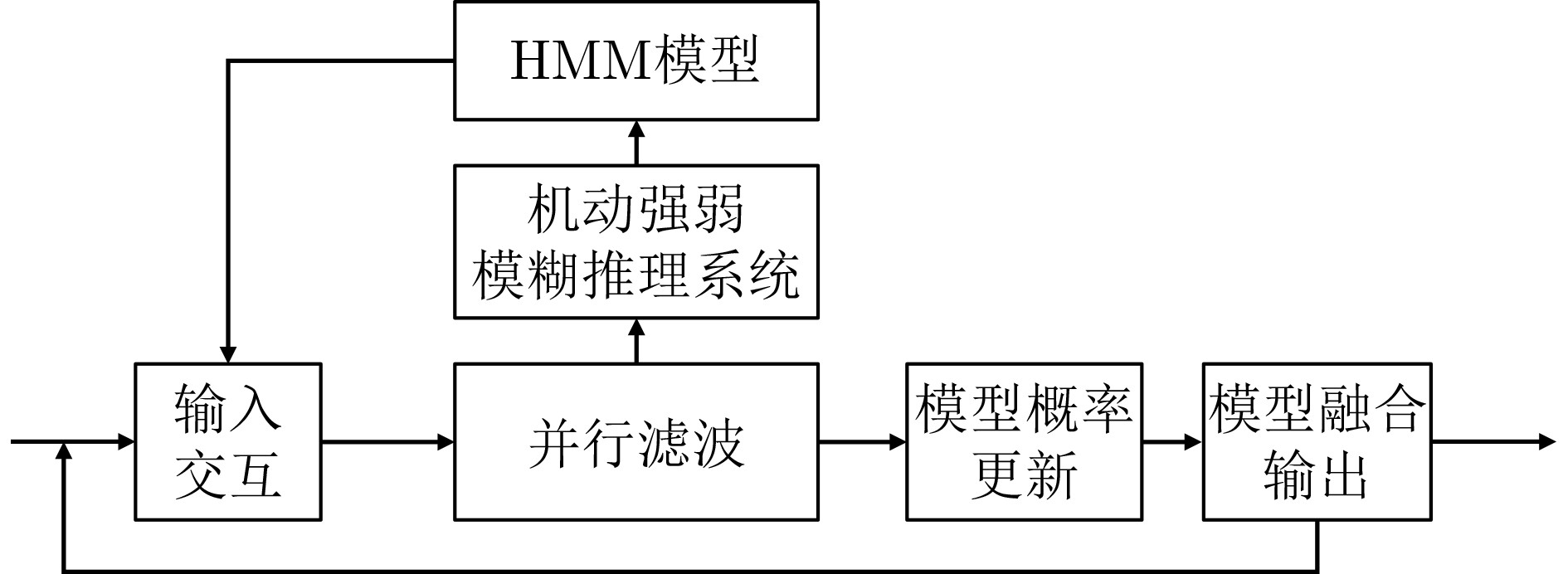
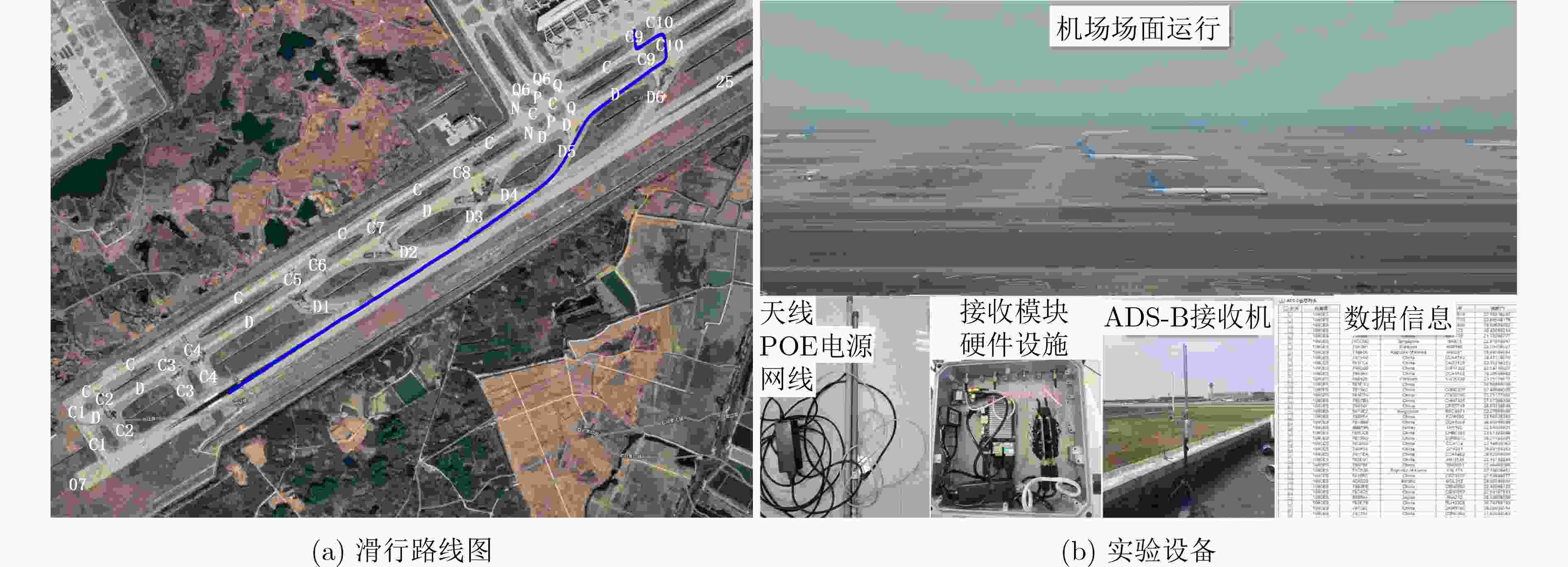
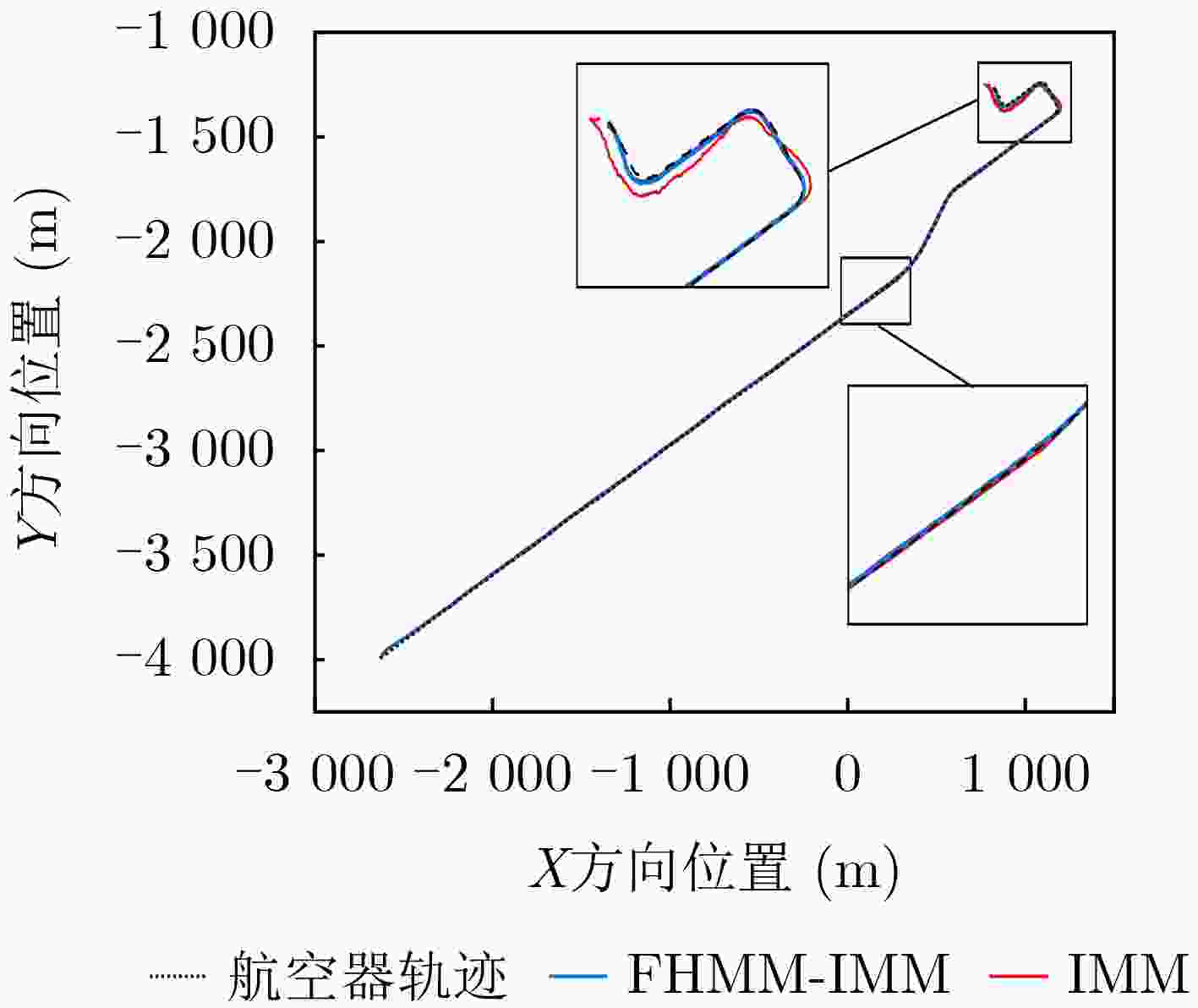
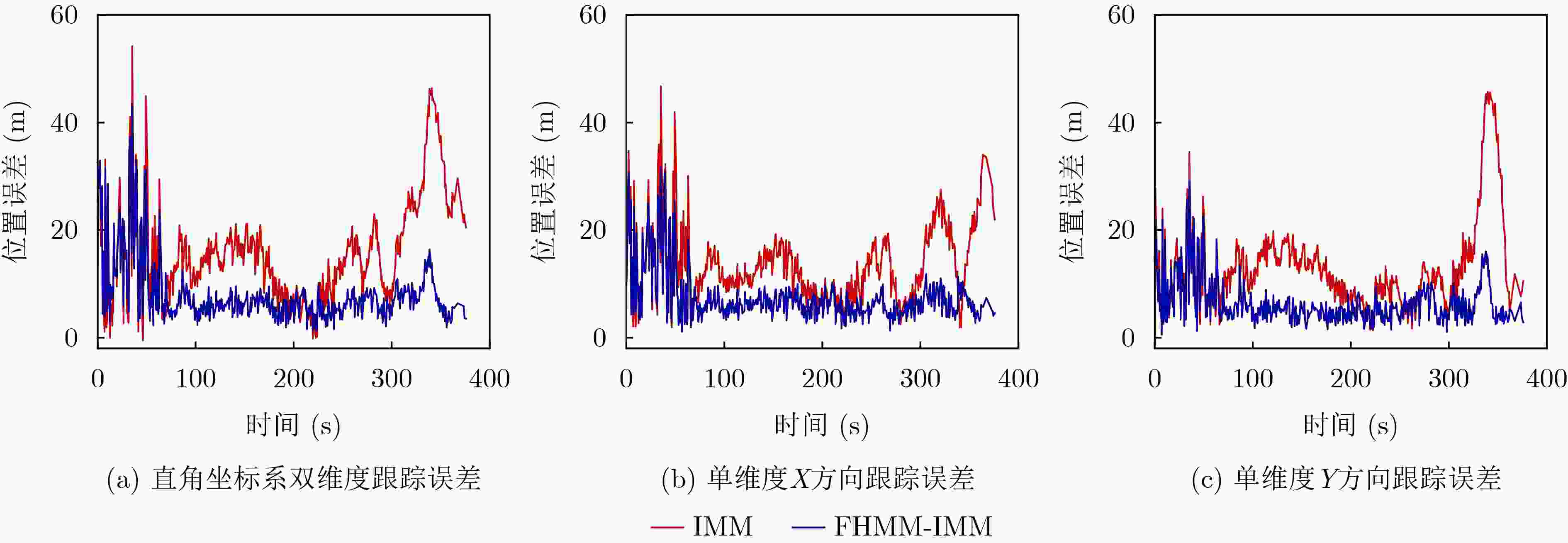
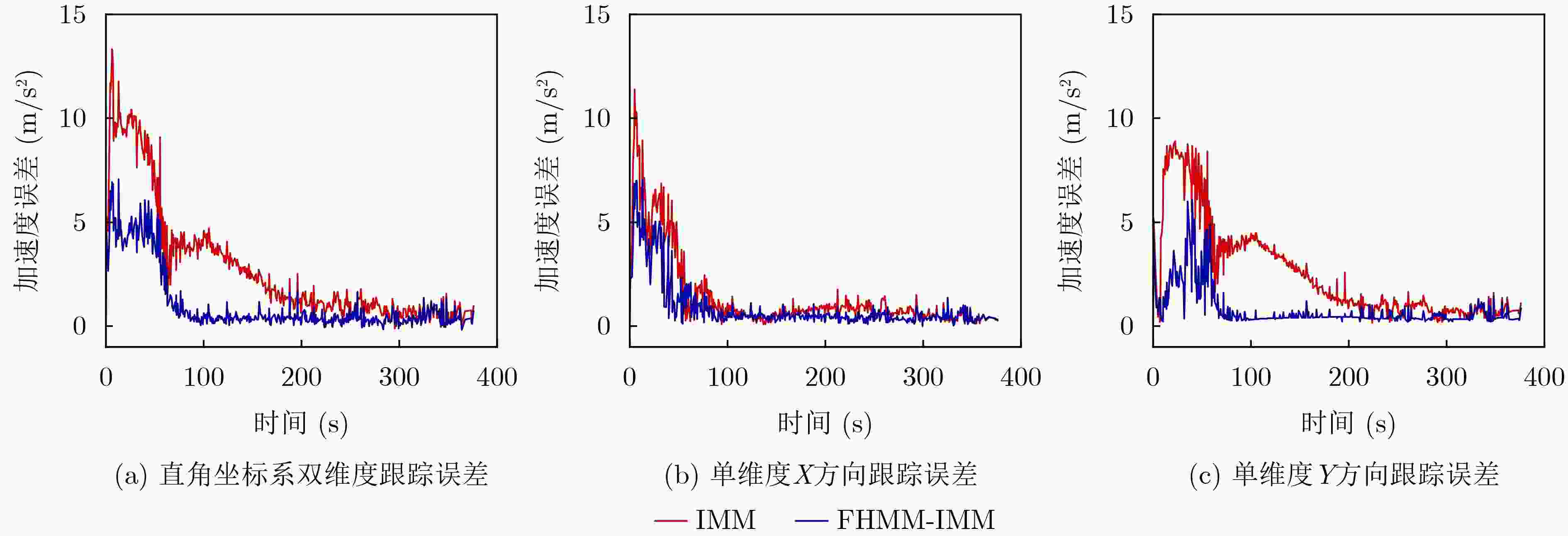
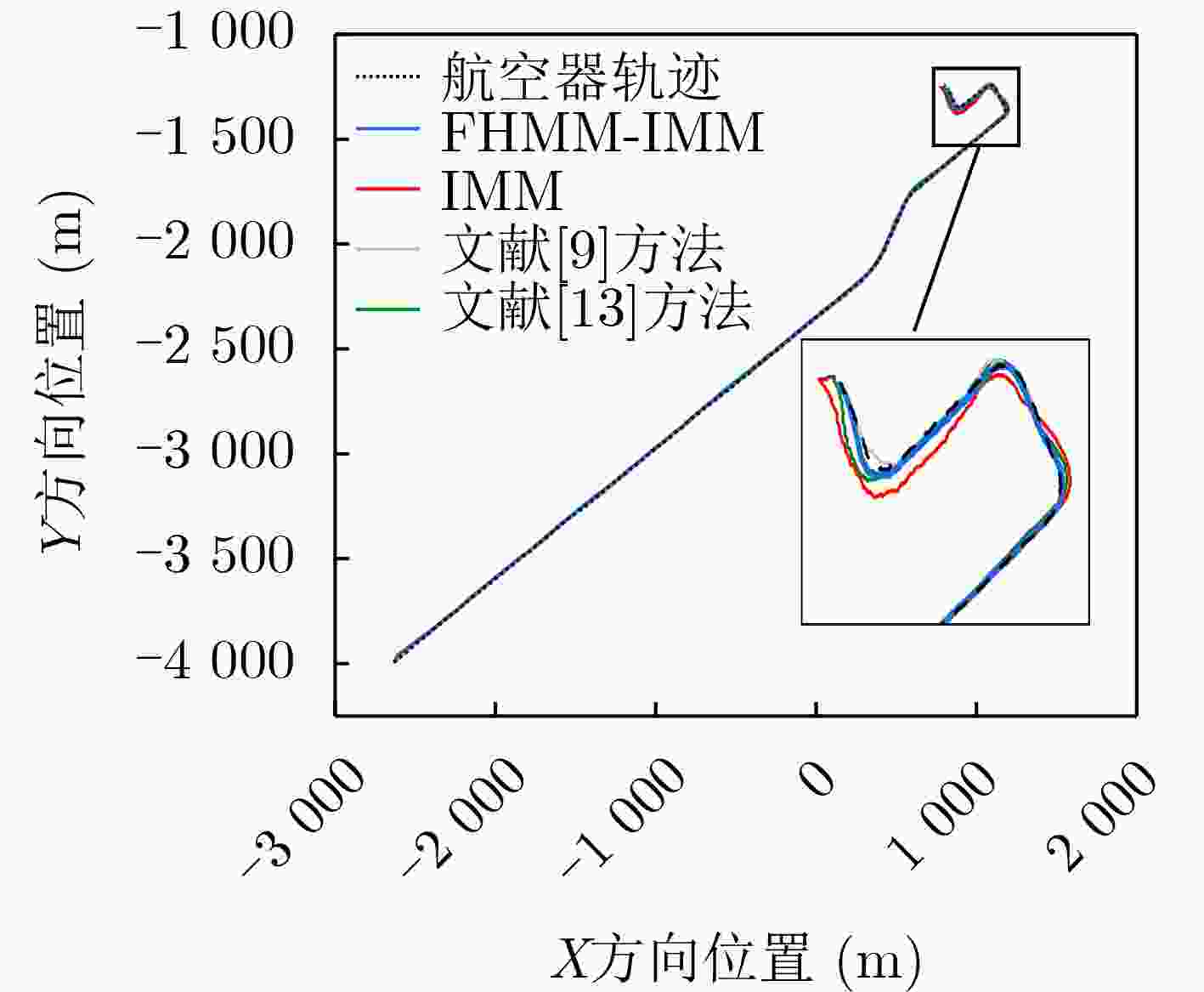
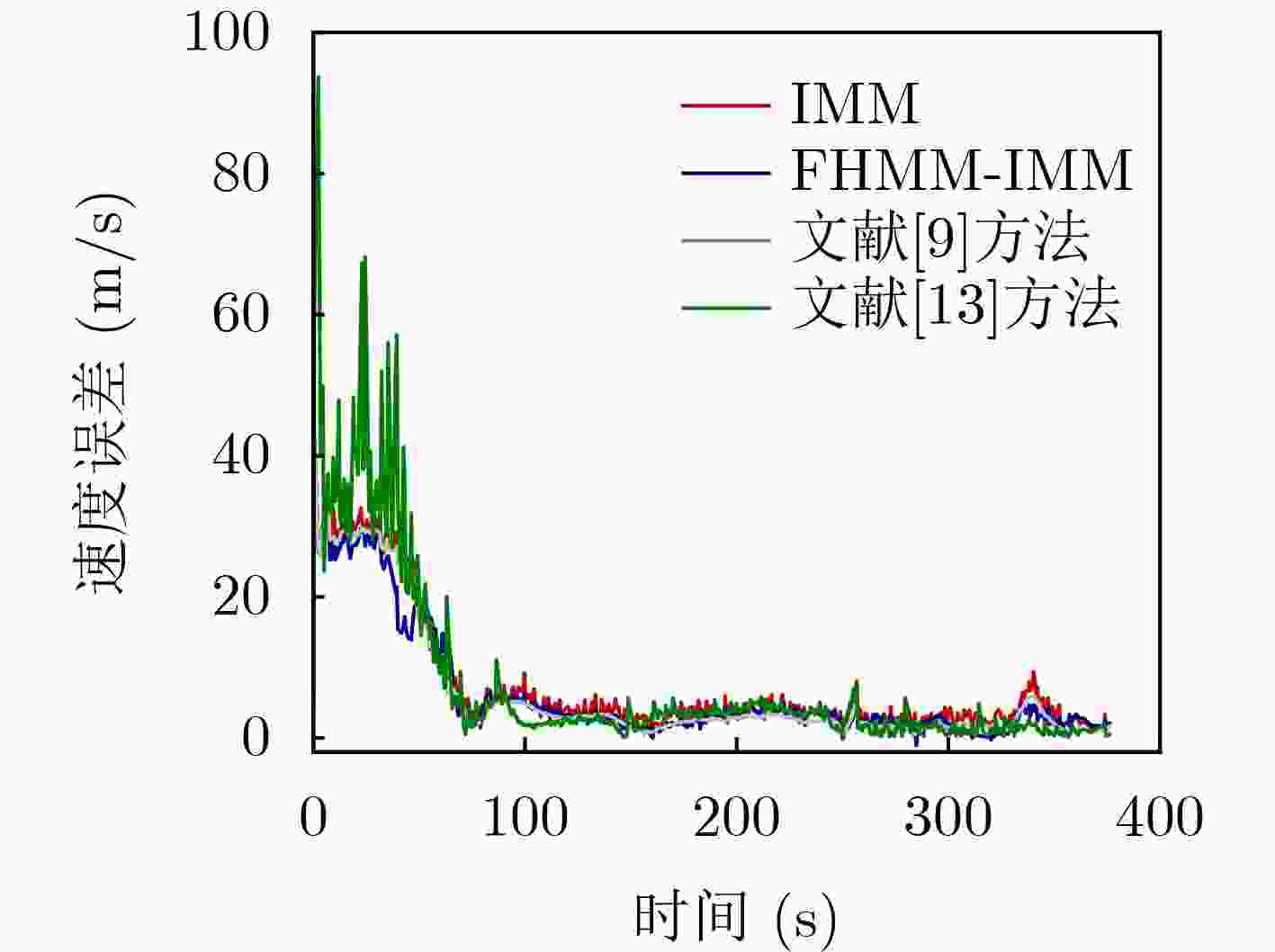
Abstract: Objective With the rapid growth of air traffic and expanding airport infrastructure, airport surfaces have become increasingly complex and congested. Higher aircraft density on taxiways and runways, increased ground vehicles, and obstacles complicate surface operations and heighten the risk of conflicts due to limited situational awareness. Pilots and ground controllers may struggle to obtain accurate environmental data, leading to potential safety hazards. To enhance surface surveillance and reduce collision risks, this study proposes an improved Interacting Multiple Model (IMM) filtering algorithm with adaptive transition probabilities. Unlike traditional IMM algorithms that rely on a fixed Markov transition probability matrix, the proposed method dynamically adjusts state transition probabilities to better adapt to operational conditions. This approach enhances tracking accuracy and improves aircraft trajectory prediction on airport surfaces, thereby increasing the safety and stability of ground operations. Methods The proposed algorithm integrates observation data and filtering residuals, constructing a fuzzy inference system for maneuver intensity using a fuzzy inference algorithm. This system infers the mapping relationship between observation data and the explicit state set in the Hidden Markov Model (HMM), deriving the corresponding state sequence. This process accurately captures target state changes, enhancing behavior prediction. The Baum-Welch algorithm in HMM is applied to solve the state transition matrix and update the observation probability matrix in real time, optimizing the adaptive update strategy for state transition probabilities. This improves model adaptability and accuracy across different environments. The algorithm integrates the fuzzy inference system for maneuver intensity with HMM and incorporates it into the IMM algorithm, forming a Fuzzy Hidden Markov-Interacting Multiple Model (FHMM-IMM) algorithm for real-time maneuvering target estimation. This approach significantly enhances tracking accuracy, particularly in complex and dynamic environments, ensuring high precision and stability for practical applications. Results and Discussions The proposed improved IMM algorithm is validated using actual airport surface ADS-B trajectory data. The results show that the algorithm adaptively adjusts parameters under non-equidistant prediction conditions, maintaining stable tracking performance (Figure 8). The position, velocity, and acceleration tracking error curves in both two-dimensional and one-dimensional Cartesian coordinates indicate a significant reduction in overall error, enhancing tracking accuracy (Figures 9, 10, and 11). Comparison with other algorithms confirms that the proposed method achieves a more stable tracking trajectory with lower errors, demonstrating superior performance (Figures 12, 13, 14, and 15). According to (Tables 2, 3, and 4), the two-dimensional position tracking accuracy improves by 63.5%, 54.3%, 40.3%, and 22.7%. The X-direction position tracking accuracy improves by 44.9%, 51.8%, 33.8%, and 35.2%, while the Y-direction position tracking accuracy improves by 63.9%, 62.9%, 52.7%, and 43.4%. The algorithm meets the real-time operational requirements of airport surface monitoring, further validating its effectiveness. Conclusions This study highlights the importance of precise four-dimensional trajectory tracking and prediction for airport surface aircraft, particularly in complex environments. Accurate trajectory tracking enhances taxiing safety and operational efficiency, addressing the challenges posed by increasing aircraft density on runways and taxiways. To improve tracking accuracy, an improved IMM algorithm with adaptive transition probabilities, based on Kalman filtering, is proposed. The main contributions are as follows: (1) A fuzzy inference system for maneuver intensity is developed, deriving explicit and hidden state sets and corresponding state sequences to capture target dynamics more accurately. (2) The FHMM-IMM algorithm is introduced for real-time estimation of maneuvering targets, incorporating time-varying state transition probabilities to enhance multi-model tracking and prediction in dynamic environments. (3) Experimental validation using real ADS-B trajectory data demonstrates that the FHMM-IMM algorithm achieves superior trajectory fitting, significantly reducing model errors. It also improves tracking accuracy for position, velocity, and acceleration in both two-dimensional and one-dimensional scenarios, verifying the effectiveness of the proposed model. These improvements provide a more precise and real-time solution for airport surface aircraft trajectory prediction and tracking, contributing to enhanced operational safety and efficiency.
- Target tracking /
- Interacting Multiple Model (IMM) /
- ADS-B /
- Transition probability matrix /
- Tracking error

HTML全文

图 1 机场场面目标跟踪预测结构示意图

下载: 全尺寸图片幻灯片

图 2 IMM算法中HMM结构图

下载: 全尺寸图片幻灯片

图 3 机动强弱模糊推理系统结构图

下载: 全尺寸图片幻灯片

图 4 输入、输出隶属度函数

下载: 全尺寸图片幻灯片

图 5 FHMM-IMM算法框架图

下载: 全尺寸图片幻灯片

图 6 航空器短时轨迹跟踪预测示意图

下载: 全尺寸图片幻灯片

图 7 场面航空器滑行路线和实验设备示意图

下载: 全尺寸图片幻灯片

图 8 IMM、FHMM-IMM跟踪轨迹与航空器真实轨迹对比图

下载: 全尺寸图片幻灯片

图 9 直角坐标系位置跟踪误差对比曲线图

下载: 全尺寸图片幻灯片

图 10 直角坐标系速度跟踪误差对比曲线图

下载: 全尺寸图片幻灯片

图 11 直角坐标系加速度跟踪误差对比曲线图

下载: 全尺寸图片幻灯片

图 12 跟踪轨迹对比图

下载: 全尺寸图片幻灯片

图 13 位置跟踪误差对比曲线图

下载: 全尺寸图片幻灯片

图 14 速度跟踪误差对比曲线图

下载: 全尺寸图片幻灯片

图 15 加速度跟踪误差对比曲线图

下载: 全尺寸图片幻灯片

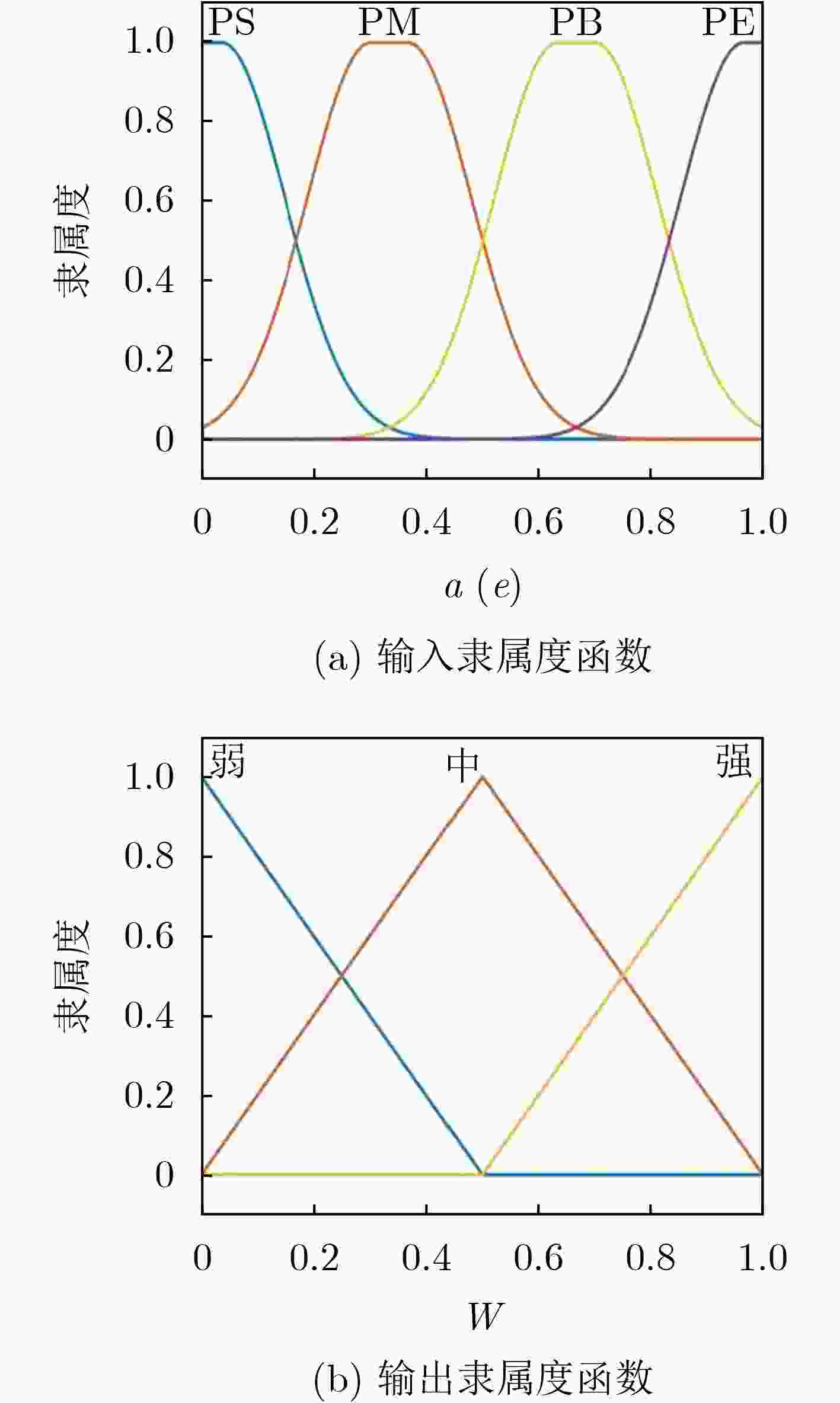
表 1 航空器机动强弱判定规则

e	a(PS)	a(PM)	a(PB)	a(PE)
PS	弱	弱	中	强
PM	弱	中	强	强
PB	中	强	强	强
PE	强	强	强	强

下载: 导出CSV

表 2 双维度上位置、速度和加速度各项评判指标对比

直角坐标双维度		位置	速度(m/s)	加速度(m/s²)
RMSE	IMM	18.857	12.854	5.157
	FHMM-IMM	6.875	11.458	3.527
	精度提高	63.5%	10.86%	31.6%
$\bar E$	IMM	14.509	9.546	2.603
	FHMM-IMM	6.637	4.980	1.657
	精度提高	54.3%	47.8%	36.3%
$\sigma$	IMM	10.238	9.765	2.580
	FHMM-IMM	6.108	8.869	1.432
	精度提高	40.3%	9.2%	44.5%
最高点	IMM	56.081	42.167	13.154
	FHMM-IMM	43.328	37.523	9.756
	精度提高	22.7%	11.0%	25.8%

下载: 导出CSV

表 3 X方向上位置、速度和加速度各项评判指标对比

X方向		位置(m)	速度(m/s)	加速度(m/s²)
RMSE	IMM	13.084	9.532	2.586
	FHMM-IMM	7.204	8.283	1.725
	精度提高	44.9%	13.1%	33.3%
$\bar E$	IMM	11.105	5.662	1.407
	FHMM-IMM	5.347	4.371	0.944
	精度提高	51.8%	22.8%	32.9%
$\sigma$	IMM	6.828	7.324	2.357
	FHMM-IMM	4.518	6.953	1.645
	精度提高	33.8%	5.1%	30.2%
最高点	IMM	45.763	34.980	11.188
	FHMM-IMM	29.649	27.161	6.972
	精度提高	35.2%	22.4%	37.7%

下载: 导出CSV

表 4 Y方向上位置、速度和加速度各项评判指标对比

Y方向		位置	速度(m/s)	加速度(m/s²)
RMSE	IMM	12.716	9.053	3.382
	FHMM-IMM	4.593	6.926	1.652
	精度提高	63.9%	23.5%	51.2%
$\bar E$	IMM	11.036	4.586	2.388
	FHMM-IMM	4.088	3.238	0.847
	精度提高	62.9%	29.4%	64.5%
$\sigma$	IMM	7.765	6.837	2.603
	FHMM-IMM	3.675	5.630	1.664
	精度提高	52.7%	17..6%	36.1%
最高点	IMM	47.285	34.396	8.858
	FHMM-IMM	26.765	32.652	6.915
	精度提高	43.4%	5.1%	21.9%

下载: 导出CSV

参考文献(23)

[1]	TANG Xinmin, ZHAO Wenjie, and GAO Shangfeng. Improved interacting multiple model algorithm airport surface target tracking based on geomagnetic sensors[J]. International Journal of Distributed Sensor Networks, 2020, 16(2): 1–11. doi: 10.1177/1550147720904563. (查阅网上资料,页码信息不确定,请确认) .
[2]	宫淑丽, 王帮峰, 吴红兰, 等. 基于IMM算法的机场场面运动目标跟踪[J]. 系统工程与电子技术, 2011, 33(10): 2322–2326. doi: 10.3969/j.issn.1001-506X.2011.10.35. GONG Shuli, WANG Bangfeng, WU Honglan, et al. Tracking of moving targets on airport surface based on IMM algorithm[J]. Systems Engineering and Electronics, 2011, 33(10): 2322–2326. doi: 10.3969/j.issn.1001-506X.2011.10.35.
[3]	汤新民, 郑鹏程. 基于大地坐标系的IMM航空器短期航迹外推[J]. 系统工程与电子技术, 2022, 44(7): 2293–2301. doi: 10.12305/j.issn.1001-506X.2022.07.26. TANG Xinmin and ZHENG Pengcheng. IMM aircraft short-tern track extrapolation based on geodetic coordinate system[J]. Systems Engineering and Electronics, 2022, 44(7): 2293–2301. doi: 10.12305/j.issn.1001-506X.2022.07.26.
[4]	LIU Zhiyong, ZHOU Kaixing, and SUN Xiucong. Satellite attitude determination using ADS-B receiver and MEMS gyro[J]. Aerospace, 2023, 10(4): 370. doi: 10.3390/aerospace10040370.
[5]	BI Yan and LI Chuankun. Multi-scale convolutional network for space-based ADS-B signal separation with single antenna[J]. Applied Sciences, 2022, 12(17): 8816. doi: 10.3390/app12178816.
[6]	THAI P, ALAM S, LILITH N, et al. A computer vision framework using convolutional neural networks for airport-airside surveillance[J]. Transportation research Part C: Emerging Technologies, 2022, 137: 103590. doi: 10.1016/j.trc.2022.103590.
[7]	AKHTAR S and HABIBI S. The interacting multiple model smooth variable structure filter for trajectory prediction[J]. IEEE Transactions on Intelligent Transportation Systems, 2023, 24(9): 9217–9239. doi: 10.1109/TITS.2023.3271295.
[8]	王小敏, 雷筱, 张亚东. 基于改进自适应IMM算法的高速列车组合定位[J]. 电子与信息学报, 2024, 46(3): 817–825. doi: 10.11999/JEIT230251. WANG Xiaomin, LEI Xiao, and ZHANG Yadong. Combined positioning of high-speed train based on improved adaptive IMM algorithm[J]. Journal of Electronics & Information Technology, 2024, 46(3): 817–825. doi: 10.11999/JEIT230251.
[9]	封普文, 黄长强, 曹林平, 等. 马尔可夫矩阵修正IMM跟踪算法[J]. 系统工程与电子技术, 2013, 35(11): 2269–2274. doi: 10.3969/j.issn.1001-506X.2013.11.07. FENG Puwen, HUANG Changqiang, CAO Linping, et al. Research on adaptive Markov matrix IMM tracking algorithm[J]. Systems Engineering and Electronics, 2013, 35(11): 2269–2274. doi: 10.3969/j.issn.1001-506X.2013.11.07.
[10]	BAZZI M, BLASQUES F, KOOPMAN S J, et al. Time-varying transition probabilities for Markov regime switching models[J]. Journal of Time Series Analysis, 2017, 38(3): 458–478. doi: 10.1111/jtsa.12211.
[11]	郭志, 董春云, 蔡远利, 等. 时变转移概率IMM-SRCKF机动目标跟踪算法[J]. 系统工程与电子技术, 2015, 37(1): 24–30. doi: 10.3969/j.issn.1001-506X.2015.01.05. GUO Zhi, DONG Chunyun, CAI Yuanli, et al. Time-varying transition probability based IMM-SRCKF algorithm for maneuvering target tracking[J]. Systems Engineering and Electronics, 2015, 37(1): 24–30. doi: 10.3969/j.issn.1001-506X.2015.01.05.
[12]	朱洪峰, 熊伟, 崔亚奇, 等. 基于加速度的马尔可夫参数自适应IMM算法[J]. 火力与指挥控制, 2019, 44(11): 46–50, 57. doi: 10.3969/j.issn.1002-0640.2019.11.010. ZHU Hongfeng, XIONG Wei, CUI Yaqi, et al. Adaptive Markov parameters IMM algorithm based on acceleration[J]. Fire Control & Command Control, 2019, 44(11): 46–50, 57. doi: 10.3969/j.issn.1002-0640.2019.11.010.
[13]	XIE Guo, SUN Lanlan, WEN Tao, et al. Adaptive transition probability matrix-based parallel IMM algorithm[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(5): 2980–2989. doi: 10.1109/TSMC.2019.2922305.
[14]	刘通, 王飞, 严忠平. 基于IMMKF算法的ADS-B监视应用目标跟踪[J]. 航空工程进展, 2024, 15(1): 182–190. doi: 10.16615/j.cnki.1674-8190.2024.01.22. LIU Tong, WANG Fei, and YAN Zhongping. ADS-B surveillance application target tracking based on IMMKF algorithm[J]. Advances in Aeronautical Science and Engineering, 2024, 15(1): 182–190. doi: 10.16615/j.cnki.1674-8190.2024.01.22.
[15]	陈光武, 王思琪, 司涌波, 等. 基于自适应交互式多卡尔曼滤波模型的组合导航算法研究[J]. 电子与信息学报, 2024, 46(12): 4493–4503. doi: 10.11999/JEIT240426. CHEN Guangwu, WANG Siqi, SI Yongbo, et al. Research on combined navigation algorithm based on adaptive interactive multi-Kalman filter modeling[J]. Journal of Electronics & Information Technology, 2024, 46(12): 4493–4503. doi: 10.11999/JEIT240426.
[16]	孙寿宇, 宫淑丽. 基于VSIMM-CKF的机场场面运动目标跟踪[J]. 武汉理工大学学报(交通科学与工程版), 2019, 43(2): 300–305. doi: 10.3963/j.issn.2095-3844.2019.02.024. SUN Shouyu and GONG Shuli. Maneuvering target tracking on airport surface based on VSIMM-CKF[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2019, 43(2): 300–305. doi: 10.3963/j.issn.2095-3844.2019.02.024.
[17]	左东广, 韩崇昭, 郑林, 等. 基于时变马尔科夫转移概率的机动目标多模型跟踪[J]. 西安交通大学学报, 2003, 37(8): 824–828. doi: 10.3321/j.issn:0253-987X.2003.08.013. ZUO Dongguang, HAN Chongzhao, ZHENG Lin, et al. Maneuvering target tracking based on time-varying Markov transition probabilities[J]. Journal of Xi'an Jiaotong University, 2003, 37(8): 824–828. doi: 10.3321/j.issn:0253-987X.2003.08.013.
[18]	冯辉, 何伊竞, 徐海祥, 等. 基于模糊推理的STPF-AIMM水面目标跟踪算法[J]. 华中科技大学学报(自然科学版), 2023, 51(8): 109–114. doi: 10.13245/j.hust.230822. FENG Hui, HE Yijing, XU Haixiang, et al. Water surface target tracking algorithm based on fuzzy inference STPF-AIMM[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2023, 51(8): 109–114. doi: 10.13245/j.hust.230822.
[19]	徐佳伟, 罗倩. 基于遗传非参数MDL-BW方法的HMM结构优化[J]. 电子学报, 2022, 50(11): 2765–2772. doi: 10.12263/DZXB.20210870. XU Jiawei, LUO Qian. HMM structure optimization based on genetic nonparametric MDL-BW method[J]. Acta Electronica Sinica, 2022, 50(11): 2765–2772. doi: 10.12263/DZXB.20210870.
[20]	赵楚楚, 王子微, 丁冠华, 等. 基于模糊逻辑的改进自适应IMM跟踪算法[J]. 信号处理, 2021, 37(5): 724–734. doi: 10.16798/j.issn.1003-0530.2021.05.005. ZHAO Chuchu, WANG Ziwei, DING Guanhua, et al. Fuzzy-logic adaptive IMM algorithm for target tracking[J]. Journal of Signal Processing, 2021, 37(5): 724–734. doi: 10.16798/j.issn.1003-0530.2021.05.005.
[21]	HAN Bing, WANG Hongchang, SU Zhigang, et al. A gated-recurrent-unit-based interacting multiple model method for small bird tracking on Lidar system[J]. Sensors, 2023, 23(18): 7933. doi: 10.3390/s23187933.
[22]	赵文杰, 汤新民, 黄忠涛, 等. 基于改进IMM算法的机场移动目标轨迹跟踪与预测[J]. 武汉理工大学学报(交通科学与工程版), 2020, 44(3): 468–473,479. doi: 10.3963/j.issn.2095-3844.2020.03.014. ZHAO Wenjie, TANG Xinmin, HUANG Zhongtao, et al. Trajectory tracking and prediction of airport moving targets based on improved IMM algorithm[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2020, 44(3): 468–473,479. doi: 10.3963/j.issn.2095-3844.2020.03.014.
[23]	International Civil Aviation Organization (ICAO). Advance Surface Movement Guidance and Control Systems (A-SMGCS) Manual[M]. ICAO, 2004. (查阅网上资料, 未找到对应的出版地信息, 请确认补充) .