Joint Design of Integrated Sensing And Communication Waveforms and Receiving Filters
-
摘要: 通感一体化波形的多普勒容忍性和低旁瓣电平对于通感一体化场景中的目标探测和信息传输至关重要,但其设计面临着诸多挑战。为此,该文提出一种基于多普勒容忍的通感一体化波形与接收滤波器联合设计方法。以最小化加权积分旁瓣电平和处理增益损失为优化指标,同时考虑发射波形的恒模约束、发射波形与通信波形之间的相位差约束以及失配滤波器的能量约束,提出了基于迭代扭曲近似算法的框架来解决波形优化设计问题。仿真结果表明,该文提出的一体化波形在小处理增益损失的情况下,在感兴趣时延区间宽度上实现了很低的旁瓣电平和误符号率,可有效提升雷达感知性能和通信质量。Abstract:
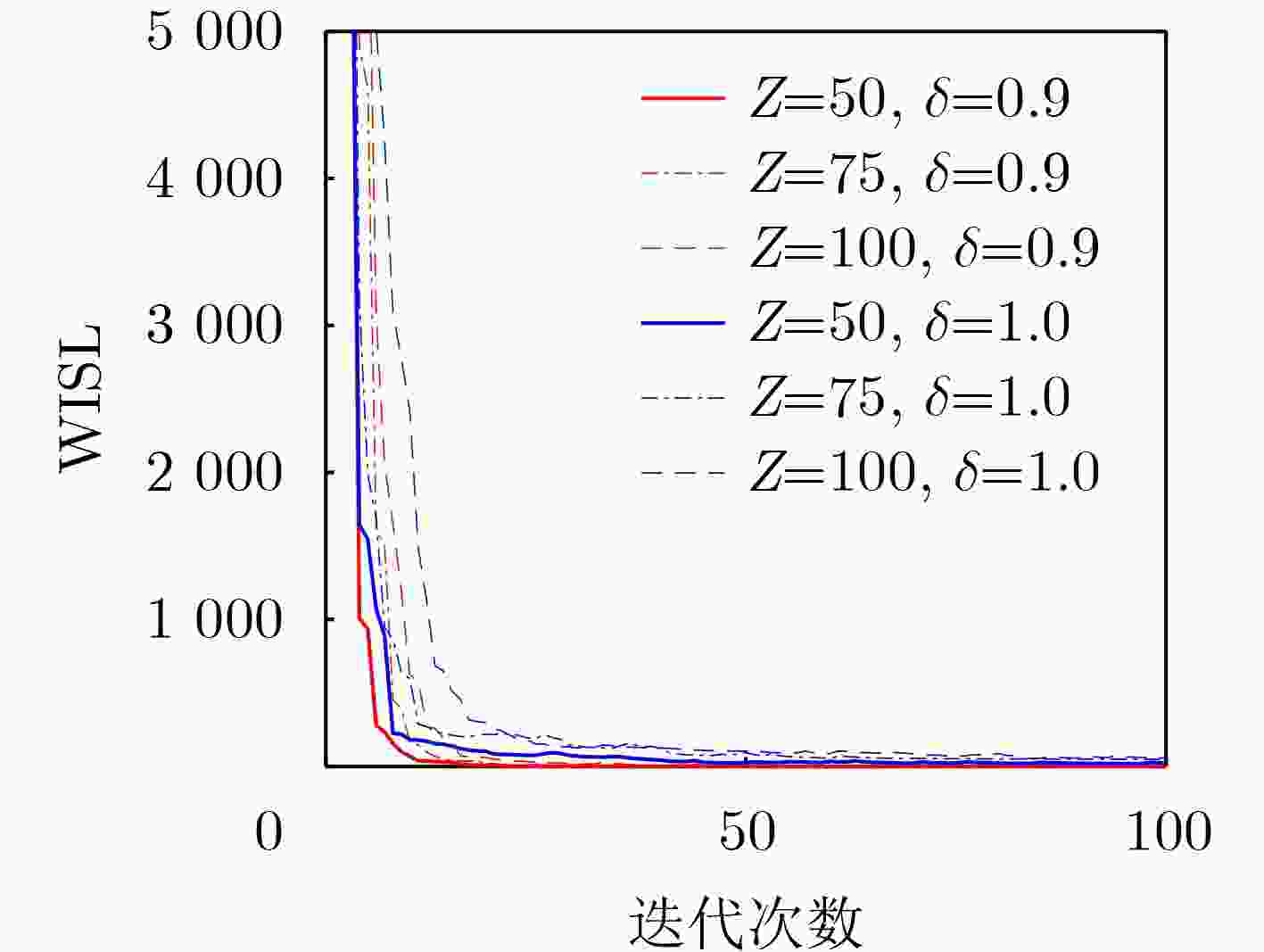
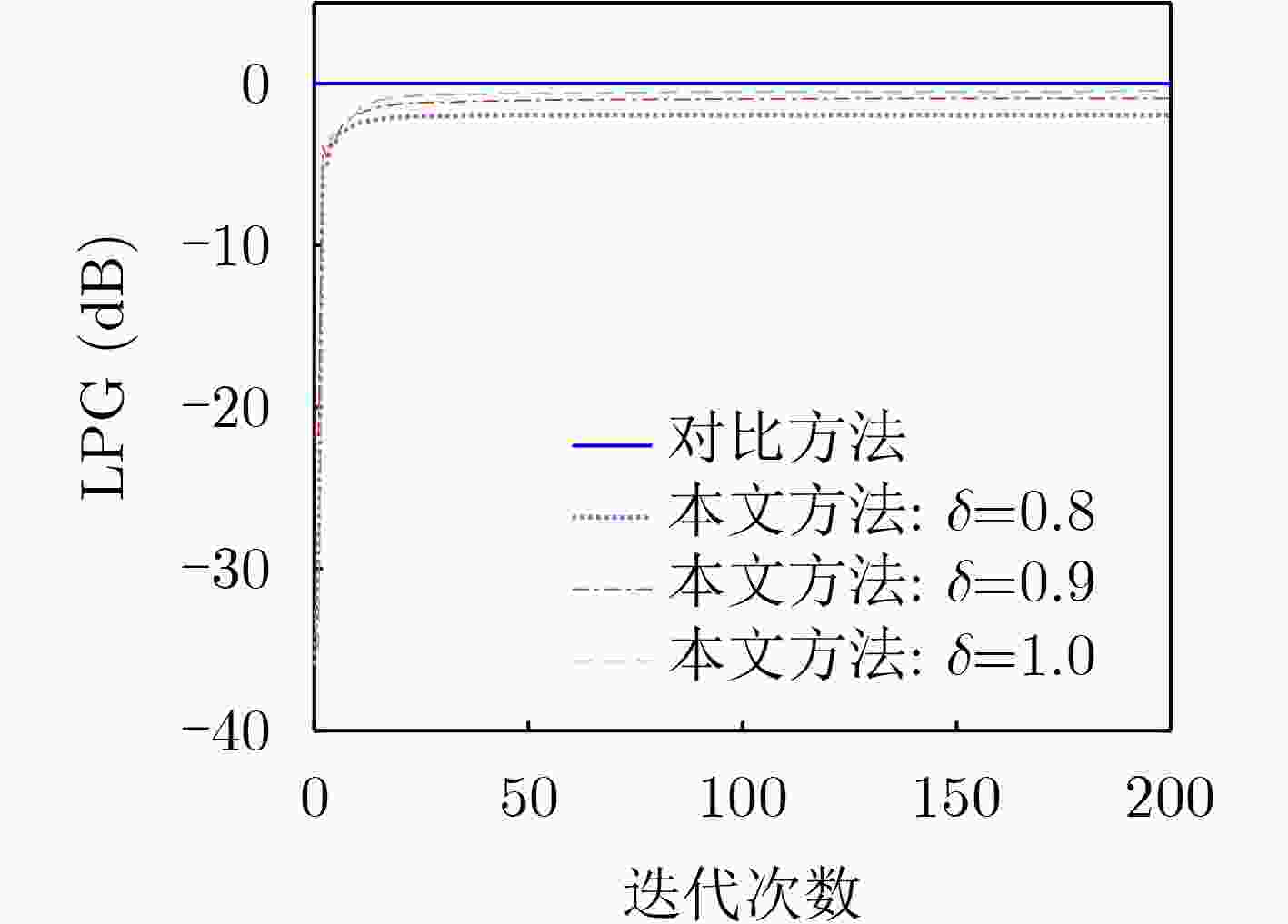
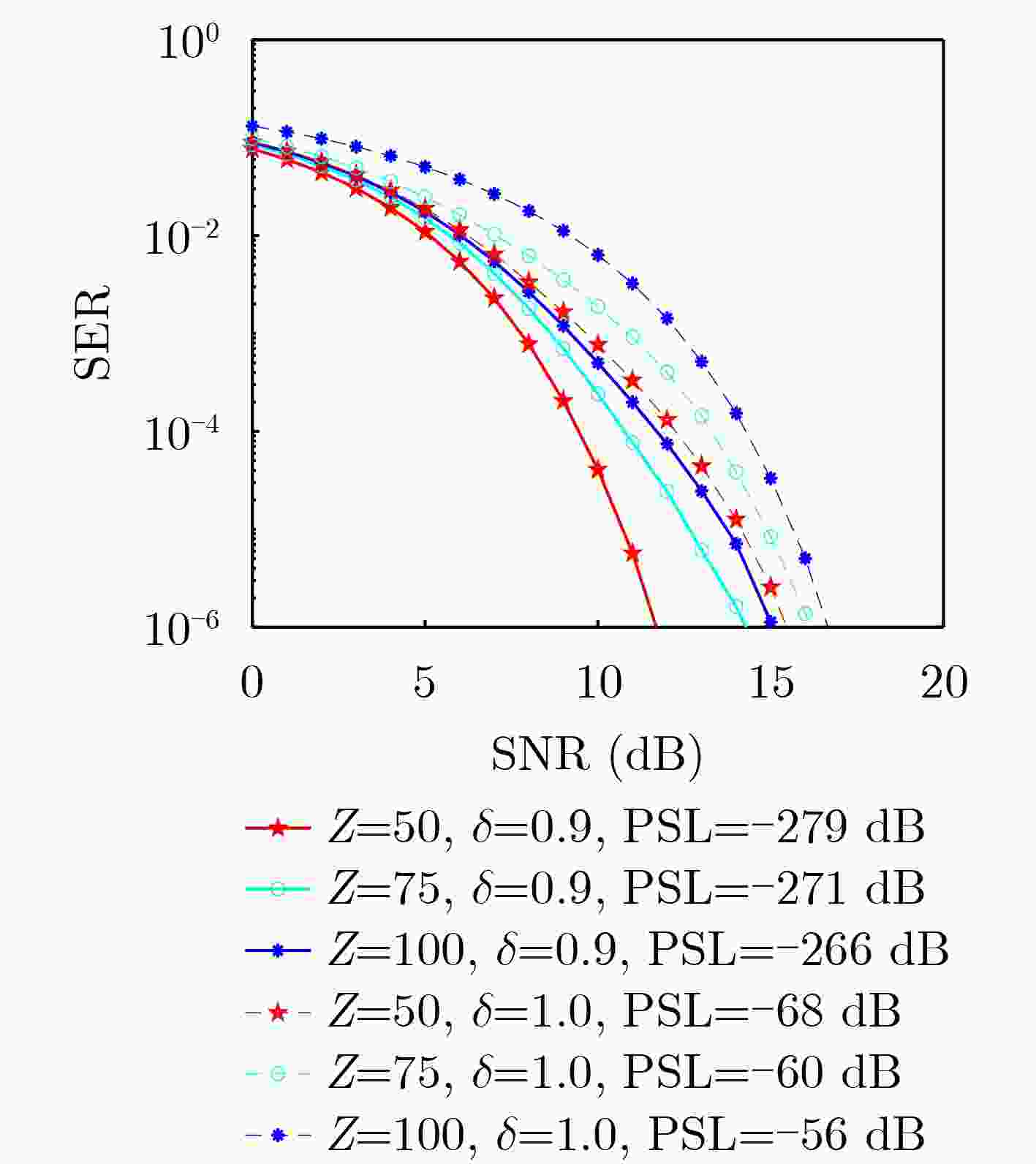
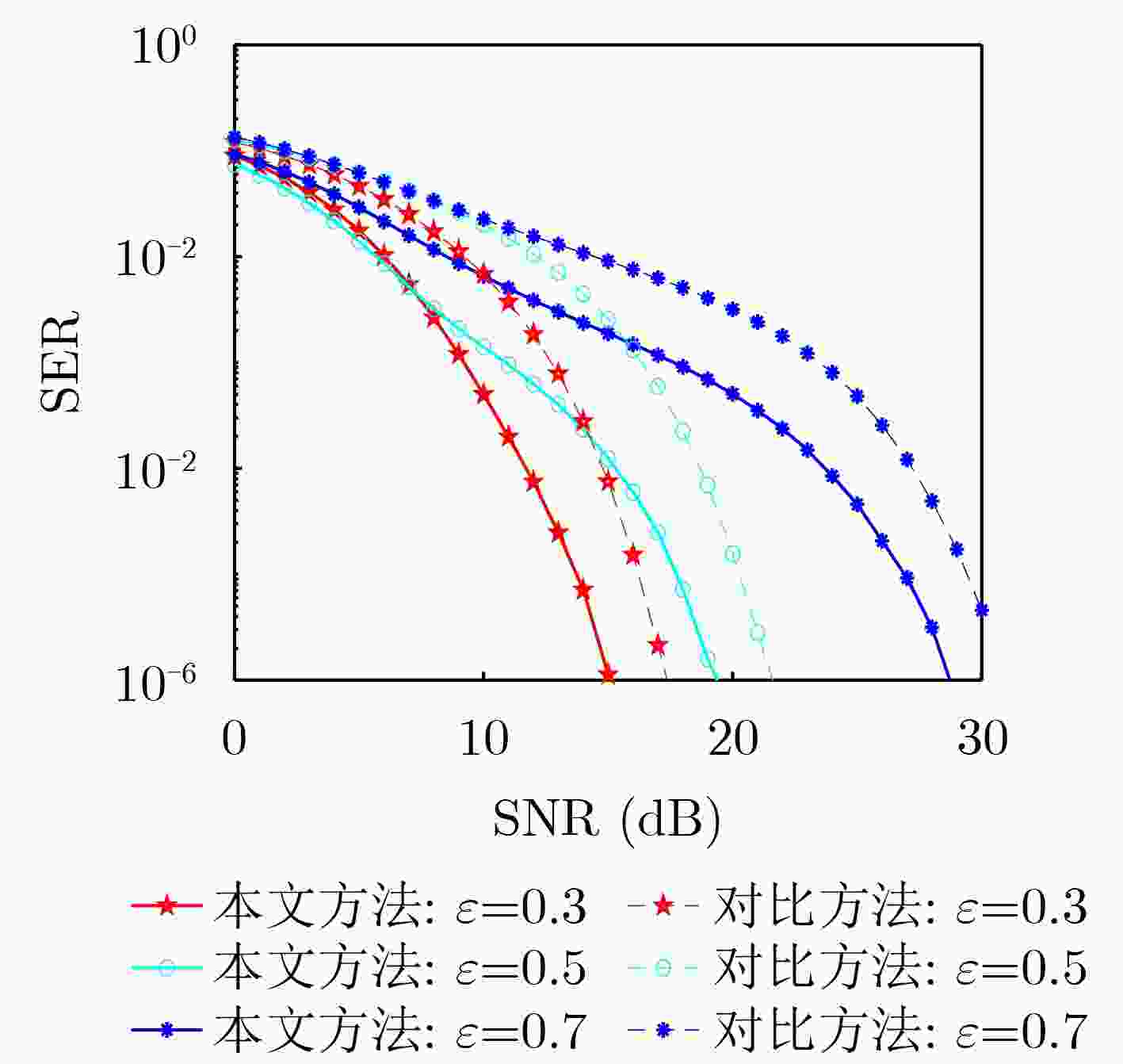
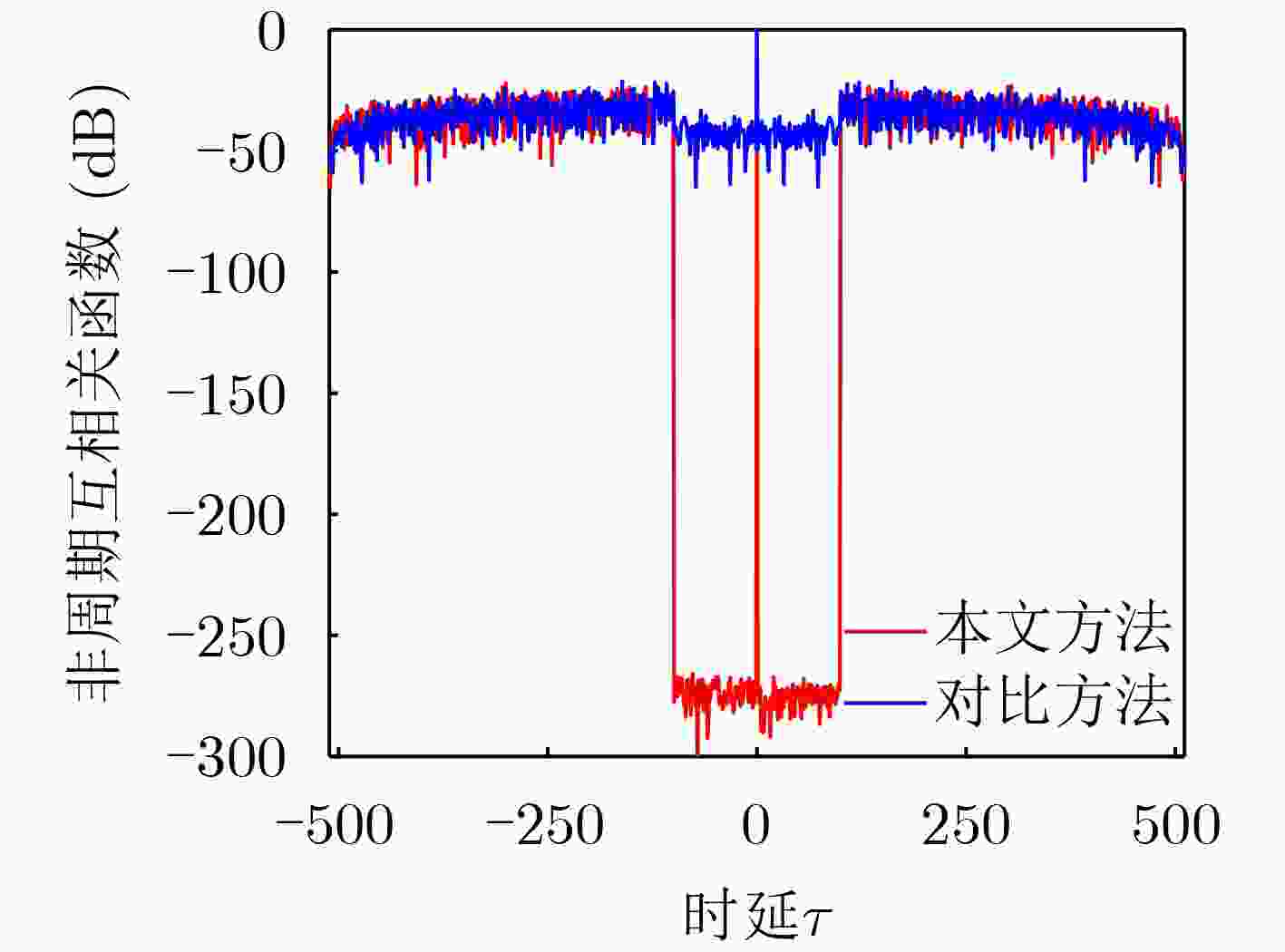
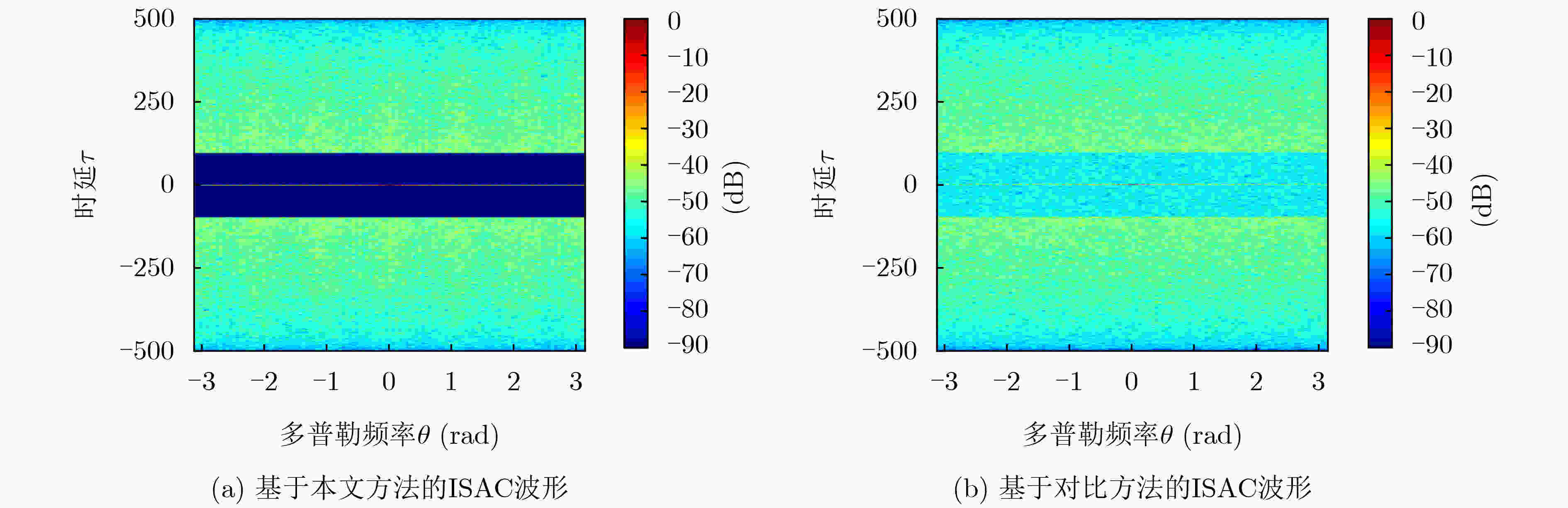
Objective With the continuous increase in wireless communication traffic and the growing scarcity of spectrum resources, the overlapping frequency bands of communication and radar systems have led to mutual interference. Therefore, Integrated Sensing And Communication (ISAC) has emerged as a critical area of research. A key technology in this field is the design of ISAC waveforms, which is of significant research interest. The Doppler resilience and low sidelobe levels of ISAC waveforms are essential for effective target detection and information transmission in ISAC scenarios. However, designing waveforms that optimize both radar and communication performance presents substantial challenges. To address these challenges, a method for the joint design of ISAC waveforms and receiving filters is proposed. An ISAC model based on mismatched filtering is proposed, and an optimization problem is formulated. The Iterative Twisted appROXimation (ITROX) algorithm is presented to solve this nonconvex problem with guaranteed convergence. This approach enables the design of unimodular ISAC waveforms with Doppler resilience, achieving enhanced performance in both communication and radar functions. Methods To design ISAC waveforms that optimize radar and communication performance, the concept of mismatched filtering is introduced to formulate an optimization problem. The requirements for Doppler-resilient ISAC waveforms are first analyzed, followed by the proposal of a waveform model based on mismatched filtering. An optimization problem is then formulated, with the objective of minimizing the Weighted Integrated Sidelobe Level (WISL) and the Loss-in-Processing Gain (LPG). Constraints include the unimodular property of the transmitted waveform, the phase difference between the transmitted ISAC waveform and the communication data-modulated waveform, and the energy of the receiving filter. To solve this nonconvex optimization problem, the task is transformed into identifying a suitable Mismatched Filtering Sequences Pair (MFSP) under multiple constraints. An ISAC waveform design algorithm based on an improved ITROX framework is proposed to simplify the optimization process. The core concept of the ITROX algorithm is to iteratively search for the optimal projection of the matrix set, with the goal of maximizing the main lobe and minimizing the sidelobes within the region of interest. This approach minimizes WISL and LPG, satisfying the objective function requirements. Additionally, the combination of the three constraints ensures that the waveform meets both communication and radar sensing requirements. The SQUAREd Iterative Method (SQUAREM) is employed to improve the algorithm's convergence speed. The balance between WISL and LPG is controlled by adjusting the coefficients. Results and Discussions The ITROX-based ISAC waveform design method proposed in this paper effectively solves the formulated optimization problem, resulting in unimodular ISAC waveforms with Doppler resilience. Compared to existing ISAC waveform methods, the proposed ISAC waveform demonstrates a lower sidelobe level and Symbol Error Rate (SER) within the region of interest, with only a minor sacrifice in LPG. This leads to significant improvements in both radar sensing and communication performance. Simulation results validate the effectiveness of the proposed ISAC waveforms. These results show that the proposed method exhibits excellent convergence, with WISL rapidly converging to a stable value as iterations increase ( Fig. 1 ). When the LPG coefficient is set to 0.9, a low sidelobe level and SER are achieved, despite a processing gain loss of 0.91 dB (Fig. 2 ,Fig. 3 ). For the same phase difference threshold, the proposed ISAC waveform exhibits a lower SER than existing methods, indicating superior communication performance (Fig. 4 ). When comparing the ISAC waveform designed by this method to existing methods with the same time-delay interval width, the proposed waveform demonstrates a lower sidelobe level, with sidelobes nearly zero, approaching ideal correlation performance (Fig. 5 ,Fig. 6 ). This leads to significant improvements in target detection by the ISAC system. Furthermore, the proposed ISAC waveform exhibits excellent Doppler resilience, maintaining low sidelobe levels within the given Doppler interval (Fig. 6 ), which contributes to improved target detection performance.Conclusions This paper proposes a method for the joint design of ISAC waveforms and receiving filters based on Doppler resilience. By integrating the concept of mismatched filtering with the ISAC model, an optimization problem is formulated to minimize WISL and LPG without compromising communication quality. Additionally, an improved ITROX algorithm is proposed to effectively solve the formulated nonconvex optimization problem. The results demonstrate that the proposed scheme maintains near-ideal correlation performance within the region of interest under specified Doppler intervals, with only a minor sacrifice in LPG, and enables communication with a low SER. Compared to existing ISAC waveform methods, the proposed ISAC waveform exhibits a lower sidelobe level and SER, showing superior radar sensing and communication performance. Furthermore, low sidelobe levels can be achieved in one or more regions of interest to meet different requirements by appropriately adjusting the weighting coefficient. Future work could explore more efficient optimization algorithms to design ISAC waveforms with enhanced Doppler resilience. -
1 基于改进ITROX算法的ISAC波形设计
输入:$ \delta $, $ \varepsilon $, $ {\omega _\tau } $, $ {{{\boldsymbol{e}}}_n} $, $ {\boldsymbol a}_n^{(0)} = {{{\boldsymbol{e}}}_n} $, $ {{A}^{(0)}} = ({\boldsymbol a}_n^{(0)}){({\boldsymbol b}_n^{(0)})^{\mathrm{H}}} $,其中
$ {\boldsymbol b}_n^{(0)} $为初始化随机相位序列for $ t = 0, 1, 2, \cdots $执行 寻找$ {{{\boldsymbol{B}}}^{(t)}} \in {\boldsymbol{\varGamma}} $(根据定理1) 对$ {{{\boldsymbol{B}}}^{(t)}} $进行奇异值分解,计算$ {\bar {\boldsymbol{a}}}_n^{(t + 1)} $和$ {\boldsymbol b}_n^{(t + 1)} $ (根据式(23)和
式(24))计算$ {\boldsymbol a}_n^{(t + 1)} = \varPi ({\bar {\boldsymbol{a}}}_n^{(t + 1)}) $ (根据式(25)) 寻找$ {{{\boldsymbol{A}}}^{(t + 1)}} = ({\boldsymbol a}_n^{(t + 1)}){({\boldsymbol b}_n^{(t + 1)})^{\mathrm{H}}} \in {\boldsymbol{\varLambda}} $ (根据定理2) end for(当收敛时) 输出:$ {\boldsymbol a}_n^{(t + 1)} $, $ {\boldsymbol b}_n^{(t + 1)} $ -
[1] CUI Gaofeng, HE Mengmin, XU Lexi, et al. Co-sharing waveform design for millimeter-wave radar communication systems[J]. China Communications, 2024, 21(6): 305–318. doi: 10.23919/JCC.ja.2021-0780. [2] LU Shihang, LIU Fan, LI Yunxin, et al. Integrated sensing and communications: Recent advances and ten open challenges[J]. IEEE Internet of Things Journal, 2024, 11(11): 19094–19120. doi: 10.1109/JIOT.2024.3361173. [3] 李博, 刘博文, 杨洪娟, 等. 海洋环境下无人机通信感知一体化波形设计[J]. 电子与信息学报, 2025, 47(3): 1–9. doi: 10.11999/JEIT240446.LI Bo, LIU Bowen, YANG Hongjuan, et al. Waveform design of UAV-enabled integrated sensing and communication in marine environment[J]. Journal of Electronics & Information Technology, 2025, 47(3): 1–9. doi: 10.11999/JEIT240446. [4] LIU Fan, CUI Yuanhao, MASOUROS C, et al. Integrated sensing and communications: Toward dual-functional wireless networks for 6G and beyond[J]. IEEE Journal on Selected Areas in Communications, 2022, 40(6): 1728–1767. doi: 10.1109/JSAC.2022.3156632. [5] 马丁友, 刘祥, 黄天耀, 等. 雷达通信一体化: 共用波形设计和性能边界[J]. 雷达学报, 2022, 11(2): 198–212. doi: 10.12000/JR21146.MA Dingyou, LIU Xiang, HUANG Tianyao, et al. Joint radar and communications: Shared waveform designs and performance bounds[J]. Journal of Radars, 2022, 11(2): 198–212. doi: 10.12000/JR21146. [6] XU Zhaoyi and PETROPULU A. A bandwidth efficient dual-function radar communication system based on a MIMO radar using OFDM waveforms[J]. IEEE Transactions on Signal Processing, 2023, 71: 401–416. doi: 10.1109/TSP.2023.3241779. [7] LIU Yongjun, LIAO Guisheng, and YANG Zhiwei. Robust OFDM integrated radar and communications waveform design based on information theory[J]. Signal Processing, 2019, 162: 317–329. doi: 10.1016/j.sigpro.2019.05.001. [8] YUAN Weijie, WEI Zhiqiang, LI Shuangyang, et al. Integrated sensing and communication-assisted orthogonal time frequency space transmission for vehicular networks[J]. IEEE Journal of Selected Topics in Signal Processing, 2021, 15(6): 1515–1528. doi: 10.1109/JSTSP.2021.3117404. [9] ZHANG Kecheng, YUAN Weijie, LI Shuangyang, et al. Radar sensing via OTFS signaling: A delay doppler signal processing perspective[C]. IEEE International Conference on Communications, Rome, Italy, 2023: 6429–6434. doi: 10.1109/ICC45041.2023.10279816. [10] ZHANG Qiuyue, ZHOU Yu, ZHANG Linrang, et al. Circulating code array for a dual-function radar-communications system[J]. IEEE Sensors Journal, 2020, 20(2): 786–798. doi: 10.1109/JSEN.2019.2944470. [11] BEKAR M, BAKER C J, HOARE E G, et al. Joint MIMO radar and communication system using a PSK-LFM waveform with TDM and CDM approaches[J]. IEEE Sensors Journal, 2021, 21(5): 6115–6124. doi: 10.1109/JSEN.2020.3043085. [12] LIU Rang, LI Ming, LIU Qian, et al. Joint waveform and filter designs for STAP-SLP-based MIMO-DFRC systems[J]. IEEE Journal on Selected Areas in Communications, 2022, 40(6): 1918–1931. doi: 10.1109/JSAC.2022.3155501. [13] LIU Fan, LIU Yafeng, LI Ang, et al. Cramér-Rao bound optimization for joint radar-communication beamforming[J]. IEEE Transactions on Signal Processing, 2022, 70: 240–253. doi: 10.1109/TSP.2021.3135692. [14] HE Hao, STOICA P, and LI Jian. Designing unimodular sequence sets with good correlations-including an application to MIMO radar[J]. IEEE Transactions on Signal Processing, 2009, 57(11): 4391–4405. doi: 10.1109/TSP.2009.2025108. [15] WANG Fulai, YIN Jiapeng, PANG Chen, et al. A unified framework of doppler resilient sequences design for simultaneous polarimetric radars[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5109615. doi: 10.1109/TGRS.2022.3144385. [16] WANG Fulai, XIA Xianggen, PANG Chen, et al. Joint design methods of unimodular sequences and receiving filters with good correlation properties and doppler tolerance[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5100214. doi: 10.1109/TGRS.2022.3233094. [17] 王佳欢, 范平志, 时巧, 等. 一种具有多普勒容忍性的通感一体化波形设计[J]. 雷达学报, 2023, 12(2): 275–286. doi: 10.12000/JR22155.WANG Jiahuan, FAN Pingzhi, SHI Qiao, et al. Doppler resilient integrated sensing and communication waveforms design[J]. Journal of Radars, 2023, 12(2): 275–286. doi: 10.12000/JR22155. [18] CHEN Yun, CHEN Zixuan, ZHANG Yunhua, et al. Joint design of doppler resilient unimodular discrete phase sequence waveform and receiving filter for multichannel radar[J]. IEEE Transactions on Signal Processing, 2024, 72: 4207–4221. doi: 10.1109/TSP.2024.3458175. [19] CHEN Yutao, CHENG Yuanbo, LIN Ronghao, et al. Joint design of binary probing sequence sets and receive filter banks for MIMO PMCW radar[J]. IEEE Transactions on Signal Processing, 2024, 72: 1620–1633. doi: 10.1109/TSP.2024.3375646. [20] SOLTANALIAN M and STOICA P. Computational design of sequences with good correlation properties[J]. IEEE Transactions on Signal Processing, 2012, 60(5): 2180–2193. doi: 10.1109/TSP.2012.2186134. [21] GU Zhi, ADHIKARY A R, ZHOU Zhengchun, et al. A computational design of aperiodic mismatched filtering sequences[C]. IEEE International Symposium on Information Theory, Espoo, Finland, 2022: 2643–2647. doi: 10.1109/ISIT50566.2022.9834377. [22] ECKART C and YOUNG G. The approximation of one matrix by another of lower rank[J]. Psychometrika, 1936, 1(3): 211–218. doi: 10.1007/BF02288367. [23] GOLUB G H and VAN LOAN C F. Matrix Computations[M]. 4th ed. Baltimore: Johns Hopkins University Press, 2013. [24] SONG Junxiao, BABU P, and PALOMAR D P. Sequence design to minimize the weighted integrated and peak sidelobe levels[J]. IEEE Transactions on Signal Processing, 2016, 64(8): 2051–2064. doi: 10.1109/TSP.2015.2510982. -





 下载:
下载:


 下载:
下载:
