Aerial Target Intention Recognition Method Integrating Information Classification Processing and Multi-scale Embedding Graph Robust Learning with Noisy Labels
-
摘要: 针对传统深度学习意图识别方法难以在噪声标签存在时获得可靠模型的问题,该文提出基于信息分类处理(ICP)网络和多尺度鲁棒学习的空中目标意图识别(ATIR)方法。首先,基于空中目标属性性质,构建基于ICP的编码器,以获得更具可分性的嵌入;随后,设计了从精细到粗糙的跨尺度嵌入融合机制,利用不同尺度的目标序列,训练多个编码器来学习判别模式;同时,利用不同尺度的互补信息,以交叉教学的方式训练每个编码器,以选择小损失样本作为干净标签;对于未选定的大损失样本,基于多尺度嵌入图和说话者-倾听者标签传播算法(SLPA),使用干净样本的标签进行校正。在不同标签噪声类型、多级噪声水平的ATIR数据集上的实验结果表明,该方法的测试准确率和Macro F1分数显著优于其他基线方法,说明其具有更强的噪声标签鲁棒性。Abstract:
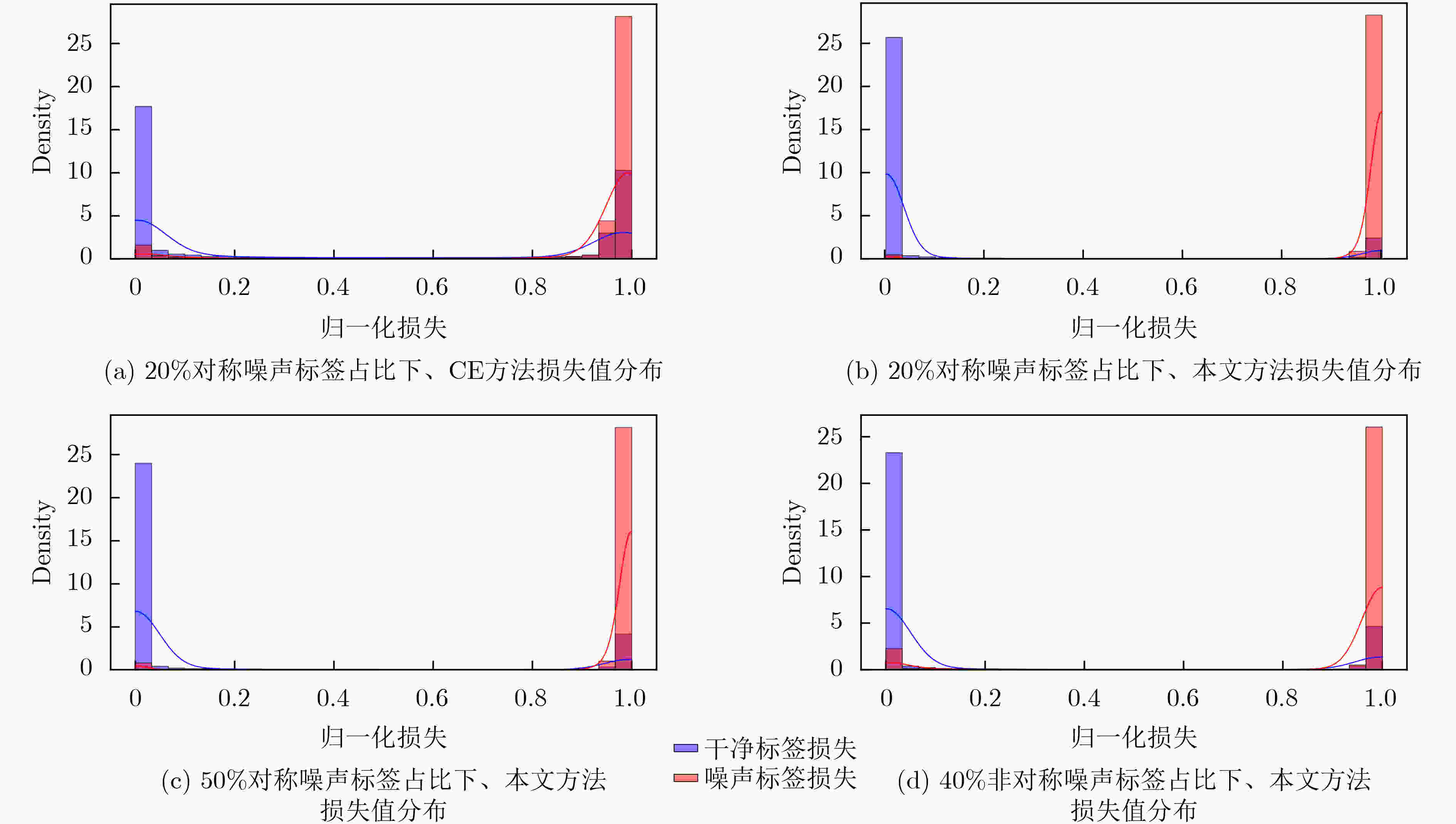
Objective Aerial Target Intention Recognition (ATIR) predicts and assesses the intentions of non-cooperative targets by integrating information acquired and processed by various sensors. Accurate recognition enhances decision-making, aiding commanders and combatants in steering engagements favorably. Therefore, robust and precise recognition methods are essential. Advances in big data and detection technologies have driven research into deep-learning-based intention recognition. However, noisy labels in target intention recognition datasets hinder the reliability of traditional deep-learning models. To address this issue, this study proposes an intention recognition method incorporating Information Classification Processing (ICP) and multi-scale robust learning. The trained model demonstrates high accuracy even in the presence of noisy labels. Methods This method integrates an ICP network, a cross-scale embedding fusion mechanism, and multi-scale embedding graph learning. The ICP network performs cross-classification processing by analyzing attribute correlations and differences, facilitating the extraction of embeddings conducive to intention recognition. The cross-scale embedding fusion mechanism employs target sequences at different scales to train multiple Deep Neural Networks (DNNs) simultaneously. It sequentially integrates robust embeddings from fine to coarse scales. During training, complementary information across scales enables a cross-teaching strategy, where each encoder selects clean-label samples based on a small-loss criterion. Additionally, multi-scale embedding graph learning establishes relationships between labeled and unlabeled samples to correct noisy labels. Specifically, for high-loss unselected samples, the Speaker-listener Label PropagAtion (SLPA) algorithm refines their labels using the multi-scale embedding graph, improving model adaptation to the class distribution of target attribute sequences. Results and Discussions When the proportion of symmetric noise is 20% ( Table 1 ), the test accuracy of the Cross-Entropy (CE) method exceeds 80%, demonstrating the effectiveness of the ICP network. The proposed method achieves both test accuracy and a Macro F1 score (MF1) above 92%. At higher noise levels—50% symmetric noise and 40% asymmetric noise (Table 1 )—the performance of other methods declines significantly. In contrast, the proposed method maintains accuracy and MF1 above 80%, indicating greater stability and robustness. This strong performance can be attributed to: (1) Cross-scale fusion, which integrates complementary information from different scales, enhancing the separability and robustness of fused embeddings. This ensures the selection of high-quality samples and prevents performance degradation caused by noisy labels in label propagation. (2) SLPA in multi-scale embedding graph learning, which stabilizes label propagation even when the dataset contains a high proportion of noisy labels.Conclusions This study proposes an intelligent method for recognizing aerial target intentions in the presence of noisy labels. The method effectively addresses noise label by integrating an ICP network, a cross-scale embedding fusion mechanism, and multi-scale embedding graph learning. First, an embedding extraction encoder based on the ICP network is constructed using acquired target attributes. The cross-scale embedding fusion mechanism then integrates encoder outputs from sequences at different scales, facilitating the extraction of multi-scale features and enhancing the reliability of clean samples identified by the small-loss criterion. Finally, multi-scale embedding graph learning, incorporating SLPA, refines noisy labels by leveraging selected clean labels. Experiments on the ATIR dataset across various noise types and levels demonstrate that the proposed method achieves significantly higher test accuracy and M F1 than other baseline approaches. Ablation studies further validate the effectiveness and robustness of the network architecture and mechanisms. -
1 信息分类处理网络
输入:空中目标属性训练集$ {\boldsymbol{\mathcal{D}}} = \left\{ {{\boldsymbol{\mathcal{X}}},{\boldsymbol{\mathcal{Y}}}} \right\} = \left\{ {\left( {{{\boldsymbol{X}}_i},{y_i}} \right)} \right\}_{i = 1}^N $;迭
代次数T输出:空中目标属性嵌入集${\boldsymbol{E}} = \left\{ {{{\boldsymbol{E}}^i}} \right\}_{i = 1}^N$ (1) 构建BaseNet1, BaseNet2, BaseNet3; (2) 令K1, K2, K3分别表示BaseNet1,BaseNet2, BaseNet3的支路网
络数量(3) 初始化所有BaseNet的参数θ (4) epoch$ \leftarrow $0 (5) While epoch < T do (6) for i = 1:N do (7) for j = 1:3 do (8) for k = 1:Kj do (9) ${\boldsymbol{E}}_{j,k}^i = {\text{BaseNe}}{{\text{t}}_{j,k}}({{\boldsymbol{X}}_{i,j}})$ //通过BaseNetj第k个支
路网络处理特征,获得基础特征(10) if Kj≥2 do (11) ${\boldsymbol{E}}_{j,{\mathrm{f}}}^i = {\left( {{\text{Fusio}}{{\text{n}}_j}} \right)^{{K_j} - 1}}\left( {{\boldsymbol{E}}_{j,1}^i,{\boldsymbol{E}}_{j,2}^i, \cdots ,{\boldsymbol{E}}_{j,{K_j}}^i} \right)$
//融合特征(12) else do (13) ${\boldsymbol{E}}_{j,{\mathrm{f}}}^i = {\boldsymbol{E}}_{j,1}^i$ (14) end (15) end (16) ${{\boldsymbol{E}}^i} = {\text{Linear}}\left( {{\text{CONCAT}}({\boldsymbol{E}}_{1,{\mathrm{f}}}^i,{\boldsymbol{E}}_{2,{\mathrm{f}}}^i,{\boldsymbol{E}}_{3,{\mathrm{f}}}^i)} \right)$ (17) end (18) epoch = epoch + 1 (19) end 2 噪声标签下融合ICP编码器和多尺度鲁棒学习的意图识别模型学习范式
输入:ICP编码器 [ICPA, ICPB, ICPC],分类器[ClassifierA, ClassifierB, ClassifierC],精细尺度目标属性序列XA,中等尺度目标属性序列
XB,粗糙尺度目标属性序列XC输出:[ICPA, ICPB, ICPC]和[ClassifierA, ClassifierB, ClassifierC] (1) 获得单个尺度嵌入 rA,rB,rC; rA = ICPA(XA),rB = ICPB(XB),rC = ICPC(XC); (2) 获得跨尺度融合嵌入vA,vB,vC; vA = rA,vB = 式(11)(rB, vA),vC = 式(11)(rC, vB); (3) 获得用于交叉学习训练的干净标签yA,yB,yC; yA = ClassifierC(vC) //利用小损失标准; yB = ClassifierA(vA) //利用小损失标准; yC = ClassifierB(vB) //利用小损失标准; (4) 获得用于分类训练的修正标签 ycA,ycB,ycC; ycA = SLPA(vA, yA),ycB = SLPA(vB, yB),ycC = SLPA(vC, yC); (5) 参数更新; 计算交叉熵损失CrossEntropy(vA, yA &ycA)并更新ICP编码器 ICPA和分类器ClassifierA; 计算交叉熵损失CrossEntropy(vB, yB &ycB)并更新ICP编码器ICPB和分类器ClassifierB; 计算交叉熵损失CrossEntropy(vC, yC &ycC)并更新ICP编码器ICPC和分类器ClassifierC。 表 1 基准方法对比实验结果(%)
方法 指标 Sym, 20% Sym, 50% Asym, 40% CE Acc 81.15 68.13 50.15 MF1 80.36 64.05 48.56 Mixup Acc 82.66 72.88 41.67 MF1 82.25 72.40 42.18 Mixup-BMM Acc 80.16 67.03 55.26 MF1 79.63 66.68 52.54 Co-teaching Acc 91.78 75.65 61.35 MF1 91.61 75.46 61.22 SIGUA Acc 80.08 74.91 67.13 MF1 79.79 74.98 66.37 SREA Acc 80.16 67.45 78.54 MF1 78.98 61.51 77.51 CTW Acc 87.78 80.36 79.76 MF1 87.63 79.53 79.36 Sel-CL Acc 78.15 73.01 68.52 MF1 77.69 71.26 66.18 本文 Acc 92.77 84.01 83.77 MF1 92.99 84.11 83.72 表 2 编码器采用不同网络架构时的意图识别性能(%)
网络架构 指标 Sym, 0% Sym, 20% FCL Acc 89.26 89.22 MF1 89.23 89.01 FCN Acc 92.60 90.49 MF1 92.58 90.26 GRU Acc 91.23 90.75 MF1 91.37 91.13 1DCNN_BiLSTM Acc 90.06 90.50 MF1 90.16 90.44 ICP Acc 96.13 92.77 MF1 96.00 92.99 表 3 消融实验结果(%)
方法 指标 Sym, 20% Sym, 50% Asym, 40% 本文 Acc 92.77 84.01 83.77 MF1 92.99 84.11 83.72 w/o cross-scale fusion Acc 92.71 73.08 69.83 MF1 92.82 74.34 64.48 w/o downsampling Acc 91.41 78.61 68.15 MF1 91.28 77.79 67.09 w/o graph learning Acc 91.03 80.64 81.46 MF1 91.09 80.45 77.74 replace SLPA with LPA Acc 90.86 83.26 81.02 MF1 90.54 83.10 80.47 w/o momentum update Acc 91.77 82.95 74.28 MF1 91.88 82.46 70.70 w/o dynamic threshold Acc 93.10 77.39 78.91 MF1 93.17 76.47 75.83 表 4 20%对称噪声标签占比下、不同尺度数目取值时的准确率(%)
尺度数目 Acc 2 0.904 4 3 0.927 7 4 0.903 2 5 0.908 2 表 5 20%对称噪声标签占比下、不同动量更新增量取值时的准确率(%)
动量更新增量 Acc 0.99 0.911 2 0.90 0.927 7 0.75 0.903 2 0.50 0.905 3 表 6 20%对称噪声标签占比下、不同最近邻数量取值时的准确率(%)
最近邻数量 Acc 5 0.911 1 10 0.927 7 15 0.913 6 表 7 20%对称标签占比下、SLPA中不同阈值取值时的准确率(%)
SLPA中阈值 Acc 0.5 0.921 1 0.6 0.927 7 0.7 0.910 5 表 8 20%对称噪声标签占比下、不同γ取值时的准确率(%)
γ Acc 0.99 0.927 7 0.95 0.903 4 0.90 0.901 1 0.80 0.897 2 -
[1] AHMED A A and MOHAMMED M F. SAIRF: A similarity approach for attack intention recognition using fuzzy min-max neural network[J]. Journal of Computational Science, 2018, 25: 467–473. doi: 10.1016/j.jocs.2017.09.007. [2] AKRIDGE C. On advanced template-based interpretation as applied to intention recognition in a strategic environment[D]. [Master dissertation], University of Central Florida, 2007. [3] GONZALEZ A J, GERBER W J, DEMARA R F, et al. Context-driven near-term intention recognition[J]. The Journal of Defense Modeling and Simulation, 2004, 1(3): 153–170. doi: 10.1177/875647930400100303. [4] CHARNIAK E and GOLDMAN R P. A Bayesian model of plan recognition[J]. Artificial Intelligence, 1993, 64(1): 53–79. doi: 10.1016/0004-3702(93)90060-O. [5] YU Quan, SONG Jinyu, YU Xiaohan, et al. To solve the problems of combat mission predictions based on multi-instance genetic fuzzy systems[J]. The Journal of Supercomputing, 2022, 78(12): 14626–14647. doi: 10.1007/s11227-022-04388-5. [6] SVENMARCKT P and DEKKER S. Decision support in fighter aircraft: From expert systems to cognitive modelling[J]. Behaviour & Information Technology, 2003, 22(3): 175–184. doi: 10.1080/0144929031000109755. [7] MENG Guanglei, ZHAO Runnan, WANG Biao, et al. Target tactical intention recognition in multiaircraft cooperative air combat[J]. International Journal of Aerospace Engineering, 2021, 2021: 9558838. doi: 10.1155/2021/9558838. [8] TRABOULSI A and BARBEAU M. Recognition of drone formation intentions using supervised machine learning[C]. 2019 International Conference on Computational Science and Computational Intelligence, Las Vegas, USA, 2019: 408–411. doi: 10.1109/CSCI49370.2019.00079. [9] 胡智勇, 刘华丽, 龚淑君, 等. 基于随机森林的目标意图识别[J]. 现代电子技术, 2022, 45(19): 1–8. doi: 10.16652/j.issn.1004-373x.2022.19.001.HU Zhiyong, LIU Huali, GONG Shujun, et al. Target intention recognition based on random forest[J]. Modern Electronics Technique, 2022, 45(19): 1–8. doi: 10.16652/j.issn.1004-373x.2022.19.001. [10] ZHANG Chenhao, ZHOU Yan, LI Hui, et al. Combat intention recognition of air targets based on 1DCNN-BiLSTM[J]. IEEE Access, 2023, 11: 134504–134516. doi: 10.1109/ACCESS.2023.3337640. [11] ZHANG Zhuo, WANG Hongfei, JIANG Wen, et al. A target intention recognition method based on information classification processing and information fusion[J]. Engineering Applications of Artificial Intelligence, 2024, 127: 107412. doi: 10.1016/j.engappai.2023.107412. [12] CHENG Cheng, LIU Xiaoyu, ZHOU Beitong, et al. Intelligent fault diagnosis with noisy labels via semisupervised learning on industrial time series[J]. IEEE Transactions on Industrial Informatics, 2023, 19(6): 7724–7732. doi: 10.1109/TII.2022.3229130. [13] ZHANG Hongyi, CISSÉ M, DAUPHIN Y N, et al. Mixup: Beyond empirical risk minimization[C]. The 6th International Conference on Learning Representations, Vancouver, Canada, 2018. [14] ARAZO E, ORTEGO D, ALBERT P, et al. Unsupervised label noise modeling and loss correction[C]. The 36th International Conference on Machine Learning, Long Beach, USA, 2019: 312–321. [15] HAN Bo, YAO Quanming, YU Xingrui, et al. Co-teaching: Robust training of deep neural networks with extremely noisy labels[C]. The 32nd International Conference on Neural Information Processing Systems, Montréal, Canada, 2018: 8536–8546. [16] HAN Bo, NIU Gang, YU Xingrui, et al. SIGUA: Forgetting may make learning with noisy labels more robust[C]. The 37th International Conference on Machine Learning, 2020: 4006–4016. [17] CASTELLANI A, SCHMITT S, and HAMMER B. Estimating the electrical power output of industrial devices with end-to-end time-series classification in the presence of label noise[C]. Proceedings of European Conference on Machine Learning and Knowledge Discovery in Databases. Bilbao, Spain, 2021: 469–484. doi: 10.1007/978-3-030-86486-6_29. [18] LI Shikun, XIA Xiaobo, GE Shiming, et al. Selective-supervised contrastive learning with noisy labels[C]. 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, USA, 2022: 316–325. doi: 10.1109/CVPR52688.2022.00041. [19] MA Peitian, LIU Zhen, ZHENG Junhao, et al. CTW: Confident time-warping for time-series label-noise learning[C]. The 32nd International Joint Conference on Artificial Intelligence, Macao, China, 2023: 4046–4054. doi: 10.24963/ijcai.2023/450. [20] 魏琦, 孙皓亮, 马玉玲, 等. 面向标签噪声的联合训练框架[J]. 中国科学: 信息科学, 2024, 54(1): 144–158. doi: 10.1360/SSI-2022-0395.WEI Qi, SUN Haoliang, MA Yuling, et al. A joint training framework for learning with noisy labels[J]. SCIENTIA SINICA Informationis, 2024, 54(1): 144–158. doi: 10.1360/SSI-2022-0395. [21] LIANG Xuefeng, LIU Xingyu, and YAO Longshan. Review–a survey of learning from noisy labels[J]. ECS Sensors Plus, 2022, 1(2): 021401. doi: 10.1149/2754-2726/ac75f5. [22] SHAN Yuxiang, LU Hailiang, and LOU Weidong. A hybrid attention and dilated convolution framework for entity and relation extraction and mining[J]. Scientific Reports, 2023, 13(1): 17062. doi: 10.1038/s41598-023-40474-1. [23] CHEN Wei and SHI Ke. Multi-scale attention convolutional neural network for time series classification[J]. Neural Networks, 2021, 136: 126–140. doi: 10.1016/j.neunet.2021.01.001. [24] ZHANG Yitian, MA Liheng, PAL S, et al. Multi-resolution time-series transformer for long-term forecasting[C]. The 27th International Conference on Artificial Intelligence and Statistics, Valencia, Spain, 2024: 4222–4230. [25] BISCHOF B and BUNCH E. Geometric feature performance under downsampling for EEG classification tasks[J]. arXiv: 2102.07669, 2021. doi: 10.48550/arXiv.2102.07669. [26] LI Junnan, WONG Yongkang, ZHAO Qi, et al. Learning to learn from noisy labeled data[C]. The 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, USA, 2019: 5046–5054. doi: 10.1109/CVPR.2019.00519. [27] XIA Xiaobo, LIU Tongliang, HAN Bo, et al. Sample selection with uncertainty of losses for learning with noisy labels[C]. The Tenth International Conference on Learning Representations, 2022. [28] GUI Xianjin, WANG Wei, and TIAN Zhanghao. Towards understanding deep learning from noisy labels with small-loss criterion[C]. The Thirtieth International Joint Conference on Artificial Intelligence, Montreal, Canada, 2021: 2469–2475. [29] 王晓莉, 薛丽. 标签噪声学习算法综述[J]. 计算机系统应用, 2021, 30(1): 10–18. doi: 10.15888/j.cnki.csa.007776.WANG Xiaoli and XUE Li. Review on label noise learning algorithms[J]. Computer Systems & Applications, 2021, 30(1): 10–18. doi: 10.15888/j.cnki.csa.007776. [30] 崔瑞博, 王峰. 动量更新与重构约束的限制视角下3D物品识别[J]. 华东师范大学学报(自然科学版), 2023(6): 61–72. doi: 10.3969/j.issn.1000-5641.2023.06.006.CUI Ruibo and WANG Feng. Momentum-updated representation with reconstruction constraint for limited-view 3D object recognition[J]. Journal of East China Normal University (Natural Science), 2023(6): 61–72. doi: 10.3969/j.issn.1000-5641.2023.06.006. [31] 邓琨, 李文平, 陈丽, 等. 一种新的基于标签传播的复杂网络重叠社区识别算法[J]. 控制与决策, 2020, 35(11): 2733–2742. doi: 10.13195/j.kzyjc.2019.0176.DENG Kun, LI Wenping, CHEN Li, et al. A novel algorithm for overlapping community detection based on label propagation in complex networks[J]. Control and Decision, 2020, 35(11): 2733–2742. doi: 10.13195/j.kzyjc.2019.0176. [32] XIE Jierui, SZYMANSKI B K, and LIU Xiaoming. SLPA: Uncovering overlapping communities in social networks via a speaker-listener interaction dynamic process[C]. The 2011 IEEE 11th International Conference on Data Mining Workshops, Vancouver, Canada, 2011: 344–349. doi: 10.1109/ICDMW.2011.154. [33] ZHANG Bowen, WANG Yidong, HOU Wenxin, et al. FlexMatch: Boosting semi-supervised learning with curriculum pseudo labeling[C]. The 35th International Conference on Neural Information Processing Systems, Red Hook, USA, 2024: 1407. [34] SONG Zihao, ZHOU Yan, CHENG Wei, et al. Robust air target intention recognition based on weight self-learning parallel time-channel transformer encoder[J]. IEEE Access, 2023, 11: 144760–144777. doi: 10.1109/ACCESS.2023.3341154. [35] WANG Jingdong, WANG Fei, ZHANG Changshui, et al. Linear neighborhood propagation and its applications[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(9): 1600–1615. doi: 10.1109/TPAMI.2008.216. [36] WANG Zhiguang, YAN Weizhong, and OATES T. Time series classification from scratch with deep neural networks: A strong baseline[C]. 2017 International Joint Conference on Neural Networks, Anchorage, USA, 2017: 1578–1585. doi: 10.1109/IJCNN.2017.7966039. -





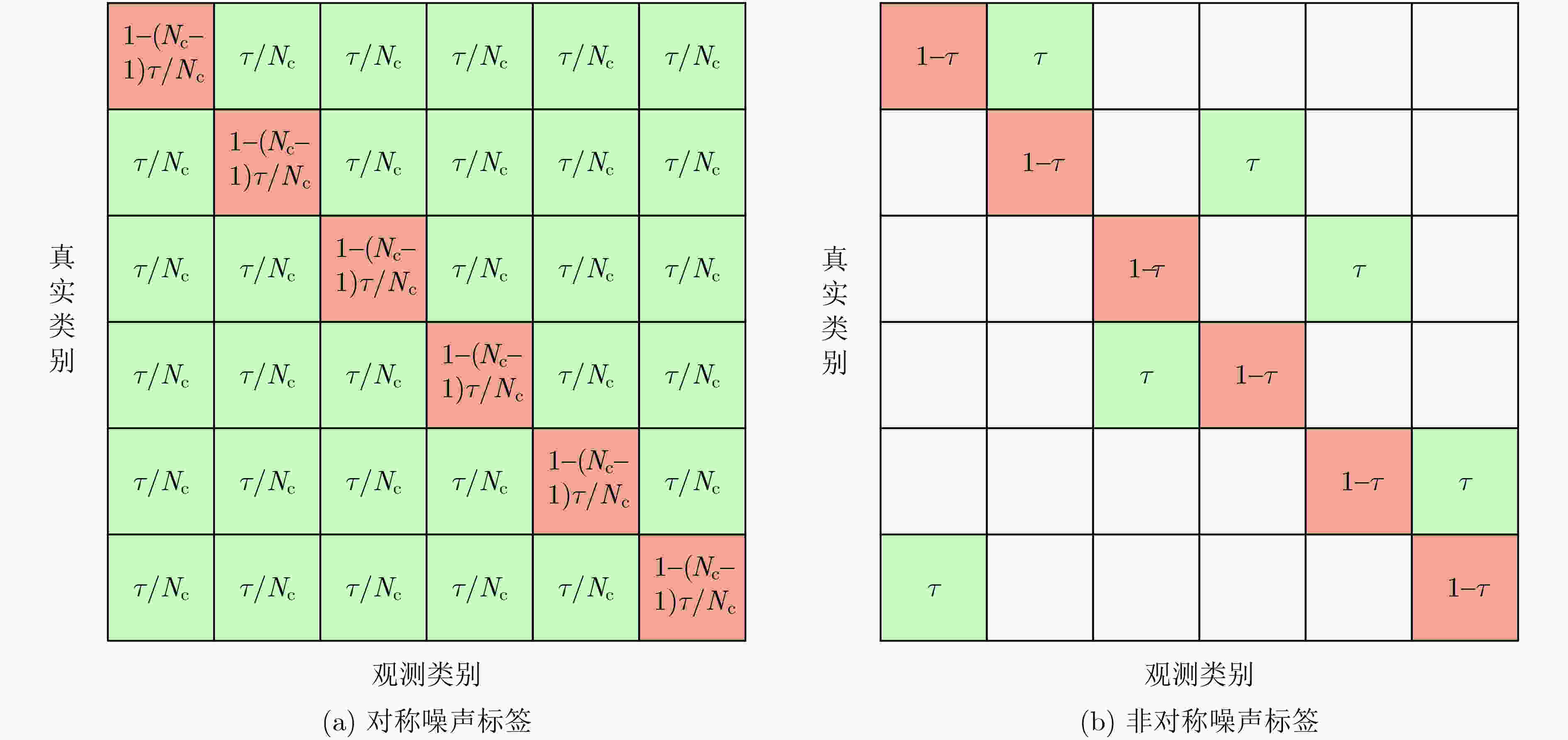
 下载:
下载:
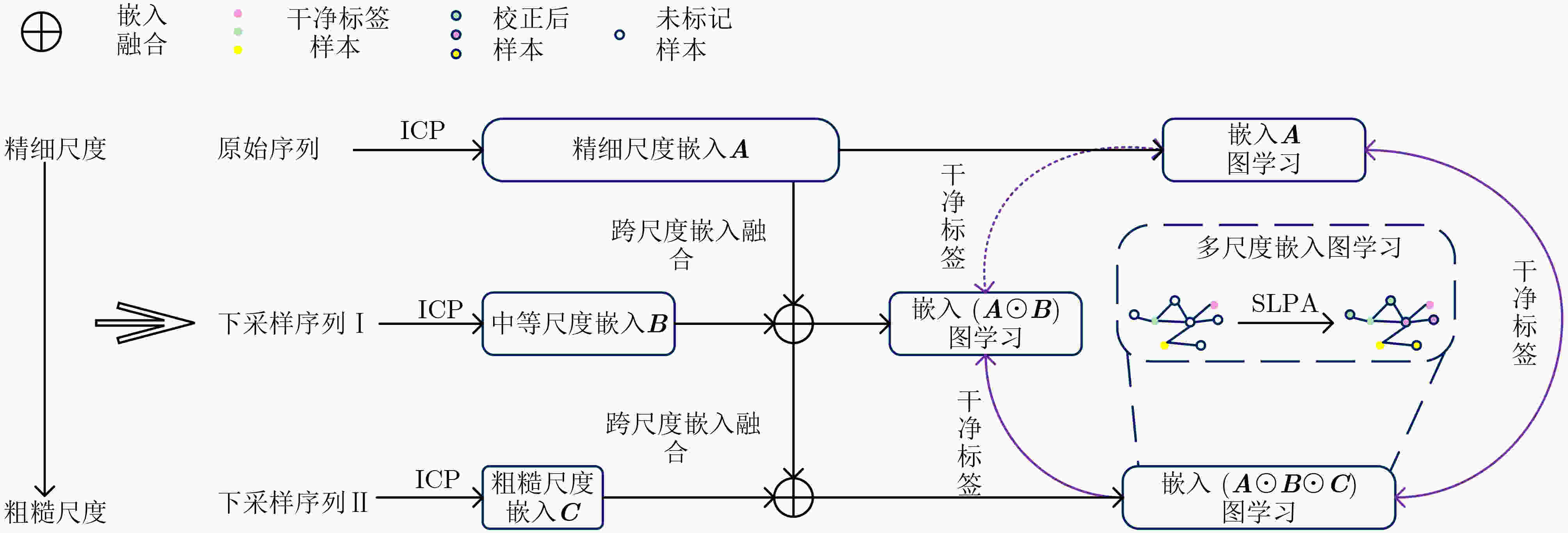
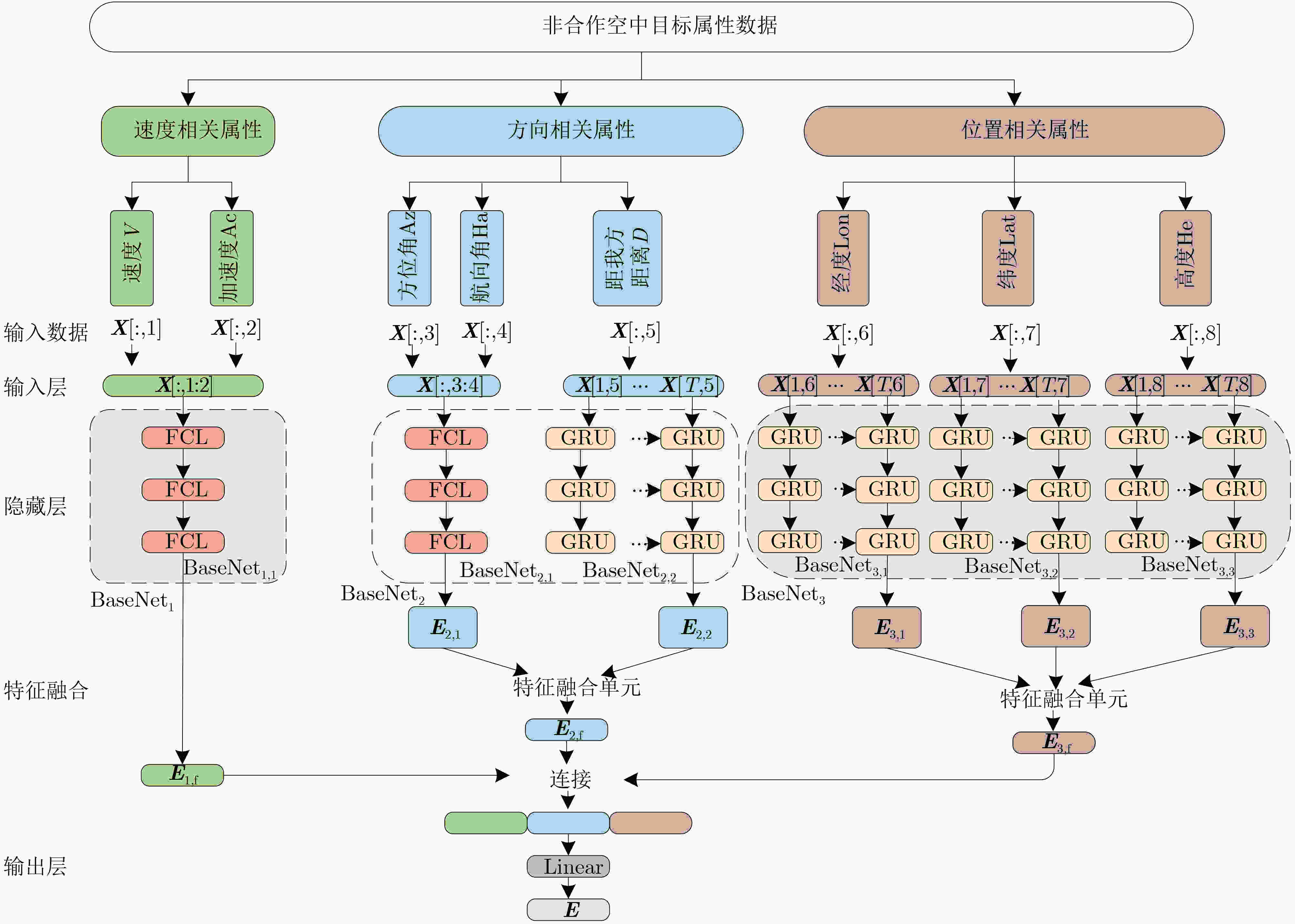
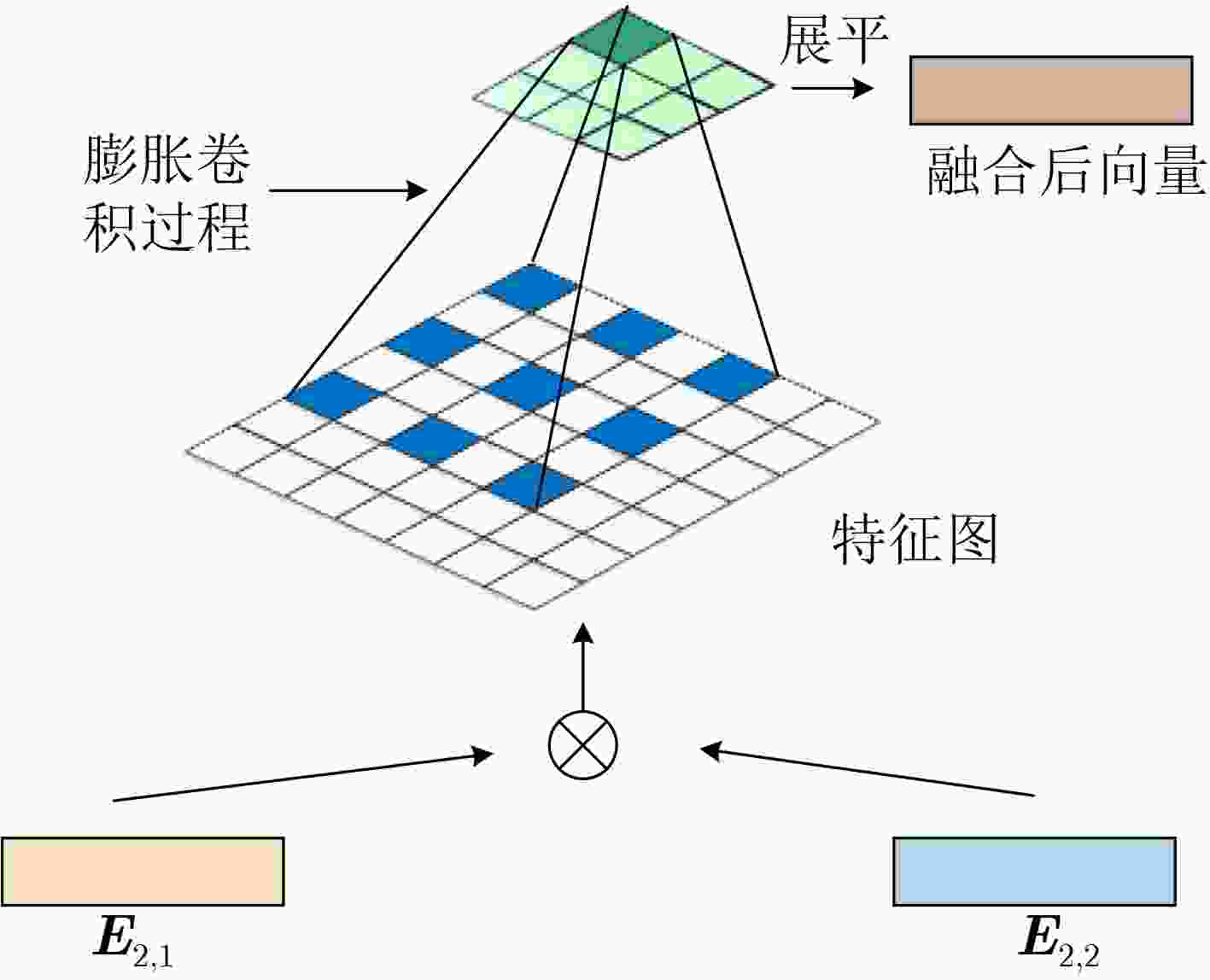


 下载:
下载:
