Low-complexity MRC Receiver Algorithm Based on OTFS System
-
摘要: 正交时频空(OTFS)因其在高速移动场景下优异的误码率性能而受到广泛研究。针对OTFS接收机运算复杂度较高问题,该文提出一种基于最大比合并(MRC)的低复杂度接收机算法。首先,其核心思想在时延多普勒域利用最大比合并算法进行迭代,对接收的多径分量进行提取和相干组合,以提高组合信号的信噪比。其次,通过引入交织器和解交织器,信道矩阵转化为稀疏的上三角海森伯矩阵,有利于后续进行矩阵分解。再次,针对符号决策过程中矩阵求逆计算量大的问题,提出一种低复杂度的LDLH分解算法。最后,在此基础上进一步改进,提出了一种复杂度进一步降低的下三角矩阵求逆算法,以降低下三角矩阵求逆的复杂度。仿真结果表明,一方面该算法误码率与最大比合并算法相同,另一方面性能显著优于高阶调制的线性最小均方误差估计(LMMSE)线性均衡器与高斯−赛德尔(GS)迭代均衡算法。Abstract:
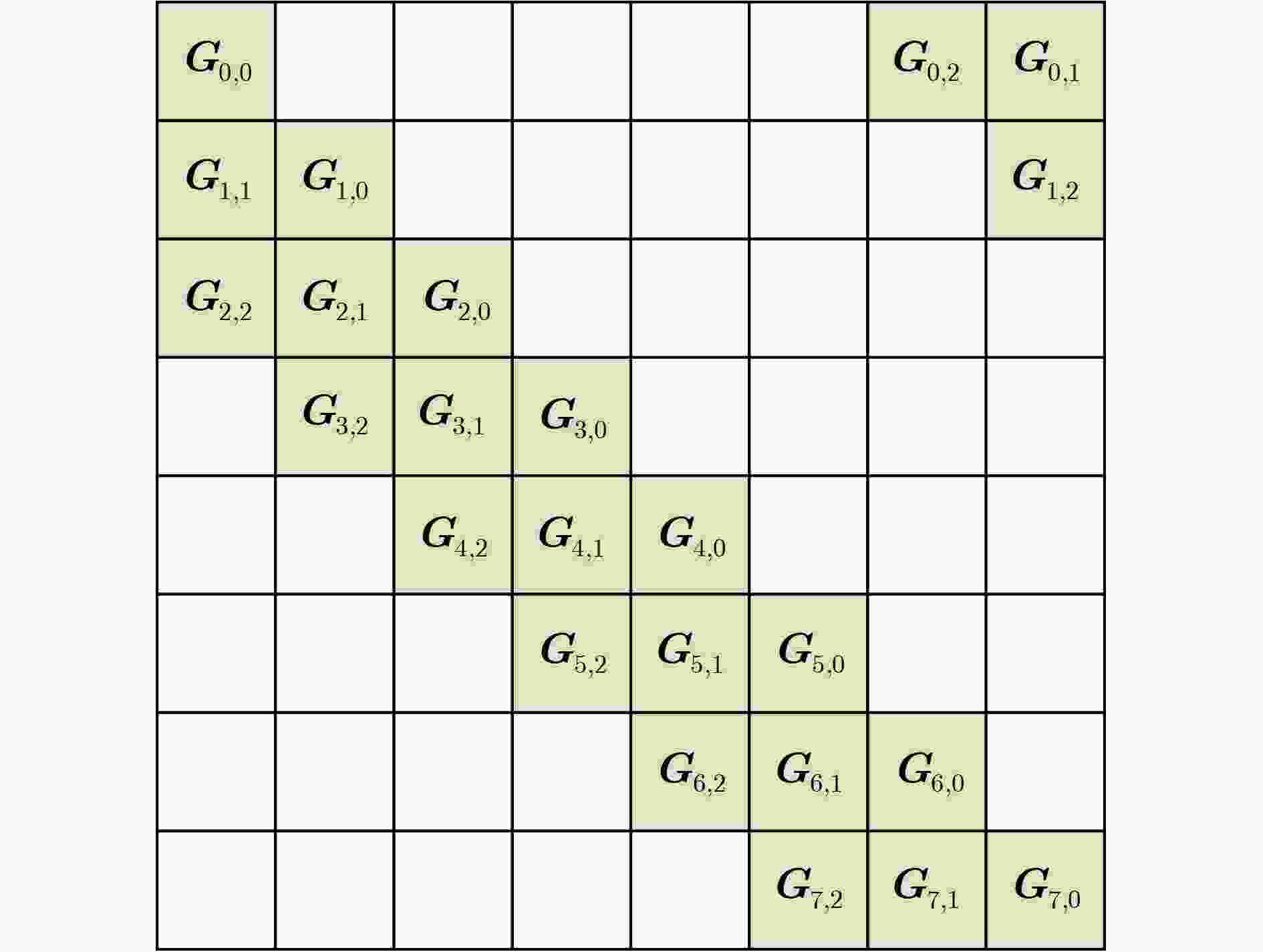
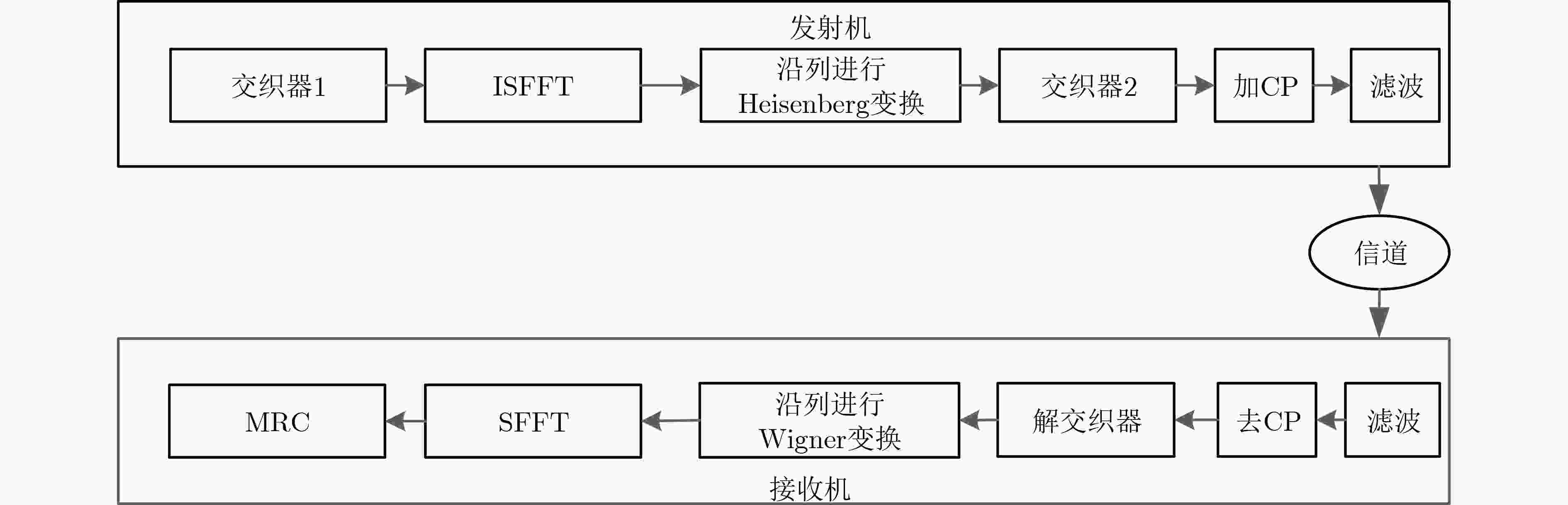
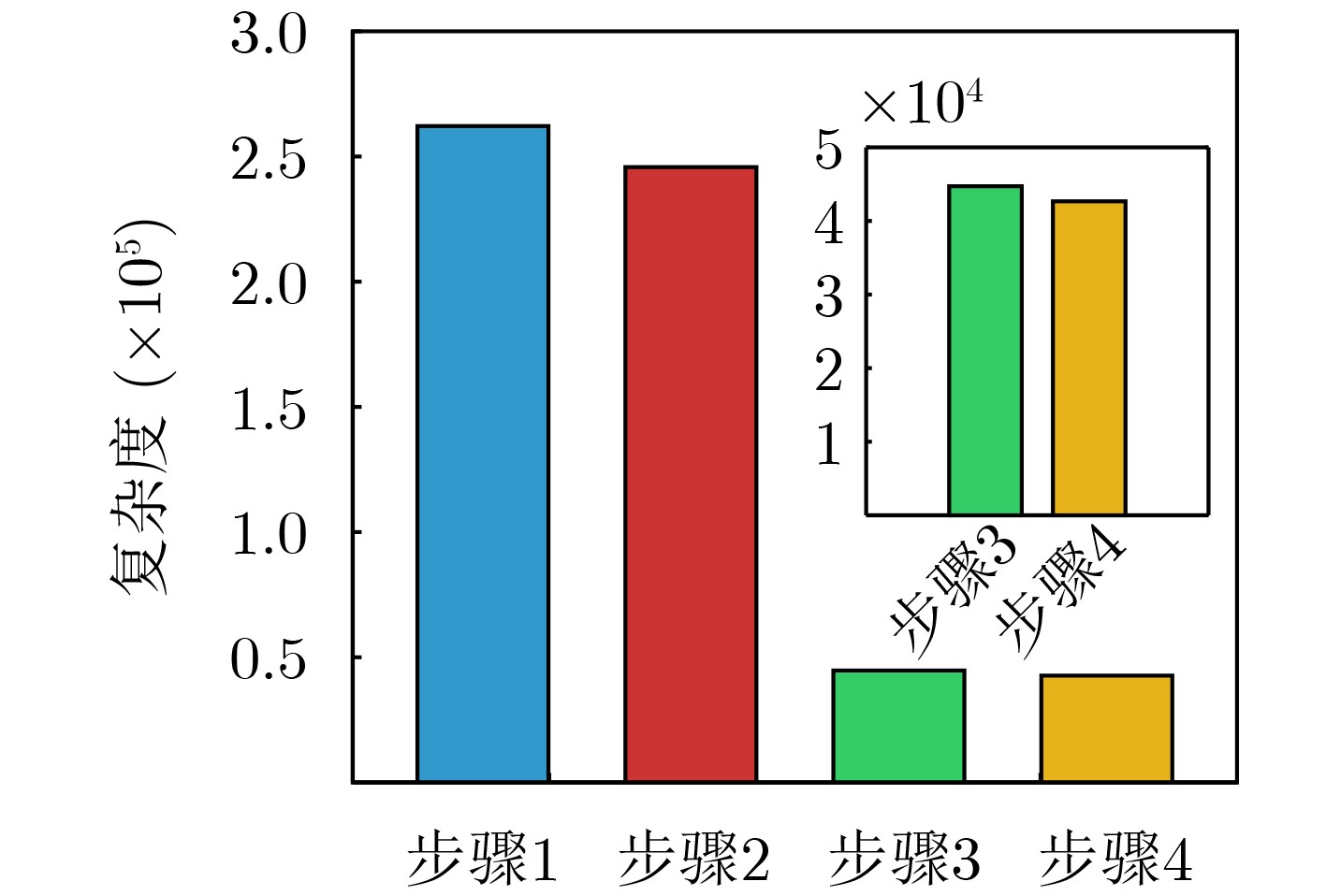
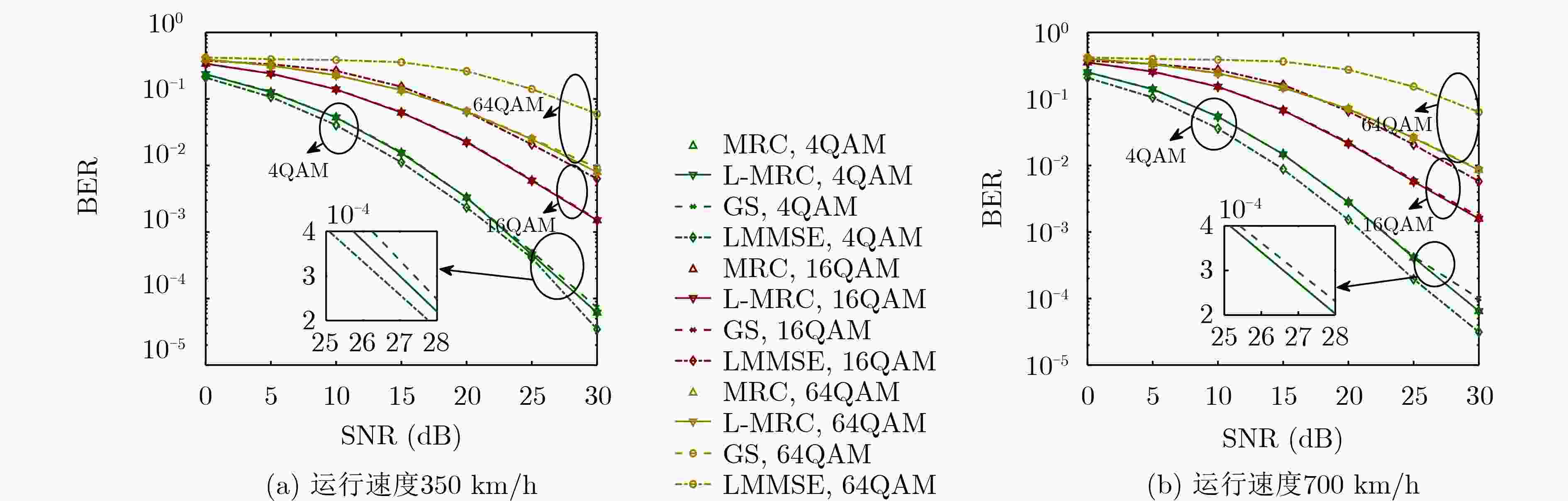
Objective Ultra-high-speed mobile applications—such as Unmanned Aerial Vehicles (UAVs), high-speed railways, satellite communications, and vehicular networks—place increasing demands on communication systems, particularly under high-Doppler conditions. Orthogonal Time Frequency Space (OTFS) modulation offers advantages in such environments due to its robustness against Doppler effects. However, conventional receiver algorithms rely on computationally intensive matrix operations, which limit their efficiency and degrade real-time performance in high-mobility scenarios. This paper proposes a low-complexity Maximum Ratio Combining (MRC) receiver for OTFS systems that avoids matrix inversion by exploiting the structural characteristics of OTFS channel matrices in the Delay-Doppler (DD) domain. The proposed receiver achieves high detection performance while substantially reducing computational complexity, supporting practical deployment in ultra-high-speed mobile communication systems. Methods The proposed low-complexity receiver algorithm applies MRC in the DD domain to iteratively extract and coherently combine multipath components. This approach enhances Bit Error Rate (BER) performance by optimizing signal aggregation while avoiding computationally intensive operations. To further reduce complexity, the algorithm incorporates interleaving and deinterleaving operations that restructure the channel matrix into a sparse upper triangular Heisenberg form. This transformation enables efficient matrix decomposition and facilitates simplified processing. To address the computational burden associated with matrix inversion during symbol detection, a low-complexity LDL decomposition algorithm is introduced. Compared with conventional matrix inversion techniques, this method substantially reduces computational overhead. Furthermore, a low-complexity inversion method for lower triangular matrices is implemented to further improve efficiency during the decision process. Simulation results confirm that the proposed receiver achieves BER performance comparable to that of traditional MRC algorithms while significantly lowering computational complexity. Results and Discussions Simulation results confirm that the proposed low-complexity MRC receiver achieves BER performance comparable to that of conventional MRC receivers while substantially improving computational efficiency under high-mobility conditions ( Fig. 3 ). The algorithm is evaluated across a range of environments, including scenarios characterized by high-speed motion and complex multipath interference. It outperforms Linear Minimum Mean Square Error (LMMSE) equalizers and Gauss–Seidel iterative equalization algorithms. Despite its reduced complexity, the proposed receiver maintains the same BER performance as traditional MRC methods. The algorithm demonstrates effective scalability as the number of symbols and subcarriers increases. Under conditions of increased system complexity, the receiver sustains computational efficiency without performance degradation (Fig. 4 ,Fig. 5 ). These results support its suitability for practical deployment in high-speed mobile communication systems employing OTFS modulation. The receiver also exhibits strong resilience to variations in wireless channel models. Across both typical urban multipath scenarios and high-velocity vehicular conditions, it maintains stable BER performance (Fig. 8 ). In addition, the receiver demonstrates robust tolerance to Doppler shift fluctuations and variable noise levels. These characteristics enable its application in dynamic environments with rapidly changing channel conditions. The algorithm’s efficiency and performance stability make it particularly well suited for real-time implementation in ultra-high-mobility networks, including UAV systems, high-speed rail communications, and other next-generation wireless platforms. By reducing computational complexity without compromising detection accuracy, the proposed receiver supports large-scale deployment of OTFS-based systems, addressing key performance and scalability challenges in emerging communication infrastructures.Conclusions This study proposes a low-complexity MRC receiver algorithm for OTFS systems. By introducing an interleaver and deinterleaver, the channel matrix is transformed into a sparse upper triangular form, enabling efficient inversion with reduced computational cost. In addition, the receiver integrates a low-complexity LDL decomposition algorithm and an upper triangular matrix inversion method to further minimize the computational burden associated with matrix operations. Simulation results confirm that the proposed receiver achieves equivalent BER performance to conventional MRC receivers. Moreover, under identical channel conditions, it demonstrates superior BER performance relative to linear receivers. -
1 低复杂度${\text{LD}}{{\text{L}}^{\text{H}}}$分解算法
输入:信道矩阵$ {{{\boldsymbol{D}}}_m} $,零矩阵$ {{\boldsymbol{G}}} $ 输出:下三角矩阵L,下三角矩阵$ {{{\boldsymbol{L}}}^{ - 1}} $,对角矩阵D (1) $ {{\boldsymbol{D}}}(1,1) = {{{\boldsymbol{D}}}_m}(1,1) $ (2) for $ {\text{ }}{i}{ = 1:}{N} $ (3) for $ j = 1:i - 1 $ (4) for $ k = 1:j - 1 $ (5) $ {\text{tem}}{{\text{p}}_{(i)}} = \displaystyle\sum\limits_{j = 1}^{i - 1} {\displaystyle\sum\limits_{k = 1}^{j - 1} {{{\boldsymbol{G}}}(i,j){{{\boldsymbol{L}}}^ * }(j,k)} } $ (6) end (7) $ {{\boldsymbol{G}}}(i,j) = {\boldsymbol{A}}(i,j) - {\text{tem}}{{\text{p}}_{(i)}} $ (8) $ {{\boldsymbol{L}}}(i,j) = {{\boldsymbol{G}}}(i,j)/{{\boldsymbol{D}}}(j,j) $ (9) end (10) for $ k = 1:i - 1 $ (11) $ {\text{tem}}{{\text{p}}_{(i)}} = \displaystyle\sum\limits_{k = 1}^{i - 1} {{{\boldsymbol{G}}}(i,k){{{\boldsymbol{L}}}^*}(i,k)} $ (12) end (13) $ {{\boldsymbol{D}}}(i,i) = {{\boldsymbol{A}}}(i,i) - {\text{tem}}{{\text{p}}_{(i)}} $ (14) end (15) for $ i = 1:MN $ (16) $ {{{\boldsymbol{L}}}^{ - 1}}(i,i) = {{\boldsymbol{L}}}(i,i) $ (17) for $ u = 1:i - 1 $ (18) $ {{{\boldsymbol{L}}}^{ - 1}}(i,u) = - {{\boldsymbol{L}}}(i,i) \cdot \displaystyle\sum\limits_{k = u}^{i - 1} {{L}(i,k){{{\boldsymbol{L}}}^{ - 1}}(k,u)} $ (19) end (20) end 表 1 MRC迭代均衡算法计算复杂度
步骤 复杂度 1 $ O({M^3}{N^3}) $ 2 $ O({M^3}{N^3} - N{M^3}) $ 3 $ O((2{M^3}{N^3} + 3{M^2}{N^2} + MN)/12) $ 4 $ O((2{M^3}{N^3} - 3{M^2}{N^2} + MN)/12) $ 表 2 系统仿真参数
参数 值 子载波个数(M) 16, 32 符号个数(N) 4,16 载波频率(GHz) 4 子载波间隔(kHz) 15 用户移动速度(km/h) 350,700 调制方案 4 QAM, 16 QAM, 64 QAM 最大时延抽头数 4 -
[1] WANG Zhenduo, CHEN Xingyu, and NING Xiaoyan. BER analysis of integrated WFRFT-OTFS waveform framework over static multipath channels[J]. IEEE Communications Letters, 2021, 25(3): 754–758. doi: 10.1109/LCOMM.2020.3040822. [2] 蒋占军, 刘庆达, 张鈜, 等. 高速移动通信系统中OTFS分数多普勒信道估计加窗研究[J]. 电子与信息学报, 2022, 44(2): 646–653. doi: 10.11999/JEIT210561.JIANG Zhanjun, LIU Qingda, ZHANG Hong, et al. Study on OTFS fractional Doppler channel estimation and windowing in high-speed mobile communication systems[J]. Journal of Electronics & Information Technology, 2022, 44(2): 646–653. doi: 10.11999/JEIT210561. [3] RAVITEJA P, HONG Yi, VITERBO E, et al. Practical pulse-shaping waveforms for reduced-cyclic-prefix OTFS[J]. IEEE Transactions on Vehicular Technology, 2019, 68(1): 957–961. doi: 10.1109/TVT.2018.2878891. [4] 王永川, 周平, 黄局. 正交时频空调制的信道估计与信号检测技术研究现状[J]. 通信学报, 2024, 45(9): 229–243. doi: 10.11959/j.issn.1000-436x.2024151.WANG Yongchuan, ZHOU Ping, and HUANG Ju. Research status of channel estimation and signal detection techniques for orthogonal time frequency space modulation[J]. Journal on Communications, 2024, 45(9): 229–243. doi: 10.11959/j.issn.1000-436x.2024151. [5] LI Shuangyang, YUAN Weijie, WEI Zhiqiang, et al. Hybrid MAP and PIC detection for OTFS modulation[J]. IEEE Transactions on Vehicular Technology, 2021, 70(7): 7193–7198. doi: 10.1109/TVT.2021.3083181. [6] LAMPEL F, ALVARADO A, and WILLEMS F M J. A sliding-window LMMSE turbo equalization scheme for OTFS[J]. IEEE Communications Letters, 2023, 27(12): 3320–3324. doi: 10.1109/LCOMM.2023.3326168. [7] RAVITEJA P, PHAN K T, HONG Yi, et al. Interference cancellation and iterative detection for orthogonal time frequency space modulation[J]. IEEE Transactions on Wireless Communications, 2018, 17(10): 6501–6515. doi: 10.1109/TWC.2018.2860011. [8] THAJ T and VITERBO E. Low complexity iterative rake decision feedback equalizer for zero-padded OTFS systems[J]. IEEE Transactions on Vehicular Technology, 2020, 69(12): 15606–15622. doi: 10.1109/TVT.2020.3044276. [9] 蒋占军, 刘庆达. 高速移动通信系统中OTFS信道估计算法研究[J]. 电子与信息学报, 2021, 43(10): 2878–2885. doi: 10.11999/JEIT200683.JIANG Zhanjun and LIU Qingda. Study on OTFS channel estimation algorithms in high-speed mobile communication systems[J]. Journal of Electronics & Information Technology, 2021, 43(10): 2878–2885. doi: 10.11999/JEIT200683. [10] YUAN Zhengdao, LIU Fei, YUAN Weijie, et al. Iterative detection for orthogonal time frequency space modulation with unitary approximate message passing[J]. IEEE Transactions on Wireless Communications, 2022, 21(2): 714–725. doi: 10.1109/TWC.2021.3097173. [11] PAN Yanjun, WU Jingxian, and YUAN Jinhong. Low complexity OTFS detection with a delay-Doppler domain CMC-MMSE receiver[C]. The ICC 2024 - IEEE International Conference on Communications, Denver, USA, 2024: 551–556. doi: 10.1109/ICC51166.2024.10622327. [12] LI Qi, YUAN Jinhong, QIU Min, et al. Low complexity turbo SIC-MMSE detection for orthogonal time frequency space modulation[J]. IEEE Transactions on Communications, 2024, 72(6): 3169–3183. doi: 10.1109/TCOMM.2024.3357431. [13] SURABHI G D and CHOCKALINGAM A. Low-complexity linear equalization for OTFS modulation[J]. IEEE Communications Letters, 2020, 24(2): 330–334. doi: 10.1109/LCOMM.2019.2956709. [14] LIN Xu, MEI Lin, LABEAU F, et al. Efficient fast-convolution based hybrid carrier system[J]. IEEE Transactions on Wireless Communications, 2022, 21(5): 3508–3522. doi: 10.1109/TWC.2021.3122880. [15] LI Shuangyang, YUAN Weijie, WEI Zhiqiang, et al. Cross domain iterative detection for orthogonal time frequency space modulation[J]. IEEE Transactions on Wireless Communications, 2022, 21(4): 2227–2242. doi: 10.1109/TWC.2021.3110125. [16] TIWARI S, DAS S S, and RANGAMGARI V. Low complexity LMMSE Receiver for OTFS[J]. IEEE Communications Letters, 2019, 23(12): 2205–2209. doi: 10.1109/LCOMM.2019.2945564. -





 下载:
下载:




 下载:
下载:
