A Beamforming Combined Iterative Dual-Maximum Ratio Combining Detection Algorithm for Orthogonal Time Frequency Space Systems
-
摘要: 正交时频空(OTFS)调制方案有望通过将复杂的时频(TF)域信道转换为稀疏的时延-多普勒(DD)域信道,实现高机动环境下的可靠通信。基于此,绝大多数研究都以DD域信道的稀疏性为前提展开讨论。然而,在市区车联网、无人机蜂群和多用户MIMO等复杂通信场景下,DD域信道可能无法保证具有一定的稀疏度。这将对接收端检测的复杂度和准确性构成极大的挑战。针对这一问题,该文提出一种结合波束成型的OTFS迭代双重最大比值合并(Dual MRC)检测算法。其主要思想是在接收端每个用户使用多天线阵列和波束成型初步分离信道多径中的不同接收角度的信号,从而提高对应信道矩阵的稀疏度并提供分集增益;进一步,利用OTFS信号在时延-时间(DT)域中具有简化运算的性质,对每个波束成型分支中的多径分量以及所有波束成型分支信号依次进行相干合并,通过不断迭代得到最优估计值。仿真结果表明,所提算法在误码率方面显著优于一些典型的检测方案;与现有性能较好的波束成型MP-MRC算法相比,在误码率性能提升的同时,达到最优值所需的迭代次数和迭代耗时均大幅降低。Abstract:
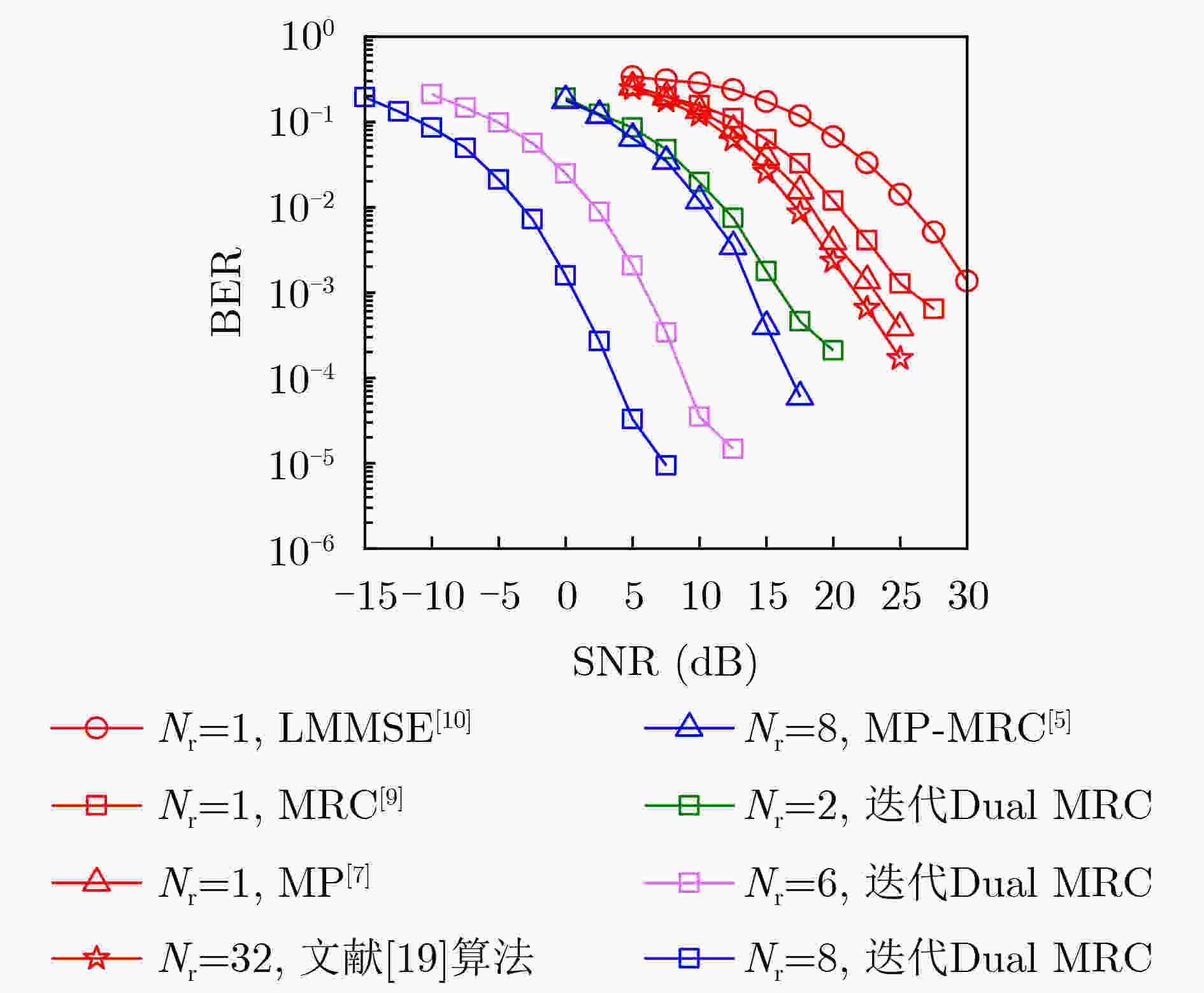
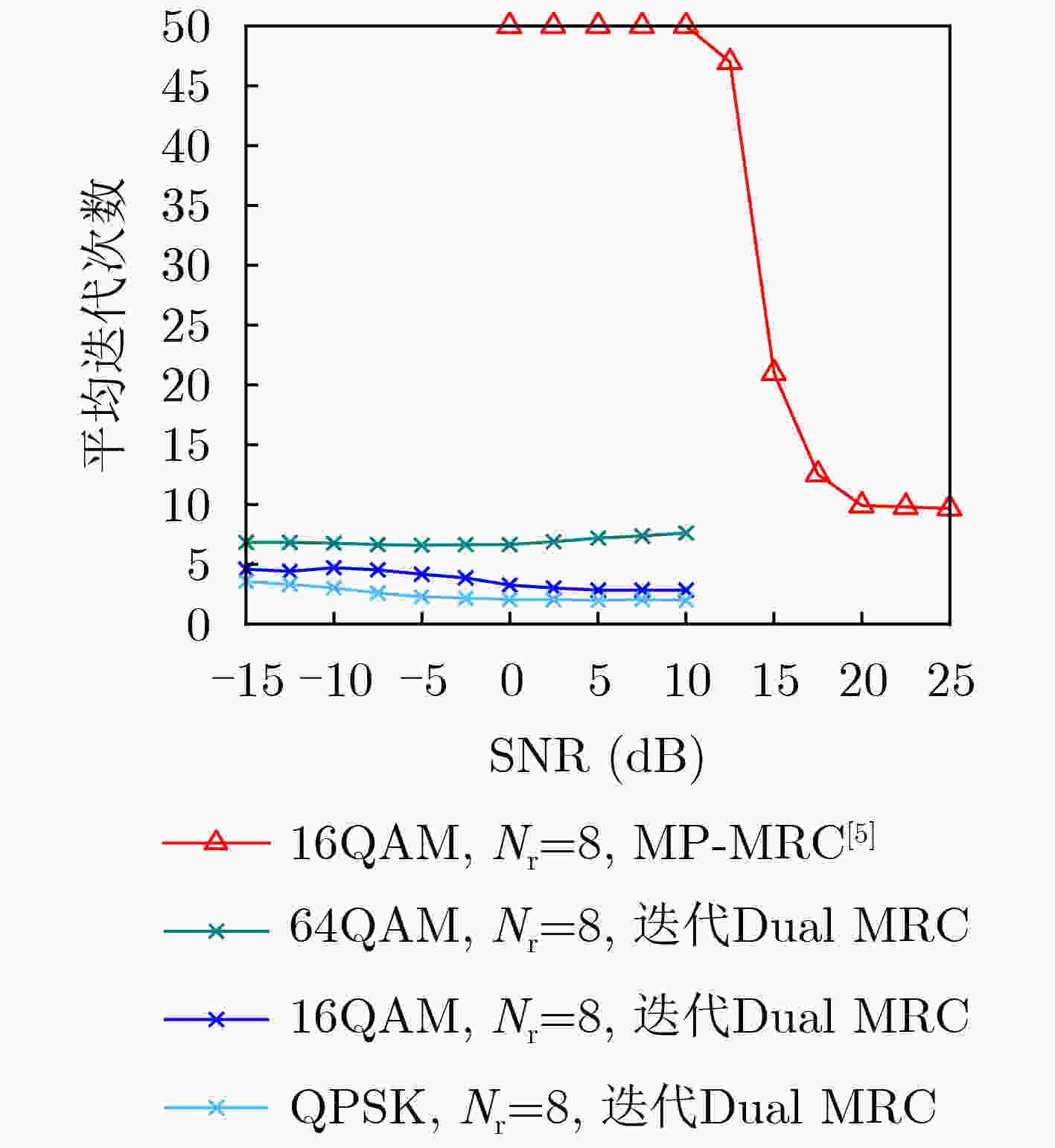
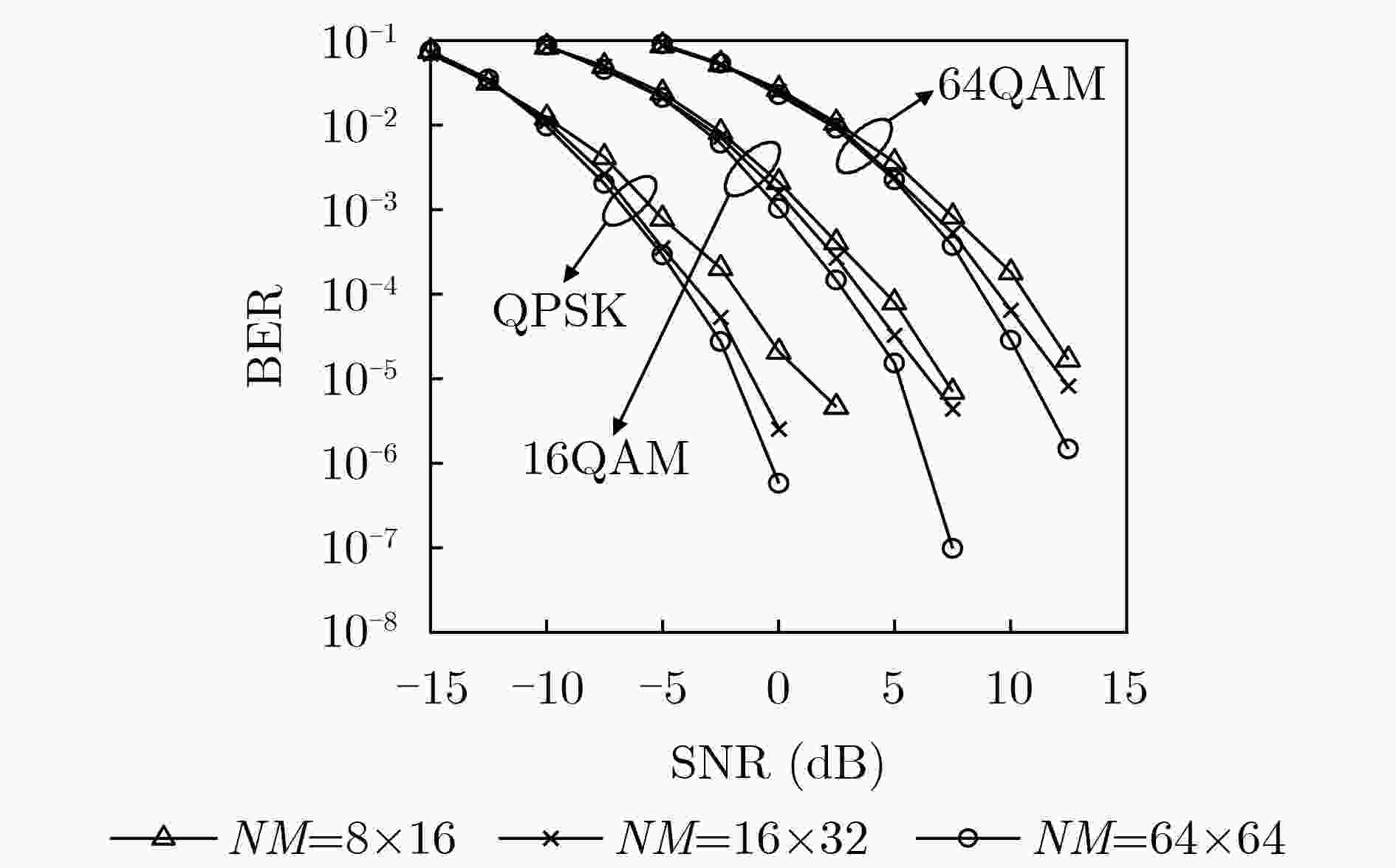
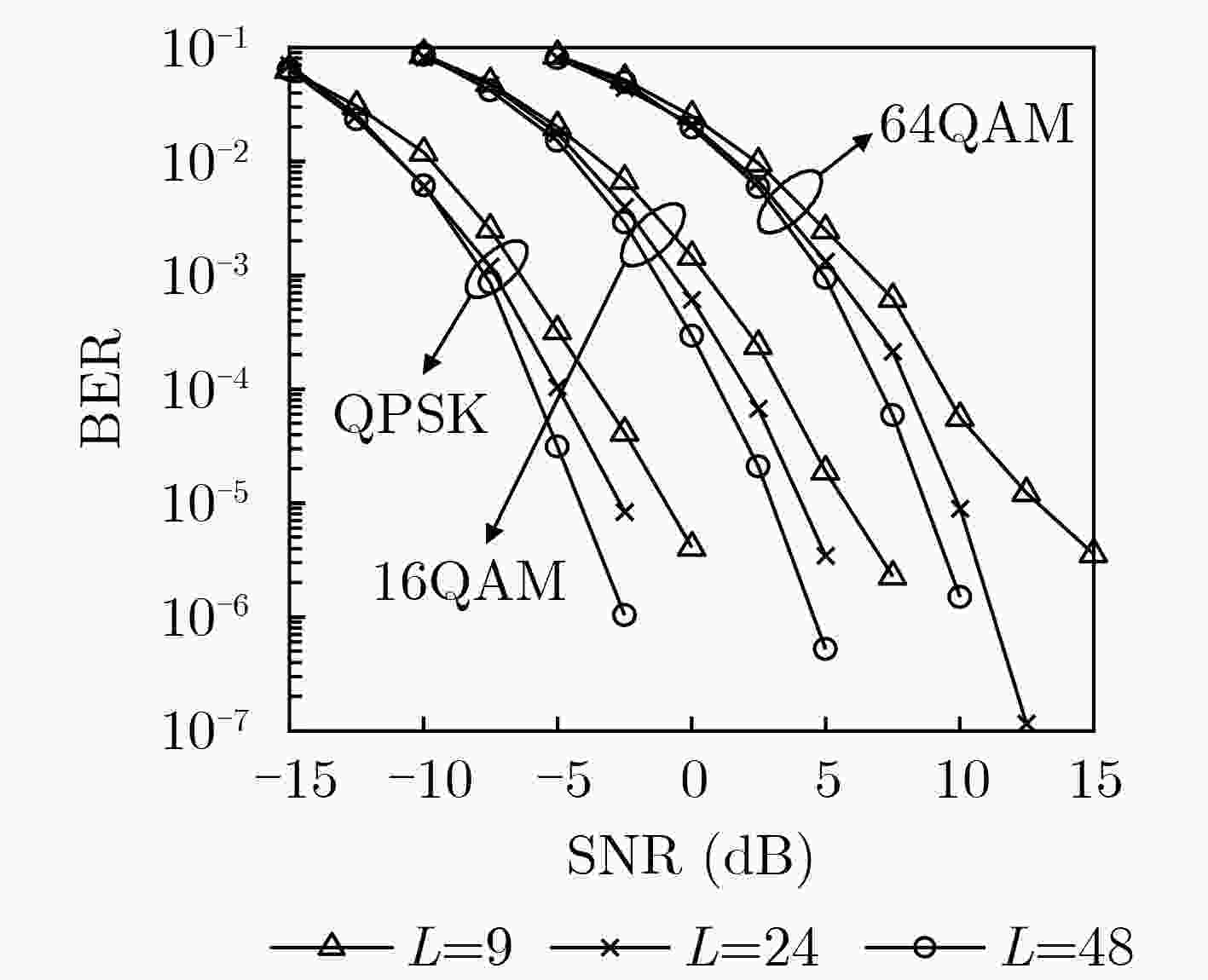
Objective The rapid advancement of wireless communication has introduced new waveform and modulation requirements for high-mobility scenarios such as vehicular networks, high-speed railways, and Low-Earth Orbit (LEO) satellites. Traditional Orthogonal Frequency Division Multiplexing (OFDM) performs poorly in such environments due to severe Inter-Carrier Interference (ICI). To address this, Orthogonal Time Frequency Space (OTFS), a two-dimensional modulation scheme that maps data in the Delay-Doppler (DD) domain, has been proposed. OTFS transforms complex Time-Frequency (TF) domain channels into sparse DD domain representations and has demonstrated improved performance over OFDM under high mobility. Signal detection plays a critical role in realizing OTFS benefits, and extensive studies have focused on DD-domain sparsity-based detection algorithms. However, in complex scenarios—such as urban vehicular networks, drone formations, and multi-user MIMO systems—DD-domain sparsity is often absent. This condition significantly increases detection complexity and degrades accuracy at the receiver. Methods A beamforming combined iterative Dual-Maximum Ratio Combining (Dual MRC) detection algorithm is proposed for OTFS systems (Algorithm 1). The approach utilizes a multi-antenna array and a beamforming network at the receiver to initially separate signals arriving from different angles within the multipath channel. This separation enhances channel matrix sparsity and provides diversity gain. By leveraging the computational simplicity of OTFS signals in the Delay-Time (DT) domain, the algorithm coherently combines multipath components within each beamforming branch and iteratively across branches. This process gradually refines the signal estimate and converges toward the optimal transmitted signal. Results and Discussions Simulation results show that the proposed algorithm significantly improves Bit Error Rate (BER) performance compared with several conventional detection methods. In particular, relative to the beamforming Message Passing-MRC (MP-MRC) algorithm, it achieves better BER performance ( Fig. 2 ) and reduces both the number of iterations and the iteration time required to reach convergence (Fig. 3 ). The algorithm also maintains robust BER performance as terminal mobility increases (Fig. 4 ), as the DD grid size $ N \times M $ expands (Fig. 5 ), and as the number of channel paths $ L $ grows (Fig. 6 ). Furthermore, compared with MP-MRC, the proposed method reduces computational complexity by two orders of magnitude while further improving detection performance (Table 2 ,Fig. 2 ).Conclusions This study addresses the limitations of existing OTFS detection algorithms using multi-antenna and beamforming receivers, which often suffer from high computational complexity or limited accuracy. A beamforming combined iterative Dual MRC detection algorithm operating in the DT domain is proposed to enhance receiver performance. Simulation results show that the proposed method substantially improves BER performance compared with conventional algorithms. In particular, relative to the beamforming-based MP-MRC algorithm, it achieves a marked reduction in computational complexity while improving detection accuracy. These results indicate that the proposed algorithm offers an effective and computationally efficient solution for OTFS signal detection in complex communication environments. -
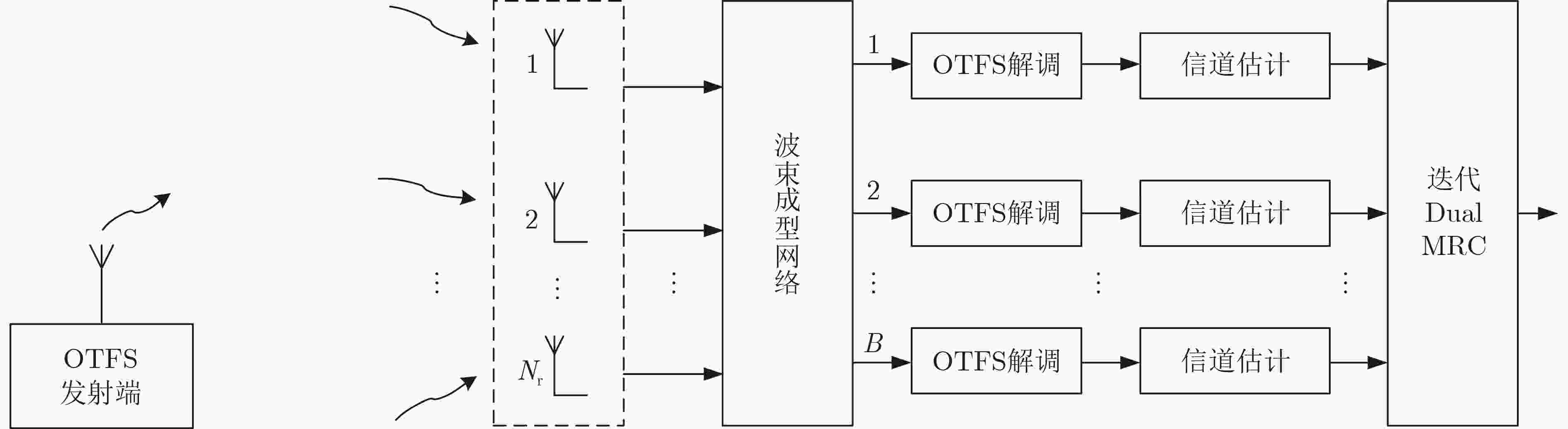
1 DT域结合波束成型的迭代Dual MRC检测算法
输入:$ {\boldsymbol{\hat {\tilde {\boldsymbol x}}}}_m^{(0)},{\boldsymbol{y}}_m^{({\theta _b})},\tilde {\boldsymbol{\upsilon}} _{m,p}^{({\theta _b})}, \forall p,m,b $ 输出:$ {{\boldsymbol{\hat {\tilde {\boldsymbol x}}}}_m},{{\boldsymbol{\tilde x}}_m} ,\forall m $ (1) for $ m = {\text{0}}:M' - {\text{1}} $ do (2) for $ b = {\text{1}}:B $ do (3) $ \Delta \tilde {\boldsymbol{y}}_m^{(0,{\theta _b})} = \tilde {\boldsymbol{y}}_m^{({\theta _b})} - \tilde {\boldsymbol{\upsilon}} _{m,p}^{({\theta _b})} \circ {\boldsymbol{\hat {\tilde {\boldsymbol x}}}}_{m - p}^{(0)} $ (4) end (5) $ {{\boldsymbol{\tilde d}}_m} = \displaystyle\sum\nolimits_{b = 0}^{B - 1} {\displaystyle\sum\nolimits_{p \in \mathcal{P}} {{{\left( {\tilde{\boldsymbol{ \upsilon}} _{m + p,p}^{({\theta _b})}} \right)}^{\text{H}}} \circ \tilde {\boldsymbol{\upsilon}} _{m + p,p}^{({\theta _b})}} } $ (6) end (7) for $ {\mathrm{iter}} = 1:{N_{{\text{iter}}}} $ do (8) $ \Delta \tilde {\boldsymbol{y}}_m^{(i,{\theta _b})} = \Delta \tilde {\boldsymbol{y}}_m^{(i - 1,{\theta _b})} $ (9) for $ m = {\text{0}}:M' - {\text{1}} $ do (10) $ \Delta {\boldsymbol{\tilde g}}_m^{(i)} = \displaystyle\sum\nolimits_{b = 0}^{B - 1} { \displaystyle\sum\nolimits_{p \in \mathcal{P}} {{{\left( {\tilde {\boldsymbol{\upsilon}} _{m + p,p}^{({\theta _b})}} \right)}^{\text{H}}} \circ \Delta \tilde {\boldsymbol{y}}_{m + p}^{(i,{\theta _b})}} } $ (11) $ {\boldsymbol{\tilde c}}_m^{(i)} = {\boldsymbol{\hat {\tilde {\boldsymbol x}}}}_m^{(i)} + \Delta {\boldsymbol{\tilde g}}_m^{(i)}{ \oslash }{\tilde {\boldsymbol{d}}_m} $ (12) $ {\boldsymbol{\hat {\tilde {\boldsymbol x}}}}_m^{(i)} = \omega {\boldsymbol{F}}_N^{\mathrm{H}}D\left( {{{\boldsymbol{F}}_N}{\boldsymbol{\tilde c}}_m^{(i)}} \right) + (1 - \omega ){\boldsymbol{\tilde c}}_m^{(i)},0 \le \omega \le 1 $ (13) for $ b = {\text{1}}:B $ do (14) for $ p \in {\mathcal{P}} $ do (15) $ \Delta \tilde {\boldsymbol{y}}_{m + p}^{(i,{\theta _b})} = \Delta \tilde {\boldsymbol{y}}_{m + p}^{(i - 1,{\theta _b})} - \tilde{\boldsymbol{ \upsilon}} _{m + p,p}^{({\theta _b})} $
$ \circ \left({\boldsymbol{\hat {\tilde {\boldsymbol x}}}}_m^{(i)} - {\boldsymbol{\tilde x}}_m^{(i - 1)}\right) $(16) end (17) end (18) end (19) if $ \left\| {\Delta \tilde {\boldsymbol{y}}_m^{(i,{\theta _b})}} \right\| \ge \left\| {\Delta \tilde {\boldsymbol{y}}_m^{(i - 1,{\theta _b})}} \right\|,\forall m,b $ (20) break (21) end (22) end 表 1 仿真参数
参数 取值 子载波数$ M $ 32 符号数$ N $ 16 载波频率 4.0 GHz 子载波间隔 15 kHz 调制方案 QPSK, 16QAM, 64QAM 信道模型 EVA[20] 接收天线数 8 终端移动速度 500 km/h 波束成型角度 [$ {30^ \circ },{60^ \circ },{90^ \circ },{120^ \circ },{150^ \circ } $] 表 3 计算总复杂度对比
检测算法 总复杂度 计算量 文献[19] $ {\mathcal{O}}(M'NB|{\mathcal{P}}|) $ $ 2.16 \times {10^4} $ 本文 $ {\mathcal{O}}[({N_{{\text{iter}}}} + {N_{\text{r}}})M'NB|{\mathcal{P}}|] $ $ 2.81 \times {10^5} $ MP-MRC[5] $ {\mathcal{O}}\left( {{N_{{\text{iter}}}}M'NBS|{\mathbb{A}}|} \right) $ $ {\text{3}}{\text{.46}} \times {10^7} $ -
[1] WU Jingxian and FAN Pingzhi. A survey on high mobility wireless communications: Challenges, opportunities and solutions[J]. IEEE Access, 2016, 4: 450–476. doi: 10.1109/ACCESS.2016.2518085. [2] WANG Chengxiang, YOU Xiaohu, GAO Xiqi, et al. On the road to 6G: Visions, requirements, key technologies, and testbeds[J]. IEEE Communications Surveys & Tutorials, 2023, 25(2): 905–974. doi: 10.1109/COMST.2023.3249835. [3] YUAN Weijie, LI Shuangyang, WEI Zhiqiang, et al. New delay Doppler communication paradigm in 6G era: A survey of orthogonal time frequency space (OTFS)[J]. China Communications, 2023, 20(6): 1–25. doi: 10.23919/JCC.fa.2022-0578.202306. [4] HADANI R, RAKIB S, TSATSANIS M, et al. Orthogonal time frequency space modulation[C]. The 2017 IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, USA, 2017: 1–6. doi: 10.1109/WCNC.2017.7925924. [5] CHENG Junqiang, JIA Chenglu, GAO Hui, et al. OTFS based receiver scheme with multi-antennas in high-mobility V2X systems[C]. The 2020 IEEE International Conference on Communications Workshops (ICC Workshops), Dublin, Ireland, 2020: 1–6. doi: 10.1109/ICCWorkshops49005.2020.9145313. [6] LIU Haoyan, LIU Yanming, YANG Min, et al. On the characterizations of OTFS modulation over multipath rapid fading channel[J]. IEEE Transactions on Wireless Communications, 2023, 22(3): 2008–2021. doi: 10.1109/TWC.2022.3208161. [7] RAVITEJA P, PHAN K T, HONG Yi, et al. Interference cancellation and iterative detection for orthogonal time frequency space modulation[J]. IEEE Transactions on Wireless Communications, 2018, 17(10): 6501–6515. doi: 10.1109/TWC.2018.2860011. [8] MA Yiyan, MA Guoyu, AI Bo, et al. Characteristics of channel spreading function and performance of OTFS in high-speed railway[J]. IEEE Transactions on Wireless Communications, 2023, 22(10): 7038–7054. doi: 10.1109/TWC.2023.3247736. [9] THAJ T and VITERBO E. Low complexity iterative rake decision feedback equalizer for zero-padded OTFS systems[J]. IEEE Transactions on Vehicular Technology, 2020, 69(12): 15606–15622. doi: 10.1109/TVT.2020.3044276. [10] TIWARI S, DAS S S, and RANGAMGARI V. Low complexity LMMSE receiver for OTFS[J]. IEEE Communications Letters, 2019, 23(12): 2205–2209. doi: 10.1109/LCOMM.2019.2945564. [11] SURABHI G D and CHOCKALINGAM A. Low-Complexity linear equalization for OTFS modulation[J]. IEEE Communications Letters, 2020, 24(2): 330–334. doi: 10.1109/LCOMM.2019.2956709. [12] LI Haotian and YU Qiyue. Doubly-iterative sparsified MMSE turbo equalization for OTFS modulation[J]. IEEE Transactions on Communications, 2023, 71(3): 1336–1351. doi: 10.1109/TCOMM.2023.3237243. [13] YUAN Weijie, WEI Zhiqiang, YUAN Jinhong, et al. A simple variational Bayes detector for orthogonal time frequency space (OTFS) modulation[J]. IEEE Transactions on Vehicular Technology, 2020, 69(7): 7976–7980. doi: 10.1109/TVT.2020.2991443. [14] XIANG Luping, LIU Yusha, YANG Lieliang, et al. Gaussian approximate message passing detection of orthogonal time frequency space modulation[J]. IEEE Transactions on Vehicular Technology, 2021, 70(10): 10999–11004. doi: 10.1109/TVT.2021.3102673. [15] LIU Fei, YUAN Zhengdao, GUO Qinghua, et al. Multi-block UAMP-based detection for OTFS with rectangular waveform[J]. IEEE Wireless Communications Letters, 2022, 11(2): 323–327. doi: 10.1109/LWC.2021.3126871. [16] YUAN Zongming, TANG Meng, CHEN Jianhua, et al. Low complexity parallel symbol detection for OTFS modulation[J]. IEEE Transactions on Vehicular Technology, 2023, 72(4): 4904–4918. doi: 10.1109/TVT.2022.3227282. [17] LI Xiang and YUAN Weijie. OTFS detection based on Gaussian mixture distribution: A generalized message passing approach[J]. IEEE Communications Letters, 2024, 28(1): 178–182. doi: 10.1109/LCOMM.2023.3318312. [18] ZHANG Zhengquan, LIU Heng, WANG Qianli, et al. A survey on low complexity detectors for OTFS systems[J]. ZTE Communications, 2021, 19(4): 3–15. doi: 10.12142/ZTECOM.202104002. [19] SHAN Yaru and WANG Fanggang. Low-complexity and low-overhead receiver for OTFS via large-scale antenna array[J]. IEEE Transactions on Vehicular Technology, 2021, 70(6): 5703–5718. doi: 10.1109/TVT.2021.3072667. [20] Technical Specification Group Radio Access Network. Evolved universal terrestrial radio access (E-UTRA); User equipment (UE) radio transmission and reception[R]. 36.101, 2020. -





 下载:
下载:



 下载:
下载:
