结合相似度预测和阈值自动求解的开集条件下毫米波雷达点云步态识别方法

杜兰; 李逸明; 薛世鲲; 石钰; 陈健; 李真芳

doi:10.11999/JEIT241034

结合相似度预测和阈值自动求解的开集条件下毫米波雷达点云步态识别方法

doi: 10.11999/JEIT241034 cstr: 32379.14.JEIT241034

西安电子科技大学雷达信号处理全国重点实验室西安 710071

基金项目: 国家自然科学基金(U21B2039, U24B20137, 62201433)，中央高校基本科研业务费专项资金(QTZX23067)

详细信息

作者简介:
杜兰：女，博士，教授，博士生导师，研究方向为雷达目标识别、雷达信号处理、机器学习

李逸明：男，博士生，研究方向为SAR图像目标识别与开放世界学习

薛世鲲：男，硕士生，研究方向为毫米波雷达步态识别与机器学习

石钰：男，博士生，研究方向为雷达目标检测识别与多模态学习

陈健：男，博士，副教授，硕士生导师，研究方向为雷达目标检测识别与机器学习

李真芳：男，博士，教授，博士生导师，研究方向为干涉/极化合成孔径雷达信号处理与系统设计

通讯作者:
杜兰　dulan@mail.xidian.edu.cn

中图分类号: TN957
计量
- 文章访问数: 323
- HTML全文浏览量: 183
- PDF下载量: 80
- 被引次数: 0
出版历程
- 收稿日期: 2024-11-20
- 修回日期: 2025-04-30
- 网络出版日期: 2025-05-16
- 刊出日期: 2025-06-30

Millimeter-wave Radar Point Cloud Gait Recognition Method Under Open-set Conditions Based on Similarity Prediction and Automatic Threshold Estimation

National Key Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China

Funds: The National Natural Science Foundation of China (U21B2039, U24B20137, 62201433), The Fundamental Research Funds for the Central Universities (QTZX23067)

摘要

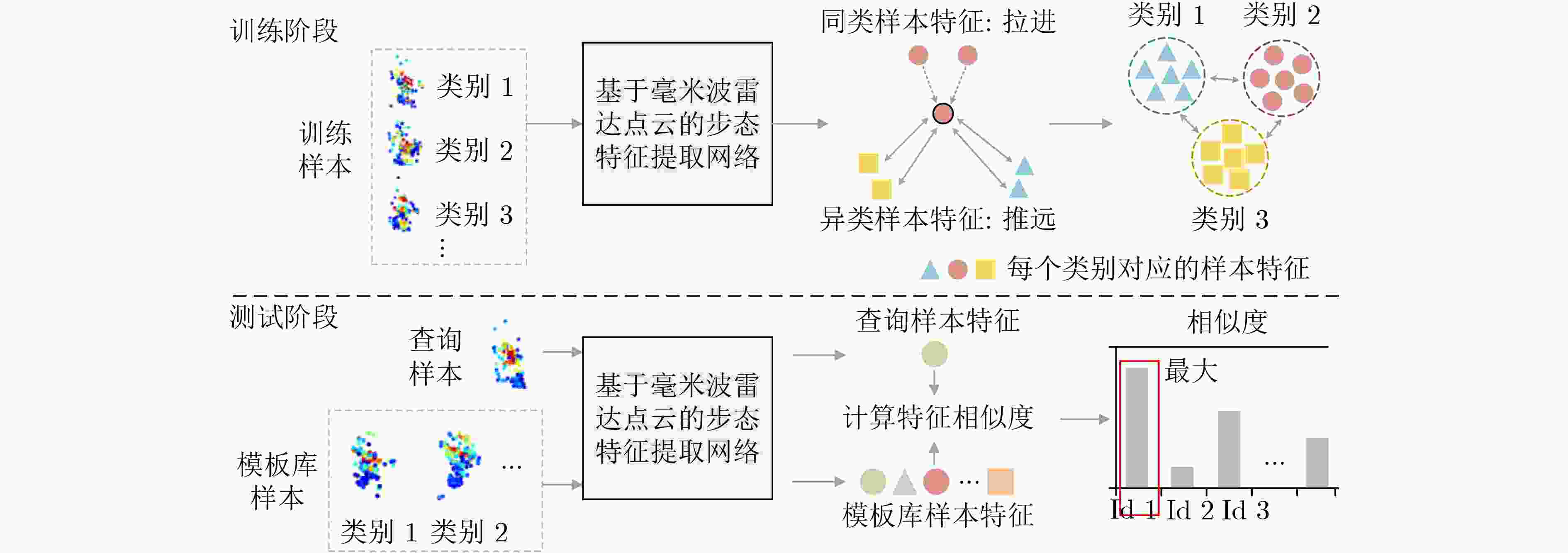
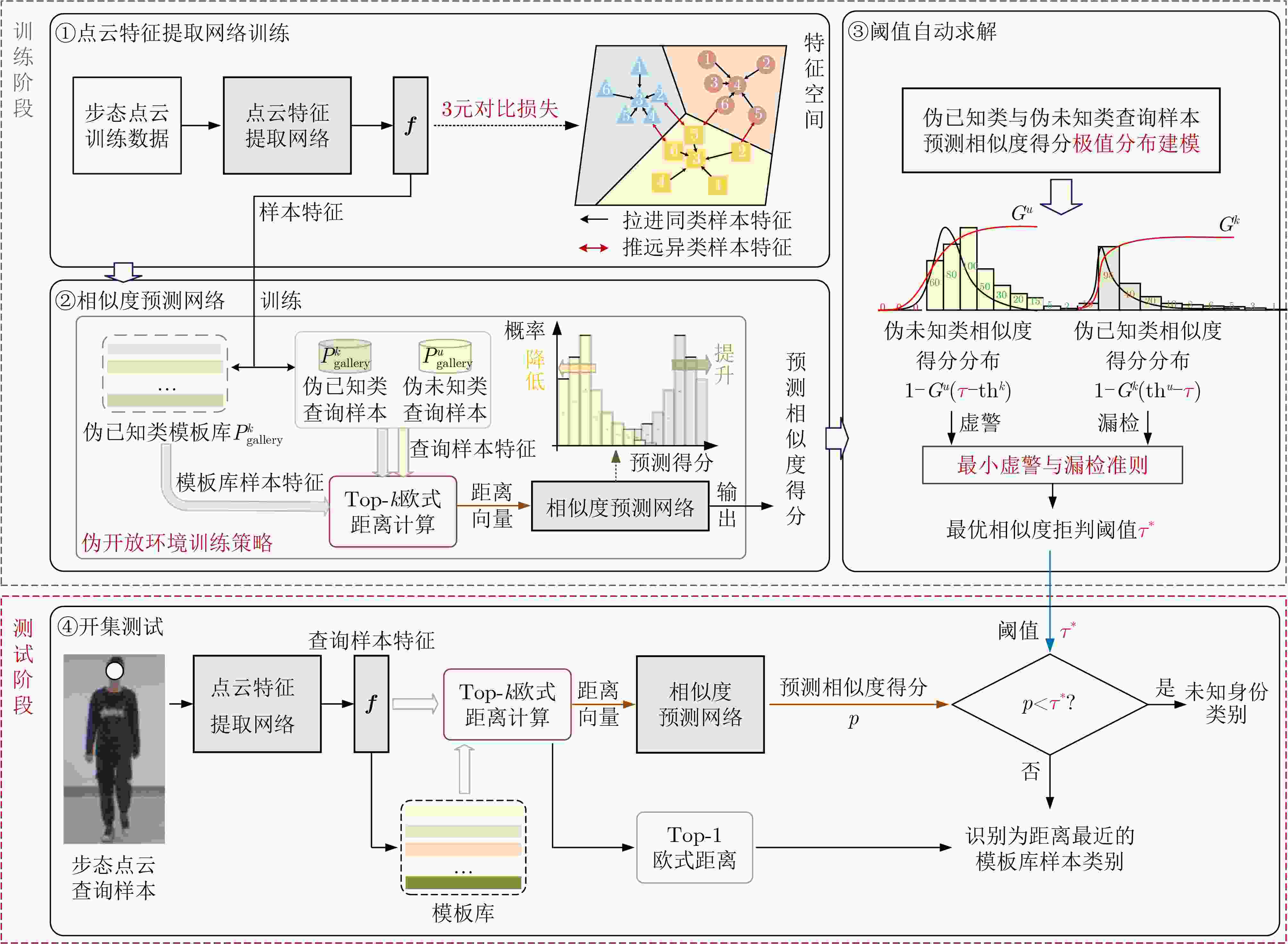
摘要: 现有的雷达步态识别方法多局限于闭集设置，即假设测试阶段的所有身份类别均已包含在模板库中，不适用于库内已知身份类别和库外未知新身份类别共存的真实开放识别环境。针对非完备身份类别模板库条件下的步态识别问题，该文提出一种结合相似度预测和阈值自动求解的开集条件下毫米波雷达点云步态识别方法。在点云特征提取的基础上，结合对潜在未知类相似度得分分布的先验认知，设计了一种伪开放环境训练策略来学习相似度预测网络，提升相似度得分空间中已知类别与未知类别的鉴别性；最后，阈值自动求解模块通过极值理论对相似度得分的极值分布进行概率拟合，并通过最小虚警与漏检准则实现未知类拒判阈值的准确求解。基于实测毫米波雷达点云数据的实验结果表明了所提方法在开集条件下具有良好的识别稳健性。
- 毫米波雷达 /
- 步态识别 /
- 开集识别 /
- 相似度预测 /
- 极值理论
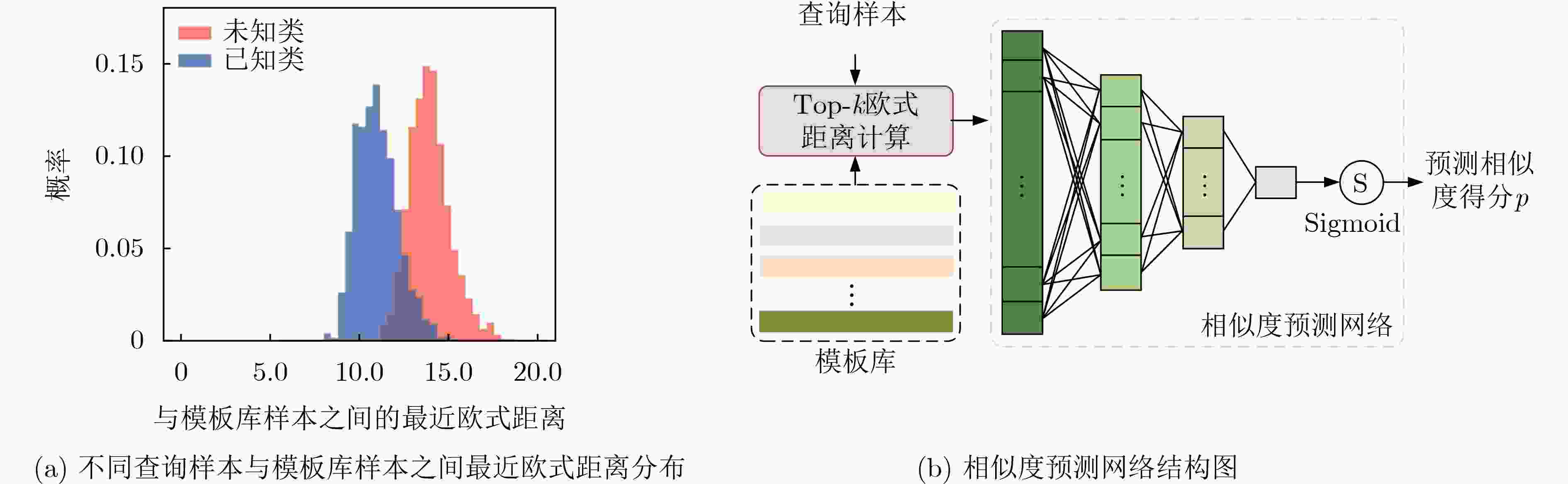
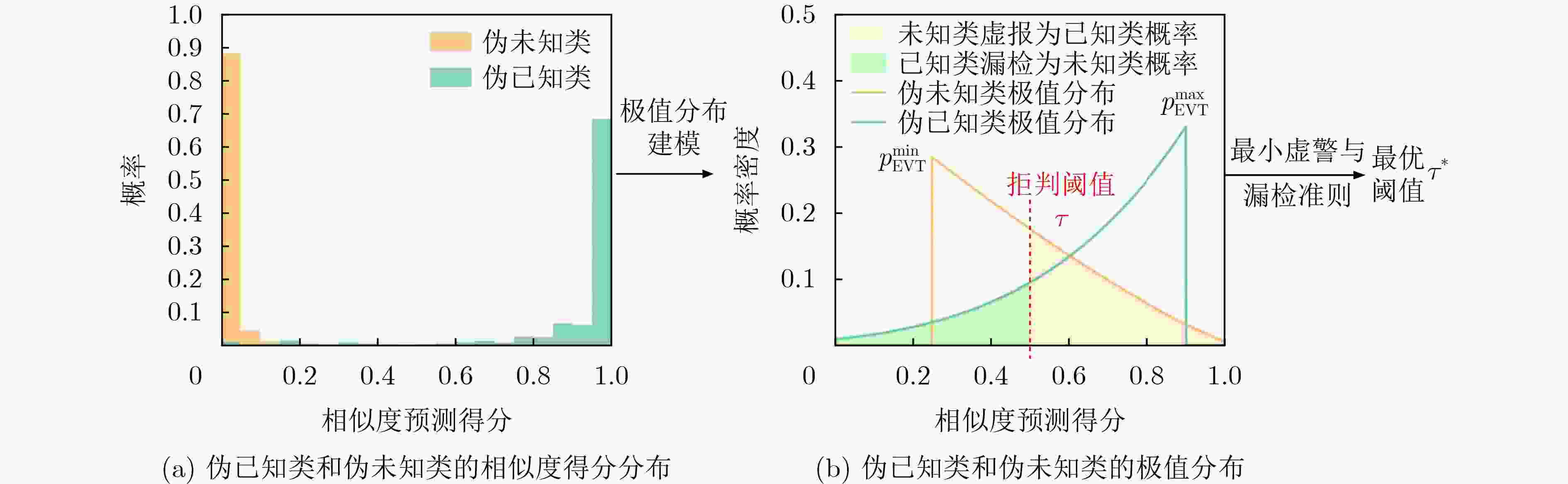
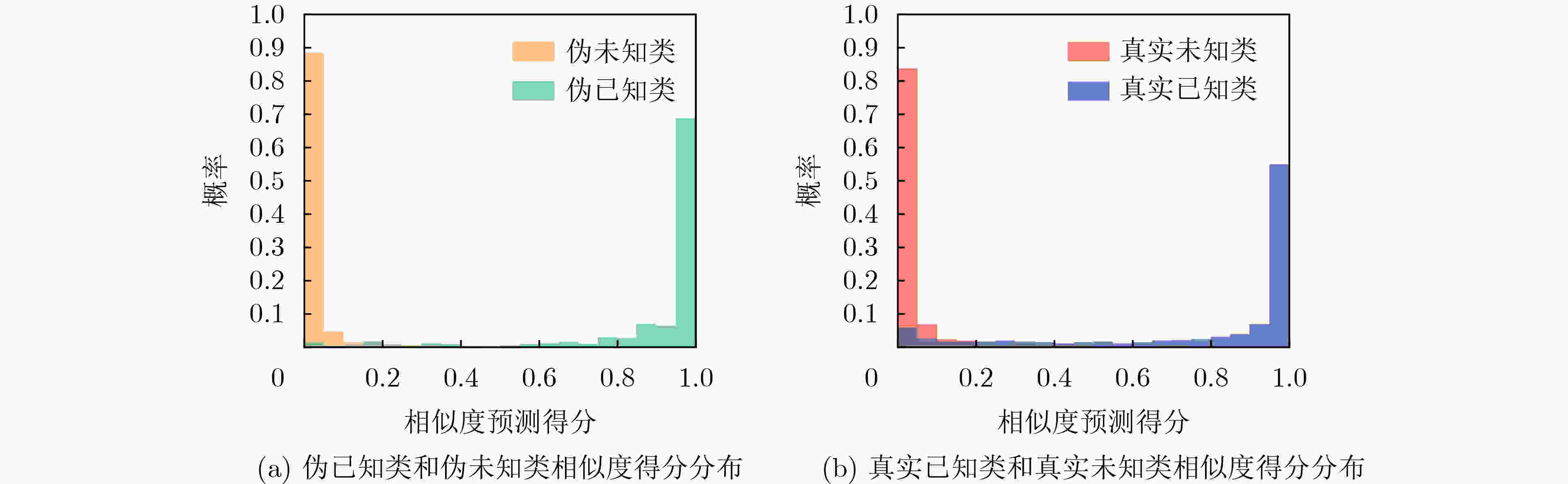
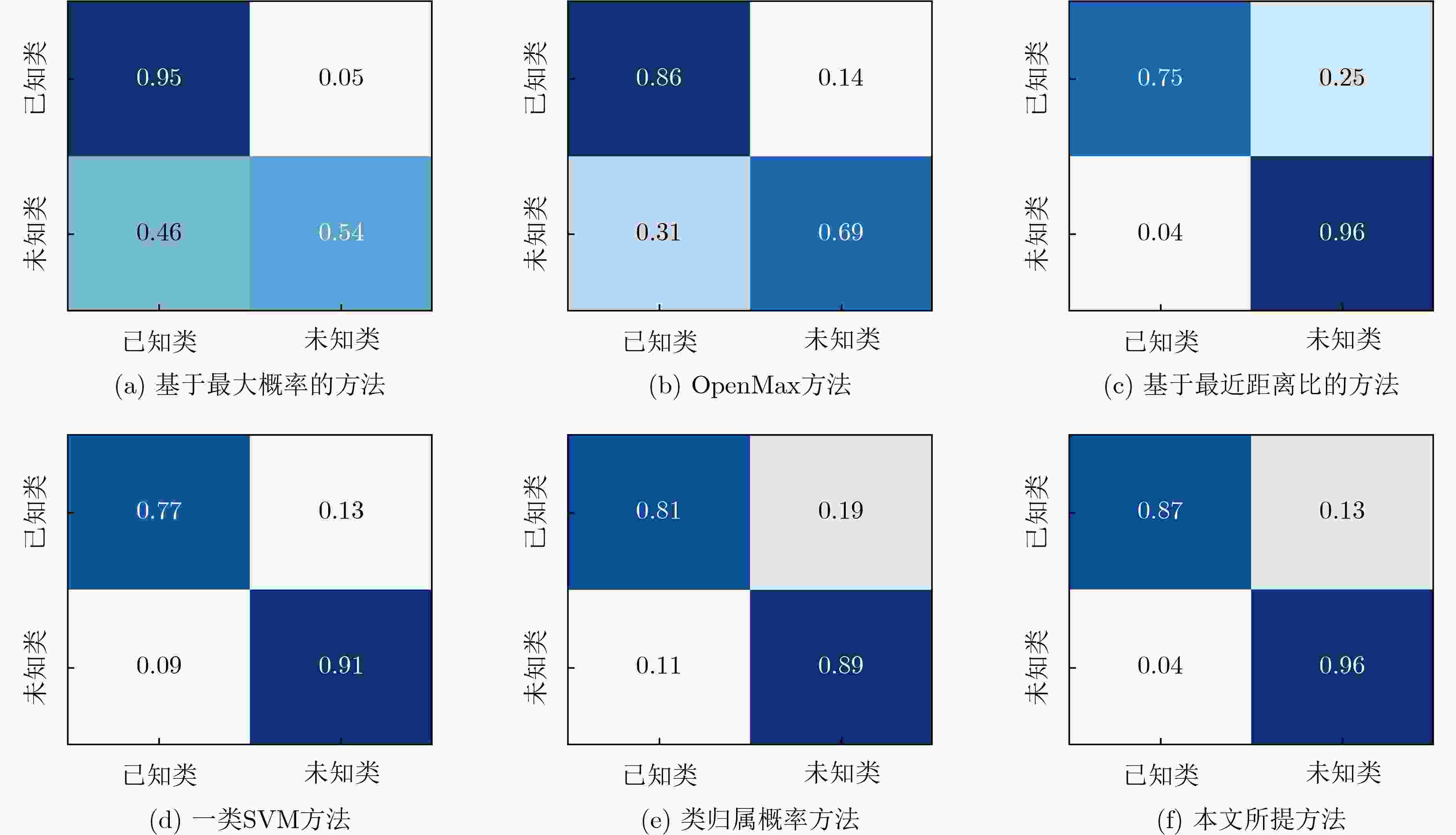
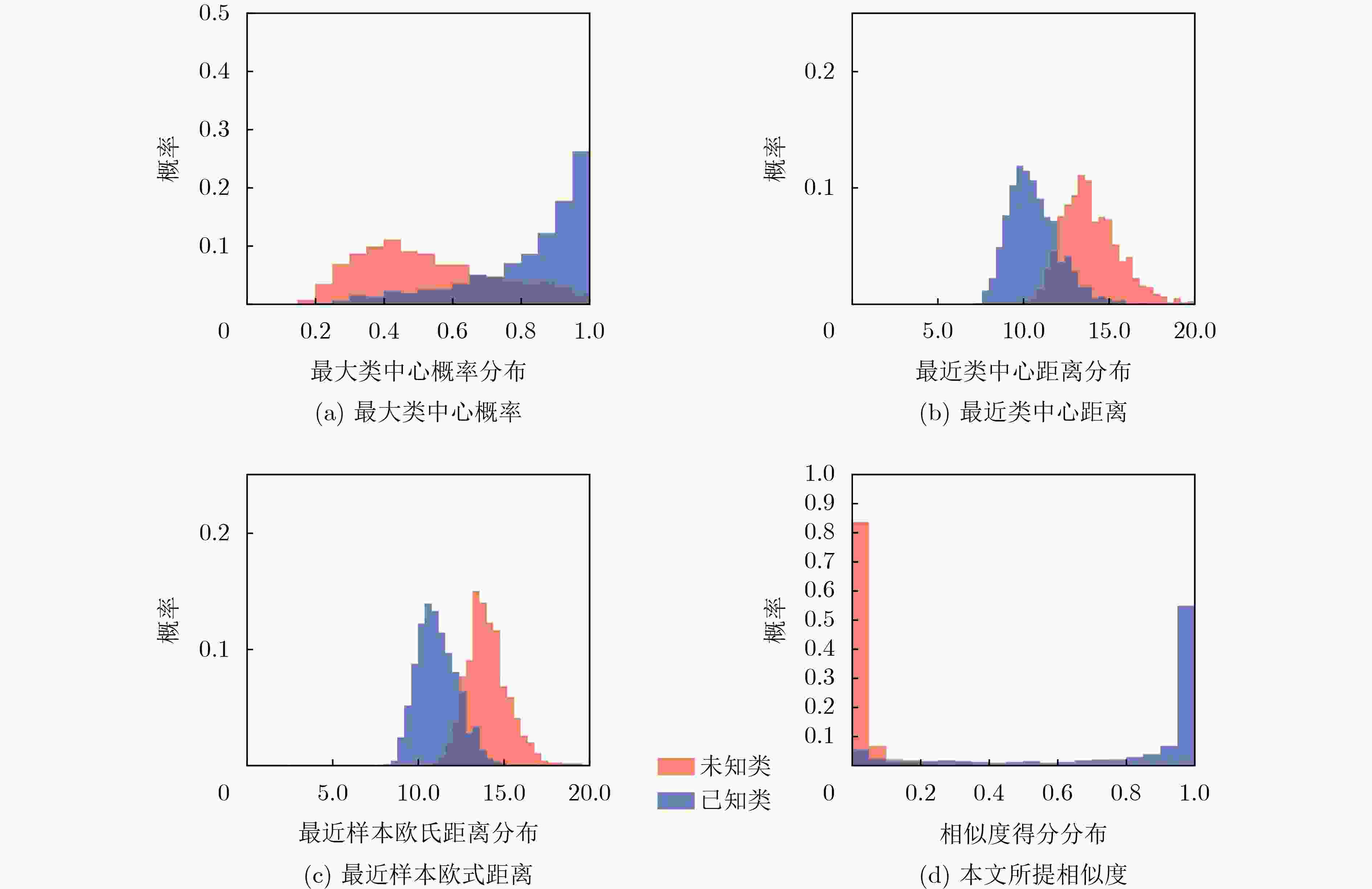
Abstract: Objective Radar-based gait recognition systems are typically developed under closed-set assumptions, limiting their applicability in real-world scenarios where unknown individuals frequently occur. This constraint presents challenges in security-critical settings such as surveillance and access control, where both accurate recognition of known individuals and reliable exclusion of unknown identities are essential. Existing methods often lack effective mechanisms to differentiate between known and unknown classes, leading to elevated false acceptance rates and security risks. To overcome this limitation, this study proposes an open-set recognition framework that integrates a similarity prediction network with an adaptive thresholding method based on Extreme Value Theory (EVT). The framework models the score distributions of known and unknown classes to enable robust identification of unfamiliar identities without requiring samples from unknown classes during training. The proposed method enhances the robustness and applicability of millimeter-wave radar-based gait recognition under open-set conditions, supporting its deployment in operational environments. Methods The proposed method comprises four key modules: point cloud feature extraction network training, similarity prediction network training, automatic threshold estimation, and open-set testing. A sequential training strategy is adopted to ensure robust learning. First, the point cloud feature extraction network is trained with a triplet loss function that encourages intra-class compactness and inter-class separability by pulling same-class samples closer and pushing different-class samples apart. This enables the network to learn stable and discriminative representations, even under variations in viewpoint or clothing. The extracted features are then input into a similarity prediction network trained to model the score distributions of known and unknown identities. By incorporating score-based constraints, the network learns a decision space in which known and unknown classes are more effectively separated. Following network optimization, an EVT-based thresholding module is employed. This module dynamically models the tail distributions of similarity scores and automatically determines a class-agnostic threshold by minimizing the joint false acceptance and false rejection rates. This adaptive and theoretically grounded strategy enhances the separation between known and unknown classes in the similarity space. Together, these modules improve the stability and accuracy of radar-based gait recognition under open-set conditions, supporting reliable operation in real-world scenarios where unfamiliar individuals may appear. Results and Discussions The proposed method improves distributional separation between known and unknown classes in the similarity score space through the similarity prediction network and distinguishes them effectively using adaptive thresholding. Experimental results show that the method consistently yields higher F1 scores across all openness levels compared with baseline approaches, indicating strong robustness to open-set variations (Table 1). Specifically, the method achieves an 87% recognition rate for known classes and a 96% rejection rate for unknown classes, outperforming all comparison methods (Fig. 7). Ablation experiments confirm that incorporating the similarity prediction module enhances recognition performance under high openness. Manually set thresholds, while effective under low openness, show substantial performance degradation under large openness (F1 score: 43.93%). In contrast, the proposed automatic thresholding module demonstrates superior generalization, improving the F1 score by 22.88% under large openness conditions (Table 2). Further analysis shows that the method significantly increases the score distribution gap between known and unknown classes, contributing to improved recognition reliability (Fig. 8). Comparative evaluations (Table 3) confirm that the method achieves superior open-set recognition performance. In addition, the employed point cloud feature extraction network captures temporal features at multiple time scales and uses an attention-based mechanism to adaptively aggregate information across frames and temporal resolutions. This contributes to more robust gait representations and further improves open-set recognition performance compared with other feature extraction networks (Table 4). Conclusions Building on previous work on robust feature extraction under complex covariate conditions, this study extends millimeter-wave radar point cloud gait recognition to open-set scenarios. The proposed method preserves the recognition strength of the original feature extraction network and enhances class discriminability by integrating a similarity prediction network. To address the limitations of manually defined rejection thresholds, an automatic threshold determination module based on EVT is introduced. Extensive experiments using measured millimeter-wave radar point cloud gait data confirm that the method reliably distinguishes between known and unknown individuals, demonstrating its effectiveness and robustness under open-set conditions.
- Millimeter-wave radar /
- Gait recognition /
- Open-set recognition /
- Similarity prediction /
- Extreme Value Theory (EVT)

HTML全文

图 1 检索任务框架下闭集步态识别模型的训练和测试流程

下载: 全尺寸图片幻灯片

图 2 结合相似度预测和阈值自动求解的开集条件下的毫米波雷达点云步态识别方法示意图

下载: 全尺寸图片幻灯片

图 3 文献[15]所提细粒度空时特征提取网络架构

下载: 全尺寸图片幻灯片

图 4 最近欧式距离分布示意图与相似度预测网络结构图

下载: 全尺寸图片幻灯片

图 5 阈值自动求解流程

下载: 全尺寸图片幻灯片

图 6 已知类和未知类样本的相似度得分分布

下载: 全尺寸图片幻灯片

图 7 不同开集步态识别方法的混淆矩阵

下载: 全尺寸图片幻灯片

图 8 不同拒判依据下的已知类和未知类分布

下载: 全尺寸图片幻灯片

表 1 不同开集步态识别方法在不同开放度条件下的F1分数(%)

开集方法	开放度
开集方法	7.42	12.29	18.35	26.15	36.75	52.86
基于最大后验概率的方法	85.99±0.71	82.61±0.49	73.39±0.83	61.77±1.85	43.93±2.56	25.85±3.52
OpenMax方法^[10]	83.18±1.23	79.07±1.21	75.37±1.08	69.95±1.64	61.66±1.79	49.35±2.45
最近距离比方法^[19]	79.08±1.31	79.76±0.99	81.57±4.38	81.42±3.65	75.21±3.35	69.16±4.11
一类SVM方法^[14]	84.87±2.85	82.78±1.12	80.73±1.83	78.74±3.09	77.45±3.88	74.38±4.13
类归属概率方法^[11]	85.83±1.77	83.35±2.38	82.69±2.09	81.67±3.78	78.86±3.83	73.93±3.73
本文方法	88.87±0.54	88.61±0.69	88.41±1.62	86.94±1.19	83.50±2.15	78.84±2.72

下载: 导出CSV

表 2 所提模块的消融实验(%)

	相似度预测模块	阈值自动求解模块	开放度
	相似度预测模块	阈值自动求解模块	7.42	18.35	36.75
Baseline	×	×	85.99	73.39	43.93
所提模块	√	×	86.69	84.54	82.35
	×	√	76.26	74.19	66.81
	√	√	88.87	88.41	83.50

下载: 导出CSV

表 3 基于不同拒判依据的方法对应开集识别F1分数(%)

拒判依据	开放度
拒判依据	7.42	18.35	36.75
最大类中心概率	76.26	74.19	66.81
最近类中心距离	85.59	80.44	74.45
最近样本欧式距离	88.56	85.57	82.51
本文所提相似度	88.87	88.41	83.50

下载: 导出CSV

表 4 不同点云特征提取网络对开集识别性能的影响(%)

不同模型	开放度
不同模型	7.42	18.35	36.75
SRPNet^[9]	33.92	32.37	16.62
HDNet^[20]	38.10	34.26	21.98
PcGaitPart^[21]	81.54	67.36	38.02
PcCSTL^[22]	84.27	71.10	41.03
本文模型	85.99	73.39	43.93

下载: 导出CSV

表 5 不同$k$值条件下模型的开集识别性能

$k$	查准率(%)	查全率(%)	F1分数(%)	准确率(%)
16	93.65	80.78	86.00	90.15
32	95.02	80.03	86.30	90.56
64	92.45	87.92	88.41	91.59
96	88.69	85.24	85.71	88.16
128	94.06	74.67	82.31	87.87

下载: 导出CSV

表 6 不同极值样本选取比例条件下模型的开集识别性能(%)

选取比例	查准率	查全率	F1分数	准确率
5	93.55	83.66	87.63	91.05
10	93.30	84.03	87.72	91.07
20	92.45	87.29	88.41	91.59
30	93.90	83.34	87.62	91.09
40	94.09	82.71	87.35	90.97
50	94.49	81.99	87.11	90.86

下载: 导出CSV

表 7 不同网格搜索步长对搜索时长和搜索精度的影响

搜索步长	搜索时长(s)	F1分数(%)
1e–5	3.872 243	88.41
1e–4	0.633 015	88.41
1e–3	0.064 913	88.25
1e–2	0.008 936	87.94
5e–1	0.000 677	86.75

下载: 导出CSV

参考文献(22)

[1]	SARKAR S, PHILLIPS P J, LIU Z, et al. The HumanID gait challenge problem: Data sets, performance, and analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(2): 162–177. doi: 10.1109/TPAMI.2005.39.
[2]	SEPAS-MOGHADDAM A and ETEMAD A. Deep gait recognition: A survey[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2023, 45(1): 264–284. doi: 10.1109/TPAMI.2022.3151865.
[3]	KALE A, SUNDARESAN A, RAJAGOPALAN A N, et al. Identification of humans using gait[J]. IEEE Transactions on Image Processing, 2004, 13(9): 1163–1173. doi: 10.1109/TIP.2004.832865.
[4]	VANDERSMISSEN B, KNUDDE N, JALALVAND A, et al. Indoor person identification using a low-power FMCW radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(7): 3941–3952. doi: 10.1109/TGRS.2018.2816812.
[5]	RICHARDS M A. Fundamentals of Radar Signal Processing[M]. New York: Mcgraw-hill, 2005.
[6]	杜兰, 陈晓阳, 石钰, 等. MMRGait-1.0: 多视角多穿着条件下的雷达时频谱图步态识别数据集[J]. 雷达学报, 2023, 12(4): 892–905. doi: 10.12000/JR22227. DU Lan, CHEN Xiaoyang, SHI Yu, et al. MMRGait-1.0: A radar time-frequency spectrogram dataset for gait recognition under multi-view and multi-wearing conditions[J]. Journal of Radars, 2023, 12(4): 892–905. doi: 10.12000/JR22227.
[7]	ZHAO Peijun, LU C X, WANG Jianan, et al. mID: Tracking and identifying people with millimeter wave radar[C]. 2019 15th International Conference on Distributed Computing in Sensor Systems (DCOSS), Santorini, Greece, 2019: 33–40. doi: 10.1109/DCOSS.2019.00028.
[8]	MENG Zhen, FU Song, YAN Jie, et al. Gait recognition for co-existing multiple people using millimeter wave sensing[C]. The 34th AAAI Conference on Artificial Intelligence, New York, USA, 2020: 849–856. doi: 10.1609/aaai.v34i01.5430.
[9]	CHENG Yuwei and LIU Yimin. Person reidentification based on automotive radar point clouds[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5101913. doi: 10.1109/TGRS.2021.3073664.
[10]	SCHEIRER W J, DE REZENDE ROCHA A, SAPKOTA A, et al. Toward open set recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(7): 1757–1772. doi: 10.1109/TPAMI.2012.256.
[11]	NI Zhongfei and HUANG Binke. Open-set human identification based on gait radar micro-Doppler signatures[J]. IEEE Sensors Journal, 2021, 21(6): 8226–8233. doi: 10.1109/JSEN.2021.3052613.
[12]	FISHER R A and TIPPETT L H C. Limiting forms of the frequency distribution of the largest or smallest member of a sample[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1928, 24(2): 180–190. doi: 10.1017/S0305004100015681.
[13]	YANG Yang, GE Yanyan, LI Beichen, et al. Multiscenario open-set gait recognition based on radar micro-Doppler signatures[J]. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 2519813. doi: 10.1109/TIM.2022.3214271.
[14]	MOON J, JUNG J, KANG E, et al. Open set user identification using gait pattern analysis based on ensemble deep neural network[J]. IEEE Sensors Journal, 2022, 22(17): 16975–16984. doi: 10.1109/JSEN.2022.3188527.
[15]	XUE Shikun, DU Lan, SHI Yu, et al. Fine-grained spatial-temporal gait recognition network based on millimeter-wave radar point cloud[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 5101316. doi: 10.1109/TGRS.2023.3345829.
[16]	BALKEMA A A and DE HAAN L. Residual life time at great age[J]. The Annals of Probability, 1974, 2(5): 792–804. doi: 10.1214/aop/1176996548.
[17]	ZHANG He and PATEL V M. Sparse representation-based open set recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(8): 1690–1696. doi: 10.1109/TPAMI.2016.2613924.
[18]	LI Yiming, DU Lan, CHEN Jian, et al. An open set recognition for SAR targets based on encoding-conditional decoding network with reject threshold adaptation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2024: 1–16. doi: 10.1109/JSTARS.2024.3416175.
[19]	MENDES JÚNIOR P R, DE SOUZA R M, DE O WERNECK R, et al. Nearest neighbors distance ratio open-set classifier[J]. Machine Learning, 2017, 106(3): 359–386. doi: 10.1007/s10994-016-5610-8.
[20]	HUANG Yanyan, WANG Yong, SHI Kun, et al. HDNet: Hierarchical dynamic network for gait recognition using millimeter-wave radar[C]. 2023–2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 2023: 1–5. doi: 10.1109/ICASSP49357.2023.10096835.
[21]	FAN Chao, PENG Yunjie, CAO Chunshui, et al. GaitPart: Temporal part-based model for gait recognition[C]. The 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, USA, 2020: 14213–14221. doi: 10.1109/CVPR42600.2020.01423.
[22]	HUANG Xiaohu, ZHU Duowang, WANG Hao, et al. Context-sensitive temporal feature learning for gait recognition[C]. The 2021 IEEE/CVF International Conference on Computer Vision, Montreal, Canada, 2021: 12889–12898. doi: 10.1109/ICCV48922.2021.01267.