Error State Kalman Filter Multimodal Fusion SLAM Based on MICP Closed-loop Detection
-
摘要: 同步定位与地图构建(SLAM)技术是移动机器人智能导航的基础。该文针对单一传感器SLAM技术存在的问题,提出一种基于激光雷达多层迭代最近点(MICP)点云匹配闭环检测的误差状态卡尔曼滤波(ESKF)多传感器紧耦合2D-SLAM算法。在完成视觉与激光雷达多模态数据的时空同步后,建立了里程计误差模型以及激光雷达与机器视觉点云匹配误差模型,并将其应用于误差状态卡尔曼滤波进行多模态数据融合,以提高SLAM的准确性和实时性。在公共数据集KITTI下进行的Gazebo环境仿真结果表明,该所提算法能够完整还原单一激光2D-SLAM无法获取到的环境障碍物信息,并能显著提高机器人轨迹估计和相对位姿估计精度。最后,采用Turtlebot2机器人在复杂实际大场景下进行了SLAM实验验证,结果表明所提多模态融合SLAM方法可以完整复原环境信息,实现实时的高精度2D地图构建。Abstract:
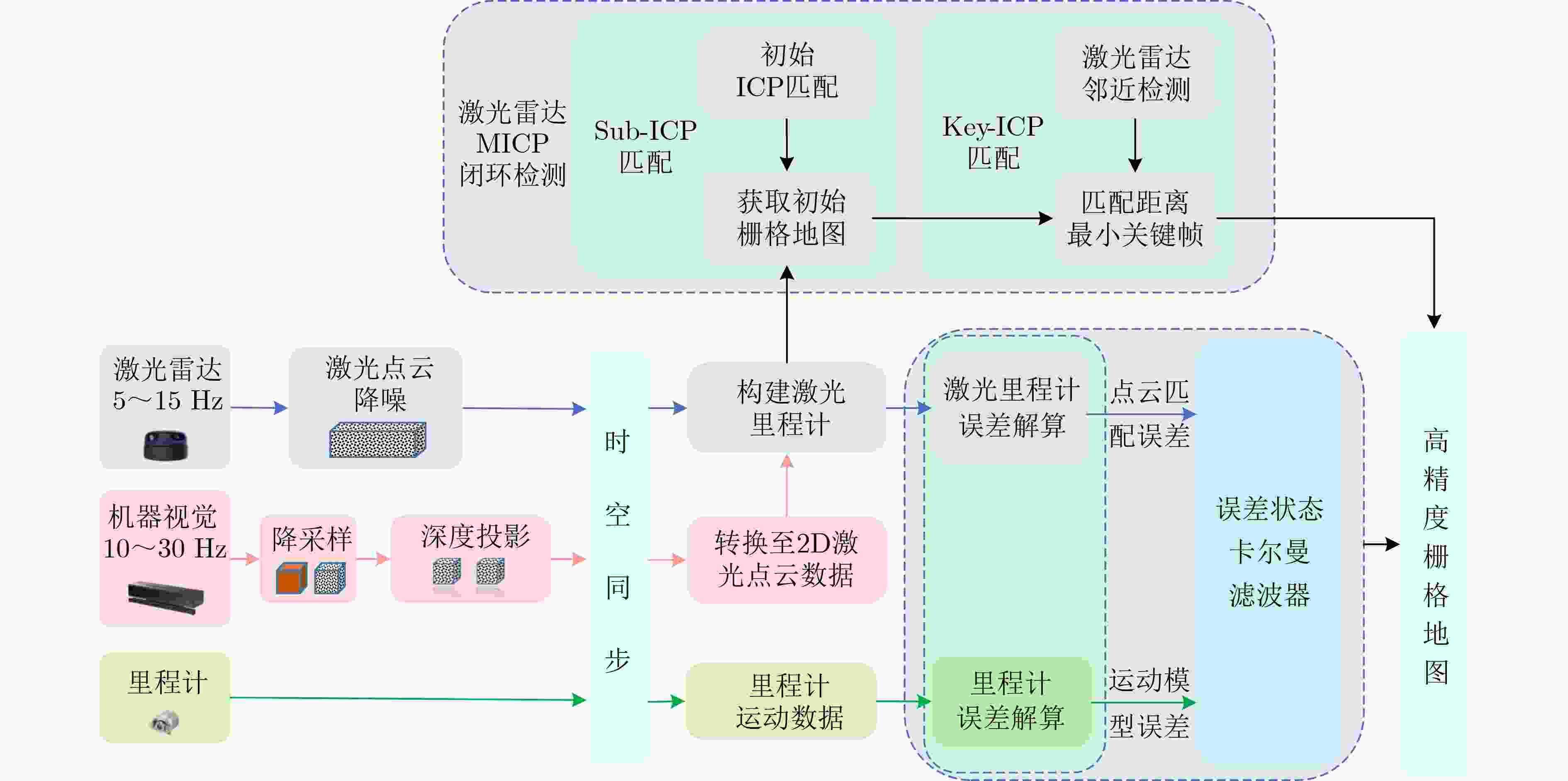
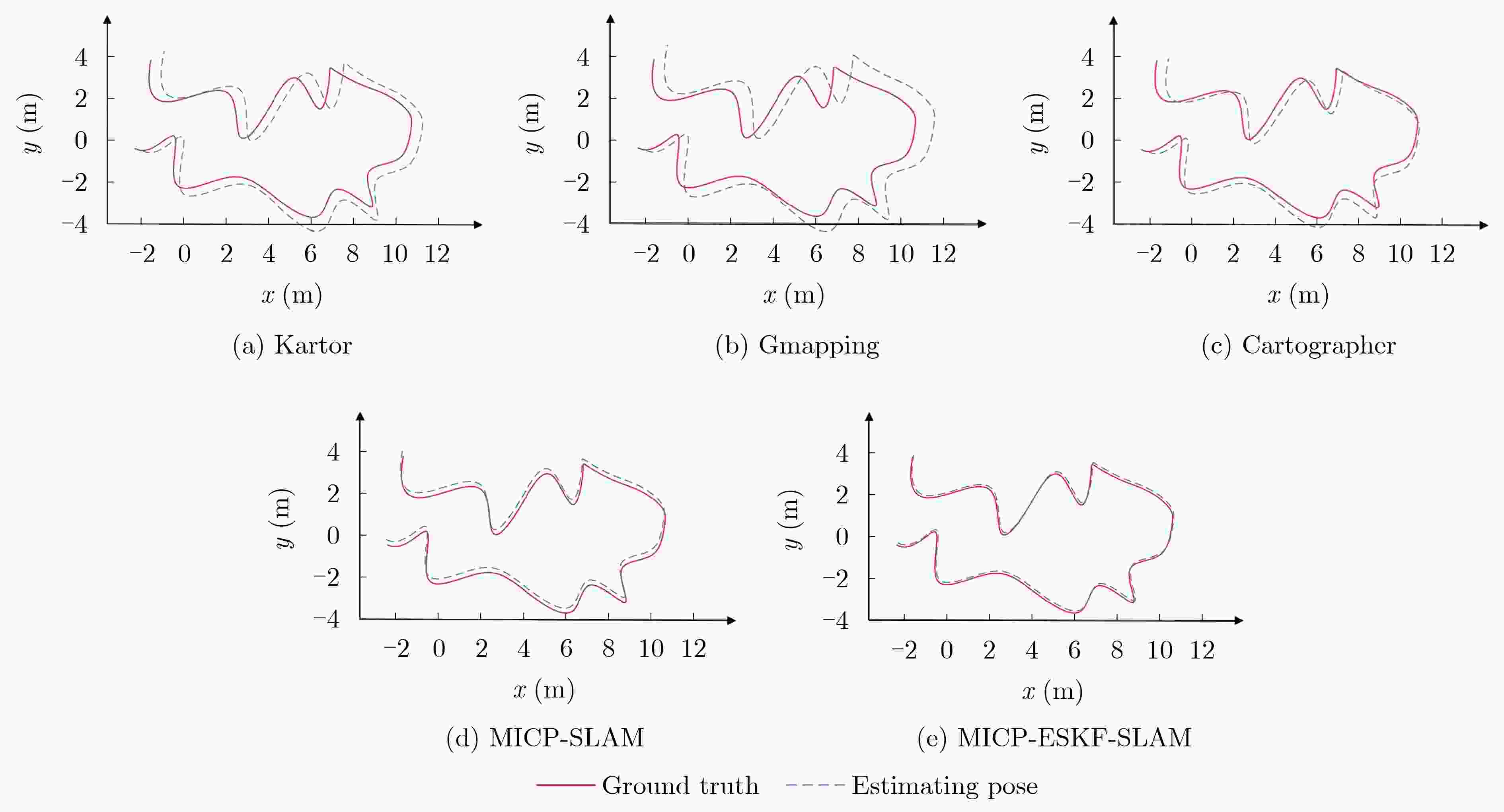
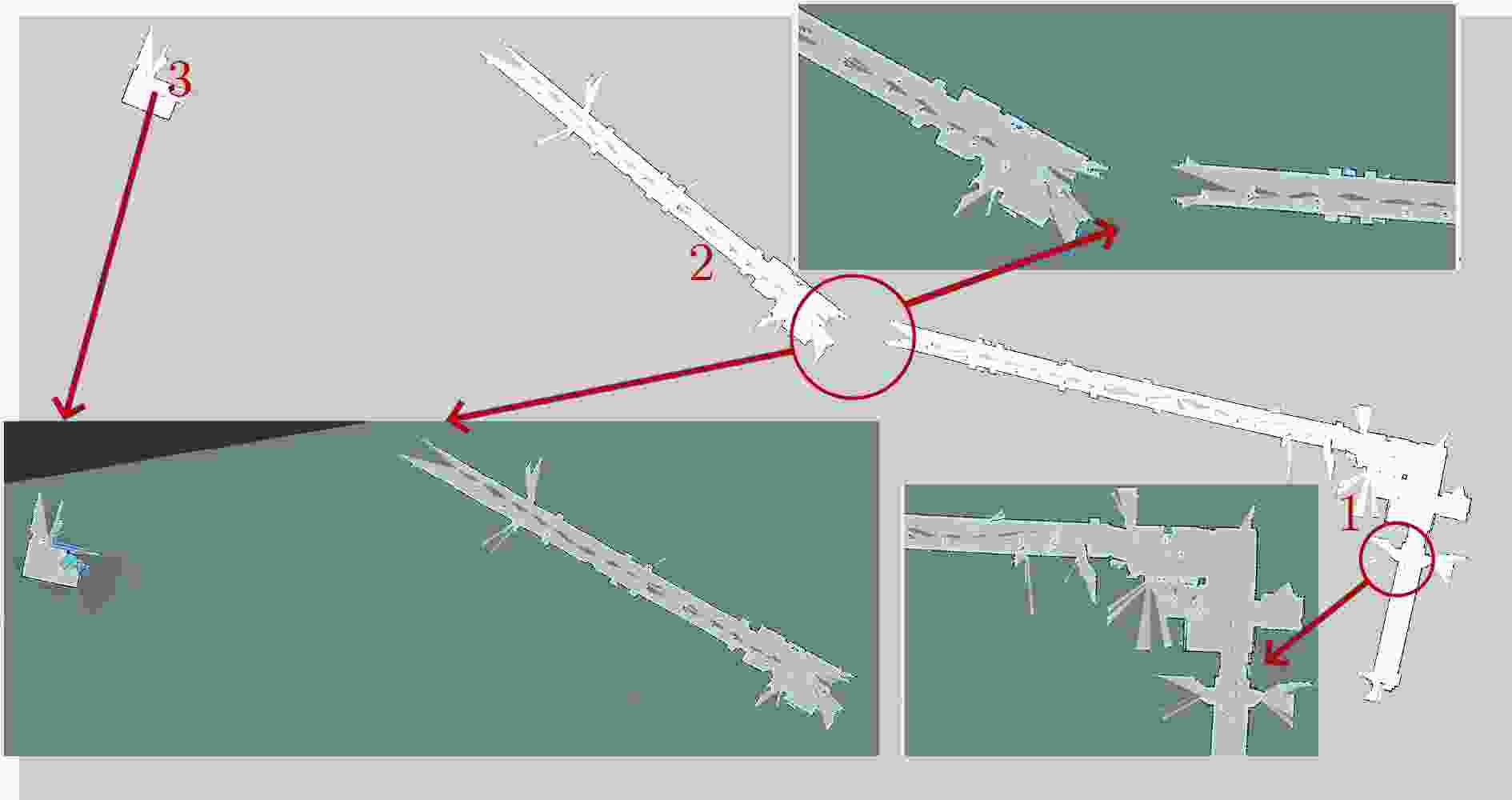
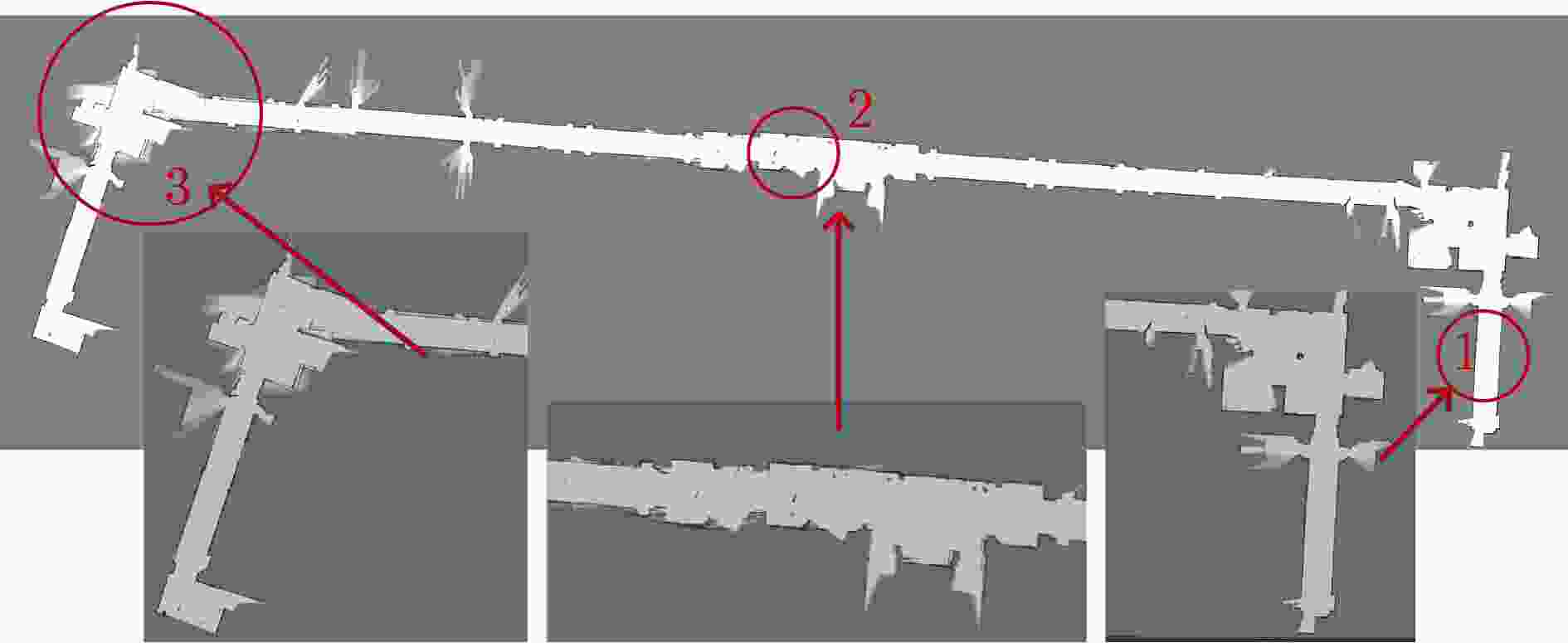
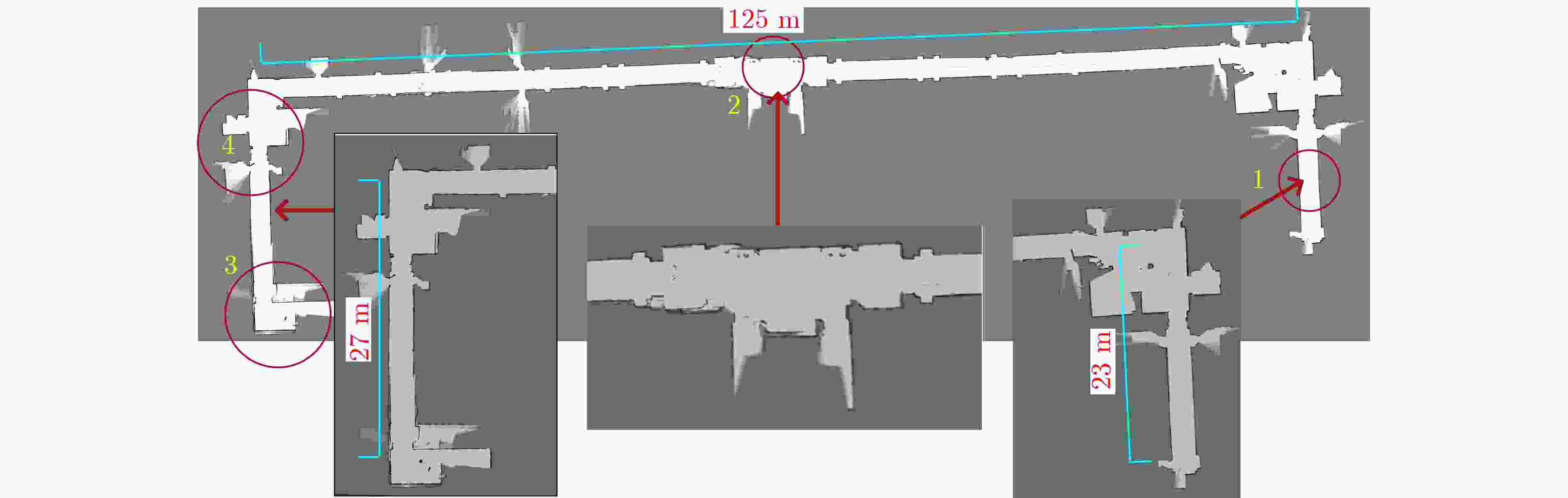
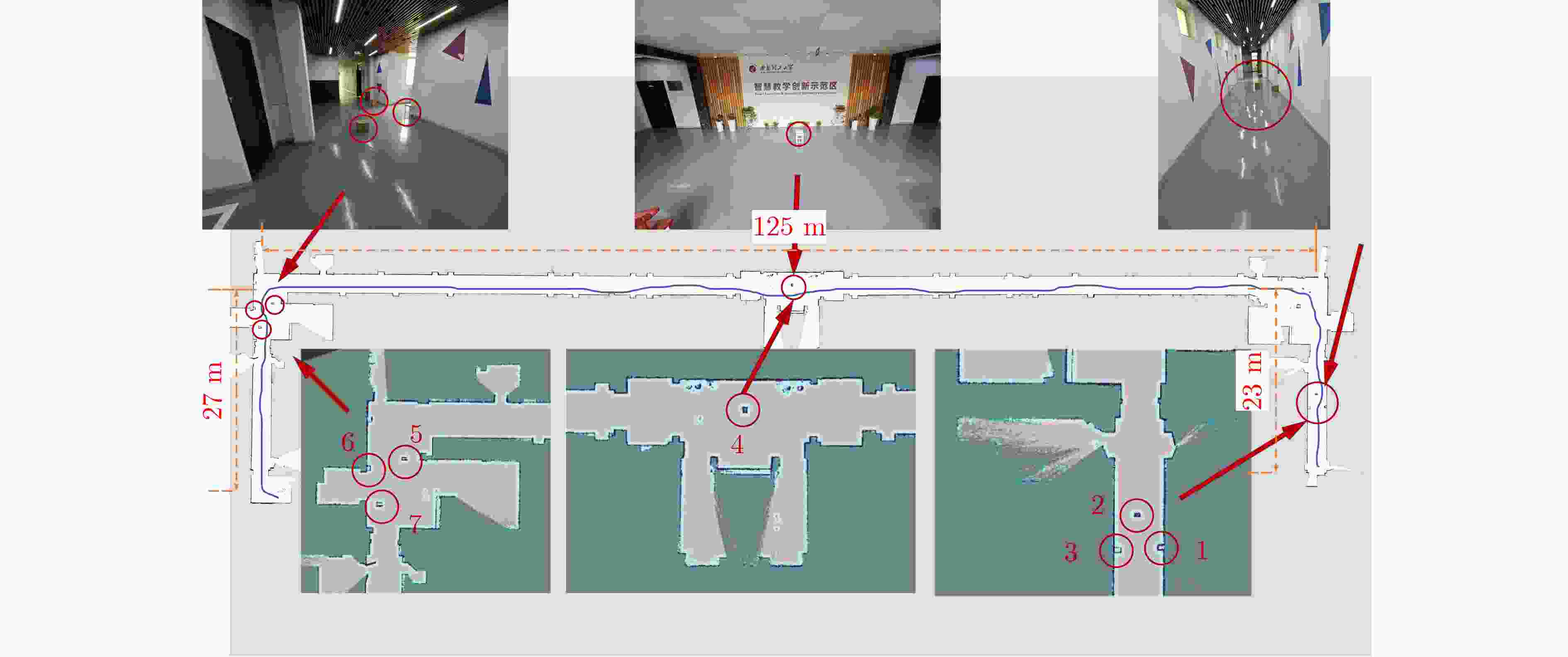
Objective Single-sensor Simultaneous Localization and Mapping (SLAM) technology has limitations, including large mapping errors and poor performance in textureless or low-light environments. The 2D-SLAM laser performs poorly in natural and dynamic outdoor environments and cannot capture object information below the scanning plane of a single-line LiDAR. Additionally, long-term operation leads to cumulative errors from sensor noise and model inaccuracies, significantly affecting positioning accuracy. This study proposes an Error State Kalman Filter (ESKF) multimodal tightly coupled 2D-SLAM algorithm based on LiDAR MICP closed-loop detection to enhance environmental information acquisition, trajectory estimation, and relative pose estimation. The proposed approach improves SLAM accuracy and real-time performance, enabling high-precision and complete environmental mapping in complex real-world scenarios. Methods Firstly, sensor data is spatiotemporally synchronized, and the LiDAR point cloud is denoised. MICP matching closed-loop detection, including initial ICP matching, sub-ICP matching, and key ICP matching, is then applied to optimize point cloud matching. Secondly, an odometer error model and a point cloud matching error model between LiDAR and machine vision are constructed. Multi-sensor data is fused using the ESKF to obtain more accurate pose error values, enabling real-time correction of the robot’s pose. Finally, the proposed MICP-ESKF SLAM algorithm is compared with several classic SLAM methods in terms of closed-loop detection accuracy, processing time, and robot pose accuracy under different data samples and experimentally validated on the Turtlebot2 robot platform. Results and Discussions This study addresses the reduced accuracy of 2D grid maps due to accumulated odometry errors in large-scale mobile robot environments. To overcome the limitations of visual and laser SLAM, the paper examines laser radar Multi-layer Iterative Closest Point (MICP) matching closed-loop detection and proposes a visual-laser odometry tightly coupled SLAM method based on the ESKF. The SLAM algorithm incorporating MICP closed-loop detection achieves higher accuracy than the Cartographer algorithm on the test set. Compared to the Karto algorithm, the proposed MICP-ESKF-SLAM algorithm shows significant improvements in detection accuracy and processing speed. As shown in Table 2 , the multimodal MICP-ESKF-SLAM algorithm has the lowest median relative pose error, approximately 3% of that of the Gmapping algorithm. The average relative pose error is reduced by about 40% compared to the MICP-SLAM algorithm, demonstrating the advantages of the proposed approach in high-precision positioning. Furthermore, multi-sensor fusion via ESKF effectively reduces cumulative errors caused by frequency discrepancies and sensor noise, ensuring timely robot pose updates and preventing map drift.Conclusions This study proposes a 2D-SLAM algorithm that integrates MICP matching closed-loop detection with ESKF. By estimating errors, optimizing state updates, and applying corrected increments to the main state, the approach mitigates cumulative drift caused by random noise and internal error propagation in dynamic environments. This enhances localization and map construction accuracy while improving the real-time performance of multi-sensor tightly coupled SLAM. The ESKF multi-sensor tightly coupled SLAM algorithm based on multi-layer ICP matching closed-loop detection is implemented on the Turtlebot2 experimental platform for large-scale scene localization and mapping. Experimental results demonstrate that the proposed algorithm effectively integrates LiDAR and machine vision data, achieving high-accuracy robot pose estimation and stable performance in dynamic environments. It enables the accurate construction of a complete, drift-free environmental map, addressing the challenges of 2D mapping in complex environments that single-sensor SLAM algorithms struggle with, thereby providing a foundation for future research on intelligent mobile robot navigation. -
1 基于MICP匹配闭环检测的ESKF多传感器紧耦合SLAM
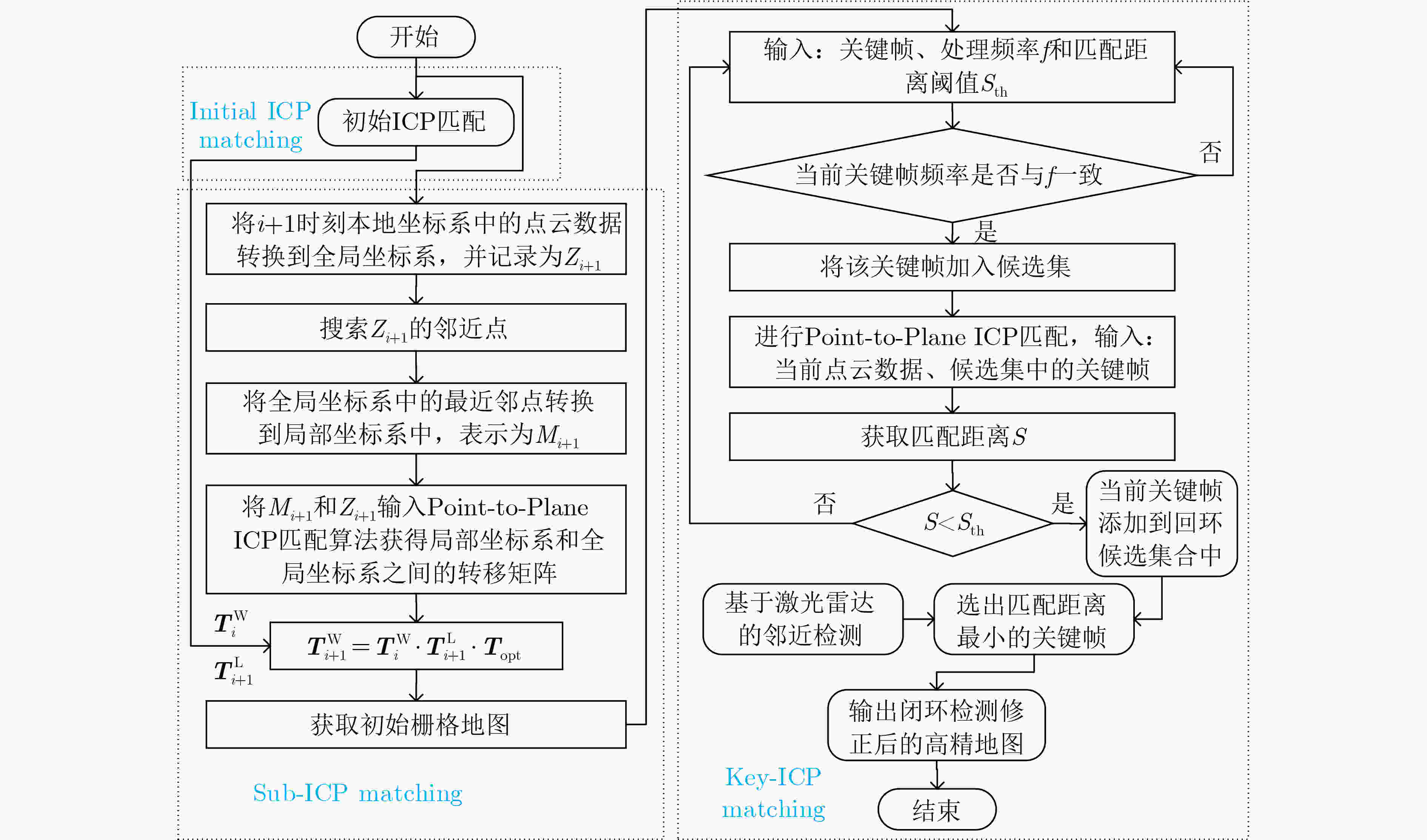
输入:$k + 1$时刻的机器人位姿${{\boldsymbol{x}}_{k + 1}}$ 1.将点云数据转换到全局坐标系,使得Sub-ICP进行初始化; 2.构建点云匹配误差数学模型${\boldsymbol{F}}$,构建里程计误差模型; 3.利用式(7)、式(17)分别得到非系统误差协方差${{\boldsymbol{Q}}_k}$,${{\boldsymbol{D}}_k}$; 4.将里程计估算的机器人位姿作为位姿预测值输入ESKF,将激
光里程计计算的位姿作为观测值输入ESKF迭代;5.通过$\delta {\hat {\boldsymbol{x}}_k}$对状态变量${{\boldsymbol{x}}_k}$进行位姿修正; 6.更新后的位姿进行定位与地图构建。 输出:修正后的高精度地图 表 1 不同数据样本下SLAM算法闭环检测精度与用时测试
数量样本 约束数量 检测精度(%) 计算占用时间(s) Cartographer MICP Karto Cartographer MICP Karto Aces 971±5 98.1 97.9 96.4 1366 1291 1405 Intel 5786 ±597.2 98.4 96.6 2691 2523 2725 MIT CSAIL 916±5 93.4 94.2 90.0 7678 7284 7862 Freiburg bldg 79 1857±5 94.1 93.2 92.9 424 393 419 Freiburg hospital 412±5 98.8 98.5 96.5 1061 894 1084 MIT Killian Court 554±5 77.3 80.1 73.1 4820 4627 4839 表 2 不同SLAM算法下的机器人相对位姿误差
SLAM算法 最大误差 平均误差 中位数误差 最小误差 均方根误差 MICP-ESKF-SLAM 0.09332 0.08214 0.01721 0.00934 0.01594 MICP-SLAM 0.15587 0.12773 0.04418 0.02021 0.05672 Gmapping 1.03219 0.54158 0.49083 0.22892 0.50026 Cartographer 0.61091 0.30171 0.21823 0.10442 0.29528 Karto 0.73019 0.44203 0.29575 0.12471 0.32757 -
[1] WANG Zhongli, CHEN Yan, MEI Yue, et al. IMU-assisted 2D SLAM method for low-texture and dynamic environments[J]. Applied Sciences, 2018, 8(12): 2534. doi: 10.3390/app8122534. [2] CHAN S H, WU P T, and FU Lichen. Robust 2D indoor localization through laser SLAM and visual SLAM fusion[C]. 2018 IEEE International Conference on Systems, Man, and Cybernetics, Miyazaki, Japan, 2018: 1263–1268. doi: 10.1109/SMC.2018.00221. [3] CHEN L H and PENG C C. A robust 2D-SLAM technology with environmental variation adaptability[J]. IEEE Sensors Journal, 2019, 19(23): 11475–11491. doi: 10.1109/JSEN.2019.2931368. [4] XU Wei and ZHANG Fu. FAST-LIO: A fast, robust LiDAR-inertial odometry package by tightly-coupled iterated Kalman filter[J]. IEEE Robotics and Automation Letters, 2021, 6(2): 3317–3324. doi: 10.1109/LRA.2021.3064227. [5] XU Wei, CAI Yixi, HE Dongjiao, et al. FAST-LIO2: Fast direct LiDAR-inertial odometry[J]. IEEE Transactions on Robotics, 2022, 38(4): 2053–2073. doi: 10.1109/TRO.2022.3141876. [6] LIANG Xiao, CHEN Haoyao, LI Yanjie, et al. Visual laser-SLAM in large-scale indoor environments[C]. 2016 IEEE International Conference on Robotics and Biomimetics, Qingdao, China, 2016: 19–24. doi: 10.1109/ROBIO.2016.7866271. [7] GAO Xiang, WANG Rui, DEMMEL N, et al. LDSO: Direct sparse odometry with loop closure[C]. 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems, Madrid, Spain, 2018: 2198–2204. doi: 10.1109/IROS.2018.8593376. [8] ZHU Zulun, YANG Shaowu, and DAI Huadong. Enhanced visual loop closing for laser-based SLAM[C]. The 2018 IEEE 29th International Conference on Application-specific Systems, Architectures and Processors, Milan, Italy, 2018: 1–4. doi: 10.1109/ASAP.2018.8445128. [9] WANG Han, WANG Chen, and XIE Lihua. Intensity scan context: Coding intensity and geometry relations for loop closure detection[C]. 2020 IEEE International Conference on Robotics and Automation, Paris, France, 2020: 2095–2101. doi: 10.1109/ICRA40945.2020.9196764. [10] FAN Yunfeng, HE Yichang, and TAN U X. Seed: A segmentation-based egocentric 3D point cloud descriptor for loop closure detection[C]. 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems, Las Vegas, USA, 2020: 5158–5163. doi: 10.1109/IROS45743.2020.9341517. [11] CHEN Dan, ZHANG Heng, TANG Linao, et al. Multimodal fusion simultaneous localization and mapping method based on multilayer point cloud matching closed-loop detection[J]. Journal of Electronic Imaging, 2024, 33(3): 033024. doi: 10.1117/1.JEI.33.3.033024. [12] CHEN Yang and MEDIONI G. Object modeling by registration of multiple range images[C]. 1991 IEEE International Conference on Robotics and Automation, Sacramento, USA, 1991: 2724–2729. doi: 10.1109/ROBOT.1991.132043. [13] 杨晶东, 杨敬辉, 洪炳熔. 一种有效的移动机器人里程计误差建模方法[J]. 自动化学报, 2009, 35(2): 168–173. doi: 10.3724/SP.J.1004.2009.00168.YANG Jingdong, YANG Jinghui, and HONG Bingrong. An efficient approach to odometric error modeling for mobile robots[J]. Acta Automatica Sinica, 2009, 35(2): 168–173. doi: 10.3724/SP.J.1004.2009.00168. [14] KÜMMERLE R, STEDER B, DORNHEGE C, et al. On measuring the accuracy of SLAM algorithms[J]. Autonomous Robots, 2009, 27(4): 387–407. doi: 10.1007/s10514-009-9155-6. [15] JULIER S, UHLMANN J, and DURRANT-WHYTE H F. A new method for the nonlinear transformation of means and covariances in filters and estimators[J]. IEEE Transactions on Automatic Control, 2000, 45(3): 477–482. doi: 10.1109/9.847726. [16] 程效军, 施贵刚, 王峰, 等. 点云配准误差传播规律的研究[J]. 同济大学学报: 自然科学版, 2009, 37(12): 1668–1672. doi: 10.3969/j.issn.0253-374x.2009.12.020.CHENG Xiaojun, SHI Guigang, WANG Feng, et al. Research on point cloud registration error propagation[J]. Journal of Tongji University: Natural Science, 2009, 37(12): 1668–1672. doi: 10.3969/j.issn.0253-374x.2009.12.020. [17] 武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 3版. 武汉: 武汉大学出版社, 2014.Surveying Adjustment Group School of Geodesy Wuhan University. Error Theory and Foundation of Surveying Adjustment[M]. 3rd ed. Wuhan: Wuhan University Press, 2014. [18] 崔文, 薛棋文, 李庆玲, 等. 基于三维点云地图和ESKF的无人车融合定位方法[J]. 工矿自动化, 2022, 48(9): 116–122. doi: 10.13272/j.issn.1671-251x.17997.CUI Wen, XUE Qiwen, LI Qingling, et al. Unmanned vehicle fusion positioning method based on 3D point cloud map and ESKF[J]. Journal of Mine Automation, 2022, 48(9): 116–122. doi: 10.13272/j.issn.1671-251x.17997. [19] WAN Guowei, YANG Xiaolong, CAI Renlan, et al. Robust and precise vehicle localization based on multi-sensor fusion in diverse city scenes[C]. 2018 IEEE International Conference on Robotics and Automation, Brisbane, Australia, 2018: 4670–4677. doi: 10.1109/ICRA.2018.8461224. [20] 郭文卓, 李林阳, 程振豪, 等. 先验地图/IMU/LiDAR的图优化和ESKF位姿估计方法对比[J]. 测绘科学, 2023, 48(4): 88–97. doi: 10.16251/j.cnki.1009-2307.2023.04.010.GUO Wenzhuo, LI Linyang, CHENG Zhenhao, et al. Comparison of prior map/IMU/LiDAR map optimization and error state Kalman filter pose estimation methods[J]. Science of Surveying and Mapping, 2023, 48(4): 88–97. doi: 10.16251/j.cnki.1009-2307.2023.04.010. [21] LIU Shengshu, LEI Yixing, and DONG Xin. Evaluation and comparison of gmapping and karto SLAM systems[C]. The 2022 12th International Conference on CYBER Technology in Automation, Control, and Intelligent Systems, Baishan, China, 2022: 295–300. doi: 10.1109/CYBER55403.2022.9907154. [22] HESS W, KOHLER D, RAPP H, et al. Real-time loop closure in 2D LIDAR SLAM[C]. Proceedings of 2016 IEEE International Conference on Robotics and Automation, Stockholm, Sweden, 2016: 1271–1278. doi: 10.1109/ICRA.2016.7487258. [23] 王勇, 陈卫东, 王景川, 等. 面向动态高遮挡环境的移动机器人自适应位姿跟踪算法[J]. 机器人, 2015, 37(1): 112–121. doi: 10.13973/j.cnki.robot.2015.0112.WANG Yong, CHEN Weidong, WANG Jingchuan, et al. Self-adaptive pose-tracking algorithm for mobile robots in dynamic and highly-occluded environments[J]. Robot, 2015, 37(1): 112–121. doi: 10.13973/j.cnki.robot.2015.0112. [24] GRISETTI G, STACHNISS C, and BURGARD W. Improving grid-based SLAM with rao-blackwellized particle filters by adaptive proposals and selective resampling[C]. 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 2005: 2432–2437. doi: 10.1109/ROBOT.2005.1570477. [25] 丁林祥, 陶卫军. ROS/Gazebo在SLAM算法评估中的应用[J]. 兵工自动化, 2022, 41(4): 87–92. doi: 10.7690/bgzdh.2022.04.018.DING Linxiang and TAO Weijun. Application of ROS/gazebo in the evaluation of SLAM algorithm[J]. Ordnance Industry Automation, 2022, 41(4): 87–92. doi: 10.7690/bgzdh.2022.04.018. -





 下载:
下载:





 下载:
下载:
