Identification of Non-Line-Of-Sight Signals Based on Direct Path Signal Residual and Support Vector Data Description
-
摘要: 非视距(NLOS)误差是限制超宽带定位准度的一个重要因素,快速准确识别出NLOS信号成为提高超宽带定位准度的前提。该文基于信道冲激响应提出了一种新型信号特征参数:直达路径(DP)信号残差,与文献提出的9个典型波形特征参数组合成不同的特征组合用于表征信号,基于此,为了使识别方法兼具样本获取成本低、环境适应能力好的特点,该文以构建在单个环境下采集单类信号数据作为分类模型的训练样本,在识别其它场景NLOS信号中有更好性能的方法为目的,设计了一种带DP信号残差训练的支持向量数据描述(SVDD)的识别方法。为了进一步提高识别准确率,将基于多层神经网络的深度特征提取技术引入SVDD中,设计了一种基于反向扩维的深度支持向量数据描述(DSVDD)的NLOS信号识别方法。实验结果表明:带DP信号残差训练的 DSVDD方法只需在单个场景采集单类信号样本,且在训练集和测试集采集自不同场景时实现了 85%以上的准确率,较只使用典型波形特征训练的SVDD提升了10%以上。
-
关键词:
- 超宽带定位 /
- 非视距信号识别 /
- 直达路径信号残差 /
- 支持向量数据描述 /
- 深度支持向量数据描述
Abstract:Objective Current machine learning-based methods for Non-Line-Of-Sight (NLOS) signal recognition either require the collection of a large amount of data from two different types of signals for various scenarios, or the trained models fail to generalize across different environments. These methods also do not simultaneously address the practical challenges of low training sample acquisition cost and good scene adaptation. This paper proposes a new NLOS recognition method that collects single-class signals from a single environment to train recognition models, which then demonstrate high accuracy when recognizing signals in different scenarios. This approach offers the advantages of low sample acquisition cost and strong environmental adaptability. Methods This paper proposes Direct Path (DP) signal residual feature parameters that exhibit significant differences between two types of signals. The effectiveness of these parameters is theoretically analyzed and combined with nine feature parameters identified in typical literature, forming various feature vectors to characterize the signals. This approach effectively enhances the accuracy of the recognition model. A class of signals with high feature similarity across different scenarios is used as training data, and a single recognition model is employed as the machine learning algorithm. The model is trained on signal samples collected in typical Line-Of-Sight (LOS) channels to improve its scene adaptability. Based on the principles of Deep Support Vector Data Description (DSVDD), a reverse-expanded DSVDD model is designed for NLOS signal recognition, further improving the model’s accuracy in recognizing samples across different scenarios. Results and Discussions As shown in Table 2 , in the signal recognition scenario where the test set and training set originate from the same scene, the Least Squares Support Vector Machine (LSSVM) model demonstrates the best recognition performance. This is achieved using hyperplanes trained with two types of signals, resulting in a recognition accuracy of over 95%. In comparison, the standard Support Vector Data Description (SVDD) model, which is trained using only single-class LOS signal samples, exhibits a performance loss relative to LSSVM, with a maximum accuracy decrease exceeding 5%. The recognition accuracy of the SVDD model trained with DP signal residual features improves compared to the standard SVDD model, with the highest accuracy difference remaining within 5% of the LSSVM model. Furthermore, the performance of the DSVDD model, trained with DP signal residuals, shows a further improvement, with the highest accuracy decrease decreased to less than 2% compared to the LSSVM model. In scenarios where the training set and test data come from different scenes, LSSVM requires two types of signals for training. However, the hyperplane trained with two types of signal samples from a single scene exhibits poor performance when recognizing signal samples from other scenarios, with a maximum accuracy of less than 75%. The SVDD model trained with DP signal residual eigenvalues incorporates features with significant differences between the two signal types, improving recognition accuracy to over 80%. Finally, the DSVDD model, trained with DP signal residual features and replacing the Gaussian kernel function in the SVDD model with a neural network, further enhances recognition accuracy, achieving a maximum accuracy exceeding 85%.Conclusions A recognition method based on DP signal residual feature training for DSVDD is proposed to address the challenges of low sample acquisition cost and strong environmental adaptability in typical NLOS signal recognition. Compared with the SVDD method, this approach improves upon feature parameters, models, and model structures by introducing features with significant differences between the two types of signals, resulting in a substantial improvement in recognition performance. Additionally, the paper designs a reverse dimensionality expansion for DSVDD and incorporates it into NLOS signal recognition, further enhancing the accuracy of the recognition model across different scene samples. Compared to other typical machine learning algorithms, the proposed method requires the collection of single-class signal data from a single scene and performs effectively in recognizing signal samples from other scenes. Although the proposed method outperforms typical single-recognition approaches, the overall performance still has room for improvement. The theoretical analysis regarding how neural networks can better explore potential relationships between features is insufficient, and the full potential of neural networks in single-recognition models has not been fully realized. Furthermore, due to time constraints, this study only simulated sample data collected from three scenarios, and the recognition performance in other typical scenarios requires further validation. -
表 1 用于NLOS信号识别的机器学习算法性能对比
LSSVM SVDD 胶囊网络算法 加权K-近邻分类 识别效果 本场景识别准确率高于95%,其它场景识别
准确率低于75%本场景识别准确率高于90%, 其它场景识别
准确率较LSSVM有所
提升,但低于80%在小样本和样本类别比例不平衡 的训练集中,识别准确率能够接近95%,相对于LSSVM有优势,其它场景的
识别效果有待验证文献[15]在6个不同场景中的识别准确率均为95%左右 训练样本数量 两类信号样本,本文取500组NLOS和500组
LOS信号单个场景的单类信号样本,本文取500组LOS信号 需要针对不同的场景采集
两类信号样本文献[15]在6个场景中为每个场景采集200组,共1 200组 代表文献 文献[12] 文献[13] 文献[14] 文献[15] 1 带DP信号残差特征训练SVDD的NLOS识别算法
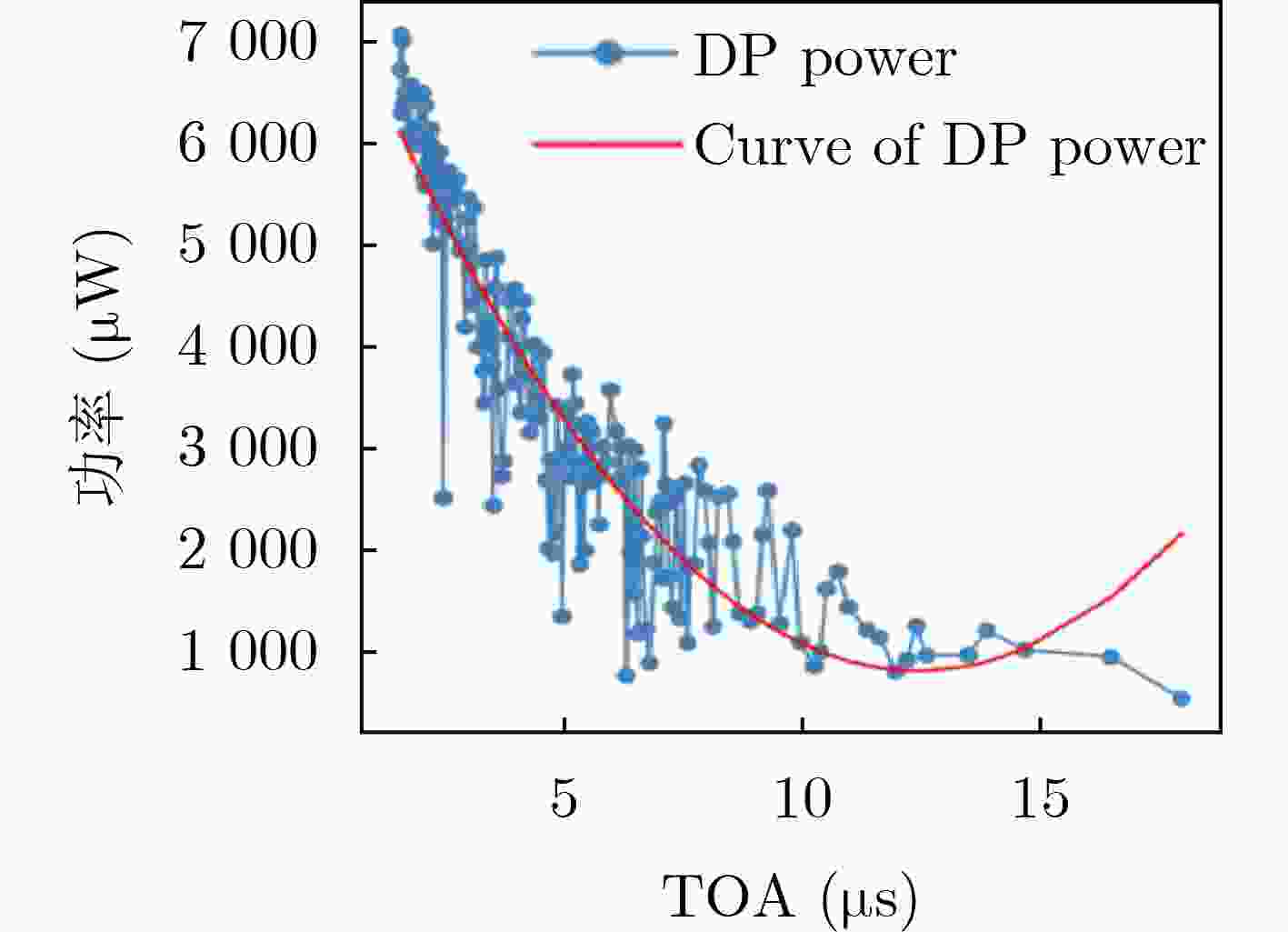
步骤1 将空旷场景采集到的500组LOS信号的CIR数据包作为训
练集,以DP信号的TOA为自变量,功率为因变量,使用最小二
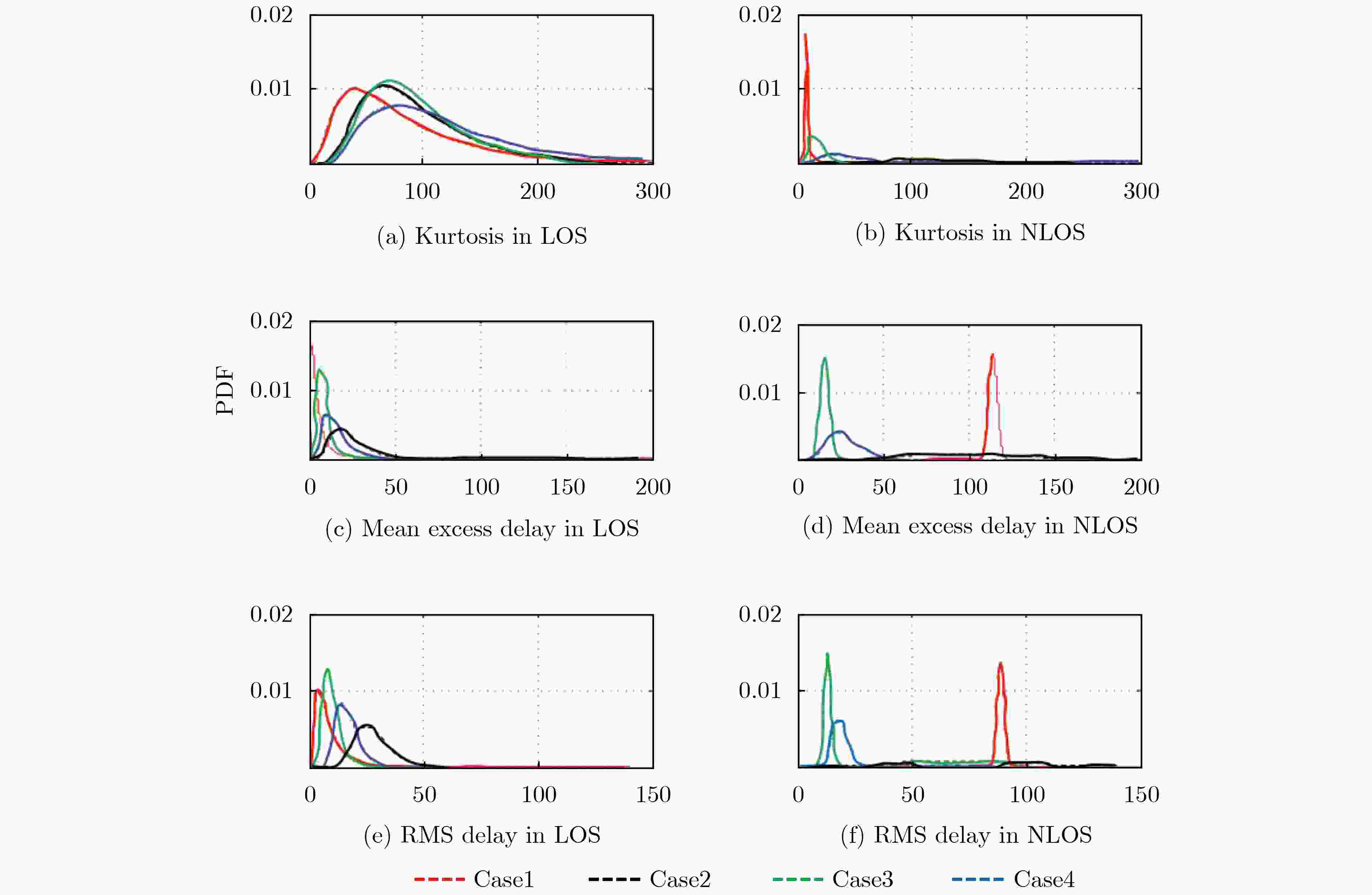
乘算法拟合出一条功率曲线:P(TOA),作为标准DP功率函数步骤2 提取训练集信号的$ \ell ,{r_{\max }},\kappa ,\tau ,\varsigma ,{t_{{\mathrm{rise}}}},\mu ,{\lambda _{{\mathrm{sp}}}},S和\varDelta $特
征,形成训练集$ {\boldsymbol{X}} \in {\mathbb{R}^{n \times d}} $步骤3 使用$ K({{\boldsymbol{x}}_i},{{\boldsymbol{x}}_j}) $核函数将$ {\boldsymbol{X}} \in {\mathbb{R}^{n \times d}} $映射到特征空间训
练SVDD模型,求出球心c和半径d1步骤4 识别未知信号类型时,提取该信号的$ \ell ,{r_{\max }},\kappa ,\tau ,\varsigma $,
${t_{{\mathrm{rise}}}}, \mu, {\lambda _{{\mathrm{sp}}}},S和\varDelta $特征步骤5 将该信号通过$ K({{\boldsymbol{x}}_i},{{\boldsymbol{x}}_j}) $映射到特征空间,求出与训练
好的SVDD超球面球心c之间的距离d2步骤6 当d2≤d1,判断为LOS信号;当d2>d1时,判断为
NLOS信号2 带DP信号残差特征训练DSVDD的NLOS识别算法
步骤1 将空旷场景采集到的500组LOS信号作为训练集,以
DP信号的TOA为自变量,功率为因变量,使用最小二乘算法拟
合出一条功率曲线P,作为标准DP功率函数步骤2 提取训练集信号的$ \ell ,{r_{\max }},\kappa ,\tau ,\varsigma ,{t_{{\text{rise}}}},\mu ,{\lambda _{{\text{sp}}}},S 和\varDelta $特
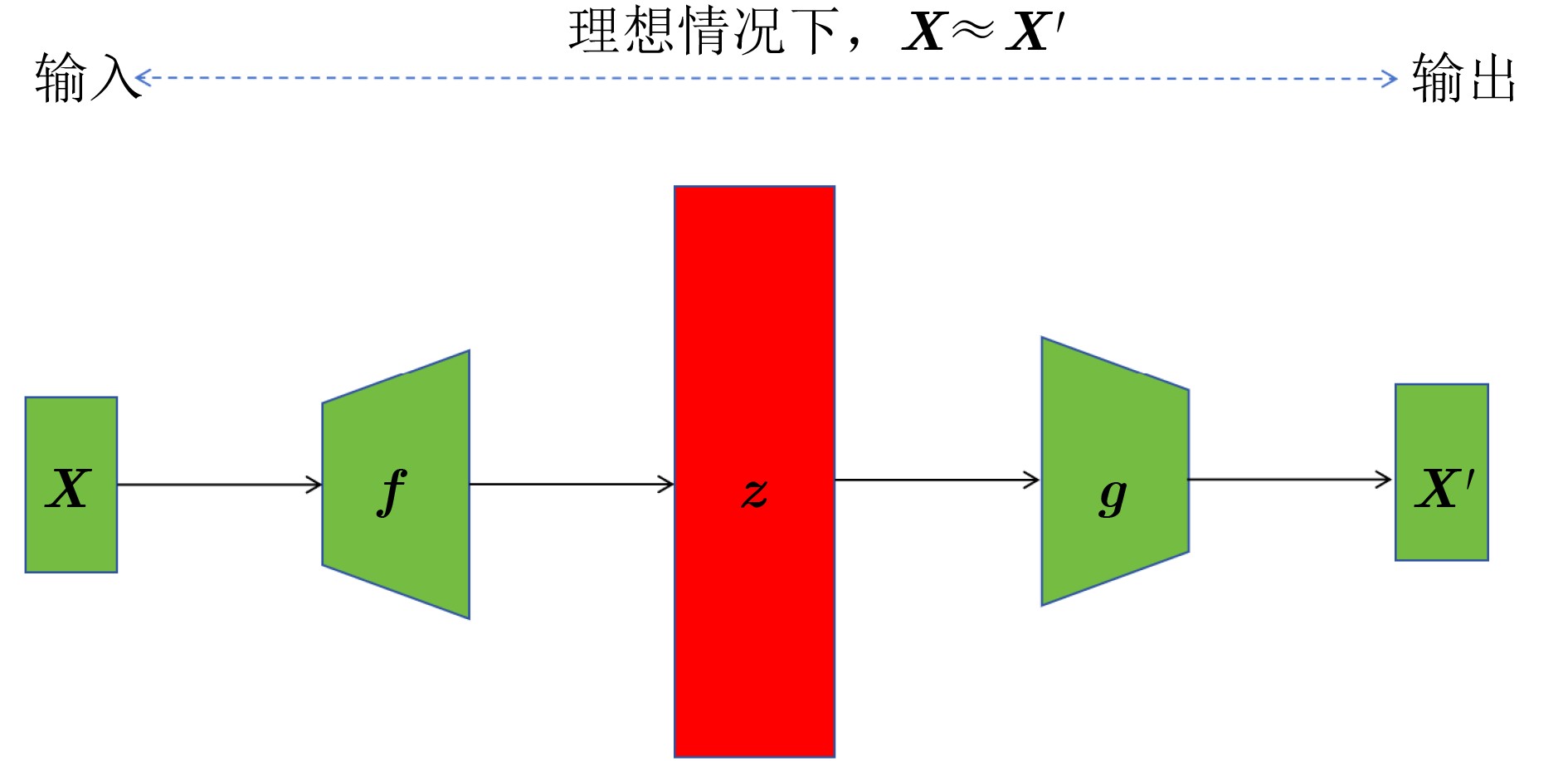
征,形成训练集$ {\boldsymbol{X}} \in {\mathbb{R}^{n \times d}} $步骤3 将$ {\boldsymbol{X}} \in {\mathbb{R}^{n \times d}} $输入预训练网络进行训练,获得初始化的
球心c和半径d1,利用$ \phi (.;{\boldsymbol{W}}):{\boldsymbol{X}} \to {\boldsymbol{F}} $将$ {\boldsymbol{X}} \in {\mathbb{R}^{n \times d}} $映射到
$ {\boldsymbol{F}} $特征空间训练DSVDD模型,不断优化神经网络的权重系数
$ {\boldsymbol{W}} $,球心c和半径d1步骤4 识别未知信号类型时,提取该信号的$ \ell ,{r_{\max }},\kappa ,\tau $,
$\varsigma ,{t_{{\text{rise}}}},\mu ,{\lambda _{{\text{sp}}}},S $和$\varDelta $特征,形成$ {\boldsymbol{X}} \in {\mathbb{R}^d} $步骤5 将$ {\boldsymbol{X}} \in {\mathbb{R}^d} $通过$ \phi (.;{\boldsymbol{W}}):{\boldsymbol{X}} \to {\boldsymbol{F}} $映射到$ {\boldsymbol{F}} $,求出与训
练好的DSVDD超球面球心C之间的距离d2步骤6 当d 2≤d1,判断为LOS信号;当d2>d1时,判断为
NLOS信号表 2 识别效果对比(%)
LSSVM SVDD 带DP信号残差训练的SVDD 带DP信号残差训练的DSVDD 训练集 场景1采集的500组LOS和500组NLOS信号 场景1采集的500组LOS信号 测试集 场景1采集的信号样本中除开测试集信号,场景2和3所有的信号 准确率 场景1 96.42 89.41 93.62 95.84 场景2 73.45 78.41 82.14 87.34 场景3 69.75 77.45 80.23 85.43 精确率 场景1 95.62 88.23 93.47 95.16 场景2 72.25 77.11 83.27 88.16 场景3 70.43 76.22 80.27 84.31 召回率 场景1 96.35 89.68 93.52 95.32 场景2 75.32 80.32 82.22 86.21 场景3 74.52 78.25 79.28 83.29 F2-score 场景1 96.20 89.39 93.51 95.29 场景2 74.69 79.66 82.43 86.59 场景3 73.66 77.84 79.48 83.49 表 3 LSSVM, SVDD、带DP信号残差训练的SVDD的最佳特征组合
特征组合 LSSVM SVDD 带DP信号残差训练的SVDD A $ \ell ,{r_{\max }},{t_{{\text{rise}}}} $ $ {r_{\max }},\tau ,{t_{{\text{rise}}}} $ $ {r_{\max }},\kappa ,\varDelta $ B $ \ell ,{r_{\max }},\varsigma ,{t_{{\text{rise}}}} $ $ \ell ,{r_{\max }},\tau ,{t_{{\text{rise}}}} $ $ {r_{\max }},\tau ,{t_{{\text{rise}}}},\varDelta $ C $ \ell ,{r_{\max }},\kappa ,\tau ,\varsigma $ $ \ell ,{r_{\max }},\kappa ,\tau ,{t_{{\text{rise}}}} $ $ {r_{\max }},\kappa ,\tau ,{t_{{\text{rise}}}},\varDelta $ D $ \ell ,{r_{\max }},\kappa ,\tau ,\varsigma ,{t_{{\text{rise}}}} $ $ \ell ,{r_{\max }},\kappa ,\tau ,\varsigma ,{t_{{\text{rise}}}} $ $ {r_{\max }},\kappa ,\tau ,{t_{{\text{rise}}}},\varsigma ,\varDelta $ E $ \ell ,{r_{\max }},\kappa ,\tau ,\varsigma ,{t_{{\text{rise}}}},\mu $ $ \ell ,{r_{\max }},\kappa ,\tau ,\varsigma ,{t_{{\text{rise}}}},\mu $ $ {r_{\max }},\kappa ,\tau ,{t_{{\text{rise}}}},\varsigma ,\mu ,\varDelta $ F $ \ell ,{r_{\max }},\kappa ,\tau ,\varsigma ,{t_{{\text{rise}}}},{\lambda _{{\text{sp}}}},S $ $ \ell ,{r_{\max }},\kappa ,\tau ,\varsigma ,{t_{{\text{rise}}}},{\lambda _{{\text{sp}}}},S $ $ \ell ,{r_{\max }},\kappa ,\tau ,\varsigma ,{t_{{\text{rise}}}},\varsigma ,S,\varDelta $ G $ \ell ,{r_{\max }},\kappa ,\tau ,\varsigma ,{t_{{\text{rise}}}},\mu ,{\lambda _{{\text{sp}}}},S $ $ \ell ,{r_{\max }},\kappa ,\tau ,\varsigma ,{t_{{\text{rise}}}},\mu ,{\lambda _{{\text{sp}}}},S $ $ \ell ,{r_{\max }},\kappa ,\tau ,\varsigma ,{t_{{\text{rise}}}},{\lambda _{{\text{sp}}}},S,\varDelta $ -
[1] DARDARI D, CONTI A, FERNER U, et al. Win. Ranging with ultrawide bandwidth signals in multipath environments[J]. Proceedings of the IEEE, 2009, 97(2): 404–426. doi: 10.1109/JPROC.2008.2008846. [2] SUWANSANTISUK W and WIN M Z. Multipath aided rapid acquisition: Optimal search strategies[J]. IEEE Transactions on Information Theory, 2007, 53(1): 174–193. doi: 10.1109/TIT.2006.887509. [3] ZHANG Guolong, DENG Zhongliang, WEN Liu, et al. An UWB location algorithm for indoor NLOS environment[C]. 2018 Ubiquitous Positioning, Indoor Navigation and Location-Based Services, Wuhan, China, 2018: 1–6. doi: 10.1109/UPINLBS.2018.8559711. [4] WANG Lei, CHEN Ruizhi, CHEN Liang, et al. A robust filter for TOA based indoor localization in mixed LOS/NLOS environment[C]. Ubiquitous Positioning, Indoor Navigation and Location-Based Services, Wuhan, China, 2018: 1–9. doi: 10.1109/UPINLBS.2018.8559862. [5] 邓锴. 基于NLOS识别和误差消除的无线定位算法研究[D]. [硕士论文], 西南交通大学, 2018.DENG Kai. Research on wireless location algortihm based on NLOS identification and error mitigation[D]. [Master dissertation], Southwest Jiaotong University, 2018. [6] FAN Zhibo, CHU Hao, WANG Fei, et al. A new non-line-of-sight localization algorithm for wireless sensor network[C]. 2020 IEEE 6th International Conference on Computer and Communications, Chengdu, China, 2020: 858–862. doi: 10.1109/ICCC51575.2020.9344936. [7] YAN Leibing, LU Yin, and ZHANG Yerong. An improved NLOS identification and mitigation approach for target tracking in wireless sensor networks[J]. IEEE Access, 2017, 5: 2798–2807. doi: 10.1109/ACCESS.2017.2677480. [8] ZHU Yuhong, MA tengfei, LI Zhijun, et al. NLOS identification and correction based on multidimensional scaling and quasi-accurate detection[J]. IEEE Access, 2019, 7: 53977–53987. doi: 10.1109/ACCESS.2019.2906866. [9] DIAO Hongxue and ZHAO Junhui. CMD-based NLOS identification and mitigation in wireless sensor networks[C]. 2019 IEEE International Conference on Communications Workshops, Shanghai, China, 2019: 1–6. doi: 10.1109/ICCW.2019.8757187. [10] MARANÒ S, GIFFORD W M, and WYMEERSCH H. NLOS identification and mitigation for localization based on UWB experimental data[J]. IEEE Journal on Selected Areas in Communications, 2010, 28(7): 1026–1035. doi: 10.1109/JSAC.2010.100907. [11] WYMEERSCH H, MARANÒ S, GIFFORD W M, et al. A machine learning approach to ranging error mitigation for UWB localization[J]. IEEE Transactions on Communications, 2012, 60(6): 1719–1728. doi: 10.1109/TCOMM.2012.042712.110035. [12] SUYKENS J A K and VANDEWALLE J. Least squares support vector machine classifiers[J]. Neural Processing Letters, 1999, 9(3): 293–300. doi: 10.1023/A:1018628609742. [13] TIAN Shiwei, ZHAO Luwen, and LI Guangxia. A support vector data description approach to NLOS identification in UWB positioning[J]. Mathematical Problems in Engineering, 2014, 2014(1): 963418. doi: 10.1155/2014/963418. [14] CUI Zhichao, LIU Tianwei, TIAN Shiwei, et al. Non-line-of-sight identification for UWB positioning using capsule networks[J]. IEEE Communications Letters, 2020, 24(10): 2187–2190. doi: 10.1109/LCOMM.2020.3003688. doi: 10.1109/LCOMM.2020.3003688. [15] 韦子辉, 解云龙, 王世昭, 等. 基于加权K-近邻分类的非视距识别方法研究[J]. 电子与信息学报, 2022, 44(8): 2842–2851. doi: 10.11999/JEIT210422.WEI Zihui, XIE Yunlong, WANG Shizhao, et al. Research on non-line-of-sight recognition method based on weighted K-nearest neighbor classification[J] Journal of Electronics & Information Technology, 2022, 44(8): 2842–2851. doi: 10.11999/JEIT210422. [16] 吴绍华, 张钦宇, 张乃通. 密集多径环境下UWB测距的NLOS误差减小方法[J]. 电子学报, 2008, 36(1): 39–45. doi: 10.3321/j.issn:0372-2112.2008.01.007.WU Shaohua, ZHANG Qinyu, and ZHANG Naitong. A NLOS error mitigation method for UWB ranging in dense multi-path environments[J]. Acat Electronica Sinica, 2008, 36(1): 39–45. doi: 10.3321/j.issn:0372-2112.2008.01.007. [17] 何建国. 超宽带室内非视距信号识别与定位研究[D]. [硕士论文], 重庆交通大学, 2024. doi: 10.27671/d.cnki.gcjtc.2024.000532.HE Jianguo. Research on recognition and localization of ultra-wideband indoor non line of sight signals[D]. [Master dissertation], Chongqing Jiaotong University, 2024. doi: 10.27671/d.cnki.gcjtc.2024.000532. [18] 刘梦琦. 超宽带定位的NLOS识别及误差减小方法[D]. [硕士论文], 中国矿业大学, 2022. doi: 10.27623/d.cnki.gzkyu.2022.000217.LIU Mengqi. NLOS Identification and mitigation in ultra-wideband positioning[D]. [Master dissertation], China University of Mining and Technology, 2022. doi: 10.27623/d.cnki.gzkyu.2022.000217. [19] GÜVENÇ İ, CHONG C C, WATANABE F, et al. NLOS identification and weighted least-squares localization for UWB systems using multipath channel statistics[J]. EURASIP Journal on Advances in Signal Processing, 2007, 2008(1): 271984. doi: 10.1155/2008/271984. [20] 王晓慧, 王延江, 邓晓刚, 等. 基于加权深度支持向量数据描述的工业过程故障检测[J]. 化工学报, 2021, 72(11): 5707–5716. doi: 10.11949/0438-1157.20210707.WANG Xiaohui, WANG Yanjiang, DENG Xiaogang, et al. Industrial process fault detection using weighted deep support vector data description[J]. CIESC Journal, 2021, 72(11): 5707–5716. doi: 10.11949/0438-1157.20210707. [21] RUFF L, GÖRNITZ N, DEECKE L, et al. Deep one-class classification[C]. Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 2018: 4390–4399. [22] 闫廷聚, 曹琰, 王依菁. 基于RFFAD_DeepSVDD的低功耗蓝牙欺骗攻击检测技术[J]. 计算机科学, 2025, 52(2): 380–387. doi: 10.11896/jsjkx.231200168. -





 下载:
下载:







 下载:
下载:
