Joint Design of Transmission Sequences and Receiver Filters Based on the Generalized Cross Ambiguity Function
-
摘要: 具有良好相关特性的正交波形集可以提高多输入多输出(MIMO)雷达系统的目标检测性能和抗干扰能力。为此,该文提出主瓣增益和动态范围约束下最小化广义互模糊函数积分旁瓣(ISL)的发射序列集和接收滤波器组联合设计方法。该方法采用最大块改进算法(MBI)将非凸优化问题分解为多个子问题,再利用连续凸近似方法(SCA)迭代求解子问题。为了进一步降低运算量,该文还提出了具有并行实现潜力的交替方向惩罚法(ADPM)求解SCA的子问题。最后,通过仿真实验从收敛速度、积分旁瓣电平等方面验证了该方法的有效性。Abstract:
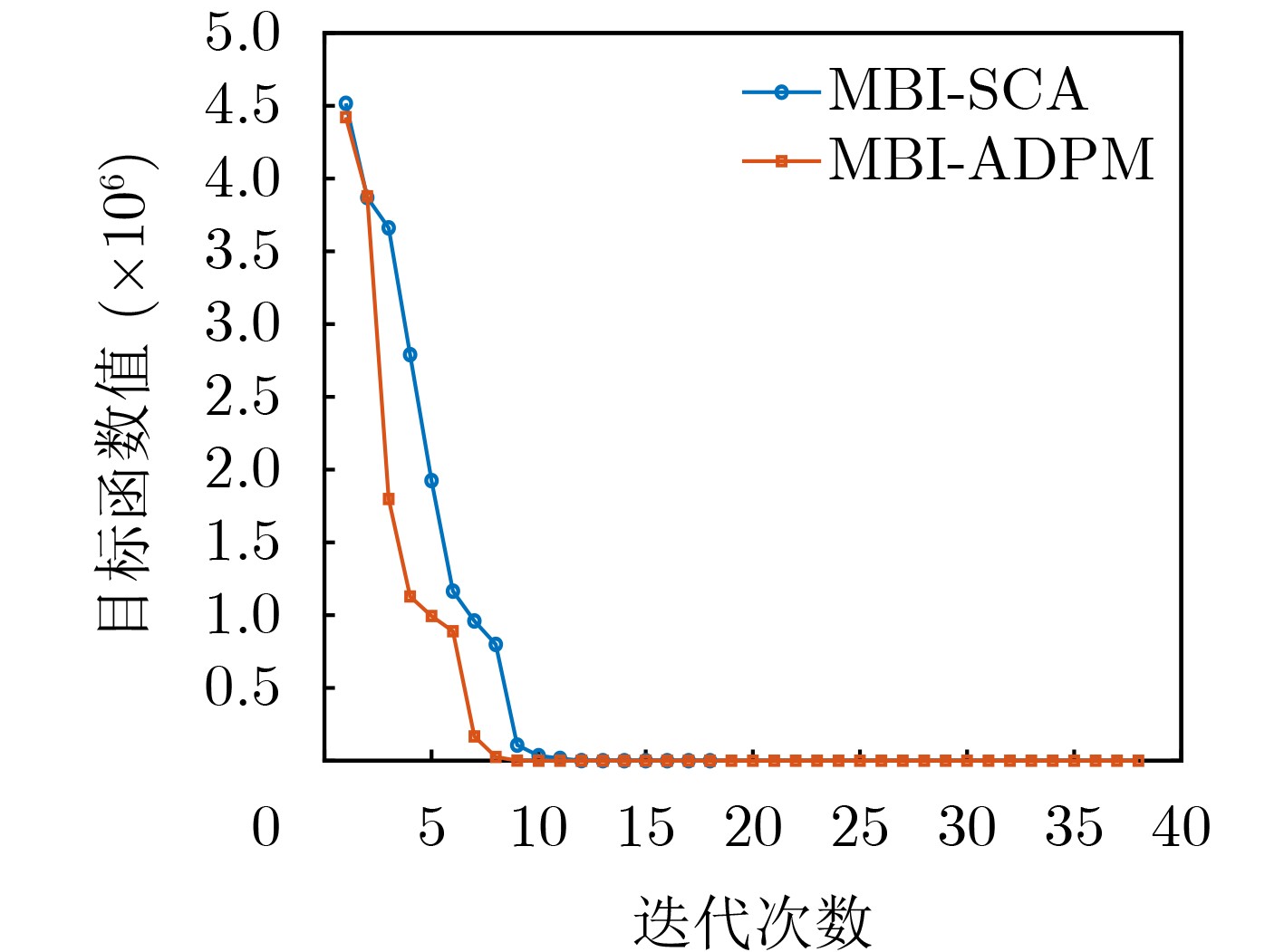
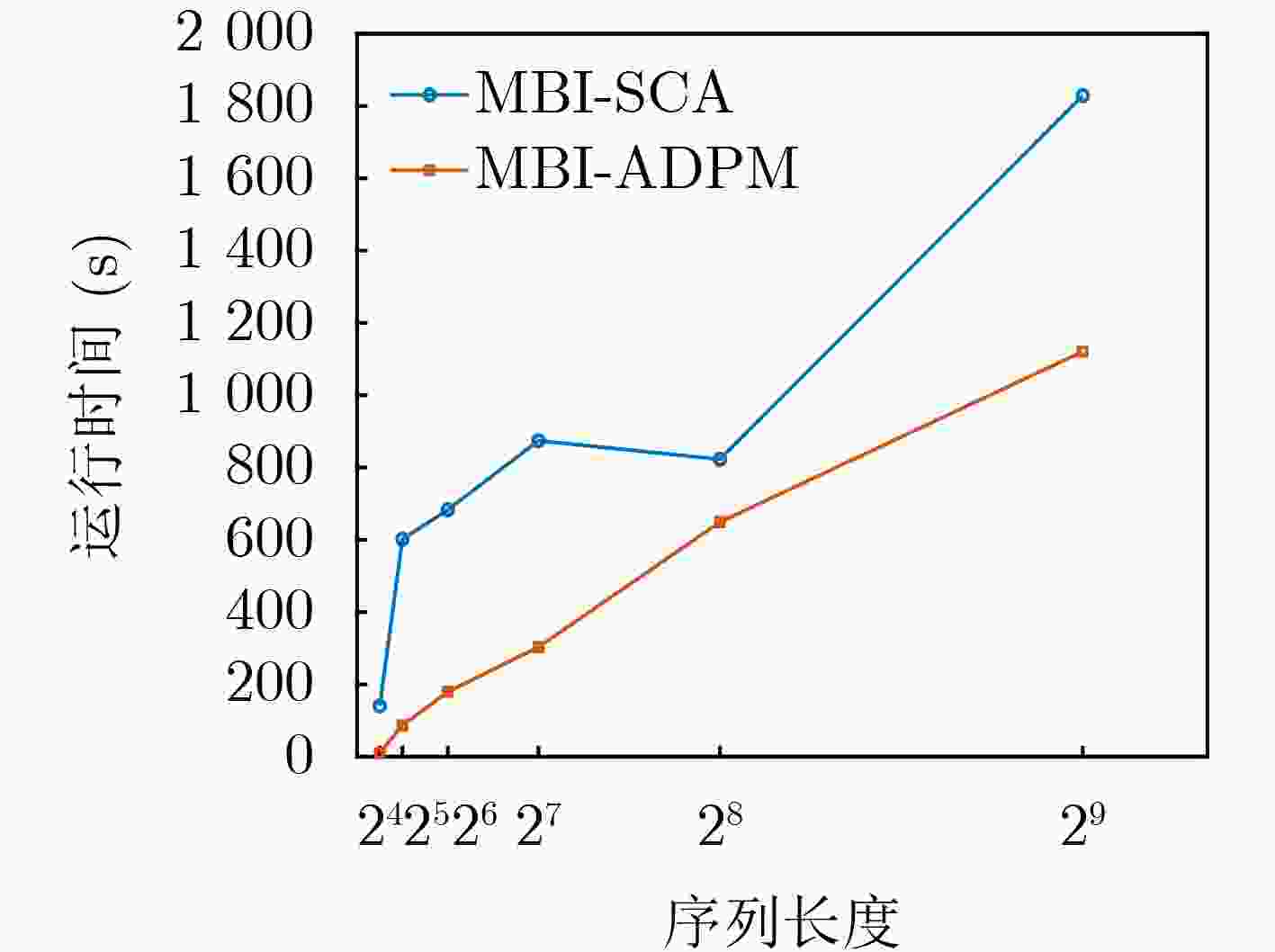
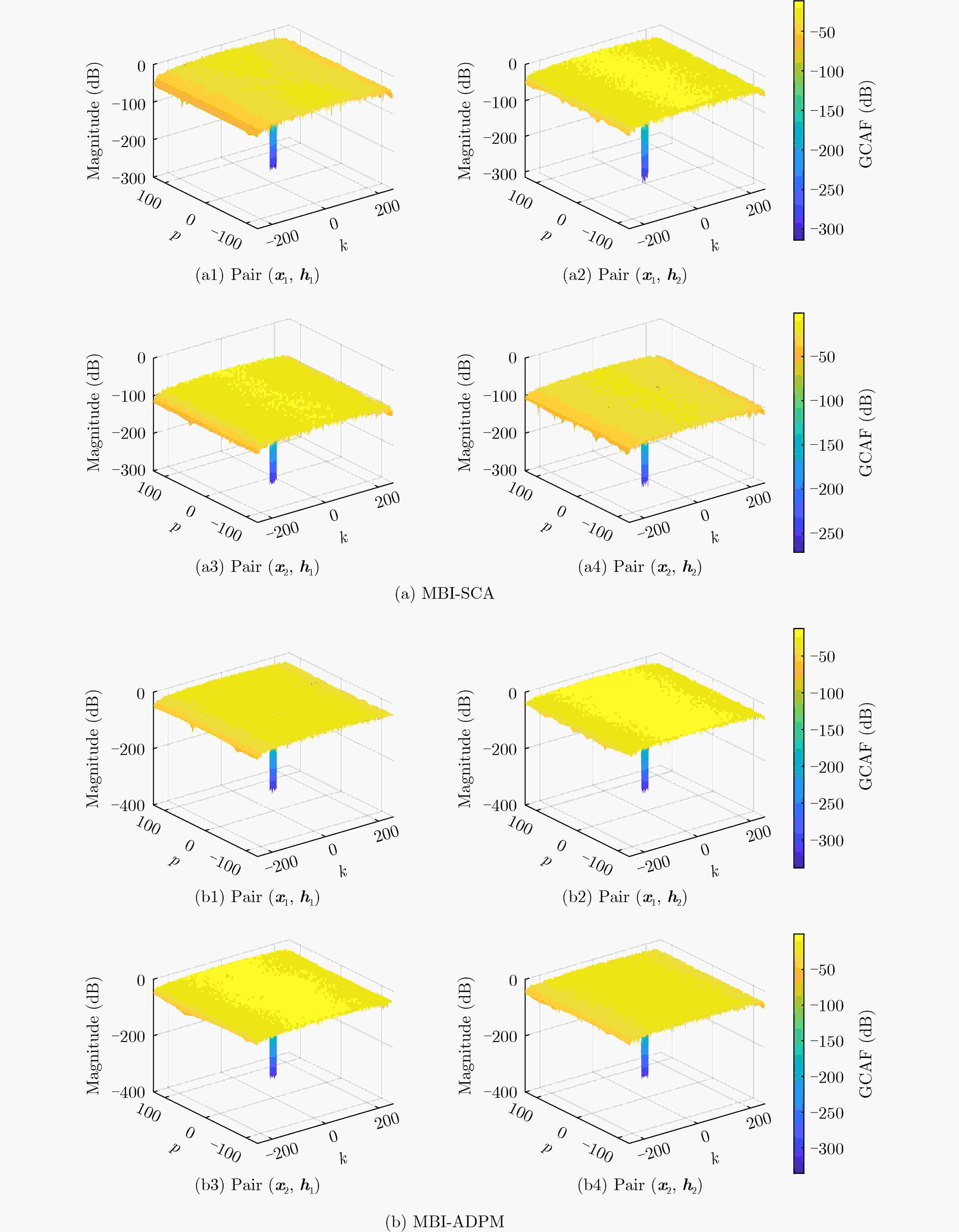
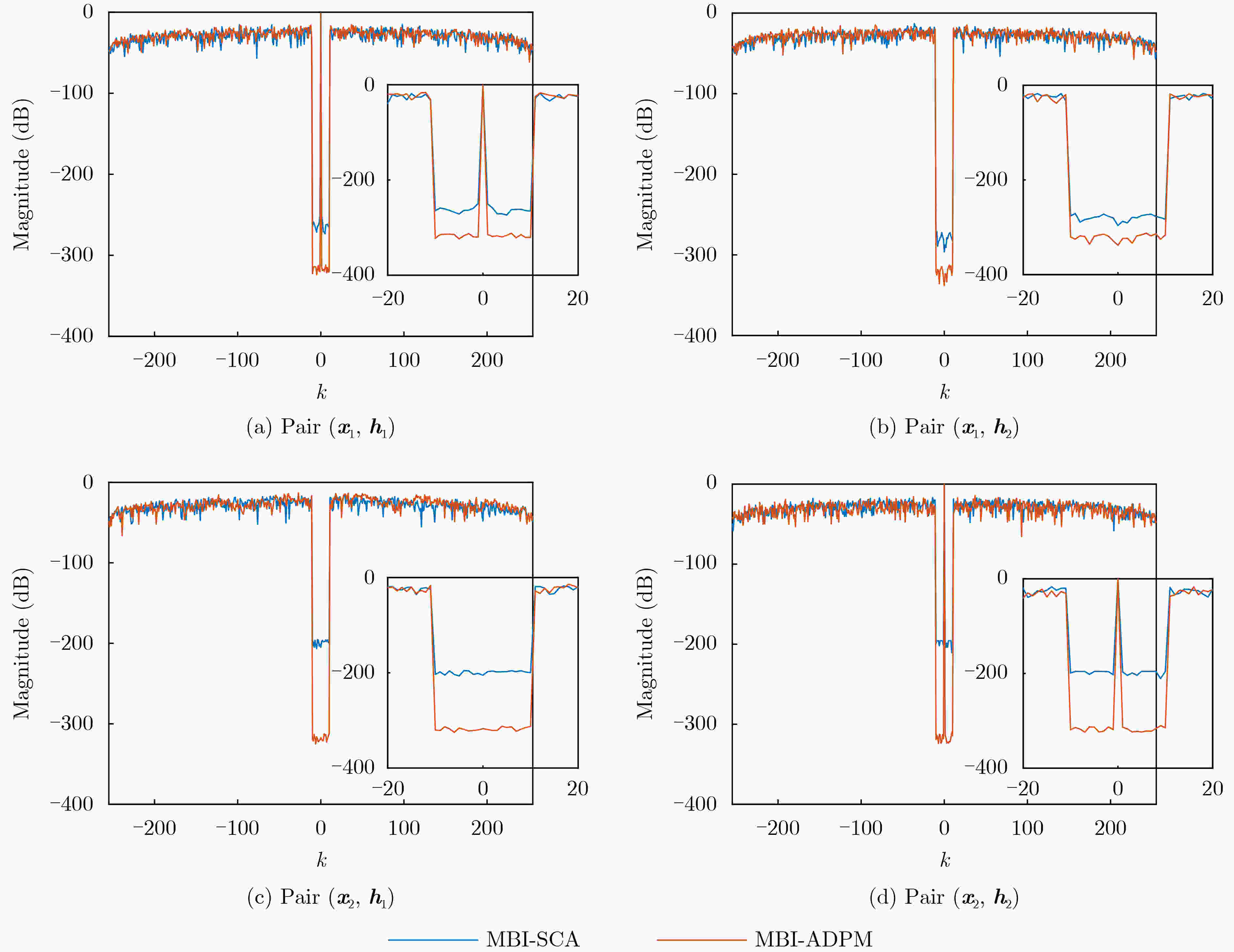
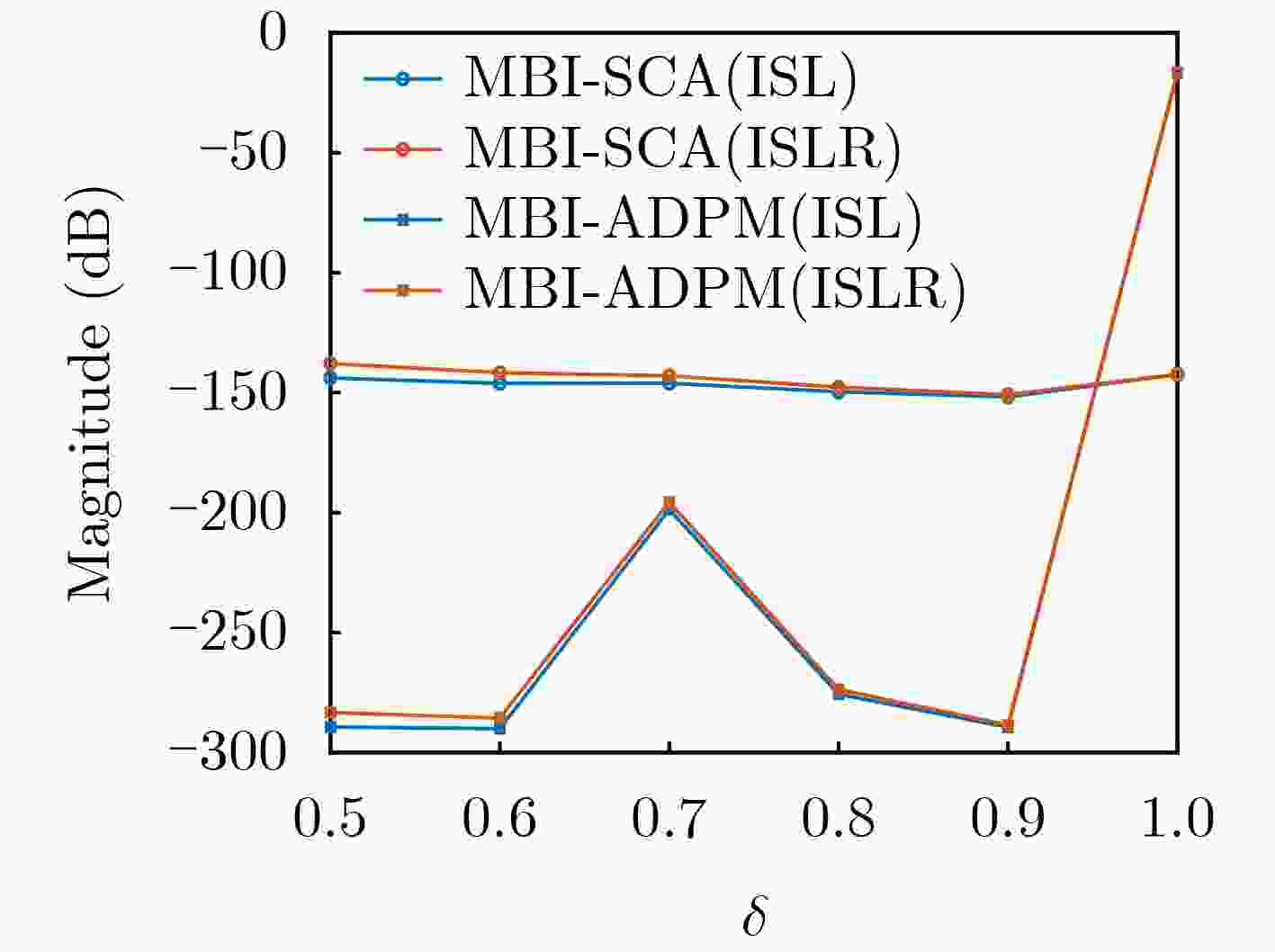
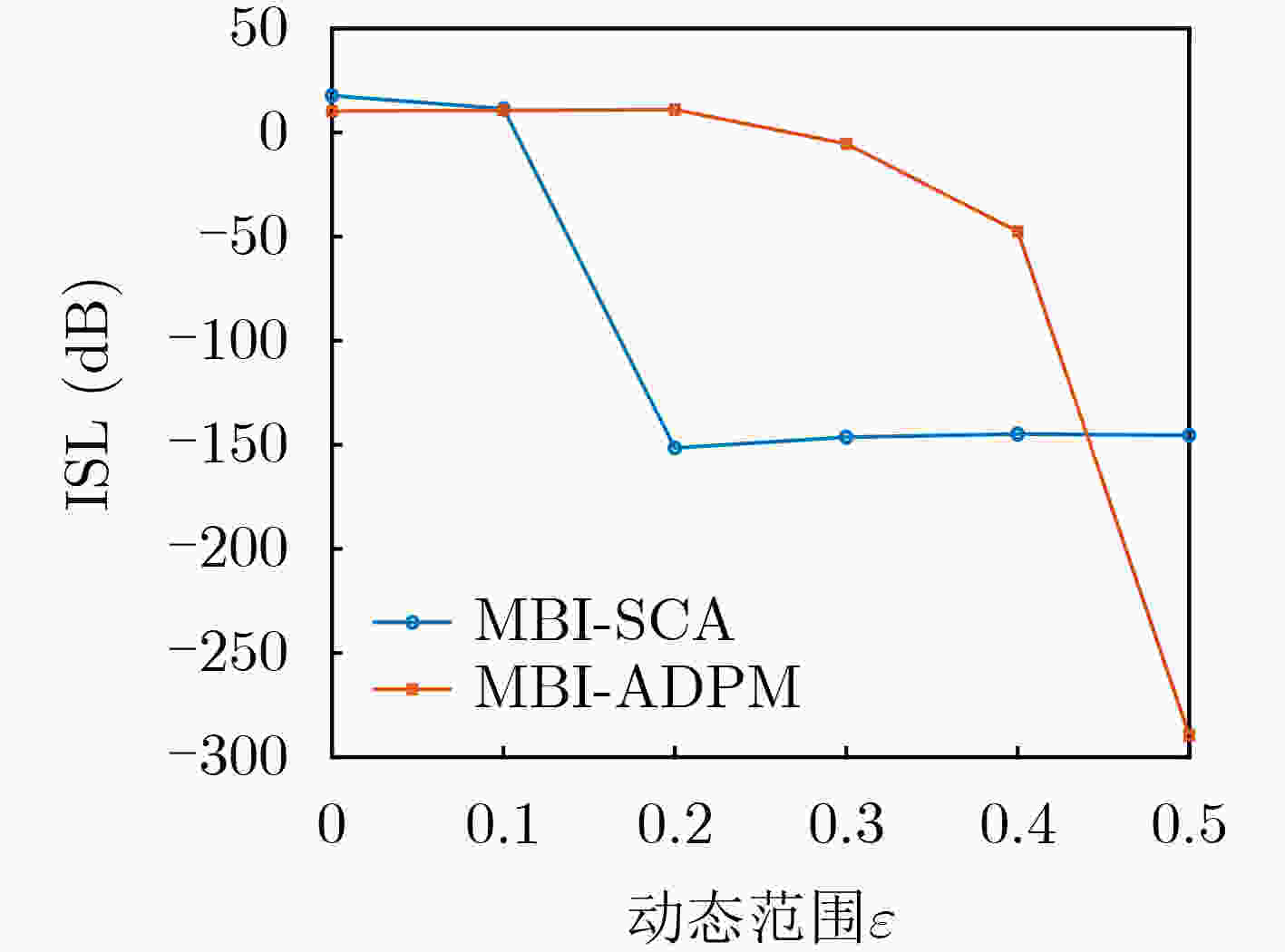
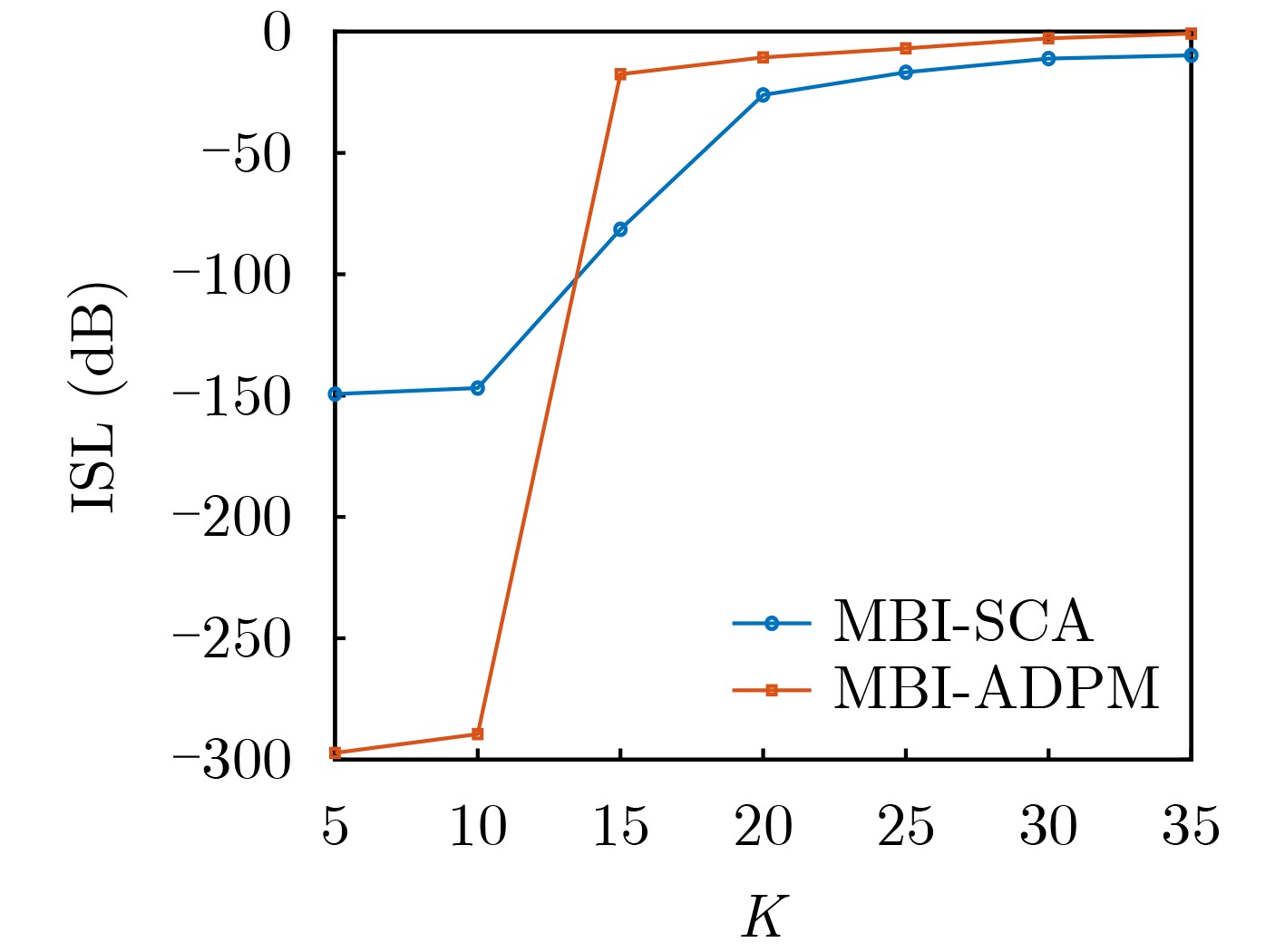
Objective A set of orthogonal waveforms with favorable correlation properties enhances target detection and anti-jamming performance in Multiple-Input Multiple-Output (MIMO) radar systems. Jointly designing the transmit sequence set and receive filter bank introduces additional degrees of freedom, reducing auto- and cross-correlation. However, research on their joint design based on the Generalized Cross Ambiguity Function (GCAF) is limited and primarily focuses on reducing the peak sidelobe level. Since a low Integrated Sidelobe Level (ISL) is also critical for radar imaging and target detection, this study formulates the joint design problem with the objective of minimizing the ISL of the GCAF, subject to mainlobe gain and dynamic range constraints. Methods This paper proposes a Maximum Block Improvement–Successive Convex Approximation (MBI-SCA) method for the nonconvex optimization problem involving High-Order Polynomials (HOP). The MBI algorithm decomposes the nonconvex problem into multiple subproblems, which are then solved iteratively using the SCA method. To further reduce computational cost, an Alternating Direction Penalty Method (ADPM) is introduced. This algorithm, which supports parallel implementation, dynamically updates the penalty factor in each iteration, ensuring the penalty term gradually converges to zero. This guarantees algorithm convergence and accelerates the search for a better feasible solution. Results and Discussions The proposed MBI-SCA algorithm converges in approximately 12 iterations, while the MBI-ADPM algorithm achieves faster convergence in about 10 iterations ( Fig. 1 ). The running time of the MBI-ADPM algorithm increases as the sequence length varies from 16 to 512, whereas the MBI-SCA algorithm exhibits an overall increase, with a decrease at ${2^8}$, likely due to an decrease in the number of iterations when the SCA method solves the subproblem (Fig. 2 ). Both algorithms demonstrate strong performance, with GCAF values in the locally optimized region significantly lower than those in the unoptimized region, all below –200 dB (Fig. 3 ). However, MBI-ADPM achieves better local optimization, reducing GCAF values to –320 dB, whereas MBI-SCA reaches only –260 dB (Fig. 4 ). The parameter $K$ determines the optimization interval’s range, and as $K$ increases from 5 to 35, the ISL values of both methods also increase. For MBI-SCA, the optimal range of the parameter $K$ is $5 \le K \le 15$, where the integral sidelobe levels remain below –50 dB, meeting the low sidelobe requirement. In contrast, MBI-ADPM performs best values of $K$ are 5 and 10, achieving an objective function value close to –300 dB (Fig. 7 ).Conclusions This paper proposes a joint design method for transmit waveforms and receive filters that minimizes the GCAF ISL under mainlobe gain and dynamic range constraints, addressing the reduction of auto- and cross-correlation integral levels in MIMO radar waveform sets. To solve the quartic nonconvex optimization problem, the original problem is first decomposed into manageable subproblems using the MBI algorithm, which are then solved iteratively with the SCA algorithm. To further reduce computational complexity, the ADPM algorithm is introduced to solve the SCA subproblems. Simulation results demonstrate that the MBI-ADPM algorithm converges faster and achieves a lower ISL than MBI-SCA for shorter distance intervals of interest. -
1 MBI算法求解问题式(8)
输入: ${\boldsymbol x}_m^{(0)}$, ${\boldsymbol h}_{m'}^{(0)}$,计算${\omega ^{(0)}} = F({\boldsymbol x}_1^{(0)},{\boldsymbol x}_2^{(0)}, \cdots ,{\boldsymbol x}_M^{(0)},{\boldsymbol h}_1^{(0)},{\boldsymbol h}_2^{(0)}, \cdots ,{\boldsymbol h}_M^{(0)})$, $t = 0$ 输出:式(8)的解$ {\boldsymbol x}_m^{(t + 1)} $, ${\boldsymbol h}_{m'}^{(t + 1)}$ 步骤1 (块更新).对$m = 1,2, \cdots ,M$,求解式(9),对$m' = 1,2, \cdots ,M$,求解式(10)。令 ${\boldsymbol{u}}_m^{(t + 1)} = \arg \mathop {\min }\limits_{{{\boldsymbol x}_m}} F({\boldsymbol x}_1^{(t)},{\boldsymbol x}_2^{(t)}, \cdots ,{{\boldsymbol x}_m},{\boldsymbol x}_{m + 1}^{(t)},{\boldsymbol x}_{m + 2}^{(t)}, \cdots ,{\boldsymbol x}_M^{(t)},{\boldsymbol h}_1^{(t)},{\boldsymbol h}_2^{(t)}, \cdots ,{\boldsymbol h}_M^{(t)})$ ${\boldsymbol{u}}_{m'}^{(t + 1)} = \arg \mathop {\min }\limits_{{{\boldsymbol h}_{m'}}} F({\boldsymbol x}_1^{(t)},{\boldsymbol x}_2^{(t)}, \cdots ,{\boldsymbol x}_M^{(t)},{\boldsymbol h}_1^{(t)},{\boldsymbol h}_2^{(t)}, \cdots ,{{\boldsymbol h}_{m'}},{\boldsymbol h}_{m' + 1}^{(t)},{\boldsymbol h}_{m' + 2}^{(t)}, \cdots ,{\boldsymbol h}_M^{(t)})$ $ y_m^{(t + 1)} = F({\boldsymbol x}_1^{(t)},{\boldsymbol x}_2^{(t)}, \cdots ,{\boldsymbol{u}}_m^{(t + 1)},{\boldsymbol x}_{m + 1}^{(t)},{\boldsymbol x}_{m + 2}^{(t)}, \cdots ,{\boldsymbol x}_M^{(t)},{\boldsymbol h}_1^{(t)},{\boldsymbol h}_2^{(t)}, \cdots ,{\boldsymbol h}_M^{(t)}) $ $ y_{m'}^{(t + 1)} = F({\boldsymbol x}_1^{(t)},{\boldsymbol x}_2^{(t)}, \cdots ,{\boldsymbol x}_M^{(t)},{\boldsymbol h}_1^{(t)},{\boldsymbol h}_2^{(t)}, \cdots ,{\boldsymbol{u}}_{m'}^{(t + 1)},{\boldsymbol h}_{m' + 1}^{(t)},{\boldsymbol h}_{m' + 2}^{(t)}, \cdots ,{\boldsymbol h}_M^{(t)}) $ 步骤2 (最大块更新).令 ${y^{(t + 1)}} = {\min _{1 \le m,m' \le M}}(y_m^{(t + 1)},y_{m'}^{(t + 1)})$ ${\boldsymbol x}_{\hat m}^{(t + 1)} = \arg \min {y^{(t + 1)}}$ 或 ${\boldsymbol h}_{\hat m}^{(t + 1)} = \arg \min {y^{(t + 1)}}$ 更新 ${\boldsymbol x}_m^{(t + 1)} = {\boldsymbol x}_m^{(t)},\forall m \ne \hat m$ $ {\boldsymbol h}_{m'}^{(t + 1)} = {\boldsymbol h}_{m'}^{(t)},\forall m' \ne \hat m' $ ${\boldsymbol x}_m^{(t + 1)} = {\boldsymbol x}_{\hat m}^{(t + 1)}$ 或 ${\boldsymbol h}_{m'}^{(t + 1)} = {\boldsymbol h}_{\hat m'}^{(t + 1)}$ ${\omega ^{(t + 1)}} = {y^{(t + 1)}}$ 步骤3 (停止准则) $|{\omega ^{(t + 1)}} - {\omega ^{(t)}}| \le {10^{ - 3}}{\omega ^{(t + 1)}}$ ,停止。否则 令$t = t + 1$,返回1。 2 SCA算法求解问题式(9)和式(10)
输入:${\boldsymbol x}_m^{(t)}$, ${\boldsymbol h}_{m'}^{(t)}$, ${\omega ^{(t)}}$ 输出:式(9)和式(10)的解$ {\boldsymbol{u}}_m^{(t + 1)} $, $ {\boldsymbol{u}}_{m'}^{(t + 1)} $ 步骤1 ${\boldsymbol x}_m^{(i)} = {\boldsymbol x}_m^{(t)}$和${\boldsymbol h}_{m'}^{(i)} = {\boldsymbol h}_{m'}^{(t)},$及${\omega ^{(i)}} = {\omega ^{(t)}}$, $i = 0$ 步骤2 CVX工具箱分别求解式(14)和式(15),得到${\boldsymbol x}_m^{(i + 1)}$,
${\boldsymbol h}_{m'}^{(i + 1)}$计算${\omega ^{(i + 1)}} = F({\boldsymbol x}_1^{(i)},{\boldsymbol x}_2^{(i)}, \cdots ,{\boldsymbol x}_m^{(i + 1)} $,
${\boldsymbol x}_{m + 1}^{(i)},{\boldsymbol x}_{m + 2}^{(i)}, \cdots ,{\boldsymbol x}_M^{(i)},{\boldsymbol h}_1^{(t)},{\boldsymbol h}_2^{(t)}, \cdots ,{\boldsymbol h}_M^{(t)})$
或${\omega ^{(i + 1)}} = F({\boldsymbol x}_1^{(t)},{\boldsymbol x}_2^{(t)}, \cdots ,{\boldsymbol x}_M^{(t)},{\boldsymbol h}_1^{(i)},{\boldsymbol h}_2^{(i)}, \cdots ,{\boldsymbol h}_{m'}^{(i + 1)}, $
${\boldsymbol h}_{m' + 1}^{(i)},{\boldsymbol h}_{m' + 2}^{(i)}, \cdots ,{\boldsymbol h}_M^{(i)})$步骤3 若$|{\omega ^{(i + 1)}} - {\omega ^{(i)}}| \le {10^{ - 3}}{\omega ^{(i + 1)}}$,输出
${\boldsymbol{u}}_m^{(t + 1)} = {\boldsymbol x}_m^{(i + 1)}$, ${\boldsymbol{u}}_{m'}^{(t + 1)} = {\boldsymbol h}_{m'}^{(i + 1)}$,否则,${\boldsymbol x}_m^{(i)} = {\boldsymbol x}_m^{(i + 1)}$,
${\boldsymbol h}_{m'}^{(i)} = {\boldsymbol h}_{m'}^{(i + 1)}$, ${\omega ^{(i)}} = {\omega ^{(i + 1)}}$,返回步骤2。3 ADPM算法求解问题式(14)
输入:${\boldsymbol x}_m^{(i)} = {\boldsymbol x}_m^{(t)}$, ${\boldsymbol h}_{m'}^{(t)}$, ${\boldsymbol{s}}_1^{(0)}$, ${\boldsymbol{s}}_2^{(0)}$, ${\boldsymbol{s}}_3^{(0)}$, $\mu _{{{\boldsymbol{s}}_1}}^{(0)}$, $\mu _{{{\boldsymbol{s}}_2}}^{(0)}$, $\mu _{{{\boldsymbol{s}}_3}}^{(0)}$计
算$\rho _{{{\boldsymbol{s}}_d}}^{(0)}$,设置$i = 0$输出:问题(14)的解${\boldsymbol x}_m^ * $ 步骤1 $i = i + 1$ 步骤2 分别通过求解问题式(18)–式(24),更新${\boldsymbol{s}}_1^{\left( {i + 1} \right)}$, ${\boldsymbol{s}}_2^{\left( {i + 1} \right)}$,
${\boldsymbol{s}}_3^{\left( {i + 1} \right)}$步骤3 通过求解问题(27),更新${\boldsymbol x}_m^{(i + 1)}$ 步骤4 若$ {e}_{{\mathrm{pri}}}^{(i+1)}\le {\varepsilon }_{{\mathrm{pri}}}^{(i+1)} $, $ {e}_{{\mathrm{dual}}}^{(i+1)}\le {\varepsilon }_{{\mathrm{dual}}}^{(i+1)} $,输出
${\boldsymbol x}_m^ * = {\boldsymbol x}_m^{(i + 1)}$,否则,返回步骤1。 -
[1] DING Mingyue, LI Yachao, WEI Jingyi, et al. Joint design of OFDM-LFM waveforms and receive filter for MIMO radar in spatial heterogeneous clutter[J]. IEEE Geoscience and Remote Sensing Letters, 2024, 21: 1–5. doi: 10.1109/LGRS.2023.3331716. [2] HATAMI M, NGUYEN N, and JUNTTI M. Waveform design for multi-carrier multiuser MIMO joint communications and sensing[C]. 2024 IEEE 25th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Lucca, Italy, 2024: 346–350. doi: 10.1109/SPAWC60668.2024.10694180. [3] YUAN Ye, TAI Xin, ZHONG Kai, et al. MIMO radar Polyphase waveform design via optimal loss function-based soft quantization[C]. IGARSS 2024 - 2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 2024: 529–533. doi: 10.1109/IGARSS53475.2024.10640743. [4] XIE Zhuang, WU Linlong, HUANG Xiaotao, et al. Cross ambiguity function shaping of cognitive MIMO radar: A synergistic approach to antenna placement and waveform design[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 5107313. doi: 10.1109/TGRS.2024.3415428. [5] WANG Jiangtao and WANG Yongchao. On the design of constant modulus probing waveforms with good correlation properties for MIMO radar via consensus-ADMM approach[J]. IEEE Transactions on Signal Processing, 2019, 67(16): 4317–4332. doi: 10.1109/TSP.2019.2928994. [6] HE Hao, STOICA P, and LI Jian. Designing unimodular sequence sets with good correlations-including an application to MIMO radar[J]. IEEE Transactions on Signal Processing, 2009, 57(11): 4391–4405. doi: 10.1109/TSP.2009.2025108. [7] FISHLER E, HAIMOVICH A, BLUM R S, et al. Spatial diversity in radars-models and detection performance[J]. IEEE Transactions on Signal Processing, 2006, 54(3): 823–838. doi: 10.1109/TSP.2005.862813. [8] LI Jian, STOICA P, XU Luzhou, et al. On parameter identifiability of MIMO radar[J]. IEEE Signal Processing Letters, 2007, 14(12): 968–971. doi: 10.1109/LSP.2007.905051. [9] BLISS D W and FORSYTHE K W. Multiple-input multiple-output (MIMO) radar and imaging: Degrees of freedom and resolution[C]. The Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, Pacific Grove, USA, 2003: 54–59. doi: 10.1109/ACSSC.2003.1291865. [10] GONG Pengcheng, LIU Jianyu, CHENG Xu, et al. Frequency-invariant beampattern synthesis for wideband MIMO radar under nulling and PAPR control[J]. IEEE Transactions on Vehicular Technology, 2024, 73(6): 7949–7961. doi: 10.1109/TVT.2023.3348495. [11] WANG Tao, LIANG Junli, SO H C, et al. Designing sequence set and mismatched filter bank with diagonal-ridge-type Doppler tolerance via relative level optimization[J]. IEEE Transactions on Signal Processing, 2024, 72: 4412–4427. doi: 10.1109/TSP.2024.3457778. [12] 巩朋成, 吴云韬. 基于ADMM改进的低截获FDA-MIMO雷达发射波束设计[J]. 通信学报, 2022, 43(4): 133–142. doi: 10.11959/j.issn.1000-436x.2022065.GONG Pengcheng and WU Yuntao. Improved transmit beamforming design based on ADMM for low probability of intercept of FDA-MIMO radar[J]. Journal on Communications, 2022, 43(4): 133–142. doi: 10.11959/j.issn.1000-436x.2022065. [13] STOICA P, LI Jian, and XIE Yao. On probing signal design for MIMO radar[J]. IEEE Transactions on Signal Processing, 2007, 55(8): 4151–4161. doi: 10.1109/TSP.2007.894398. [14] LEVANON N. Noncoherent radar pulse compression based on complementary sequences[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(2): 742–747. doi: 10.1109/TAES.2009.5089554. [15] HU Su, LIU Zilong, GUAN Yongliang, et al. Training sequence design for efficient channel estimation in MIMO-FBMC systems[J]. IEEE Access, 2017, 5: 4747–4758. doi: 10.1109/ACCESS.2017.2688399. [16] SCHMIDT K U. Complementary sets, generalized reed–muller codes, and power control for OFDM[J]. IEEE Transactions on Information Theory, 2007, 53(2): 808–814. doi: 10.1109/TIT.2006.889723. [17] XIA Meng, CHEN Shichuan, and YANG Xiaoniu. Novel method for designing waveform with good correlation properties based on high-order norm unified representation[J]. IEEE Access, 2022, 10: 108440–108452. doi: 10.1109/ACCESS.2022.3213321. [18] BU Yi, YANG Jing, YU Xianxiang, et al. Fast optimization for unimodular sequences design with good correlation properties[C]. 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 2020: 1–6. doi: 10.1109/RadarConf2043947.2020.9266632. [19] HAIMOVICH A M, BLUM R S, and CIMINI L J. MIMO radar with widely separated antennas[J]. IEEE Signal Processing Magazine, 2008, 25(1): 116–129. doi: 10.1109/MSP.2008.4408448. [20] HUANG C W, CHEN Lifu, and SU B. Waveform design for optimal PSL under spectral and unimodular constraints via alternating minimization[J]. IEEE Transactions on Signal Processing, 2023, 71: 2518–2531. doi: 10.1109/TSP.2023.3291454. [21] CHEN Zihao, LIANG Junli, WANG Tao, et al. Generalized MBI algorithm for designing sequence set and mismatched filter bank with ambiguity function constraints[J]. IEEE Transactions on Signal Processing, 2022, 70: 2918–2933. doi: 10.1109/TSP.2022.3181346. [22] WANG Fulai, YIN Jiapeng, PANG Chen, et al. A unified framework of Doppler resilient sequences design for simultaneous polarimetric radars[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5109615. doi: 10.1109/TGRS.2022.3144385. [23] RAEI E, ALAEE-KERAHROODI M, SHANKAR B, et al. Range-ISL minimization and spectral shaping in MIMO radar systems via waveform design[C]. ICASSP 2023 - 2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 2023: 1–5. doi: 10.1109/ICASSP49357.2023.10096518. [24] QIANG Xiaomin, XU Jiacen, REN Lixiang, et al. Joint design of mismatched filter and phase coded waveform via mainlobe broadening[C]. 2023 8th International Conference on Signal and Image Processing (ICSIP), Wuxi, China, 2023: 1004–1008. doi: 10.1109/ICSIP57908.2023.10270925. [25] CUI Guolong, FU Yue, YU Xianxiang, et al. Local ambiguity function shaping via unimodular sequence design[J]. IEEE Signal Processing Letters, 2017, 24(7): 977–981. doi: 10.1109/LSP.2017.2700396. [26] ALAEE-KERAHROODI M, MODARRES-HASHEMI M, and NAGHSH M M. Designing sets of binary sequences for MIMO radar systems[J]. IEEE Transactions on Signal Processing, 2019, 67(13): 3347–3360. doi: 10.1109/TSP.2019.2914878. [27] WANG Fulai, XIA Xianggen, PANG Chen, et al. Joint design methods of unimodular sequences and receiving filters with good correlation properties and Doppler tolerance[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5100214. doi: 10.1109/TGRS.2022.3233094. [28] RABASTE O and SAVY L. Mismatched filter optimization for radar applications using quadratically constrained quadratic programs[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(4): 3107–3122. doi: 10.1109/TAES.2015.130769. [29] SOLTANALIAN M, TANG Bo, LI Jian, et al. Joint design of the receive filter and transmit sequence for active sensing[J]. IEEE Signal Processing Letters, 2013, 20(5): 423–426. doi: 10.1109/LSP.2013.2250279. [30] STOICA P, HE Hao, and LI Jian. Optimization of the receive filter and transmit sequence for active sensing[J]. IEEE Transactions on Signal Processing, 2012, 60(4): 1730–1740. doi: 10.1109/TSP.2011.2179652. [31] ARLERY F, KASSAB R, TAN U, et al. Efficient gradient method for locally optimizing the periodic/aperiodic ambiguity function[C]. 2016 IEEE Radar Conference (RadarConf), Philadelphia, USA, 2016: 1–6. doi: 10.1109/RADAR.2016.7485309. [32] CHEN Bilian, HE Simai, LI Zhening, et al. Maximum block improvement and polynomial optimization[J]. SIAM Journal on Optimization, 2012, 22(1): 87–107. doi: 10.1137/110834524. [33] BOYD S and VANDENBERGHE L. Convex Optimization[M]. Cambridge, UK: Cambridge University Press, 2004. [34] 万环, 余显祥, 全智, 等. 基于交替方向惩罚法的低精度量化MIMO雷达恒模波形设计方法[J]. 雷达学报, 2022, 11(4): 557–569. doi: 10.12000/JR22072.WAN Huan, YU Xianxiang, QUAN Zhi, et al. Constant modulus waveform design for low-resolution quantization MIMO radar based on an alternating direction penalty method[J]. Journal of Radars, 2022, 11(4): 557–569. doi: 10.12000/JR22072. [35] YU Xianxiang, CUI Guolong, YANG Jing, et al. MIMO radar transmit–receive design for moving target detection in signal-dependent clutter[J]. IEEE Transactions on Vehicular Technology, 2020, 69(1): 522–536. doi: 10.1109/TVT.2019.2951399. [36] YU Xianxiang, CUI Guolong, YANG Jing, et al. Quadratic optimization for unimodular sequence design via an ADPM framework[J]. IEEE Transactions on Signal Processing, 2020, 68: 3619–3634. doi: 10.1109/TSP.2020.2998637. [37] GHADIMI E, TEIXEIRA A, SHAMES I, et al. Optimal parameter selection for the alternating direction method of multipliers (ADMM): Quadratic problems[J]. IEEE Transactions on Automatic Control, 2015, 60(3): 644–658. doi: 10.1109/TAC.2014.2354892. -





 下载:
下载:


 下载:
下载:
