低信噪比条件下目标螺旋桨参数估计方法

韩闯; 冷冰; 兰朝凤; 邢博闻

doi:10.11999/JEIT240790

低信噪比条件下目标螺旋桨参数估计方法

doi: 10.11999/JEIT240790 cstr: 32379.14.JEIT240790

韩闯¹,
冷冰¹,
兰朝凤¹,
邢博闻^2, ,

1.
哈尔滨理工大学测控技术与通信工程学院哈尔滨 150080
2.
上海海洋大学工程学院上海 201306

基金项目: 国家自然科学基金(11804068)，黑龙江省自然科学基金(LH2020F033)，黑龙江省省属本科高校优秀青年教师基础研究支持计划(YQJH2024077)

详细信息

作者简介:
韩闯：男，副教授，研究方向为水下目标识别、水声信号处理

冷冰：男，硕士生，研究方向为水声信号处理

兰朝凤：女，副教授，研究方向为语音信号处理与分析、水声信号处理

邢博闻：男，副教授，研究方向为水声信号处理、海洋环境监测

通讯作者:
邢博闻　bwxing@shou.edu.cn

中图分类号: TN911.23
计量
- 文章访问数: 66
- HTML全文浏览量: 31
- PDF下载量: 12
- 被引次数: 0
出版历程
- 收稿日期: 2024-09-12
- 修回日期: 2025-06-06
- 网络出版日期: 2025-06-24

Estimation Method of Target Propeller Parameters under Low Signal-to-noise Ratio

1.
School of Measurement and Control Technology and Communication Engineering, Harbin University of Science and Technology, Harbin 150080, China
2.
College of Engineering Science and Technology, Shanghai Ocean University, Shanghai 201306, China

Funds: The National Natural Science Foundation of China (11804068), The Natural Science Foundation of Heilongjiang Province (LH2020F033), Heilongjiang Provincial Undergraduate Colleges and Universities Outstanding Young Teachers Basic Research Support Program (YQJH2024077)

摘要

摘要: 螺旋桨广泛应用于各类航空与航海设备中，如无人机、直升机以及水下舰船，尤其在水下目标探测中，目标的螺旋桨能提供丰富的特征信息。螺旋桨的微动产生的微多普勒频率能够反映其结构和动态行为，成为识别海洋目标的重要指标。准确识别水下目标螺旋桨的参数，如桨叶数目、桨叶长度以及转速等，对于目标的身份识别具有重要意义。然而，水下探测环境复杂多变，杂波干扰成为常态，对微动特征精准提取构成了挑战，尤其是强杂波背景下，信号处理的难度显著增加。以水下目标螺旋桨参数识别为例，该文针对低信噪比条件下螺旋桨参数估计的挑战，提出一种基于复数域变分模态分解(CVMD)和正交匹配追踪(OMP)算法的新方法。首先分析了螺旋桨回波信号的复杂特性，探讨了传统方法在噪声环境下的局限性。随后，引入CVMD算法对信号进行分解和去噪处理，有效提高了信号的分离能力和抗噪声能力。通过时频分析获取目标闪烁参数，并将其作为先验信息对稀疏字典进行降维处理，降低正交匹配追踪算法的运算量，提高了微动特征参数的估计精度，利用OMP算法，精确提取了螺旋桨的微多普勒特征，实验结果验证了方法的有效性和稳定性。最后，比较了CVMD-OMP方法与传统方法在不同信噪比条件下的性能表现，展示了其在水下声学目标识别中的应用潜力和优势。
- 微多普勒 /
- 信号去噪 /
- 特征提取 /
- 复数域变分模态分解 /
- 正交匹配追踪
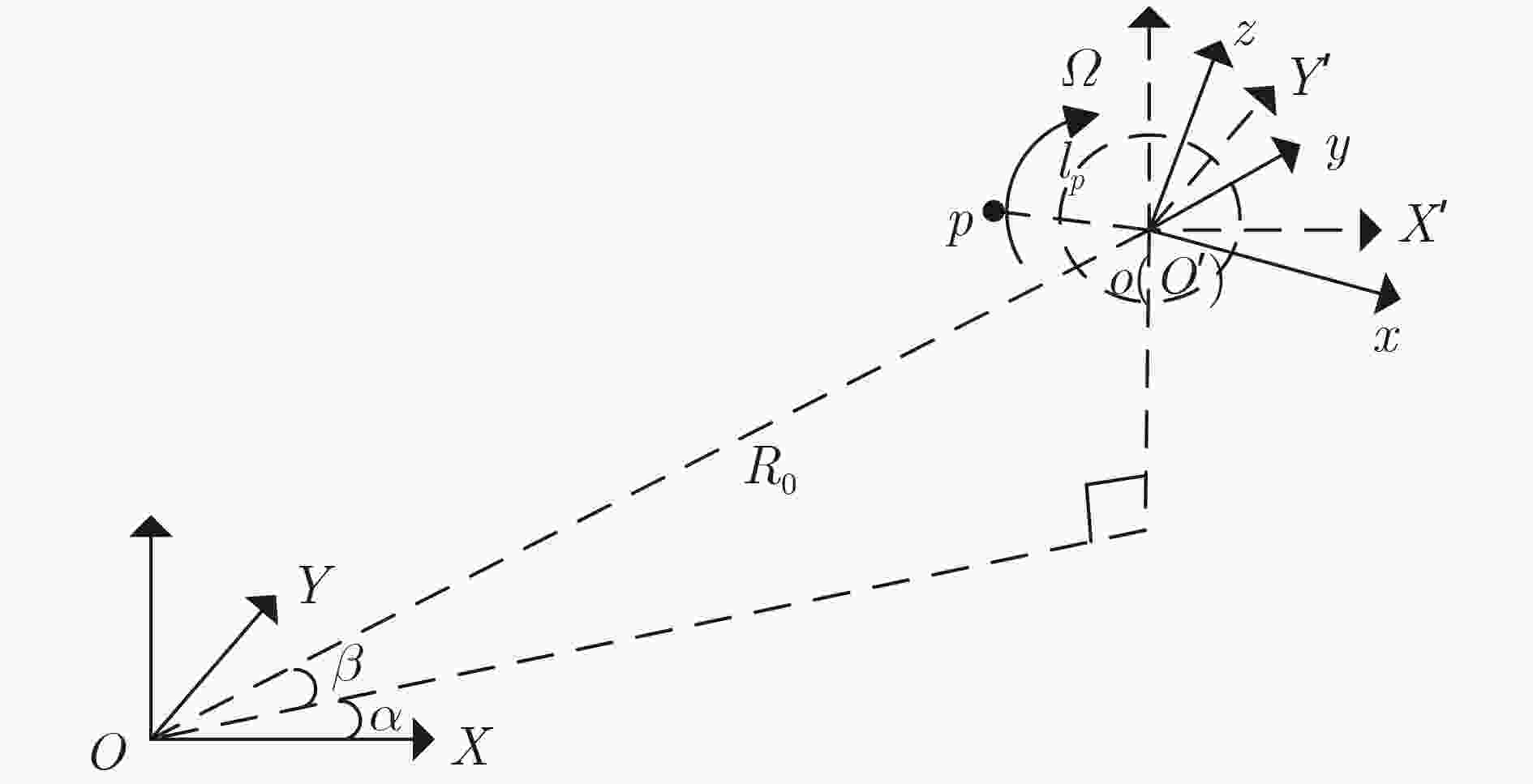
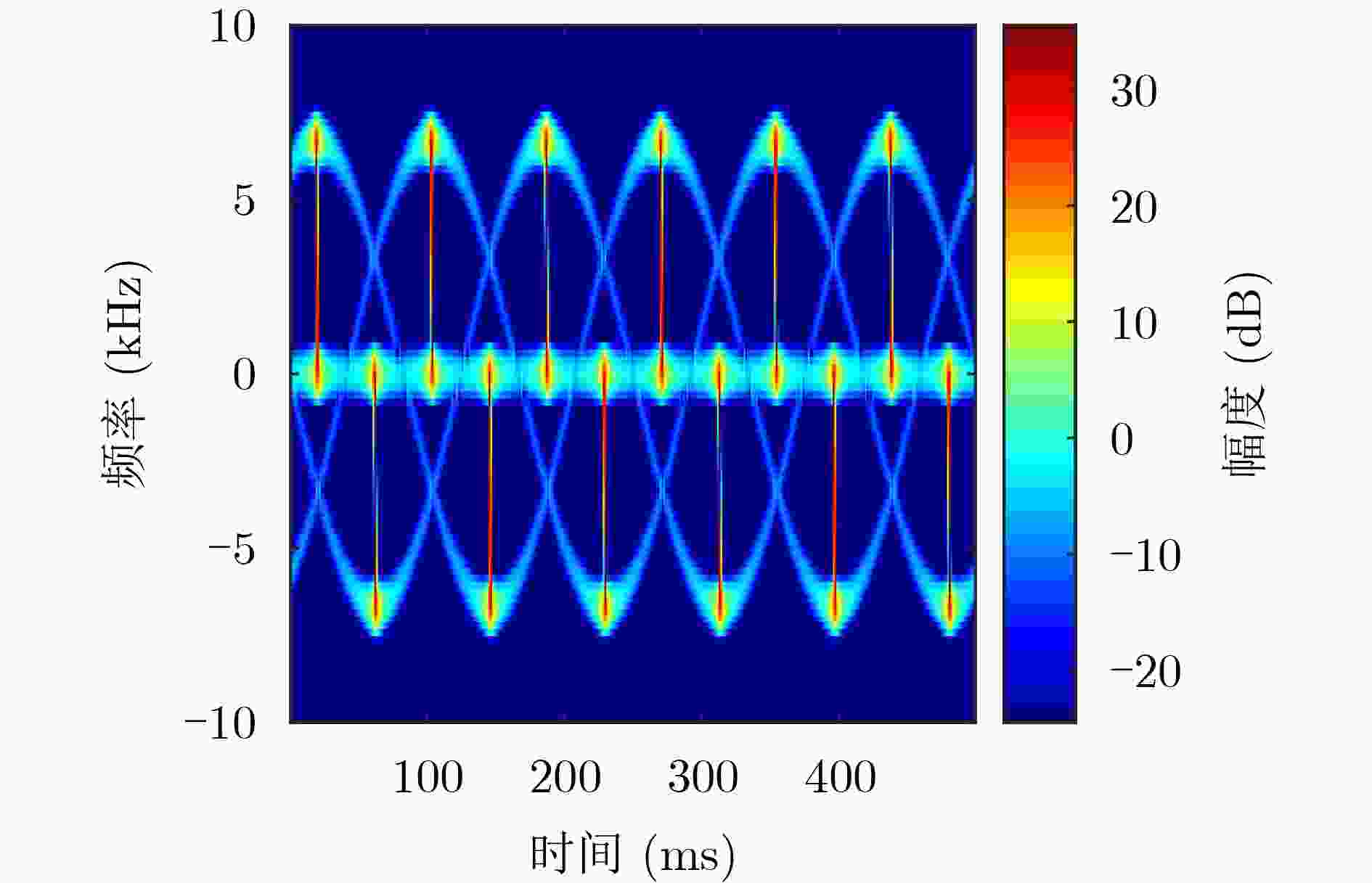
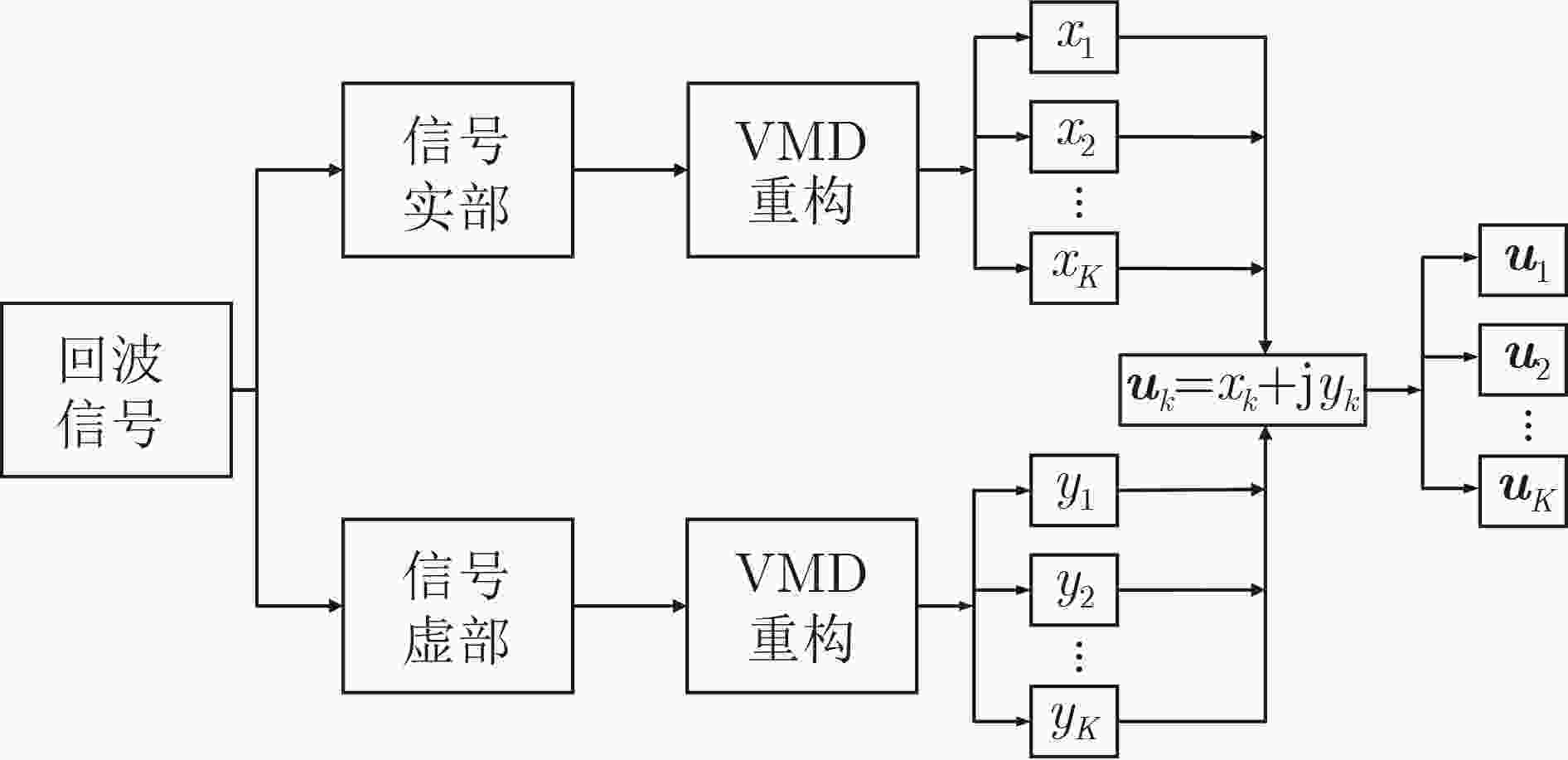
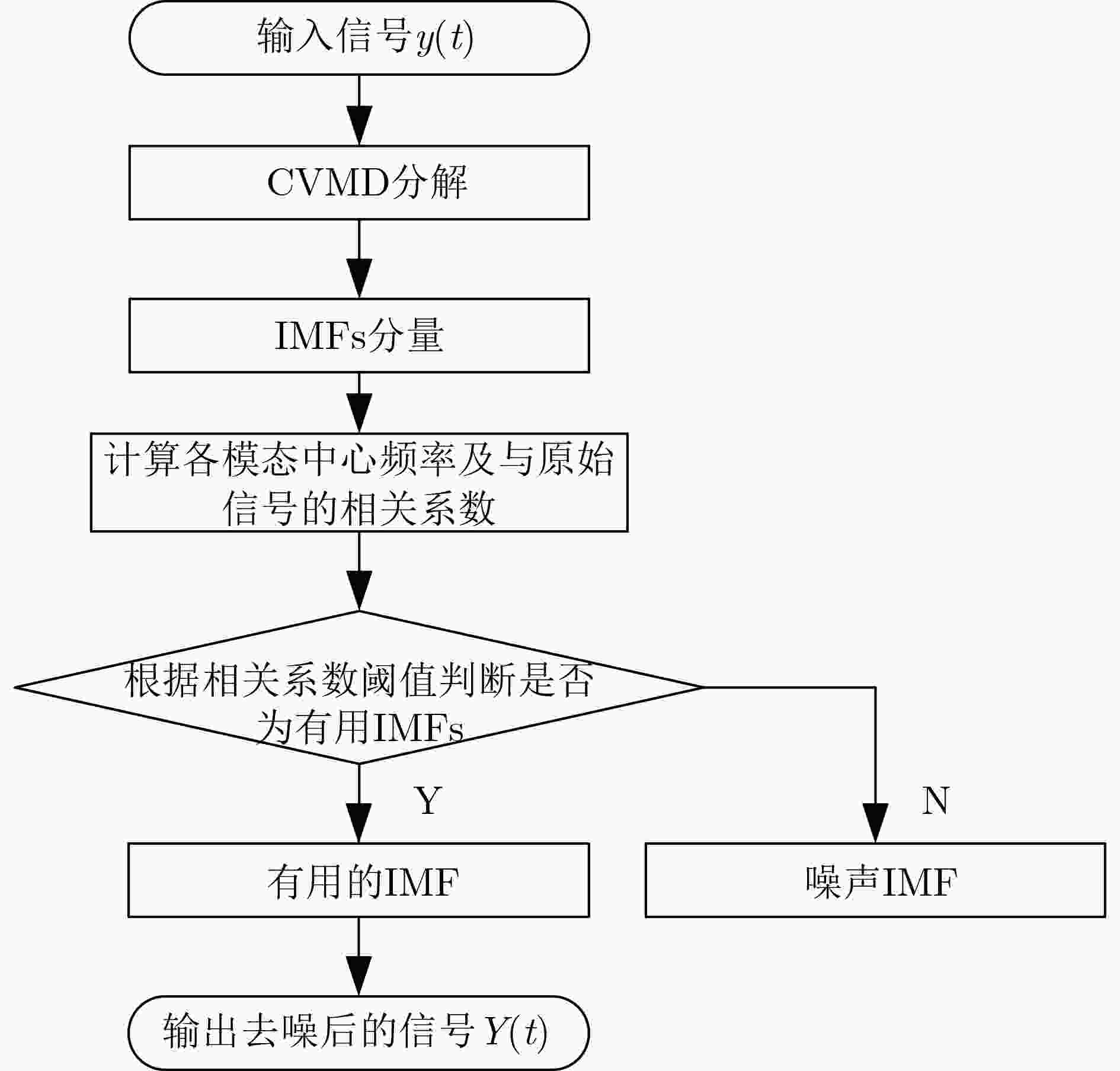
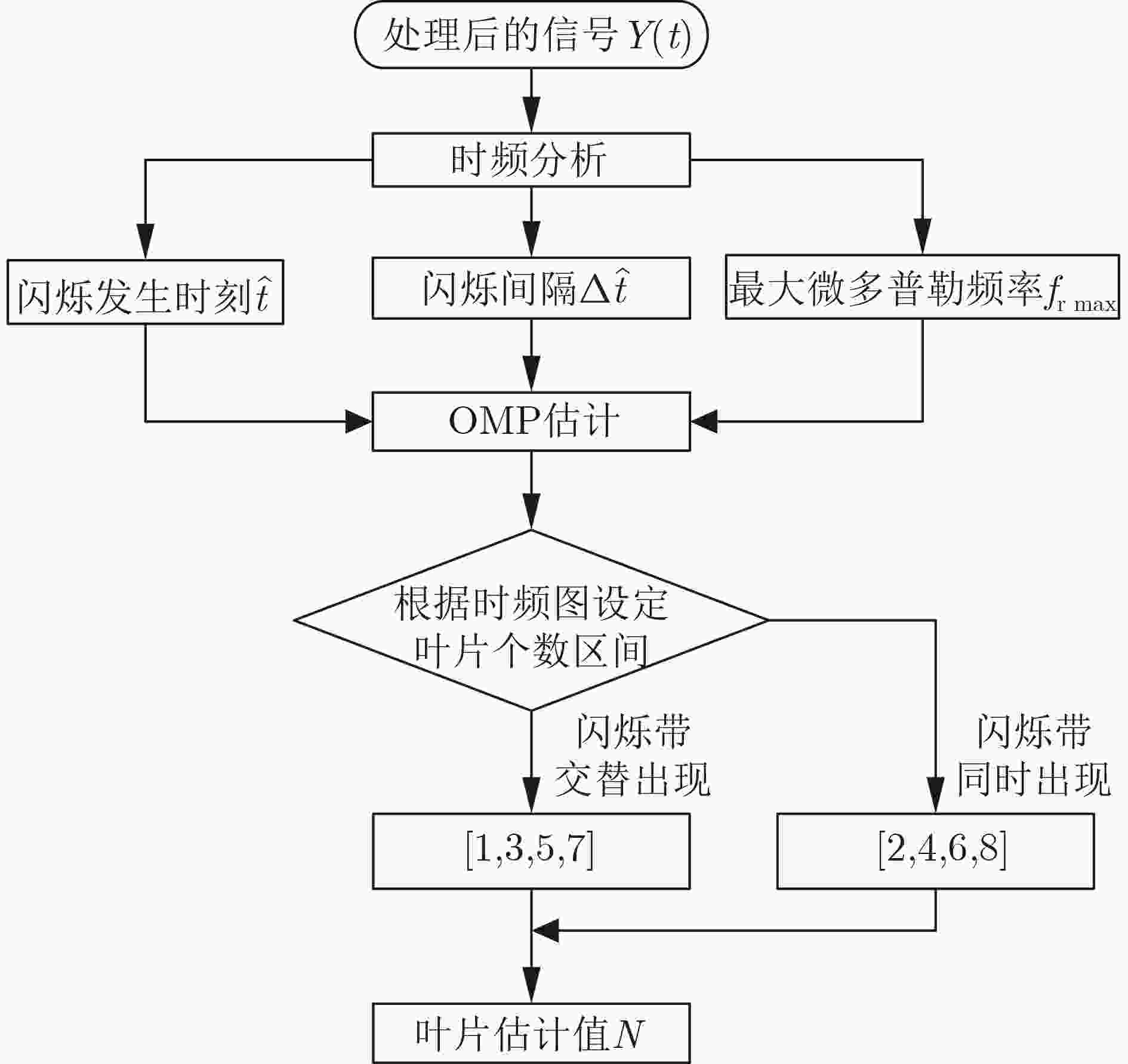
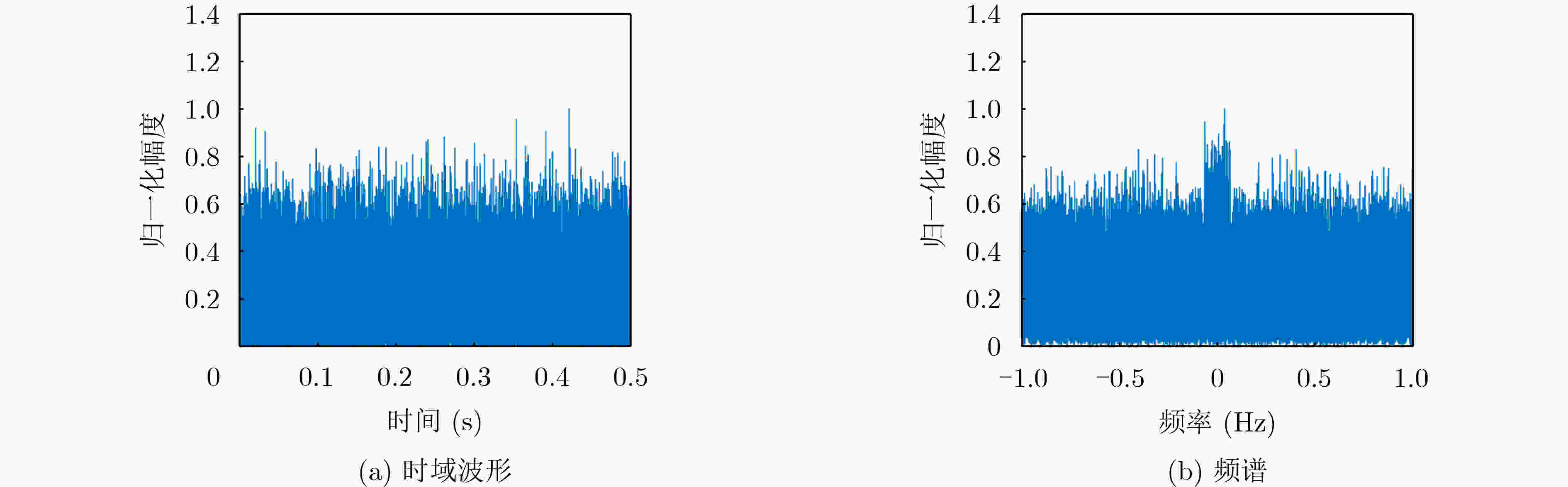
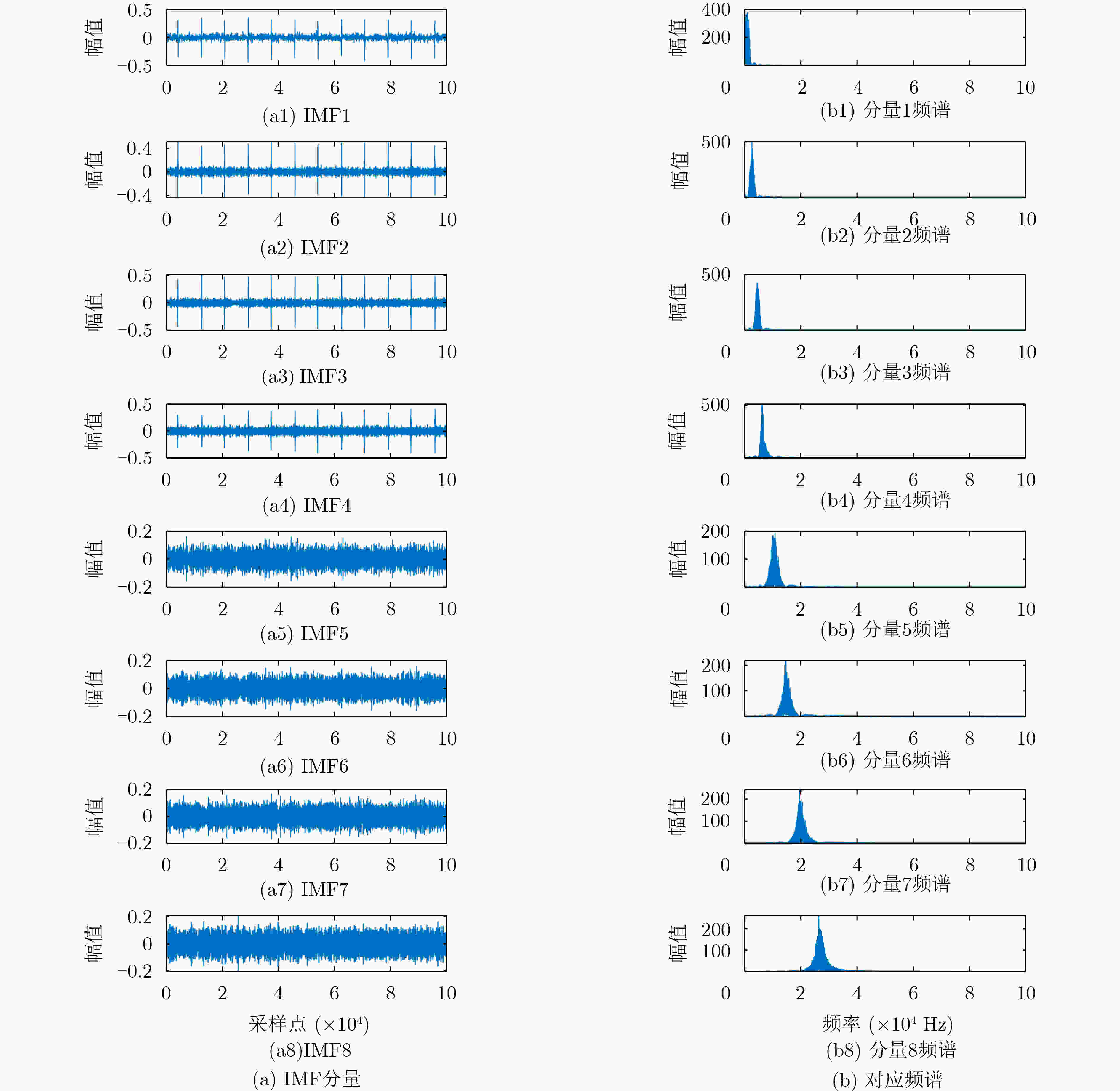
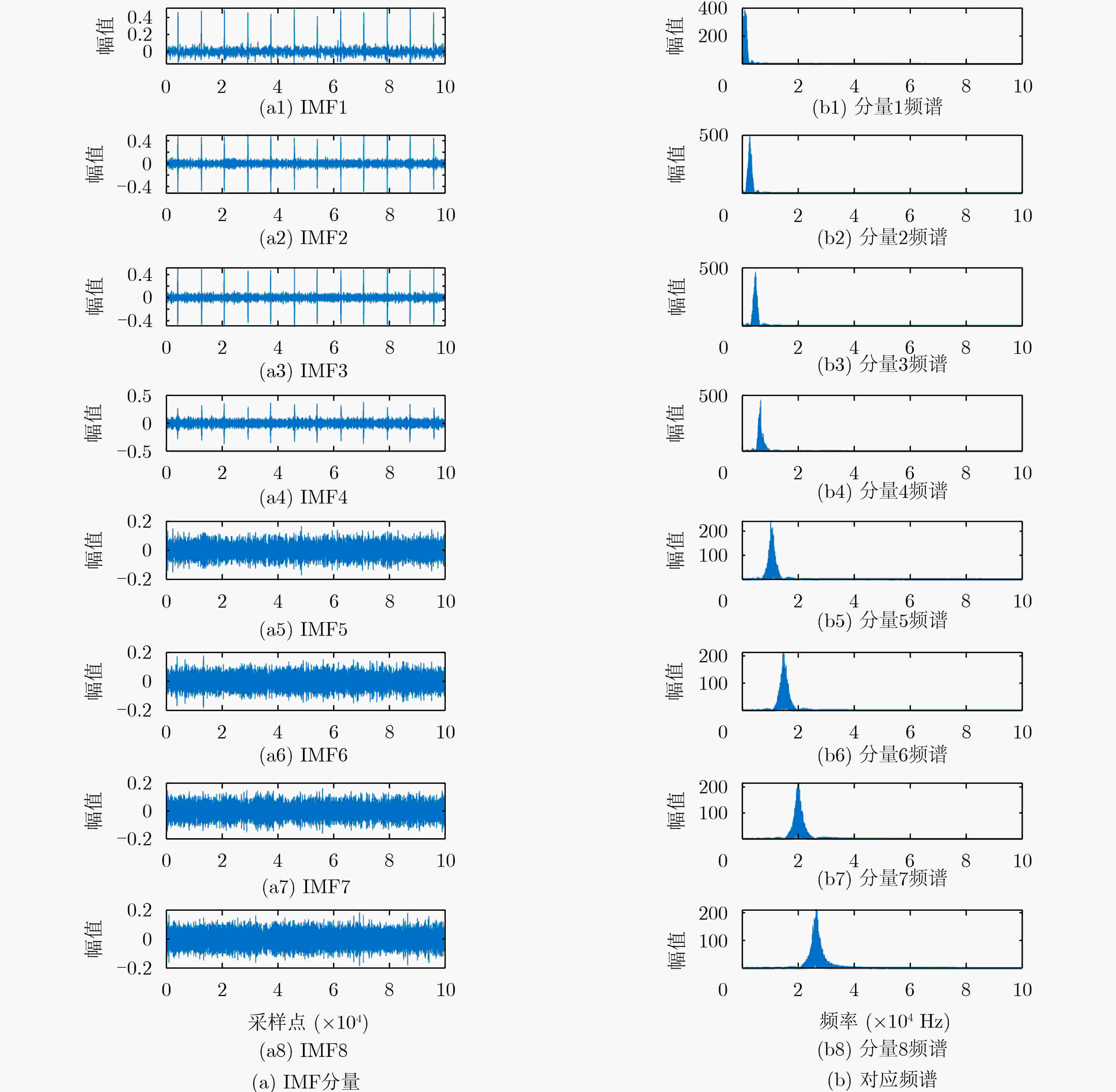
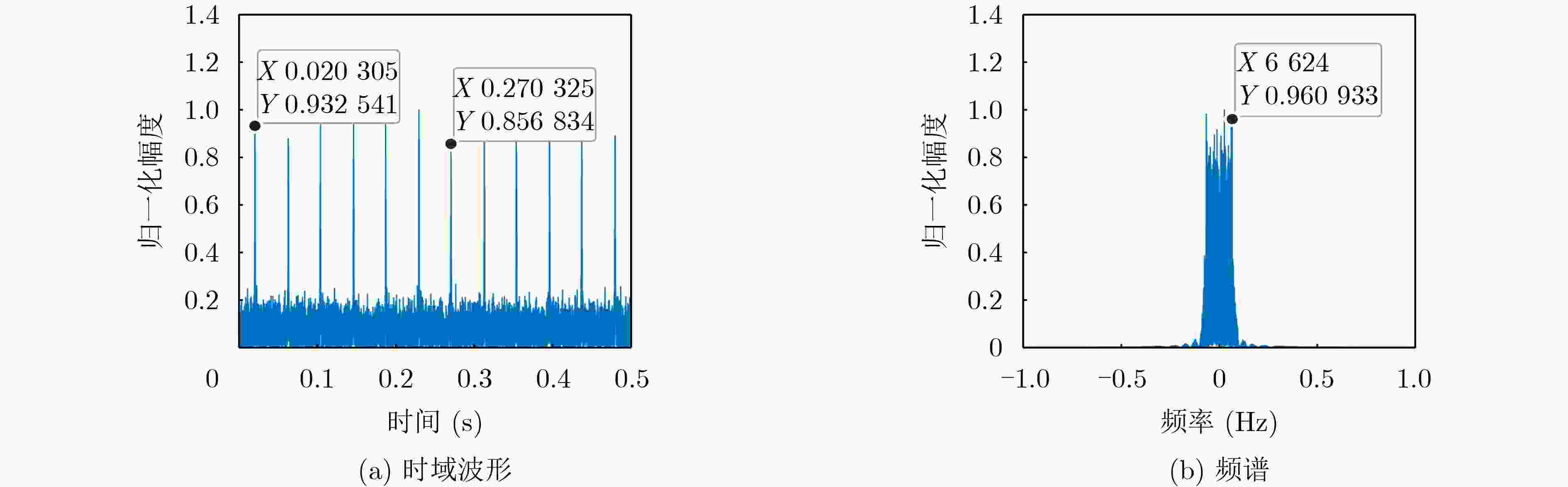
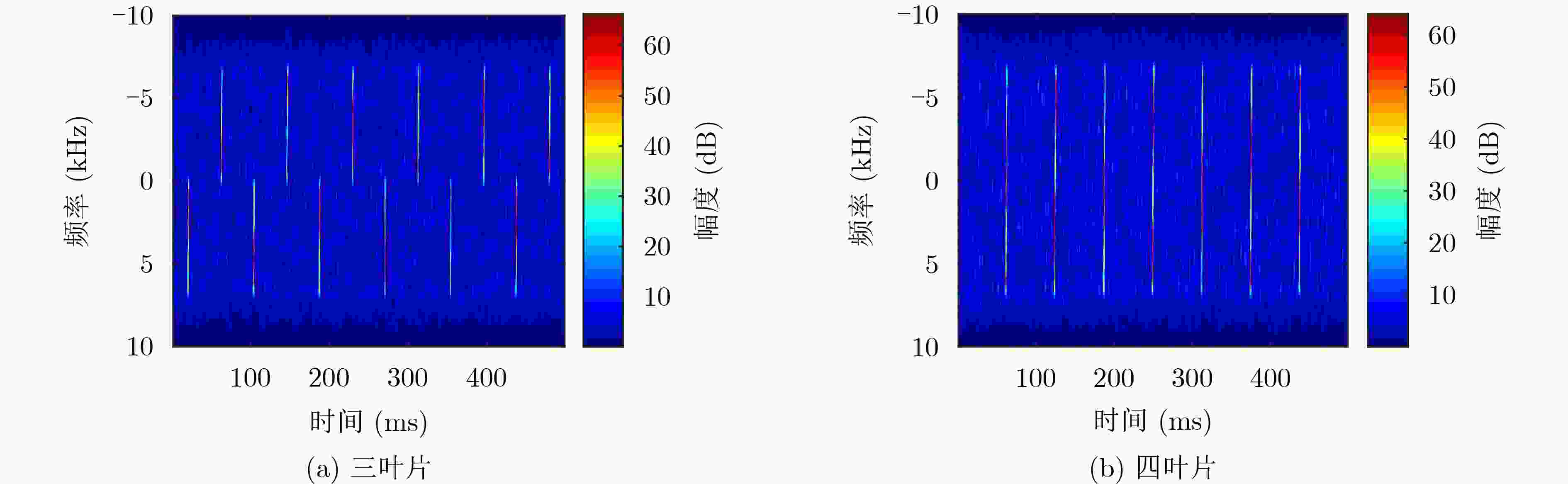
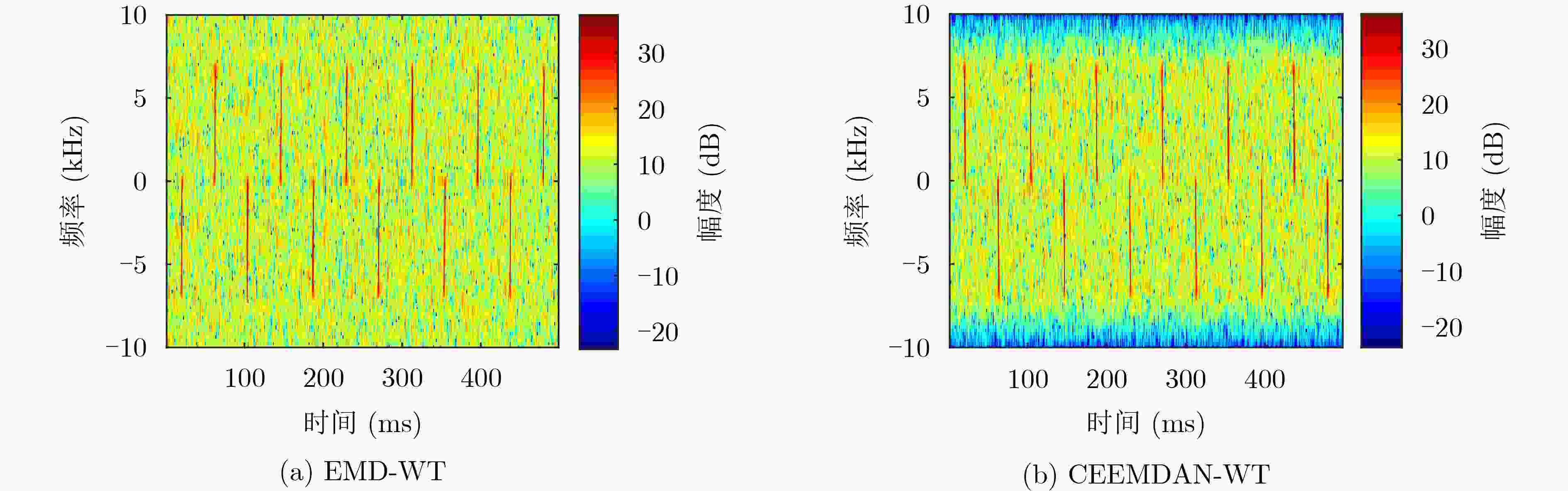
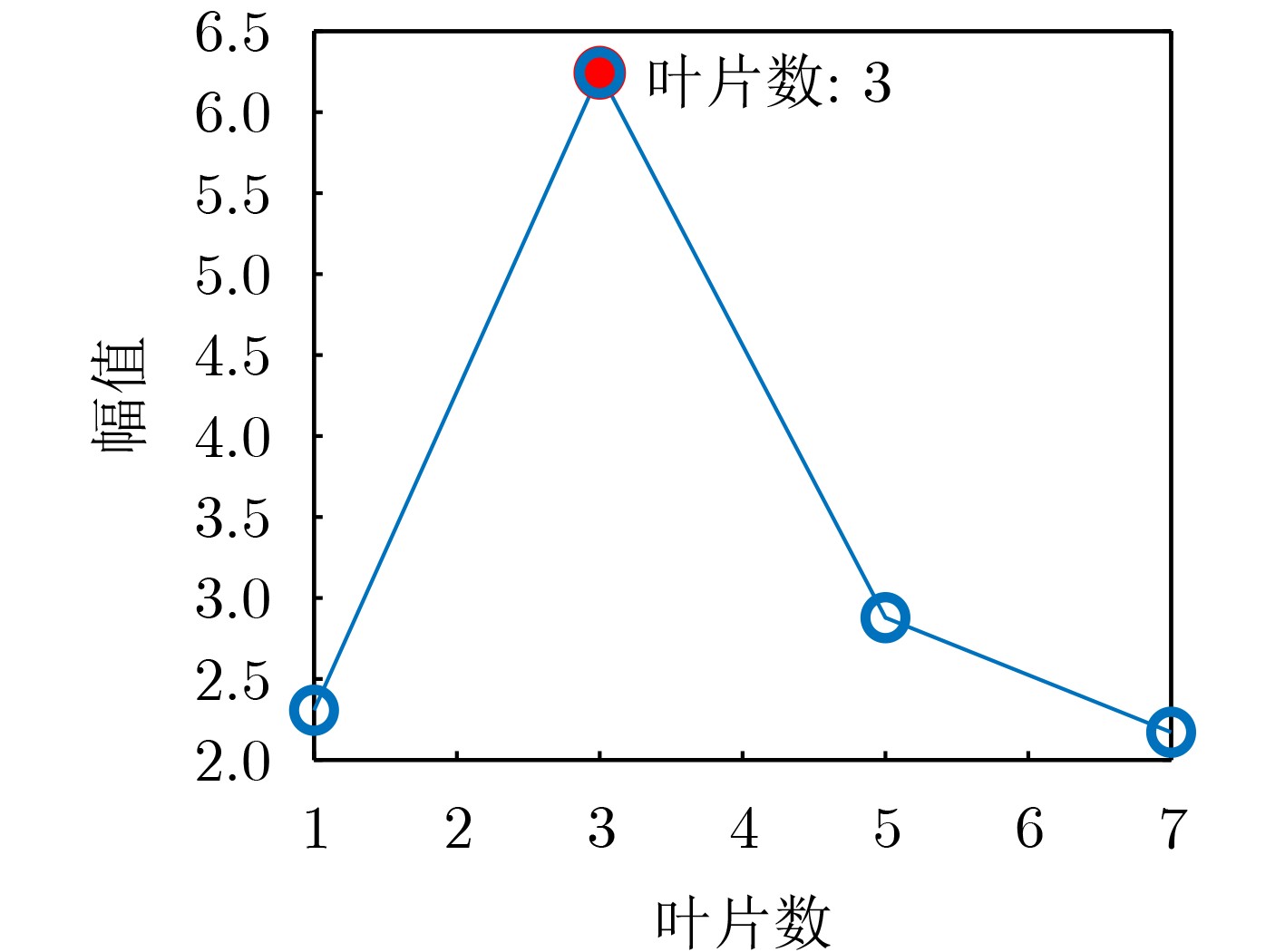
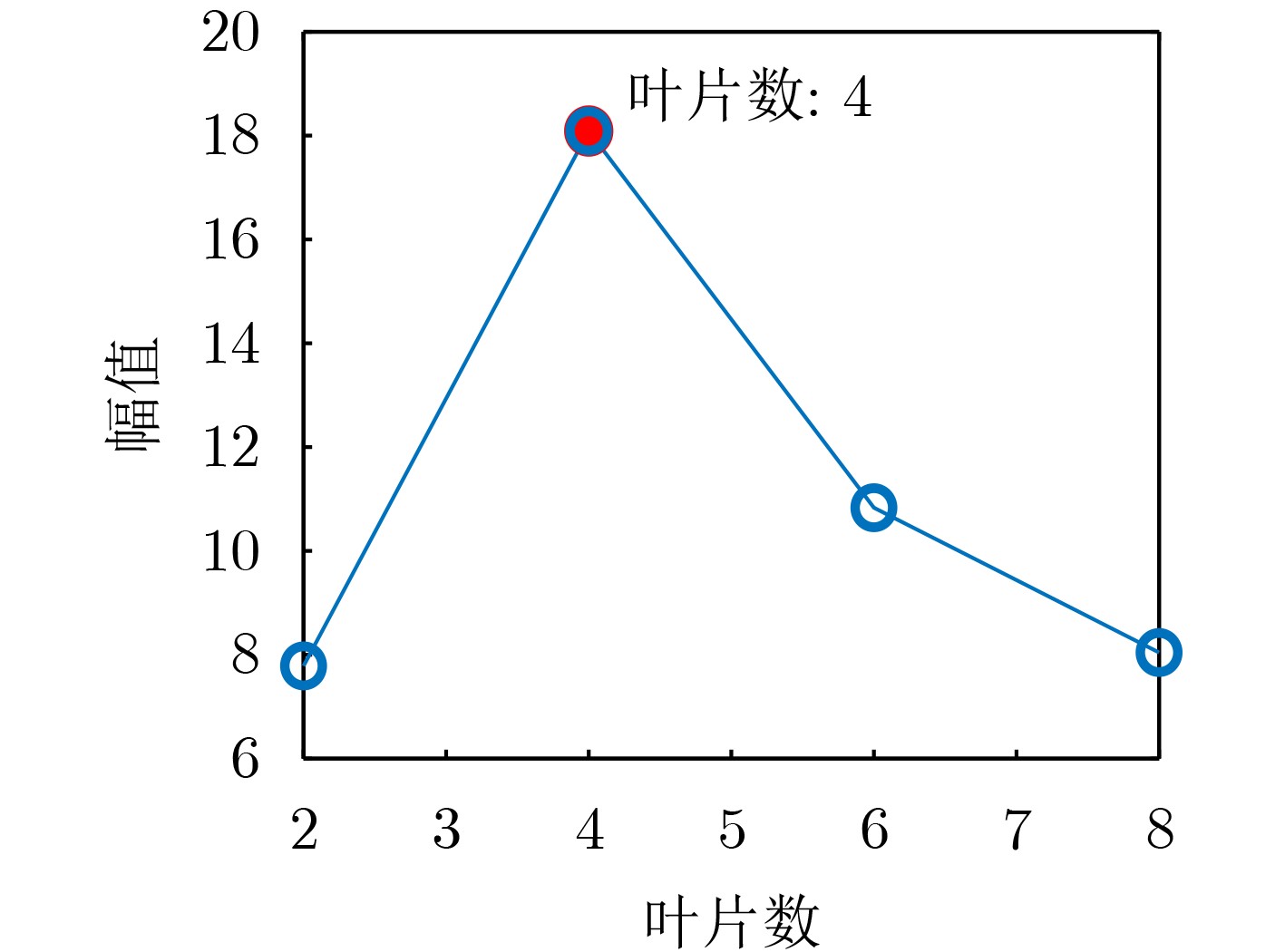
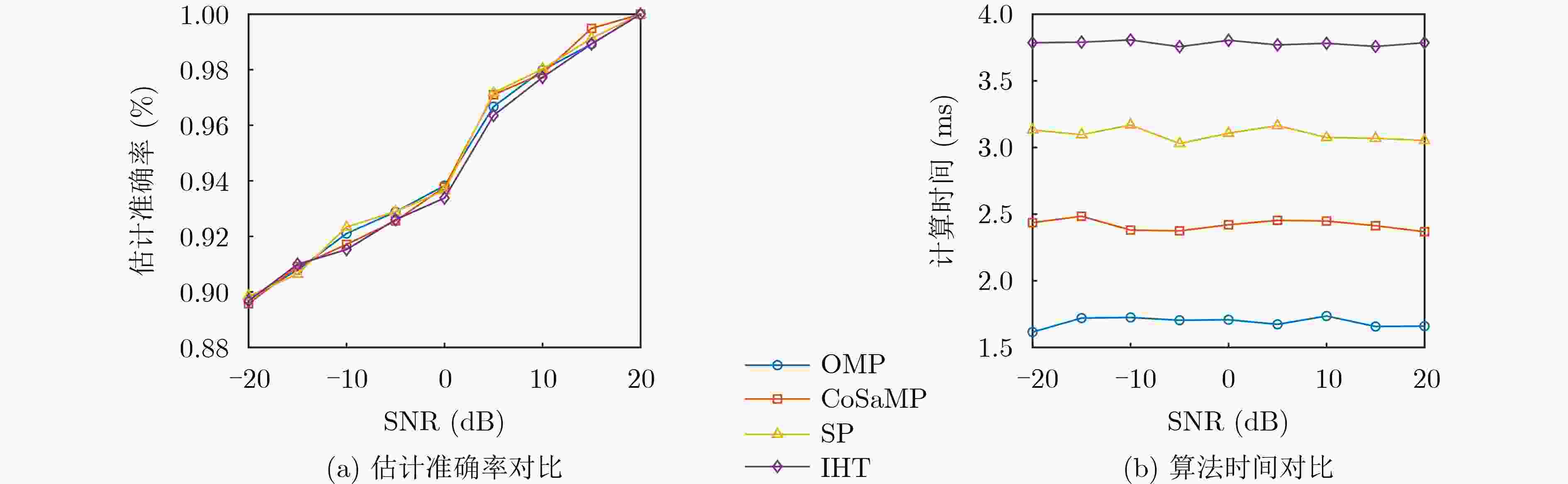
Abstract: Objective Accurate estimation of underwater propeller parameters—such as blade number, blade length, and rotational speed—is critical for target identification in marine environments. However, low Signal-to-Noise Ratio (SNR) conditions, caused by complex underwater clutter and ambient noise, substantially degrade the performance of conventional micro-Doppler feature extraction methods. Existing approaches, including Fourier Transform (FT), wavelet analysis, and Hilbert-Huang Transform (HHT), are limited in handling non-stationary signals and are highly susceptible to noise, leading to unreliable parameter estimation. To address these limitations, this study proposes a method that integrates Complex Variational Mode Decomposition (CVMD) for signal denoising with Orthogonal Matching Pursuit (OMP) for sparse parameter estimation. The combined approach improves robustness against noise while maintaining computational efficiency. This method contributes to advancing underwater acoustic target recognition in interference-rich environments and offers a theoretical basis for improving the reliability of marine detection systems. Methods The proposed method integrates CVMD and OMP to improve the estimation of propeller parameters in low-SNR environments. The approach consists of three sequential phases: signal decomposition and denoising, time-frequency feature extraction, and sparse parameter estimation. This structure enhances robustness to noise while maintaining computational efficiency. CVMD extends conventional Variational Mode Decomposition (VMD) to the complex domain, enabling adaptive decomposition of propeller echo signals into Intrinsic Mode Functions (IMFs) with preserved spectral symmetry. Unlike standard VMD, which cannot process complex-valued signals directly, CVMD treats the real and imaginary parts of the noisy signal separately. The decomposition is formulated as a constrained optimization problem, where IMFs are iteratively extracted by minimizing the total bandwidth of all modes. A correlation-based thresholding scheme is then used to identify and discard noise-dominated IMFs. The remaining signal-related IMFs are reconstructed to obtain a denoised signal, effectively isolating micro-Doppler features from background clutter. Time-frequency analysis is subsequently applied to the denoised signal to extract key scintillation parameters, including blade parity, scintillation intervals, and the maximum instantaneous micro-Doppler frequency. These parameters are used as prior information to constrain the parameter search space and reduce computational burden. Blade parity, inferred from the symmetry of the time-frequency distribution, narrows the candidate blade number range by half. Scintillation intervals and frequency bounds are also used to define physical constraints for sparse estimation. A sparse dictionary is constructed using Sinusoidal Frequency-Modulated (SFM) atoms, each corresponding to a candidate blade number. The OMP algorithm iteratively selects the atom most correlated with the residual signal, updates the sparse coefficient vector, and refines the residual until convergence. Incorporating prior information into dictionary design significantly reduces its dimensionality, transforming a multi-parameter estimation problem into an efficient single-parameter search. This step allows precise estimation of the blade number with minimal computational cost. Once the blade number is determined, the blade length and rotational speed are derived analytically using the relationships between the micro-Doppler frequency, scintillation period, and geometric parameters of the propeller. Results and Discussions The proposed CVMD-OMP framework demonstrates robust performance in propeller parameter estimation under low-SNR conditions, as verified through comprehensive simulations. The denoising efficacy of CVMD is illustrated by the reconstruction of distinct time-frequency features from heavily noise-corrupted propeller echoes (Fig. 10). By decomposing the complex-valued signal into IMFs and retaining only signal-dominant components, CVMD achieves a 12.4 dB improvement in SNR and reduces the Mean Square Error (MSE) to 0.009 at SNR = −10 dB, outperforming conventional methods such as EMD-WT and CEEMDAN-WT (Table 3). Time-frequency analysis of the denoised signal reveals clear periodic scintillation patterns (Fig. 11), which enable accurate extraction of blade parity and scintillation intervals. Guided by these prior features, the OMP algorithm achieves 91.9% accuracy in blade number estimation at SNR = −10 dB (Table 4). Accuracy improves progressively with increasing SNR, reaching 98% at SNR = 10 dB, highlighting the method’s adaptability to varying noise levels. The sparse dictionary, refined through prior-informed dimensionality reduction, maintains high precision while minimizing computational complexity. Comparative evaluations confirm that OMP outperforms CoSaMP and Subspace Pursuit (SP) in both estimation accuracy and computational efficiency. The execution time is reduced to 1.73 ms for single-parameter estimation (Fig. 15, Table 5). Parameter estimation consistency is further validated through the calculation of blade length and rotational speed. At SNR = −10 dB, the Mean Absolute Error (MAE) for blade length is 0.021 m, and 0.31 rad/s for rotational speed (Table 6). Both errors decrease significantly with improved SNR, demonstrating the method’s robustness across diverse noise conditions. The framework remains stable in multi-blade configurations, with extracted time-frequency characteristics closely matching theoretical expectations (Figs. 2 and 3). The integration of CVMD and OMP effectively balances accuracy and computational efficiency under low-SNR conditions. By leveraging prior-informed dimensionality reduction, the framework achieves a 90% reduction in computational load relative to conventional techniques. Future research will extend this framework to multi-target environments and validate its performance using real-world underwater acoustic datasets. Conclusions This study addresses the challenge of estimating underwater propeller parameters under low SNR conditions by proposing a novel framework that integrates CVMD and OMP. CVMD demonstrates strong capability in suppressing noise while preserving key micro-Doppler features, allowing reliable extraction of target signatures from severely corrupted signals. By incorporating time-frequency characteristics as prior knowledge, OMP enables accurate and efficient blade number estimation, substantially reducing computational complexity. The proposed framework shows high adaptability to varying noise levels and propeller configurations, ensuring robust performance in complex underwater environments. Its balance between estimation accuracy and computational efficiency supports real-time application in acoustic target recognition. The consistency of results with theoretical models further supports the method’s physical interpretability and practical relevance. Future work will extend this approach to multi-target scenarios and validate its effectiveness using experimental acoustic datasets, advancing the deployment of model-driven methods in real-world marine detection systems.
- Micro-doppler /
- Signal denoising /
- Feature extraction /
- Complex Variational Mode Decomposition (CVMD) /
- Orthogonal Matching Pursuit(OMP)

HTML全文

图 1 声探测设备与螺旋桨的空间几何关系

下载: 全尺寸图片幻灯片

图 2 理想三叶片回波信号仿真结果图

下载: 全尺寸图片幻灯片

图 3 理想三叶片回波信号时频图

下载: 全尺寸图片幻灯片

图 4 回波信号CVMD重构基本流程

下载: 全尺寸图片幻灯片

图 5 CVMD实现带噪回波去噪流程图

下载: 全尺寸图片幻灯片

图 6 OMP估计叶片数流程图

下载: 全尺寸图片幻灯片

图 7 三叶片带噪信号仿真结果图

下载: 全尺寸图片幻灯片

图 8 带噪信号CVMD实部分解结果

下载: 全尺寸图片幻灯片

图 9 带噪信号CVMD虚部分解结果

下载: 全尺寸图片幻灯片

图 10 CVMD去噪后的信号波形和频谱

下载: 全尺寸图片幻灯片

图 11 CVMD处理后信号时频图

下载: 全尺寸图片幻灯片

图 12 CVMD处理后信号时频图

下载: 全尺寸图片幻灯片

图 13 奇数叶片OMP估计结果

下载: 全尺寸图片幻灯片

图 14 偶数叶片OMP估计结果

下载: 全尺寸图片幻灯片

图 15 估计算法的性能与效率对比

下载: 全尺寸图片幻灯片

表 1 每个模态的相关系数

	IMF1	IMF2	IMF3	IMF4	IMF5	IMF6	IMF7	IMF8
实部相关系数	0.437 5	0.477 7	0.464 4	0.285 3	0.009 2	0.003 1	0.001 4	0.000 7
虚部相关系数	0.435 4	0.472 9	0.465 9	0.309 6	0.009 4	0.003 2	0.001 5	0.000 7

下载: 导出CSV

表 2 CVMD去噪效果指标

	SNR(dB)	MSE	NCC	SNR(dB)	MSE	NCC
去噪前	–10.401 1	0.143 0	0.299 3	–8.648 2	0.090 3	0.373 8
去噪后	1.757 3	0.009 9	0.748 6	3.830 8	0.005 9	0.827 7
去噪前	–6.184 9	0.045 2	0.489 0	–3.021 8	0.014 4	0.705 8
去噪后	5.540 8	0.003 9	0.855 5	5.985 9	0.003 6	0.864 8

下载: 导出CSV

表 3 不同去噪方法指标对比

分解方法	ΔSNR(dB)	MSE	NCC
EMD-WT	3.2	0.032	0.65
CCEMDAN-WT	5.1	0.021	0.73
CVMD	12.4	0.009	0.85

下载: 导出CSV

表 4 不同信噪比下叶片数估计准确率(%)

SNR (dB)	OMP	CoSaMP	SP	IHT
–10	91.9	92.2	91.8	91.6
–5	92.5	93.1	92.9	92.8
0	94.4	94.0	94.1	94.4
5	96.2	96.7	96.8	96.4
10	98.0	97.6	97.5	98.0

下载: 导出CSV

表 5 不同信噪比下单次估计耗时(ms)

SNR (dB)	OMP	CoSaMP	SP	IHT
–10	1.73	2.30	3.10	3.83
–5	1.82	2.37	3.07	3.88
0	1.66	2.31	3.11	3.79
5	1.70	2.44	3.06	3.69
10	1.69	2.35	3.12	3.75

下载: 导出CSV

表 6 不同信噪比下螺旋桨参数的估计结果

SNR(dB)	桨叶数估计准确率(%)	桨长MAE(m)	转速MAE(r/s)
–10	91.9	0.021	0.31
–5	92.5	0.015	0.23
0	94.4	0.010	0.18
5	96.2	0.008	0.11
10	98.0	0.004	0.07

下载: 导出CSV

参考文献(23)

[1]	CHEN V C, LI F, HO S S, et al. Micro-Doppler effect in radar: Phenomenon, model, and simulation study[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(1): 2–21. doi: 10.1109/TAES.2006.1603402.
[2]	CHEN V C. The Micro-Doppler Effect in Radar[M]. Boston: Artech House, 2011: 5–25.
[3]	CHEN V C, TAHMOUSH D, and MICELI W J. Radar Micro-Doppler Signature: Processing and Applications[M]. UK: The Institution of Engineering and Technology, 2014: 187–227.
[4]	TAHMOUSH D. Review of micro-Doppler signatures[J]. IET Radar, Sonar & Navigation, 2015, 9(9): 1140–1146. doi: 10.1049/iet-rsn.2015.0118.
[5]	LI Yuxing and WANG Long. A novel noise reduction technique for underwater acoustic signals based on complete ensemble empirical mode decomposition with adaptive noise, minimum mean square variance criterion and least mean square adaptive filter[J]. Defence Technology, 2020, 16(3): 543–554. doi: 10.1016/j.dt.2019.07.020.
[6]	HUANG N E and SHEN S S P. Hilbert-Huang Transform and its Applications[M]. Singapore: World Scientific Publishing, 1998: 1–202.
[7]	夏赛强, 向虎, 陈文峰, 等. 基于CEMD的旋翼微动目标杂波抑制方法[J]. 航空学报, 2018, 39(9): 322082. doi: 10.7527/S1000-6893.2018.22082. XIA Saiqiang, XIANG Hu, CHEN Wenfeng, et al. Clutter suppression method for rotor micro-motion target based on CEMD[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(9): 322082. doi: 10.7527/S1000-6893.2018.22082.
[8]	DRAGOMIRETSKIY K and ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531–544. doi: 10.1109/TSP.2013.2288675.
[9]	YANG Degui, LI Jin, LIANG Buge, et al. A multi-rotor drone micro-motion parameter estimation method based on CVMD and SVD[J]. Remote Sensing, 2022, 14(14): 3326. doi: 10.3390/rs14143326.
[10]	李中余, 桂亮, 海宇, 等. 基于变分模态分解与优选的超高分辨ISAR成像微多普勒抑制方法[J]. 雷达学报, 2024, 13(4): 852–865. doi: 10.12000/JR24043. LI Zhongyu, GUI Liang, HAI Yu, et al. Ultrahigh-resolution ISAR micro-Doppler suppression methodology based on variational mode decomposition and mode optimization[J]. Journal of Radars, 2024, 13(4): 852–865. doi: 10.12000/JR24043.
[11]	SAFFARI A, ZAHIRI S H, and KHISHE M. Automatic recognition of sonar targets using feature selection in micro-Doppler signature[J]. Defence Technology, 2023, 20: 58–71. doi: 10.1016/j.dt.2022.05.007.
[12]	周毅恒, 杨军, 夏赛强, 等. 闪烁现象下旋翼目标微动参数估计方法[J]. 系统工程与电子技术, 2022, 44(1): 54–63. doi: 10.12305/j.issn.1001-506X.2022.01.08. ZHOU Yiheng, YANG Jun, XIA Saiqiang, et al. Estimation method of micro-motion parameters for rotor targets under flashing[J]. Systems Engineering and Electronics, 2022, 44(1): 54–63. doi: 10.12305/j.issn.1001-506X.2022.01.08.
[13]	唐波, 谭思炜, 张静远. 水下声探测系统载体振动干扰分析及抑制方法[J]. 国防科技大学学报, 2022, 44(6): 89–94. doi: 10.11887/j.cn.202206011. TANG Bo, TAN Siwei, and ZHANG Jingyuan. Vibration interference analysis of underwater acoustic detection system and its suppressing method[J]. Journal of National University of Defense Technology, 2022, 44(6): 89–94. doi: 10.11887/j.cn.202206011.
[14]	周烨, 温玮, 韩建辉, 等. 基于声固耦合的水下复杂目标声散射研究[J]. 水下无人系统学报, 2020, 28(1): 51–56. doi: 10.11993/j.issn.2096-3920.2020.01.008. ZHOU Ye, WEN Wei, HAN Jianhui, et al. Research on acoustic scattering of underwater complicated target based on sound-solid coupling[J]. Journal of Unmanned Undersea Systems, 2020, 28(1): 51–56. doi: 10.11993/j.issn.2096-3920.2020.01.008.
[15]	张天翼. 基于微多普勒的窄带雷达目标分类系统设计[D]. [硕士论文], 哈尔滨工程大学, 2019. ZHANG Tianyi. Design of narrow-band radar target recognition air target classification system based on micro-Doppler[D]. [Master dissertation], Harbin Engineering University, 2019.
[16]	任科. 基于窄带雷达的目标微多普勒特征提取研究[D]. [博士论文], 西安电子科技大学, 2021. doi: 10.27389/d.cnki.gxadu.2021.003236. REN Ke. Study on micro-Doppler feature extraction of targets based on narrowband radar[D]. [Ph. D. dissertation], Xidian University, 2021. doi: 10.27389/d.cnki.gxadu.2021.003236.
[17]	TANG Bo, ZHANG Linsen, and TAN Siwei. Parameter estimation of underwater propeller based on inverse Radon transform[J]. Journal of Measurements in Engineering, 2022, 10(4): 179–187. doi: 10.21595/jme.2022.22781.
[18]	XIA Saiqiang, YANG Jun, CAI Wanyong, et al. Adaptive complex variational mode decomposition for micro-motion signal processing applications[J]. Sensors, 2021, 21(5): 1637. doi: 10.3390/s21051637.
[19]	CUI Xiaolong, HUANG Jie, LI Chaoshun, et al. Three-dimensional instantaneous orbit map for rotor-bearing system based on a novel multivariate complex variational mode decomposition algorithm[J]. Mechanical Systems and Signal Processing, 2022, 178: 109211. doi: 10.1016/j.ymssp.2022.109211.
[20]	TANAKA T and MANDIC D P. Complex empirical mode decomposition[J]. IEEE Signal Processing Letters, 2007, 14(2): 101–104. doi: 10.1109/LSP.2006.882107.
[21]	张朝伟, 夏赛强, 杨军, 等. 低信噪比条件下直升机微动特征提取方法[J]. 雷达科学与技术, 2021, 19(6): 689–696. doi: 10.3969/j.issn.1672-2337.2021.06.007. ZHANG Chaowei, XIA Saiqiang, YANG Jun, et al. An extraction method for helicopter micro-motion features under low SNR[J]. Radar Science and Technology, 2021, 19(6): 689–696. doi: 10.3969/j.issn.1672-2337.2021.06.007.
[22]	杜立彬, 王政凯, 吕志超, 等. 基于辐射噪声特征的舰船目标识别分类方法综述[J]. 数字海洋与水下攻防, 2023, 6(5): 613–621. doi: 10.19838/j.issn.2096-5753.2023.05.012. DU Libin, WANG Zhengkai, LYU Zhichao, et al. A review of ship target recognition and classification methods based on radiated noise features[J]. Digital Ocean & Underwater Warfare, 2023, 6(5): 613–621. doi: 10.19838/j.issn.2096-5753.2023.05.012.
[23]	施晶, 朱明, 沈华, 等. 基于VMD和小波阈值的水听器信号去噪方法[J]. 传感技术学报, 2020, 33(7): 1003–1012. doi: 10.3969/j.issn.1004-1699.2020.07.013. SHI Jing, ZHU Ming, SHEN Hua, et al. Denoising method of hydrophone signal based on VMD and wavelet threshold[J]. Chinese Journal of Sensors and Actuators, 2020, 33(7): 1003–1012. doi: 10.3969/j.issn.1004-1699.2020.07.013.