Joint Task Allocation, Communication Base Station Association and Flight Strategy Optimization Design for Distributed Sensing Unmanned Aerial Vehicles
-
摘要: 针对多无人机(UAV)分布式感知开展研究,为协调各UAV行为,该文设计了任务感知-数据回传协议,并建立了UAV任务分配、数据回传基站关联与飞行策略联合优化混合整数非线性规划问题模型。鉴于该问题数学结构的复杂性,以及集中式优化算法设计面临计算复杂度高且信息交互开销大等不足,提出将该问题转化为协作式马尔可夫博弈(MG),定义了基于成本-效用复合的收益函数。考虑到MG问题连续-离散动作空间复杂耦合特点,设计了基于独立学习者(IL)的复合动作表演评论家(MA-IL-CA2C)的MG问题求解算法。仿真分析结果表明,相对于基线算法,所提算法能显著提高系统收益并降低网络能耗。Abstract:
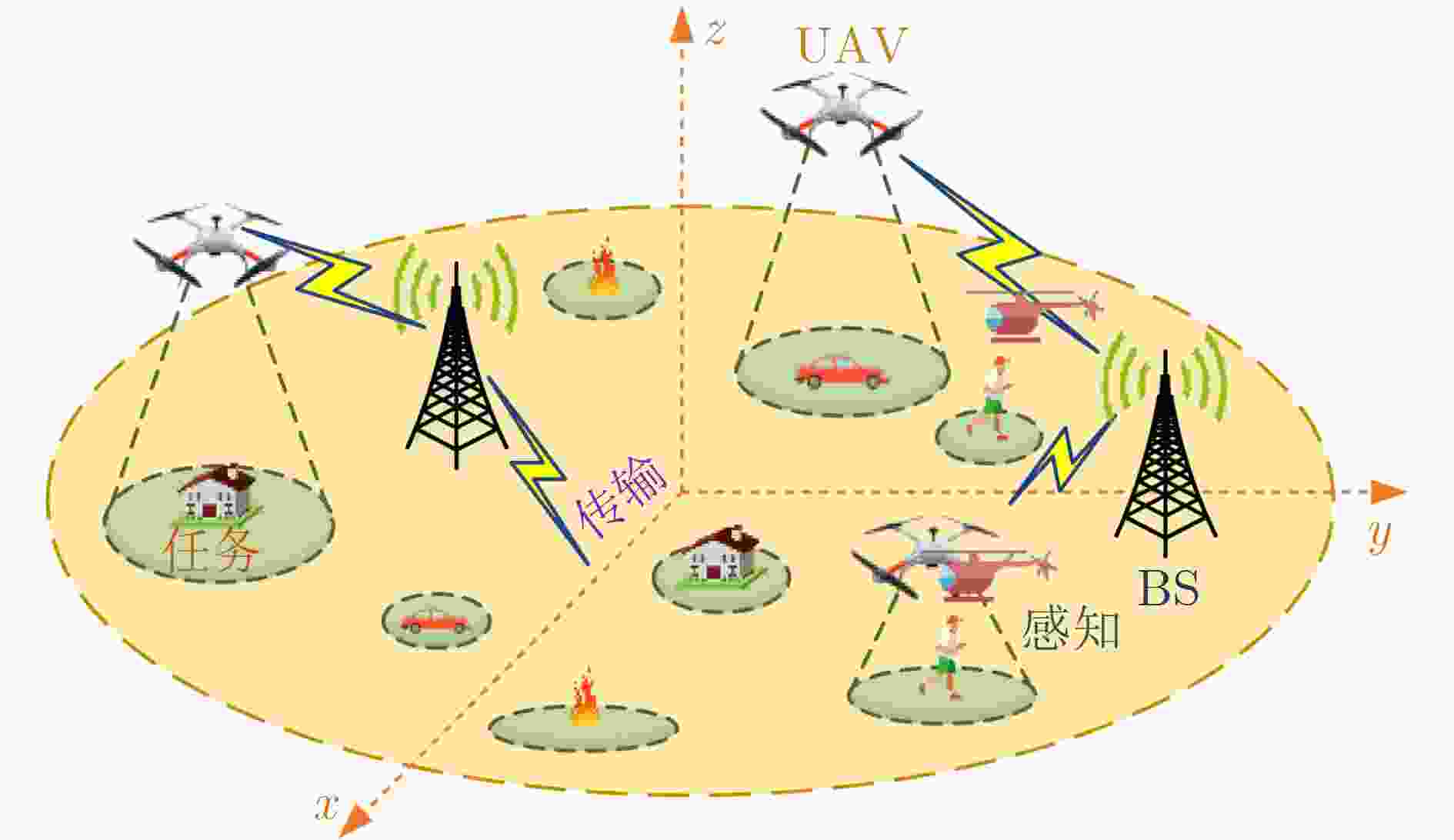
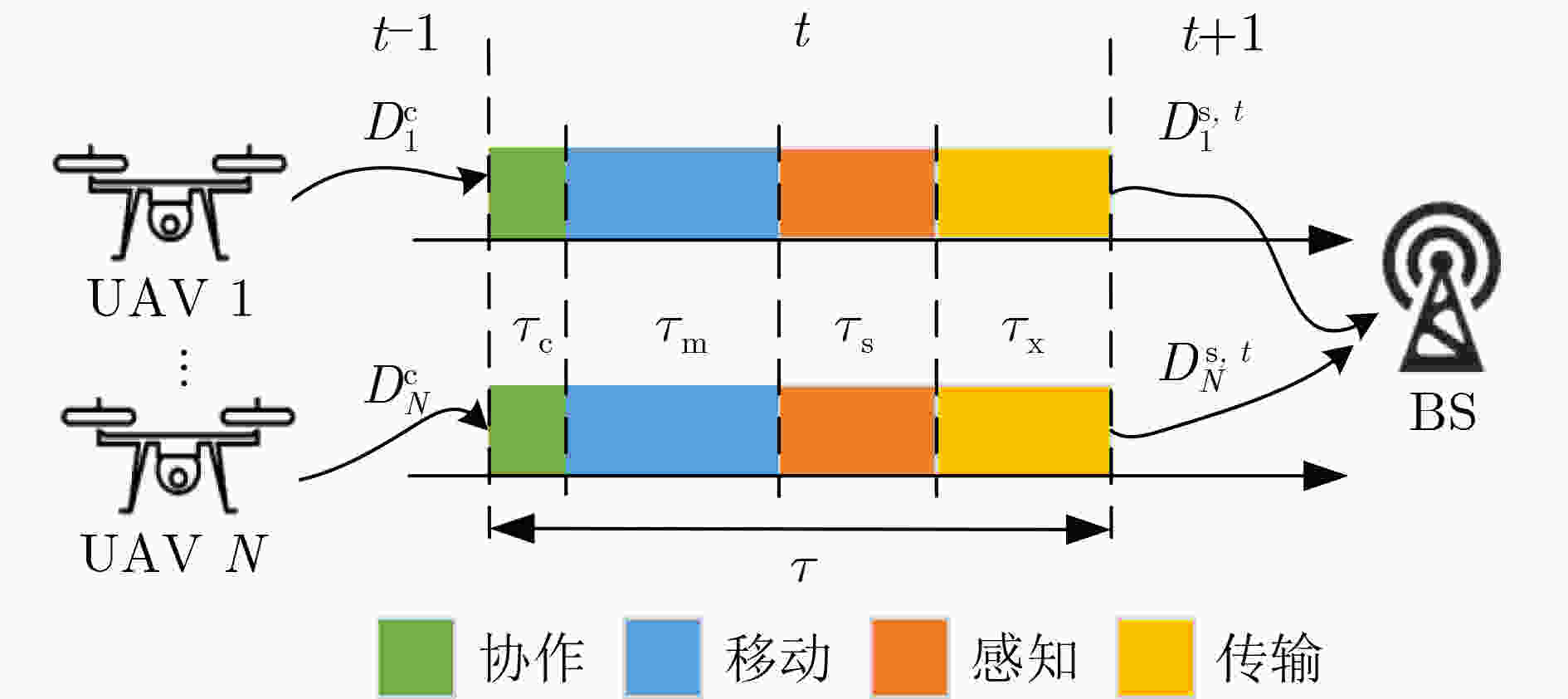
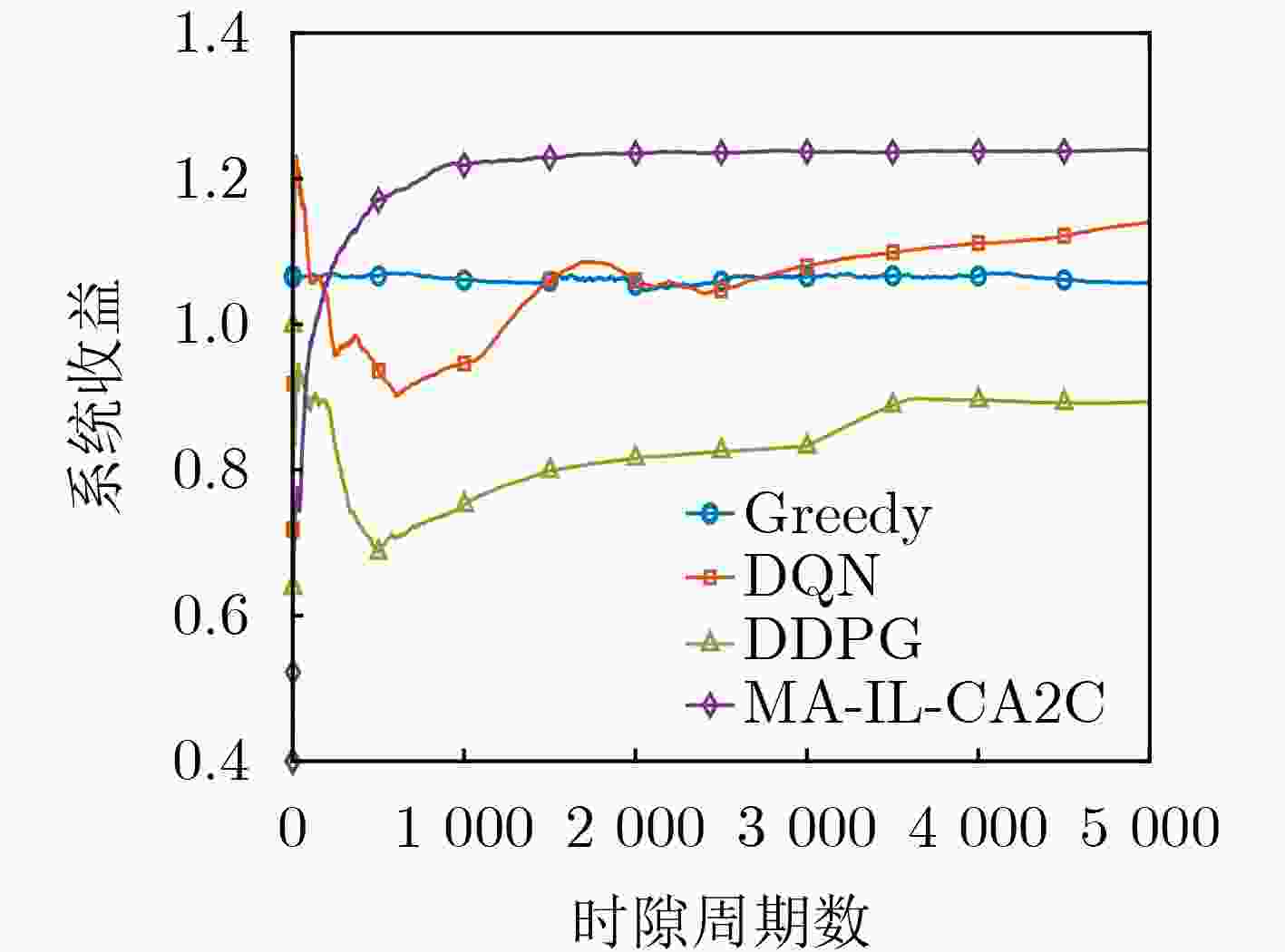
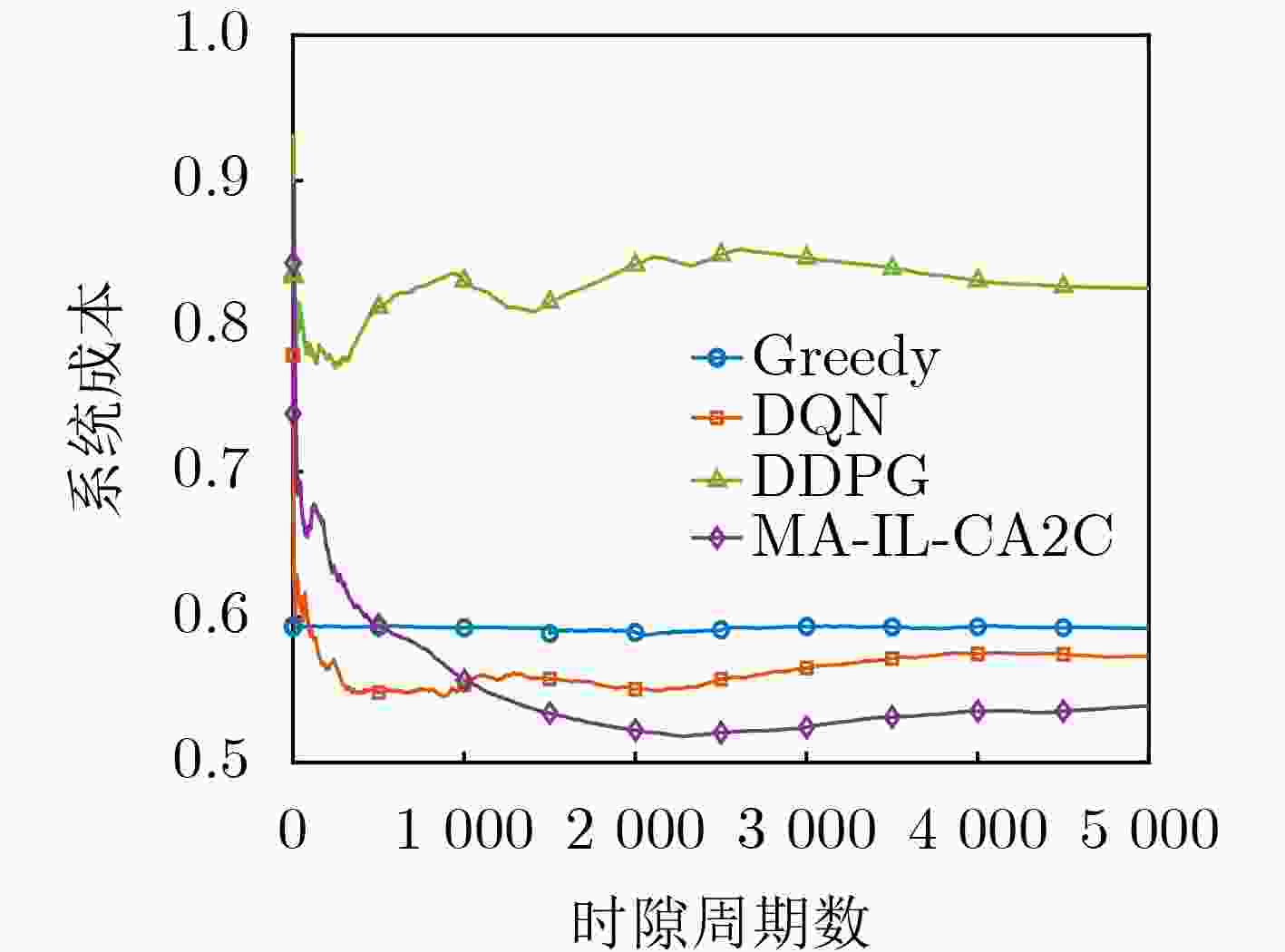
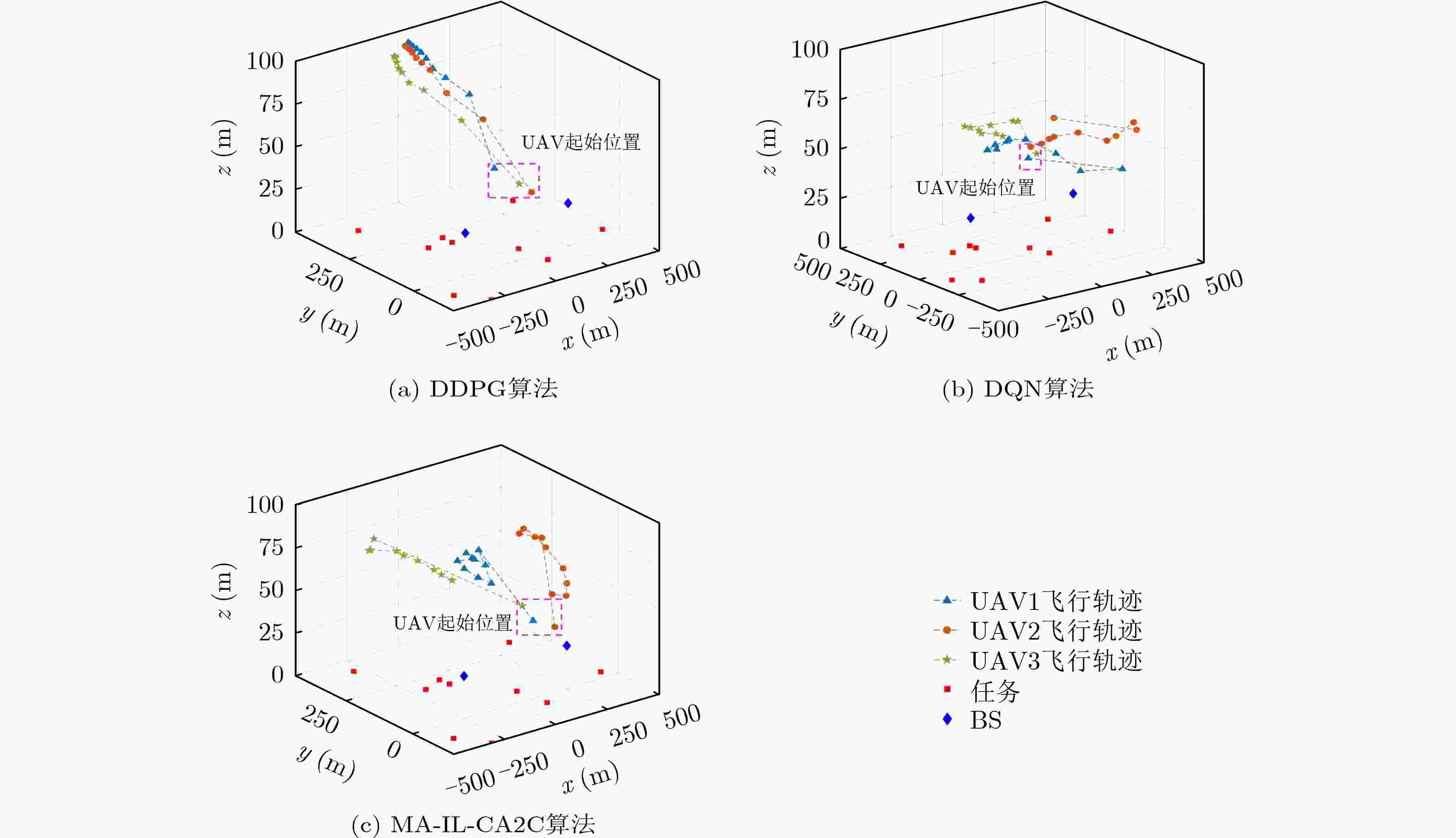
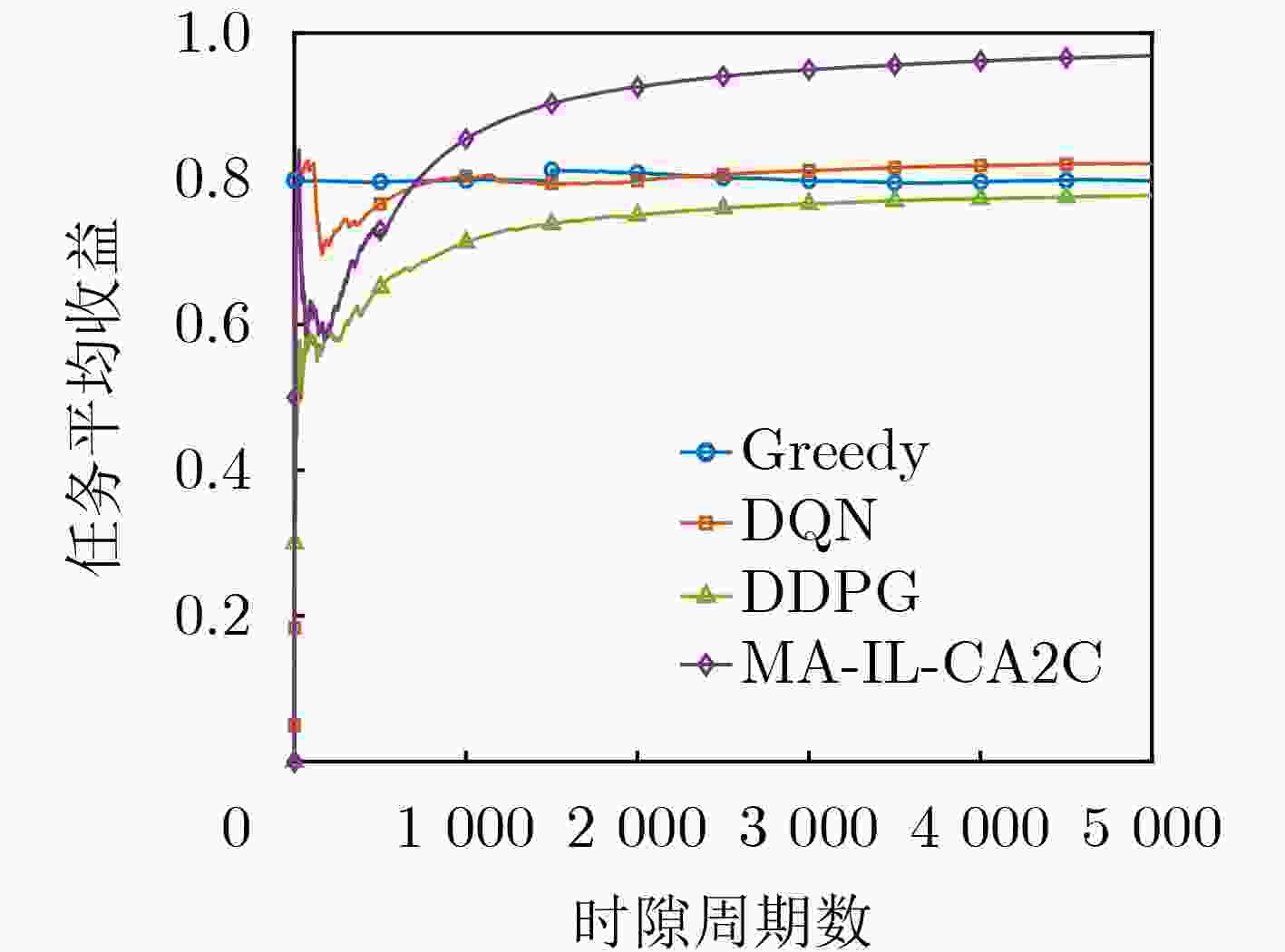
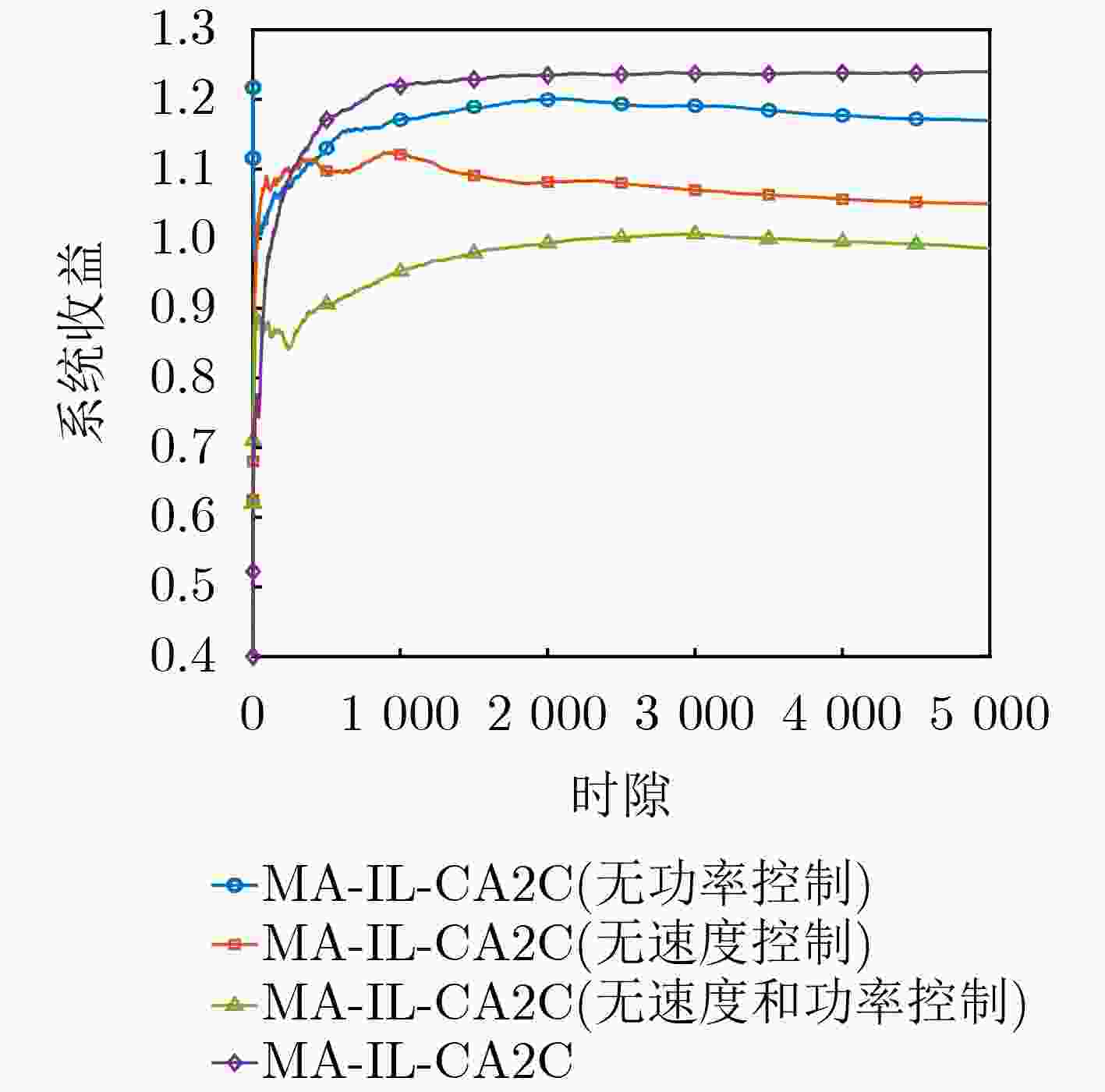
Objective The demand for Unmanned Aerial Vehicles (UAVs) in distributed sensing applications has increased significantly due to their low cost, flexibility, mobility, and ease of deployment. In these applications, the coordination of multi-UAV sensing tasks, communication strategies, and flight trajectory optimization presents a significant challenge. Although there have been preliminary studies on the joint optimization of UAV communication strategies and flight trajectories, most existing work overlooks the impact of the randomly distributed and dynamically updated task airspace model on the optimal design of UAV communication and flight strategies. Furthermore, accurate UAV energy consumption modeling is often lacking when establishing system design goals. Energy consumption during flight, sensing, and data transmission is a critical issue, especially given the UAV’s limited payload capacity and energy supply. Achieving an accurate energy consumption model is essential for extending UAV operational time. To address the requirements of multiple UAVs performing distributed sensing, particularly when tasks are dynamically updated and data must be transmitted to ground base stations, this paper explores the optimal design of joint UAV sensing task allocation, base station association for data backhaul, flight strategy planning, and transmit power control. Methods To coordinate the relationships among UAVs, base stations, and sensing tasks, a protocol framework for multi-UAV distributed task sensing applications is first proposed. This framework divides the UAVs’ behavior during distributed sensing into four stages: cooperation, movement, sensing, and transmission. The framework ensures coordination in the UAVs’ movement to the task area, task sensing, and the backhaul transmission of sensed data. A sensing task model based on dynamic updates, a UAV movement model, a UAV sensing behavior model, and a data backhaul transmission model are then established. A revenue function, combining task sensing utility and task execution costs, is designed, leading to a joint optimization problem of UAV task allocation, communication base station association, and flight strategy. The objective is to maximize the long-term weighted utility-cost. Given that the optimization problem involves high-dimensional decision variables in both discrete and continuous forms, and the objective function is non-convex with respect to these variables, the problem is a typical non-convex Mixed-Integer Non-Linear Programming (MINLP) problem. It falls within the NP-Hard complexity class. Centralized optimization algorithms for this formulation require a central node with high computational capacity and the collection of substantial additional information, such as channel state and UAV location data. This results in high information-interaction overhead and poor scalability. To overcome these challenges, the problem is reformulated as a Markov Game (MG). An effective algorithm is designed by leveraging the distributed coordination concept of Multi-Agent (MA) systems and the exploration capability of deep Reinforcement Learning (RL) within the optimization solution space. Specifically, due to the complex coupling between the continuous and discrete action spaces in the MG problem, a novel solution algorithm called Multi-Agent Independent-Learning Compound-Action Actor-Critic (MA-IL-CA2C) based on Independent Learning (IL) is proposed. The core idea is as follows: first, the independent-learning algorithm is applied to extend single-agent RL to a MA environment. Then, deep learning is used to represent the high-dimensional action and state spaces. To handle the combined discrete and continuous action spaces, the UAV action space is decomposed into discrete and continuous components, with the DQN algorithm applied to the discrete space and the DDPG algorithm to the continuous space. Results and Discussions The computational complexity of action selection and training for the proposed MA-IL-CA2C algorithm is theoretically analyzed. The results show that its complexity is almost equivalent to that of the two benchmark algorithms, DQN and DDPG. Additionally, the performance of the proposed algorithm is simulated and analyzed. When compared with the DQN, DDPG, and Greedy algorithms, the MA-IL-CA2C algorithm demonstrates lower network energy consumption throughout the network operation ( Fig. 6 ), improved system revenue (Fig. 5 ,Fig. 8 , andFig. 9 ), and optimized UAV flight strategies (Fig. 7 ).Conclusions This paper addresses and solves the optimal design problems of joint UAV sensing task allocation, data backhaul base station association, flight strategy planning, and transmit power control for multi-UAV distributed task sensing. A new MA-IL-CA2C algorithm based on IL is proposed. The simulation results show that the proposed algorithm achieves better system revenue while minimizing UAV energy consumption. -
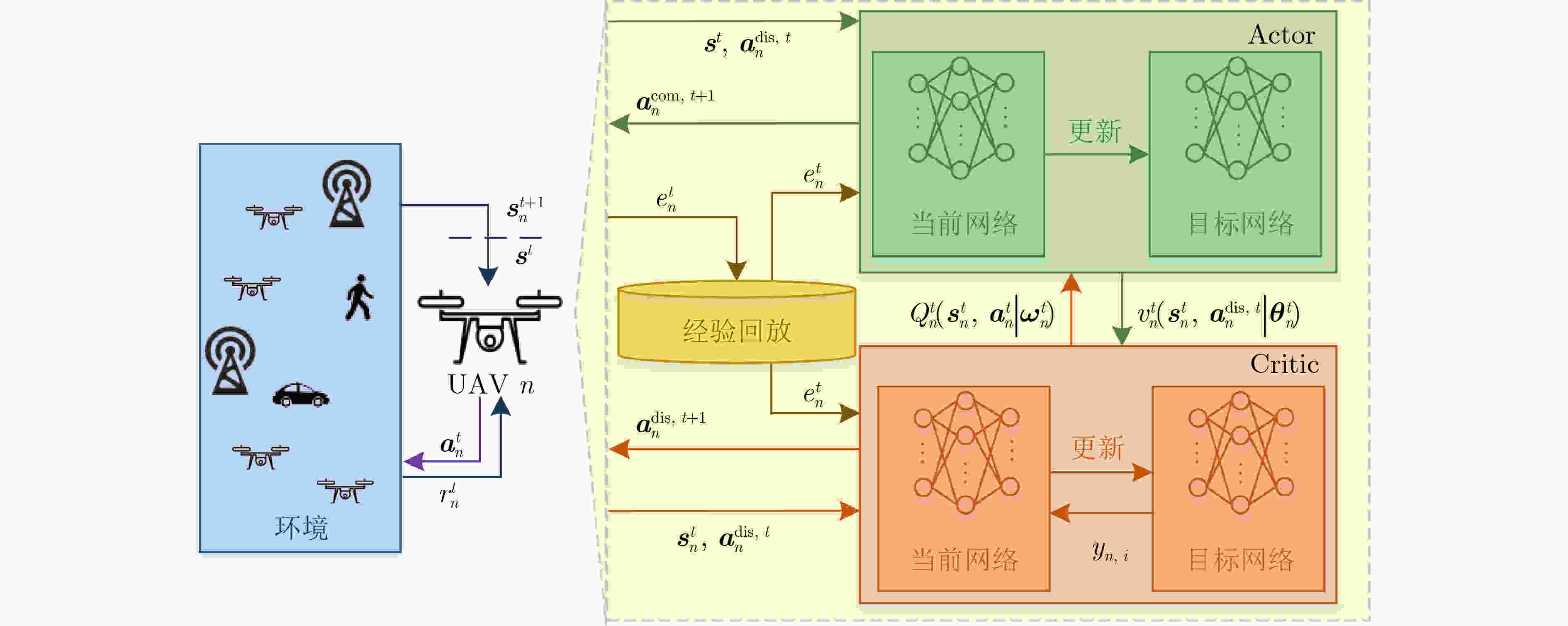
1 MA-IL-CA2C算法
(1)初始化:设置$t = 0$,最大决策周期数$T$,选择经验回放模块
容量$ {N_{\mathrm{c}}} $,批量大小${N_{\mathrm{b}}}$,网络学习率${\alpha _{{\boldsymbol{\theta}} _n^t}}$和$ {\alpha _{{\boldsymbol{\omega}} _n^t}} $,软更新参数
$ \rho $;(2)对于每个智能体$n \in \mathcal{N}$: 随机初始化网络参数$ {{\boldsymbol{\theta}} }_n^t $, $ {\hat {\boldsymbol{\theta}} }_n^t $, $ {{\boldsymbol{\omega}} }_n^t $, $ {\hat {\boldsymbol{\omega}} }_n^t $,并设置初始状态${{\boldsymbol s}^0}$; #主循环 (3)如果$t \le T$: (a)对于每个智能体$n \in \mathcal{N}$: 根据式(28),在${\boldsymbol{s}}_n^t$处选择离散动作$ {\boldsymbol a}_n^{{\text{dis}},t} $,即选择感知任务$m$和$ {\text{B}}{{\text{S}}_k} $; #协作阶段 在控制信道上反馈决策$D_n^{\mathrm{c}} = \left\{ {n,{\boldsymbol a}_n^{{\mathrm{dis}},t}} \right\}$,并接收其余
UAV的决策信息;根据离散动作$ {\boldsymbol a}_n^{{\mathrm{dis}},t} $决定连续动作${\boldsymbol a}_n^{{\text{con}},t}{ = v}_n^t\left( {{{\boldsymbol s}^t},{\boldsymbol a}_n^{{\mathrm{dis}},t}} \right)$,
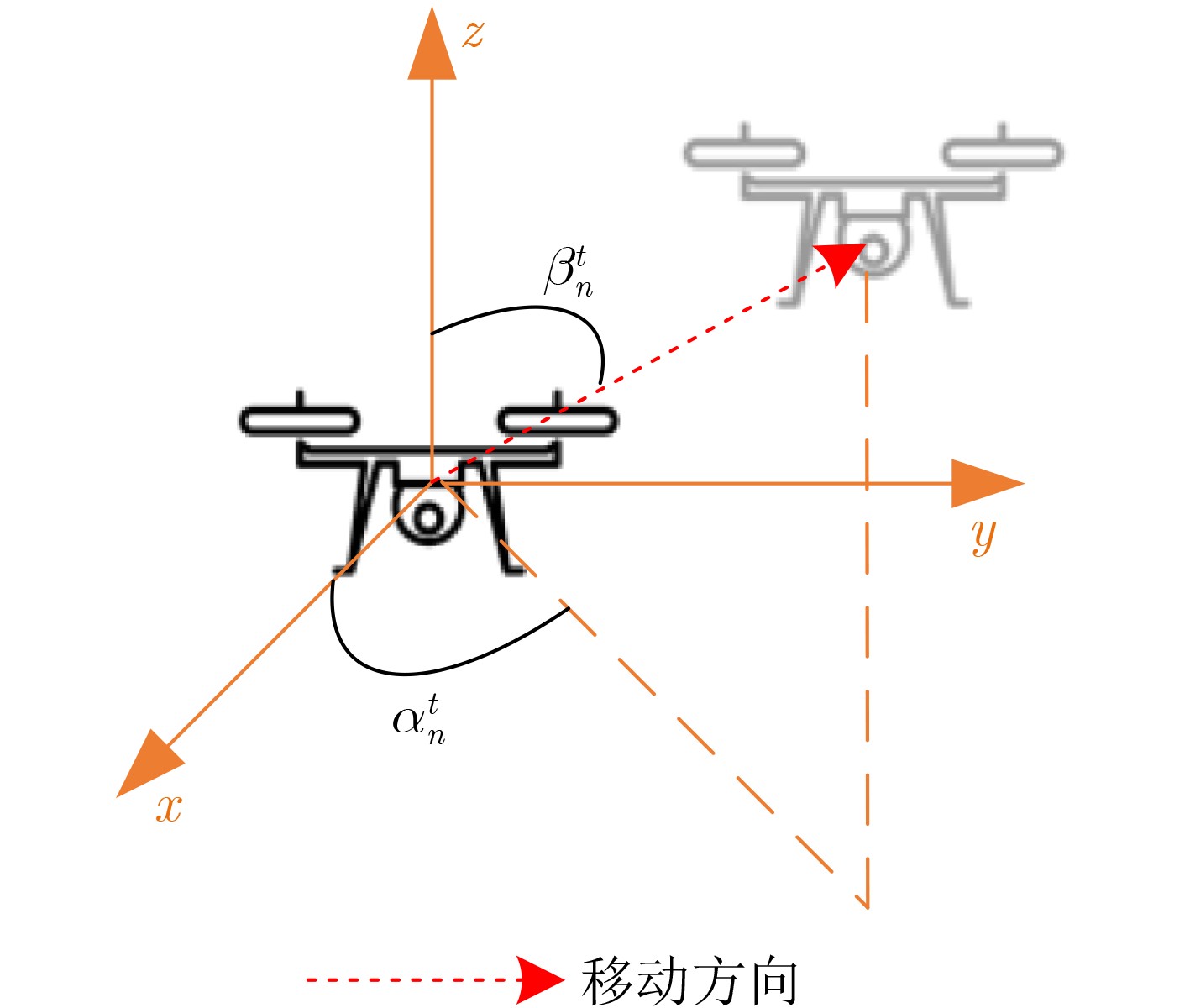
即决定飞行方向角$ \delta _n^t $、移动速度$ v_n^t $和发射功率$ P_n^t $;#移动阶段 基于飞行方向角$ {\boldsymbol{\delta}} _n^t $和移动速度$ v_n^t $,飞行至感知位置$ {\boldsymbol{x}}_n^{{\mathrm{s}},t} $; #感知阶段 执行感知任务并收集任务数据$D_n^{s,t}$; #传输阶段 以发射功率$ P_n^t $将任务数据回传给$ {\text{B}}{{\text{S}}_k} $; 根据式(23)获得收益$ r_n^{t + 1} $,观察得到${{\boldsymbol s}^{t + 1}}$; 将经验元组$ \left( {{{\boldsymbol s}^t},{\boldsymbol a}_n^t,r_n^{t + 1},{{\boldsymbol s}^{t + 1}}} \right) $存入经验回放模块${\mathcal{D}_n}$中; 如果$ t \gt {N_{\mathrm{c}}} $: 从经验回放模块${\mathcal{D}_n}$中移除旧的经验元组; #训练网络 在经验回放模块${\mathcal{D}_n}$中随机抽取一个批量${N_{\mathrm{b}}}$的经验元组
$ \left( {{{\boldsymbol s}^t},{\boldsymbol a}_n^t,r_n^{t + 1},{{\boldsymbol s}^{t + 1}}} \right) $;根据式(29)–式(34),更新当前网络参数$ {{\boldsymbol{\theta}} }_n^t $与$ {{\boldsymbol{\omega}} }_n^t $; 根据式(36)和式(37),更新目标网络参数$ {\hat {\boldsymbol{\theta}} }_n^t $与$ {\hat {\boldsymbol{\omega}} }_n^t $; (b)令$t = t + 1$, ${{\boldsymbol s}^t} \leftarrow {{\boldsymbol s}^{t + 1}}$; (4)重复步骤(3),直至算法结束。 表 1 仿真参数
参数 数值 UAV数目$N$,感知任务数目$M$,BS数目$K$ 3, 10, 2 网络范围半径${r_{\text{c}}}$ 500 m 信道带宽$ W $ 1 MHz BS高度$ {H_0} $ 25 m UAV最大与最低高度${h_{\min }},{h_{\max }}$ 50 m, 100 m UAV最大飞行速度$ {v_{\max }} $ 15 m/s UAV最大发射功率$ {P_{\max }} $ 30 dBm 感知参数$\lambda $ 0.01 环境参数${\mathrm{a}},{\mathrm{b}}$ 9.61, 0.16 LoS和NLoS额外路径损耗${\eta ^{{\text{LoS}}}},{\eta ^{{\text{NLoS}}}}$ 1 dB, 20 dB 载波频率${f_{\text{c}}}$ 2 GHz 噪声功率${N_0}$ –96 dBm 表 2 模型超参数
超参数 数值 Actor网络与Critic网络初始学习率$ {\alpha _{{\boldsymbol{\theta}} _n^t}} $,$ {\alpha _{{\boldsymbol{\omega}} _n^t}} $ 0.001, 0.002 软更新权重$\rho $ 0.01 贪婪率$\varepsilon $ 0.1 激活函数 ReLu 批量大小${N_{\text{b}}}$ 64 经验回放模块大小${N_{\text{c}}}$ 20 000 DQN网络初始学习率 0.01 DQN目标网络更新周期 100 Actor网络和Critic网络层数 4,4 隐层神经元数 128 -
[1] SHRESTHA R, ROMERO D, and CHEPURI S P. Spectrum surveying: Active radio map estimation with autonomous UAVs[J]. IEEE Transactions on Wireless Communications, 2023, 22(1): 627–641. doi: 10.1109/TWC.2022.3197087. [2] NOMIKOS N, GKONIS P K, BITHAS P S, et al. A survey on UAV-aided maritime communications: Deployment considerations, applications, and future challenges[J]. IEEE Open Journal of the Communications Society, 2023, 4: 56–78. doi: 10.1109/OJCOMS.2022.3225590. [3] HARIKUMAR K, SENTHILNATH J, and SUNDARAM S. Multi-UAV oxyrrhis marina-inspired search and dynamic formation control for forest firefighting[J]. IEEE Transactions on Automation Science and Engineering, 2019, 16(2): 863–873. doi: 10.1109/TASE.2018.2867614. [4] QU Yuben, SUN Hao, DONG Chao, et al. Elastic collaborative edge intelligence for UAV Swarm: Architecture, challenges, and opportunities[J]. IEEE Communications Magazine, 2024, 62(1): 62–68. doi: 10.1109/MCOM.002.2300129. [5] ZHANG Tao, ZHU Kun, ZHENG Shaoqiu, et al. Trajectory design and power control for joint radar and communication enabled multi-UAV cooperative detection systems[J]. IEEE Transactions on Communications, 2023, 71(1): 158–172. doi: 10.1109/TCOMM.2022.3224751. [6] PAN Hongyang, LIU Yanheng, SUN Geng, et al. Joint power and 3D trajectory optimization for UAV-Enabled wireless powered communication networks with obstacles[J]. IEEE Transactions on Communications, 2023, 71(4): 2364–2380. doi: 10.1109/TCOMM.2023.3240697. [7] NGUYEN P X, NGUYEN V D, NGUYEN H V, et al. UAV-assisted secure communications in terrestrial cognitive radio networks: Joint power control and 3D trajectory optimization[J]. IEEE Transactions on Vehicular Technology, 2021, 70(4): 3298–3313. doi: 10.1109/TVT.2021.3062283. [8] ZENG Shuhao, ZHANG Hongliang, DI Boya, et al. Trajectory optimization and resource allocation for OFDMA UAV relay networks[J]. IEEE Transactions on Wireless Communications, 2021, 20(10): 6634–6647. doi: 10.1109/TWC.2021.3075594. [9] LI Peiming and XU Jie. Fundamental rate limits of UAV-enabled multiple access channel with trajectory optimization[J]. IEEE Transactions on Wireless Communications, 2020, 19(1): 458–474. doi: 10.1109/TWC.2019.2946153. [10] GUAN Yue, ZOU Sai, PENG Haixia, et al. Cooperative UAV trajectory design for disaster area emergency communications: A multiagent PPO method[J]. IEEE Internet of Things Journal, 2024, 11(5): 8848–8859. doi: 10.1109/JIOT.2023.3320796. [11] SILVIRIANTI, NAROTTAMA B, and SHIN S Y. Layerwise quantum deep reinforcement learning for joint optimization of UAV trajectory and resource allocation[J]. IEEE Internet of Things Journal, 2024, 11(1): 430–443. doi: 10.1109/JIOT.2023.3285968. [12] HU Jingzhi, ZHANG Hongliang, SONG Lingyang, et al. Cooperative internet of UAVs: Distributed trajectory design by multi-agent deep reinforcement learning[J]. IEEE Transactions on Communications, 2020, 68(11): 6807–6821. doi: 10.1109/TCOMM.2020.3013599. [13] WU Fanyi, ZHANG Hongliang, WU Jianjun, et al. Cellular UAV-to-device communications: Trajectory design and mode selection by Multi-Agent deep reinforcement learning[J]. IEEE Transactions on Communications, 2020, 68(7): 4175–4189. doi: 10.1109/TCOMM.2020.2986289. [14] DAI Xunhua, LU Zhiyu, CHEN Xuehan, et al. Multiagent RL-based joint trajectory scheduling and resource allocation in NOMA-assisted UAV swarm network[J]. IEEE Internet of Things Journal, 2024, 11(8): 14153–14167. doi: 10.1109/JIOT.2023.3340669. [15] ZHANG Zhongyu, LIU Yunpeng, LIU Tianci, et al. DAGN: A real-time UAV remote sensing image vehicle detection framework[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(11): 1884–1888. doi: 10.1109/LGRS.2019.2956513. [16] YANG Jun, YOU Xinghui, WU Gaoxiang, et al. Application of reinforcement learning in UAV cluster task scheduling[J]. Future Generation Computer Systems, 2019, 95: 140–148. doi: 10.1016/j.future.2018.11.014. [17] NOBAR S K, AHMED M H, MORGAN Y, et al. Resource allocation in cognitive radio-enabled UAV communication[J]. IEEE Transactions on Cognitive Communications and Networking, 2022, 8(1): 296–310. doi: 10.1109/TCCN.2021.3103531. [18] CHEN Jiming, LI Junkun, and LAI T H. Energy-efficient intrusion detection with a barrier of probabilistic sensors: Global and local[J]. IEEE Transactions on Wireless Communications, 2013, 12(9): 4742–4755. doi: 10.1109/TW.2013.072313.122083. [19] SHAKHOV V V and KOO I. Experiment design for parameter estimation in probabilistic sensing models[J]. IEEE Sensors Journal, 2017, 17(24): 8431–8437. doi: 10.1109/JSEN.2017.2766089. [20] YANG Qianqian, HE Shibo, LI Junkun, et al. Energy-efficient probabilistic area coverage in wireless sensor networks[J]. IEEE Transactions on Vehicular Technology, 2015, 64(1): 367–377. doi: 10.1109/TVT.2014.2300181. [21] AL-HOURANI A, KANDEEPAN S, and LARDNER S. Optimal LAP altitude for maximum coverage[J]. IEEE Wireless Communications Letters, 2014, 3(6): 569–572. doi: 10.1109/LWC.2014.2342736. [22] ZHANG Xinyu and SHIN K G. E-MiLi: Energy-minimizing idle listening in wireless networks[J]. IEEE Transactions on Mobile Computing, 2012, 11(9): 1441–1454. doi: 10.1109/TMC.2012.112. [23] ZHU Changxi, DASTANI M, and WANG Shihan. A survey of multi-agent deep reinforcement learning with communication[J]. Autonomous Agents and Multi-Agent Systems, 2024, 38(1): 4. doi: 10.1007/s10458-023-09633-6. [24] 喻莞芯. 基于多智能体强化学习的无人机集群网络优化设计[D]. [硕士论文], 重庆大学, 2022. doi: 10.27670/d.cnki.gcqdu.2022.001082.YU Wanxin. Optimization design of UAV cluster network based on multi-agent reinforcement learning[D]. [Master dissertation], Chongqing University, 2022. doi: 10.27670/d.cnki.gcqdu.2022.001082. [25] SUTTON R S and BARTO A G. Reinforcement Learning: An Introduction[M]. Cambridge, USA: MIT Press, 1998. [26] WOOD L F. Training neural networks[P]. US, 4914603A, 1990. [27] SIPPER M. A serial complexity measure of neural networks[C]. IEEE International Conference on Neural Networks, San Francisco, USA, 1993: 962–966. doi: 10.1109/ICNN.1993.298687. [28] GUO Shaoai and ZHAO Xiaohui. Multi-agent deep reinforcement learning based transmission latency minimization for delay-sensitive cognitive satellite-UAV networks[J]. IEEE Transactions on Communications, 2023, 71(1): 131–144. doi: 10.1109/TCOMM.2022.3222460. -





 下载:
下载:


 下载:
下载:
