融合电离层延迟改正与多频信号优化的全球导航卫星系统部分模糊度解算方法

张旭; 杨杰

doi:10.11999/JEIT240682

融合电离层延迟改正与多频信号优化的全球导航卫星系统部分模糊度解算方法

doi: 10.11999/JEIT240682

张旭^{1, 2},
杨杰^1, ,

1.
安徽理工大学电气与信息工程学院淮南 232001
2.
武汉理工大学信息工程学院武汉 430070

基金项目: 国家重点研发计划(2020YFB1710800)，国家自然科学基金(51879211)，安徽理工大学引进人才基金(2024yjrc177)

详细信息

作者简介:
张旭：男，讲师，研究方向为组合导航定位

杨杰：女，教授，研究方向为人工智能与导航定位

通讯作者:
杨杰　jieyang509@163.com

中图分类号: TN967.1
计量
- 文章访问数: 87
- HTML全文浏览量: 29
- PDF下载量: 8
- 被引次数: 0
出版历程
- 收稿日期: 2024-07-31
- 修回日期: 2025-04-08
- 网络出版日期: 2025-04-29

Global Navigation Satellite System Partial Ambiguity Resolution Method Integrating Ionospheric Delay Correction and Multi-frequency Signal Optimization

ZHANG Xu^{1, 2},
YANG Jie^{1
, ,}

1.
School of Electrical and Information Engineering, Anhui University of Science and Technology, Huainan 232001, China
2.
School of Information Engineering, Wuhan University of Technology, Wuhan 430070, China

Funds: The National Key Research and Development Program of China (2020YFB1710800), The National Natural Science Foundation of China (51879211), The Scientific Research Foundation for High-level Talents of Anhui University of Science and Technology (2024yjrc177)

摘要

摘要: 针对全球导航卫星系统(GNSS)在遮挡环境下定位精度受限以及差分方法在较长基线时难以消除电离层延迟的问题，该文提出一种改进的部分模糊度解算(MPAR)方法。该方法融合了无几何模式下的基于电离层延迟改正模型的级联整数解算(ICIR)与几何模式下的最小二乘降相关平差(LAMBDA)。通过引入电离层延迟改正模型并将其融入ICIR方法中，有效解决了电离层延迟误差对模糊度解算(AR)的影响，提高了长基线条件下的定位精度。同时，为提升观测值质量不佳时的数据利用率，本研究利用卫星三频最优子集信息辅助非三频子集进行AR。具体而言，对最优子集卫星采用改进的ICIR方法进行解算，而对非三频卫星子集则结合最优子集的辅助信息，采用LAMBDA方法进行解算。两阶段解算策略不仅降低了计算复杂度，还显著提高了AR的成功率和可靠性，从而全面提升了GNSS定位的性能。实验结果表明，MPARICIR方法在各种基线条件和卫星数据质量下均表现出优异的定位精度和稳定性。
- 全球导航卫星系统 /
- 模糊度解算 /
- 电离层延迟改正模型 /
- 级联整数解算 /
- 最小二乘降相关平差
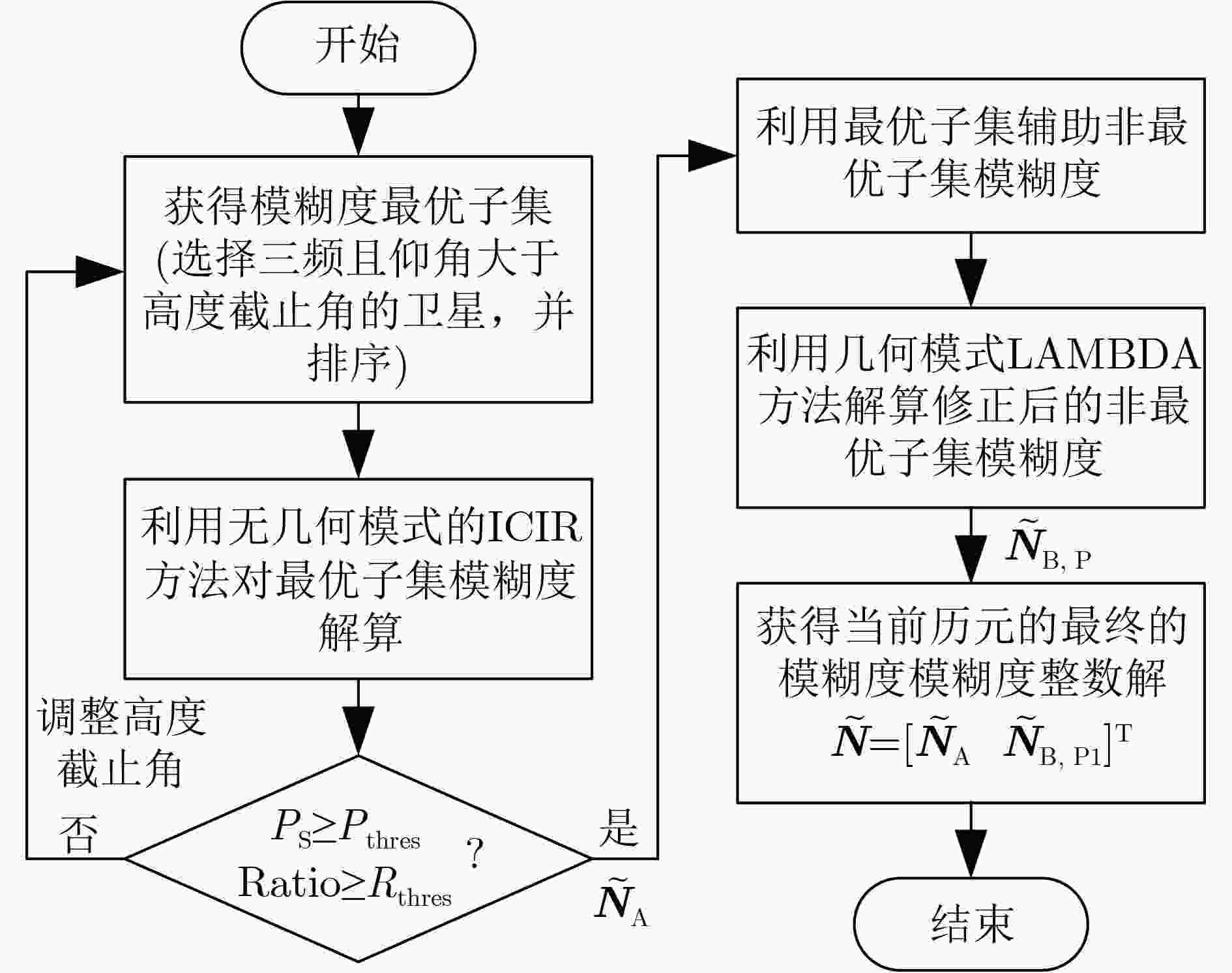
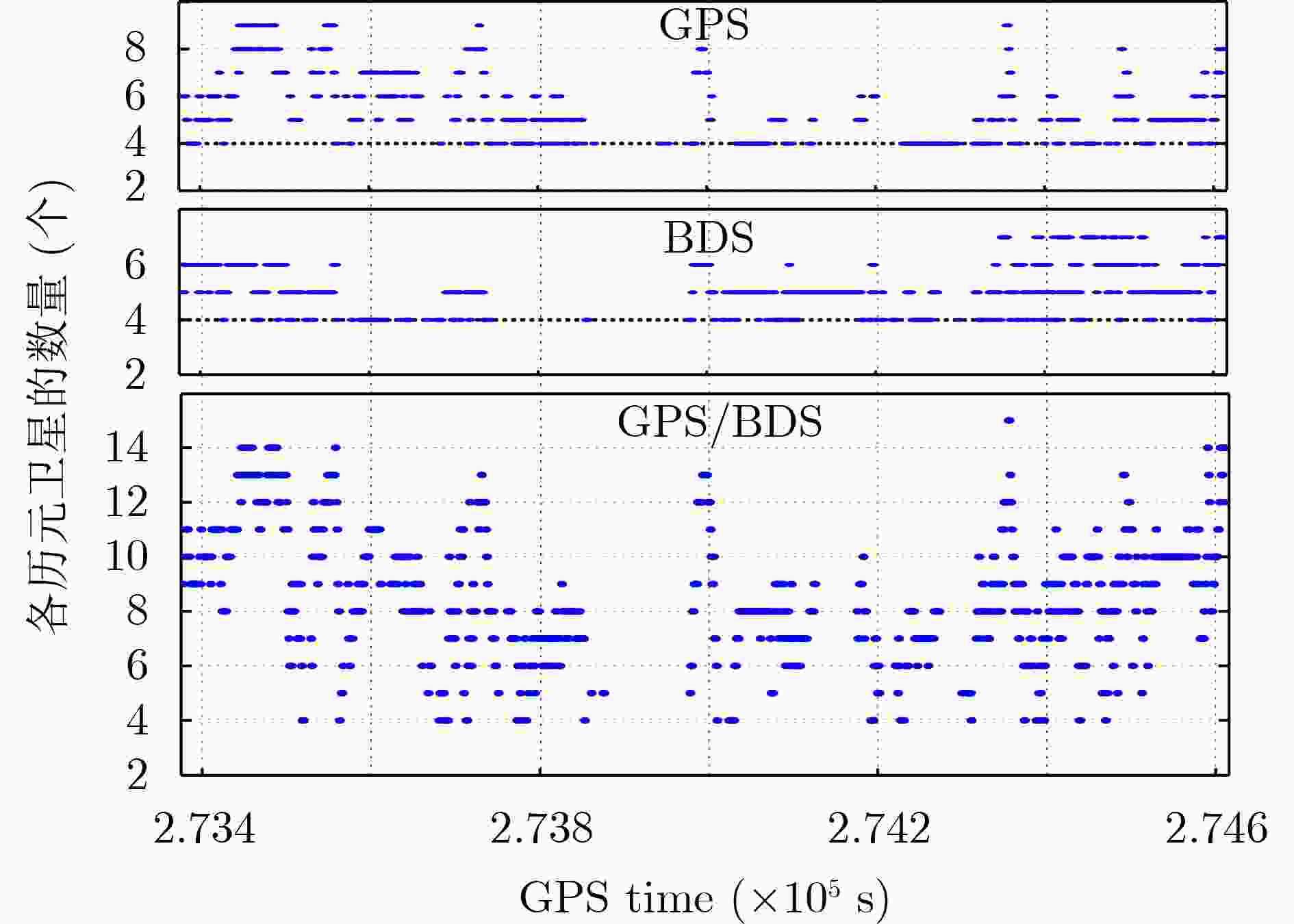
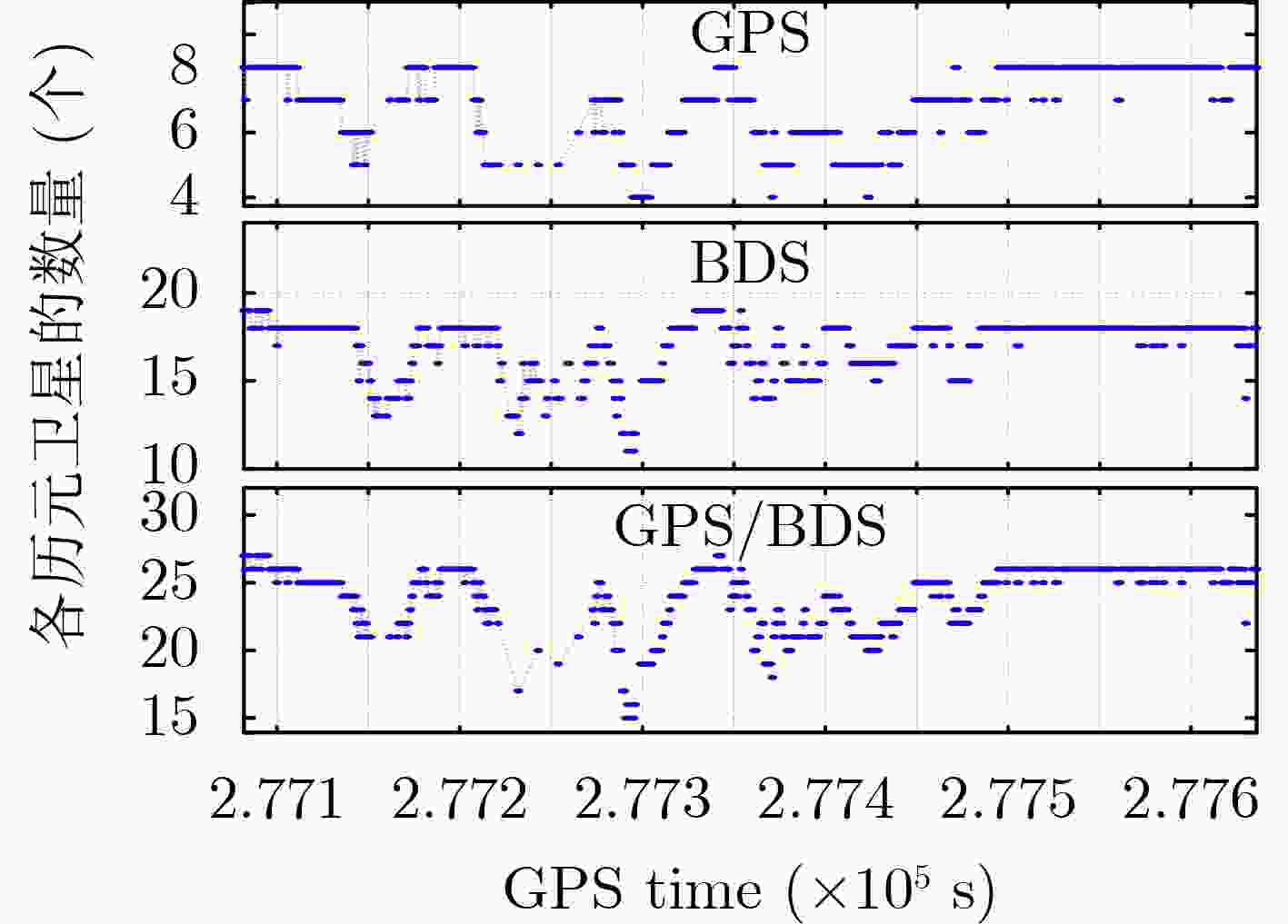
Abstract: Objective Global Navigation Satellite System (GNSS) high-precision positioning is widely applied due to its accuracy. However, the integrity of the Ambiguity Resolution (AR) process remains limited, particularly in occluded environments and over long baselines. Traditional AR methods are often affected by ionospheric delay errors, which become substantial when the ionospheric conditions differ between reference and rover stations. This paper proposes a Modified Partial Ambiguity Resolution (MPAR) method that integrates ionospheric delay correction models with multi-frequency signal optimization. The combined approach improves GNSS positioning accuracy and reliability under varied environmental and baseline conditions. Methods To reduce the effect of ionospheric delay on AR, this study incorporates an Ionospheric delay correction model into the geometry-free Cascade Integer Resolution (ICIR) method. ICIR resolves the integer ambiguities of Extra-Wide Lane (EWL), Wide Lane (WL), and Narrow Lane (NL) combinations using carrier phase measurements with different wavelengths. The ionospheric delay correction model enables compensation for differential delays between stations, improving AR accuracy, particularly over long baselines. To further enhance data usage—especially in cases of low-quality observations—a two-stage partial AR strategy is employed. In the first stage, the ICIR method is applied to an optimal subset of satellites selected based on tri-frequency availability and high elevation angles. For the non-optimal subset, which may include satellites with limited frequencies or weaker signal quality, the Least-Squares AMBiguity Decorrelation Adjustment (LAMBDA) method is used in geometric mode, with assistance from the ambiguity-fixed results of the optimal subset. This integrated approach reduces computational complexity and improves the AR success rate and reliability. The MPAR method proceeds as follows: (1) select the optimal satellite subset based on frequency availability and elevation angle; (2) apply the ICIR method to resolve ambiguities in this subset; (3) use the fixed ambiguities from the optimal subset to assist in resolving ambiguities for the non-optimal subset via the LAMBDA method; (4) obtain the final integer ambiguity solution for the full epoch. Results and Discussions The proposed MPAR method is validated using two datasets collected under different environments: one from Tokyo, characterized by complex urban occlusion and long baselines (approximately 1 700 meters), and another from Wuhan, featuring an open campus environment and short baselines (approximately 600 meters). The results show that the MPAR method outperforms traditional PAR methods in positioning accuracy, AR success rate, and computational efficiency. As shown in (Fig. 3) and (Fig. 5), satellite visibility in the Tokyo dataset is significantly affected by occlusion, leading to fewer available satellites compared to the Wuhan dataset. Despite these challenges, the MPAR method achieves the highest success rate and the lowest Average Standard Deviation (ASD) in all tested scenarios, including GPS, BDS, and dual-system modes (Table 2 and Table 4). In the Tokyo dataset, the MPAR method reduces the ASD by up to 40% compared to traditional methods, reflecting its robustness in complex environments. The AR success rate also significantly improves with the MPAR method. As presented in (Table 3) and (Table 5), the MPAR method achieves AR success rates exceeding 90% in all tested scenarios, with a peak rate of 99.4% in the GPS/BDS dual-system mode of the Wuhan dataset. These results demonstrate the effectiveness of the proposed method in enhancing AR reliability under challenging conditions. In terms of computational efficiency, the MPAR method exhibits balanced performance. Although the use of the ionospheric delay correction model slightly increases computational complexity, the overall efficiency remains competitive, with an average solution time of approximately 0.13 seconds per epoch (Table 3 and Table 5). This performance supports the suitability of the MPAR method for real-time applications. Furthermore, Table 3 (Tokyo dataset) and Table 5 (Wuhan dataset) summarize the performance metrics of the five AR methods evaluated. The MPARICIR method achieves the highest AR success rates across all systems and environments, reaching 93.1% and 99.4% for the Tokyo and Wuhan datasets, respectively. Notably, the MPARICIR method maintains a high success rate while reducing computation time compared to other methods, indicating its efficiency. These results support the effectiveness and robustness of the proposed MPARICIR method in improving GNSS positioning performance. Conclusions This study proposes an MPAR method for high-precision GNSS positioning. By integrating ionospheric delay correction models with multi-frequency signal optimization, MPAR combines the strengths of geometry-free and geometry-based AR strategies. The method effectively reduces the effect of ionospheric delay, particularly over long baselines and in occluded environments. Experimental results confirm that MPAR improves positioning accuracy, AR success rate, and computational efficiency relative to conventional methods. Its consistent performance across varied environments and baseline lengths highlights its suitability for broad application in high-precision GNSS positioning.

HTML全文

图 1 基于ICIR的MPAR方法解算流程

下载: 全尺寸图片幻灯片

图 2 两组数据集数据采集环境与卫星定位轨迹对比

下载: 全尺寸图片幻灯片

图 3 东京数据集不同系统下各历元卫星数量

下载: 全尺寸图片幻灯片

图 4 东京数据集在不同系统模式下的各方向定位结果平均标准差

下载: 全尺寸图片幻灯片

图 5 武汉数据集不同系统下各历元卫星数量

下载: 全尺寸图片幻灯片

图 6 武汉数据集在不同系统模式下的各方向定位结果平均标准差

下载: 全尺寸图片幻灯片

表 1 数据集信息与实验设置

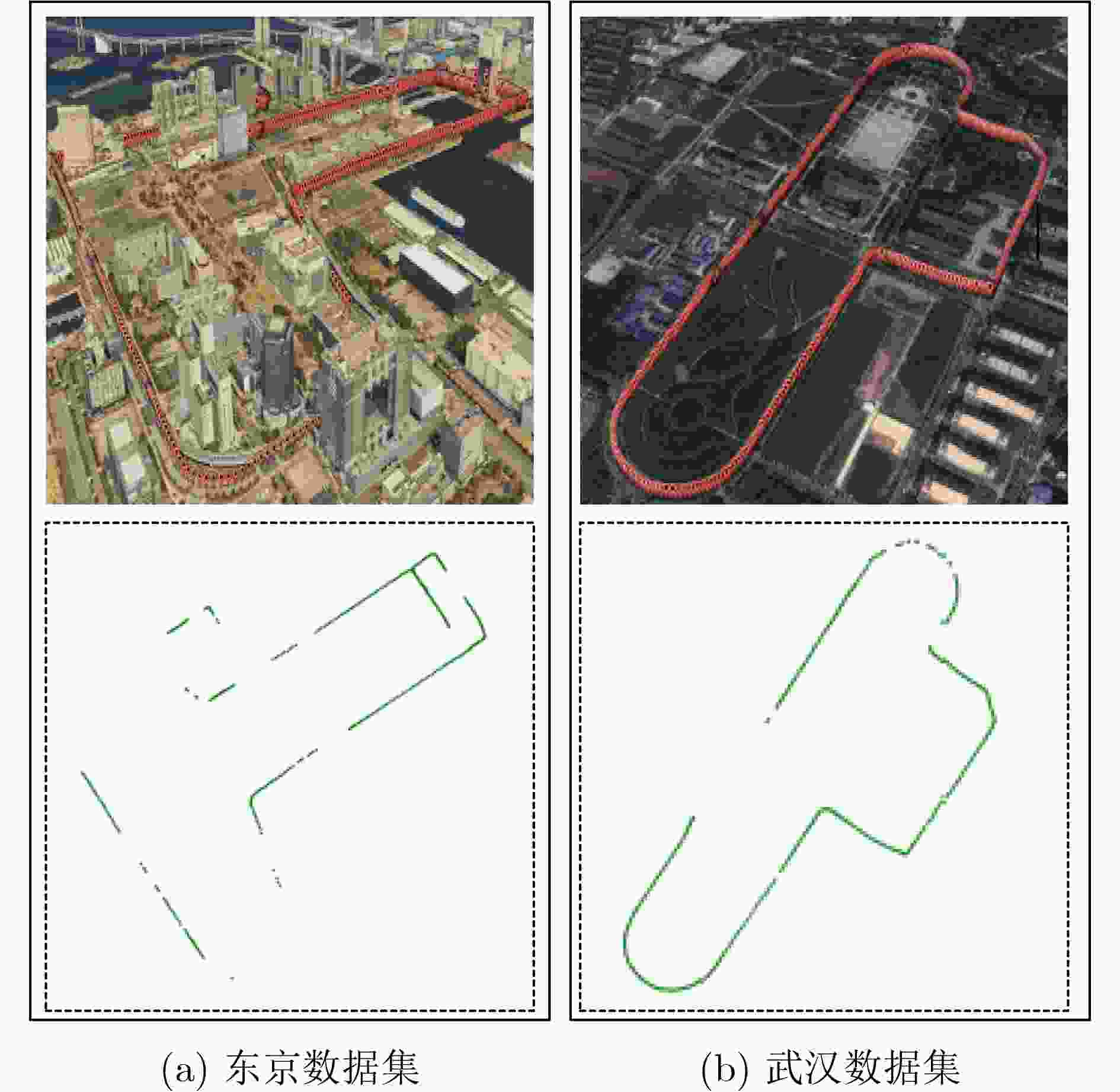
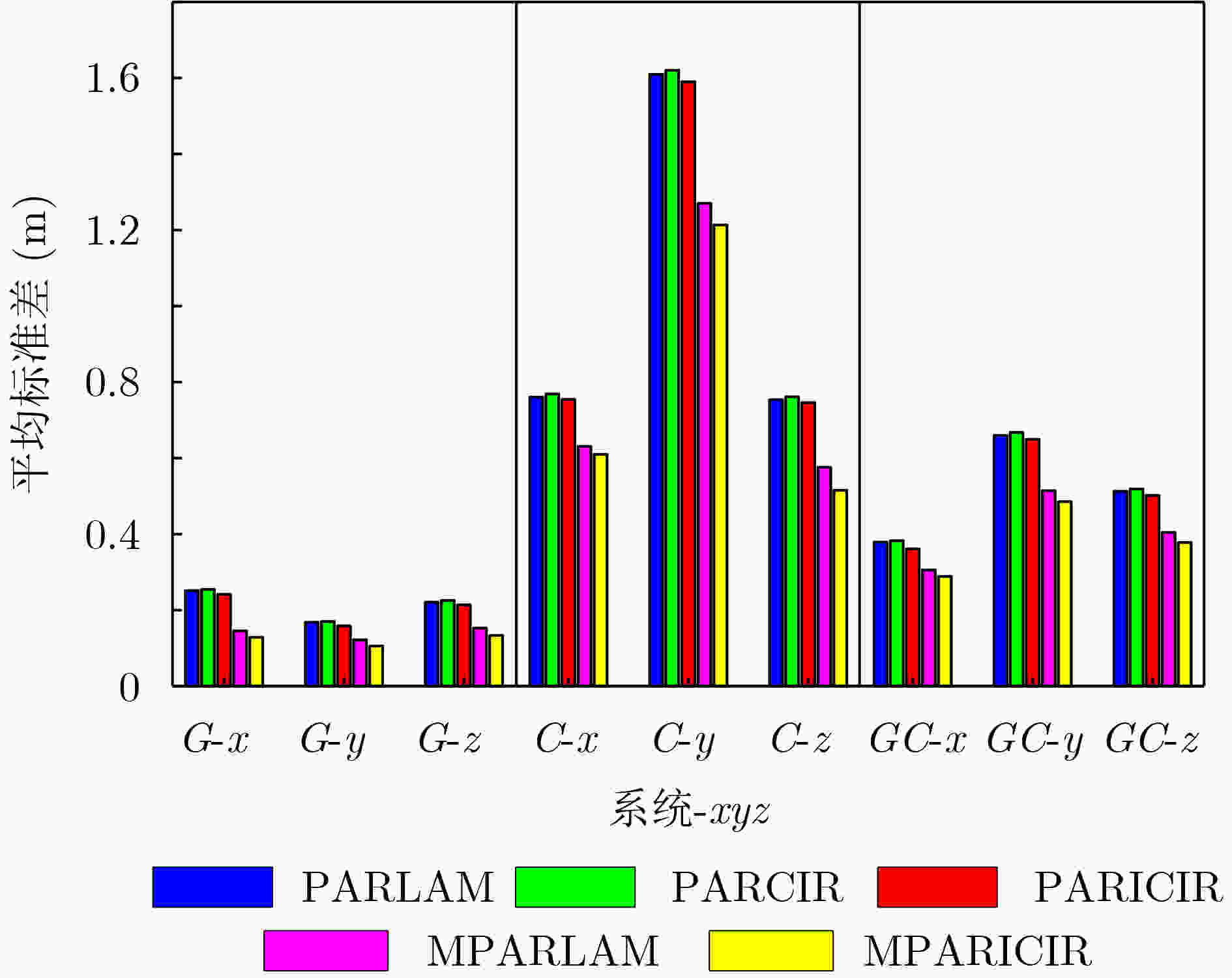
数据集	采集时间	基线长度(km)	路径长度(km)	高度截止角(º)	采样频率(Hz)	遮挡
武汉	04:58:02～05:07:16	0.6	2.1	15	1	少
东京	03:56:15～04:16:56	1.7	6.4	15	1	多

下载: 导出CSV

表 2 东京数据集xyz方向定位结果平均标准差具体数据(m)

平均标准差		PAR LAM	PAR CIR	PARI CIR	MPAR LAM	MPAR ICIR
G	x	0.251 5	0.254 6	0.241 5	0.145 1	0.128 4
	y	0.168 1	0.169 8	0.158 6	0.121 9	0.105 4
	z	0.220 8	0.225 4	0.213 8	0.152 9	0.133 5
C	x	0.760 3	0.768 7	0.754 2	0.630 7	0.609 8
	y	1.609 9	1.620 5	1.590 4	1.270 6	1.213 5
	z	0.753 8	0.761 3	0.745 7	0.575 8	0.515 4
GC	x	0.378 8	0.382 5	0.361 3	0.305 6	0.288 5
	y	0.659 5	0.667 6	0.649 5	0.514 2	0.485 3
	z	0.512 6	0.518 7	0.501 9	0.404 4	0.377 8

下载: 导出CSV

表 3 东京数据集5种模糊度解算方法性能对比

东京数据集		PAR LAM	PAR CIR	PARI CIR	MPAR LAM	MPAR ICIR
总历元数		1 242
G	可定位历元	795	795	795	795	795
	固定解历元	649	646	656	739	745
	浮点解历元	146	149	139	56	50
	成功率(%)	81.6	79.5	82.5	93.0	93.7
	解算时间(s)	0.152	0.124	0.126	0.157	0.131
C	可定位历元	621	621	621	637	637
	固定解历元	528	523	532	548	552
	浮点解历元	93	98	89	89	85
	成功率(%)	85.0	84.2	85.7	86.0	86.7
	解算时间(s)	0.127	0.113	0.108	0.130	0.110
GC	可定位历元	943	943	943	943	943
	固定解历元	790	788	796	872	878
	浮点解历元	153	155	147	71	65
	成功率(%)	83.8	83.6	84.4	92.5	93.1
	解算时间(s)	0.142	0.127	0.129	0.147	0.132

下载: 导出CSV

表 4 武汉数据集xyz方向定位结果平均标准差具体数据(m)

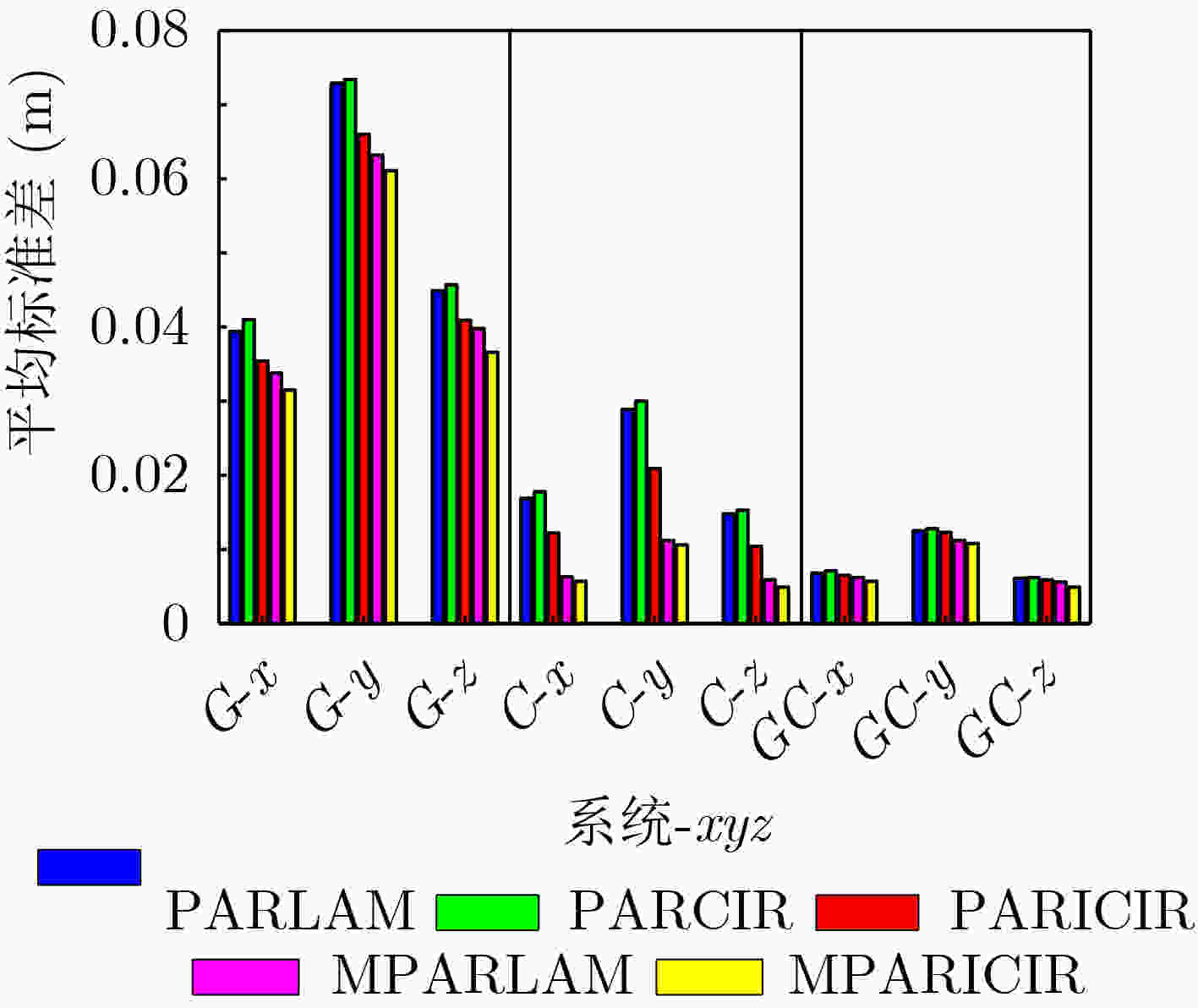
平均标准差		PAR LAM	PAR CIR	PAR ICIR	MPAR LAM	MPAR ICIR
G	x	0.039 4	0.041 0	0.035 4	0.033 8	0.031 5
	y	0.072 9	0.073 4	0.066 0	0.063 2	0.061 1
	z	0.044 9	0.045 7	0.040 9	0.039 8	0.036 6
C	x	0.016 9	0.017 8	0.012 2	0.006 3	0.005 7
	y	0.028 9	0.030 0	0.020 9	0.011 2	0.010 6
	z	0.014 8	0.015 3	0.010 4	0.005 9	0.004 9
GC	x	0.006 8	0.007 1	0.006 5	0.006 2	0.005 7
	y	0.012 5	0.012 8	0.012 3	0.011 2	0.010 8
	z	0.006 1	0.006 2	0.005 9	0.005 6	0.004 9

下载: 导出CSV

表 5 武汉数据集5种模糊度解算方法性能对比

武汉数据集		PAR LAM	PAR CIR	PAR ICIR	MPAR LAM	MPAR ICIR
总历元数		555
G	可定位历元	492	492	492	492	492
	固定解历元	462	460	464	472	478
	浮点解历元	30	32	28	20	14
	成功率(%)	93.7	93.5	94.3	96.1	97.2
	解算时间(s)	0.137	0.120	0.123	0.139	0.130
C	可定位历元	526	526	526	529	529
	固定解历元	449	446	479	510	523
	浮点解历元	77	80	47	19	6
	成功率(%)	85.4	84.8	91.1	96.4	98.9
	解算时间(s)	0.161	0.142	0.136	0.167	0.139
GC	可定位历元	537	537	537	537	537
	固定解历元	519	516	525	529	534
	浮点解历元	18	21	12	8	3
	成功率(%)	96.6	96.1	97.8	98.5	99.4
	解算时间(s)	0.183	0.166	0.151	0.173	0.158

下载: 导出CSV

参考文献(20)

[1]	CHEN Jiajia, WANG Jun, YUAN Hong, et al. Performance analysis of a GNSS multipath detection and mitigation method with two low-cost antennas in RTK positioning[J]. IEEE Sensors Journal, 2022, 22(6): 4827–4835. doi: 10.1109/JSEN.2021.3068767.
[2]	KHODABANDEH A, ZAMINPARDAZ S, and NADARAJAH N. A study on multi-GNSS phase-only positioning[J]. Measurement Science and Technology, 2021, 32(9): 095005. doi: 10.1088/1361-6501/abeced.
[3]	CAI Jianqing, GRAFAREND E W, and HU Congwei. The total optimal search criterion in solving the mixed integer linear model with GNSS carrier phase observations[J]. GPS Solutions, 2009, 13(3): 221–230. doi: 10.1007/s10291-008-0115-y.
[4]	ZHANG Zhetao, LI Bofeng, HE Xiufeng, et al. Models, methods and assessment of four-frequency carrier ambiguity resolution for BeiDou-3 observations[J]. GPS Solutions, 2020, 24(4): 96. doi: 10.1007/s10291-020-01011-z.
[5]	TEUNISSEN P J G. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation[J]. Journal of Geodesy, 1995, 70(1/2): 65–82. doi: 10.1007/BF00863419.
[6]	周非, 杨铁军, 黄顺吉. 基线约束辅助整周模糊度求解研究[J]. 电子学报, 2004, 32(9): 1549–1552. doi: 10.3321/j.issn:0372-2112.2004.09.037. ZHOU Fei, YANG Tiejun, and HUANG Shunji. Research of ambiguity resolution with baseline constraint[J]. Acta Electronica Sinica, 2004, 32(9): 1549–1552. doi: 10.3321/j.issn:0372-2112.2004.09.037.
[7]	GUO Jiang, GENG Jianghui, ZENG Jing, et al. GPS/Galileo/BDS phase bias stream from Wuhan IGS analysis center for real-time PPP ambiguity resolution[J]. GPS Solutions, 2024, 28(2): 67. doi: 10.1007/s10291-023-01610-6.
[8]	ZHANG Zhiteng, LI Bofeng, GAO Yang, et al. Asynchronous and time-differenced RTK for ocean applications using the BeiDou short message service[J]. Journal of Geodesy, 2023, 97(1): 7. doi: 10.1007/s00190-023-01699-0.
[9]	刘增军, 彭竞, 吕志成, 等. 一种适用于长基线的改进CIR算法[J]. 国防科技大学学报, 2013, 35(2): 93–98. doi: 10.3969/j.issn.1001-2486.2013.02.017. LIU Zengjun, PENG Jing, LV Zhicheng, et al. An improved CIR for long baseline[J]. Journal of National University of Defense Technology, 2013, 35(2): 93–98. doi: 10.3969/j.issn.1001-2486.2013.02.017.
[10]	TANG Weiming, DENG Chenlong, SHI Chuang, et al. Triple-frequency carrier ambiguity resolution for Beidou navigation satellite system[J]. GPS Solutions, 2014, 18(3): 335–344. doi: 10.1007/s10291-013-0333-9.
[11]	NING Yafei and YUAN Yunbin. A modified geometry- and ionospheric-free combination for static three-carrier ambiguity resolution[J]. GPS Solutions, 2017, 21(4): 1633–1645. doi: 10.1007/s10291-017-0642-5.
[12]	TANG Weiming, SHEN Mingxing, DENG Chenlong, et al. Network-based triple-frequency carrier phase ambiguity resolution between reference stations using BDS data for long baselines[J]. GPS Solutions, 2018, 22(3): 73. doi: 10.1007/s10291-018-0737-7.
[13]	PU Yakun, SONG Min, YUAN Yunbin, et al. Triple-frequency ambiguity resolution for GPS/Galileo/BDS between long-baseline network reference stations in different ionospheric regions[J]. GPS Solutions, 2022, 26(4): 146. doi: 10.1007/s10291-022-01336-x.
[14]	JI Shengyue, CHEN Wu, ZHAO Chunmei, et al. Single epoch ambiguity resolution for Galileo with the CAR and LAMBDA methods[J]. GPS Solutions, 2007, 11(4): 259–268. doi: 10.1007/s10291-007-0057-9.
[15]	HAN Houzeng, WANG Jian, WANG Jinling, et al. Reliable partial ambiguity resolution for single-frequency GPS/BDS and INS integration[J]. GPS Solutions, 2017, 21(1): 251–264. doi: 10.1007/s10291-016-0519-z.
[16]	YAN Zhongbao and ZHANG Xiaohong. The performance of three-frequency GPS PPP-RTK with partial ambiguity resolution[J]. Atmosphere, 2022, 13(7): 1014. doi: 10.3390/atmos13071014.
[17]	LI Xin, LI Xingxing, JIANG Zihao, et al. A unified model of GNSS phase/code bias calibration for PPP ambiguity resolution with GPS, BDS, Galileo and GLONASS multi-frequency observations[J]. GPS Solutions, 2022, 26(3): 84. doi: 10.1007/s10291-022-01269-5.
[18]	ZHANG Xu and YANG Jie. MPARELAM: A robust approach for ambiguity resolution in complex RTK positioning scenarios[J]. IEEE Sensors Journal, 2023, 23(17): 19582–19589. doi: 10.1109/JSEN.2023.3293461.
[19]	CHEN Guang’e, LI Bofeng, ZHANG Zhiteng, et al. Integer ambiguity resolution and precise positioning for tight integration of BDS-3, GPS, GALILEO, and QZSS overlapping frequencies signals[J]. GPS Solutions, 2022, 26(1): 26. doi: 10.1007/s10291-021-01203-1.
[20]	FENG Shaojun and JOKINEN A. Integer ambiguity validation in high accuracy GNSS positioning[J]. GPS Solutions, 2017, 21(1): 79–87. doi: 10.1007/s10291-015-0506-9.