Cross-Entropy Iteration Aided Time-Hopping Pattern Estimation and Multi-hop Coherent Combining Algorithm
-
摘要: 作为全球化通信网络的重要组成部分,卫星通信因其能够实现全球无缝覆盖和构建天地一体化信息网络而备受关注。跳时(TH)作为一种常用的卫星通信方式,具备强大的抗干扰能力、灵活的频谱利用和高安全性。该文提出一种适用于卫星通信的TH图案随机变化系统,以进一步增强数据传输过程的安全性。针对发射功率受限的问题,该文提出多跳信号相干合并策略,并进一步在该策略指导下,面对接收信号信噪比(SNR)低的约束,提出了交叉熵(CE)迭代辅助的跳时图案与多跳载波相位联合估计算法,以合并信噪比损失为目标函数,自适应调整待估参数的概率分布,从而快速收敛至最优解附近。仿真实验证明了该算法在迭代收敛速度、参数估计误差以及合并解调误码率等方面的优异性能。与传统算法相比,所提算法在保持较低复杂度的同时,误码率(BER)性能接近理论最优,有效提高了卫星TH通信系统在复杂环境下的稳定性和可靠性。Abstract:
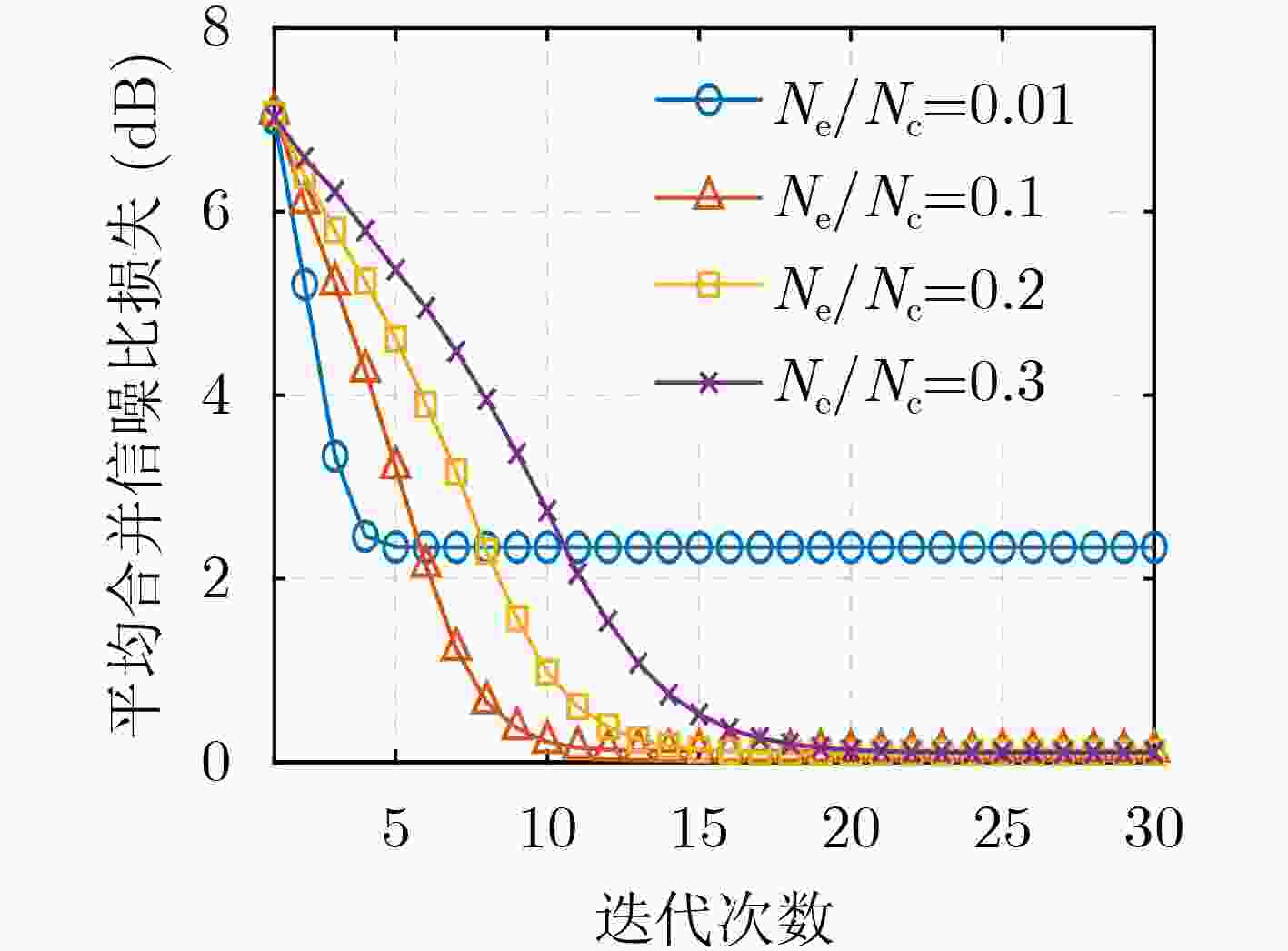
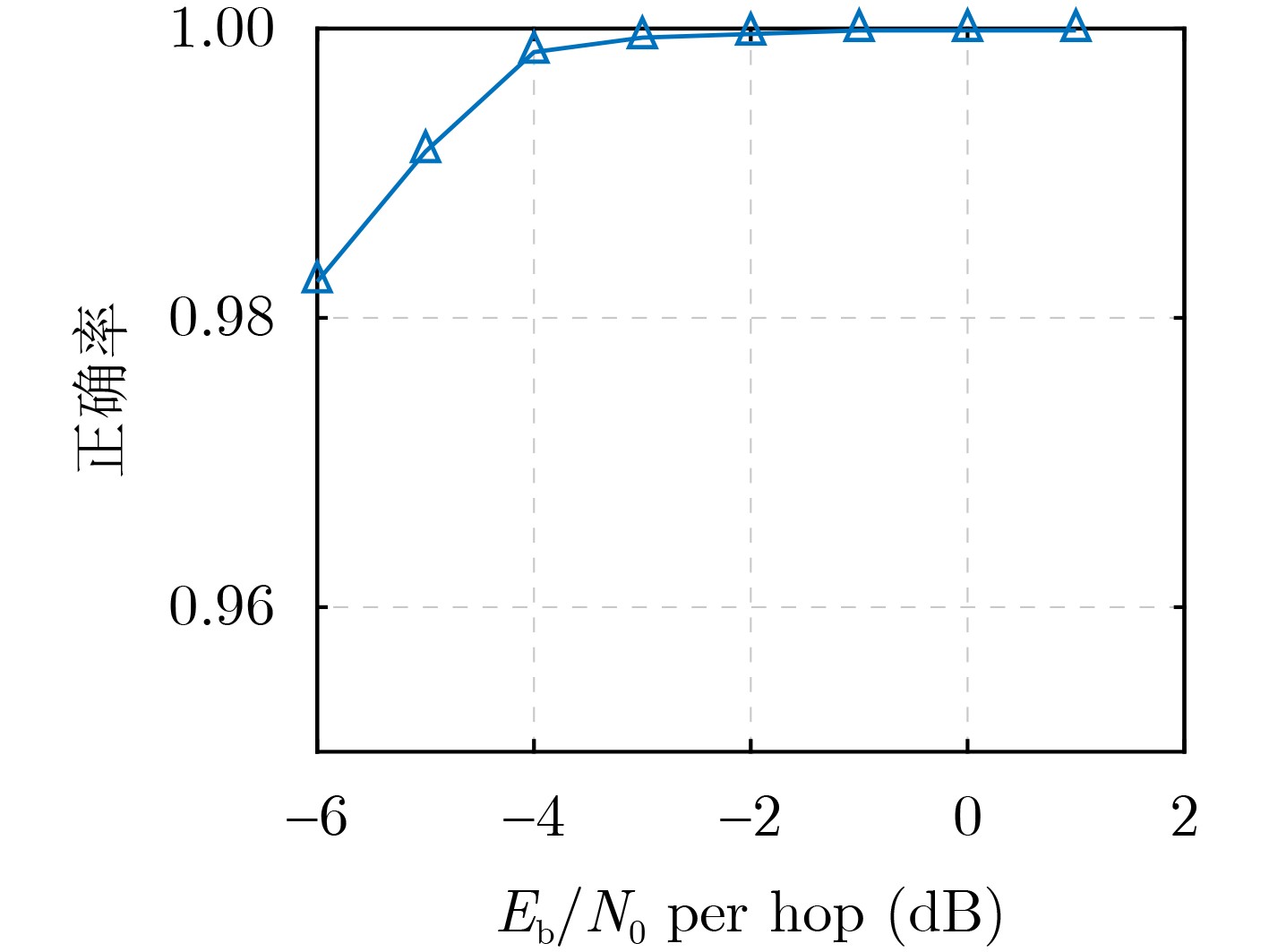
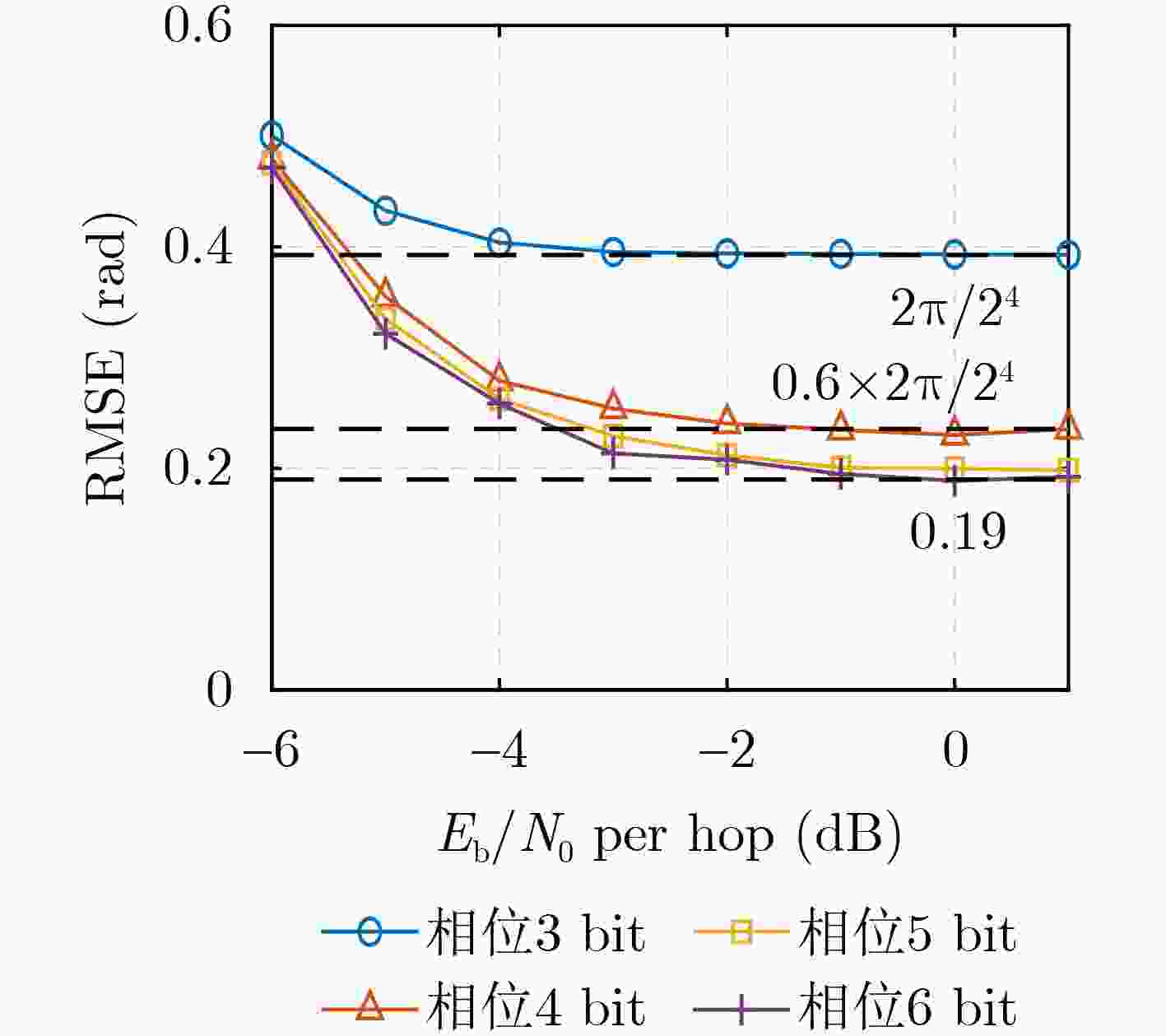
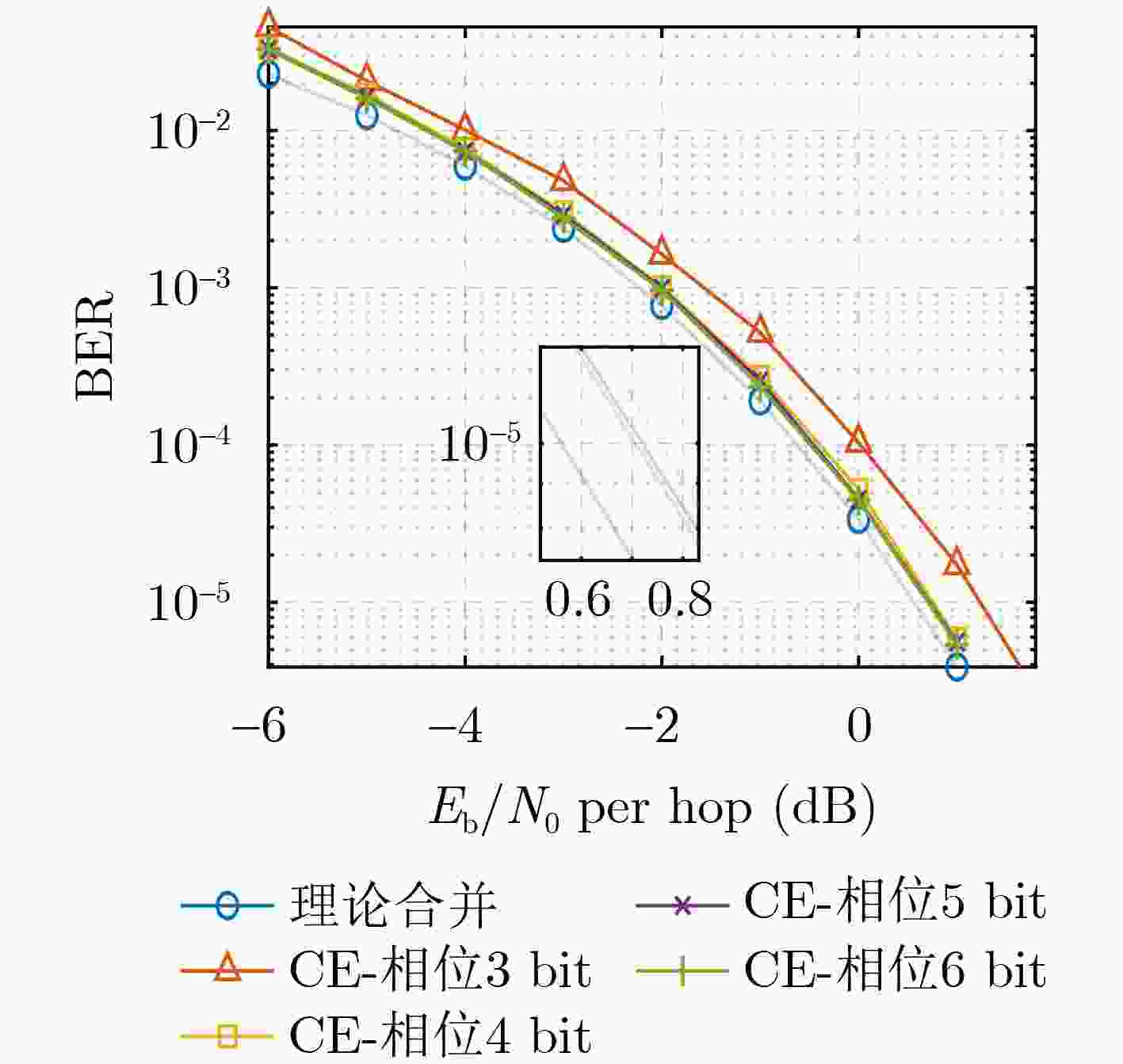
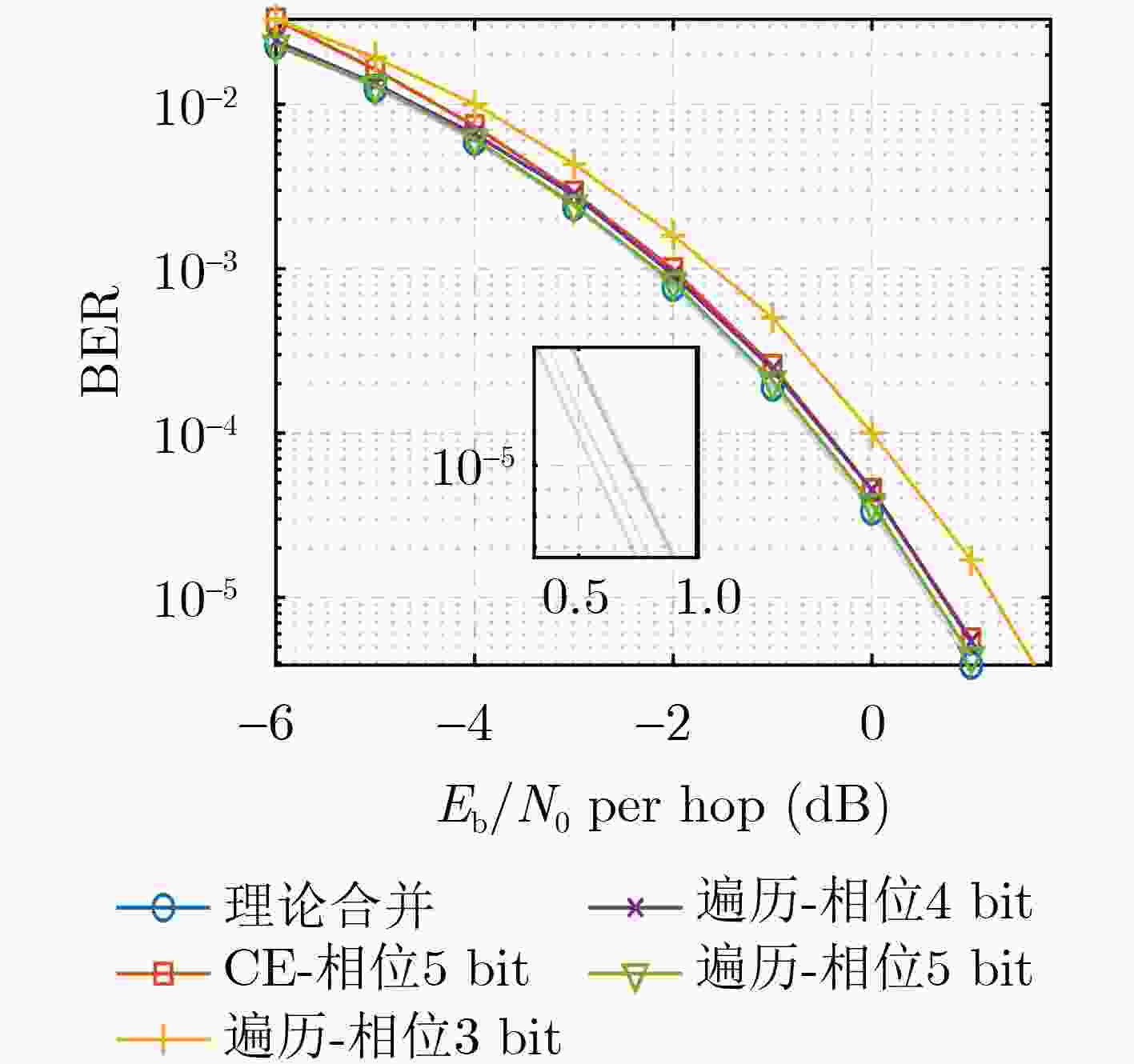
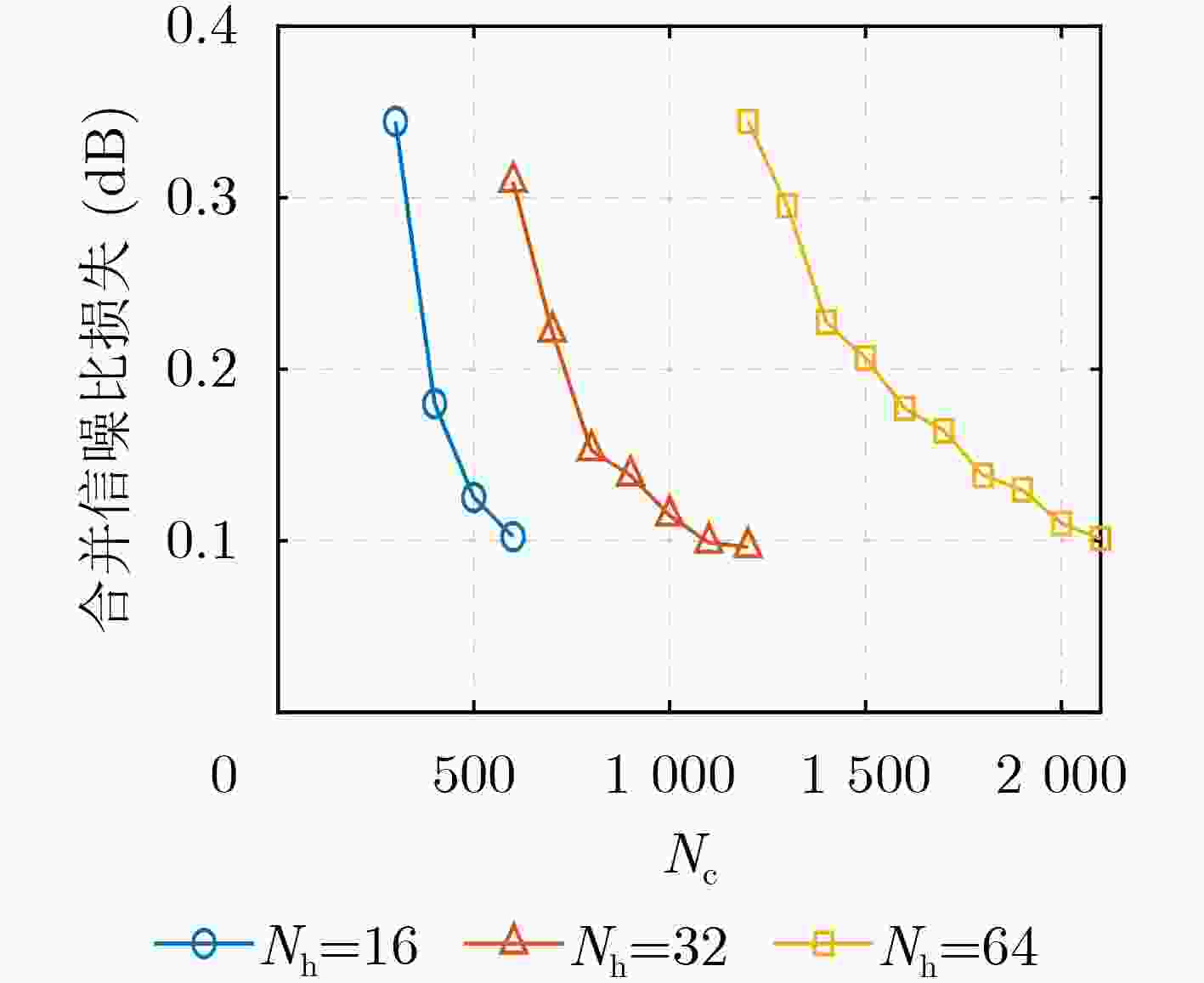
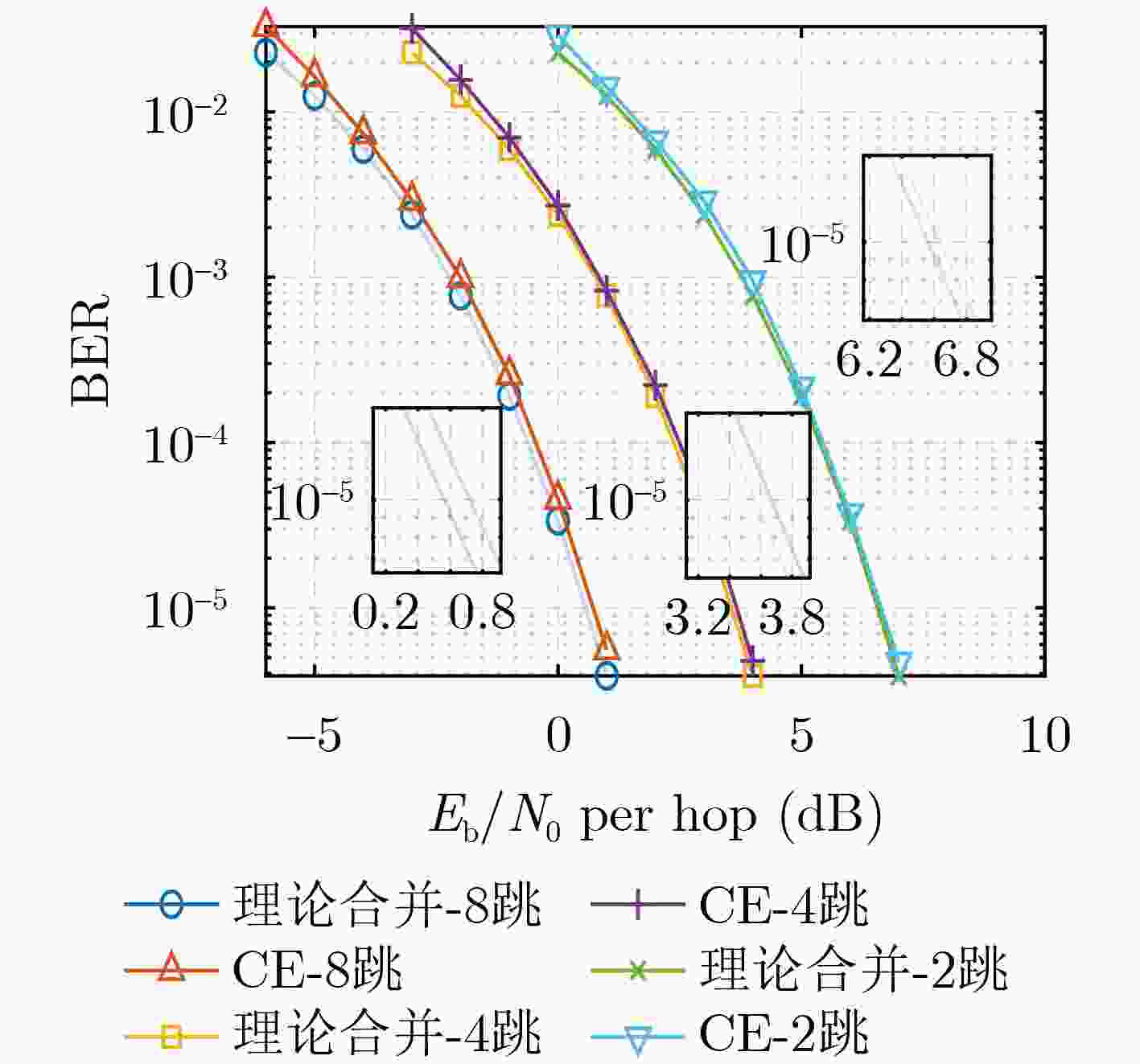
Objective: As a vital component of the global communication network, satellite communication attracts significant attention for its capacity to provide seamless global coverage and establish an integrated space-ground information network. Time-Hopping (TH), a widely used technique in satellite communication, is distinguished by its strong anti-jamming capabilities, flexible spectrum utilization, and high security levels. In an effort to enhance data transmission security, a system utilizing randomly varying TH patterns has been developed. To tackle the challenge of limited transmission power, symbols are distributed across different time slots and repeatedly transmitted according to random TH patterns. At the receiver end, a coherent combining strategy is implemented for signals originating from multiple time slots. To minimize Signal-to-Noise Ratio (SNR) loss during this combining process, precise estimation of TH patterns and multi-hop carrier phases is essential. The randomness of the TH patterns and multi-hop carrier phases further complicates parameter estimation by increasing its dimensionality. Additionally, the low transmission power leads to low-SNR conditions for the received signals in each time slot, complicating parameter estimation even more. Traditional exhaustive search methods are hindered by high computational complexity, highlighting the pressing need for low-complexity multidimensional parameter estimation techniques tailored specifically for TH communication systems. Methods: Firstly, a TH communication system featuring randomly varying TH patterns is developed, where the time slot index of the signal in each time frame is determined by the TH code. Both parties involved in the communication agree that this TH code will change randomly within a specified range. Building on this foundation, a mathematical model for estimating TH patterns and multi-hop carrier phases is derived from the perspective of maximum likelihood estimation, framing it as a multidimensional nonlinear optimization problem. Moreover, guided by a coherent combining strategy and constrained by low SNR conditions at the receiver, a Cross-Entropy (CE) iteration aided algorithm is proposed for the joint estimation of TH patterns and multi-hop carrier phases. This algorithm generates multiple sets of TH code and carrier phase estimates randomly based on a predetermined probability distribution. Using the SNR loss of the combined signal as the objective function, the CE method incorporates an adaptive importance sampling strategy to iteratively update the probability distribution of the estimated parameters, facilitating rapid convergence towards optimal solutions. Specifically, in each iteration, samples demonstrating superior performance are selected according to the objective function to calculate the probability distribution for the subsequent iteration, thereby enhancing the likelihood of reaching the optimal solution. Additionally, to account for the randomness inherent in the iterations, a global optimal vector set is established to document the parameter estimates that correspond to the minimum SNR loss throughout the iterative process. Finally, simulation experiments are conducted to assess the performance of the proposed algorithm in terms of iterative convergence speed, parameter estimation error, and the combined demodulation Bit Error Rate (BER). Results and Discussions: The estimation errors for the TH code and carrier phase were simulated to evaluate the parameter estimation performance of the proposed algorithm. With an increase in SNR, the accuracy of TH code estimation approaches unity. When a small phase quantization bit width is applied, the Root Mean Square Error (RMSE) of the carrier phase estimation is primarily constrained by the grid search step size. Conversely, as the phase quantization bit width increases, the RMSE gradually converges to a fixed value. Regarding the influence of phase quantization on combined demodulation, as the phase quantization bit width increases, nearly theoretical BER performance can be achieved. A comparison between the proposed algorithm and the exhaustive search method reveals that the proposed algorithm significantly reduces the number of search trials compared to the grid search method, with minimal loss in BER performance. An increase in the variation range of the TH code necessitates a larger number of candidate groups for the CE method to maintain a low combining SNR loss. However, with a greater TH code variation range, the number of search iterations and its growth rate in the proposed algorithm are significantly lower than those in the exhaustive search method. Regarding transmission power in the designed TH communication method, as the number of hops in the multi-hop combination increases, the required SNR per hop decreases for the same BER performance, indicating that maximum transmission power can be correspondingly reduced. Conclusions: A TH communication system with randomly varying TH patterns tailored for satellite communication applications has been designed. This includes the presentation of a multi-hop signal coherent combining technique. To address the multidimensional parameter estimation challenge associated with TH patterns and multi-hop carrier phases under low SNR conditions, a CE iteration-aided algorithm has been proposed. The effectiveness of this algorithm is validated through simulations, and its performance regarding iterative convergence characteristics, parameter estimation error, and BER performance has been thoroughly analyzed. The results indicate that, in comparison to the conventional grid search method, the proposed algorithm achieves near-theoretical optimal BER performance while maintaining lower complexity. -
1 交叉熵迭代辅助的跳时图案估计与相干合并算法
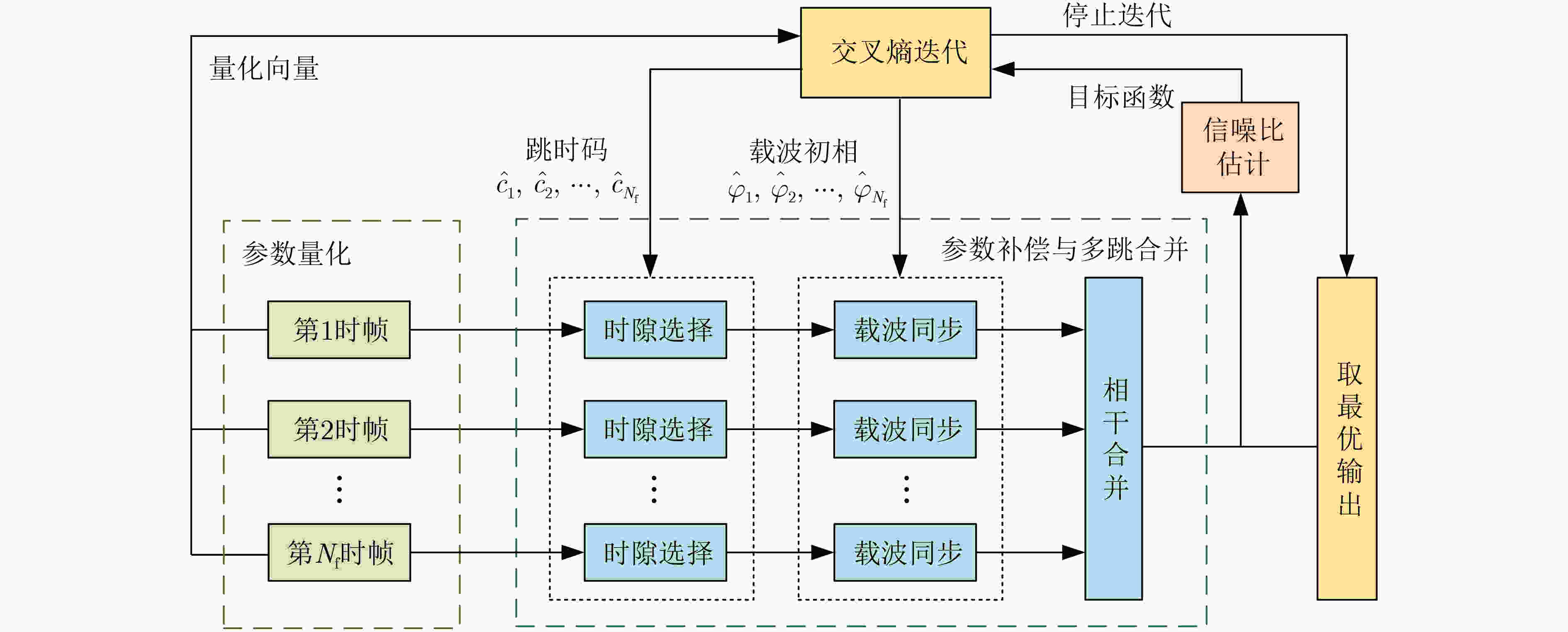
输入:载波初相和跳时码的量化候选组数$ {N_{\rm c}} $,优选组数$ {N_{\rm e}} $,平滑系数$ \alpha $,最大迭代次数$ {I_{\max}} $,$ {N_{\rm f}} $帧数据,载波初相量化比特位数$ {D_1} $,
跳时码量化比特位数$ {D_2} $;初始化:$ {N_{\rm f}} $帧信号的载波初相和跳时码量化比特生成概率$ {\hat {\boldsymbol{p}}^1} = 0.5 \times {{{{\textit{1}}}}_{1 \times {N_{\rm f}}({D_1} + {D_2})}} $,$ {\hat {\boldsymbol{p}}^i} $元素为0或1的个数$ M = 0 $,迭代次数$ i = 1 $; while $ M \lt {N_{\rm f}}({D_1} + {D_2}) $ && $ 1 \le i \le {I_{\max}} $ do (1) 根据概率$ {\hat {\boldsymbol{p}}^i} $生成$ {N_{\rm c}} $组候选组参数向量; (2) 根据每组参数向量对$ {N_{\rm f}} $帧数据分别进行时隙选择与载波初相补偿,并进行多跳信号的相干合并; (3) 对每组参数向量得到的合并信号进行合并信噪比损失估计,将共$ {N_{\rm c}} $组估计结果按照从小到大排序; (4) 取合并信噪比损失最小的前$ {N_{\rm e}} $组作为优选组,计算优选组量化比特为1的概率$ {{\boldsymbol{p}}^{i + 1}} $,更新概率向量$ {\hat {\boldsymbol{p}}^{i + 1}} $; (5) 将合并信噪比损失最小的一组参数向量记为$ {\boldsymbol{q}}_{{\mathrm{tmp}}}^i $,其损失记为$ \gamma _{{\mathrm{tmp}}}^i $; if $ i = = 1 $ then $ {{\boldsymbol{q}}_{{\mathrm{opt}}}} = {\boldsymbol{q}}_{{\mathrm{tmp}}}^i $; $ {\gamma _{\min }} = \gamma _{{\mathrm{tmp}}}^i $; else if $\gamma _{{\mathrm{tmp}}}^i \lt {\gamma _{\min }}$ then $ {{\boldsymbol{q}}_{{\mathrm{opt}}}} = {\boldsymbol{q}}_{{\mathrm{tmp}}}^i $; $ {\gamma _{\min }} = \gamma _{{\mathrm{tmp}}}^i $; end if (6) 更新$ {\hat {\boldsymbol{p}}^{i + 1}} $元素为0或1的个数$ M $,$ i = i + 1 $; end while 输出:$ {N_{\rm f}} $帧载波初相和跳时码的最优组合$ {{\boldsymbol{q}}_{{\mathrm{opt}}}} $ 表 1 仿真参数
参数名称 参数设置 调制方式 BPSK 信道类型 AWGN 跳数 2, 4, 8 每时帧的时隙数 4, 16, 32, 64 每跳的符号数 1 000 表 2 不同跳时码变化范围的搜索次数
跳时码量化位数 4 5 6 候选组数 600 1200 2100 迭代次数 30 38 51 所提算法搜索次数(相位5 bit量化) 18 000 45 600 107 100 遍历法搜索次数(相位3 bit量化) 256 264 272 遍历法搜索次数(相位4 bit量化) 264 272 280 遍历法搜索次数(相位5 bit量化) 272 280 288 -
[1] ZHOU Di, SHENG Min, LI Jiandong, et al. Aerospace integrated networks innovation for empowering 6G: A survey and future challenges[J]. IEEE Communications Surveys & Tutorials, 2023, 25(2): 975–1019. doi: 10.1109/COMST.2023.3245614. [2] GERACI G, LÓPEZ-PÉREZ D, BENZAGHTA M, et al. Integrating terrestrial and non-terrestrial networks: 3D opportunities and challenges[J]. IEEE Communications Magazine, 2023, 61(4): 42–48. doi: 10.1109/MCOM.002.2200366. [3] QUY V K, CHEHRI A, QUY N M, et al. Innovative trends in the 6G Era: A comprehensive survey of architecture, applications, technologies, and challenges[J]. IEEE Access, 2023, 11: 39824–39844. doi: 10.1109/ACCESS.2023.3269297. [4] SCHOLTZ R. Multiple access with time-hopping impulse modulation[C]. IEEE Military Communications Conference, Boston, USA, 1993: 447–450. doi: 10.1109/MILCOM.1993.408628. [5] WELBORN M L. System considerations for ultra-wideband wireless networks[C]. 2001 IEEE Radio and Wireless Conference, Waltham, USA, 2001: 5–8. doi: 10.1109/RAWCON.2001.947480. [6] ALI T, SIDDIQUA P, and MATIN M A. Performance evaluation of different modulation schemes for ultra wide band systems[J]. Journal of Electrical Engineering, 2014, 65(3): 184–188. doi: 10.2478/jee-2014-0029. [7] YANG Liuqing and GIANNAKIS G B. Timing ultra-wideband signals with dirty templates[J]. IEEE Transactions on Communications, 2005, 53(11): 1952–1963. doi: 10.1109/TCOMM.2005.858663. [8] WU Tao, JI Zhiyong, and ZHAO Yubin. An adaptive UWB synchronization algorithm based on the IEEE 802.15. 4–2020 protocol[C]. 2023 IEEE International Conferences on Internet of Things (iThings) and IEEE Green Computing & Communications (GreenCom) and IEEE Cyber, Physical & Social Computing (CPSCom) and IEEE Smart Data (SmartData) and IEEE Congress on Cybermatics (Cybermatics), Danzhou, China, 2023: 647–653. doi: 10.1109/iThings-GreenCom-CPSCom-SmartData-Cybermatics60724.2023.00117. [9] NAVARRO M and NAJAR M. Frequency domain joint TOA and DOA estimation in IR-UWB[J]. IEEE Transactions on Wireless Communications, 2011, 10(10): 1–11. doi: 10.1109/TWC.2011.072511.090933. [10] DIACONESCU F. Blind detection of impulse radio UWB time-hopping pulses using the phase space transformation[C]. The 2019 11th International Conference on Electronics, Computers and Artificial Intelligence, Pitesti, Romania, 2019: 1–4. doi: 10.1109/ECAI46879.2019.9042136. [11] DIACONESCU F. Impulse radio UWB blind detection using cross recurrence plot[C]. Proceedings of the 2020 13th International Conference on Communications, Bucharest, Romania, 2020: 397–400. doi: 10.1109/COMM48946.2020.9141986. [12] BORIO D and ODRISCOLL C. Design of a general pseudolite pulsing scheme[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(1): 2–16. doi: 10.1109/TAES.2013.110277. [13] LIU Tong, LIU Jian, WANG Jing, et al. Pseudolites to support location services in smart cities: Review and prospects[J]. Smart Cities, 2023, 6(4): 2081–2105. doi: 10.3390/smartcities6040096. [14] CHEONG J W. Signal processing and collective detection for locata positioning system[D]. [Ph. D. dissertation], University of New South Wales, 2012. [15] HU Yi, YU Baoguo, SONG Maozhong, et al. Pulse position detection of the pseudo random time-hopping pseudolite for the participative GNSS receivers[J]. IEEE Access, 2020, 8: 216151–216161. doi: 10.1109/ACCESS.2020.3040960. [16] LIU Xu, YAO Zheng, and LU Mingquan. Robust time-hopping pseudolite signal acquisition method based on dynamic Bayesian network[J]. GPS Solutions, 2021, 25(2): 38. doi: 10.1007/s10291-020-01066-y. -





 下载:
下载:


 下载:
下载:
