Two-stage Constrained Weighted Least Squares method for Multistatic Passive Localization of a Moving Object Under Unknown Transmitter Position and Velocity
-
摘要: 针对发射站位置与速度未知时的运动目标定位问题,该文提出一种低复杂度的两阶段定位算法。首先,利用直接路径时间迟延和多普勒频移量测构建一个基于约束加权最小二乘(CWLS)模型获得发射站的位置和速度。然后,将发射站位置和速度估计值代入直接路径和间接路径联合模型,建立基于CWLS的目标位置和速度估计模型,利用拟牛顿法求解目标的位置和速度。理论分析和仿真结果显示所提算法定位性能达到克拉美罗下界(CRLB)。
-
关键词:
- 多基外辐射源定位 /
- 运动目标 /
- 未知发射站位置和速度 /
- 约束加权最小二乘 /
- 拟牛顿法
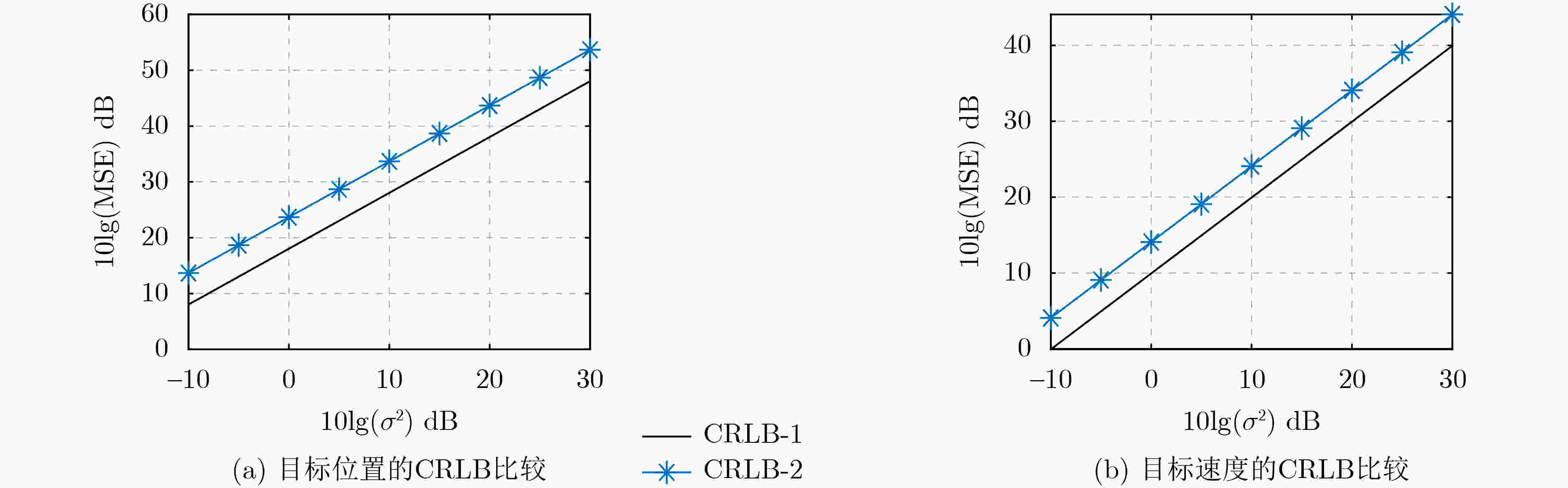
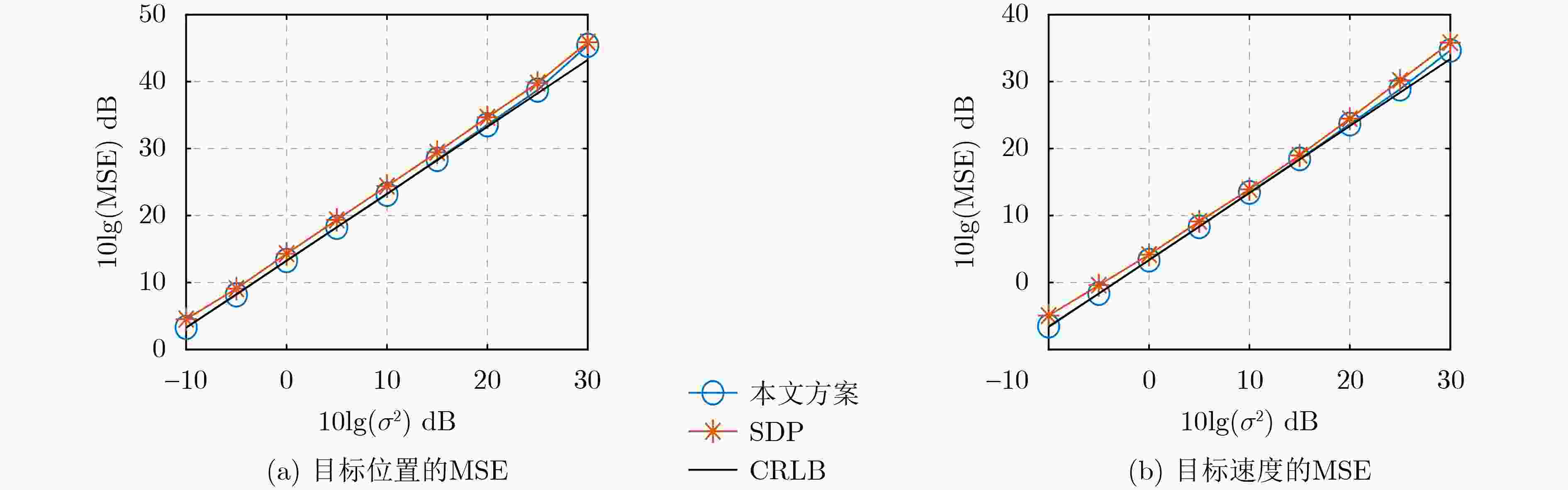
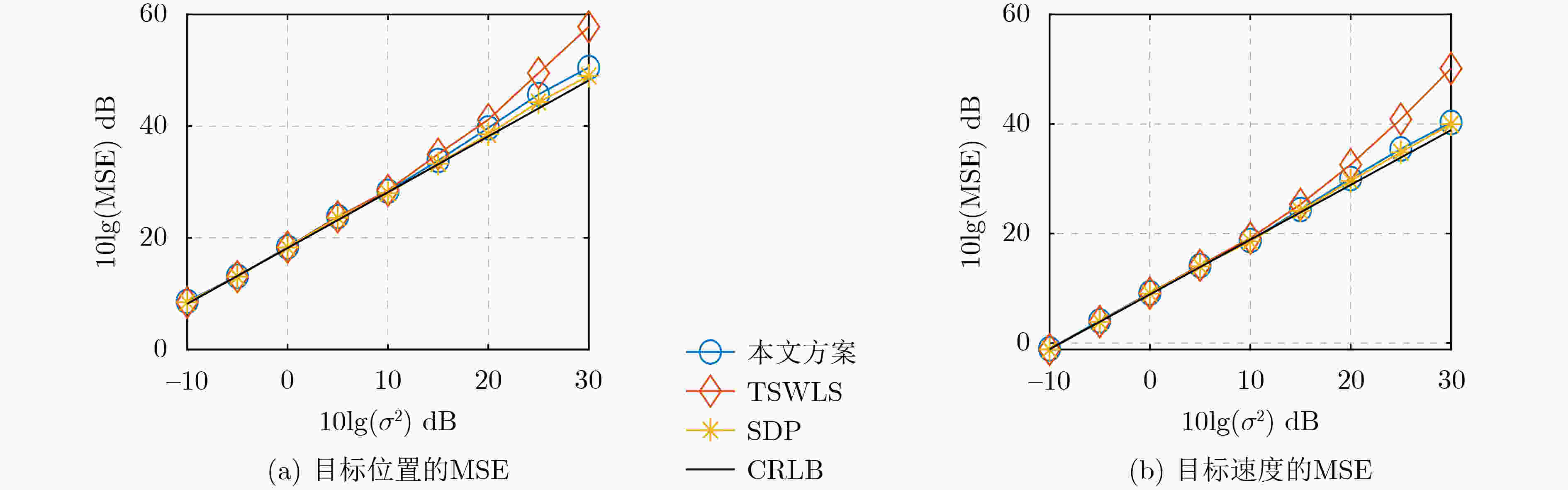
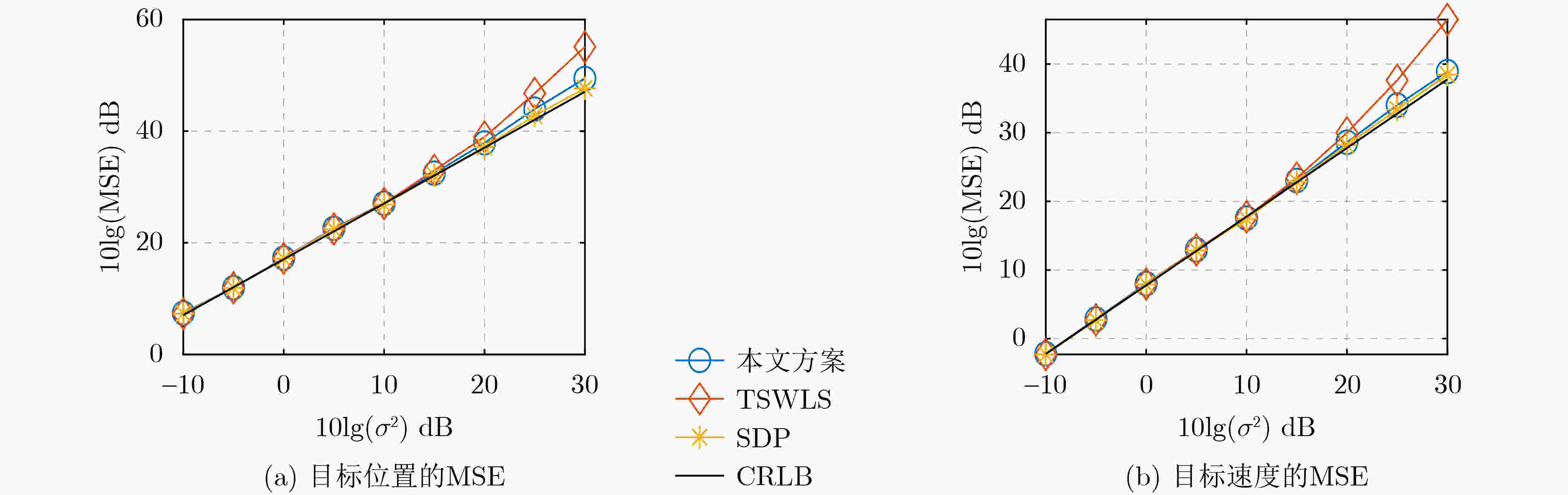
Abstract:Objective This study addresses target localization in multistatic passive radar systems under conditions where the transmitter’s position and velocity are unknown. Multistatic passive radar systems utilize covert deployment, exhibit resilience to jamming, and provide wide-area coverage. Conventional localization techniques rely on precise transmitter state information, which is often unavailable due to the mobility of transmitters mounted on dynamic platforms. Environmental disturbances can further introduce inaccuracies in position and velocity measurements. In non-cooperative scenarios, direct acquisition of transmitter state information is typically infeasible. Existing localization methods, such as the Two-Step Weighted Least Squares (TSWLS) approach, exhibit a threshold effect under high noise conditions, while the Semi-Definite Programming (SDP) method achieves Cramér-Rao Lower Bound (CRLB) accuracy but incurs excessive computational costs, limiting real-time applicability. To address these challenges, a localization algorithm is formulated that enables high-precision tracking of moving targets under uncertain transmitter conditions while maintaining relatively low computational complexity. Methods Multistatic passive radar localization systems employ two receiving channels: the reference channel, which receives direct signals from the transmitter, and the surveillance channel, which captures signals reflected from the target. Delay-Doppler cross-correlation between the reflected and reference signals enables the measurement of time delay and Doppler shift. The time delay from the reference channel corresponds to the distance between the transmitter and receivers, denoted as the Direct Range (DR), while the associated Doppler shift represents the Direct Range Rate (DRR). Similarly, the bistatic time delay from the surveillance channel corresponds to the sum of the distances between the target, transmitter, and receivers, referred to as the Bistatic Range (BR), with the associated Doppler shift representing the Bistatic Range Rate (BRR). A two-stage localization algorithm is proposed for estimating the positions and velocities of both the target and transmitter. In the first stage, a Constrained Weighted Least Squares (CWLS) problem is formulated using DR and DRR measurements to estimate the transmitter’s position and velocity. In the second stage, the estimated transmitter state is incorporated into the DR/DRR and BR/BRR measurements to construct a new CWLS problem. This problem is then solved using the Quasi-Newton method to determine the position and velocity of the moving target. Results and Discussions Compared with traditional localization approaches that rely solely on indirect path information (BR/BRR), incorporating direct path information (DR/DRR) for joint estimation improves target localization accuracy when the transmitter’s position and velocity are unknown ( Figure 1 ). The performance of the proposed two-stage localization algorithm is evaluated through Monte Carlo simulations and compared with the TSWLS method, the SDP approach, and the CRLB. Estimation accuracy is assessed using the Mean Squared Error (MSE), while algorithm complexity is evaluated based on runtime. In scenarios with only four receivers, the TSWLS algorithm fails to provide accurate estimates, whereas the proposed algorithm maintains localization performance, with deviations occurring only when noise reaches 25 dB (Figure 2 ). When five receivers with uncorrelated noise are used, the TSWLS algorithm deviates from the CRLB and exhibits a threshold effect at a measurement noise level of 10 dB. At 30 dB, the proposed algorithm reduces the MSE for target position estimation by approximately 7 m2 compared to the TSWLS algorithm, slightly outperforming the SDP algorithm, and reduces the MSE for target velocity estimation by approximately 10 (m/s)2, approaching the localization accuracy of the SDP algorithm (Figure 3 ). When 5 receivers with correlated noise are used, the TSWLS algorithm begins to deviate from the CRLB at a noise variance of 15 dB and exhibits significant performance degradation at 30 dB. Under these conditions, the proposed algorithm reduces the MSE for target position estimation by approximately 5 m2 compared to the TSWLS algorithm, slightly outperforming the SDP algorithm, and reduces the MSE for target velocity estimation by approximately 7 (m/s)2, achieving localization accuracy comparable to the SDP algorithm (Figure 4 ). While the SDP algorithm has higher computational complexity and longer runtime, the proposed algorithm achieves a shorter runtime while maintaining localization accuracy, demonstrating good real-time performance (Table 1 ).Conclusions This study investigates the localization of a moving target in a multistatic passive radar system when the transmitter’s position and velocity are unknown. By leveraging time delay and Doppler frequency shift measurements from both direct and indirect paths, a quadratic constraint model is formulated and iteratively solved using the Quasi-Newton method. Simulation results demonstrate that the proposed algorithm can achieve CRLB accuracy even under high-noise conditions. Compared with localization algorithms based on joint transmitter and target estimation using TSWLS and SDP, the proposed algorithm achieves lower computational complexity and enables three-dimensional moving target localization with only four receivers. The proposed method, designed for a single-transmitter multiple-receiver system, can be directly extended to multiple-transmitter multiple-receiver configurations. Additionally, this method assumes time synchronization between the transmitter and receivers. Future research will focus on extending multistatic passive radar localization to scenarios where the transmitter is not synchronized with the receivers. -
表 1 不同算法平均耗时比较(5个接收站)
求解算法 TSWLS SDP 所提算法 平均耗时(ms) 0.552 4 393.463 5 3.316 0 -
[1] 万显荣. 基于低频段数字广播电视信号的外辐射源雷达发展现状与趋势[J]. 雷达学报, 2012, 1(2): 109–123. doi: 10.3724/SP.J.1300.2012.20027.WAN Xianrong. An overview on development of passive radar based on the low frequency band digital broadcasting and TV signals[J]. Journal of Radars, 2012, 1(2): 109–123. doi: 10.3724/SP.J.1300.2012.20027. [2] 万显荣, 易建新, 占伟杰, 等. 基于多照射源的被动雷达研究进展与发展趋势[J]. 雷达学报, 2020, 9(6): 939–958. doi: 10.12000/JR20143.WAN Xianrong, YI Jianxin, ZHAN Weijie, et al. Research progress and development trend of the multi-illuminator-based passive radar[J]. Journal of Radars, 2020, 9(6): 939–958. doi: 10.12000/JR20143. [3] MALANOWSKI M and KULPA K. Two methods for target localization in multistatic passive radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 572–580. doi: 10.1109/TAES.2012.6129656. [4] 王鼎, 魏帅. 基于外辐射源的约束总体最小二乘定位算法及其理论性能分析[J]. 中国科学: 信息科学, 2015, 45(11): 1466–1489. doi: 10.1360/N112014-00397.WANG Ding and WEI Shuai. The constrained-total-least- squares localization algorithm and performance analysis based on an external illuminator[J]. Scientia Sinica Informationis, 2015, 45(11): 1466–1489. doi: 10.1360/N112014-00397. [5] NIU Ruixin, BLUM R S, VARSHNEY P K, et al. Target localization and tracking in noncoherent multiple-input multiple-output radar systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1466–1489. doi: 10.1109/TAES.2012.6178073. [6] DU Yanshen and WEI Ping. An explicit solution for target localization in noncoherent distributed MIMO radar systems[J]. IEEE Signal Processing Letters, 2014, 21(9): 1093–1097. doi: 10.1109/LSP.2014.2325999. [7] YANG H and CHUN J. An improved algebraic solution for moving target localization in noncoherent MIMO radar systems[J]. IEEE Transactions on Signal Processing, 2016, 64(1): 258–270. doi: 10.1109/TSP.2015.2477803. [8] 赵勇胜, 赵拥军, 赵闯, 等. 一种新的分布式MIMO雷达系统运动目标定位代数解算法[J]. 电子与信息学报, 2018, 40(3): 548–556. doi: 10.11999/JEIT170510.ZHAO Yongsheng, ZHAO Yongjun, ZHAO Chuang, et al. New algebraic algorithm for moving target localization in distributed MIMO radar systems[J]. Journal of Electronics & Information Technology, 2018, 40(3): 548–556. doi: 10.11999/JEIT170510. [9] AMIRI R, BEHNIA F, and SADR M A M. Positioning in MIMO radars based on constrained least squares estimation[J]. IEEE Communications Letters, 2017, 21(10): 2222–2225. doi: 10.1109/LCOMM.2017.2724541. [10] 万显荣, 武冰倩, 易建新, 等. 面向外辐射源雷达发射站定位的合作无人机航迹规划方法研究[J]. 电子与信息学报, 2024, 46(5): 2057–2064. doi: 10.11999/JEIT231293.WAN Xianrong, WU Bingqian, YI Jianxin, et al. UAV path planning method for passive radar transmitter localization[J]. Journal of Electronics & Information Technology, 2024, 46(5): 2057–2064. doi: 10.11999/JEIT231293. [11] ZHANG Yang and HO K C. Multistatic localization in the absence of transmitter position[J]. IEEE Transactions on Signal Processing, 2019, 67(18): 4745–4760. doi: 10.1109/TSP.2019.2929960. [12] ZHAO Yongsheng, HU Dexiu, ZHAO Yongjun, et al. Moving target localization in distributed MIMO radar with transmitter and receiver location uncertainties[J]. Chinese Journal of Aeronautics, 2019, 32(7): 1705–1715. doi: 10.1016/j.cja.2018.12.029. [13] 王鼎, 高卫港, 聂福全, 等. 校正源存在下抑制部分同步时钟偏差和传感器位置误差的时差定位闭式解[J]. 航空学报, 2023, 44(16): 328057. doi: 10.7527/S1000-6893.2022.28057.WANG Ding, GAO Weigang, NIE Fuquan, et al. A closed-form solution for TDOA source localization with calibration emitter in presence of partial synchronization clock biases and sensor location uncertainties[J]. Acta Aeronautica et Astronautica Sinica, 2023, 44(16): 328057. doi: 10.7527/S1000-6893.2022.28057. [14] WANG Gang, JIANG Zhenguo, and HO K C. Multistatic localization aided by a calibration object in the absence of synchronization and transmitter position[J]. IEEE Transactions on Wireless Communications, 2024, 23(6): 6362–6377. doi: 10.1109/TWC.2023.3331104. [15] 白璐, 郑瑞超, 王刚. 未知发射机位置的闭式解椭圆定位方法[J]. 传感技术学报, 2023, 36(12): 1893–1899. doi: 10.3969/j.issn.1004-1699.2023.12.009.BAI Lu, ZHENG Ruichao, and WANG Gang. Closed-form solution for elliptic localization with unknown transmitter position[J]. Chinese Journal of Sensors and Actuators, 2023, 36(12): 1893–1899. doi: 10.3969/j.issn.1004-1699.2023.12.009. [16] WU Wenjun, WANG Gang, and HO K C. Multistatic localization by differential time delays and time differences of arrival in the absence of transmitter position[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(5): 7020–7034. doi: 10.1109/TAES.2023.3287814. [17] ZHANG Yang and HO K C. Multistatic moving object localization by a moving transmitter of unknown location and offset[J]. IEEE Transactions on Signal Processing, 2020, 68: 4438–4453. doi: 10.1109/TSP.2020.3008752. [18] WANG Gang, ZHANG Ruichao, and HO K C. Elliptic localization of a moving object by transmitter at unknown position and velocity: A semidefinite relaxation approach[J]. IEEE Transactions on Mobile Computing, 2023, 22(5): 2675–2692. doi: 10.1109/TMC.2021.3123330. [19] RAO S S. Engineering Optimization Theory and Practice[M]. 4th ed. Hoboken, New Jersey: John Wiley & Sons, Inc. , 2009. doi: 10.1002/9780470549124. -





 下载:
下载:


 下载:
下载:
