Throughput Maximization for Double RIS-Assisted MISO Systems
-
摘要: 近年来,有源可重构智能表面(ARIS)技术获得了学术界的广泛关注。然而,ARIS在多RIS辅助无线通信系统中的应用还缺乏相关研究。针对此问题,该文提出基于双RIS辅助的无线通信系统模型。模型假设基站(BS)和用户之间的直连链路受阻,仅通过RIS形成的反射链路进行通信。在此基础上,根据ARIS与被动RIS(PRIS)的不同组合情况,提出4种RIS组合模型。模型的目标是优化基站波束赋形、RIS的相移矩阵和功率分配因子,以最大化系统通信容量。由于该优化问题为非凸问题,该文采用了交替优化算法(AO)与连续凸逼近(SCA)对问题进行处理。仿真结果表明,无论基站发射功率高或低,TAAR组合模型的性能均显著优于传统单ARIS配置。Abstract:
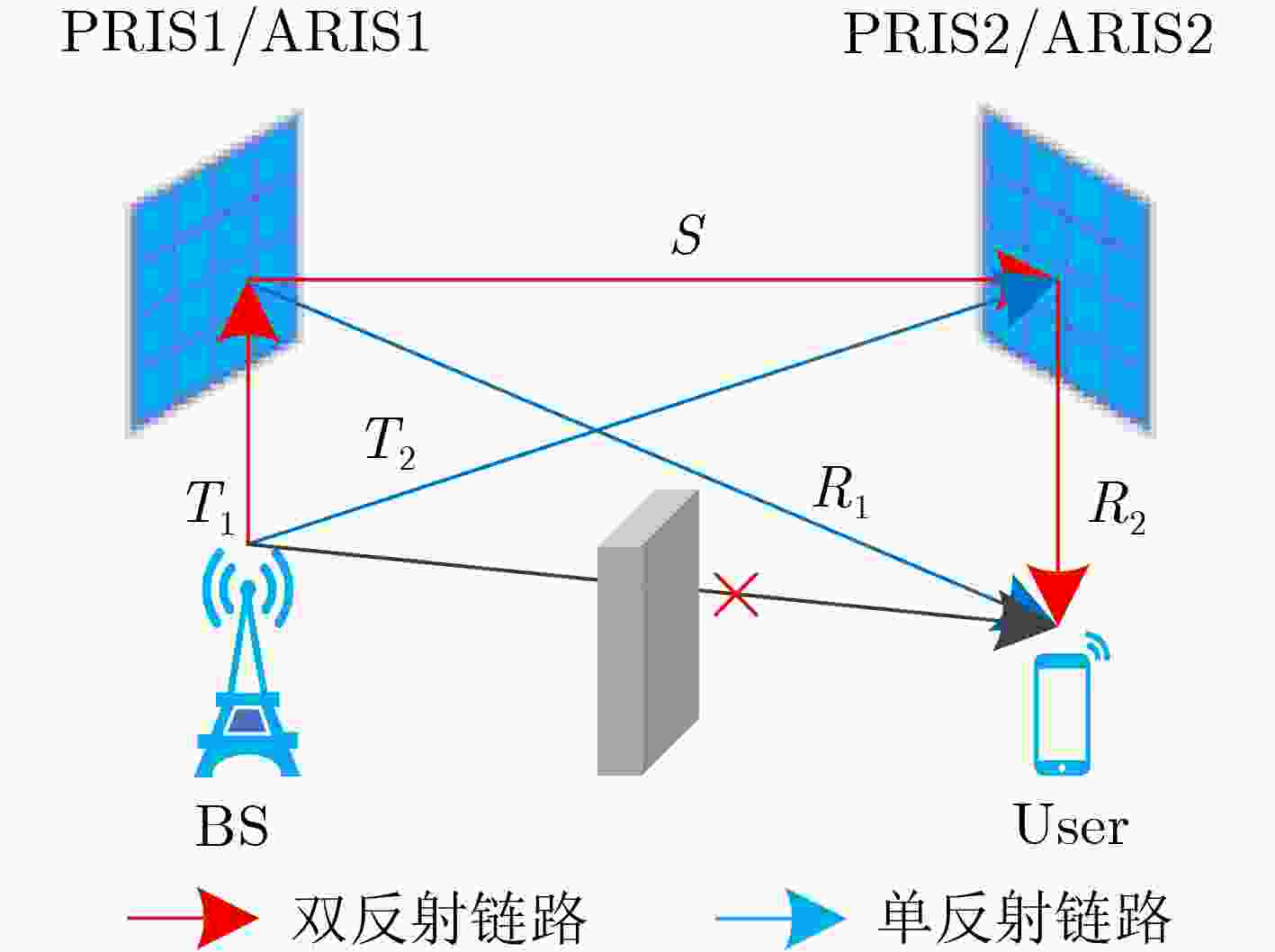
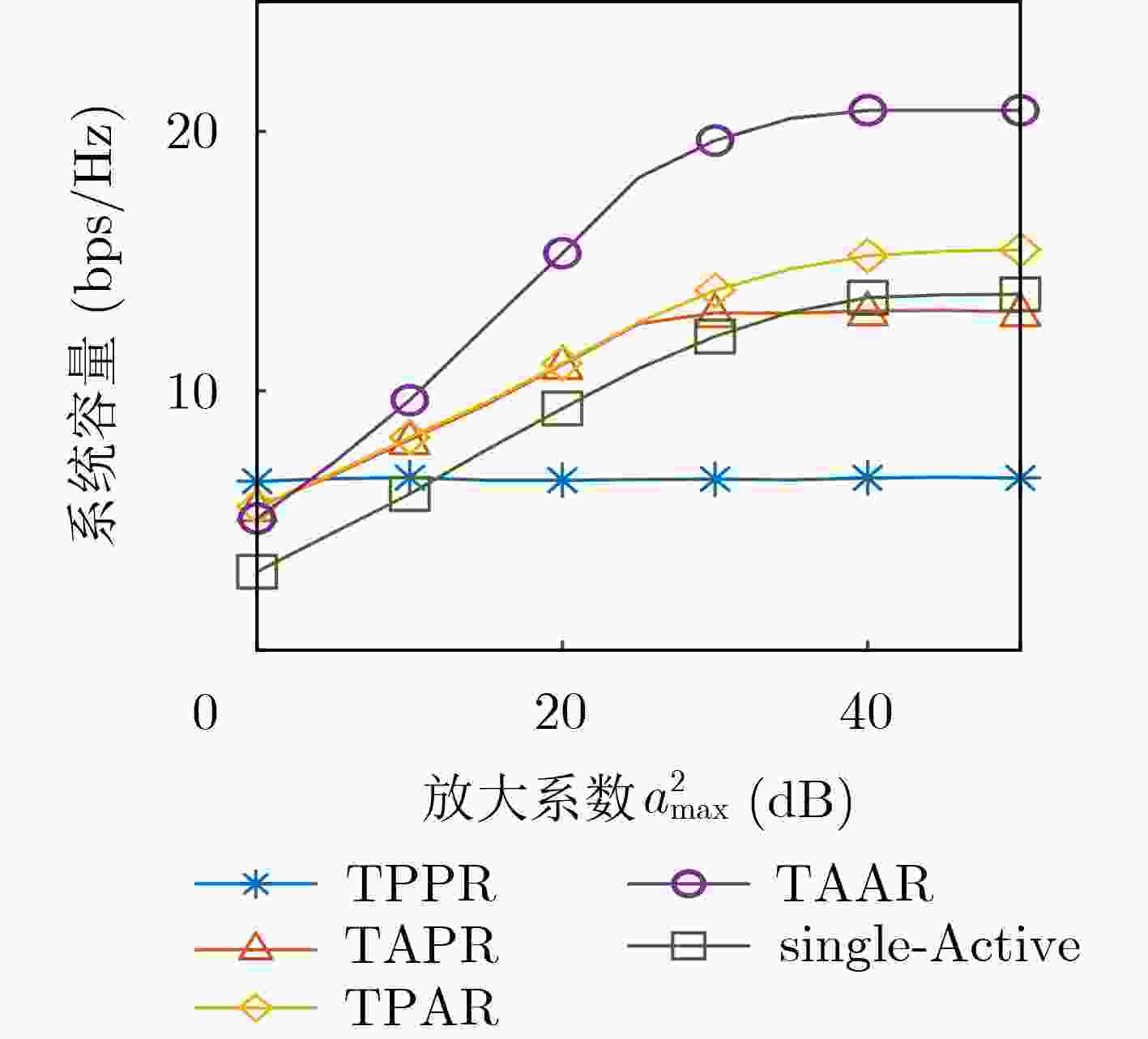
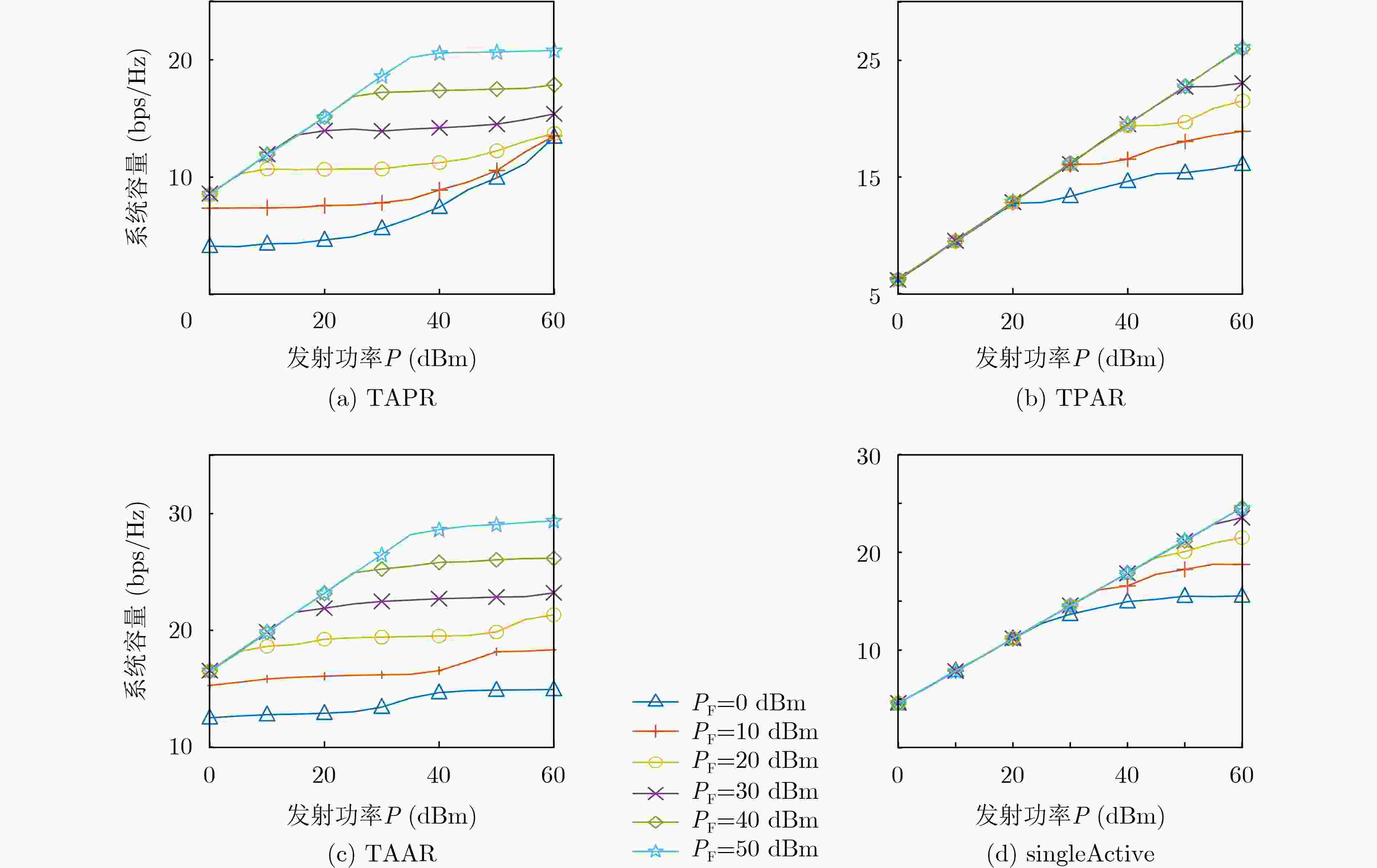
Objective With the continuous advancement of research on Reconfigurable Intelligent Surfaces (RIS), various application scenarios have emerged. Among these, Active Reconfigurable Intelligent Surfaces (ARIS) attracts significant attention from the academic community. While some studies focus on dual Passive RIS-assisted communication systems, others investigate dual RIS-assisted systems incorporating ARIS. Existing literature consistently demonstrates that dual RIS configurations outperform single RIS setups in terms of achievable Signal-to-Noise Ratio (SNR), power gain, and energy transfer efficiency, with dual RIS systems achieving approximately ten times higher energy transfer efficiency.However, most existing studies on RIS focus on optimizing the performance of reflection coefficients in one or more distributed RIS-aided systems, primarily serving users within their respective coverage areas, without sufficiently addressing the benefits of single-reflection links. While dual RIS systems can effectively mitigate the limitations of antenna numbers and improve transmission reliability and efficiency, single-reflection links can still significantly enhance channel capacity, especially under low transmission power conditions. This paper proposes a novel approach wherein dual-reflection links and two single-reflection links jointly serve users. The goal is to maximize the downlink capacity of dual RIS-assisted Multiple-Input Single-Output (MISO) systems by strategically configuring the interaction between the two RISs. Methods In this paper, four combinatorial models of RIS are investigated: the Transmitter-PRIS PRIS-Receiver (TPPR), Transmitter-ARIS PRIS-Receiver (TAPR), Transmitter-PRIS ARIS-Receiver (TPAR), and Transmitter-ARIS ARIS-Receiver (TAAR). The optimization objective of all models is to maximize the communication rate by optimizing the antenna beamforming vector of the base station and the phase shift matrix of the RIS. Due to the coupling of the three variables in the objective function, the model is non-convex, making it difficult to obtain an optimal solution. To address the coupling problem, the Alternating Optimization (AO) algorithm is employed, where one phase shift vector is fixed while the other is optimized alternately. To tackle the non-convex problem, SCA is applied to iteratively approximate the optimal solution by solving a series of convex subproblems. Results and Discussions Building on the research methods outlined above and employing the SCA and AO algorithms, experimental results are obtained. The system capacity of each combination model increases with rising amplification power ( Fig. 2 ). However, once the amplification factor reaches a certain threshold, the capacity curves of all models begin to flatten due to the constraints imposed by the maximum amplification power.Further demonstration of the system capacity performance of different combination models as transmit power increases is shown in (Fig. 3 ). Across all dual-RIS combination models, system capacity improves with higher transmit power and outperforms the Single-Active model in all scenarios.In (Fig. 3(a) ), under low transmit power conditions, regions of the curves corresponding to higher amplification power overlap due to the constraint of the amplification factor. As transmit power increases, system capacity stabilizes, which can be attributed to the proximity of ARIS to the base station, allowing it to receive stronger signals. Under high transmit power, system capacity continues to improve due to the influence of PRIS. Unlike ARIS, PRIS reflects the optimized signal path without being constrained by amplification power. Consequently, as transmit power increases, the signal strength received by PRIS is enhanced.In (Fig. 3(b) ), system capacity increases with transmit power, showing trends similar to those in (Fig. 3(a) ). In the TPAR combined model, the amplification factor constraint dominates, causing the system capacity curves to exhibit similar behavior across different amplification power levels. Under low transmit power, the signal strength at ARIS does not exceed the maximum amplification power budget. As transmit power increases, the amplification power constraint increasingly affects system capacity, leading to a gradual slowdown in the curve’s upward trend until it flattens. At high transmit power levels, the system capacity curve of the TPAR model levels off due to the low signal strength received by ARIS when it is positioned farther from the base station. This positioning necessitates higher transmit power to overcome the amplified power constraint. Thus, it is recommended that ARIS be deployed as close to the user as possible.In (Fig. 3(c) ), the TAAR combined model leverages the characteristics of both ARIS and PRIS in a dual ARIS-assisted scenario. Under low transmit power conditions, significant capacity gains are achieved. However, at high transmit power, the system capacity is constrained by the maximum amplification power of ARIS and eventually levels off. The system capacity trends in (Fig. 3(a) ) and (Fig. 3(b) ) consistently increase with higher transmit power. This is because both combination models integrate the advantages of PRIS and ARIS, ensuring high performance under both high and low transmit power conditions.In (Fig. 3(d)) , where ARIS is positioned on the user side, comparison with (Fig. 3(c) ) reveals that, under high transmit power, the system capacity of both combination models is nearly identical, regardless of the amplification power level. This suggests that in strong transmit power scenarios, the additional gains from ARIS are limited.Conclusions This paper provides an in-depth analysis of the optimization of dual RIS-assisted MISO communication systems, confirming their superiority over single RIS configurations. However, several potential research directions remain unexplored. Most current studies assume ideal channel models, whereas real-world applications often involve complex channel conditions that significantly affect system performance. Future research could investigate the performance of dual RIS systems under these practical conditions, paving the way for more robust and applicable solutions. -
1 基于AO算法的信道对齐流程
(1) 初始化参数${\boldsymbol{\theta}} _1^{(0)}$, ${\boldsymbol{\theta}} _2^{(0)}$, ${{\boldsymbol{\omega }}^{(0)}}$迭代数$n = 0$,收敛门限$\varepsilon $ (2) 利用初始参数计算$ \gamma _{{\text{TPPR}}}^n $的值 (3) 迭代开始: (4) 固定${{{\boldsymbol{\theta}}} _2}$, ${\boldsymbol{\omega }}$,求解式(15)得到${{{\boldsymbol{\theta}}} _1}$ (5) 固定${{{\boldsymbol{\theta}}} _1}$, ${\boldsymbol{\omega }}$,求解式(16)得到${{{\boldsymbol{\theta}}} _2}$ (6) 固定${{{\boldsymbol{\theta}}} _1}$,${{{\boldsymbol{\theta}}} _2}$,求解式(17)得到${\boldsymbol{\omega }}$ (7) 使用${{{\boldsymbol{\theta}}} _1}$,${{{\boldsymbol{\theta}}} _2}$, ${\boldsymbol{\omega }}$,计算$\gamma _{{\text{TPPR}}}^{n + 1}$的值 (8) 判断$\left| {\gamma _{{\text{TPPR}}}^{n + 1} - \gamma _{{\text{TPPR}}}^n} \right| \le \varepsilon $或$n \ge 100$是否成立,若不满
足条件,$n = n + 1$返回步骤4(9) 结束循环 (10) 得到最优解${{{\boldsymbol{\theta}}} _1}$, ${{{\boldsymbol{\theta}}} _2}$, ${\boldsymbol{\omega }}$ 2 基于SCA的AO算法流程
(1) 初始化参数${{\boldsymbol{\theta}}} _1^{(0)}$, ${{\boldsymbol{\theta}}} _2^{(0)}$, ${{\boldsymbol{\omega }}^{(0)}}$, ${\tau _0}$, ${\kappa _0}$,迭代数$n = 0$,收敛
门限$\varepsilon $(2) 计算$\gamma _{{\text{TAPR}}}^n$的值 (3) 迭代开始: (4) 固定${{{\boldsymbol{\theta}}} _2}$, ${\boldsymbol{\omega }}$,求解问题(P2.1),将解进行高斯随机化后得
到${{\boldsymbol{\theta}}} _1^{n + 1}$(5) 固定${{{\boldsymbol{\theta}}} _1}$, ${\boldsymbol{\omega }}$,求解问题(P2.2),将解进行高斯随机化后得
到${{\boldsymbol{\theta}}} _2^{n + 1}$(6) 固定${{{\boldsymbol{\theta}}} _1}$, ${{{\boldsymbol{\theta}}} _2}$,求解问题(P2.3)得到${{\boldsymbol{\omega }}^{n + 1}}$ (7) 使用${{\boldsymbol{\theta}}} _1^{n + 1}$, ${{\boldsymbol{\theta}}} _2^{n + 1}$,${{\boldsymbol{\omega }}^{n + 1}}$,计算$\gamma _{{\text{TAPR}}}^{n + 1}$的值 (8) 判断收敛条件$\left| {\gamma _{{\text{TAPR}}}^{n + 1} - \gamma _{{\text{TAPR}}}^n} \right| \le \varepsilon $或$n \ge 100$是否成
立,若满足条件,迭代结束,否则,$n = n + 1$返回步
骤4(9) 得到最优解${{{\boldsymbol{\theta}}} _1}$, ${{{\boldsymbol{\theta}}} _2}$, ${\boldsymbol{\omega }}$ -
[1] SIDDIQI M Z and MIR T. Reconfigurable intelligent surface-aided wireless communications: An overview[J]. Intelligent and Converged Networks, 2022, 3(1): 33–63. doi: 10.23919/ICN.2022.0007. [2] 张力康, 杜清河, 卢忱, 等. 面向6G的RIS辅助通信系统的信道估计技术[J]. 移动通信, 2024, 48(6): 75–80. doi: 10.3969/j.issn.1006-1010.20240425-0002.ZHANG Likang, DU Qinghe, LU Chen, et al. Overview of channel estimation for reconfigurable intelligent surface-assisted communications towards 6G system[J]. Mobile Communications, 2024, 48(6): 75–80. doi: 10.3969/j.issn.1006-1010.20240425-0002. [3] JIANG Hao, ZHANG Zaichen, XIONG Baiping, et al. A 3D stochastic channel model for 6G wireless double-IRS cooperatively assisted MIMO communications[C]. 2021 13th International Conference on Wireless Communications and Signal Processing, Changsha, China, 2021. doi: 10.1109/WCSP52459.2021.9613605. [4] GORTY V K. Channel estimation for double IRS assisted broadband single-user SISO communication[C]. 2022 IEEE International Conference on Signal Processing and Communications, Bangalore, India, 2022: 1–5. doi: 10.1109/SPCOM55316.2022.9840513. [5] ZHENG Beixiong, YOU Changsheng, and ZHANG Rui. Efficient channel estimation for double-IRS aided multi-user MIMO system[J]. IEEE Transactions on Communications, 2021, 69(6): 3818–3832. doi: 10.1109/TCOMM.2021.3064947. [6] BAZZI S and XU Wen. IRS parameter optimization for channel estimation MSE minimization in double-IRS aided systems[J]. IEEE Wireless Communications Letters, 2022, 11(10): 2170–2174. doi: 10.1109/LWC.2022.3196126. [7] YOU Changsheng, ZHENG Beixiong, and ZHANG Rui. Wireless communication via double IRS: Channel estimation and passive beamforming designs[J]. IEEE Wireless Communications Letters, 2021, 10(2): 431–435. doi: 10.1109/LWC.2020.3034388. [8] HAN Yitao, ZHANG Shuowen, DUAN Lingjie, et al. Cooperative double-IRS aided communication: Beamforming design and power scaling[J]. IEEE Wireless Communications Letters, 2020, 9(8): 1206–1210. doi: 10.1109/LWC.2020.2986290. [9] WU Qingqing and ZHANG Rui. Intelligent reflecting surface enhanced wireless network via joint active and passive beamforming[J]. IEEE Transactions on Wireless Communications, 2019, 18(11): 5394–5409. doi: 10.1109/TWC.2019.2936025. [10] HAN Yitao, ZHANG Shuowen, DUAN Lingjie, et al. Double-IRS aided MIMO communication under LoS channels: Capacity maximization and scaling[J]. IEEE Transactions on Communications, 2022, 70(4): 2820–2837. doi: 10.1109/TCOMM.2022.3151893. [11] ZHENG Beixiong, YOU Changsheng, and ZHANG Rui. Double-IRS assisted multi-user MIMO: Cooperative passive beamforming design[J]. IEEE Transactions on Wireless Communications, 2021, 20(7): 4513–4526. doi: 10.1109/TWC.2021.3059945. [12] DING Gengfa, YANG Feng, DING Lianghui, et al. Analysis and optimization of a double-IRS cooperatively assisted system with a quasi-static phase shift design[J]. IEEE Transactions on Wireless Communications, 2023, 22(7): 4416–4433. doi: 10.1109/TWC.2022.3225474. [13] KUMAR C and KASHYAP S. On the power transfer efficiency and feasibility of wireless energy transfer using double IRS[J]. IEEE Transactions on Vehicular Technology, 2023, 72(5): 6165–6180. doi: 10.1109/TVT.2022.3231636. [14] FU Min and ZHANG Rui. Active and passive IRS jointly aided communication: Deployment design and achievable rate[J]. IEEE Wireless Communications Letters, 2023, 12(2): 302–306. doi: 10.1109/LWC.2022.3224457. [15] LI Xinhao, YOU Changsheng, KANG Zhenyu, et al. Double-active-IRS aided wireless communication with total amplification power constraint[J]. IEEE Communications Letters, 2023, 27(10): 2817–2821. doi: 10.1109/LCOMM.2023.3298070. [16] KANG Zhenyu, YOU Changsheng, and ZHANG Rui. Double-active-IRS aided wireless communication: Deployment optimization and capacity scaling[J]. IEEE Wireless Communications Letters, 2023, 12(11): 1821–1825. doi: 10.1109/LWC.2023.3294258. [17] NGUYEN T A, NGUYEN H V, DO D T, et al. Performance analysis of downlink double-IRS systems relying on non-orthogonal multiple access[J]. IEEE Access, 2023, 11: 110208–110220. doi: 10.1109/ACCESS.2023.3322373. [18] HU Xiaoling, ZHONG Caijun, ZHANG Yu, et al. Location information aided multiple intelligent reflecting surface systems[J]. IEEE Transactions on Communications, 2020, 68(12): 7948–7962. doi: 10.1109/TCOMM.2020.3020577. [19] TEJAS K S, UDAYKUMAR M, VARUN R, et al. Intelligent reflecting surface assisted wireless communication for coverage enhancement[C]. 2023 International Conference on Smart Systems for applications in Electrical Sciences, Tumakuru, India, 2023. doi: 10.1109/ICSSES58299.2023.10200009. [20] 王丹, 陈小梦, 王勇芳. 可重构智能表面辅助无线通信的用户分配[J]. 电子与信息学报, 2022, 44(7): 2425–2430. doi: 10.11999/JEIT211473.WANG Dan, CHEN Xiaomeng, and WANG Yongfang. User assignment for wireless communication assisted by reconfigurable intelligent surfaces[J]. Journal of Electronics & Information Technology, 2022, 44(7): 2425–2430. doi: 10.11999/JEIT211473. [21] 王华华, 孙宸, 朱鹏云. 可重构智能表面辅助双功能雷达通信系统的联合波束优化[J]. 电子与信息学报, 2024, 46(1): 222–228. doi: 10.11999/JEIT221537.WANG Huahua, SUN Chen, and ZHU Pengyun. Joint beamforming optimization for RIS-assisted dual-functional radar-communication systems[J]. Journal of Electronics & Information Technology, 2024, 46(1): 222–228. doi: 10.11999/JEIT221537. -





 下载:
下载:


 下载:
下载:
