偏差未补偿自适应边缘化容积卡尔曼滤波跟踪方法

邓洪高; 余润华; 纪元法; 吴孙勇; 孙少帅

doi:10.11999/JEIT240469

偏差未补偿自适应边缘化容积卡尔曼滤波跟踪方法

doi: 10.11999/JEIT240469

邓洪高^{1, 4},
余润华^{1, 2},
纪元法^{1, 2, 4},
吴孙勇^{2, 3, ,},
孙少帅¹

1.
桂林电子科技大学信息与通信学院桂林 541004
2.
桂林电子科技大学广西精密导航技术与应用重点实验室桂林 541004
3.
桂林电子科技大学数学与计算科学学院桂林 541004
4.
卫星导航定位与位置服务国家地方联合工程研究中心桂林 541004

基金项目: 广西重点研发项目(AB23026150, AB23026147)，国家自然科学基金(U23A20280)

详细信息

作者简介:
邓洪高：男，研究员，研究方向为雷达信号处理和卫星导航

余润华：男，硕士生，研究方向为雷达多目标跟踪、空间误差配准和多源信息融合

纪元法：男，教授，研究方向为卫星导航和信号处理

吴孙勇：男，教授，研究方向为雷达信号处理、多目标检测与跟踪和多源信息融合

孙少帅：女，硕士，研究方向为项目管理

通讯作者:
吴孙勇　wusunyong121991@163.com

中图分类号: V243.2; TN953
计量
- 文章访问数: 107
- HTML全文浏览量: 25
- PDF下载量: 27
- 被引次数: 0
出版历程
- 收稿日期: 2024-06-11
- 修回日期: 2024-11-30
- 网络出版日期: 2024-12-09

An Adaptive Target Tracking Method Utilizing Marginalized Cubature Kalman Filter with Uncompensated Biases

DENG Honggao^{1, 4},
YU Runhua^{1, 2},
JI Yuanfa^{1, 2, 4},
WU Sunyong^{2, 3
, ,},
SUN Shaoshuai¹

1.
School of Information and Communication, Guilin University of Electronic Technology, Guilin 541004, China
2.
Guangxi Key Laboratory of Precision Navigation Technology and Application, Guilin University of Electronic Technology, Guilin 541004, China
3.
School of Mathematics and Computing Science, Guilin University of Electronic Science and Technology, Guilin, 541004, China
4.
National & Local Joint Engineering Research Center of Satellite Navigation Positioning and Location Service, Guilin 541004, China

Funds: Guangxi Key Research and Development Project (AB23026150, AB23026147), The National Natural Science Foundation of China (U23A20280)

摘要

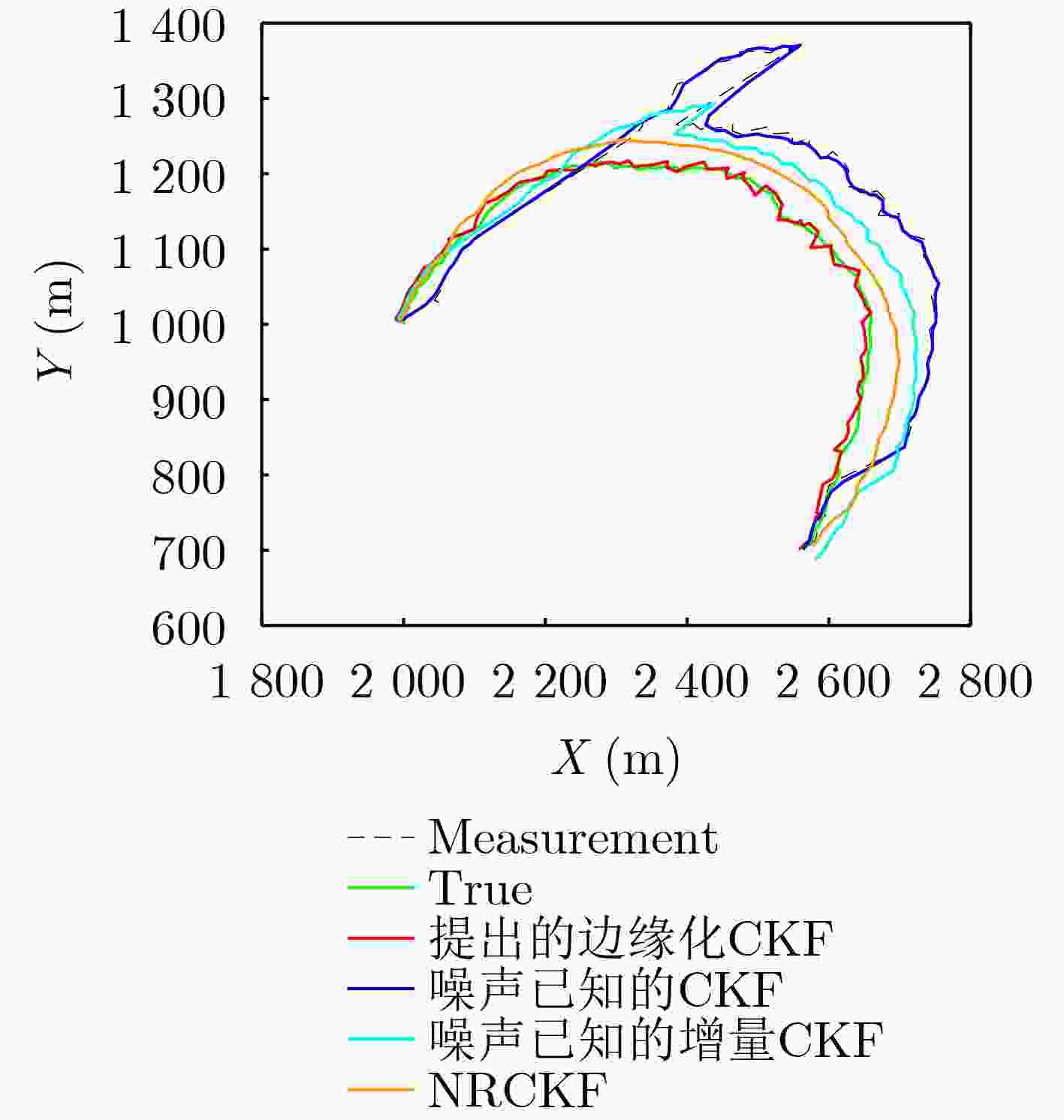
摘要: 针对存在突变测量偏差和未知时变量测噪声场景下的目标跟踪问题，该文提出一种偏差未补偿自适应边缘化容积卡尔曼滤波跟踪方法。首先通过建立差分量测方程来消除恒定的测量偏差，同时构建满足beta-Bernoulli分布的指示变量识别突变测量偏差，将相邻时刻目标状态扩维以满足实时滤波需求，利用逆Wishart分布建模未知量测噪声协方差矩阵，从而建立目标状态、指示变量、噪声协方差矩阵的联合分布，并通过变分贝叶斯推断来求解各个参数的近似后验。为减小滤波负担，对扩维后的状态向量进行边缘化处理，结合容积卡尔曼滤波方法实现边缘化容积卡尔曼滤波跟踪。仿真实验结果表明，所提方法能够同时处理突变测量偏差和未知时变量测噪声，从而对目标进行有效跟踪。
- 突变测量偏差 /
- Beta-Bernoulli分布 /
- 逆Wishart分布 /
- 变分贝叶斯推断 /
- 边缘化容积卡尔曼滤波
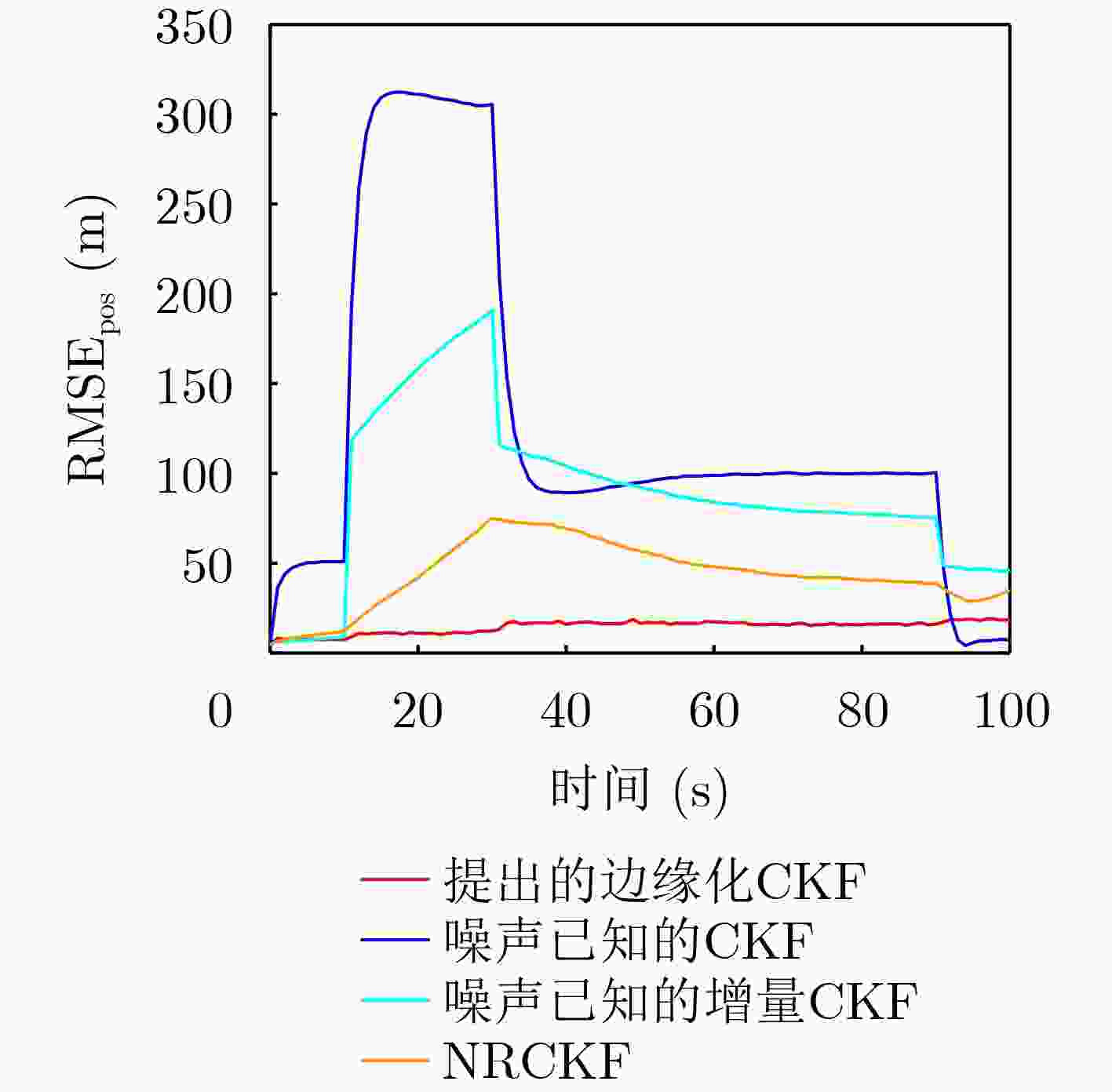
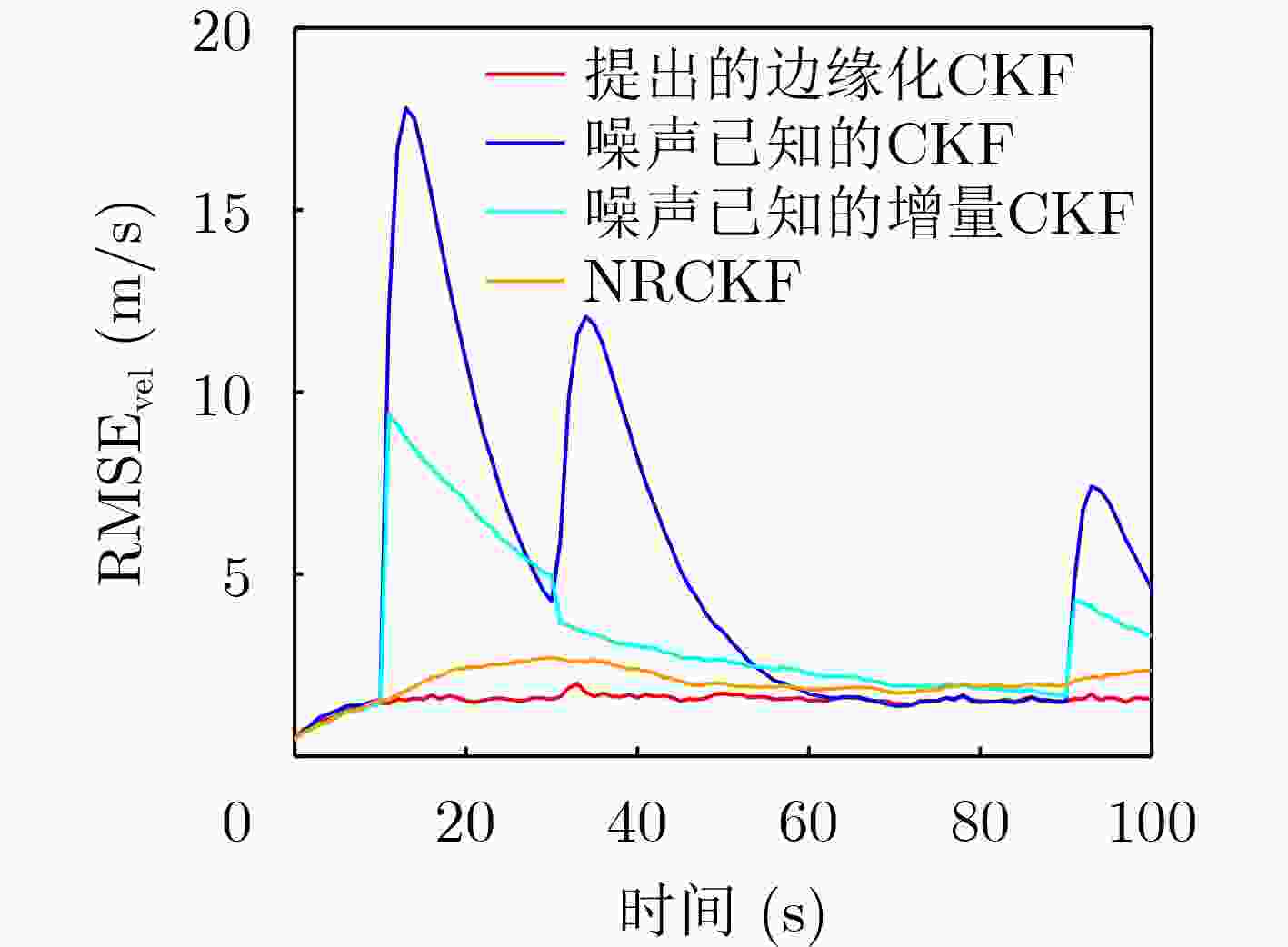
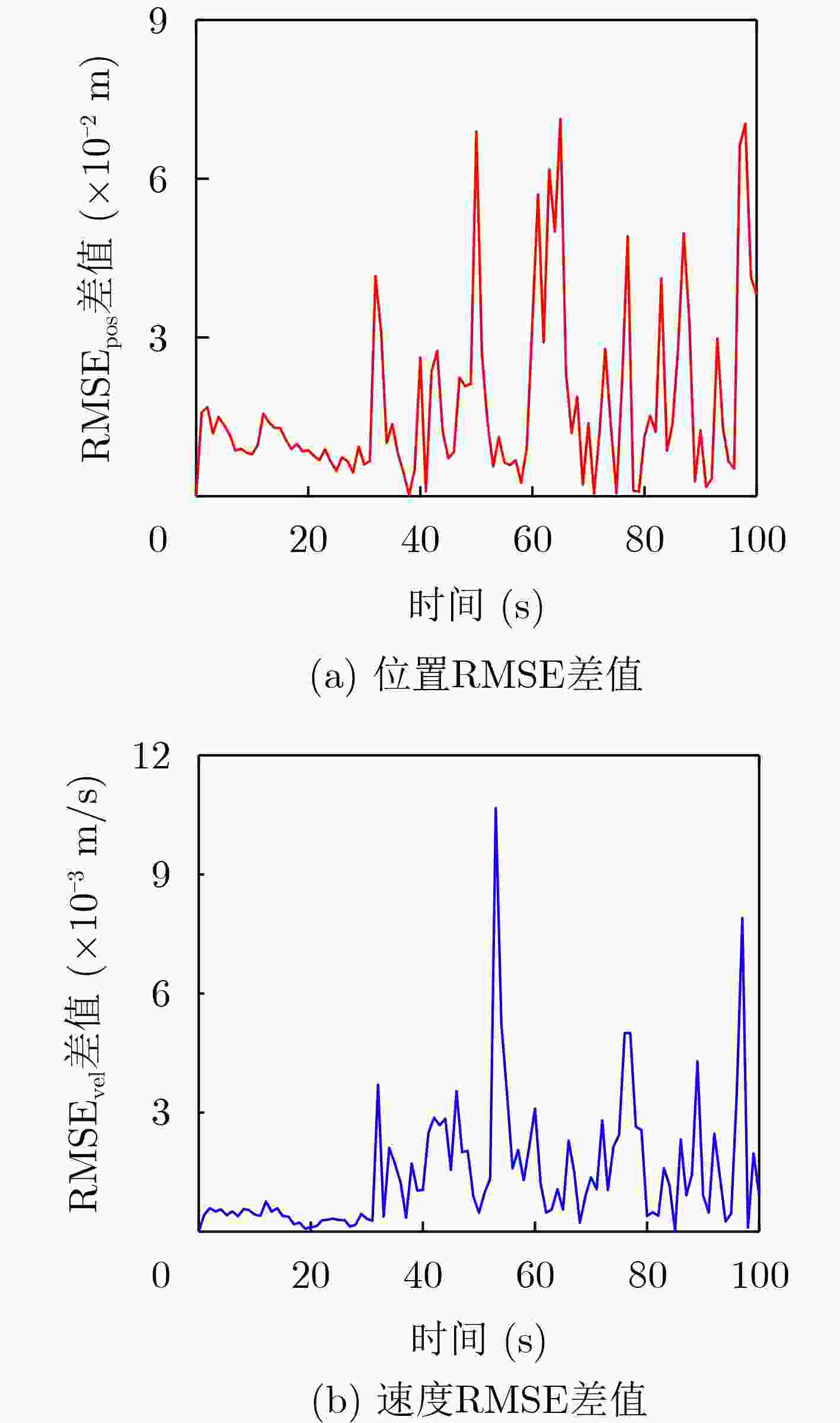
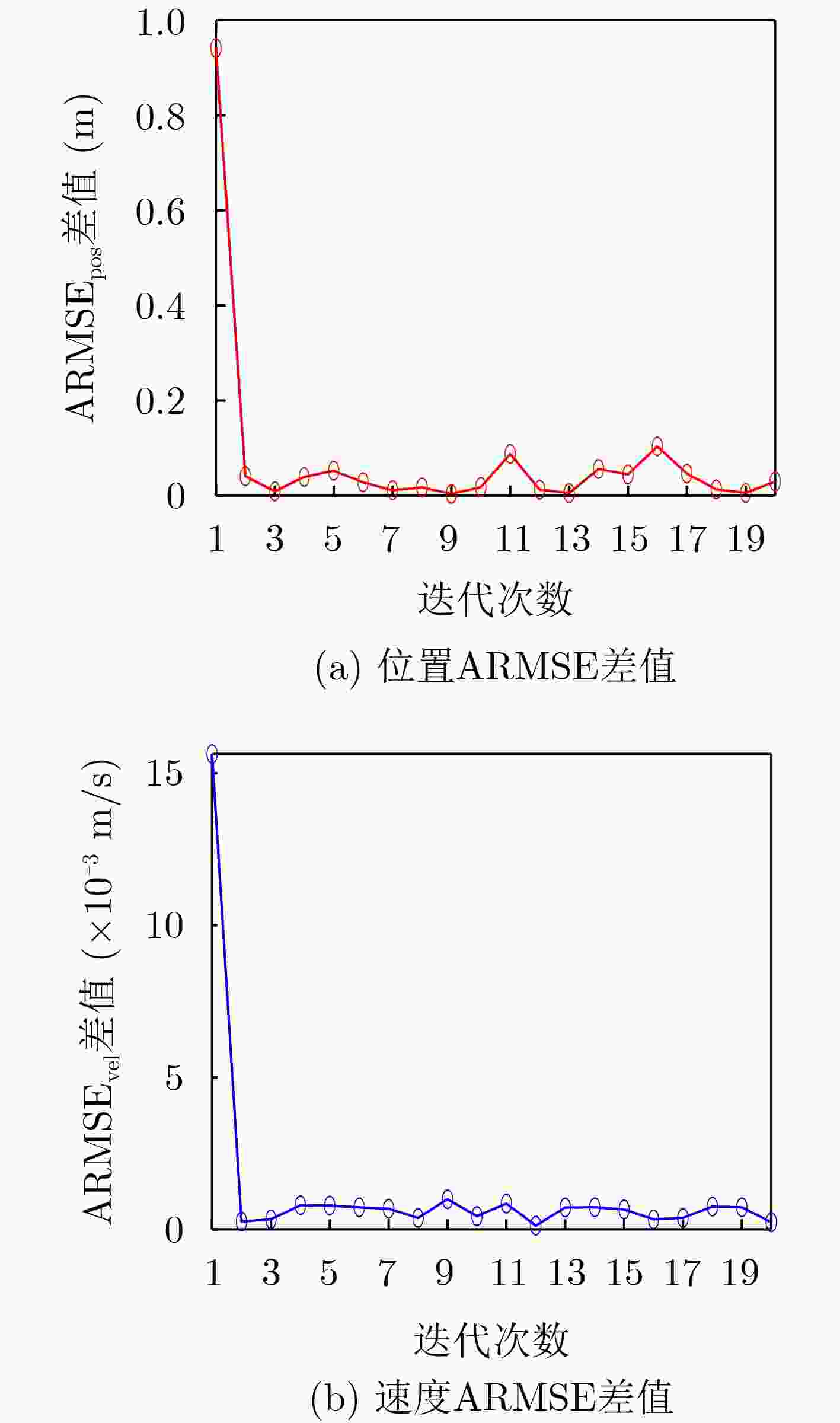
Abstract: Objective In radar target tracking, tracking accuracy is often influenced by sensor measurement biases and measurement noise. This is particularly true when measurement biases change abruptly and measurement noise is unknown and time-varying. Ensuring effective target tracking under these conditions poses a significant challenge. An adaptive target tracking method is proposed, utilizing a marginalized cubature Kalman filter to address this issue. Methods (1) Initially, measurements taken at adjacent time points are differentiated to formulate the differential measurement equation, thereby effectively mitigating the influence of measurement biases that are either constant or change gradually between adjacent observations. Concurrently, the target states at these moments are expanded to create an extended state vector facilitating real-time filtering. (2) Following the differentiation of measurements, sudden changes in measurement biases may cause the differential measurement at the current moment to be classified as outliers. To identify the occurrence of these abrupt bias changes, a Beta-Bernoulli indicator variable is established. If such a change is detected, the differential measurement for that moment is disregarded, and the predicted state is adopted as the updated state. In the absence of any abrupt changes, standard filtering procedures are conducted. The Gaussian measurement noise, despite having unknown covariance, continues to follow a Gaussian distribution after differentiation, allowing its covariance matrix to be modeled using the inverse Wishart distribution. (3) A joint distribution is formulated for the target state, indicator variables, and the covariance matrix of the measurement noise. The approximate posteriors of each parameter are derived using variational Bayesian inference. (4) To mitigate the increased filtering burden arising from the high-dimensional extended state vector, the extended target state is marginalized, and a marginalized cubature Kalman filter for target tracking is implemented in conjunction with the cubature Kalman filtering method. Results and Discussions The target tracking performance is clearly illustrated, indicating that the proposed method accurately identifies abrupt measurement biases while effectively managing unknown time-varying measurement noise. This leads to a tracking performance that significantly exceeds that of the comparative methods. The findings further support the conclusions by examining the Root Mean Square Error (RMSE). Additionally, the stability of the proposed method is demonstrated. The results reveal that the computational load associated with the proposed method is greatly reduced through marginalization processing. This reduction occurs because, during the variational Bayesian iteration process, cubature sampling and integration are performed multiple times. Once the target state is marginalized, the dimensionality of the cubature sampling is halved, and the number of sampling points for each variational iteration is also reduced by half. As a result, the computational load during the nonlinear propagation of the sampling points decreases, with the amount of computation reduction increasing with the number of variational iterations. Furthermore, the results demonstrate that marginalization does not compromise tracking accuracy, thereby further validating the effectiveness of marginalization processing. This finding also confirms that marginalization processing can be extended to other nonlinear variational Bayesian filters based on deterministic sampling, providing a means to reduce computational complexity. Conclusions This paper proposes an adaptive marginalized cubature Kalman filter to improve target tracking in scenarios with measurement biases and unknown time-varying measurement noise. The approach incorporates measurement differencing to eliminate constant biases, constructs indicator variables to detect abrupt biases, and models the unknown measurement noise covariance matrix using the inverse Wishart distribution. A joint posterior distribution of the parameters is established, and the approximate posteriors are solved through variational Bayesian inference. Additionally, marginalization of the target state is performed before implementing tracking within the CKF framework, reducing the filtering burden. The results of our simulation experiments yield the following conclusions: (1) The proposed method demonstrates superior target tracking performance compared to existing techniques in scenarios involving abrupt measurement biases and unknown measurement noise; (2) The marginalization processing strategy significantly alleviates the filtering burden of the proposed filter, making it applicable to more complex nonlinear variational Bayesian filters, such as robust nonlinear random finite set filters, to reduce filtering complexity; (3) This filtering methodology can be extended to target tracking scenarios in higher dimensions.
- Abrupt measurement biases /
- Beta-Bernoulli distribution /
- Inverse Wishart distribution /
- Variational Bayesian inference /
- Marginalized cubature Kalman filter

HTML全文

图 1 跟踪效果

下载: 全尺寸图片幻灯片

图 2 E[r]值变化图

下载: 全尺寸图片幻灯片

图 3 不同方法的位置RMSE

下载: 全尺寸图片幻灯片

图 4 不同方法的速度RMSE

下载: 全尺寸图片幻灯片

图 5 不同方法的位置ARMSE

下载: 全尺寸图片幻灯片

图 6 不同方法的速度ARMSE

下载: 全尺寸图片幻灯片

图 7 不同$\varepsilon $值的位置ARMSE

下载: 全尺寸图片幻灯片

图 8 不同$\varepsilon $值的速度ARMSE

下载: 全尺寸图片幻灯片

图 9 边缘化处理前后的RMSE差值

下载: 全尺寸图片幻灯片

图 10 边缘化处理前后的ARMSE差值

下载: 全尺寸图片幻灯片

1 偏差未补偿自适应边缘化容积卡尔曼滤波跟踪算法

输入：状态估计值${{\boldsymbol{\tilde x}}_{0\|0}}$，误差协方差${{\boldsymbol{P}}_{0\|0}}$，逆Wishart分布参数　${u_{0\|0}}$, ${{\boldsymbol{U}}_{0\|0}}$，贝塔分布参数${\alpha _0}$, ${\beta _0}$，初始时刻伯努利变量的期望　值${\text{E}}[{r_0}]$，遗忘因子$ \rho $，迭代次数N。
输出：${{\boldsymbol{\tilde x}}_{k\|k}}$,${{\boldsymbol{P}}_{k\|k}}$, ${u_{k\|k}}$, ${{\boldsymbol{U}}_{k\|k}}$。
(1) for k = 1:K
(2) 　通过式(23)计算${{\boldsymbol{\tilde x}}_{k\|k - 1}}$, ${{\boldsymbol{P}}_{k\|k - 1}}$, $ {{\boldsymbol{C}}_{k\|k - 1}} $；
(3) 　计算：$ {u_{k\|k - 1}} = \rho {u_{k - 1\|k - 1}} $, ${{\boldsymbol{U}}_{k\|k - 1}} = \rho {{\boldsymbol{U}}_{k - 1\|k - 1}}$；
(4) 　初始化：$ {\boldsymbol{\tilde x}}_{k\|k}^{{\text{(0)}}} = {{\boldsymbol{\tilde x}}_{k\|k - 1}} $, ${\boldsymbol{P}}_{k\|k}^{{\text{(0)}}} = {{\boldsymbol{P}}_{k\|k - 1}}$, 　　　　$ u_{k\|k}^{(0)} = {u_{k\|k - 1}} $, $ {\boldsymbol{U}}_{k\|k}^{(0)} = {{\boldsymbol{U}}_{k\|k - 1}} $；
(5) 　for i = 0:N
(6) 　　通过式(14)计算${{\stackrel \frown{{\boldsymbol{R}}} }}_k^{(i + 1)}$；
(7) 　　通过式(35)计算${\boldsymbol{\tilde x}}_{k\|k}^{{\text{(}}i{\text{ + 1)}}}$, ${\boldsymbol{P}}_{k\|k}^{{\text{(}}i{\text{ + 1)}}}$；
(8) 　　通过式(18)计算${({\text{E}}[{r_k}])^{(i + 1)}}$；
(9) 　　根据式(34)判断传感器测量偏差是否突变
(10) 　　若传感器测量偏差突变：
(11) 　　 ${{\boldsymbol{\tilde x}}_{k\|k}} = {\boldsymbol{\tilde x}}_{k\|k}^{{\text{(}}0{\text{)}}}$, ${{\boldsymbol{P}}_{k\|k}} = {\boldsymbol{P}}_{k\|k}^{(0)}$；
(12) 　　 ${u_{k\|k}} = u_{k\|k}^{(0)}$, ${{\boldsymbol{U}}_{k\|k}} = {\boldsymbol{U}}_{k\|k}^{(0)}$；
(13) 　　跳出循环；
(14) 　若传感器测量偏差不突变：
(15) 　　 ${{\boldsymbol{\tilde x}}_{k\|k}} = {\boldsymbol{\tilde x}}_{k\|k}^{{\text{(}}i{\text{ + 1)}}}$,${{\boldsymbol{P}}_{k\|k}} = {\boldsymbol{P}}_{k\|k}^{(i + 1)}$；
(16) 　　通过式(21)计算$\alpha _k^{(i + 1)}$和$\beta _k^{(i + 1)}$；
(17) 　　通过式(22)计算$u_{k\|k}^{(i + 1)}$和$ {\boldsymbol{U}}_{k\|k}^{(i + 1)} $；
(18) 　　 ${u_{k\|k}} = u_{k\|k}^{{\text{(}}i{\text{ + 1)}}}$, $ {{\boldsymbol{U}}_{k\|k}} = {\boldsymbol{U}}_{k\|k}^{(i + 1)} $；
(19)　　计算迭代停止阈值$\kappa $：　　　　　　$\kappa = \|\|{\boldsymbol{\tilde x}}_{k\|k}^{{\text{(}}i + 1{\text{)}}} - {\boldsymbol{\tilde x}}_{k\|k}^{{\text{(}}i{\text{)}}}\|\|/\|\|{\boldsymbol{\tilde x}}_{k\|k}^{{\text{(}}i{\text{)}}}\|\|$；
(20) 　　当$\kappa \le {10^{ - 6}}$时：
(21) 　　　跳出循环。
(22)　　 end for
(23) end for

下载: 导出CSV

表 1 运行时间对比(s)

方法	时间
传统CKF	1.038 1
增量CKF	1.210 0
NRCKF	11.343 8
提出的方法(非边缘化)	12.866 4
提出的方法(边缘化)	7.333 3

下载: 导出CSV

表 2 仅测量偏差${{\boldsymbol{b}}_k}$变化时各方法ARMSE对比

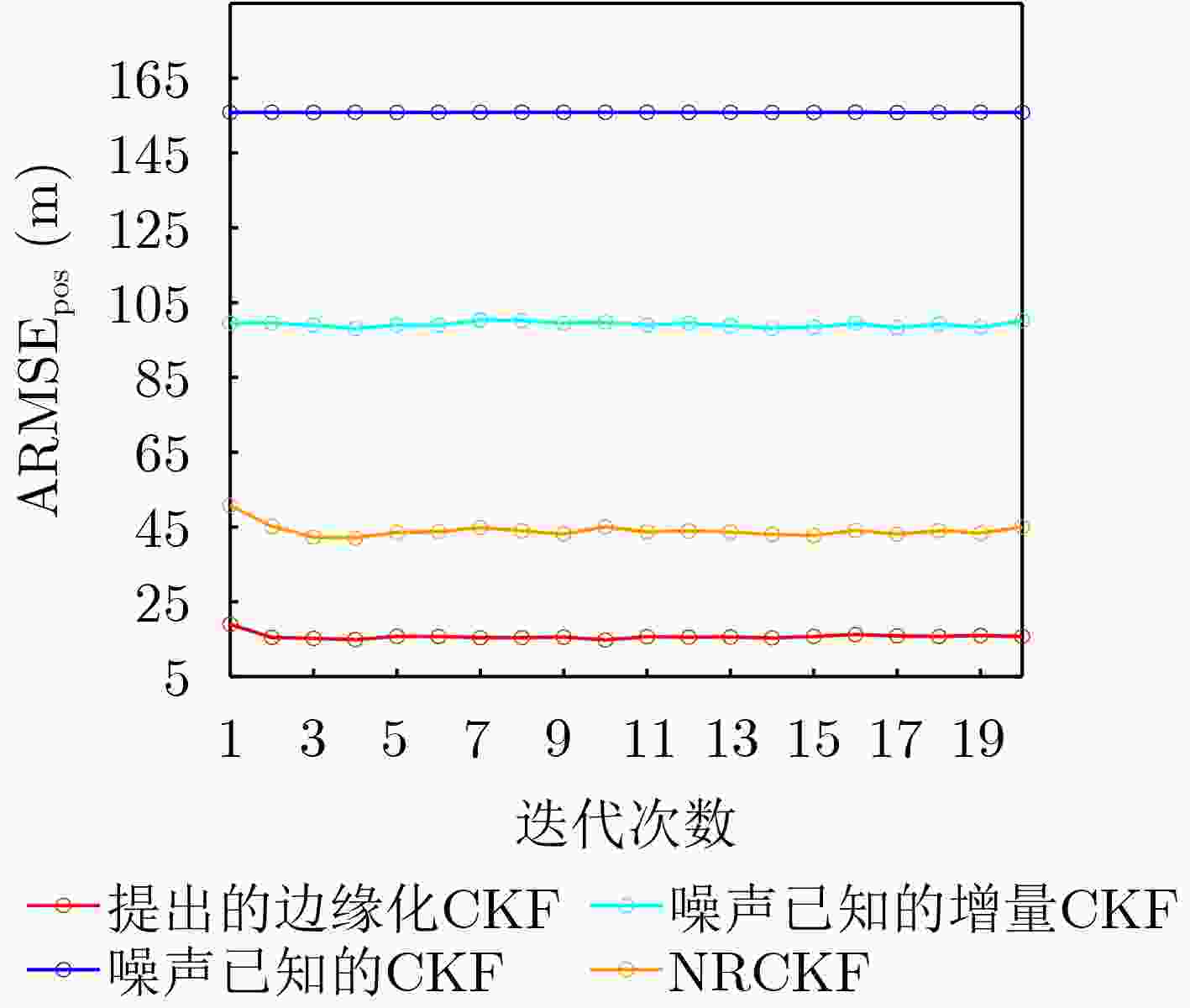
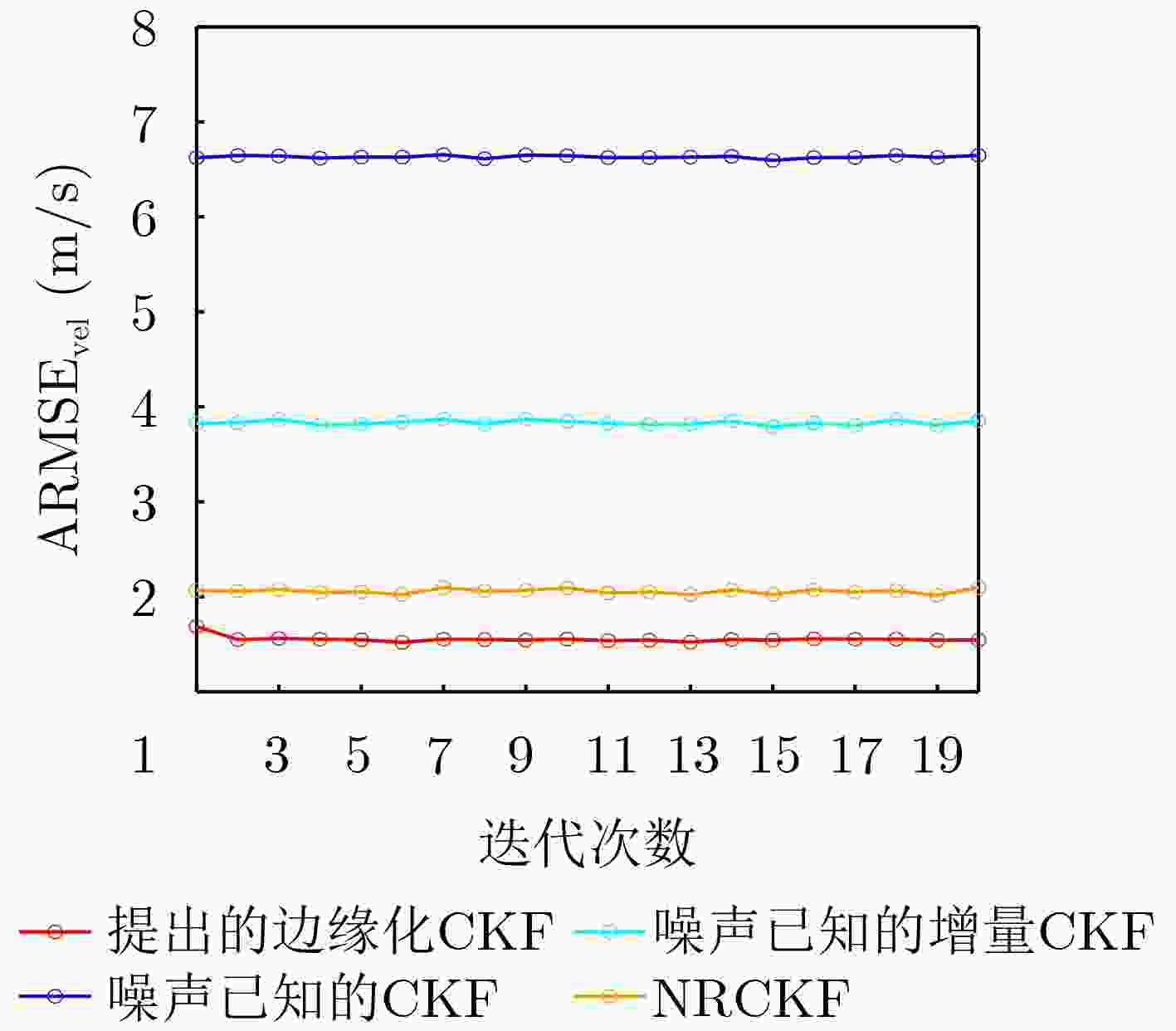
	传统CKF	增量CKF	NRCKF	提出的边缘化CKF
${\text{ARMS}}{{\text{E}}_{{\text{pos}}}}$(m)	155.359 1	78.411 8	47.686 8	15.359 0
${\text{ARMS}}{{\text{E}}_{{\text{vel}}}}$(m/s)	6.533 4	3.533 9	2.062 2	1.549 0

下载: 导出CSV

表 3 仅量测协方差矩阵${{\boldsymbol{R}}_k}$变化时各方法ARMSE对比

	传统CKF	增量CKF	NRCKF	提出的边缘化CKF
${\text{ARMS}}{{\text{E}}_{{\text{pos}}}}$(m)	49.822 0	29.690 6	22.204 5	9.597 0
${\text{ARMS}}{{\text{E}}_{{\text{vel}}}}$(m/s)	1.481 2	1.655 1	1.696 7	1.518 7

下载: 导出CSV

参考文献(21)

[1]	LIN X and BAR-SHALOM Y. Multisensor target tracking performance with bias compensation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(3): 1139–1149. doi: 10.1109/TAES.2006.248212.
[2]	董云龙, 张焱. 雷达系统偏差精确配准技术研究综述[J]. 现代雷达, 2024, 46(3): 1–8. doi: 10.16592/j.cnki.1004-7859.2024.03.001. DONG Yunlong and ZHANG Yan. A review of radar system deviation accurate registration technology[J]. Modern Radar, 2024, 46(3): 1–8. doi: 10.16592/j.cnki.1004-7859.2024.03.001.
[3]	崔亚奇, 熊伟, 何友. 基于MLR的机动平台传感器误差配准算法[J]. 航空学报, 2012, 33(1): 118–128. doi: 11-1929/V.20111213.1132.001. CUI Yaqi, XIONG Wei, and HE You. Mobile platform sensor registration algorithm based on MLR[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(1): 118–128. doi: 11-1929/V.20111213.1132.001.
[4]	XIU Jianjuan, DONG Kai, and HE You. Systematic error real-time registration based on modified input estimation[J]. Journal of Systems Engineering and Electronics, 2016, 27(5): 986–992. doi: 10.21629/JSEE.2016.05.06.
[5]	GENG Han, LIANG Yan, LIU Yurong, et al. Bias estimation for asynchronous multi-rate multi-sensor fusion with unknown inputs[J]. Information Fusion, 2018, 39: 139–153. doi: 10.1016/j.inffus.2017.03.002.
[6]	CHUGHTAI A H, MAJAL A, TAHIR M, et al. Variational-based nonlinear Bayesian filtering with biased observations[J]. IEEE Transactions on Signal Processing, 2022, 70: 5295–5307. doi: 10.1109/TSP.2022.3217921.
[7]	HUANG Yulong, JIA Guangle, CHEN Badong, et al. A new robust Kalman filter with adaptive estimate of time-varying measurement bias[J]. IEEE Signal Processing Letters, 2020, 27: 700–704. doi: 10.1109/LSP.2020.2983552.
[8]	傅惠民, 吴云章, 娄泰山. 欠观测条件下的增量Kalman滤波方法[J]. 机械强度, 2012, 34(1): 43–47. doi: 10.16579/j.issn.1001.9669.2012.01.014. FU Huimin, WU Yunzhang, and LOU Taishan. Incremental Kalman filter method under poor observation condition[J]. Journal of Mechanical Strength, 2012, 34(1): 43–47. doi: 10.16579/j.issn.1001.9669.2012.01.014.
[9]	傅惠民, 娄泰山, 吴云章. 欠观测条件下的扩展增量Kalman滤波方法[J]. 航空动力学报, 2012, 27(4): 777–781. doi: 10.13224/j.cnki.jasp.2012.04.004. FU Huimin, LOU Taishan, and WU Yunzhang. Extended incremental Kalman filter method under poor observation condition[J]. Journal of Aerospace Power, 2012, 27(4): 777–781. doi: 10.13224/j.cnki.jasp.2012.04.004.
[10]	马丽丽, 赵甜甜, 陈金广. 欠观测条件下的增量容积卡尔曼滤波[J]. 计算机工程, 2014, 40(10): 228–231,238. doi: 10.3969/j.issn.1000-3428.2014.10.043. MA Lili, ZHAO Tiantian, and CHEN Jinguang. Incremental cubature Kalman filtering under poor observation condition[J]. Computer Engineering, 2014, 40(10): 228–231,238. doi: 10.3969/j.issn.1000-3428.2014.10.043.
[11]	傅惠民, 吴云章, 娄泰山. 自适应无迹增量滤波方法[J]. 航空动力学报, 2013, 28(2): 259–263. doi: 10.13224/j.cnki.jasp.2013.02.008. FU Huimin, WU Yunzhang, and LOU Taishan. Adaptive unscented incremental filter method[J]. Journal of Aerospace Power, 2013, 28(2): 259–263. doi: 10.13224/j.cnki.jasp.2013.02.008.
[12]	孙小君, 周晗, 闫广明. 基于新息的自适应增量Kalman滤波器[J]. 电子与信息学报, 2020, 42(9): 2223–2230. doi: 10.11999/JEIT190493. SUN Xiaojun, ZHOU Han, and YAN Guangming. Adaptive incremental Kalman filter based on innovation[J]. Journal of Electronics & Information Technology, 2020, 42(9): 2223–2230. doi: 10.11999/JEIT190493.
[13]	LOU Taishan, YANG Ning, WANG Yan, et al. Target tracking based on incremental center differential Kalman filter with uncompensated biases[J]. IEEE Access, 2018, 6: 66285–66292. doi: 10.1109/ACCESS.2018.2879118.
[14]	黄玉龙, 张勇刚, 武哲民, 等. 带有色厚尾量测噪声的鲁棒高斯近似滤波器和平滑器[J]. 自动化学报, 2017, 43(1): 114–131. doi: 10.16383/j.aas.2017.c150810. HUANG Yulong, ZHANG Yonggang, WU Zhemin, et al. Robust Gaussian approximate filter and smoother with colored heavy tailed measurement noise[J]. Acta Automatica Sinica, 2017, 43(1): 114–131. doi: 10.16383/j.aas.2017.c150810.
[15]	WANG Guoqing, ZHAO Jiaxiang, YANG Chunyu, et al. Robust Kalman filter for systems with colored heavy-tailed process and measurement noises[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2023, 70(11): 4256–4260. doi: 10.1109/TCSII.2023.3283547.
[16]	WANG Hongwei, LI Hongbin, FANG Jun, et al. Robust Gaussian Kalman filter with outlier detection[J]. IEEE Signal Processing Letters, 2018, 25(8): 1236–1240. doi: 10.1109/LSP.2018.2851156.
[17]	HOSTETTLER R and SÄRKKÄ S. Rao-blackwellized Gaussian smoothing[J]. IEEE Transactions on Automatic Control, 2019, 64(1): 305–312. doi: 10.1109/TAC.2018.2828087.
[18]	JIA Guangle, HUANG Yulong, ZHANG Yonggang, et al. A novel adaptive Kalman filter with unknown probability of measurement loss[J]. IEEE Signal Processing Letters, 2019, 26(12): 1862–1866. doi: 10.1109/LSP.2019.2951464.
[19]	GRANSTRÖM K and ORGUNER U. On the reduction of Gaussian inverse Wishart mixtures[C]. 2012 15th International Conference on Information Fusion, Singapore, 2012: 2162–2169.
[20]	GU Peng, JING Zhongliang, and WU Liangbin. Robust adaptive multi-target tracking with unknown measurement and process noise covariance matrices[J]. IET Radar, Sonar & Navigation, 2022, 16(4): 735–747. doi: 10.1049/rsn2.12216.
[21]	ZHU Jiangbo, XIE Weixin, and LIU Zongxiang. Student’s t-based robust Poisson multi-Bernoulli mixture filter under heavy-tailed process and measurement noises[J]. Remote Sensing, 2023, 15(17): 4232. doi: 10.3390/rs15174232.