Electromagnetic Sensitivity Analysis of Curved Boundaries under the Method of Accompanying Variables
-
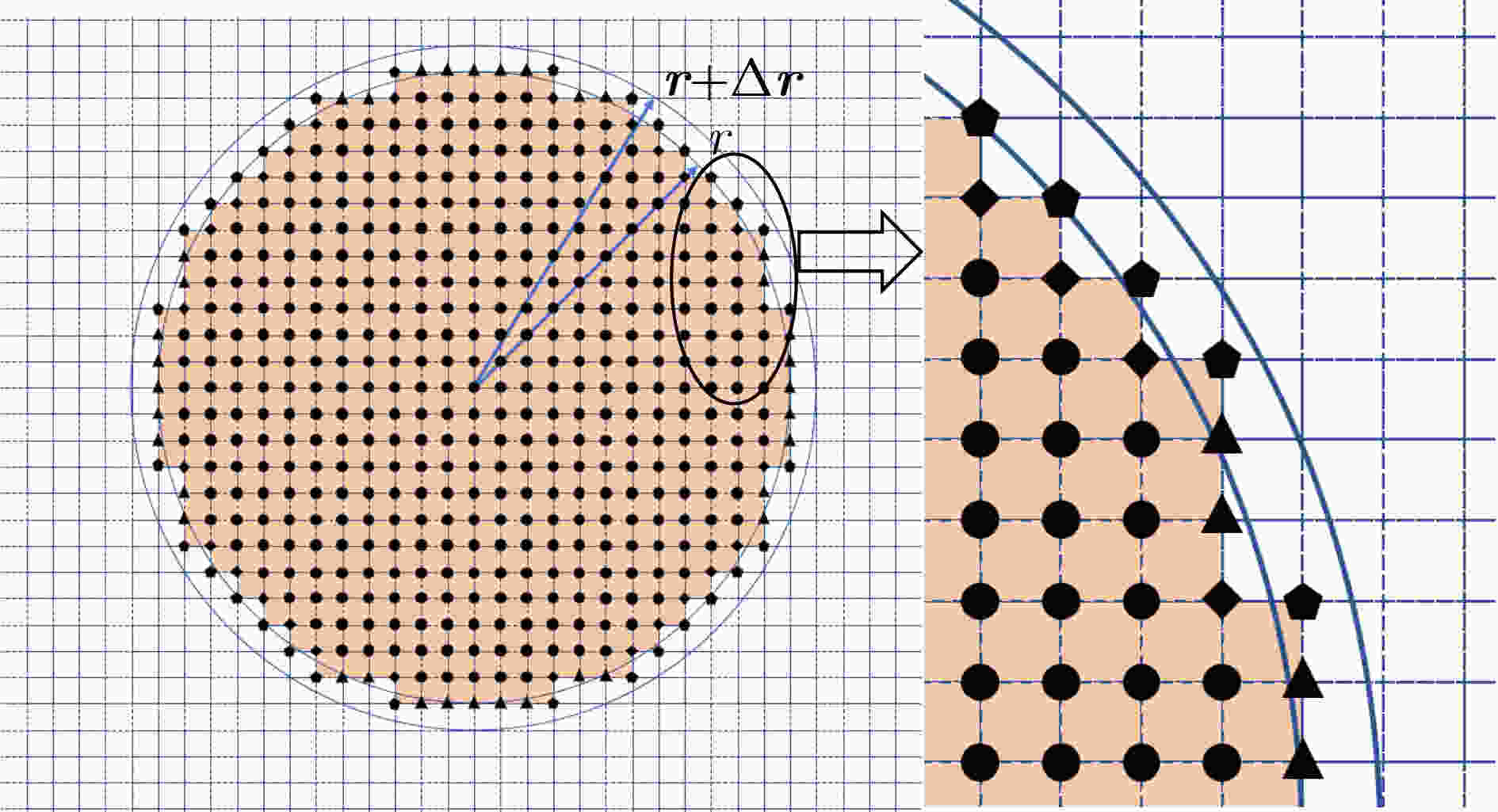
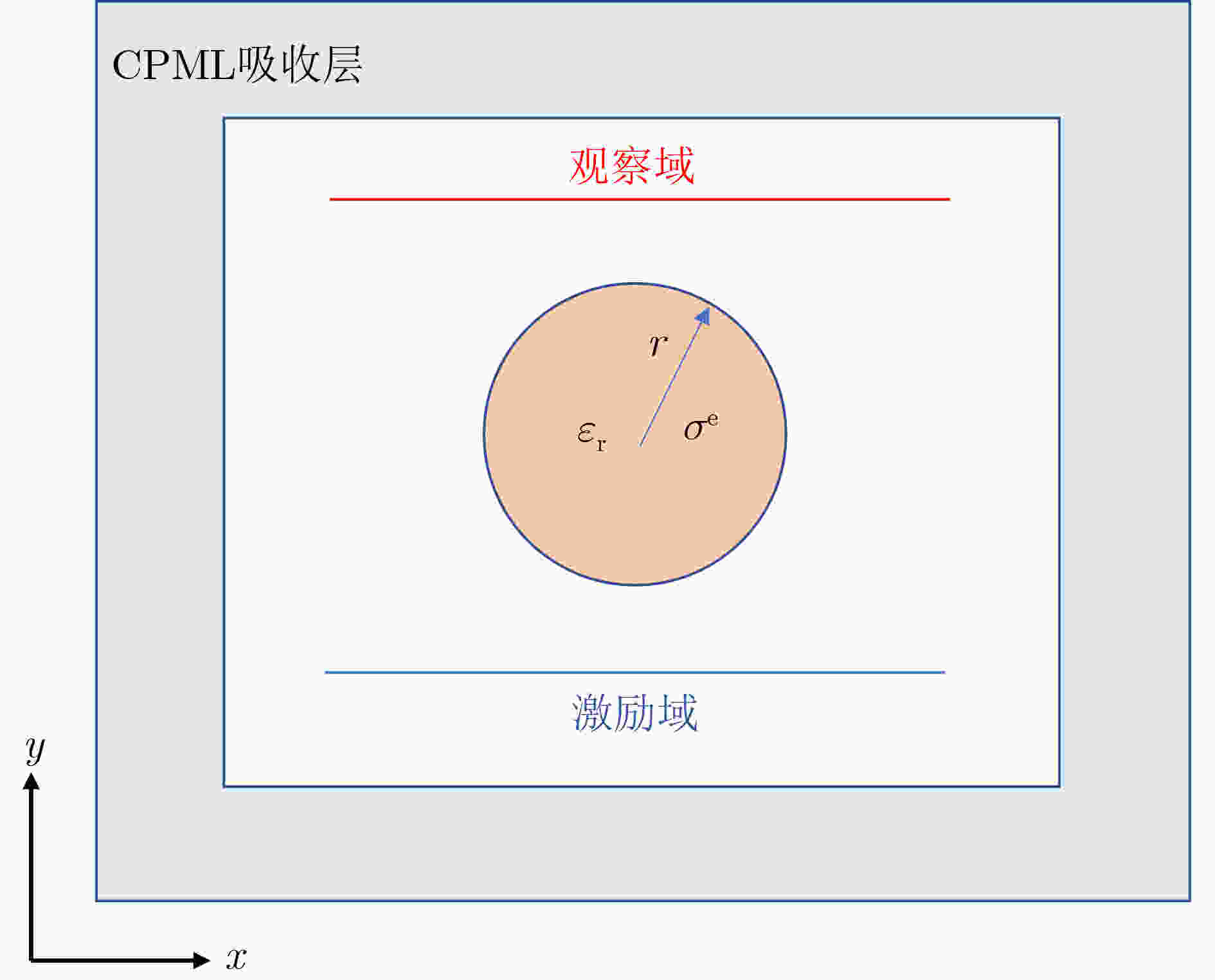
摘要: 电磁灵敏度分析是评估设计参数变化对电磁性能影响的一种方法,它通过计算灵敏度信息指导结构模型分析,以满足设计规范。商业软件在进行电磁结构优化设计时,常通过调整几何结构并使用传统算法,但这种方法计算耗时且资源占用大。为了提高模型设计的效率,该文提出一种稳定高效的处理方案,即伴随变量法(AVM),利用仅有2次算法模拟条件下,实现在参数变换上进行1~2阶灵敏度估计。当前AVM的绝大多数应用局限在矩形边界参数的灵敏度分析,该文首次开拓性地将AVM拓展到弧形边界参数的灵敏度分析。基于固定的本构参数、频率依赖性目标函数以及瞬态脉冲函数的3种不同情形设计的条件,实现了对弧形结构的电磁灵敏度的高效分析。与有限差分方法(FDM)相比,该方法在计算效率上得到了显著的提高。该方法有效实施显著拓宽了AVM在弧形边界上的应用范围,可应用于等离子体模型的电磁结构、复杂天线模型的边缘结构等优化问题上。当计算资源较少的情况下,可满足电磁结构优化的可靠性和稳定性。Abstract: Sensitivity analysis an evaluation method for the influence with variations of the design parameters on electromagnetic performance, which is utilized to calculate sensitivity information. This information guides the analysis of structural models to ensure compliance with design specifications. In the optimization design of electromagnetic structures by commercial software, traditional algorithms are often employed, involving adjustments to the geometry. However, this approach is known to be extensive in terms of computational time and resource consumption. In order to enhance the efficiency of model design, a stable and efficient processing scheme is proposed in the paper, known as the Adjoint Variable Method (AVM). This method achieves estimation of 1st~2nd order sensitivity on parameter transformations with only two algorithmic simulation conditions required. The application of AVM has predominantly been confined to the sensitivity analysis of rectangular boundary parameters, with this paper making the first extension of AVM to the sensitivity analysis of arc boundary parameters. Efficient analysis of the electromagnetic sensitivity of curved structures is accomplished based on the conditions designed for three distinct scenarios: fixed intrinsic parameters, frequency-dependent objective functions, and transient impulse functions. Compared to the Finite-Difference Method (FDM), a significant enhancement in computational efficiency is achieved by the proposed method. The effective implementation of the method substantially expands the application scope of AVM to curved boundaries, which can be utilized in optimization problems such as the electromagnetic structures of plasma models and the edge structures of complex antenna models. When computational resources are limited, the reliability and stability of electromagnetic structure optimization can be ensured by the application of the proposed method.
-
表 1 本构无关目标函数下AVM和FDM之间的范数误差
误差类型 $ {\varepsilon _{\mathrm{r}}} $ $ {\sigma ^{\mathrm{e}}} $ $ r $ AVM和CFD 2.0255 ×10–35.1667 ×10–46.2553 ×10–2AVM和FFD 2.7232 ×10–35.5774 ×10–47.3643 ×10–3AVM和BFD 1.3269 ×10–34.7567 ×10–41.4296 ×10–1表 2 频率相关目标函数下AVM和FDM之间的范数误差
误差类型 $ {\varepsilon _{\mathrm{r}}} $ $ {\sigma ^{\mathrm{e}}} $ r 实部 虚部 实部 虚部 实部 虚部 AVM和CFD 0.0099 0.0459 0.0551 0.0101 0.1178 0.1132 AVM和FFD 0.0137 0.0594 0.0573 0.0101 0.1145 0.2525 AVM和BFD 0.0013 0.0820 0.0533 0.0104 0.1287 0.1842 表 3 瞬态函数下AVM和FDM之间的范数误差
误差类型 $ {\varepsilon _{\mathrm{r}}} $ (×10–2) $ {\sigma ^{\mathrm{e}}} $ (×10–3) r (×10–1) AVM和CFD 0.3689 4.0714 1.1738 AVM和FFD 1.3879 4.9260 1.3187 AVM和BFD 1.9305 4.1873 1.3244 -
[1] RAO S S. Engineering Optimization Theory and Practice[M]. 4th ed. Hoboken: John Wiley & Sons, 2009. [2] ANTONIOU A and LU Wusheng. Practical Optimization Algorithms and Engineering Applications[M]. New York: Springer, 2007. [3] WU J C, WANG S P, WANG Y H, et al. Sensitivity analysis of design parameters in transverse flux induction heating device[J]. IEEE Transactions on Applied Superconductivity, 2020, 30(4): 0600406. doi: 10.1109/TASC.2020.2973604. [4] DU Guanghui, HUANG Na, ZHAO Yanyun, et al. Comprehensive sensitivity analysis and multiphysics optimization of the rotor for a high speed permanent magnet machine[J]. IEEE Transactions on Energy Conversion, 2021, 36(1): 358–367. doi: 10.1109/TEC.2020.3005568. [5] BAKER R D. A methodology for sensitivity analysis of models fitted to data using statistical methods[J]. IMA Journal of Management Mathematics, 2001, 12(1): 23–39. doi: 10.1093/imaman/12.1.23. [6] CABANA K, CANDELO J E, and CASTILLO R. Statistical analysis of voltage sensitivity in distribution systems integrating DG[J]. IEEE Latin America Transactions, 2016, 14(10): 4304–4309. doi: 10.1109/TLA.2016.7786309. [7] LI Hui, DU Yuanbo, YANG Xian, et al. Optimization of operation parameters in a cesium atomic fountain clock using Monte Carlo method[J]. IEEE Access, 2021, 9: 132140–132149. doi: 10.1109/ACCESS.2021.3113161. [8] KIM H, LEE J, LEE J, et al. Topology optimization of a magnetic resonator using finite-difference time-domain method for wireless energy transfer[J]. IEEE Transactions on Magnetics, 2016, 52(3): 7003304. doi: 10.1109/TMAG.2015.2478444. [9] ZHONG Shuangying, RAN Chongxi, and LIU Song. The optimal force-gradient symplectic finite-difference time-domain scheme for electromagnetic wave propagation[J]. IEEE Transactions on Antennas and Propagation, 2016, 64(12): 5450–5454. doi: 10.1109/TAP.2016.2606543. [10] MORI T, MURAKAMI R, SATO Y, et al. Shape optimization of wideband antennas for microwave energy harvesters using FDTD[J]. IEEE Transactions on Magnetics, 2015, 51(3): 8000804. doi: 10.1109/TMAG.2014.2359677. [11] FENG Feng, XUE Jianguo, ZHANG Jianan, et al. Concise and compatible MOR-based self-adjoint EM sensitivity analysis for fast frequency sweep[J]. IEEE Transactions on Microwave Theory and Techniques, 2023, 71(9): 3829–3840. doi: 10.1109/TMTT.2023.3248167. [12] NA Weicong, LIU Ke, ZHANG Wanrong, et al. Advanced EM optimization using adjoint-sensitivity-based multifeature surrogate for microwave filter design[J]. IEEE Microwave and Wireless Technology Letters, 2024, 34(1): 1–4. doi: 10.1109/LMWT.2023.3329783. [13] NIKOLOVA N K, BANDLER J W, and BAKR M H. Adjoint techniques for sensitivity analysis in high-frequency structure CAD[J]. IEEE Transactions on Microwave Theory and Techniques, 2004, 52(1): 403–419. doi: 10.1109/TMTT.2003.820905. [14] ZHANG Yu, AHMED O S, and BAKR M H. Adjoint sensitivity analysis of plasmonic structures using the FDTD method[J]. Optics Letters, 2014, 39(10): 3002–3005. doi: 10.1364/OL.39.003002. [15] HARMON J J, KEY C, ESTEP D, et al. Adjoint-based accelerated adaptive refinement in frequency domain 3-D finite element method scattering problems[J]. IEEE Transactions on Antennas and Propagation, 2021, 69(2): 940–949. doi: 10.1109/TAP.2020.3016162. [16] HUANG Zhengyu, JIANG Feng, CHEN Zian, et al. A 3-D total-field/scattered-field plane-wave source for the unconditionally stable associated hermite FDTD method[J]. IEEE Antennas and Wireless Propagation Letters, 2024, 23(2): 628–632. doi: 10.1109/LAWP.2023.3331381. [17] 叶志红, 张玉, 鲁唱唱. 端接复杂电路传输线网络的电磁耦合时域并行计算方法[J]. 电子与信息学报, 2024, 46(2): 713–719. doi: 10.11999/JEIT230098.YE Zhihong, ZHANG Yu, and LU Changchang. Time domain parallel calculation method for the coupling of transmission line network terminated with complex circuits[J]. Journal of Electronics & Information Technology, 2024, 46(2): 713–719. doi: 10.11999/JEIT230098. [18] ZHU Guocui, NIU Kaikun, LI Minquan, et al. High-order ME-CFS-PML implementations for terminating the FDTD domain composed of arbitrary media[J]. IEEE Transactions on Microwave Theory and Techniques, 2024, 72(4): 2414–2426. doi: 10.1109/TMTT.2023.33158373. [19] ZHAO Sihan, WEI Bing, HE Xinbo, et al. 2-D hybrid cylindrical FDTD method with unconditional stability[J]. IEEE Microwave and Wireless Technology Letters, 2023, 33(7): 955–958. doi: 10.1109/LMWT.2023.3261918. -





 下载:
下载:





 下载:
下载:
