Two-stage Long-correlation Signal Acquisition Method for Through-the-earth Communication of the Ground Electrode Current Field
-
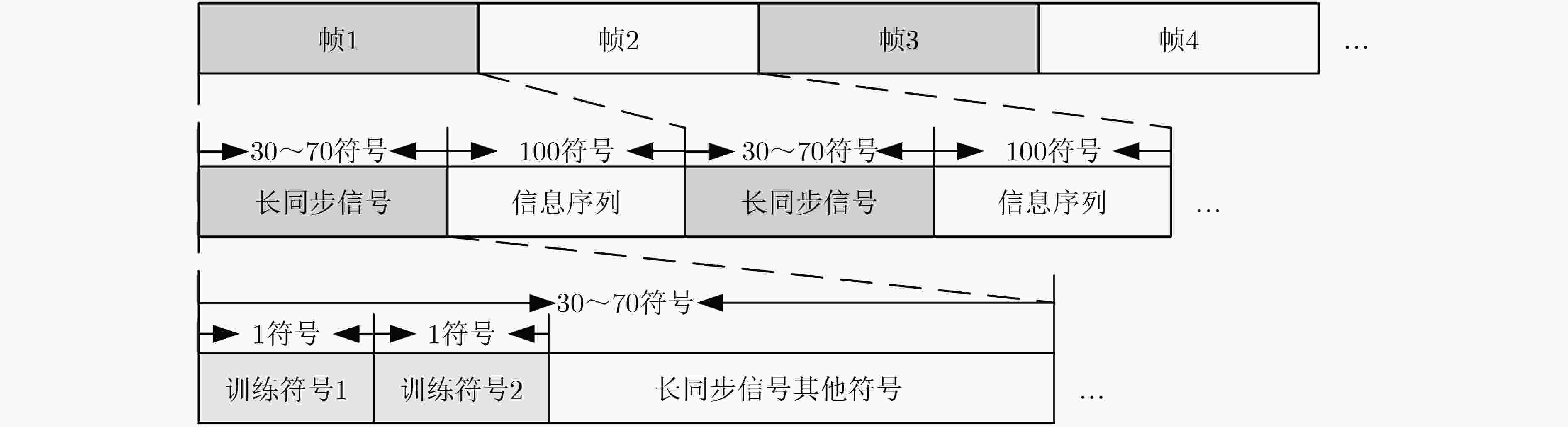
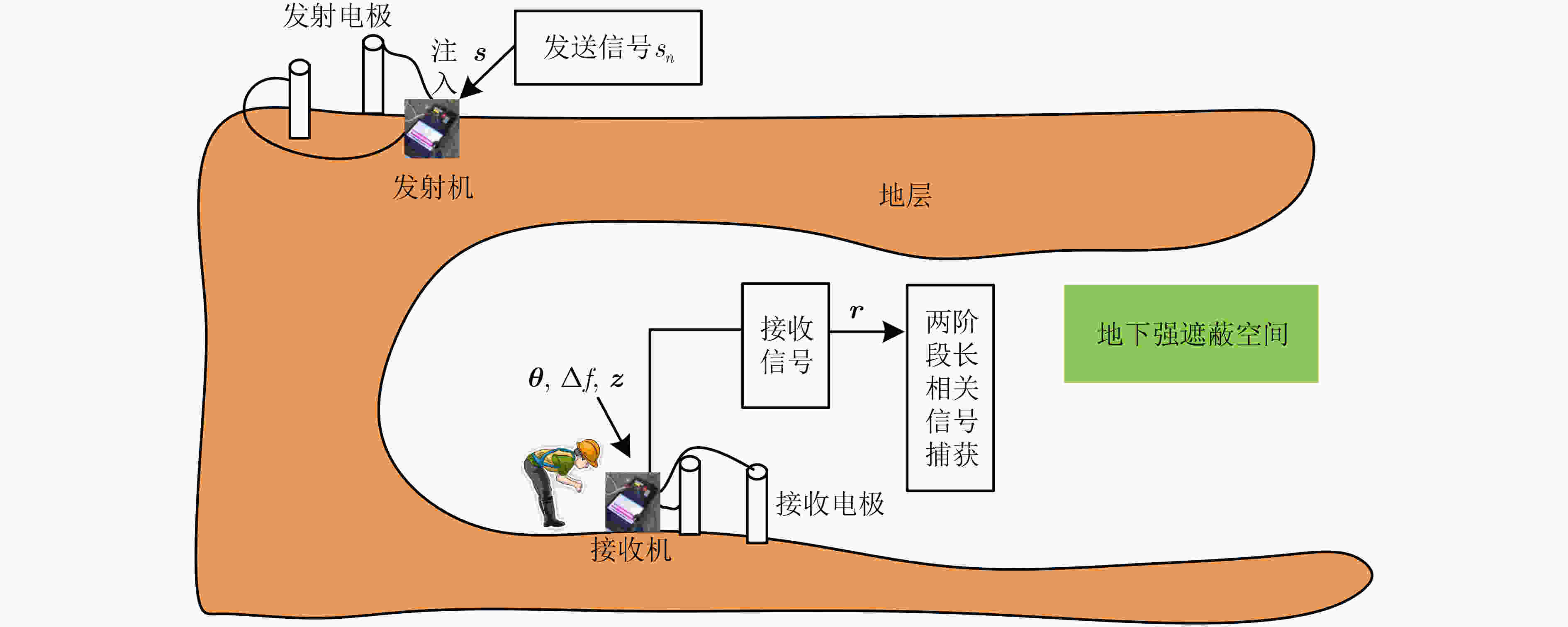
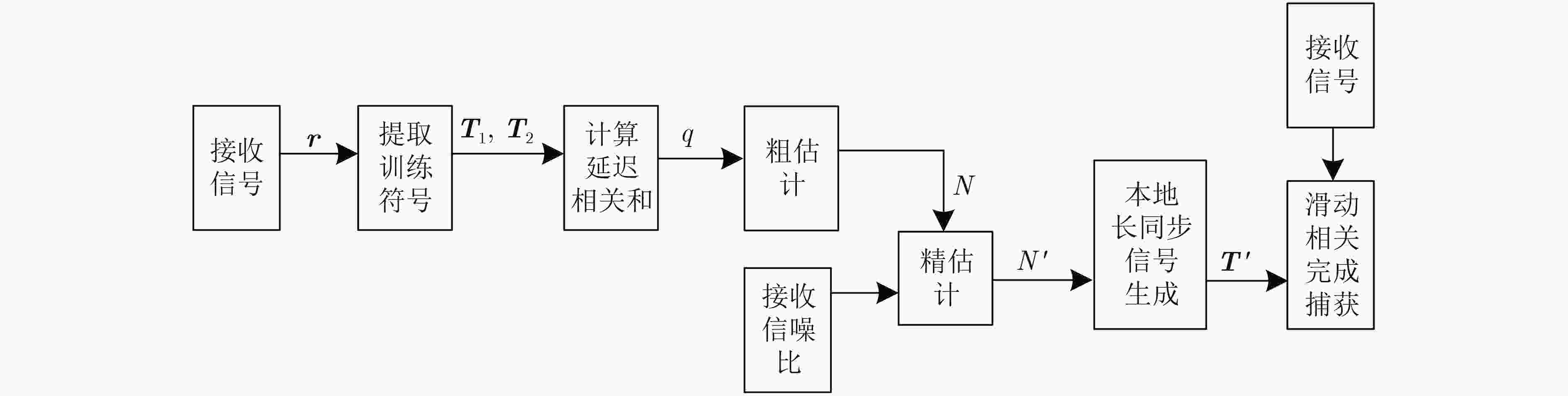
摘要: 地电极电流场透地通信可以为地下强遮蔽空间信息传输提供解决方案。针对接收的电流场信号信噪比(SNR)低、易畸变且受载波频偏影响大导致捕获困难的问题,该文设计一种长同步信号帧结构,在此基础上提出一种联合频偏粗估计和精估计的两阶段长相关信号捕获算法。该算法第1阶段利用接收时域信号中的训练符号,依据最大似然算法进行采样间隔偏差粗估计,并计算采样点补偿间隔粗估计值。第2阶段结合粗估计值和接收信噪比,确定采样点补偿间隔精估计值的遍历范围,进而设计本地补偿后的长相关模板信号,实现电流场信号的精确捕获。本研究在距离地面30.26 m的地下强遮蔽空间中进行了算法性能验证。实验结果表明,与传统的滑动相关算法相比,该文所提算法具有更高的捕获成功概率。Abstract: Wireless through-the-earth communication provides a solution for information transmission in heavily shielded space. The received current field signal has low Signal-to-Noise Ratio (SNR), is easily distorted, and is greatly affected by carrier frequency offset, making signal acquisition difficult. In this paper, a long synchronization signal frame structure is designed and a two-stage long correlation signal acquisition algorithm is proposed that combines coarse and fine frequency offset estimation. In the first stage, the training symbols in the received time-domain signal are used for coarse estimation of sampling interval deviation based on the maximum likelihood algorithm, and the coarse estimation value of the sampling point compensation interval is calculated. In the second stage, the coarse estimation value and the received SNR are combined to determine the traversal range of the fine estimation value of the sampling point compensation interval. A long correlation template signal with local compensation is designed to achieve accurate acquisition of the current field signal. The algorithm’s performance is verified in a heavily shielded space located 30.26 m below the ground. Experimental results show that compared to traditional sliding correlation algorithms, the proposed algorithm has a higher acquisition success probability.
-
1 基于粗估计值$ \text{N} $遍历计算频偏修正后本地长同步信号
输入:$ {{\mathrm{Sync}}\_L} $ //本地长同步信号 输出:$ {{\mathrm{Sync}}\_L}{'} $ //频偏修正后本地长同步信号 (1) for $ {N'} $ = $ {N}{-}{x} $ to $ {N}{+}{x} $ do // $ {N'} $在范围内遍历 (2) $ {i} $ = $ {i} $ +1 // $ {i} $的初始值为0 (3) if $\vartheta < 0$ $ {{\mathrm{Sync}}\_L}{'}{(}{i}{)} $ = interpolation ($ {{\mathrm{Sync}}\_L} $, $ {N'}{(}{i}{)} $) //在本地长同步信号信号上每隔$ {N'}{(}{i}{)} $个点插入1个样值,生
成第$ {i} $个频偏修正后本地长同步信号(4) else $ {{\mathrm{Sync}}\_L}{'}{(}{i}{)} $ = decline ($ {{\mathrm{Syn}}{\mathrm{c}}\_L} $, $ {N'}{(}{i}{)} $) //在本地长同步信号信号上每隔$ {N'}{(}{i}{)} $个点去除1个采样点 (5) end (6) end (7) return $ {{\mathrm{Sync}}\_L}{'}{(}{i}{)} $ 2 采样点补偿间隔精估计值计算
输入:$ \text{Sync\_L}{'} $ // 频偏修正后本地长同步信号 $ {R} $// 接收信号 输出:$ {N'} $// $ \text{Sync\_L}{'} $与$ {R} $滑动相关峰值最大时对应的采样点补
偿间隔精估计值(1) for $ {i} $ = 1 To $ {{l}}_{{1}}{-}{{l}}_{{2}}{-1} $ do // 相关滑动窗口,共有$ {{l}}_{{1}}{-}{{l}}_{{2}}{-1} $个。 (2) $ {g}{(}{i}{)} $ = corr($ {R} $, $ \text{Sync\_L}{'}{(}{i}{)} $) // $ {R} $与 $ \text{Sync\_L}{'}{(}{i}{)} $进行滑动相关 (3) $ {{K}}_{{i}} $ = max($ {d}{(}{i}{)} $) //获取相关峰值 (4) end (5) $ {N'} $=find(max($ {{K}}_{{i}}{} $)) //获取相关峰值最大时对应的采样点补偿间隔精估计值 (6) return $ {N'} $ 表 1 仿真参数
参数名称 参数值 发送信号载波频率(Hz) 10 发射机时钟频率(MHz) 10 收发机时钟频率偏差(PPM) 0.1 [16] 收发机采样频率(Hz) 500 信道类型 加性高斯白噪声信道 信噪比(dB) –3~6 同步信号长度 30~70符号 表 2 不同算法捕获成功概率在不同同步信号点数下达到95%所需信噪比(dB)
接收同步信号
点数滑动相关
捕获算法粗估计捕获
算法长相关捕获
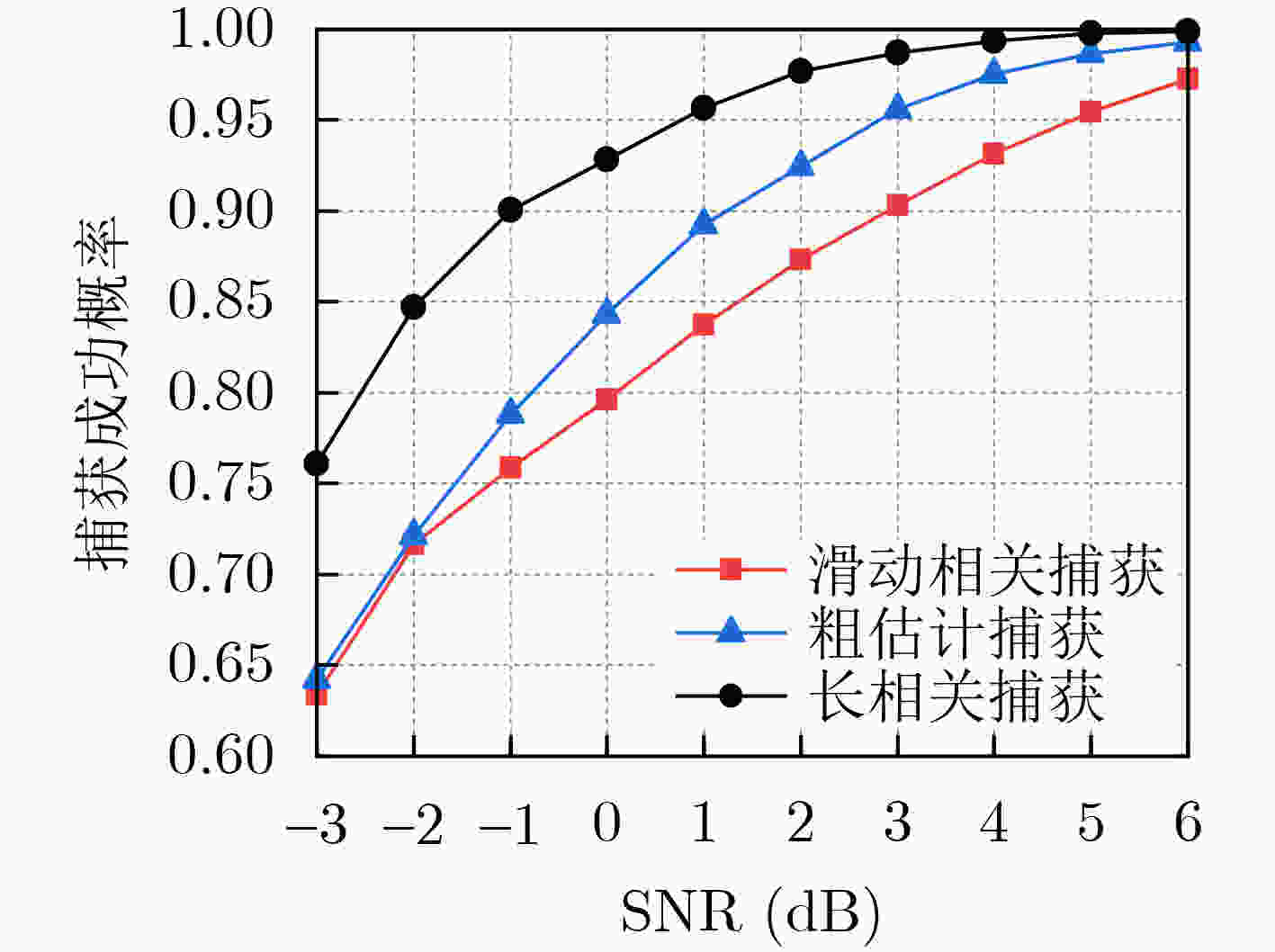
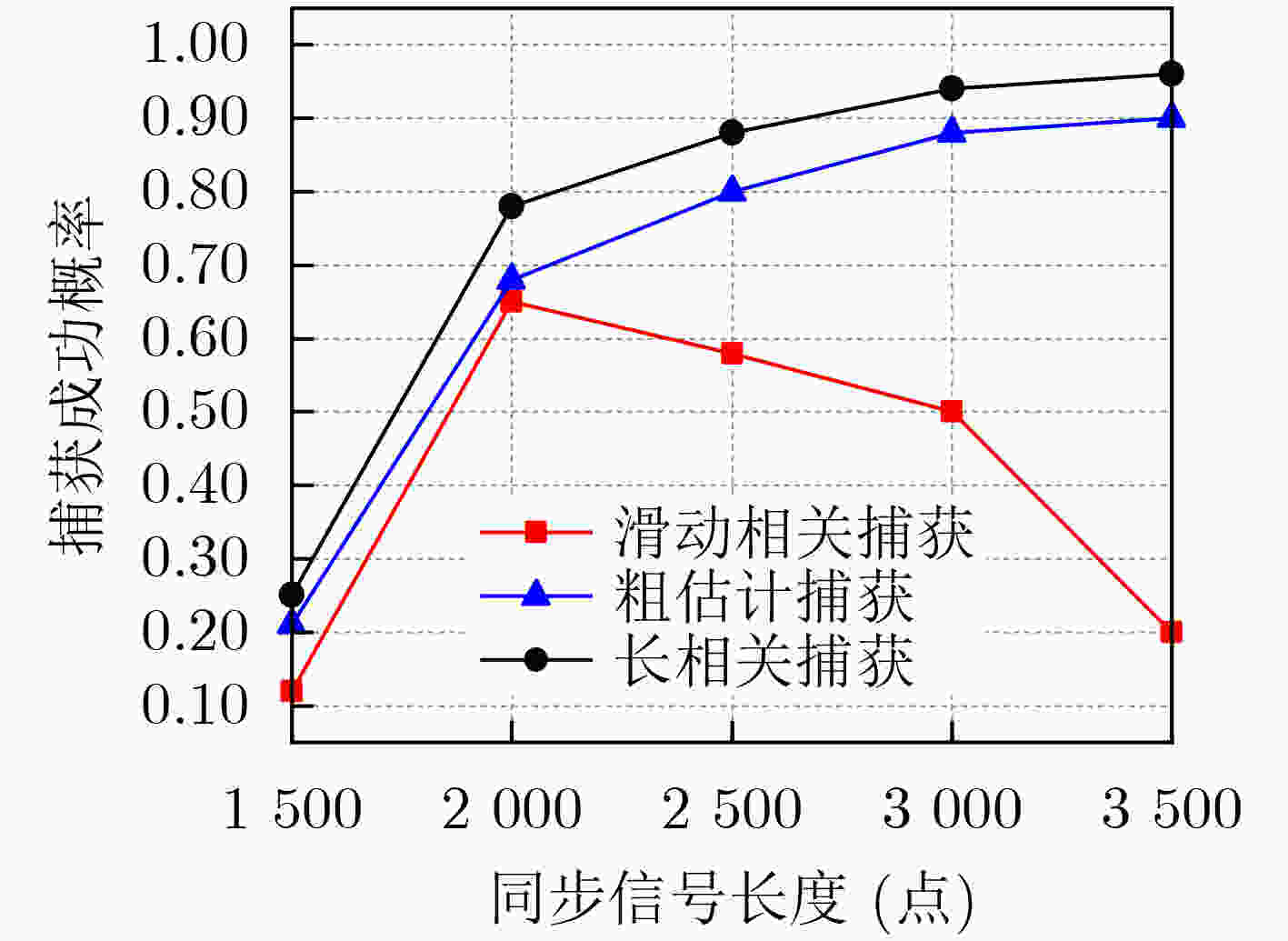
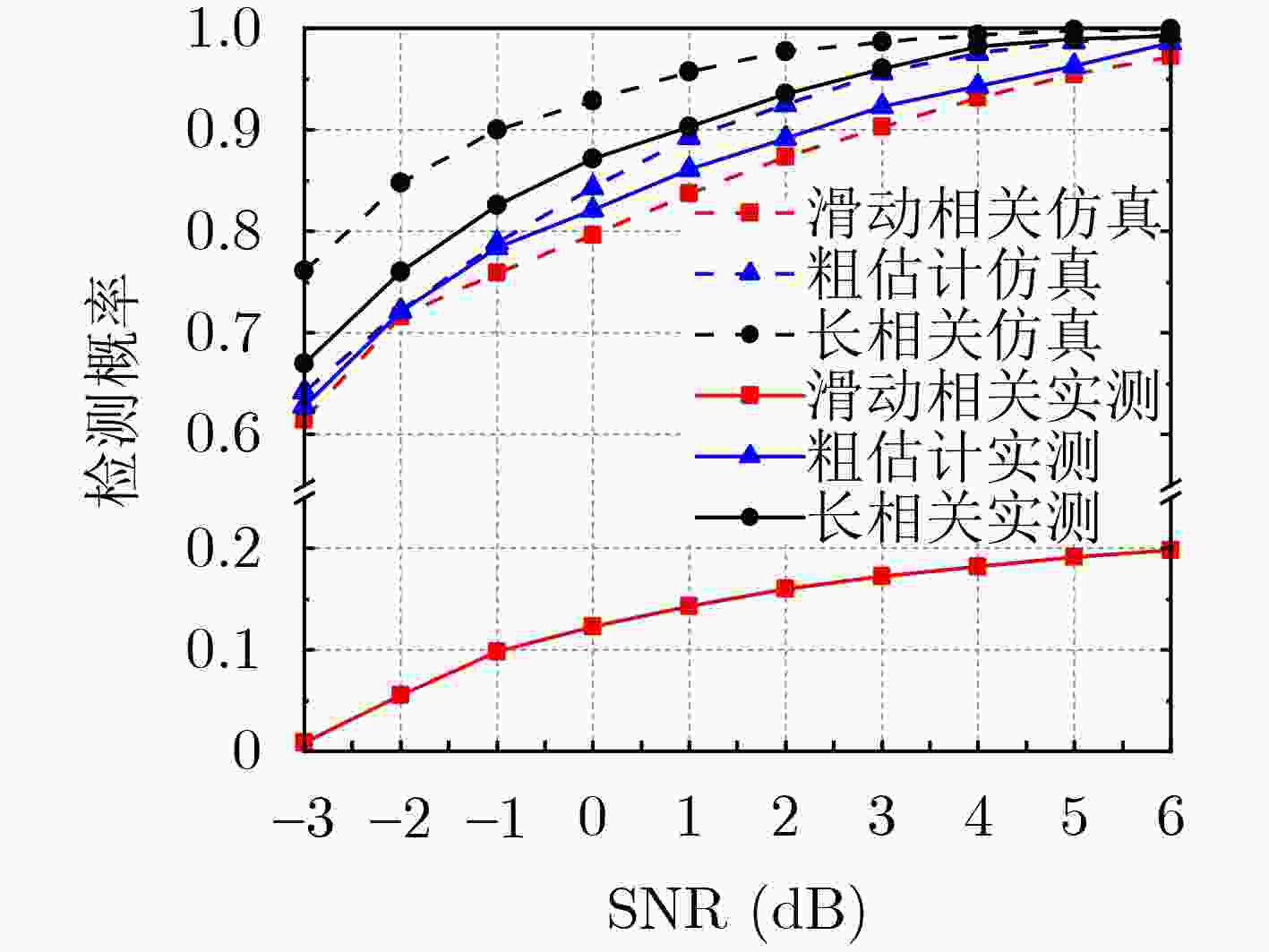
算法1 500 6 4 3 2 000 5 2 0 2 500 – 0 –2 3 000 – –1 –2 3 500 – –2 –4 -
[1] MA Honglei, LIU Erwu, WANG Rui, et al. Antenna optimization for decode-and-forward relay in magnetic induction communications[J]. IEEE Transactions on Vehicular Technology, 2020, 69(3): 3449–3453. doi: 10.1109/TVT.2019.2963357. [2] JULTHOCHAI S, KHAMSALEE P, and WONGSAN R. An experimental study of performance enhancement of medium-frequency small loop antennas for through-the-earth at 350 kHz[C]. 2023 20th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Nakhon Phanom, Thailand, 2023: 1–4. doi: 10.1109/ECTI-CON58255.2023.10153298. [3] ZHOU Chenming, SNYDER D P, EPSTEIN B, et al. Measurement of ambient magnetic field noise for through-the-earth (TTE) communications and historical comparisons[J]. IEEE Transactions on Electromagnetic Compatibility, 2024, 66(3): 720–727. doi: 10.1109/TEMC.2024.3354735. [4] DAMIANO N W, YAN Lincan, WHISNER B, et al. Simulation and measurement of through-the-earth, extremely low-frequency signals using copper-clad steel ground rods[J]. IEEE Transactions on Industry Applications, 2017, 53(5): 5088–5095. doi: 10.1109/TIA.2017.2703625. [5] WU Lipeng, ZHANG Wenwei, SONG Xianjin, et al. Research on electromagnetic field characteristics of rotating-magnet based mechanical antenna through the earth[J]. International Journal of Applied Electromagnetics and Mechanics, 2024, 72(2): 123–139. doi: 10.3233/JAE-230080. [6] PRUEKCHATSIRI C, JANTAUPALEE A, KHAMSALEE P, et al. An experimental study of electrodes for through-the-earth 350 kHz MF Communication[C]. 2023 IEEE International Symposium On Antennas And Propagation (ISAP), Kuala Lumpur, Malaysia, 2023: 1–2. doi: 10.1109/ISAP57493.2023.10389116. [7] ZHOU Chenming, SYNDER D P, EPSTEIN B, et al. Magnetic field noise in the ultra-low frequency (ULF) band and historical comparisons[C]. 2022 IEEE International Symposium on Electromagnetic Compatibility & Signal/Power Integrity (EMCSI), Spokane, USA, 2022: 439–442. doi: 10.1109/EMCSI39492.2022.9889418. [8] CHAVES B P and BRAGA A J. An analytical propagation model based on dyadic green’s functions for TTE communications in an arbitrary stratified soil[J]. IEEE Transactions on Antennas and Propagation, 2022, 70(11): 11240–11245. doi: 10.1109/TAP.2022.3184524. [9] 龚永俭, 张长轩, 程立康, 等. 地电场环境干扰跟踪分析关键问题研究[J]. 高原地震, 2020, 32(1): 26–38. doi: 10.3969/j.issn.1005-586X.2020.01.005.GONG Yongjian, ZHANG Changxuan, CHENG Likang, et al. Study on key problems of tracking analysis of the geoelectric field environmental interference[J]. Plateau Earthquake Research, 2020, 32(1): 26–38. doi: 10.3969/j.issn.1005-586X.2020.01.005. [10] JANTAUPALEE A, KHAMSALEE P, and WONGSAN R. Low-frequency wave propagation in the cave[C]. 2023 20th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Nakhon Phanom, Thailand, 2023: 1–4. doi: 10.1109/ECTI-CON58255.2023.10153170. [11] 杨天绘. 基于电流场传播的矿井透地通信系统研究[D]. [硕士论文], 西安电子科技大学, 2017.YANG Tianhui. Research on through-the-earth communication system for mines based on current field propagation[D]. [Master dissertation], Xidian University, 2017. [12] YANG Liu, ZHANG Hang, CAI Yang, et al. Blind carrier frequency offset estimation for MIMO-OFDM systems based on the banded structure of covariance matrices for constant modulus signals[J]. IEEE Access, 2018, 6: 51804–51813. doi: 10.1109/ACCESS.2018.2870278. [13] 侯文壮. 地下防空洞无线透地通信系统设计与实现[D]. [硕士论文], 哈尔滨工程大学, 2023.HOU Wenzhuang. Design and implementation of wireless through-the-earth communication system for underground air raid shelters[D]. [Master dissertation], Harbin Engineering University, 2023. [14] ZHANG Gan, XU Zhan, CHEN Jinhui, et al. OFDM signal design based on electrode-based through-the-earth communication[C]. 2021 20th International Conference on Ubiquitous Computing and Communications (IUCC/CIT/DSCI/SmartCNS), London, UK, 2021: 40–45. doi: 10.1109/IUCC-CIT-DSCI-SmartCNS55181.2021.00021. [15] JANTAUPALEE A, WONGSAN R, KHAMSALEE P, et al. A study of radio wave propagation in the cave for developing the through-the-earth application[J]. GEOMATE Journal, 2024, 26(118): 74–86. [16] 王菊凤, 张宇, 黄徐瑞晗, 等. 对相对频率偏差的探讨与思考[J]. 计量与测试技术, 2022, 49(9): 1–3. doi: 10.15988/j.cnki.1004-6941.2022.9.001.WANG Jufeng, ZHANG Yu, HUANG Xuruihan, et al. Discussion and reflection on relative frequency offset[J]. Metrology & Measurement Technique, 2022, 49(9): 1–3. doi: 10.15988/j.cnki.1004-6941.2022.9.001. -





 下载:
下载:




 下载:
下载:
