方向感知增强的轻量级自监督单目深度估计方法

程德强; 徐帅; 吕晨; 韩成功; 江鹤; 寇旗旗

doi:10.11999/JEIT240189

方向感知增强的轻量级自监督单目深度估计方法

doi: 10.11999/JEIT240189

程德强¹,
徐帅¹,
吕晨¹,
韩成功¹,
江鹤¹,
寇旗旗^2, ,

1.
中国矿业大学信息与控制工程学院徐州 221116
2.
中国矿业大学计算机科学与技术学院徐州 221116

基金项目: 国家自然科学基金(52304182)，徐州市推动科技创新专项资金项目(KC23401)

详细信息

作者简介:
程德强：男，教授，研究方向为图像处理

徐帅：男，硕士生，研究方向为深度估计

吕晨：男，博士生，研究方向为深度估计

韩成功：男，博士生，研究方向为深度估计

江鹤：男，讲师，研究方向为图像处理

寇旗旗：男，副教授，研究方向为图像处理，模式识别

通讯作者:
寇旗旗　kouqiqi@cumt.edu.cn

中图分类号: TN911.73; TP391.41
计量
- 文章访问数: 34
- HTML全文浏览量: 16
- PDF下载量: 8
- 被引次数: 0
出版历程
- 收稿日期: 2024-03-20
- 修回日期: 2024-07-01
- 网络出版日期: 2024-07-05

Lightweight Self-supervised Monocular Depth Estimation Method with Enhanced Direction-aware

1.
School of Information and Control Engineering, China University of Mining and Technology, Xuzhou 221116, China
2.
School of Computer Science and Technology, China University of Mining and Technology, Xuzhou 221116, China

Funds: The National Natural Science Foundation of China (52304182), The Promoting Science and Technology Innovation Special Funds Program of Xuzhou City (KC23401)

摘要

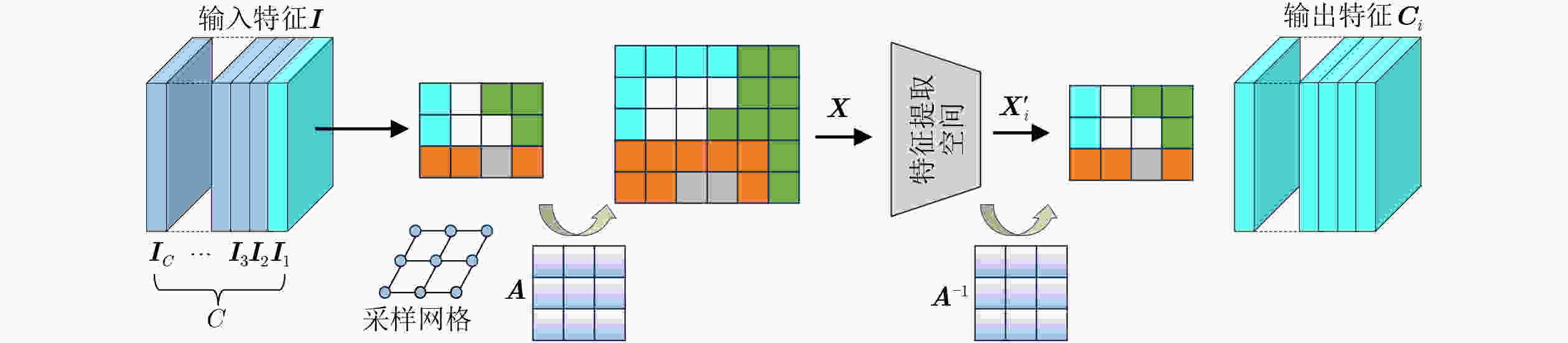
摘要: 为解决现有单目深度估计网络复杂度高、在弱纹理区域精度低等问题，该文提出一种基于方向感知增强的轻量级自监督单目深度估计方法(DAEN)。首先，引入迭代扩展卷积模块(IDC)作为编码器的主体，提取远距离像素的相关性；其次，设计方向感知增强模块(DAE)增强垂直方向的特征提取，为深度估计模型提供更多的深度线索；此外，通过聚合视差图特征改善解码器上采样过程中的细节丢失问题；最后，采用特征注意力模块(FAM)连接编解码器，有效利用全局上下文信息解决弱纹理区域的不适应问题。在KITTI数据集上的实验结果表明，该文模型参数量仅2.9M，取得$ \delta $指标89.2%的先进性能。在Make3D数据集上验证DAEN的泛化性，结果表明，该文模型各项指标均优于目前主流的方法，在弱纹理区域具有更好的深度预测性能。
- 图像处理 /
- 深度估计 /
- 自监督学习 /
- 方向感知
Abstract: To address challenges such as high complexity in monocular depth estimation networks and low accuracy in regions with weak textures, a Direction-Aware Enhancement-based lightweight self-supervised monocular depth estimation Network (DAEN) is proposed in this paper. Firstly, the Iterative Dilated Convolution module (IDC) is introduced as the core of the encoder to extract correlations among distant pixels. Secondly, the Directional Awareness Enhancement module (DAE) is designed to enhance feature extraction in the vertical direction, providing the depth estimation model with additional depth cues. Furthermore, the problem of detail loss during the decoder upsampling process is addressed through the aggregation of disparity map features. Lastly, the Feature Attention Module (FAM) is employed to connect the encoder and decoder, effectively leveraging global contextual information to resolve adaptability issues in regions with weak textures. Experimental results on the KITTI dataset demonstrate that the proposed method has a model parameter count of only 2.9M, achieving an advanced performance with $ \delta $ metric of 89.2%. The generalization of DAEN is validated on the Make3D datasets, with results indicating that the proposed method outperforms current state-of-the-art methods across various metrics, particularly exhibiting superior depth prediction performance in regions with weak textures.
- Image processing /
- Depth estimation /
- Self-supervised learning /
- Direction-aware

HTML全文

图 1 整体框架图

下载: 全尺寸图片幻灯片

图 2 DAE

下载: 全尺寸图片幻灯片

图 3 FAM

下载: 全尺寸图片幻灯片

图 4 基于视差融合的深度解码器

下载: 全尺寸图片幻灯片

图 5 KITTI数据集上可视化分析

下载: 全尺寸图片幻灯片

图 6 KITTI数据集上深度估计细节

下载: 全尺寸图片幻灯片

图 7 Make3d数据集上可视化分析

下载: 全尺寸图片幻灯片

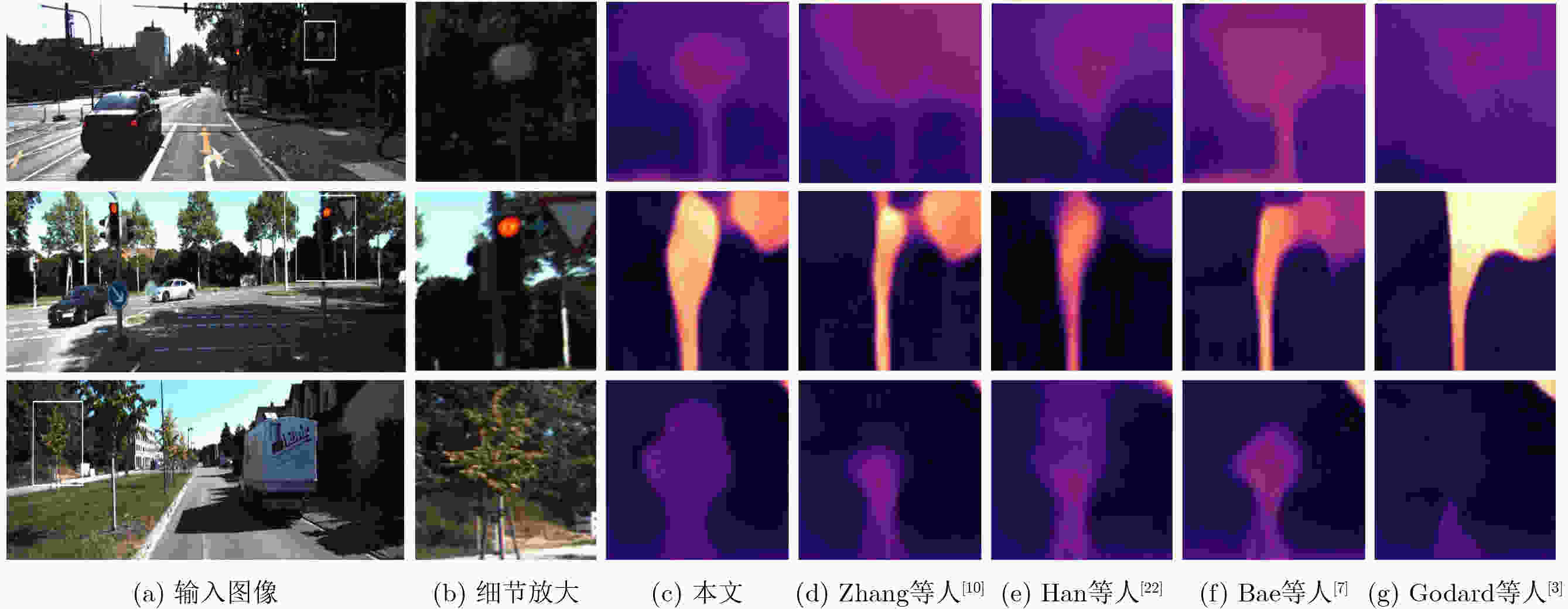
表 1 KITTI数据集上的定量结果

方法	时间	训练方法	骨干网络	AbsRel	SqRel	RMS	RMSlog	$ \delta <125 $	$ \delta < 1.25^{2} $	$ \delta < 1.25^{3} $	参数量(M)
方法	时间	训练方法	骨干网络	越小越好				越大越好			参数量(M)
Yin等人^[18]	2018	M	CNN	0.149	1.060	5.567	0.226	0.796	0.935	0.975	31.6
Wang等人^[19]	2018	M	CNN	0.151	1.257	5.583	0.228	0.810	0.936	0.974	28.1
Godard等人^[3]	2019	M	CNN	0.115	0.903	4.863	0.193	0.887	0.959	0.981	14.3
Godard等人^[3]	2019	M	CNN	0.110	0.831	4.642	0.187	0.883	0.962	0.982	32.5
Klingner等人^[17]	2020	Mse	CNN	0.113	0.835	4.693	0.191	0.879	0.961	0.981	16.3
Johnston等人^[20]	2020	M	CNN	0.111	0.941	4.817	0.189	0.885	0.961	0.981	14.3
Yan等人^[21]	2021	M	CNN	0.110	0.812	4.686	0.187	0.882	0.962	0.983	18.8
Lyu等人^[5]	2021	M	CNN	0.116	0.845	4.841	0.190	0.866	0.957	0.982	3.1
Zhou等人^[16]	2021	M	CNN	0.114	0.815	4.712	0.193	0.876	0.959	0.981	3.5
Zhou等人^[16]	2021	M	CNN	0.112	0.806	4.704	0.191	0.878	0.960	0.981	3.8
Han等人^[22]	2022	M	CNN	0.111	0.816	4.694	0.189	0.884	0.961	0.982	14.7
Varma等人^[8]	2022	M	XRFM	0.112	0.838	4.771	0.188	0.879	0.960	0.982	21.6
Bae等人^[7]	2023	M	XRFM	0.118	0.942	4.840	0.193	0.873	0.956	0.981	23.9
Bae等人^[7]	2023	M	CNN+XRFM	0.104	0.846	4.580	0.183	0.891	0.962	0.982	34.4
Zhang等人^[10]	2023	M	CNN+XRFM	0.107	0.765	4.561	0.183	0.886	0.963	0.983	3.1
本文	2023	M	CNN+XRFM	0.105	0.768	4.552	0.182	0.892	0.964	0.984	2.9
Zhou等人^[16]	2021	M*	CNN	0.112	0.773	4.581	0.189	0.879	0.960	0.982	3.5
Zhou等人^[16]	2021	M*	CNN	0.108	0.748	4.470	0.185	0.889	0.963	0.982	3.8
Lyu等人^[5]	2021	M*	CNN	0.106	0.755	4.472	0.181	0.892	0.966	0.984	14.7
Varma等人^[8]	2022	M*	XRFM	0.104	0.799	4.547	0.181	0.893	0.963	0.982	21.6
Zhang等人^[10]	2023	M*	CNN+XRFM	0.102	0.746	4.444	0.179	0.896	0.965	0.983	3.1
本文	2023	M*	CNN+XRFM	0.100	0.738	4.421	0.177	0.902	0.966	0.984	2.9

下载: 导出CSV

表 2 Make3D数据集的定量结果

方法	AbsRel	SqRel	RMS	RMSlog
Godard等人^[3]	0.322	3.589	7.417	0.163
Zhou等人^[16]	0.334	3.285	7.212	0.169
Zhang等人^[10]	0.305	3.060	6.981	0.158
本文	0.296	2.977	6.651	0.147

下载: 导出CSV

表 3 KITTI数据集上不同方法的消融实验结果

方法	DAE	FAM	FDD	参数量	AbsRel	SqRel	RMS	RMSlog	$ \delta < 125 $	$ \delta < 1.25^{2} $	$ \delta \times 125^{3} $
基准网络				3.1M	0.107	0.765	4.561	0.183	0.886	0.963	0.983
本文	√			3.1M	0.105	0.799	4.582	0.183	0.890	0.963	0.983
		√		3.3M	0.106	0.785	4.623	0.184	0.887	0.963	0.982
			√	2.5M	0.106	0.801	4.610	0.183	0.888	0.962	0.983
	√	√		3.3M	0.107	0.808	4.585	0.184	0.889	0.963	0.983
	√		√	2.5M	0.106	0.761	4.596	0.184	0.892	0.963	0.984
		√	√	2.9M	0.107	0.805	4.609	0.185	0.888	0.963	0.983
	√	√	√	2.9M	0.105	0.768	4.552	0.182	0.892	0.964	0.984

下载: 导出CSV

表 4 DAEN模型5折交叉验证法实验结果

	AbsRel	SqRel	RMS	RMSlog	$ \delta < 125 $	$ \delta < 1.25^{2} $	$ \delta < 125^{3} $	验证时间(s)
Fold1	0.105	0.784	4.535	0.182	0.892	0.963	0.983	62.62
Fold2	0.106	0.732	4.568	0.183	0.892	0.963	0.982	59.31
Fold3	0.105	0.805	4.526	0.181	0.891	0.964	0.983	61.18
Fold4	0.105	0.801	4.565	0.182	0.891	0.964	0.984	61.45
Fold5	0.106	0.772	4.533	0.182	0.892	0.964	0.983	60.25
平均结果	0.105	0.779	4.545	0.182	0.892	0.964	0.983	60.96

下载: 导出CSV

表 5 不同方向感知增强模块数量的模型结果对比

方法	FLOPs(G)	AbsRel	SqRel	RMS	RMSlog	$ \delta< 125 $	$ \delta < 1.25^{2} $	$ \delta < 125^{3} $
1(本文)	6.1	0.105	0.768	4.552	0.182	0.892	0.964	0.984
2	8.3	0.106	0.770	4.556	0.183	0.890	0.964	0.984
3	11.2	0.108	0.782	4.560	0.184	0.887	0.963	0.984

下载: 导出CSV

表 6 不同设置的放大因子对模型性能的影响

方法	参数量(M)	AbsRel	SqRel	RMS	RMSlog	$ \delta < 125 $	$ \delta < 1.25^{2} $	$ \delta < 125^{3} $
可训练	3.1	0.106	0.762	4.481	0.182	0.890	0.963	0.984
固定(本文)	2.9	0.105	0.768	4.552	0.182	0.892	0.964	0.984

下载: 导出CSV

参考文献(22)

[1]	邓慧萍, 盛志超, 向森, 等. 基于语义导向的光场图像深度估计[J]. 电子与信息学报, 2022, 44(8): 2940–2948. doi: 10.11999/JEIT210545. DENG Huiping, SHENG Zhichao, XIANG Sen, et al. Depth estimation based on semantic guidance for light field image[J]. Journal of Electronics & Information Technology, 2022, 44(8): 2940–2948. doi: 10.11999/JEIT210545.
[2]	程德强, 张华强, 寇旗旗, 等. 基于层级特征融合的室内自监督单目深度估计[J]. 光学精密工程, 2023, 31(20): 2993–3009. doi: 10.37188/OPE.20233120.2993. CHENG Deqiang, ZHANG Huaqiang, and KOU Qiqi, et al. Indoor self-supervised monocular depth estimation based on level feature fusion[J]. Optics and Precision Engineering, 2023, 31(20): 2993–3009. doi: 10.37188/OPE.20233120.2993.
[3]	GODARD C, AODHA O M, FIRMAN M, et al. Digging into self-supervised monocular depth estimation[C]. 2019 IEEE/CVF International Conference on Computer Vision, Seoul, South Korea, 2019: 3827–3837. doi: 10.1109/ICCV.2019.00393.
[4]	WANG Zhou, BOVIK A C, SHEIKH H R, et al. Image quality assessment: From error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600–612. doi: 10.1109/TIP.2003.819861.
[5]	LYU Xiaoyang, LIU Liang, WANG Mengmeng, et al. HR-Depth: High resolution self-supervised monocular depth estimation[C]. 35th AAAI Conference on Artificial Intelligence, Palo Alto, USA, 2021: 2294–2301. doi: 10.1609/aaai.v35i3.16329.
[6]	DOSOVITSKIY A, BEYER L, KOLESNIKOV A, et al. An image is worth 16x16 words: Transformers for image recognition at scale[C]. 9th International Conference on Learning Representations, Vienna, Austria, 2021.
[7]	BAE J, MOON S, and IM S. Deep digging into the generalization of self-supervised monocular depth estimation[C]. 36th AAAI Conference on Artificial Intelligence, Washington, USA, 2023: 187–196. doi: 10.1609/aaai.v37i1.25090.
[8]	VARMA A, CHAWLA H, ZONOOZ B, et al. Transformers in self-supervised monocular depth estimation with unknown camera intrinsics[C]. The 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications, 2022: 758–769.
[9]	HAN Wencheng, YIN Junbo, and SHEN Jianbing. Self-supervised monocular depth estimation by direction-aware cumulative convolution network[C]. 2023 IEEE/CVF International Conference on Computer Vision, Paris, France, 2023: 8579–8589. doi: 10.1109/ICCV51070.2023.00791.
[10]	ZHANG Ning, NEX F, VOSSELMAN G, et al. Lite-Mono: A lightweight CNN and transformer architecture for self-supervised monocular depth estimation[C]. 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, Canada, 2023: 18537–18546. doi: 10.1109/CVPR52729.2023.01778.
[11]	CHEN L C, PAPANDREOU G, SCHROFF F, et al. Rethinking atrous convolution for semantic image segmentation[EB/OL]. https://arxiv.org/abs/1706.05587, 2017.
[12]	DENG Jia, DONG Wei, SOCHER R, et al. ImageNet: A large-scale hierarchical image database[C]. 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, USA, 2009: 248–255. doi: 10.1109/CVPR.2009.5206848.
[13]	GEIGER A, LENZ P, and URTASUN R. Are we ready for autonomous driving? The KITTI vision benchmark suite[C]. 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, USA, 2012: 3354–3361. doi: 10.1109/CVPR.2012.6248074.
[14]	EIGEN D, PUHRSCH C, and FERGUS R. Depth map prediction from a single image using a multi-scale deep network[C]. The 27th International Conference on Neural Information Processing Systems, Montreal, Canada, 2014: 2366–2374.
[15]	SAXENA A, SUN Min, and NG A Y. Make3D: Learning 3D scene structure from a single still image[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(5): 824–840. doi: 10.1109/TPAMI.2008.132.
[16]	ZHOU Zhongkai, FAN Xinnan, SHI Pengfei, et al. R-MSFM: Recurrent multi-scale feature modulation for monocular depth estimating[C]. 18th IEEE/CVF International Conference on Computer Vision, Montreal, Canada, 2021: 12757–12766. doi: 10.1109/ICCV48922.2021.01254.
[17]	KLINGNER M, TERMÖHLEN J A, MIKOLAJCZYK J, et al. Self-supervised monocular depth estimation: Solving the dynamic object problem by semantic guidance[C]. 16th European Conference on Computer Vision, Glasgow, UK, 2020: 582–600. doi: 10.1007/978-3-030-58565-5_35.
[18]	YIN Zhichao and SHI Jianping. GeoNet: Unsupervised learning of dense depth, optical flow and camera pose[C]. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, USA, 2018: 1983–1992. doi: 10.1109/CVPR.2018.00212.
[19]	WANG Chaoyang, BUENAPOSADA J M, ZHU Rui, et al. Learning depth from monocular videos using direct methods[C]. 31st IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, USA, 2018: 2022–2030. doi: 10.1109/CVPR.2018.00216.
[20]	JOHNSTON A and CARNEIRO G. Self-supervised monocular trained depth estimation using self-attention and discrete disparity volume[C]. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, USA, 2020: 4755–4764. doi: 10.1109/CVPR42600.2020.00481.
[21]	YAN Jiaxing, ZHAO Hong, BU Penghui, et al. Channel-wise attention-based network for self-supervised monocular depth estimation[C]. 9th International Conference on 3D Vision, London, USA, 2021: 464–473. doi: 10.1109/3DV53792.2021.00056.
[22]	HAN Chenggong, CHENG Deqiang, KOU Qiqi, et al. Self-supervised monocular Depth estimation with multi-scale structure similarity loss[J]. Multimedia Tools and Applications, 2022, 82(24): 38035–38050. doi: 10.1007/S11042-022-14012-6.