Multi-Stage Game-based Topology Deception Method Using Deep Reinforcement Learning
-
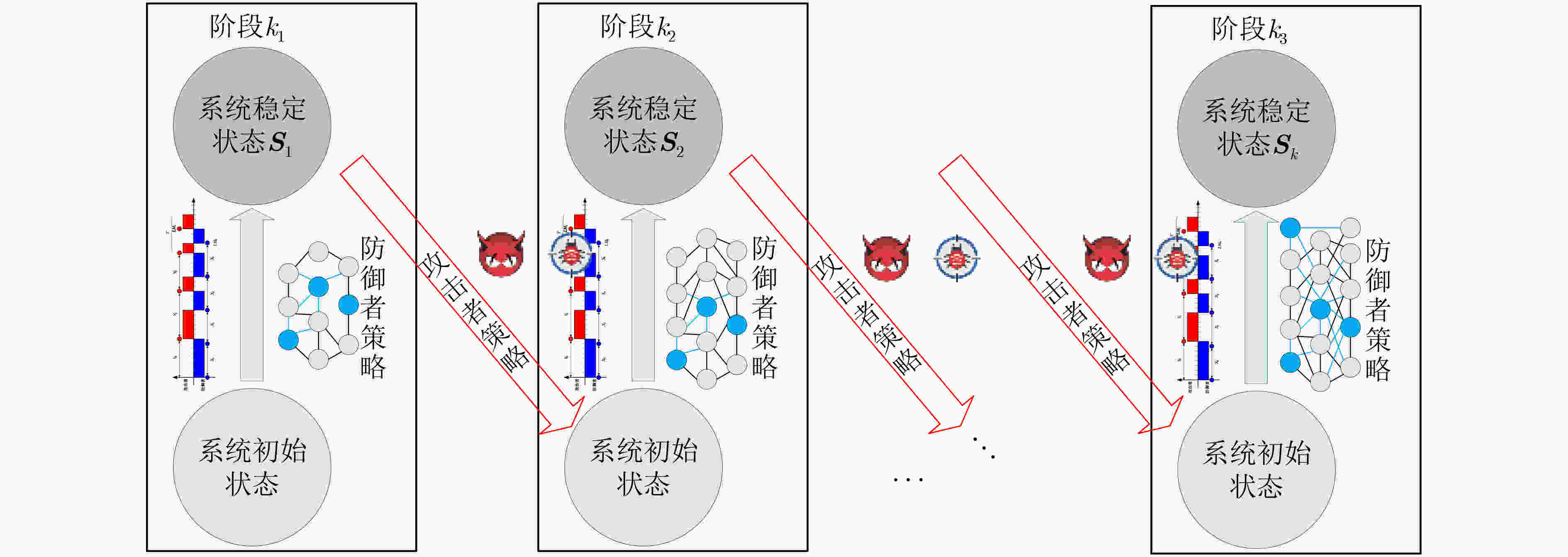
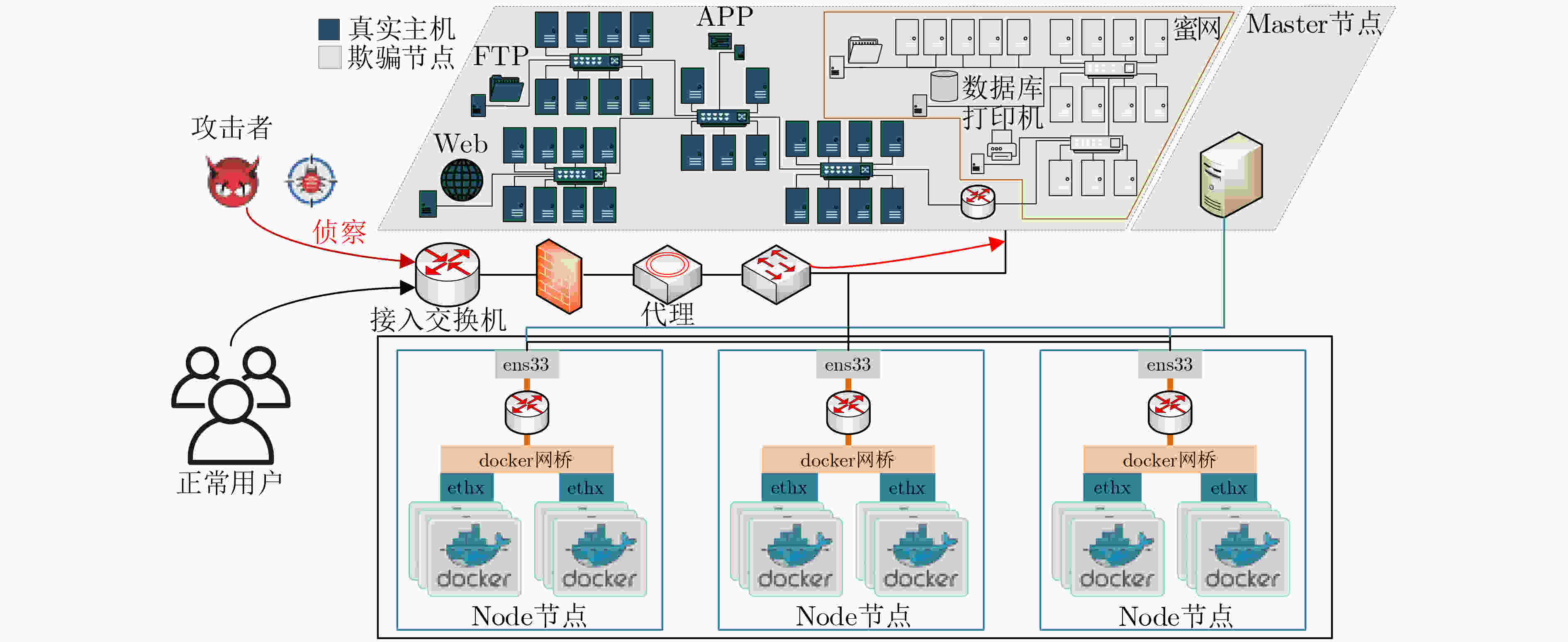
摘要: 针对当前网络拓扑欺骗防御方法仅从空间维度进行决策,没有考虑云原生网络环境下如何进行时空多维度拓扑欺骗防御的问题,该文提出基于深度强化学习的多阶段Flipit博弈网络拓扑欺骗防御方法来混淆云原生网络中的侦察攻击。首先分析了云原生网络环境下的拓扑欺骗攻防模型,接着在引入折扣因子和转移概率的基础上,构建了基于Flipit的多阶段博弈网络拓扑欺骗防御模型。在分析博弈攻防策略的前提下,构建了基于深度强化学习的拓扑欺骗生成方法求解多阶段博弈模型的拓扑欺骗防御策略。最后,通过搭建实验环境,验证了所提方法能够有效建模分析云原生网络的拓扑欺骗攻防场景,且所提算法相比于其他算法具有明显的优势。
-
关键词:
- 云原生网络 /
- 拓扑欺骗 /
- 多阶段Flipit博弈 /
- 深度强化学习 /
- 深度确定性策略梯度算法
Abstract: Aiming at the problem that current network topology deception methods only make decisions in the spatial dimension without considering how to perform spatio-temporal multi-dimensional topology deception in cloud-native network environments, a multi-stage Flipit game topology deception method with deep reinforcement learning to obfuscate reconnaissance attacks in cloud-native networks. Firstly, the topology deception defense-offense model in cloud-native complex network environments is analyzed. Then, by introducing a discount factor and transition probabilities, a multi-stage game-based network topology deception model based on Flipit is constructed. Furthermore under the premise of analyzing the defense-offense strategies of game models, a topology deception generation method is developed based on deep reinforcement learning to solve the topology deception strategy of multi-stage game models. Finally, through experiments, it is demonstrated that the proposed method can effectively model and analyze the topology deception defense-offense scenarios in cloud-native networks. It is shown that the algorithm has significant advantages compared to other algorithms. -
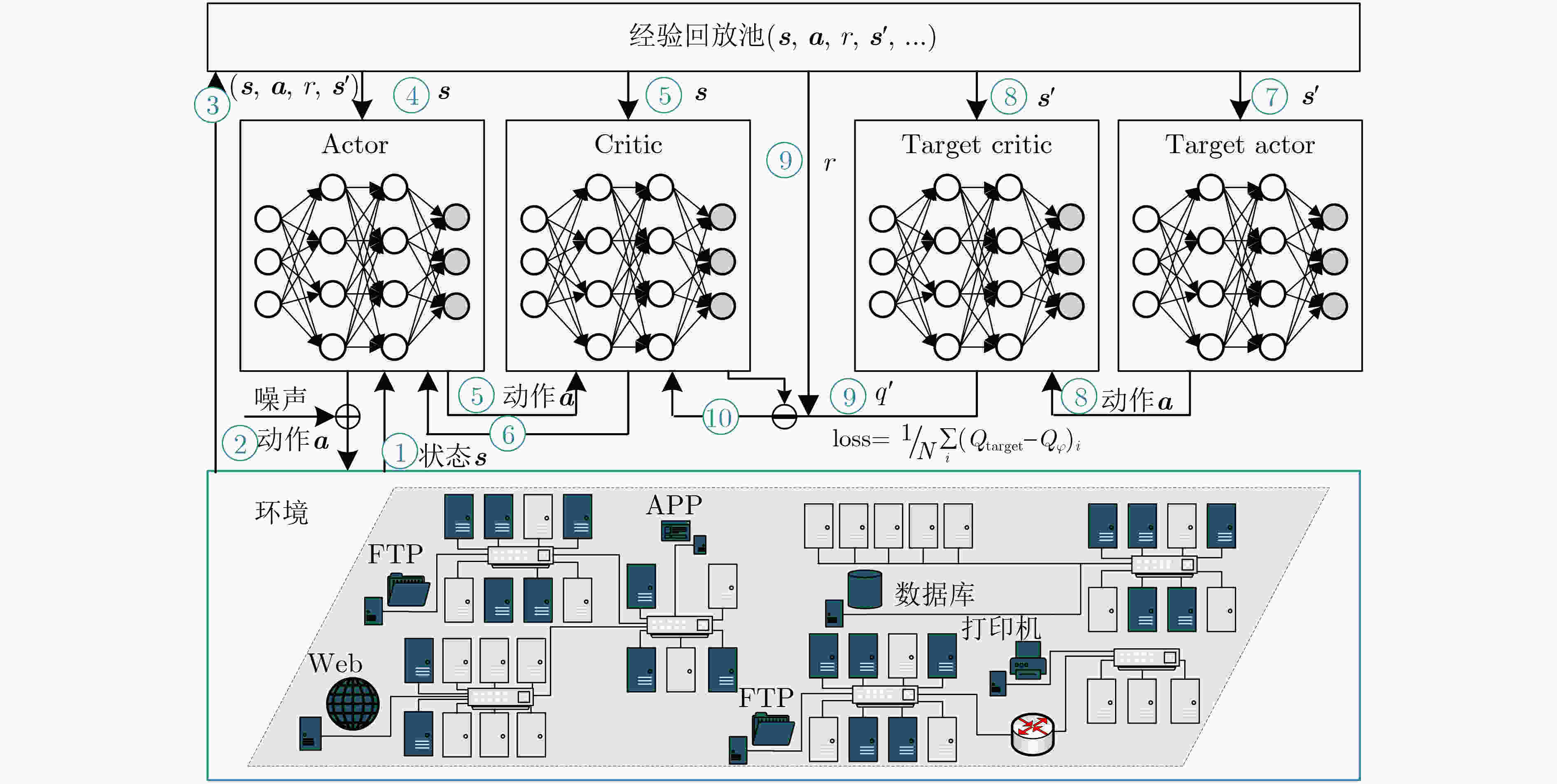
1 基于DDPG算法的最佳网络拓扑欺骗方法
Input:当前网络环境中攻击者的侦察策略$ \lambda_{k} $和防御者采取变换
欺骗策略产生的开销$ C_{{\mathrm{D}}}^{k} $Output: 防御者最佳的网络拓扑欺骗策略$ T_{k} $ 1 初始化经验回访池$D \leftarrow \varnothing $,初始化Actor网络参数$ \theta $,初始化
Critic网络参数$ \varphi $2 对Target Actor网络参数和Target Critic网络参数进行赋值,
即$ \theta^{\prime} \leftarrow \theta_{,} \varphi^{\prime} \leftarrow \varphi $3 for epi=1, 2, ···, M do //不断迭代,训练神经网络直至收敛 4 初始化环境状态$ {\boldsymbol{s}}_{0} $和随机噪声$ {\boldsymbol{n}} $ 5 初始化状态行为轨迹$\tau \leftarrow \varnothing $ 6 for t = 1, 2, ···, K do //不断迭代获取经验回放数据,根据
存储的经验回放数据对神经网络训练7 获取当前状态$ {\boldsymbol{s}}_{t} $//获取当前攻击者在阶段$k$时网络环境中
采取的策略$ \lambda_{k} $8 从Actor网络中输出行为$ {\boldsymbol{a}}_{t} $//选取防御者的拓扑欺骗策略
$ T $9 将行为${{\boldsymbol{a}}_t}$加上噪声${{\boldsymbol{n}}_t}$输入到环境中,得到奖励${r_t}$和下一
状态${{\boldsymbol{s}}_{t + 1}}$10 将得到的轨迹存入经验回访池$ \tau \leftarrow \tau \cup\left({\boldsymbol{s}}_{t}, {\boldsymbol{a}}_{t}, \tau_{t}\right) $ 11 end for 12 $ D \in D \cup \tau $ 13 从经验回访池中采样一定数量的轨迹值$ \left({\boldsymbol{s}}_{t}, {\boldsymbol{a}}_{t}, r_{t},{\boldsymbol{s}}_{t+1}\right) $
进行训练14 根据式(4)、式(6)更新Actor网络参数$ \theta $和Critic网络参数$ \varphi $ 15 根据式(7)更新Target Actor和Target Critic网络参数 16 end for 17 end 表 1 8个阶段之间的转移概率
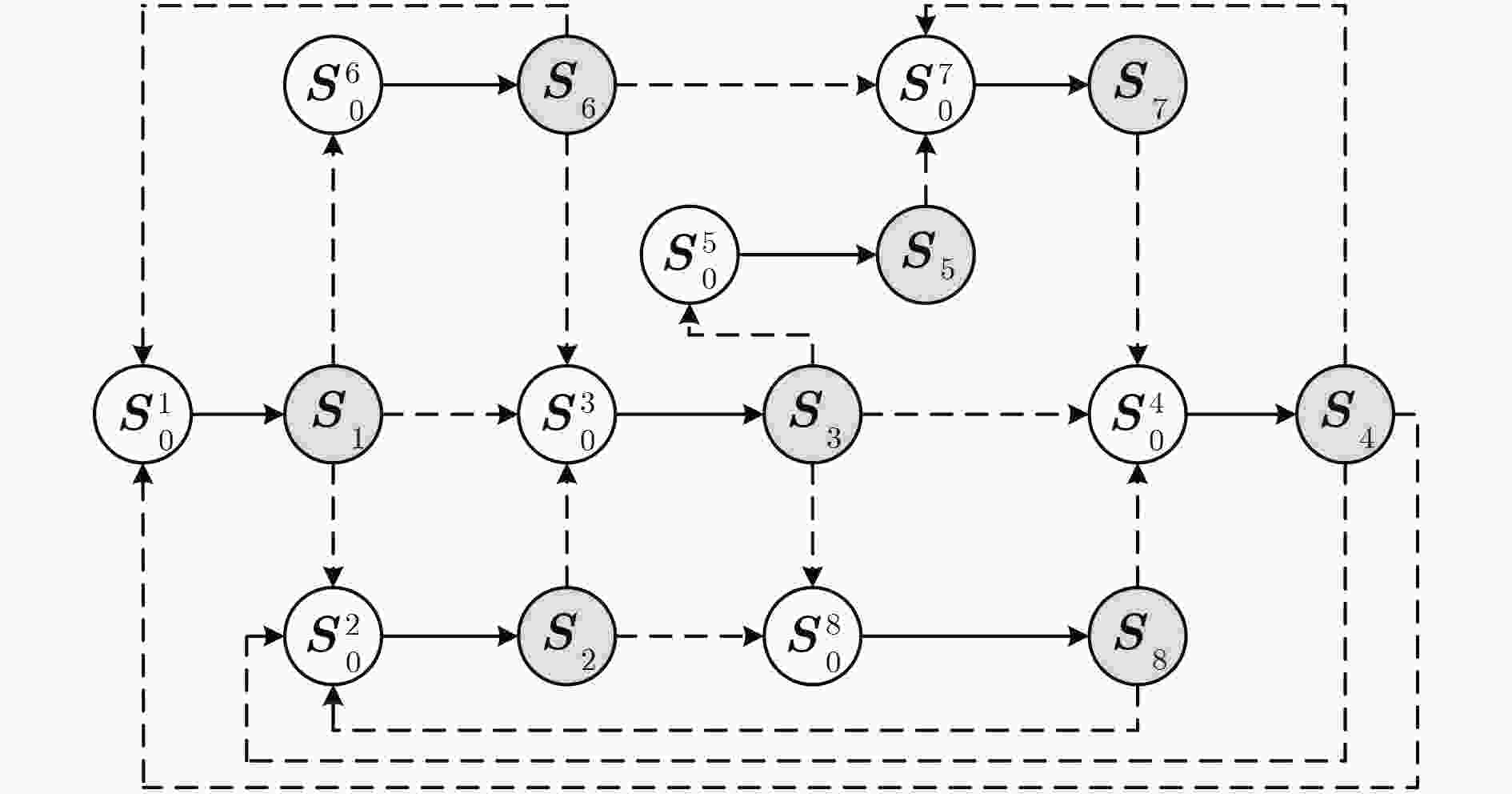
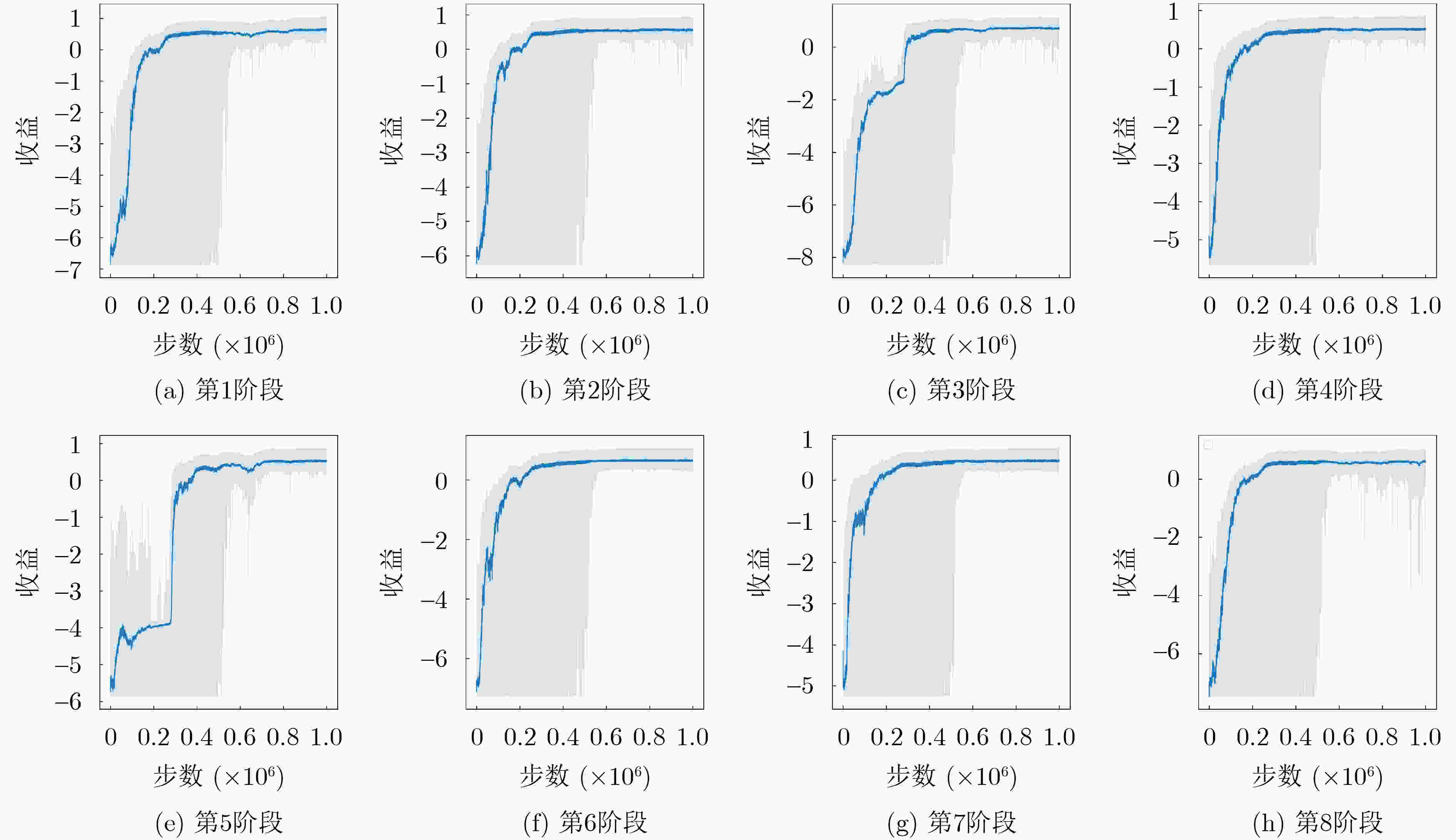
阶段跳变 $ {\boldsymbol{S}}_{1} \rightarrow {\boldsymbol{S}}_{2}^{t} $ $ {\boldsymbol{S}}_{1} \rightarrow {\boldsymbol{S}}_{0}^{3} $ $ {\boldsymbol{S}}_{1} \rightarrow {\boldsymbol{S}}_{0}^{6} $ $ {\boldsymbol{S}}_{2} \rightarrow {\boldsymbol{S}}_{0}^{3} $ $ {\boldsymbol{S}}_{2} \rightarrow {\boldsymbol{S}}_{0}^{8} $ $ {\boldsymbol{S}}_{3} \rightarrow {\boldsymbol{S}}_{0}^{4} $ 跳变概率 $ \eta(2 \mid 1)=0.7 $ $ \eta(3 \mid 1)=0.2 $ $ \eta(6 \mid 1)=0.1 $ $ \eta(3 \mid 2)=0.7 $ $ \eta(8 \mid 2)=0.3 $ $ \eta(4 \mid 3)=0.6 $ 阶段跳变 $ {\boldsymbol{S}}_{3} \rightarrow {\boldsymbol{S}}_{0}^{5} $ $ {\boldsymbol{S}}_{3} \rightarrow {\boldsymbol{S}}_{0}^{8} $ $ {\boldsymbol{S}}_{4} \rightarrow s_{0}^{7} $ $ {\boldsymbol{S}}_{4} \rightarrow {\boldsymbol{S}}_{0}^{2} $ $ {\boldsymbol{S}}_{4} \rightarrow {\boldsymbol{S}}_{0}^{1} $ $ {\boldsymbol{S}}_{5} \rightarrow {\boldsymbol{S}}_{0}^{7} $ 跳变概率 $ \eta(5 \mid 3)=0.2 $ $ \eta(8 \mid 3)=0.2 $ $ \eta(7 \mid 4)=0.2 $ $ \eta {(2|4) }=0.4 $ $ \eta(1 \mid 4)=0.4 $ $ \eta ( 7 \mid 5)=0.9 $ 阶段跳变 $ {\boldsymbol{S}}_{6} \rightarrow {\boldsymbol{S}}_{0}^{1} $ $ {\boldsymbol{S}}_{6} \rightarrow {\boldsymbol{S}}_{0}^{3} $ $ {\boldsymbol{S}}_{6} \rightarrow {\boldsymbol{S}}_{0}^{7} $ $ {\boldsymbol{S}}_{7} \rightarrow {\boldsymbol{S}}_{0}^{4} $ $ {\boldsymbol{S}}_{8} \rightarrow {\boldsymbol{S}}_{0}^{2} $ $ {\boldsymbol{S}}_{8} \rightarrow {\boldsymbol{S}}_{0}^{4} $ 跳变概率 $ \eta(1 \mid 6)=0.2 $ $ \eta(3 \mid 6)=0.8 $ $ \eta(7 \mid 6)=0.8 $ $ \eta(4 \mid 7)=0.6 $ $ \eta(2 \mid 8)=0.9 $ $ \eta(4 \mid 8)=0.8 $ 表 2 仿真参数设置
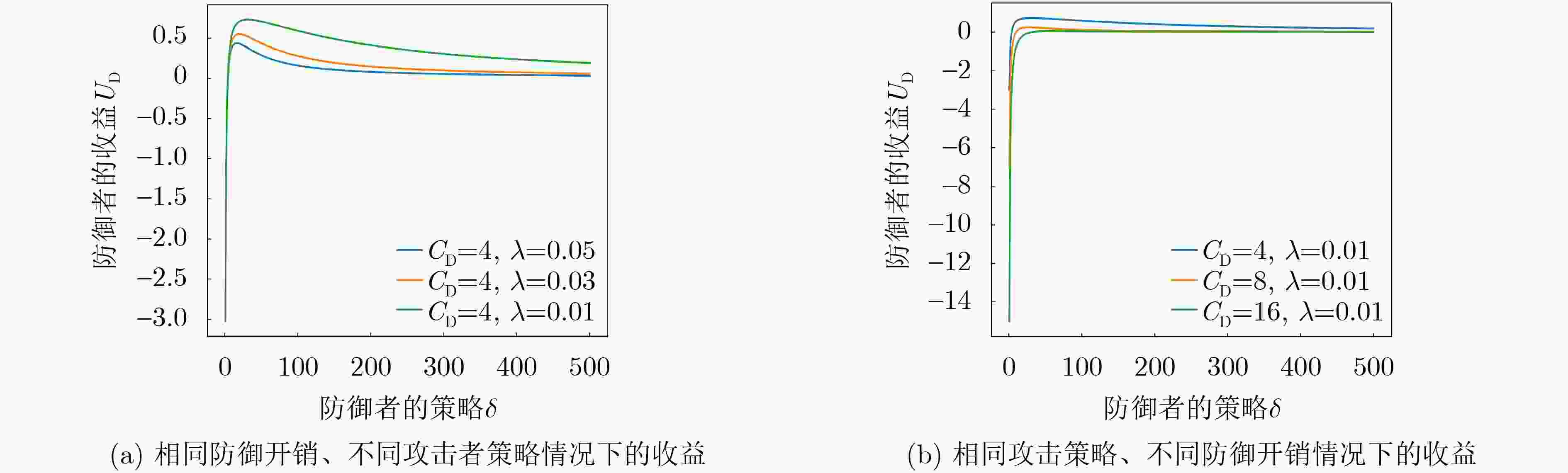
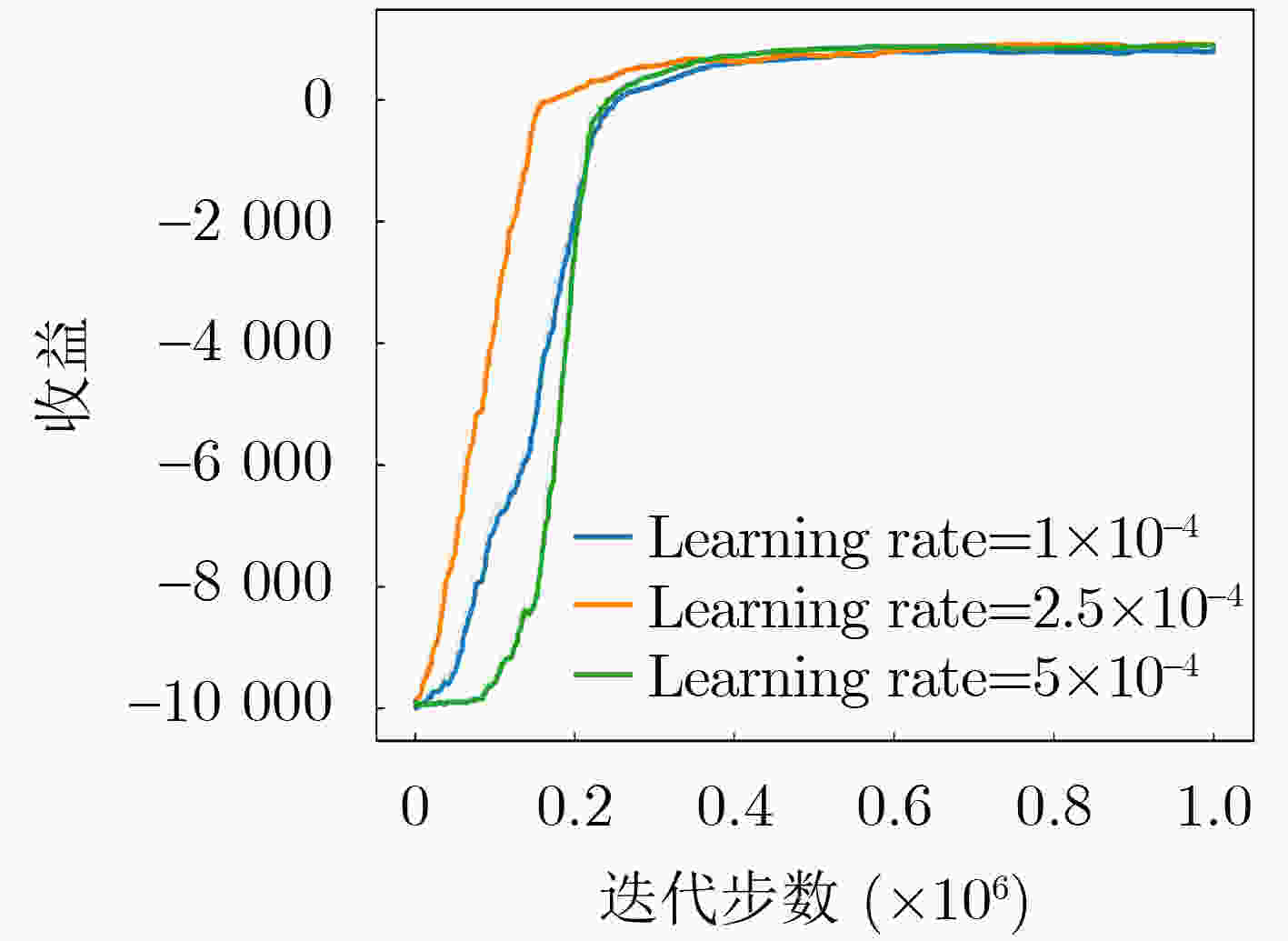
实验参数 实验参数的值 攻击者的策略$ {\lambda} $ [0.01, 0.20] 防御者的策略$ T $ [1, 100] 防御者的开销$ C_{{\mathrm{D}}} $ 4 学习率 $2.5 \times {10^{ - 4}}$ 表 3 DTG-DDPG与其他方法的定性比较
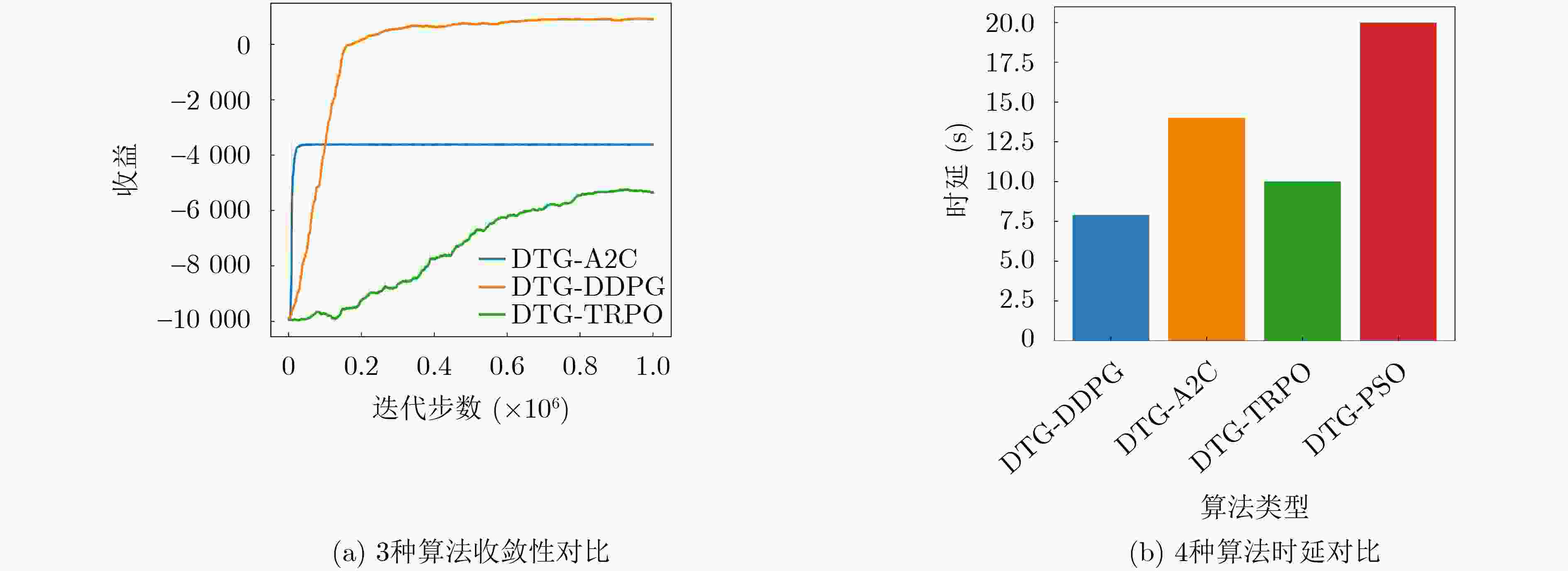
文献 博弈模型 求解方法 攻防过程 决策目标 实时决策 实验场景 Sayed等人[7] 动态博弈 强化学习Q-learning 多阶段 单目标空间策略 未考虑 NetworkX Horák等人[8] 随机博弈 无 多阶段 单目标空间策略 未考虑 传统网络 Milani等人[9] Stackelberg博弈 神经架构搜索算法 单阶段 单目标空间策略 未考虑 传统网络 Wang等人[10] 马尔可夫决策过程 强化学习Q-learning 多阶段 多目标时空策略 考虑 传统网络 Li等人[11] 马尔可夫决策过程 深度强化学习PPO 多阶段 多目标时空策略 考虑 云计算网络 DTG-DDPG Flipit博弈 深度强化学习DDPG 多阶段 多目标时空策略 考虑 云原生网络 -
[1] DUAN Qiang. Intelligent and autonomous management in cloud-native future networks—A survey on related standards from an architectural perspective[J]. Future Internet, 2021, 13(2): 42. doi: 10.3390/fi13020042. [2] ARMITAGE J. Cloud Native Security Cookbook[M]. O’Reilly Media, Inc. , 2022: 15–20. [3] TÄRNEBERG W, SKARIN P, GEHRMANN C, et al. Prototyping intrusion detection in an industrial cloud-native digital twin[C]. 2021 22nd IEEE International Conference on Industrial Technology, Valencia, Spain, 2021: 749–755. doi: 10.1109/ICIT46573.2021.9453553. [4] STOJANOVIĆ B, HOFER-SCHMITZ K, and KLEB U. APT datasets and attack modeling for automated detection methods: A review[J]. Computers & Security, 2020, 92: 101734. doi: 10.1016/j.cose.2020.101734. [5] TRASSARE S T, BEVERLY R, and ALDERSON D. A technique for network topology deception[C]. 2013 IEEE Military Communications Conference, San Diego, USA, 2013: 1795–1800. doi: 10.1109/MILCOM.2013.303. [6] MEIER R, TSANKOV P, LENDERS V, et al. NetHide: Secure and practical network topology obfuscation[C]. 27th USENIX Conference on Security Symposium, Baltimore, USA, 2018: 693–709. [7] SAYED A, ANWAR A H, KIEKINTVELD C, et al. Honeypot allocation for cyber deception in dynamic tactical networks: A game theoretic approach[C]. 14th International Conference on Decision and Game Theory for Security, Avignon, France, 2023: 195–214. doi: 10.1007/978-3-031-50670-3_10. [8] HORÁK K, ZHU Quanyan, and BOŠANSKÝ B. Manipulating adversary’s belief: A dynamic game approach to deception by design for proactive network security[C]. 8th International Conference on Decision and Game Theory for Security, Vienna, Austria, 2017: 273–294. doi: 10.1007/978-3-319-68711-7_15. [9] MILANI S, SHEN Weiran, CHAN K S, et al. Harnessing the power of deception in attack graph-based security games[C]. 11th International Conference on Decision and Game Theory for Security, College Park, USA, 2020: 147–167. doi: 10.1007/978-3-030-64793-3_8. [10] WANG Shuo, PEI Qingqi, WANG Jianhua, et al. An intelligent deployment policy for deception resources based on reinforcement learning[J]. IEEE Access, 2020, 8: 35792–35804. doi: 10.1109/ACCESS.2020.2974786. [11] LI Huanruo, GUO Yunfei, HUO Shumin, et al. Defensive deception framework against reconnaissance attacks in the cloud with deep reinforcement learning[J]. Science China Information Sciences, 2022, 65(7): 170305. doi: 10.1007/s11432-021-3462-4. [12] KANG M S, GLIGOR V D, and SEKAR V. SPIFFY: Inducing cost-detectability tradeoffs for persistent link-flooding attacks[C]. 23rd Annual Network and Distributed System Security Symposium, San Diego, USA, 2016: 53–55. [13] KIM J, NAM J, LEE S, et al. BottleNet: Hiding network bottlenecks using SDN-based topology deception[J]. IEEE Transactions on Information Forensics and Security, 2021, 16: 3138–3153. doi: 10.1109/TIFS.2021.3075845. [14] VAN DIJK M, JUELS A, OPREA A, et al. FlipIt: The game of “stealthy takeover”[J]. Journal of Cryptology, 2013, 26(4): 655–713. doi: 10.1007/s00145-012-9134-5. [15] DORASZELSKI U and ESCOBAR J F. A theory of regular Markov perfect equilibria in dynamic stochastic games: Genericity, stability, and purification[J]. Theoretical Economics, 2010, 5(3): 369–402. doi: 10.3982/TE632. [16] NILIM A and GHAOUI L E. Robust control of Markov decision processes with uncertain transition matrices[J]. Operations Research, 2005, 53(5): 780–798. doi: 10.1287/opre.1050.0216. [17] 张勇, 谭小彬, 崔孝林, 等. 基于Markov博弈模型的网络安全态势感知方法[J]. 软件学报, 2011, 22(3): 495–508. doi: 10.3724/SP.J.1001.2011.03751.ZHANG Yong, TAN Xiaobin, CUI Xiaolin, et al. Network security situation awareness approach based on Markov game model[J]. Journal of Software, 2011, 22(3): 495–508. doi: 10.3724/SP.J.1001.2011.03751. [18] China national vulnerability database of information security[DB/OL]. https://www.cnnvd.org.cn/home/aboutUs, 2015. -






 下载:
下载:



 下载:
下载:
