基于反障碍距离加权的复杂场景电磁频谱地图构建方法

陶诗飞; 吴昱江; 罗佳; 丁浩; 王元贺

doi:10.11999/JEIT231374

基于反障碍距离加权的复杂场景电磁频谱地图构建方法

doi: 10.11999/JEIT231374 cstr: 32379.14.JEIT231374

1.
南京理工大学电子工程与光电技术学院南京 210094
2.
电磁空间安全全国重点实验室成都 610036
3.
南京理工大学工程训练中心南京 210094

基金项目: 电磁空间安全全国重点实验室开放基金

详细信息

作者简介:
陶诗飞：男，副研究员，研究方向为电子侦查、目标识别、电磁隐身技术

吴昱江：男，硕士生，研究方向为电磁态势感知、电磁频谱地图构建

罗佳：男，高级工程师，研究方向为电子对抗技术

丁浩：男，高级工程师，研究方向为频谱管理、频谱监测、频谱作战

王元贺：男，硕士生，研究方向为电磁态势感知

通讯作者:
陶诗飞　s.tao@njust.edu.cn

中图分类号: TN97
计量
- 文章访问数: 230
- HTML全文浏览量: 266
- PDF下载量: 51
- 被引次数: 0
出版历程
- 收稿日期: 2023-12-13
- 修回日期: 2024-02-28
- 网络出版日期: 2024-03-08
- 刊出日期: 2024-08-30

Radio Environment Map Construction Method for Complex Scenes Based on Inverse Obstacle Distance Weighted

1.
School of Electronic and Optical Engineering, Nanjing University of Science and Technology, NanJing 210094, China
2.
National Key Laboratory of Electromagnetic Space Security, Chengdu 610036, China
3.
Engineering Training Center, Nanjing University of Science and Technology, NanJing 210094, China

Funds: The National Key Laboratory of Electromagnetic Space Secunrity

摘要

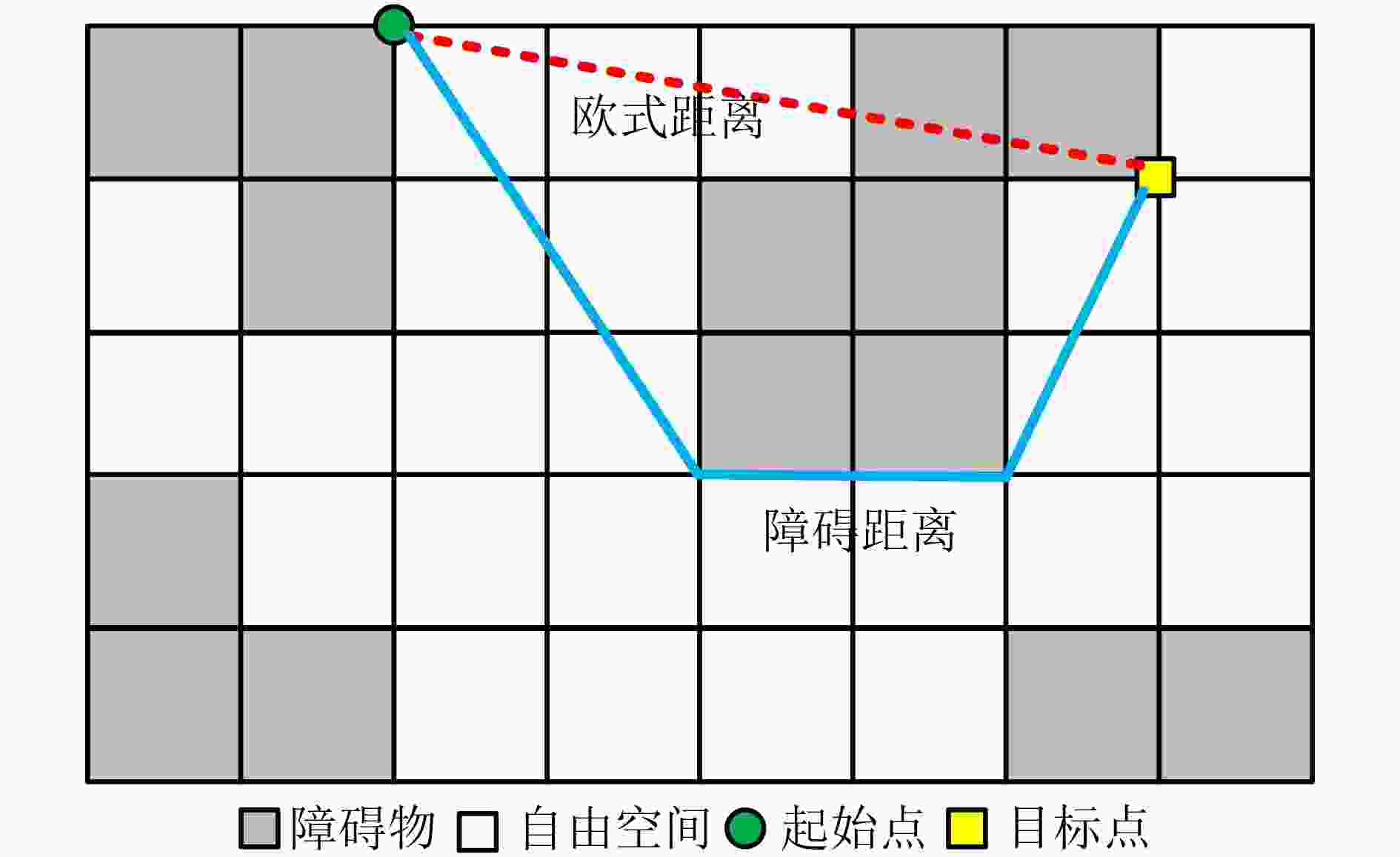
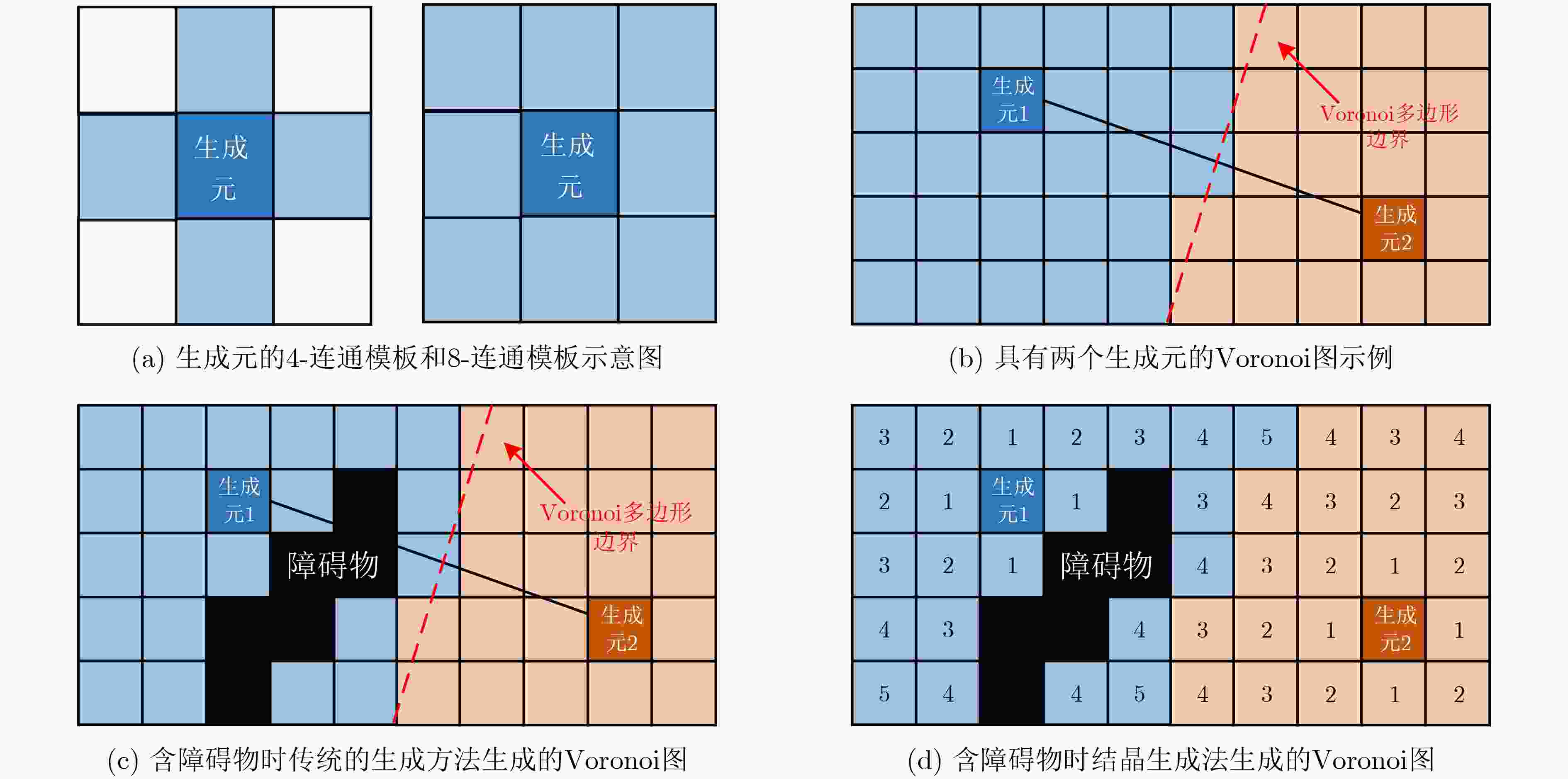
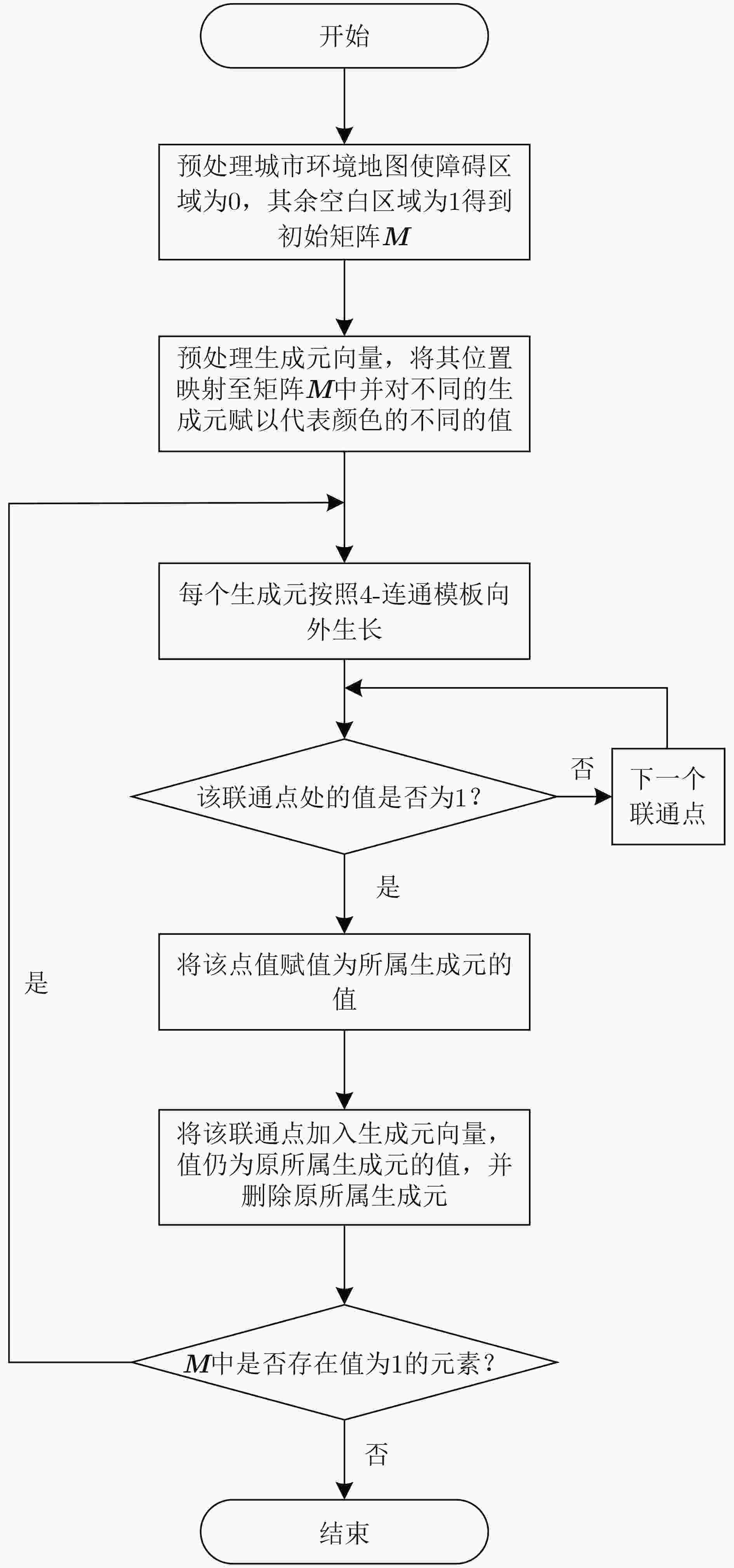
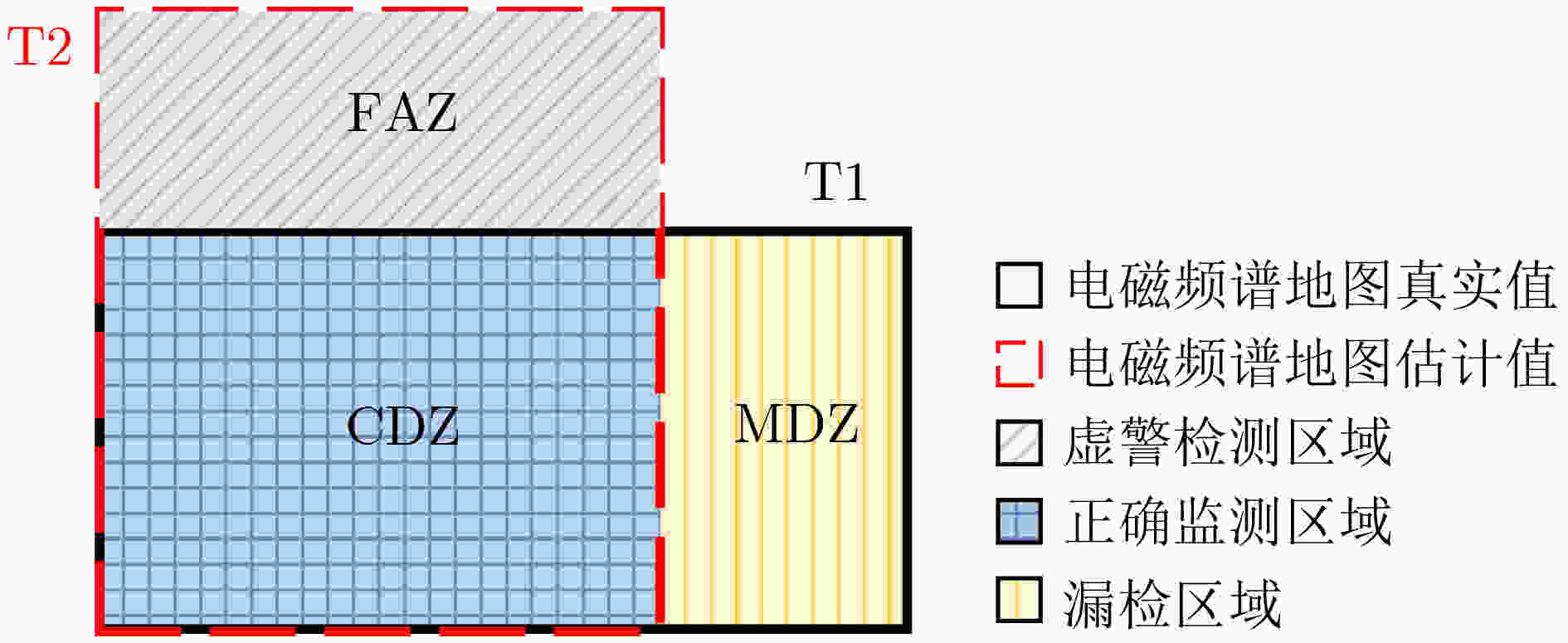
摘要: 针对复杂场景中存在电磁波不可穿透的障碍物导致电磁频谱地图(REMs)构建性能不佳、反距离加权(IDW)算法受限于插值邻域的人工选择等问题，该文提出一种基于Voronoi图的反障碍距离加权(VIODW)的复杂场景电磁频谱地图构建算法。该算法通过创建包含障碍物的Voronoi图，为每一个待插值点自适应选定插值邻域用于电磁频谱数据构建，并利用任意角度路径寻优(ANYA)算法计算得到待插值点与插值邻域内每个监测站点之间的障碍距离，最后以障碍距离的反幂次作为权重加权获得待插值点处的电磁频谱数据，实现高精度的复杂场景电磁频谱地图构建。理论分析和仿真结果表明，该方法具有良好的构建精度，能够准确拟合出电磁波在复杂场景中的功率分布情况，为复杂场景下电磁频谱地图高精度构建提供了一种有效方法。
- 电磁频谱地图 /
- 反距离加权插值 /
- 障碍距离 /
- 复杂场景
Abstract: Addressing the issues of inadequate performance in constructing Radio Environment Maps (REMs) in complex scenarios due to non-penetrable obstacles for electromagnetic waves, and the arbitrary selection of interpolation neighborhoods imposed by Inverse Distance Weighted (IDW), a Voronoi-based Inverse Obstacle Distance Weighted algorithm (VIODW) is proposed in this paper. This algorithm adaptively defines interpolation neighborhoods for each interpolation point by creating Voronoi diagrams incorporating obstacles for numerical computation. Then, using the ANY-Angle (ANYA) Algorithm to calculate the obstacle distance between the interpolation point and each monitoring station within the interpolation neighborhood. Finally, by calculating the weighted mean with the inverse power of the obstacle distance as the weight, the value at the point is obtained, achieving high-precision construction of REMs in complex scenarios. Both theoretical analysis and simulation results demonstrate that this method offers excellent construction accuracy and can accurately model the power distribution of electromagnetic waves in complex scenarios. Hence, it provides an effective approach for high-precision REM construction in complex scenarios.
- Radio Environment Map(REM) /
- Inverse Distance Weighted(IDW) interpolation /
- Obstacle distance /
- Complex scenarios

HTML全文

图 1 基于反障碍距离加权的复杂场景电磁频谱地图构建流程

下载: 全尺寸图片幻灯片

图 2 障碍距离与欧式距离的示意图

下载: 全尺寸图片幻灯片

图 3 结晶生成法示意图

下载: 全尺寸图片幻灯片

图 4 障碍Voronoi图结晶生成法流程框图

下载: 全尺寸图片幻灯片

图 5 区域覆盖指标中3种区域位置示意图

下载: 全尺寸图片幻灯片

图 6 城市环境复杂场景示意图

下载: 全尺寸图片幻灯片

图 7 不同数量监测站点下各算法的区域覆盖指标性能对比

下载: 全尺寸图片幻灯片

图 8 监测站点数量为500时各算法重构得到的REM占用轮廓可视化效果

下载: 全尺寸图片幻灯片

图 9 监测站点数量为500时各算法重构得到的REM可视化效果

下载: 全尺寸图片幻灯片

表 1 不同数量电磁监测站点下各算法的RMSE对比

算法	50	100	200	500	1 000	2 000	3 000
IDW1	9.235 6	8.386 5	8.436 8	8.350 7	7.840 8	7.471 4	6.665 9
IDW2	6.662 7	4.748 4	4.513 7	4.053 2	3.458 2	3.268 8	2.773 6
IDW3	5.619 2	3.625 4	3.279 7	2.362 6	1.784 6	1.258 6	0.961 8
MSM	6.295 3	3.610 5	3.441 1	2.137 6	1.663 8	0.973 1	0.653 1
VIODW	4.761 9	3.185 5	2.518 8	1.689 5	1.332 0	0.846 7	0.623 1

下载: 导出CSV

参考文献(22)

[1]	YILMAZ H B, TUGCU T, ALAGÖZ F, et al. Radio environment map as enabler for practical cognitive radio networks[J]. IEEE Communications Magazine, 2013, 51(12): 162–169. doi: 10.1109/MCOM.2013.6685772.
[2]	ROMERO D and KIM S J. Radio map estimation: A data-driven approach to spectrum cartography[J]. IEEE Signal Processing Magazine, 2022, 39(6): 53–72. doi: 10.1109/MSP.2022.3200175.
[3]	PESKO M, JAVORNIK T, KOŠIR A, et al. Radio environment maps: The survey of construction methods[J]. KSII Transactions on Internet and Information Systems, 2014, 8(11): 3789–3809. doi: 10.3837/tiis.2014.11.008.
[4]	陈智博, 胡景明, 张邦宁, 等. 基于张量Tucker分解的频谱地图构建算法[J]. 电子与信息学报, 2023, 45(11): 4161–4169. doi: 10.11999/JEIT230796. CHEN Zhibo, HU Jingming, ZHANG Bangning, et al. Spectrum map construction algorithm based on tensor Tucker decomposition[J]. Journal of Electronics & Information Technology, 2023, 45(11): 4161–4169. doi: 10.11999/JEIT230796.
[5]	XING Yue, SONG Qifan, and CHENG Guang. Benefit of interpolation in nearest neighbor algorithms[J]. SIAM Journal on Mathematics of Data Science, 2022, 4(2): 935–956. doi: 10.1137/21M1437457.
[6]	AZPURUA M A and DOS RAMOS K. A comparison of spatial interpolation methods for estimation of average electromagnetic field magnitude[J]. Progress in Electromagnetics Research M, 2010, 14: 135–145. doi: 10.2528/PIERM10083103.
[7]	SHEPARD D. A two-dimensional interpolation function for irregularly-spaced data[C]//The 1968 23rd ACM National Conference, 1968: 517–524. doi: 10.1145/800186.810616.
[8]	MAITI P and MITRA D. Ordinary kriging interpolation for indoor 3D REM[J]. Journal of Ambient Intelligence and Humanized Computing, 2023, 14(10): 13285–13299. doi: 10.1007/s12652-022-03784-2.
[9]	XIE Yunfeng, CHEN Tongbin, LEI Mei, et al. Spatial distribution of soil heavy metal pollution estimated by different interpolation methods: Accuracy and uncertainty analysis[J]. Chemosphere, 2011, 82(3): 468–476. doi: 10.1016/j.chemosphere.2010.09.053.
[10]	MERWADE V M, MAIDMENT D R, and GOFF J A. Anisotropic considerations while interpolating river channel bathymetry[J]. Journal of Hydrology, 2006, 331(3/4): 731–741. doi: 10.1016/j.jhydrol.2006.06.018.
[11]	MUELLER T G, PUSULURI N B, MATHIAS K K, et al. Map quality for ordinary kriging and inverse distance weighted interpolation[J]. Soil Science Society of America Journal, 2004, 68(6): 2042–2047. doi: 10.2136/sssaj2004.2042.
[12]	LU G Y and WONG D W. An adaptive inverse-distance weighting spatial interpolation technique[J]. Computers & Geosciences, 2008, 34(9): 1044–1055. doi: 10.1016/j.cageo.2007.07.010.
[13]	史利民, 王仁宏. 几种基于散乱数据拟合的局部插值方法[J]. 数学研究与评论, 2006, 26(2): 283–291. doi: 10.3770/j.issn:1000-341X.2006.02.014. SHI Limin and WANG Renhong. Some local methods for scattered data interpolation[J]. Journal of Mathematical Research and Exposition, 2006, 26(2): 283–291. doi: 10.3770/j.issn:1000-341X.2006.02.014.
[14]	RENKA R J. Multivariate interpolation of large sets of scattered data[J]. ACM Transactions on Mathematical Software, 1988, 14(2): 139–148. doi: 10.1145/45054.45055.
[15]	段平, 盛业华, 李佳, 等. 自适应的IDW插值方法及其在气温场中的应用[J]. 地理研究, 2014, 33(8): 1417–1426. doi: 10.11821/dlyj201408003. DUAN Ping, SHENG Yehua, LI Jia, et al. Adaptive IDW interpolation method and its application in the temperature field[J]. Geographical Research, 2014, 33(8): 1417–1426. doi: 10.11821/dlyj201408003.
[16]	CAO Yu, TANG Xiaobo, LI Jie, et al. Flow field distribution and structural strength performance evaluation of fixed offshore wind turbine based on digital twin technology[J]. Ocean Engineering, 2023, 288: 116156. doi: 10.1016/j.oceaneng.2023.116156.
[17]	夏海洋, 查淞, 黄纪军, 等. 电磁频谱地图构建方法研究综述及展望[J]. 电波科学学报, 2020, 35(4): 445–456. doi: 10.13443/j.cjors.2020040801. XIA Haiyang, ZHA Song, HUANG Jijun, et al. Survey on the construction methods of spectrum map[J]. Chinese Journal of Radio Science, 2020, 35(4): 445–456. doi: 10.13443/j.cjors.2020040801.
[18]	MCGARVEY R G and CAVALIER T M. A global optimal approach to facility location in the presence of forbidden regions[J]. Computers & Industrial Engineering, 2003, 45(1): 1–15. doi: 10.1016/S0360-8352(03)00028-7.
[19]	HARABOR D D, GRASTIEN A, ÖZ D, et al. Optimal any-angle pathfinding in practice[J]. Journal of Artificial Intelligence Research, 2016, 56: 89–118. doi: 10.1613/jair.5007.
[20]	曹清洁. 障碍Voronoi图的结晶生成及其应用[J]. 计算机应用与软件, 2007, 24(8): 147–149, 197. doi: 10.3969/j.issn.1000-386X.2007.08.055. CAO Qingjie. The crystal growth of Voronoi diagrams with obstacles and its application[J]. Computer Applications and Software, 2007, 24(8): 147–149, 197. doi: 10.3969/j.issn.1000-386X.2007.08.055.
[21]	周璧华, 陈彬, 高成, 等. 钢筋网及钢筋混凝土电磁脉冲屏蔽效能研究[J]. 电波科学学报, 2000, 15(3): 251–259. doi: 10.3969/j.issn.1005-0388.2000.03.001. ZHOU Bihua, CHEN Bin, GAO Cheng, et al. Study on EMP shielding effectiveness of wire-mesh reinforcement and reinforced-concrete[J]. Chinese Journal of Radio Science, 2000, 15(3): 251–259. doi: 10.3969/j.issn.1005-0388.2000.03.001.
[22]	YAPAR Ç, LEVIE R, KUTYNIOK G, et al. Real-time outdoor localization using radio maps: A deep learning approach[J]. IEEE Transactions on Wireless Communications, 2023, 22(12): 9703–9717. doi: 10.1109/TWC.2023.3273202.