Research on Construction Methods of Low Correlation zone Complementary Sequence Sets
-
摘要: 完备互补序列是一类具有理想相关函数性质的信号,在多址接入通信系统、雷达波形设计等领域具有广泛的应用。然而完备互补序列集合大小不超过其子序列数目。为扩展互补序列数目,该文研究了非周期低相关区互补序列集的构造方法,首先提出了两类有限域上的映射函数,进而得到两类参数渐近达到最优的低相关区互补序列集。该类低相关区互补序列集相比完备互补序列集具有更多的序列数目,在通信系统中可支持更多的用户。Abstract: Perfect complementary sequence is a kind of signal with ideal correlation function, which is widely used in multiple access communication system, radar waveform design and so on. However, the set size of perfect complementary sequences is at most equal to the number of its subsequences. In order to expand the number of complementary sequences, the construction methods of aperiodic low correlation zone complementary sequence set are studied in this paper. First, two kinds of mapping functions on finite fields are proposed, and then two kinds of low correlation zone complementary sequence set with asymptotically optimal parameters are obtained. The number of these kinds of low correlation zone complementary sequence set are more than that of the perfect complementary sequence set, thereby supporting more users in the communication system.
-
表 1 例1中集合$ {\boldsymbol{C}} $的部分互补序列
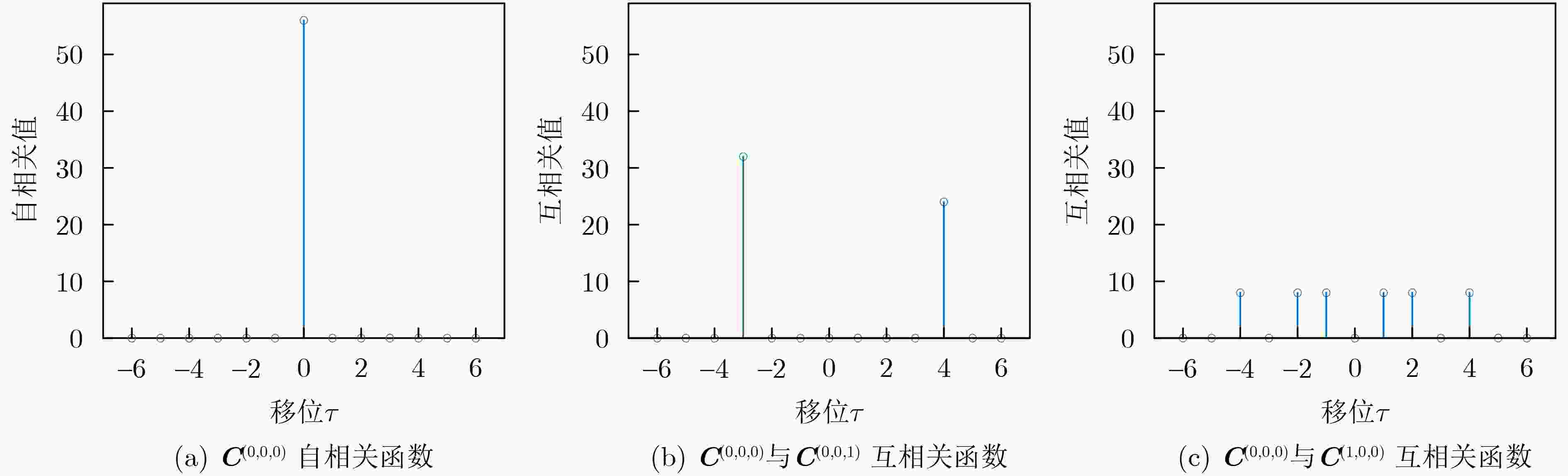
$ {{\boldsymbol{C}}^{(0,0,0)}} $ $ {{\boldsymbol{C}}^{(0,0,1)}} $ $ {{\boldsymbol{C}}^{(0,1,0)}} $ $ {{\boldsymbol{C}}^{(0,1,1)}} $ $ \begin{gathered} \omega _{56}^0\omega _{56}^0\omega _{56}^0\omega _{56}^0\omega _{56}^0\omega _{56}^0\omega _{56}^0 \\ \omega _{56}^7\omega _{56}^{14}\omega _{56}^{28}\omega _{56}^{21}\omega _{56}^{42}\omega _{56}^{49}\omega _{56}^{35} \\ \omega _{56}^{14}\omega _{56}^{28}\omega _{56}^0\omega _{56}^{42}\omega _{56}^{28}\omega _{56}^{42}\omega _{56}^{14} \\ \omega _{56}^{21}\omega _{56}^{42}\omega _{56}^{28}\omega _{56}^7\omega _{56}^{14}\omega _{56}^{35}\omega _{56}^{49} \\ \omega _{56}^{28}\omega _{56}^0\omega _{56}^0\omega _{56}^{28}\omega _{56}^0\omega _{56}^{28}\omega _{56}^{28} \\ \omega _{56}^{35}\omega _{56}^{14}\omega _{56}^{28}\omega _{56}^{49}\omega _{56}^{42}\omega _{56}^{21}\omega _{56}^7 \\ \omega _{56}^{42}\omega _{56}^{28}\omega _{56}^0\omega _{56}^{14}\omega _{56}^{28}\omega _{56}^{14}\omega _{56}^{42} \\ \omega _{56}^{49}\omega _{56}^{42}\omega _{56}^{28}\omega _{56}^{35}\omega _{56}^{14}\omega _{56}^7\omega _{56}^{21} \\ \end{gathered} $ $ \begin{gathered} \omega _{56}^0\omega _{56}^0\omega _{56}^0\omega _{56}^0\omega _{56}^0\omega _{56}^0\omega _{56}^0 \\ \omega _{56}^{21}\omega _{56}^{42}\omega _{56}^{49}\omega _{56}^{35}\omega _{56}^7\omega _{56}^{14}\omega _{56}^{28} \\ \omega _{56}^{42}\omega _{56}^{28}\omega _{56}^{42}\omega _{56}^{14}\omega _{56}^{14}\omega _{56}^{28}\omega _{56}^0 \\ \omega _{56}^7\omega _{56}^{14}\omega _{56}^{35}\omega _{56}^{49}\omega _{56}^{21}\omega _{56}^{42}\omega _{56}^{28} \\ \omega _{56}^{28}\omega _{56}^0\omega _{56}^{28}\omega _{56}^{28}\omega _{56}^{28}\omega _{56}^0\omega _{56}^0 \\ \omega _{56}^{49}\omega _{56}^{42}\omega _{56}^{21}\omega _{56}^7\omega _{56}^{35}\omega _{56}^{14}\omega _{56}^{28} \\ \omega _{56}^{14}\omega _{56}^{28}\omega _{56}^{14}\omega _{56}^{42}\omega _{56}^{42}\omega _{56}^{28}\omega _{56}^0 \\ \omega _{56}^{35}\omega _{56}^{14}\omega _{56}^7\omega _{56}^{21}\omega _{56}^{49}\omega _{56}^{42}\omega _{56}^{28} \\ \end{gathered} $ $ \begin{gathered} \omega _{56}^0\omega _{56}^8\omega _{56}^{16}\omega _{56}^{24}\omega _{56}^{32}\omega _{56}^{40}\omega _{56}^{48} \\ \omega _{56}^7\omega _{56}^{22}\omega _{56}^{44}\omega _{56}^{45}\omega _{56}^{18}\omega _{56}^{33}\omega _{56}^{27} \\ \omega _{56}^{14}\omega _{56}^{36}\omega _{56}^{16}\omega _{56}^{10}\omega _{56}^4\omega _{56}^{26}\omega _{56}^6 \\ \omega _{56}^{21}\omega _{56}^{50}\omega _{56}^{44}\omega _{56}^{31}\omega _{56}^{46}\omega _{56}^{19}\omega _{56}^{41} \\ \omega _{56}^{28}\omega _{56}^8\omega _{56}^{16}\omega _{56}^{52}\omega _{56}^{32}\omega _{56}^{12}\omega _{56}^{20} \\ \omega _{56}^{35}\omega _{56}^{22}\omega _{56}^{44}\omega _{56}^{17}\omega _{56}^{18}\omega _{56}^5\omega _{56}^{55} \\ \omega _{56}^{42}\omega _{56}^{36}\omega _{56}^{16}\omega _{56}^{38}\omega _{56}^4\omega _{56}^{54}\omega _{56}^{34} \\ \omega _{56}^{49}\omega _{56}^{50}\omega _{56}^{44}\omega _{56}^3\omega _{56}^{46}\omega _{56}^{47}\omega _{56}^{13} \\ \end{gathered} $ $ \begin{gathered} \omega _{56}^0\omega _{56}^8\omega _{56}^{16}\omega _{56}^{24}\omega _{56}^{32}\omega _{56}^{40}\omega _{56}^{48} \\ \omega _{56}^{21}\omega _{56}^{50}\omega _{56}^9\omega _{56}^3\omega _{56}^{39}\omega _{56}^{54}\omega _{56}^{20} \\ \omega _{56}^{42}\omega _{56}^{36}\omega _{56}^2\omega _{56}^{38}\omega _{56}^{46}\omega _{56}^{12}\omega _{56}^{48} \\ \omega _{56}^7\omega _{56}^{22}\omega _{56}^{51}\omega _{56}^{17}\omega _{56}^{53}\omega _{56}^{26}\omega _{56}^{20} \\ \omega _{56}^{28}\omega _{56}^8\omega _{56}^{44}\omega _{56}^{52}\omega _{56}^4\omega _{56}^{40}\omega _{56}^{48} \\ \omega _{56}^{49}\omega _{56}^{50}\omega _{56}^{37}\omega _{56}^{31}\omega _{56}^{11}\omega _{56}^{54}\omega _{56}^{20} \\ \omega _{56}^{14}\omega _{56}^{36}\omega _{56}^{30}\omega _{56}^{10}\omega _{56}^{18}\omega _{56}^{12}\omega _{56}^{48} \\ \omega _{56}^{35}\omega _{56}^{22}\omega _{56}^{23}\omega _{56}^{45}\omega _{56}^{25}\omega _{56}^{26}\omega _{56}^{20} \\ \end{gathered} $ $ {{\boldsymbol{C}}^{(1,0,0)}} $ $ {{\boldsymbol{C}}^{(1,0,1)}} $ $ {{\boldsymbol{C}}^{(1,1,0)}} $ $ {{\boldsymbol{C}}^{(1,1,1)}} $ $ \begin{gathered} \omega _{56}^0\omega _{56}^0\omega _{56}^0\omega _{56}^0\omega _{56}^0\omega _{56}^0\omega _{56}^0 \\ \omega _{56}^0\omega _{56}^{21}\omega _{56}^{35}\omega _{56}^{14}\omega _{56}^{49}\omega _{56}^{42}\omega _{56}^{28} \\ \omega _{56}^0\omega _{56}^{42}\omega _{56}^{14}\omega _{56}^{28}\omega _{56}^{42}\omega _{56}^{28}\omega _{56}^0 \\ \omega _{56}^0\omega _{56}^7\omega _{56}^{49}\omega _{56}^{42}\omega _{56}^{35}\omega _{56}^{14}\omega _{56}^{28} \\ \omega _{56}^0\omega _{56}^{28}\omega _{56}^{28}\omega _{56}^0\omega _{56}^{28}\omega _{56}^0\omega _{56}^0 \\ \omega _{56}^0\omega _{56}^{49}\omega _{56}^7\omega _{56}^{14}\omega _{56}^{21}\omega _{56}^{42}\omega _{56}^{28} \\ \omega _{56}^0\omega _{56}^{14}\omega _{56}^{42}\omega _{56}^{28}\omega _{56}^{14}\omega _{56}^{28}\omega _{56}^0 \\ \omega _{56}^0\omega _{56}^{35}\omega _{56}^{21}\omega _{56}^{42}\omega _{56}^7\omega _{56}^{14}\omega _{56}^{28} \\ \end{gathered} $ $\begin{gathered} \omega _{56}^0\omega _{56}^0\omega _{56}^0\omega _{56}^0\omega _{56}^0\omega _{56}^0\omega _{56}^0 \\ \omega _{56}^{14}\omega _{56}^{49}\omega _{56}^{42}\omega _{56}^{28}\omega _{56}^0\omega _{56}^{21}\omega _{56}^{35} \\ \omega _{56}^{28}\omega _{56}^{42}\omega _{56}^{28}\omega _{56}^0\omega _{56}^0\omega _{56}^{42}\omega _{56}^{14} \\ \omega _{56}^{42}\omega _{56}^{35}\omega _{56}^{14}\omega _{56}^{28}\omega _{56}^0\omega _{56}^7\omega _{56}^{49} \\ \omega _{56}^0\omega _{56}^{28}\omega _{56}^0\omega _{56}^0\omega _{56}^0\omega _{56}^{28}\omega _{56}^{28} \\ \omega _{56}^{14}\omega _{56}^{21}\omega _{56}^{42}\omega _{56}^{28}\omega _{56}^0\omega _{56}^{49}\omega _{56}^7 \\ \omega _{56}^{28}\omega _{56}^{14}\omega _{56}^{28}\omega _{56}^0\omega _{56}^0\omega _{56}^{14}\omega _{56}^{42} \\ \omega _{56}^{42}\omega _{56}^7\omega _{56}^{14}\omega _{56}^{28}\omega _{56}^0\omega _{56}^{35}\omega _{56}^{21} \\ \end{gathered} $ $\begin{gathered} \omega _{56}^0\omega _{56}^8\omega _{56}^{16}\omega _{56}^{24}\omega _{56}^{32}\omega _{56}^{40}\omega _{56}^{48} \\ \omega _{56}^0\omega _{56}^{29}\omega _{56}^{51}\omega _{56}^{38}\omega _{56}^{25}\omega _{56}^{26}\omega _{56}^{20} \\ \omega _{56}^0\omega _{56}^{50}\omega _{56}^{30}\omega _{56}^{52}\omega _{56}^{18}\omega _{56}^{12}\omega _{56}^{48} \\ \omega _{56}^0\omega _{56}^{15}\omega _{56}^9\omega _{56}^{10}\omega _{56}^{11}\omega _{56}^{54}\omega _{56}^{20} \\ \omega _{56}^0\omega _{56}^{36}\omega _{56}^{44}\omega _{56}^{24}\omega _{56}^4\omega _{56}^{40}\omega _{56}^{48} \\ \omega _{56}^0\omega _{56}^1\omega _{56}^{23}\omega _{56}^{38}\omega _{56}^{53}\omega _{56}^{26}\omega _{56}^{20} \\ \omega _{56}^0\omega _{56}^{22}\omega _{56}^2\omega _{56}^{52}\omega _{56}^{46}\omega _{56}^{12}\omega _{56}^{48} \\ \omega _{56}^0\omega _{56}^{43}\omega _{56}^{37}\omega _{56}^{10}\omega _{56}^{39}\omega _{56}^{54}\omega _{56}^{20} \\ \end{gathered} $ $ \begin{gathered} \omega _{56}^0\omega _{56}^8\omega _{56}^{16}\omega _{56}^{24}\omega _{56}^{32}\omega _{56}^{40}\omega _{56}^{48} \\ \omega _{56}^{14}\omega _{56}^1\omega _{56}^2\omega _{56}^{52}\omega _{56}^{32}\omega _{56}^5\omega _{56}^{27} \\ \omega _{56}^{28}\omega _{56}^{50}\omega _{56}^{44}\omega _{56}^{24}\omega _{56}^{32}\omega _{56}^{26}\omega _{56}^6 \\ \omega _{56}^{42}\omega _{56}^{43}\omega _{56}^{30}\omega _{56}^{52}\omega _{56}^{32}\omega _{56}^{47}\omega _{56}^{41} \\ \omega _{56}^0\omega _{56}^{36}\omega _{56}^{16}\omega _{56}^{24}\omega _{56}^{32}\omega _{56}^{12}\omega _{56}^{20} \\ \omega _{56}^{14}\omega _{56}^{29}\omega _{56}^2\omega _{56}^{52}\omega _{56}^{32}\omega _{56}^{33}\omega _{56}^{55} \\ \omega _{56}^{28}\omega _{56}^{22}\omega _{56}^{44}\omega _{56}^{24}\omega _{56}^{32}\omega _{56}^{54}\omega _{56}^{34} \\ \omega _{56}^{42}\omega _{56}^{15}\omega _{56}^{30}\omega _{56}^{52}\omega _{56}^{32}\omega _{56}^{19}\omega _{56}^{13} \\ \end{gathered} $ 表 2 渐近最优LCZ-CSS参数
$ p $,$ n $,$ q $ $ K $ $ M $ $ N $ $ Z $ $ {\rho _{{\text{LCZ}}}} $ $ p = 2,n = 3,q = 8 $ 112 8 7 3 1.3655 $ p = 3,n = 2,q = 9 $ 144 9 8 3 1.3312 $ p = 2,n = 4,q = 16 $ 1200 16 15 3 1.1434 $ p = 5,n = 2,q = 25 $ 4800 25 24 3 1.0871 $ p = 7,n = 2,q = 49 $ 15872 32 31 3 1.0426 表 3 例2中集合$ {\boldsymbol{C}} $的部分互补序列
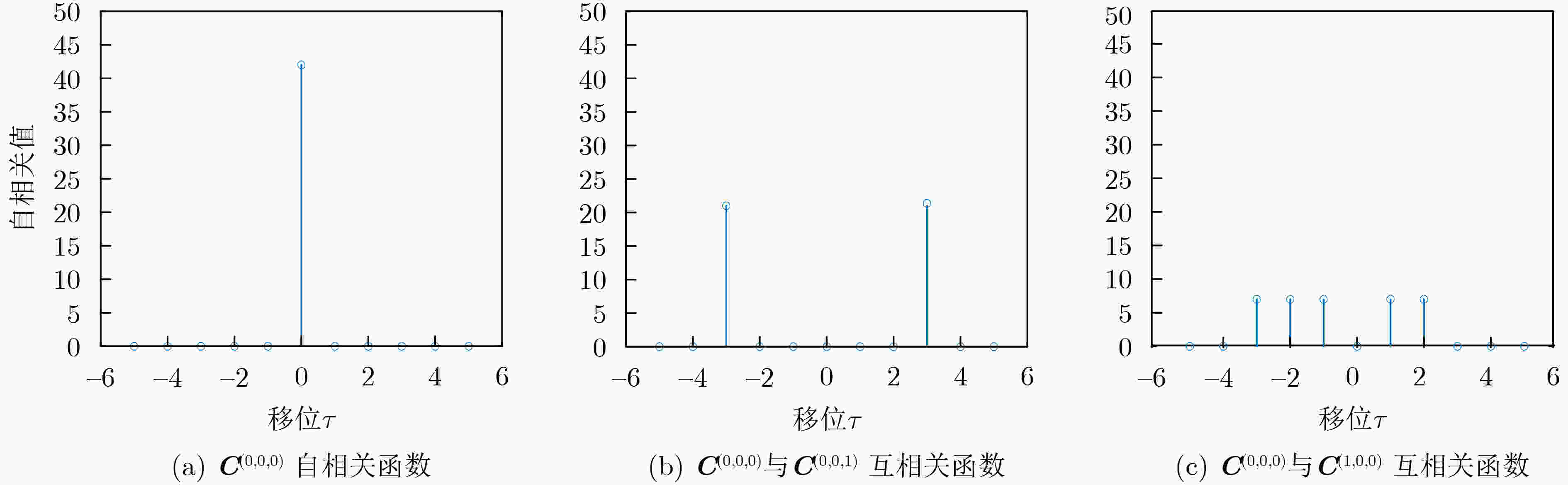
$ {{\boldsymbol{C}}^{(0,0,0)}} $ $ {{\boldsymbol{C}}^{(0,0,1)}} $ $ {{\boldsymbol{C}}^{(0,1,0)}} $ $ {{\boldsymbol{C}}^{(0,1,1)}} $ $ {{\boldsymbol{C}}^{(0,2,0)}} $ $ {{\boldsymbol{C}}^{(0,2,1)}} $ $ {{\boldsymbol{C}}^{(1,0,0)}} $ $ {{\boldsymbol{C}}^{(1,0,1)}} $ $ {{\boldsymbol{C}}^{(1,1,0)}} $ $ {{\boldsymbol{C}}^{(1,1,1)}} $ $ \begin{gathered} \begin{array}{*{20}{l}} {132645} \\ {264513} \\ {326451} \\ {451326} \\ {513264} \\ {645132} \\ 000000 \end{array} \end{gathered} $ $ \begin{array}{*{20}{l}} {645132} \\ {513264} \\ {451326} \\ {326451} \\ {264513} \\ {132645} \\ {000000} \end{array} $ $ \begin{array}{*{20}{l}} {326451} \\ {451326} \\ {513264} \\ {645132} \\ {000000} \\ {132645} \\ {264513} \end{array} $ $ \begin{array}{*{20}{l}} {451326} \\ {326451} \\ {264513} \\ {132645} \\ {000000} \\ {645132} \\ {513264} \end{array} $ $ \begin{gathered} \begin{array}{*{20}{l}} {264513} \\ {326451} \\ {451326} \\ {513264} \\ {645132} \\ {000000} \\ 132645 \end{array} \end{gathered} $ $ \begin{array}{*{20}{l}} {513264} \\ {451326} \\ {326451} \\ {264513} \\ {132645} \\ {000000} \\ {645132} \end{array} $ $ \begin{array}{*{20}{l}} {132645} \\ {305624} \\ {541603} \\ {014652} \\ {250631} \\ {423610} \\ {666666} \end{array} $ $ \begin{array}{*{20}{l}} {645132} \\ {624305} \\ {603541} \\ {652014} \\ {631250} \\ {610423} \\ {666666} \end{array} $ $ \begin{gathered} \begin{array}{*{20}{l}} {326451} \\ {562430} \\ {035416} \\ {201465} \\ {444444} \\ {610423}\\153402 \end{array} \end{gathered} $ $ \begin{array}{*{20}{l}} {451326} \\ {430562} \\ {416035} \\ {465201} \\ {444444} \\ {423610} \\ {402153} \end{array} $ 表 4 渐近最优非周期QCSS参数比较
文献 $ K $ $ M $ $ N $ $Z$ $ {\delta _{\max }} $ 字符集大小 约束条件 文献[10]定理4 $ N{q_1}{q_2} $,其中
$ N = {\text{lcm}}({q_1} - 1,{q_2} - 1) $$ {q_1}{q_2} $ $ {\text{lcm}}({q_1} - 1,{q_2} - 1) $ $ {q_1} - 1 $ $ {q_1}{q_2} $ $ {\text{lcm}}(N,{q_1}{q_2}) $ $ {q_1} $,$ {q_2} $为素数幂$ 3 \le {q_1} < {q_2} $ 文献[19] $ {2^n}({2^n} - 1)\left\lfloor {{{({2^n} - 1)} \mathord{\left/ {\vphantom {{({2^n} - 1)} Z}} \right. } Z}} \right\rfloor $ $ {2^n} $ $ {2^n} - 1 $ $ 0 < Z \le {2^n} - 1 $ $ {2^n} $ 2 $ n \ge 3 $ 文献[20] $N \times F(N)$ $N$ $N$ $N$ $N$ $N$ $N \ge 2$为任意整数 文献[21] ${p^{n + 1}}(p - 1)$ ${p^{n + 1}}$ ${p^m}$ ${p^m}$ ${p^m}$ $q$ $n \le m - 1$是任意非负整数,$p|q$ 本文定理1 $ q(q - 1)\left\lfloor {{{(q - 1)} \mathord{\left/ {\vphantom {{(q - 1)} Z}} \right. } Z}} \right\rfloor $ $ q $ $ q - 1 $ $0 < Z \le q - 1$ $ q $ $ q(q - 1) $ $ q \ge 3 $是素数幂 本文定理2 $ {q^2}\left\lfloor {{{(q - 1)} \mathord{\left/ {\vphantom {{(q - 1)} Z}} \right. } Z}} \right\rfloor $ $ q $ $ q - 1 $ $0 < Z \le q - 1$ $ q $ $ q $ 注:${\text{lcm}}$表示最大公约数,$F(N)$是$F(N) \times N$佛罗伦萨矩阵存在的最大行数,$p$是素数。 -
[1] CHEN H H, YEH J F, and SUEHIRO N. A multicarrier CDMA architecture based on orthogonal complementary codes for new generations of wideband wireless communications[J]. IEEE Communications Magazine, 2001, 39(10): 126–135. doi: 10.1109/35.956124. [2] ABEBE A T and KANG C G. Multiple codebook-based non-orthogonal multiple access[J]. IEEE Wireless Communications Letters, 2020, 9(5): 683–687. doi: 10.1109/LWC.2020.2965939. [3] CHEN Y M and CHEN Jianwei. On the design of near-optimal sparse code multiple access codebooks[J]. IEEE Transactions on Communications, 2020, 68(5): 2950–2962. doi: 10.1109/TCOMM.2020.2974213. [4] LI Fengjie, JIANG Yi, DU Cheng, et al. Construction of Golay complementary matrices and its applications to MIMO omnidirectional transmission[J]. IEEE Transactions on Signal Processing, 2021, 69: 2100–2113. doi: 10.1109/TSP.2021.3067467. [5] SU Dongliang, JIANG Yi, WANG Xin, et al. Omnidirectional precoding for massive MIMO with uniform rectangular array—Part I: Complementary codes-based schemes[J]. IEEE Transactions on Signal Processing, 2019, 67(18): 4761–4771. doi: 10.1109/TSP.2019.2931205. [6] CHEN Xu, FENG Zhiyong, WEI Zhiqing, et al. Code-division OFDM joint communication and sensing system for 6G machine-type communication[J]. IEEE Internet of Things Journal, 2021, 8(15): 12093–12105. doi: 10.1109/JIOT.2021.3060858. [7] SHARMA S and KOIVUNEN V. Multicarrier DS-CDMA based integrated sensing and communication waveform designs[C]. MILCOM 2022–2022 IEEE Military Communications Conference (MILCOM), Rockville, USA, 2022: 95–101. doi: 10.1109/MILCOM55135.2022.10017835. [8] 陈晓玉, 彭秀英, 王成瑞, 等. 周期准互补序列集构造法[J]. 电子与信息学报, 2022, 44(11): 4034–4040. doi: 10.11999/JEIT210881.CHEN Xiaoyu, PENG Xiuying, WANG Chengrui, et al. Constructions of periodic quasi-complementary sequence sets[J]. Journal of Electronics & Information Technology, 2022, 44(11): 4034–4040. doi: 10.11999/JEIT210881. [9] 陈晓玉, 王成瑞, 刘凡. 新的周期准互补序列集构造方法[J]. 通信学报, 2023, 44(5): 206–212. doi: 10.11959/j.issn.1000-436x.2023100.CHEN Xiaoyu, WANG Chengrui, and LIU Fan. New construction method of periodic quasi-complementary sequence set[J]. Journal on Communications, 2023, 44(5): 206–212. doi: 10.11959/j.issn.1000-436x.2023100. [10] LI Yubo, TIAN Liying, and XU Chengqian. Constructions of asymptotically optimal aperiodic quasi-complementary sequence sets[J]. IEEE Transactions on Communications, 2019, 67(11): 7499–7511. doi: 10.1109/TCOMM.2019.2933517. [11] DAS S, PARAMPALLI U, MAJHI S, et al. New optimal Z-complementary code sets based on generalized paraunitary matrices[J]. IEEE Transactions on Signal Processing, 2020, 68: 5546–5558. doi: 10.1109/TSP.2020.3021977. [12] SARKAR P, MAJHI S, and LIU Zilong. Pseudo-Boolean functions for optimal Z-complementary code sets with flexible lengths[J]. IEEE Signal Processing Letters, 2021, 28: 1350–1354. doi: 10.1109/LSP.2021.3091886. [13] WU S W, ŞAHIN A, HUANG Zhenming, et al. Z-complementary code sets with flexible lengths from generalized boolean functions[J]. IEEE Access, 2021, 9: 4642–4652. doi: 10.1109/ACCESS.2020.3047955. [14] LI Yu, YAN Tongjiang, and LV Chuan. Construction of a near-optimal quasi-complementary sequence set from almost difference set[J]. Cryptography and Communications, 2019, 11(4): 815–824. doi: 10.1007/s12095-018-0330-5. [15] LUO Gaojun, CAO Xiwang, SHI Minjia, et al. Three new constructions of asymptotically optimal periodic quasi-complementary sequence sets with small alphabet sizes[J]. IEEE Transactions on Information Theory, 2021, 67(8): 5168–5177. doi: 10.1109/TIT.2021.3068474. [16] LIU Tao, XU Chengqian, and LI Yubo. Multiple complementary sequence sets with low inter-set cross-correlation property[J]. IEEE Signal Processing Letters, 2019, 26(6): 913–917. doi: 10.1109/LSP.2019.2902752. [17] ZHOU Zhengchun, LIU Fangrui, ADHIKARY A R, et al. A generalized construction of multiple complete complementary codes and asymptotically optimal aperiodic quasi-complementary sequence sets[J]. IEEE Transactions on Communications, 2020, 68(6): 3564–3571. doi: 10.1109/TCOMM.2020.2978182. [18] LIU Zilong, GUAN Yongliang, NG B C, et al. Correlation and set size bounds of complementary sequences with low correlation zone[J]. IEEE Transactions on Communications, 2011, 59(12): 3285–3289. doi: 10.1109/TCOMM.2011.071111.100608. [19] LIU Tao, XU Chengqian, and LI Yubo. Binary complementary sequence set with low correlation zone[J]. IEEE Signal Processing Letters, 2020, 27: 1550–1554. doi: 10.1109/LSP.2020.3018628. [20] ADHIKARY A R, FENG Yanghe, ZHOU Zhengchun, et al. Asymptotically optimal and near-optimal aperiodic quasi-complementary sequence sets based on Florentine rectangles[J]. IEEE Transactions on Communications, 2022, 70(3): 1475–1485. doi: 10.1109/TCOMM.2021.3132364. [21] SARKAR P, LI Chunlei, MAJHI S, et al. New correlation bound and construction of quasi-complementary sequence sets[J]. IEEE Transactions on Information Theory, 2024, 70(3): 2201–2223. doi: 10.1109/TIT.2024.3352895. -





 下载:
下载:


 下载:
下载:
