A Review of Progress in Super-Resolution Reconstruction of Polarimetric Radar Image Target
-
摘要: 成像雷达具有全天时、全天候的观测能力,能够通过成像处理获得目标雷达图像信息,是对地观测、侦察监视等民用和军用领域中的重要遥感设备。高分辨率雷达图像能够提供目标的详细轮廓和精细结构,有利于后续目标分类识别等应用。对获取的雷达图像,如何利用信号和信息处理等理论方法进一步提升分辨率,突破分辨率瑞利极限,具有重要的科学研究和实际应用价值。另一方面,作为电磁波的重要属性之一,极化在目标特性的获取和挖掘中发挥着重要作用,能够为目标超分辨率重建带来丰富信息。为此,该文梳理了极化雷达图像目标超分辨率重建的概念及性能评价指标,并重点归纳整理了极化雷达图像目标超分辨率重建方法及其应用。最后,总结了现有方法的局限性并展望了未来的技术发展趋势。Abstract: Radar possesses the capability for all-day, all-weather observation and can generate radar target images through image processing. It serves as an indispensable piece of remote sensing equipment in various civil and military applications, including earth observation, and surveillance. High-resolution radar images can provide a detailed outline and fine structure of the target, which is conducive to subsequent applications such as target classification and recognition. For the acquired radar images, how to use theoretical methods such as signal and information processing to further improve the resolution and break through the Rayleigh limit has important scientific research and practical application value. On the other hand, polarization, a crucial attribute of electromagnetic waves, plays a significant role in the acquisition and analysis of target characteristics, and can provide rich information for super-resolution reconstruction. Accordingly, this work initially elucidates the concept of polarimetric radar image super-resolution reconstruction, summarizes the performance evaluation metrics, and primarily focuses on the methods of polarimetric radar image super-resolution reconstruction and their applications. Lastly, the limitations of existing methods are summarized and potential future trends in technology are forecasted.
-
Key words:
- Radar image /
- Polarization /
- Super-resolution reconstruction /
- Signal processing /
- Deep learning
-
图 3 单极化SAR图像车辆目标超分辨率重建对比结果[37]
图 4 单极化SAR图像建筑区域超分辨率重建对比结果[61]
图 5 单极化SAR图像舰船目标超分辨率重建对比结果[41]
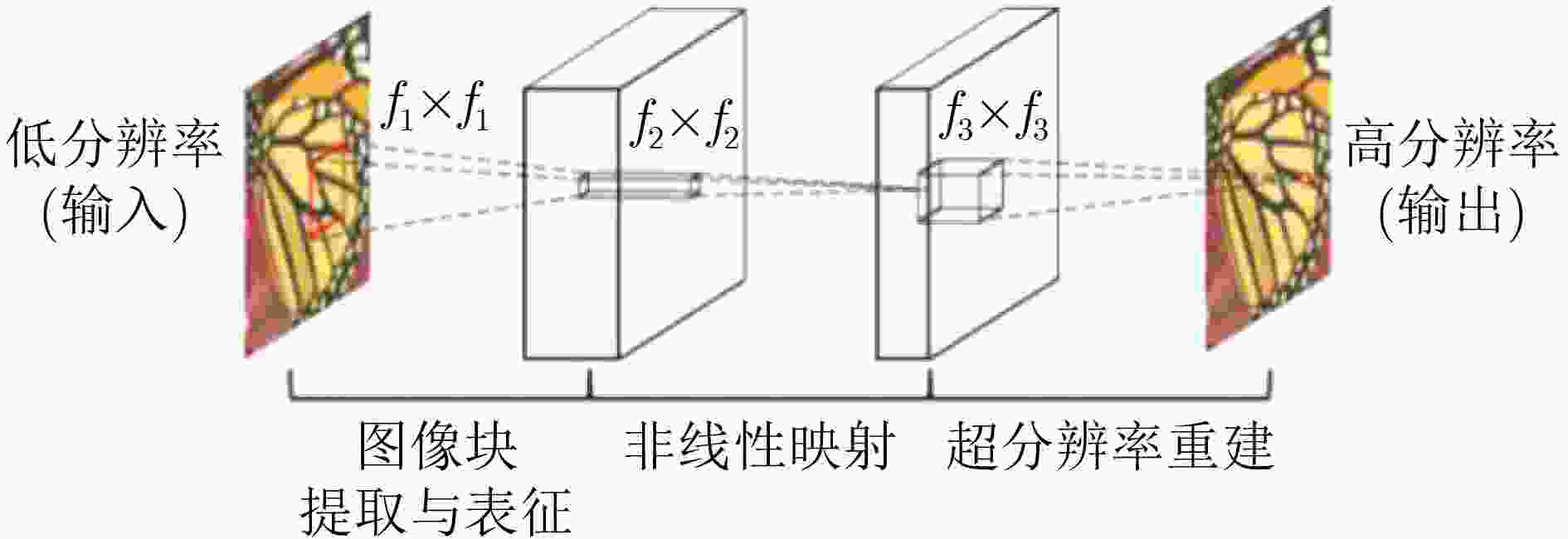
图 6 SRCNN网络模型结构[71]
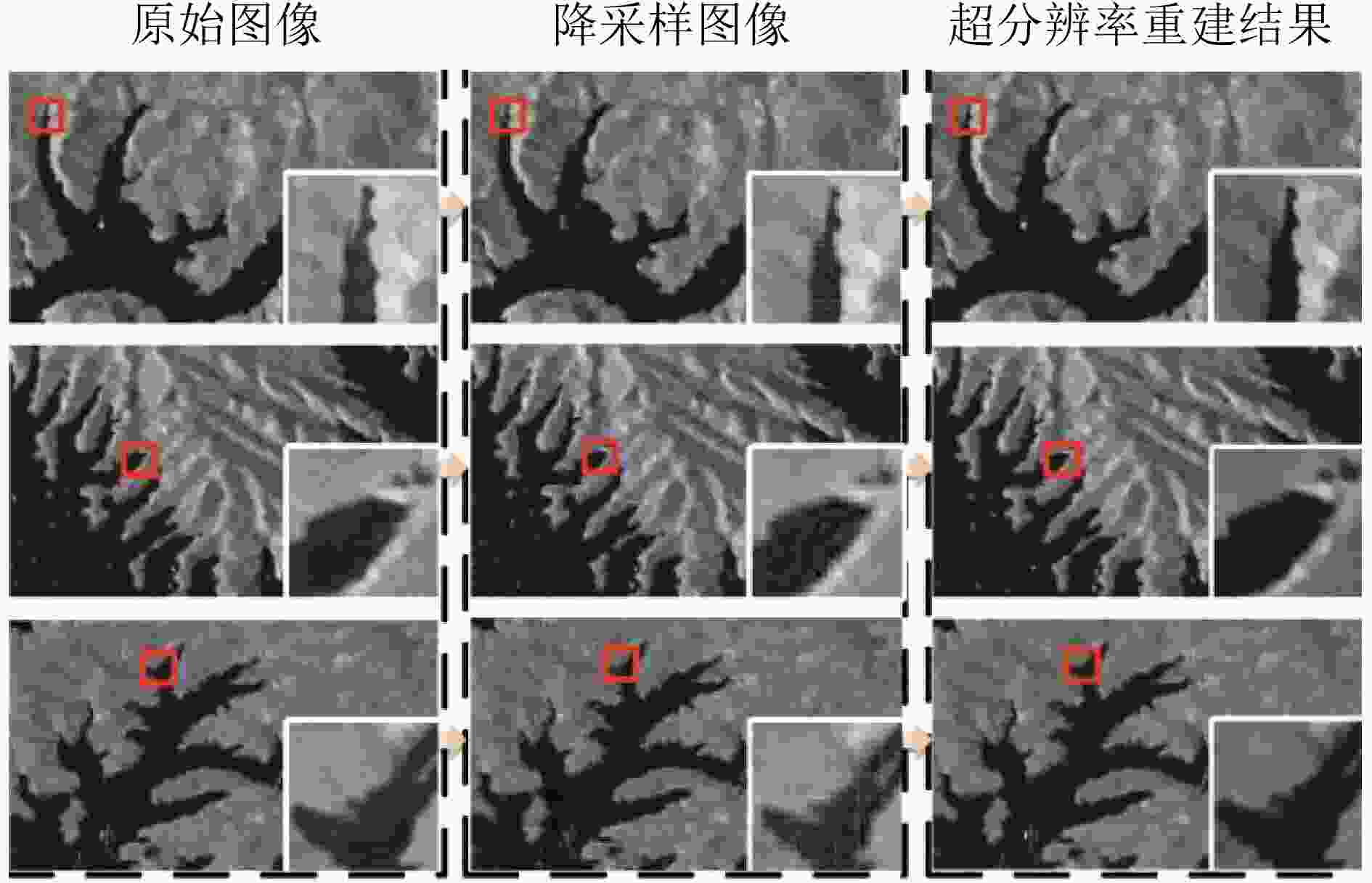
图 8 水域场景SAR图像超分辨率重建结果[3]
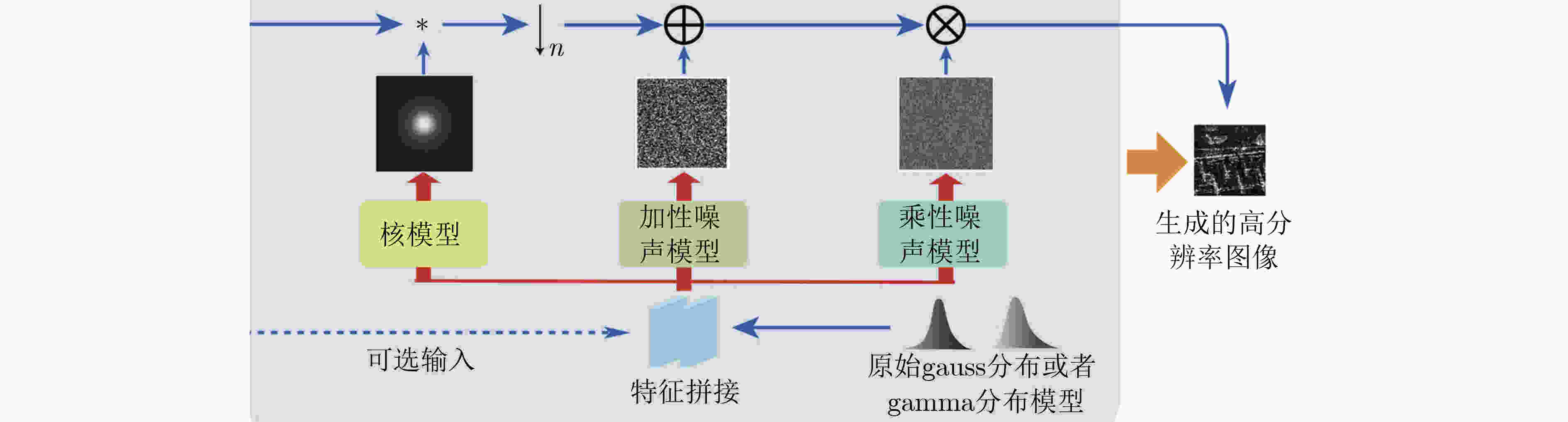
图 9 SAR图像降质模型[7]
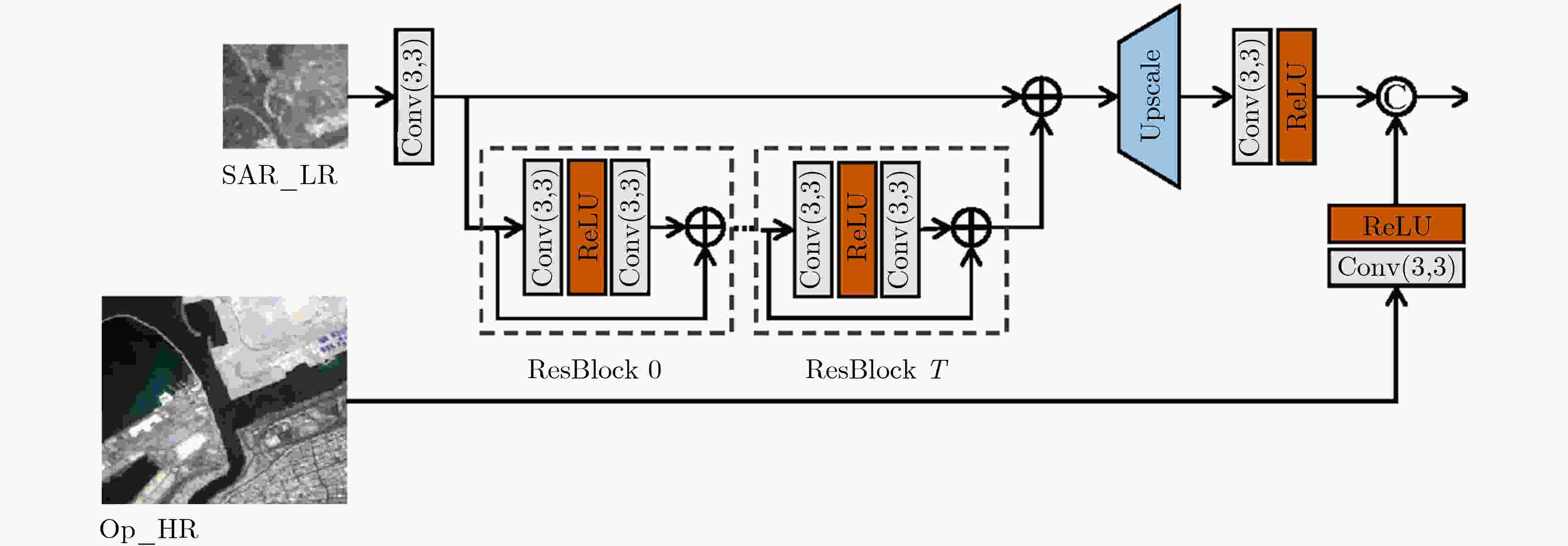
图 10 光学图像辅助的OGRN网络结构[58]
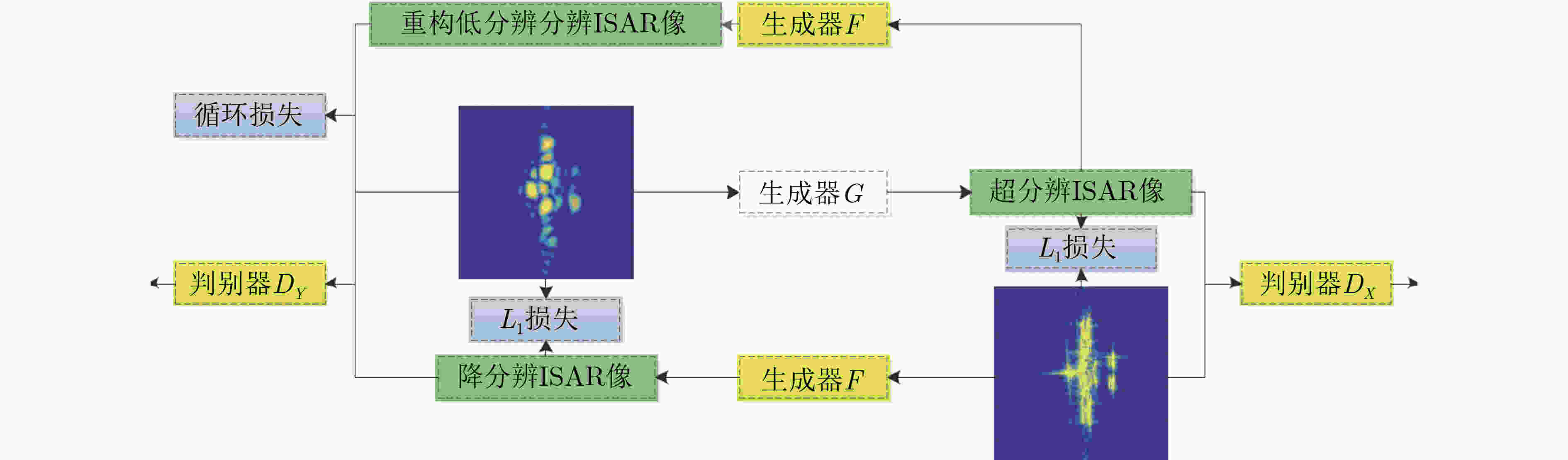
图 11 CycleGAN网络结构[46]
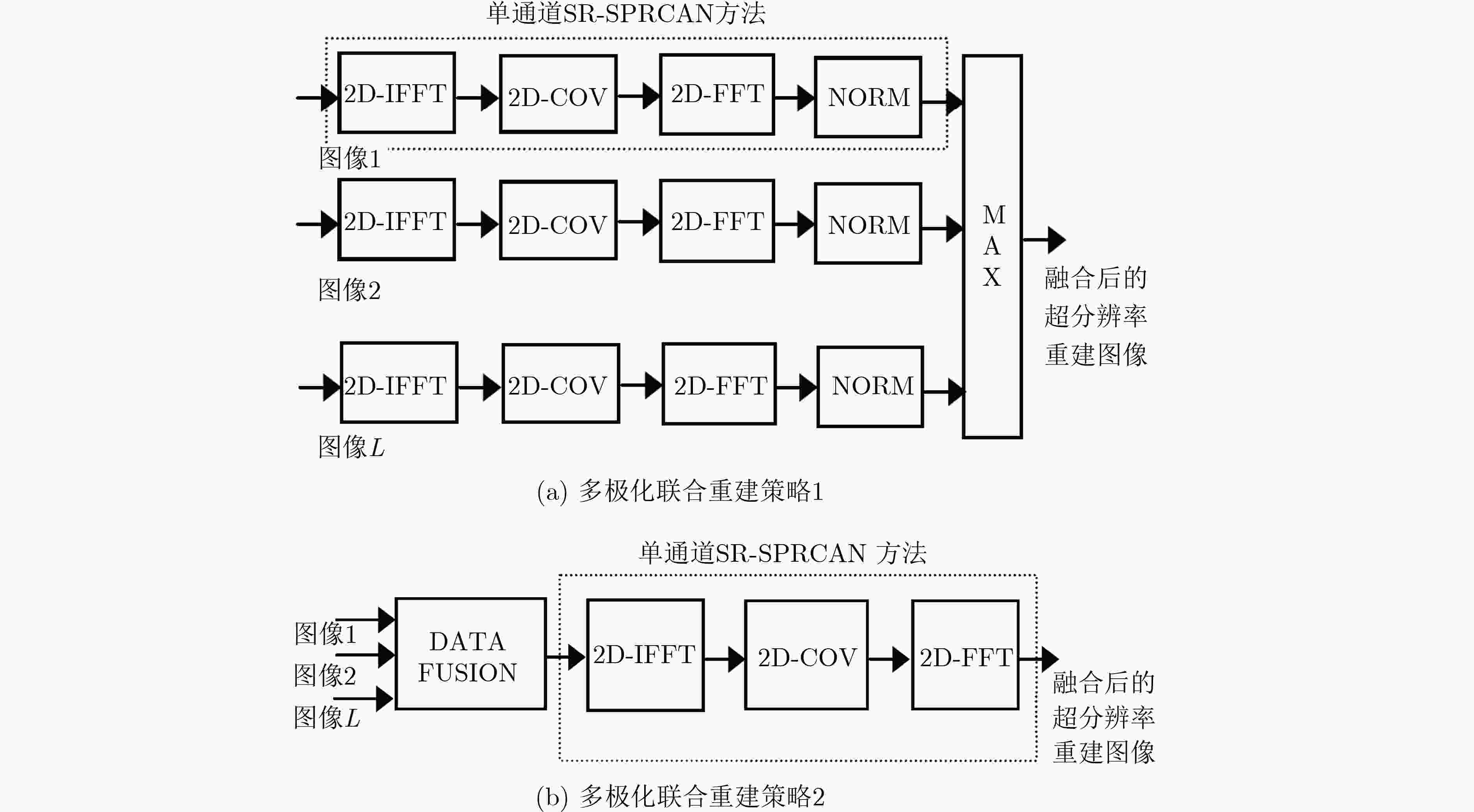
图 12 极化雷达图像目标超分辨率重建中的多极化联合策略[85]
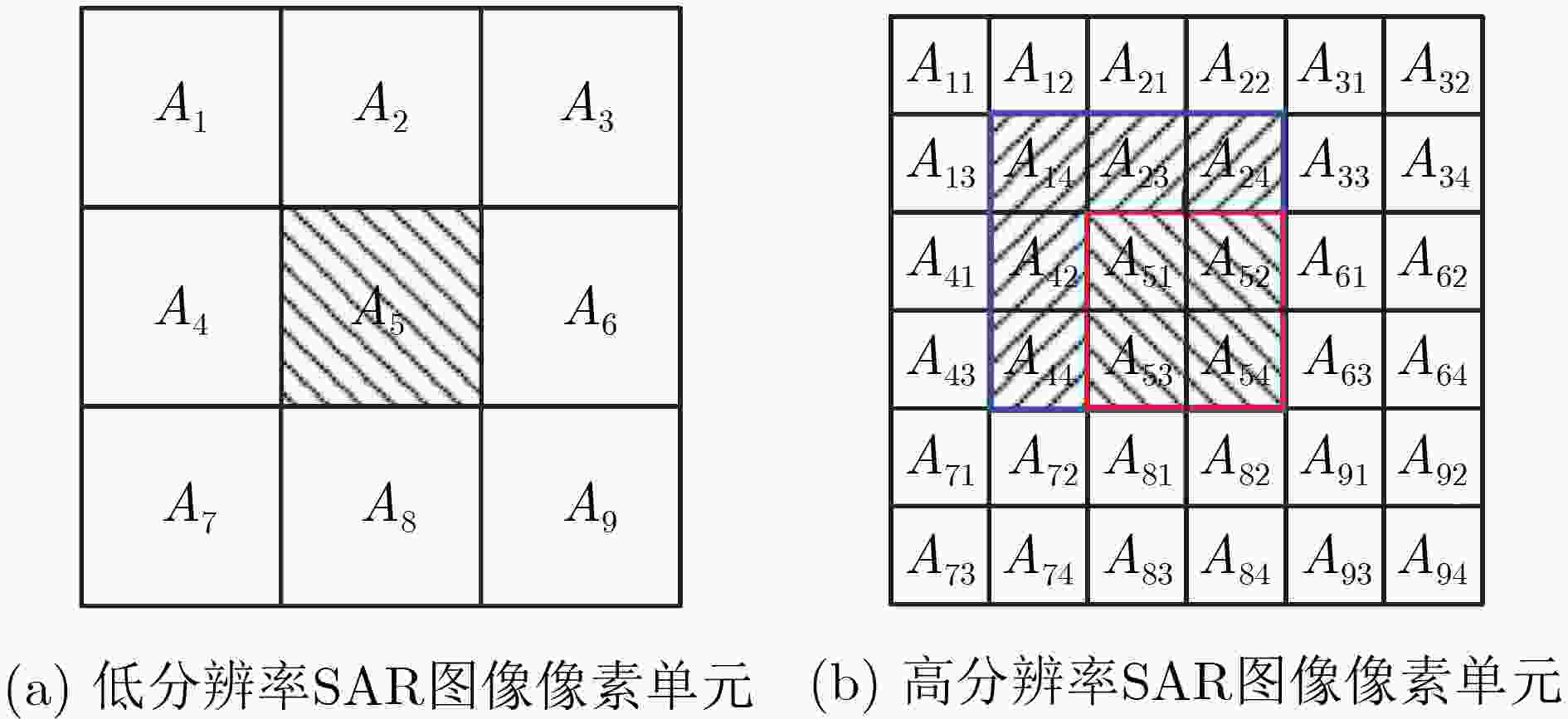
图 13 低分辨率与高分辨率SAR图像像素单元示意图[84]
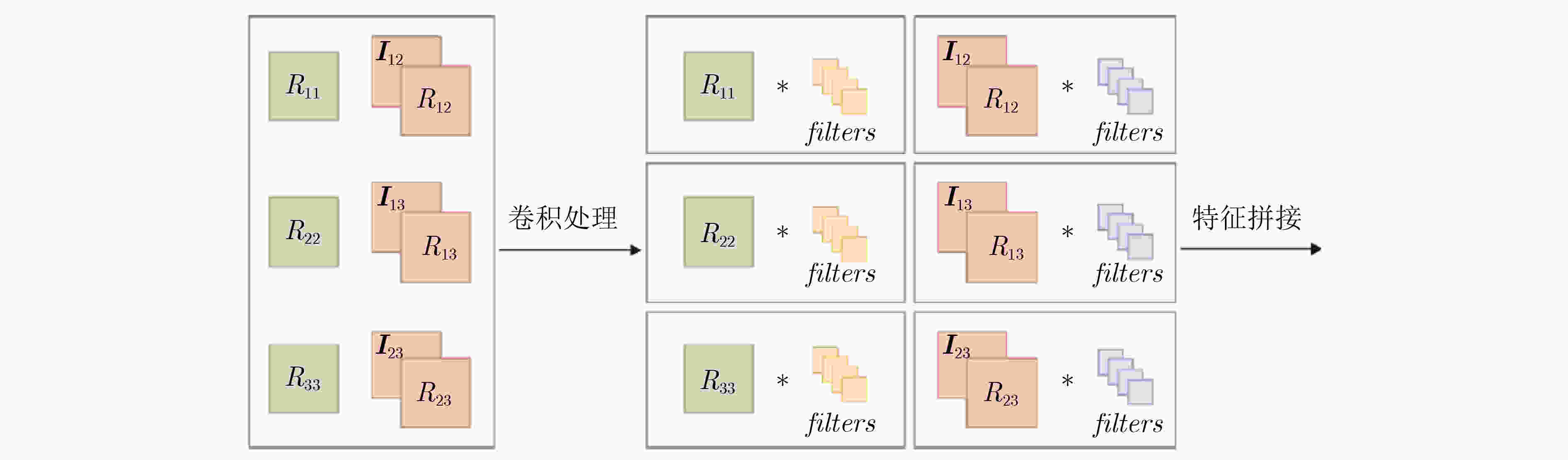
图 14 复数卷积模块[5]
图 15 港口区域全极化SAR图像超分辨率重建结果对比[53]
图 17 空间目标简缩极化ISAR图像NLSAN方法超分辨率重建结果中感兴趣区域选取[17]
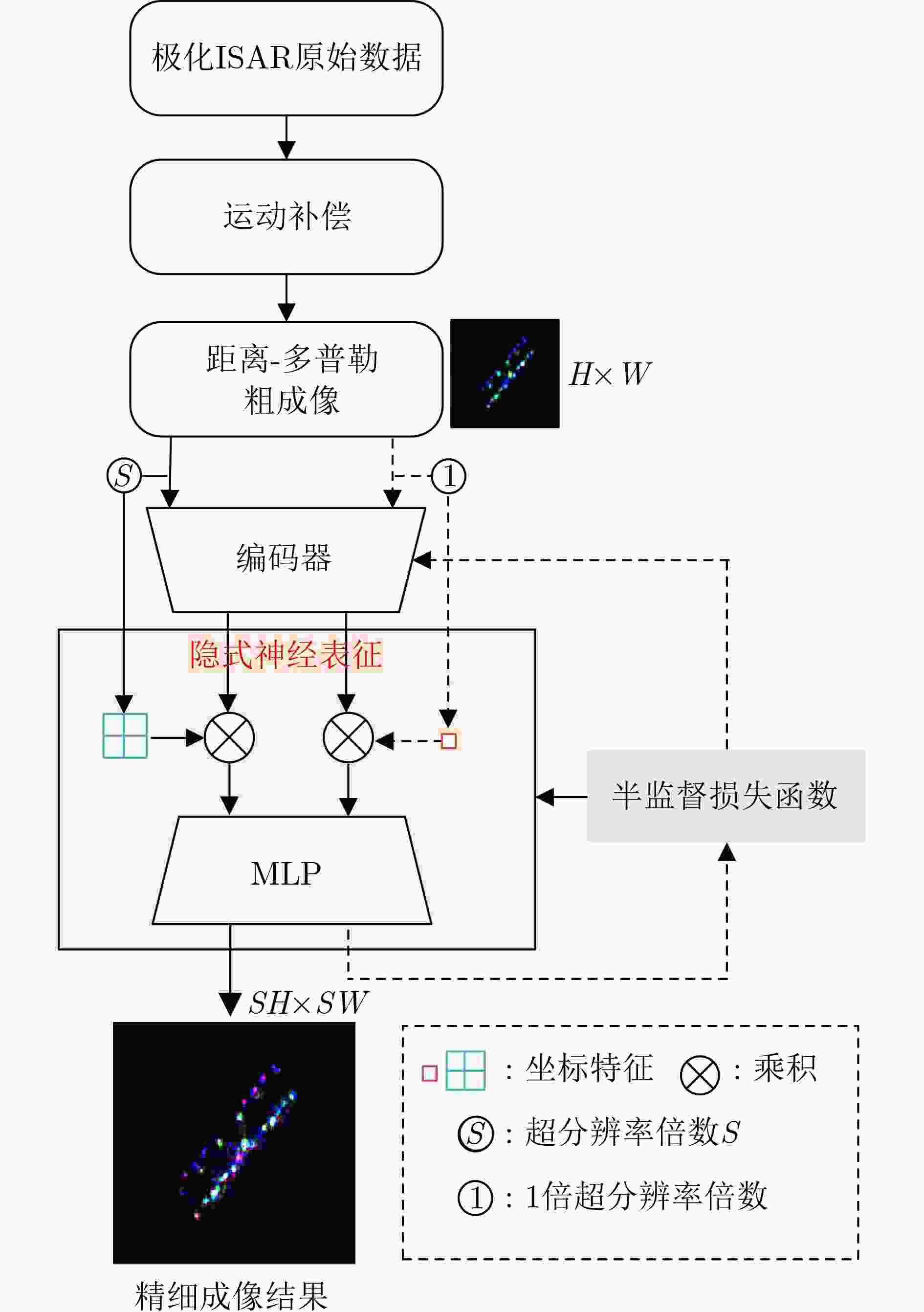
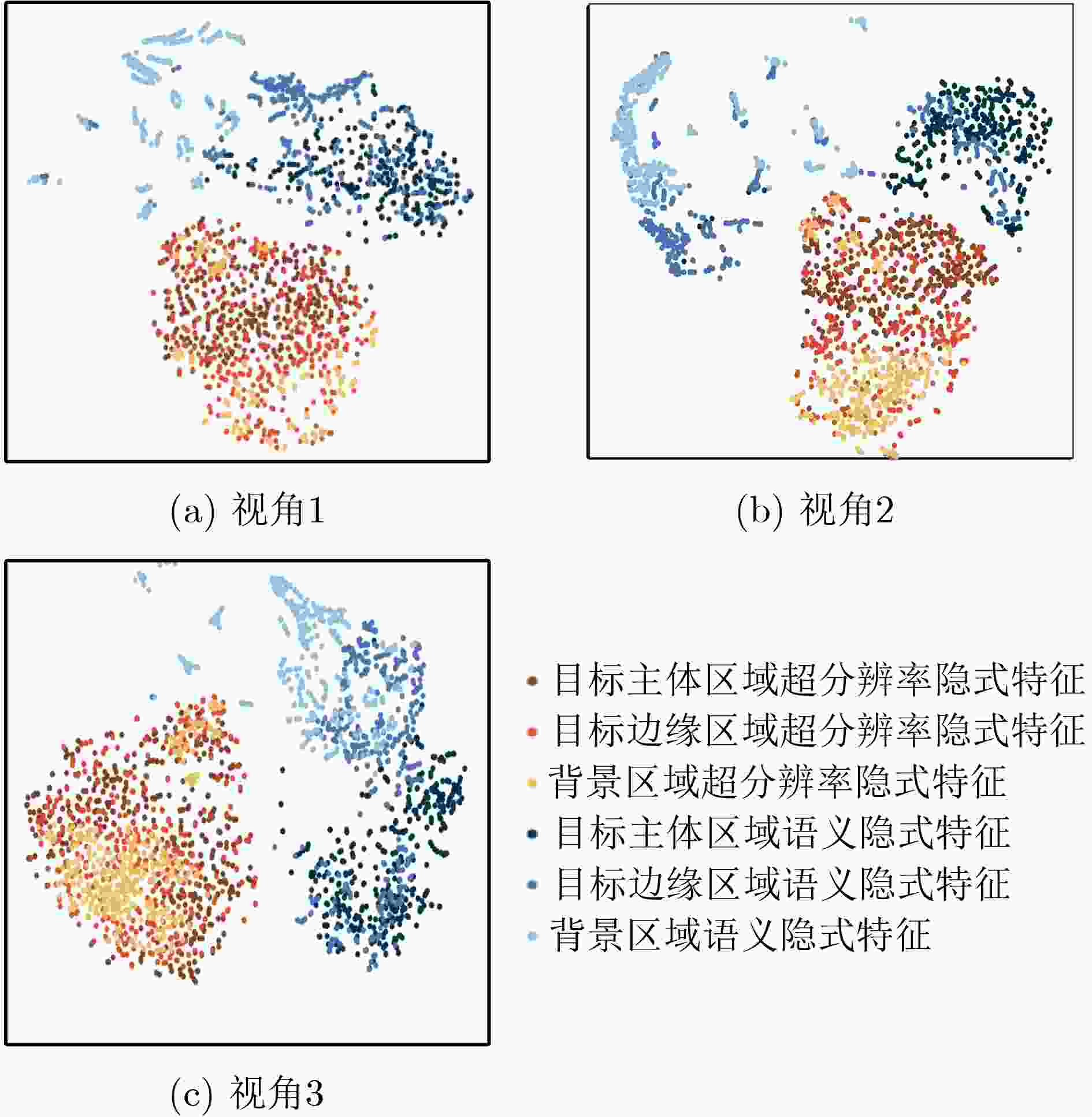
图 18 不同类型感兴趣区域超分辨率与语义隐式特征可视化[17]
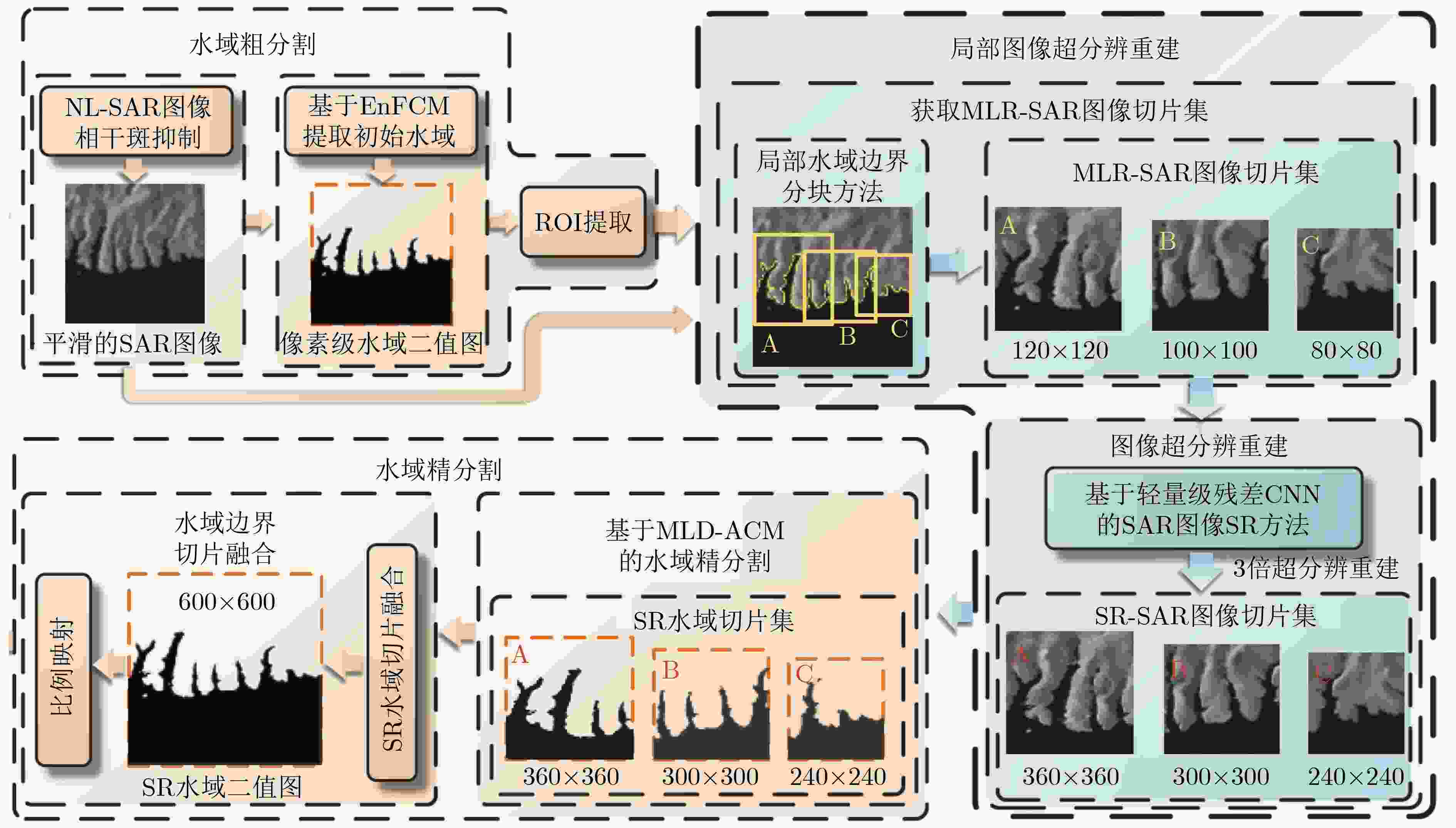
图 19 基于局部超分辨重建的SAR图像高精度水域分割方法[3]
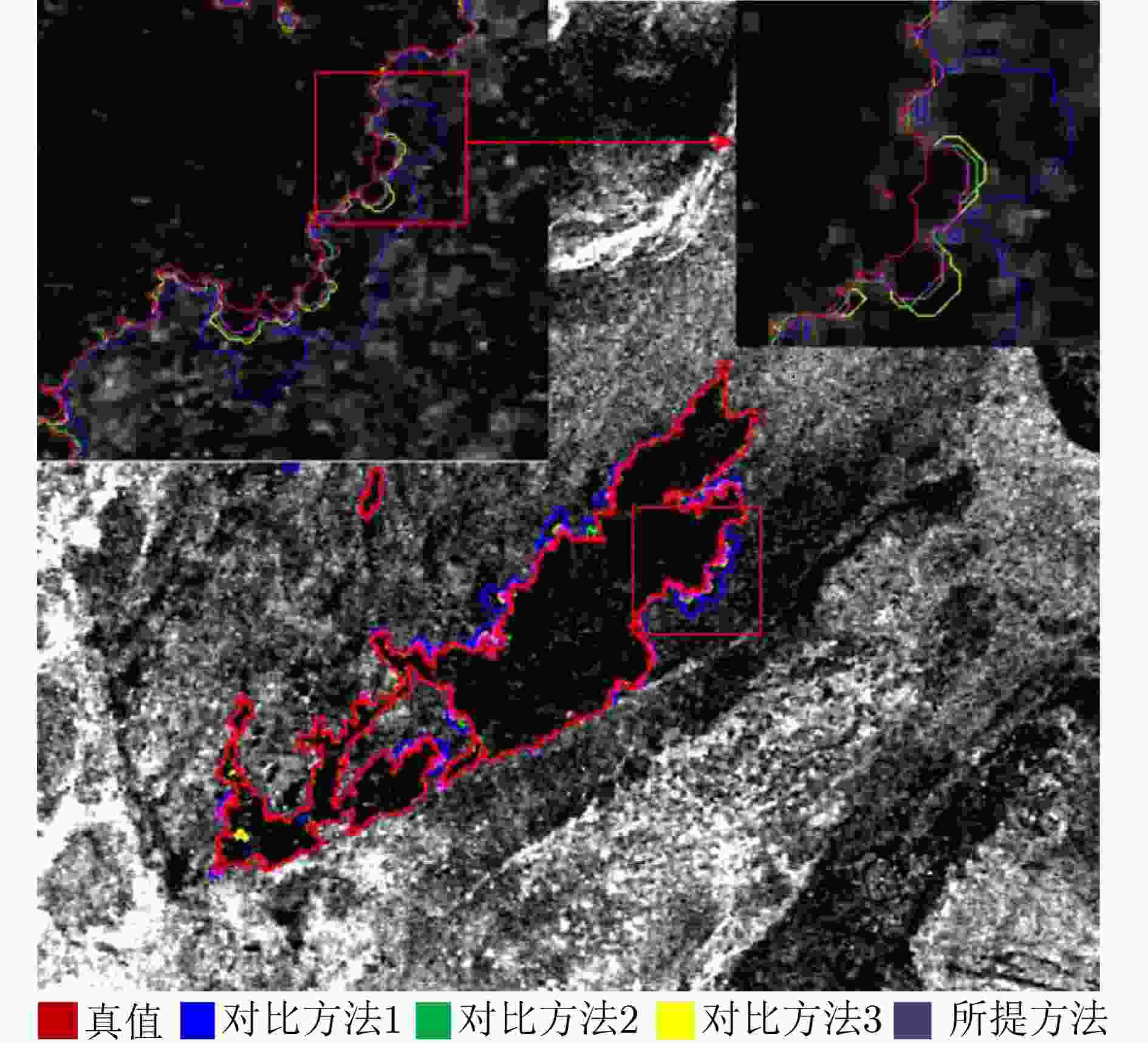
图 20 丹江口水库SAR图像水域分割对比结果[3]。
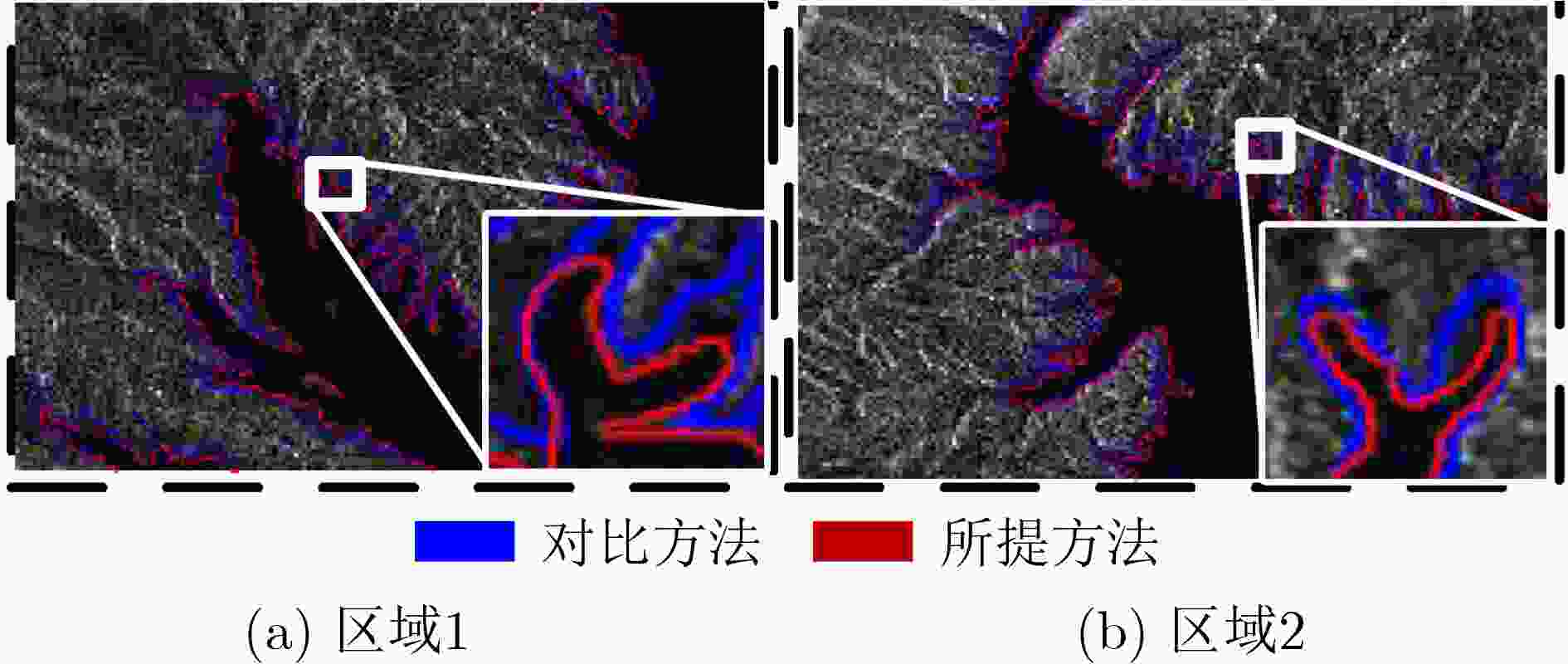
图 21 多庆错湖区域SAR图像水域分割对比结果[4]。
图 22 Flevoland区域全极化SAR地物分类结果对比[5]
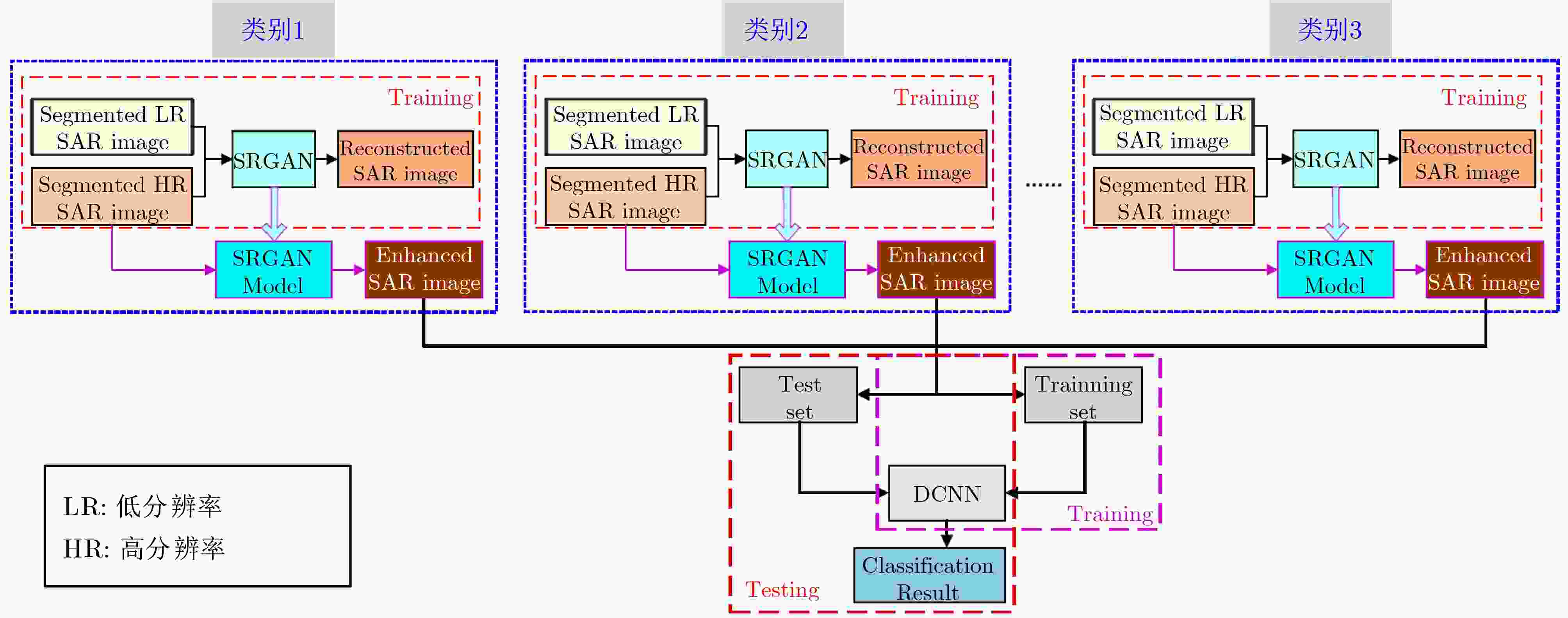
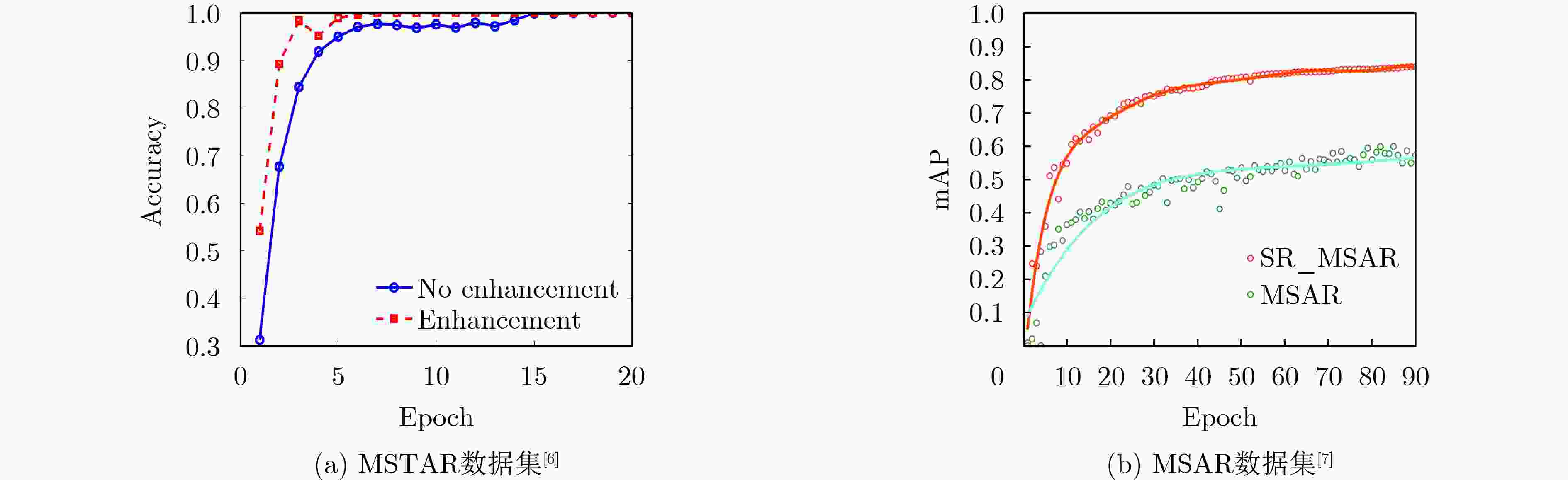
图 23 结合超分辨率重建网络和深度学习分类网络的SAR图像目标识别方法[6]
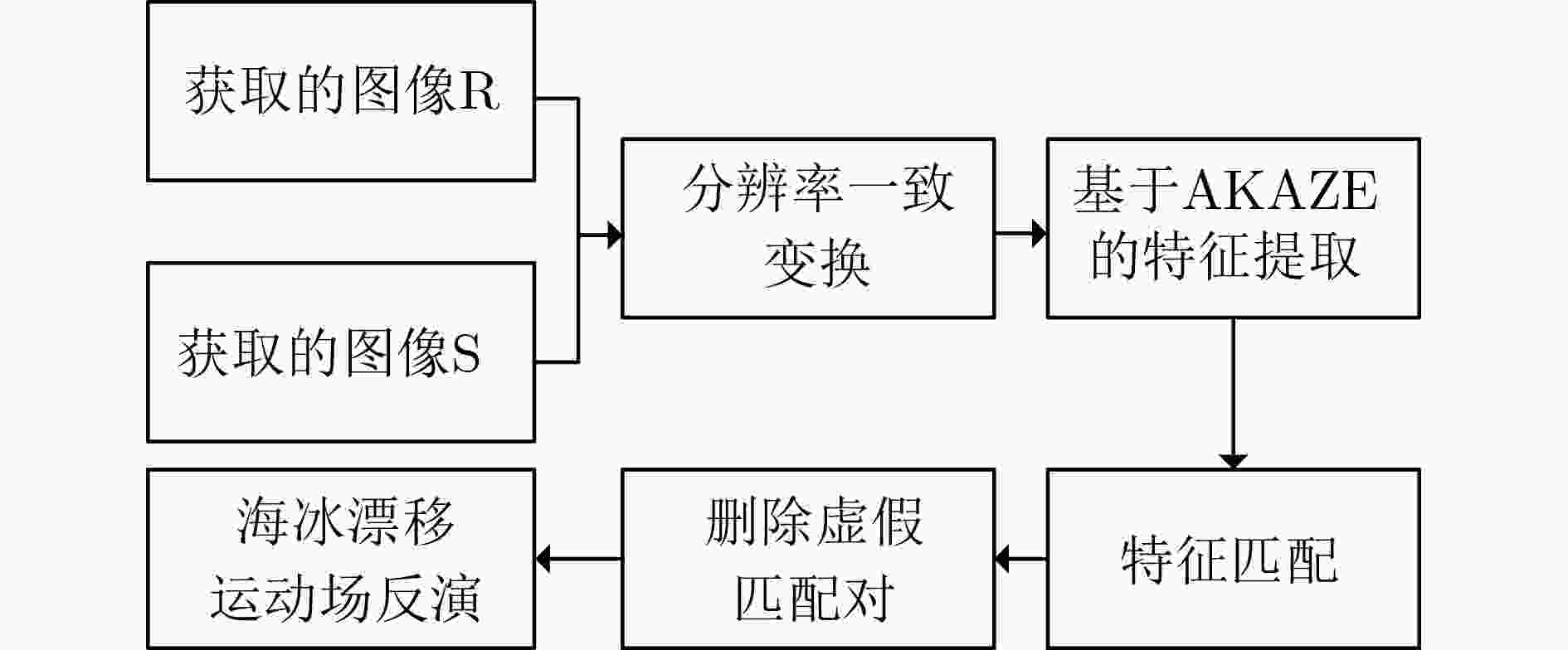
图 25 结合超分辨率重建模型的海冰漂移跟踪模型[8]
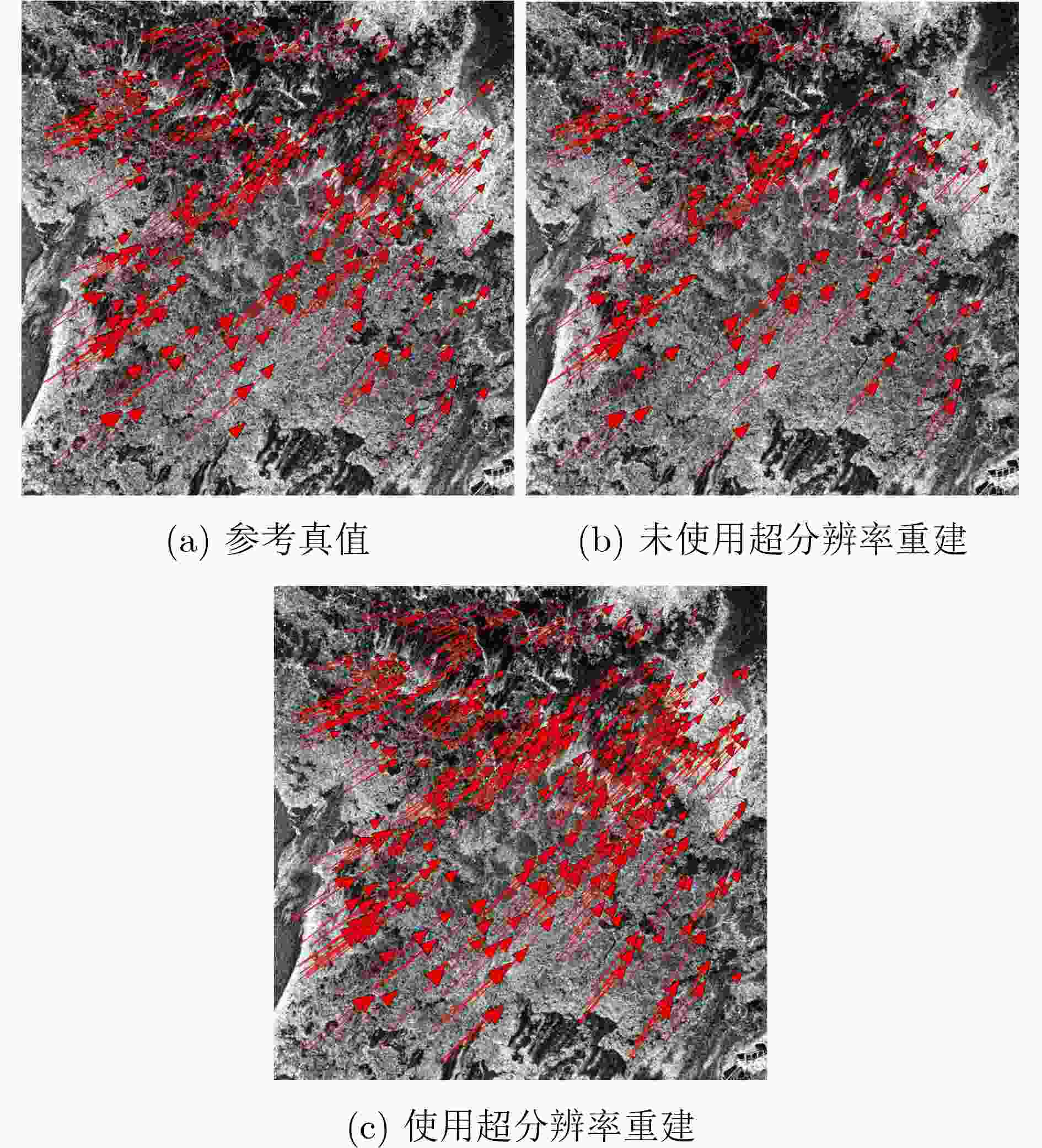
图 26 海冰漂移速度场对比结果[8]
表 1 基于点目标的极化雷达图像目标超分辨率重建定量评价指标
评价指标 是否需要参考图像 含义 计算公式 变量与符号说明 距离向3 dB主瓣宽度[17,39–43] 否 距离向瑞利极限值 ${\delta _{\text{r}}} = \left\{ {y\left| {{{{\hat {\boldsymbol{I}}}}_{\max }} \ge {\hat {\boldsymbol{I}}}\left( y \right) \ge 0.707{{{\hat {\boldsymbol{I}}}}_{\max }}} \right.} \right\}$ ${\hat {\boldsymbol{I}}}$为超分辨率重建图像幅度特征图,$ {{\hat {\boldsymbol{I}}}_{\max }} $为主瓣峰值,$y$为距离向坐标 方位向3 dB主瓣宽度[17,39–43] 否 方位向瑞利极限值 ${\delta _{\text{a}}} = \left\{ {x\left| {{{{\hat {\boldsymbol{I}}}}_{\max }} \ge {\hat {\boldsymbol{I}}}\left( x \right) \ge 0.707{{{\hat {\boldsymbol{I}}}}_{\max }}} \right.} \right\}$ $x$为方位向坐标 峰值旁瓣比(Peak Side Lobe Ratio, PSLR)[42–44] 否 第一旁瓣与主瓣峰值的比值,能够表征弱目标被强目标旁瓣压制的程度 $ {\text{PSLR}} = 20\lg \left( {{{{{{\hat {\boldsymbol{I}}}}_{{\text{SideLobe}}}}} \mathord{\left/ {\vphantom {{{{{\hat I}}_{{\text{SideLobe}}}}} {{{{\hat I}}_{\max }}}}} \right. } {{{{\hat {\boldsymbol{I}}}}_{\max }}}}} \right) $ $ {{\hat {\boldsymbol{I}}}_{{\text{SideLobe}}}} $为第一旁瓣峰值 积分旁瓣比(Integrate Side Lobe Ratio, ISLR) [42] 否 旁瓣能量与主瓣能量的比值,能够表征对旁瓣的抑制能力 $ {\text{ISLR}} = 20\lg \left( {{{{E_{{\text{SideLobe}}}}} \mathord{\left/ {\vphantom {{{E_{{\text{SideLobe}}}}} {{E_{{\text{MainLobe}}}}}}} \right. } {{E_{{\text{MainLobe}}}}}}} \right) $ $ {E_{{\text{SideLobe}}}} $为旁瓣总能量,$ {E_{{\text{MainLobe}}}} $为主瓣总能量 距离向分辨率增强指数(Intersection Amplitude Value, IAV)[45] 是 参考图像与超分辨率重建图像中两个不完全孤立的点目标距离向回波幅值交叉点取值的差 $ {\text{IA}}{{\text{V}}_{\text{r}}}{\text{ = IAV}}_{\text{r}}^{{\text{hr}}} - {\text{IAV}}_{\text{r}}^{{\text{sr}}} $ $ {\text{IAV}}_{\text{r}}^{{\text{hr}}} $和$ {\text{IAV}}_{\text{r}}^{{\text{sr}}} $分别为参考图像与超分辨率重建图像中两个不完全孤立的点目标距离向回波幅值交叉点取值 方位向分辨率增强指数(Intersection Amplitude Value, IAV)[45] 是 参考图像与超分辨率重建图像中两个不完全孤立的点目标方位向回波幅值交叉点取值的差 $ {\text{IA}}{{\text{V}}_{\text{a}}}{\text{ = IAV}}_{\text{a}}^{{\text{hr}}} - {\text{IAV}}_{\text{a}}^{{\text{sr}}} $ $ {\text{IAV}}_{\text{a}}^{{\text{hr}}} $和$ {\text{IAV}}_{\text{a}}^{{\text{sr}}} $分别为参考图像与超分辨率重建图像中两个不完全孤立的点目标方位向回波幅值交叉点取值 峰值点匹配准确率[46] 是 重建后强散射点位置保持
精度– – 表 2 基于面目标的极化雷达图像目标超分辨率重建定量评价指标
评价指标 是否需要参考图像 含义 计算公式 变量与符号说明 图像熵[44,47–51] 否 图像平均信息量 $ {\text{Entropy}} = - \sum\limits_{y = 1}^H {\sum\limits_{x = 1}^W {\frac{{{{\left| {{\hat {\boldsymbol{I}}}\left( {x,y} \right)} \right|}^2}}}{Q} {{\lg }}\frac{{{{\left| {{\hat {\boldsymbol{I}}}\left( {x,y} \right)} \right|}^2}}}{Q}} }$ $ Q $为超分辨率重建图像总能量。$H$与$W$分别为图像距离向与方位向的
像素数图像对比度(Image Contrast, IC)[42,48] 否 超分辨率重建图像强度标准差与方差
的比值$ {\text{IC}} = {{{\text{std}}\left( {{{{\hat {\boldsymbol{I}}}}^2}} \right)} \mathord{\left/ {\vphantom {{{\text{std}}\left( {{{{\hat I}}^2}} \right)} {{\text{mean}}\left( {{{{\hat I}}^2}} \right)}}} \right. } {{\text{mean}}\left( {{{{\hat {\boldsymbol{I}}}}^2}} \right)}} $ $ {\text{std}}\left( \cdot \right) $为数据标准差,$ {\text{mean}}\left( \cdot \right) $为数据均值 图像信噪比(Signal-to-noise Ratio, SNR)[48] 否 超分辨率重建图像目标区域强度与背景区域强度的比值 $ {\text{SNR}} = 20\lg \left[ {\dfrac{{{\text{mean}}\left( {{\hat {\boldsymbol{I}}}_{{\text{target}}}^2} \right)}}{{{\text{mean}}\left( {{\hat {\boldsymbol{I}}}_{{\text{background}}}^2} \right)}}} \right] $ $ {\hat {\boldsymbol{I}}}_{{\text{target}}}^2 $为目标区域图像强度,$ {\hat {\boldsymbol{I}}}_{{\text{background}}}^2 $为背景区域图像强度 平均绝对误差(Mean Absolute Error, MAE)[5,43,52,53] 是 超分辨率重建图像与参考图像幅度值之间绝对误差的平均值 $ {\text{MAE}} = {\left\| {{\hat {\boldsymbol{I}}} - {{\boldsymbol{I}}}} \right\|_1} $ $ {{\boldsymbol{I}}} $为参考图像幅度特征图,${\left\| \cdot \right\|_1}$为矩阵1范数 均方误差(Mean Square Error, MSE)[44] 是 超分辨率重建图像与参考图像幅度值之间差值平方的平均值 $ {\text{MSE}} = \left\| {{\hat {\boldsymbol{I}}} - {{\boldsymbol{I}}}} \right\|_2^2 $ ${\left\| \cdot \right\|_2}$为矩阵2范数 均方根误差(Root Mean Square Error, RMSE)[30,43,54] 是 均方误差的算数
平方根$ {\text{RMSE}} = {\left\| {{\hat {\boldsymbol{I}}} - {{\boldsymbol{I}}}} \right\|_2} $ – 平均归一化均方根误差(Average Normalized Root Mean Square Error, NRMSE)[55] 是 归一化的均方根误差 $ {\text{NRMSE}} = \dfrac{{{{\left\| {{\hat {\boldsymbol{I}}} - {{\boldsymbol{I}}}} \right\|}_2}}}{{{{\left\| {{\hat {\boldsymbol{I}}}} \right\|}_2}{{\left\| {{\boldsymbol{I}}} \right\|}_2}}} $ – 峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)[3–5,8,43,44,46,49,51–53,56–59] 是 超分辨率重建图像最大强度与均方误差强度的比值 $ {\text{PSNR = 10lg}}\dfrac{{{{\boldsymbol{I}}}_{\max }^2}}{{{\text{MSE}}}} $ – 结构相似度(Structural Similarity, SSIM)[4,8,43,46,49,57–59] 是 超分辨率重建图像与参考图像结构
相似程度$ {\text{SSIM = }}L\left( {{\hat {\boldsymbol{I}}}{\text{,}}{{\boldsymbol{I}}}} \right){{C}}\left( {{\hat {\boldsymbol{I}}}{\text{,}}{{\boldsymbol{I}}}} \right){{S}}\left( {{\hat {\boldsymbol{I}}}{\text{,}}{{\boldsymbol{I}}}} \right) $ $ {{L}}\left( \cdot \right) $为亮度相似程度,$ {{C}}\left( \cdot \right) $为对比度相似程度,$ {{S}}\left( \cdot \right) $为结构相似
程度[60]特征相似性指标(Feature Similarity Index Metric, FSIM)[61,62] 是 超分辨率重建图像与参考图像特征相似程度,取值越接近1,相似性越高 $ \begin{gathered} {\text{FSIM}} = \\ \frac{{\displaystyle\sum\limits_{y = 1}^H {\displaystyle\sum\limits_{x = 1}^W {{\text{S}}'\left[ {{\hat {\boldsymbol{I}}}\left( {x,y} \right){\text{,}}{{\boldsymbol{I}}}\left( {x,y} \right)} \right]{\text{P}}{{\text{C}}_{\text{m}}}\left[ {{\hat {\boldsymbol{I}}}\left( {x,y} \right){\text{,}}{{\boldsymbol{I}}}\left( {x,y} \right)} \right]} } }}{{\displaystyle\sum\limits_{y = 1}^H {\displaystyle\sum\limits_{x = 1}^W {{\text{P}}{{\text{C}}_{\text{m}}}\left[ {{\hat {\boldsymbol{I}}}\left( {x,y} \right){\text{,}}{{\boldsymbol{I}}}\left( {x,y} \right)} \right]} } }} \\ \end{gathered} $ $ {\text{S}}'\left( \cdot \right) $为超分辨率重建图像与参考图像的局部相似性,$ {\text{P}}{{\text{C}}_{\text{m}}}\left( \cdot \right) $为对应的最大相位一致性[63] 皮尔逊相关系数[8] 是 参考图像与超分辨率重建图像协方差与标注差的比值 $ {\text{P = }}\frac{{\displaystyle\sum\limits_{y = 1}^H {\displaystyle\sum\limits_{x = 1}^W {\left[ {{\hat {\boldsymbol{I}}}\left( {x,y} \right) - {\text{mean}}\left( {{\boldsymbol{I}}} \right)} \right]} } \left[ {{\hat {\boldsymbol{I}}}\left( {x,y} \right) - {\text{mean}}\left( {{\hat {\boldsymbol{I}}}} \right)} \right]}}{{{{\left\| {{\hat {\boldsymbol{I}}}} \right\|}_2}{{\left\| {{\boldsymbol{I}}} \right\|}_2}}} $ – 边缘保持指数(Edge Preservation Index, EPI)[62] 是 针对乘性噪声的图像距离向边缘保持度量 $ \begin{gathered} {\text{EPI = }} \\ \frac{{\displaystyle\sum\limits_{y = 1}^H {\displaystyle\sum\limits_{x = 1}^W {\left[ {\Delta {\hat {\boldsymbol{I}}}\left( {x,y} \right) - {\text{mean}}\left( {\Delta {\hat {\boldsymbol{I}}}} \right)} \right]\left[ {\Delta {{\boldsymbol{I}}}\left( {x,y} \right) - {\text{mean}}\left( {\Delta {{\boldsymbol{I}}}} \right)} \right]} } }}{{{{\left\| {\Delta {\hat {\boldsymbol{I}}} - {\text{mean}}\left( {\Delta {\hat I}} \right)} \right\|}_2}{{\left\| {\Delta {{\boldsymbol{I}}} - {\text{mean}}\left( {\Delta {{\boldsymbol{I}}}} \right)} \right\|}_2}}} \\ \end{gathered} $ $ \Delta {\hat {\boldsymbol{I}}} $为超分辨率重建图像的边缘滤波特征图,$ \Delta {{\boldsymbol{I}}} $为参考图像的边缘滤波特征图[64] 距离向边缘保持度量指标(Edge Preservation Index-ROA, EPI-ROA)[57] 是 针对乘性噪声的图像距离向边缘保持度量 $ {\text{EPI - RO}}{{\text{A}}_{\text{r}}}{\text{ = }}\frac{{\displaystyle\sum\limits_{y = 1}^H {\displaystyle\sum\limits_{x = 1}^W {\left[ {{{{\hat {\boldsymbol{I}}}\left( {x,y + 1} \right)}/ {{\hat {\boldsymbol{I}}}\left( {x,y} \right)}}} \right]} } }}{{\displaystyle\sum\limits_{y = 1}^H {\sum\limits_{x = 1}^W {\left[ {{{{{\boldsymbol{I}}}\left( {x,y + 1} \right)} \mathord{\left/ {\vphantom {{{I}\left( {x,y + 1} \right)} {{I}\left( {x,y} \right)}}} \right. } {{{\boldsymbol{I}}}\left( {x,y} \right)}}} \right]} } }} $ – 方位向边缘保持度量指标(Edge Preservation Index-ROA, EPI-ROA)[57] 是 针对乘性噪声的图像方位向边缘保持度量 $ {\text{EPI - RO}}{{\text{A}}_{\text{a}}}{\text{ = }}\frac{{\displaystyle\sum\limits_{y = 1}^H {\displaystyle\sum\limits_{x = 1}^W {\left[ {{{{\hat {\boldsymbol{I}}}\left( {x + 1,y} \right)} \mathord{\left/ {\vphantom {{{\hat I}\left( {x + 1,y} \right)} {{\hat I}\left( {x,y} \right)}}} \right. } {{\hat {\boldsymbol{I}}}\left( {x,y} \right)}}} \right]} } }}{{\displaystyle\sum\limits_{y = 1}^H {\displaystyle\sum\limits_{x = 1}^W {\left[ {{{{{\boldsymbol{I}}}\left( {x + 1,y} \right)} \mathord{\left/ {\vphantom {{{{\boldsymbol{I}}}\left( {x + 1,y} \right)} {{{\boldsymbol{I}}}\left( {x,y} \right)}}} \right. } {{{\boldsymbol{I}}}\left( {x,y} \right)}}} \right]} } }} $ – Pauli相似性指标[16] 是 全极化雷达图像Pauli矢量重建精度 ${{R}} = \dfrac{{{{\left\| {{{\boldsymbol{k}}}_{{\text{sr}}}^{}{{\boldsymbol{k}}}_{{\text{hr}}}^{\text{H}}} \right\|}_1}}}{{{{\left\| {{{\boldsymbol{k}}}_{{\text{sr}}}^{}} \right\|}_1}{{\left\| {{{\boldsymbol{k}}}_{{\text{hr}}}^{}} \right\|}_1}}}$ ${{\boldsymbol{k}}}_{{\text{sr}}}^{}$为超分辨率重建图像Pauli矢量,${{\boldsymbol{k}}}_{{\text{hr}}}^{}$为参考图像Pauli矢量 表 3 基于深度学习的极化雷达图像超分辨率重建方法研究现状
极化模式 网络模型结构 文献 学习方式 损失函数 升采样方式 升采样阶段 单极化 Shallow CNN [42] 监督学习 ${L_2}$/${L_{{\text{SSIM}}}}$ Bicubic 前升采 Shallow CNN [73] 监督学习 ${L_2}$ Bicubic 前升采 ResNet [43] 监督学习 ${L_2}$/${L_{{\text{SSIM}}}}$ 反卷积 后升采 ResNet [3] 监督学习 ${L_2}$ 反卷积 后升采 ResNet [4] 监督学习 ${L_1}$ 亚像素卷积重排 后升采 ResNet [57] 监督学习 ${L_2}$/$ {L_{{\text{Content}}}} $ 反卷积 后升采 ResNet [8] 监督学习 ${L_1}$/${L_{{\text{Edge}}}}$ Bicubic 后升采 ResNet [58] 监督学习 ${L_1}$ Bicubic 后升采 GAN [74] 监督学习 ${L_2}$/${L_{{\text{GAN}}}}$/$ {L_{{\text{Content}}}} $/$ {L_{{\text{Style}}}} $ – – GAN [75] 监督学习 ${L_1}$/${L_{{\text{GAN}}}}$ – – GAN [49] 监督学习 ${L_1}$/${L_{{\text{GAN}}}}$/$ {L_{{\text{Content}}}} $ – – GAN [73] 监督学习 ${L_{{\text{GAN}}}}$/$ {L_{{\text{Content}}}} $ – – GAN [46] 监督学习 ${L_{{\text{GAN}}}}$/${L_{{\text{CycleGAN}}}}$ – – GAN [7] 无监督学习 ${L_2}$/${L_{{\text{SSIM}}}}$ – – 双极化 ResNet [52] 监督学习 ${L_1}$/${L_{{\text{Phy}}}}$ 反卷积 前升采 隐式神经表征 [17] 半监督学习 ${L_2}$/${L_{{\text{Self}}}}$/${L_{{\text{Penalty}}}}$/${L_{{\text{CE}}}}$ Bilinear 后升采 全极化 ResNet [5,76] 监督学习 ${L_2}$ 反卷积 前升采 ResNet [53] 监督学习 ${L_{\text{F}}}$/${L_{{\text{Phy}}}}$ 反卷积 前升采 ResNet [77] 监督学习 ${L_{\text{C}}}$/${L_{{\text{Edge}}}}$ 反卷积 前升采 ResNet [15] 监督学习 ${L_1}$ 亚像素卷积重排 后升采 隐式神经表征 [78] 半监督学习 ${L_1}$/${L_{{\text{Self}}}}$ Bilinear 后升采 -
[1] 陈思伟. 成像雷达极化旋转域解译理论与应用[M]. 北京: 科学出版社, 2023: 1–251.CHEN Siwei. Imaging Radar Polarimetric Rotation Domain Interpretation[M]. Beijing: Science Press, 2023: 1–251. [2] CHEN Siwei, WANG Xuesong, XIAO Shunping, et al. Target Scattering Mechanism in Polarimetric Synthetic Aperture Radar[M]. Singapore: Springer, 2018: 1–225. doi: 10.1007/978-981-10-7269-7. [3] 李宁, 牛世林. 基于局部超分辨重建的高精度SAR图像水域分割方法[J]. 雷达学报, 2020, 9(1): 174–184. doi: 10.12000/JR19096.LI Ning and NIU Shilin. High-precision water segmentation from synthetic aperture radar images based on local super-resolution restoration technology[J]. Journal of Radars, 2020, 9(1): 174–184. doi: 10.12000/JR19096. [4] 陈嘉琪, 刘祥梅, 李宁, 等. 一种超分辨SAR图像水域分割算法及其应用[J]. 电子与信息学报, 2021, 43(3): 700–707. doi: 10.11999/jeit200366.CHEN Jiaqi, LIU Xiangmei, LI Ning, et al. A high-precision water segmentation algorithm for SAR image and its application[J]. Journal of Electronics & Information Technology, 2021, 43(3): 700–7076. doi: 10.11999/jeit200366. [5] SHEN Huanfeng, LIN Liupeng, LI Jie, et al. A residual convolutional neural network for polarimetric SAR image super-resolution[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2020, 161: 90–108. doi: 10.1016/j.isprsjprs.2020.01.006. [6] SHI Xiaoran, ZHOU Feng, YANG Shuang, et al. Automatic target recognition for synthetic aperture radar images based on super-resolution generative adversarial network and deep convolutional neural network[J]. Remote Sensing, 2019, 11(2): 135. doi: 10.3390/rs11020135. [7] ZHANG Chongqi, ZHANG Ziwen, DENG Yao, et al. Blind super-resolution for SAR images with speckle noise based on deep learning probabilistic degradation model and SAR priors[J]. Remote Sensing, 2023, 15(2): 330. doi: 10.3390/rs15020330. [8] MEN Peng, GUO Hao, AN Jubai, et al. Large-resolution difference heterogeneous SAR image sea ice drift tracking using a smooth edge-guide Super-resolution residual network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5212519. doi: 10.1109/tgrs.2023.3296462. [9] 高勋章, 张志伟, 刘梅, 等. 雷达像智能识别对抗研究进展[J]. 雷达学报, 2023, 12(4): 696–712. doi: 10.12000/jr23098.GAO Xunzhang, ZHANG Zhiwei, LIU Mei, et al. Intelligent radar image recognition countermeasures: A review[J]. Journal of Radars, 2023, 12(4): 696–712. doi: 10.12000/jr23098. [10] CHEN Siwei and TAO Chensong. PolSAR image classification using polarimetric-feature-driven deep convolutional neural network[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(4): 627–631. doi: 10.1109/LGRS.2018.2799877. [11] LI Mingdian, XIAO Shunping, and CHEN Siwei. Three-dimension polarimetric correlation pattern interpretation tool and its application[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5238716. doi: 10.1109/TGRS.2022.3222691. [12] CHEN Siwei, LI Mingdian, CUI Xingchao, et al. Polarimetric roll-invariant features and applications for polarimetric synthetic aperture radar ship detection: A comprehensive summary and investigation[J]. IEEE Geoscience and Remote Sensing Magazine, 2024, 12(1): 36–66. doi: 10.1109/MGRS.2023.3328472. [13] CHEN Siwei. Polarimetric coherence pattern: A visualization and characterization tool for PolSAR data investigation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(1): 286–297. doi: 10.1109/TGRS.2017.2746662. [14] CHEN Siwei, WANG Xuesong, and SATO M. Urban damage level mapping based on scattering mechanism investigation using fully polarimetric SAR data for the 3. 11 east Japan earthquake[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(12): 6919–6929. doi: 10.1109/TGRS.2016.2588325. [15] LI Mingdian, CUI Xingchao, YANG Chengli, et al. Polarimetric ISAR super-resolution based on group residual attention network[C]. 2022 IEEE 10th International Conference on Information, Communication and Networks (ICICN), Zhangye, China, 2022: 566–571. doi: 10.1109/ICICN56848.2022.10006508. [16] LI Mingdian, DENG Junwu, XIAO Shunping, et al. Semi-supervised implicit neural representation for polarimetric ISAR image super-resolution[J]. IEEE Geoscience and Remote Sensing Letters, 2023, 20: 3505505. doi: 10.1109/LGRS.2023.3287283. [17] LI Mingdian, DENG Junwu, XIAO Shunping, et al. NLSAN: A non-local scene awareness network for compact polarimetric ISAR image super-resolution[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5111416. doi: 10.1109/TGRS.2023.3331822. [18] 崔兴超, 李郝亮, 付耀文, 等. 空间目标散射结构极化旋转域辨识[J]. 电子与信息学报, 2022, 45(6): 2105–2114. doi: 10.11999/JEIT220493.CUI Xingchao, LI Haoliang, FU Yaowen, et al. Scattering structure recognition of space target in polarimetric rotation domain[J]. Journal of Electronics & Information Technology, 2023, 45(6): 2105–2114. doi: 10.11999/JEIT220493. [19] 李郝亮, 陈思伟. 海面角反射体电磁散射特性与雷达鉴别研究进展与展望[J]. 雷达学报, 2023, 12(4): 738–761. doi: 10.12000/jr23100.LI Haoliang and CHEN Siwei. Electromagnetic scattering characteristics and radar identification of sea corner reflectors: Advances and prospects[J]. Journal of Radars, 2023, 12(4): 738–761. doi: 10.12000/JR23100. doi: 10.12000/jr23100. [20] 许璐, 张红, 王超, 等. 简缩极化SAR数据处理与应用研究进展[J]. 雷达学报, 2020, 9(1): 55–72. doi: 10.12000/JR19106.XU Lu, ZHANG Hong, WANG Chao, et al. Progress in the processing and application of compact polarimetric SAR[J]. Journal of Radars, 2020, 9(1): 55–72. doi: 10.12000/JR19106. [21] CZERWINSKI M G and USOFF J M. Development of the haystack ultrawideband satellite imaging radar[J]. Lincoln Laboratory Journal, 2014, 21(1): 28–44. [22] 呼鹏江. 空天目标逆合成孔径雷达精细成像技术研究[D]. [博士论文], 国防科技大学, 2018. doi: 10.27052/d.cnki.gzjgu.2018.000338.HU Pengjiang. Research on inverse synthetic aperture radar fine imaging technology of aerospace targets[D]. [Ph. D. dissertation], National University of Defense Technology, 2018. doi: 10.27052/d.cnki.gzjgu.2018.000338. [23] CUMMING I G, WONG F H, 洪文, 胡东辉, 译. 合成孔径雷达成像: 算法与实现[M]. 北京: 电子工业出版社, 2007: 1–428.CUMMING I G, WONG F H, HONG Wen and HU Donghui. translation. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation[M]. Beijing: Publishing House of Electronics Industry, 2007: 1–428. [24] SOUMEKH M. Synthetic Aperture Radar Signal Processing with MATLAB Algorithms[M]. New York: Jone Wiley & Sons, 1999: 1–648. [25] BORISON S L, BOWLING S B, and CUOMO K M. Super-resolution methods for wideband radar[J]. The Lincoln Laboratory Journal, 1992, 5(3): 441–461. [26] JONSSON R. Regularization based super resolution imaging using FFT: s[C]. SPIE 5808, Algorithms for Synthetic Aperture Radar Imagery XII, Orlando, USA, 2005: 122–131. doi: 10.1117/12.604347. [27] FARINA A, PRODI F, and VINELLI F. Application of superresolution techniques to radar imaging[J]. Journal of Systems Engineering and Electronics, 1994, 5(1): 1–14. [28] 冉承其, 王正明. 基于基追踪的SAR图像超分辨处理[J]. 宇航学报, 2006, 27(1): 51–56. doi: 10.3321/j.issn:1000-1328.2006.01.011.RAN Chengqi and WANG Zhengming. Super-resolution processing of SAR image by basis pursuit method[J]. Journal of Astronautics, 2006, 27(1): 51–56. doi: 10.3321/j.issn:1000-1328.2006.01.011. [29] ZHANG Ping and YANG Ruliang. A new superresolution SAR imaging algorithm based on extrapolation[C]. 2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, USA, 2008: 407–410. doi: 10.1109/IGARSS.2008.4779744. [30] HE Chu, LIU Longzhu, XU Lianyu, et al. Learning based compressed sensing for SAR image super-resolution[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2012, 5(4): 1272–1281. doi: 10.1109/jstars.2012.2189555. [31] DU Chuan, XIE Pengfei, ZHANG Lei, et al. Conditional prior probabilistic generative model with similarity measurement for ISAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4013205. doi: 10.1109/LGRS.2021.3073691. [32] HARRIS J L. Diffraction and resolving power[J]. Journal of the Optical Society of America, 1964, 54(7): 931–936. doi: 10.1364/josa.54.000931. [33] MOSER B B, RAUE F, FROLOV S, et al. Hitchhiker's guide to super-resolution: Introduction and recent advances[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2023, 45(8): 9862–9882. doi: 10.1109/TPAMI.2023.3243794. [34] WANG Zhihao, CHEN Jian, and HOI S C H. Deep learning for image super-resolution: A survey[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 43(10): 3365–3387. doi: 10.1109/TPAMI.2020.2982166. [35] 邢孟道, 保铮, 李真芳, 等. 雷达成像算法进展[M]. 北京: 电子工业出版社, 2014: 1–262.XING Mengdao, BAO Zheng, LI Zhenfang, et al. Progress of Radar Imaging Algorithm[M]. Beijing: Publishing House of Electronics Industry, 2014: 1–262. [36] LIPPS R and KERR D. Polar reformatting for ISAR imaging[C]. 1998 IEEE Radar Conference, RADARCON'98. Challenges in Radar Systems and Solutions, Dallas, USA 1998: 275–280. doi: 10.1109/NRC.1998.678014. [37] 朱正为, 周建江. 基于联合聚焦/超分辨贝叶斯模型的雷达目标超分辨重建[J]. 系统工程与电子技术, 2011, 33(6): 1261–1264. doi: 10.3969/j.issn.1001-506X.2011.06.13.ZHU Zhengwei and ZHOU Jianjiang. Radar target image super-resolution reconstruction based on bayesian joint focus/super-resolution model[J]. Systems Engineering and Electronics, 2011, 33(6): 1261–1264. doi: 10.3969/j.issn.1001-506X.2011.06.13. [38] 张倩. SAR图像质量评估及其目标识别应用[D]. [博士论文], 中国科学技术大学, 2011.ZHANG Qian. Quality assessment and target recognition in SAR images[D]. [Ph. D. dissertation], University of Science and Technology of China, 2011. [39] 王光新, 王正明, 王卫威. 基于Cauchy稀疏分布的SAR图像超分辨算法[J]. 宇航学报, 2008, 29(1): 299–303. doi: 10.3873/j.issn.1000-1328.2008.01.054.WANG Guangxin, WANG Zhengming, and WANG Weiwei. SAR image super-resolution based on sparse cauchy distribution[J]. Journal of Astronautics, 2008, 29(1): 299–303. doi: 10.3873/j.issn.1000-1328.2008.01.054. [40] 汪雄良, 王正明, 赵侠, 等. 基于lk范数正则化方法的SAR图像超分辨[J]. 宇航学报, 2005, 26(S1): 77–82. doi: 10.3321/j.issn:1000-1328.2005.z1.015.WANG Xiongliang, WANG Zhengming, ZHAO Xia, et al. SAR image super-resolution based on regularization of lk norm[J]. Journal of Astronautics, 2005, 26(S1): 77–82. doi: 10.3321/j.issn:1000-1328.2005.z1.015. [41] 曲长文, 徐舟, 陈天乐. 稀疏条件下基于散射点估计的SAR切片超分辨重建[J]. 电子与信息学报, 2015, 37(1): 71–77. doi: 10.11999/JEIT140121.QU Changwen, XU Zhou, and CHEN Tianle. Super-resolution reconstruction of SAR section based on scattering center estimation and sparse constraint[J]. Journal of Electronics & Information Technology, 2015, 37(1): 71–77. doi: 10.11999/JEIT140121. [42] QI Mingrui, CHEN Chen, and YANG Qingwei. Single ISAR image enhancement based on convolutional neural network[C]. SPIE 12166, Seventh Asia Pacific Conference on Optics Manufacture and 2021 International Forum of Young Scientists on Advanced Optical Manufacturing (APCOM and YSAOM 2021), Hong Kong, China, 2022: 121665R. doi: 10.1117/12.2617683. [43] ADDABBO P, BERNARDI M L, BIONDI F, et al. Super-resolution of synthetic aperture radar complex data by deep-learning[J]. IEEE Access, 2023, 11: 23647–23658. doi: 10.1109/ACCESS.2023.3251565. [44] YANG Ting, SHI Hongyin, LANG Manyun, et al. ISAR imaging enhancement: Exploiting deep convolutional neural network for signal reconstruction[J]. International Journal of Remote Sensing, 2020, 41(24): 9447–9468. doi: 10.1080/01431161.2020.1799449. [45] QIN Dan, LIU Diyang, GAO Xunzhang, et al. ISAR resolution enhancement using residual network[C]. 2019 IEEE 4th International Conference on Signal and Image Processing (ICSIP), Wuxi, China, 2019: 788–792. doi: 10.1109/SIPROCESS.2019.8868757. [46] 易拓源, 户盼鹤, 刘振. 基于改进CycleGAN的ISAR图像超分辨方法[J]. 信号处理, 2023, 39(2): 323–334. doi: 10.16798/j.issn.1003-0530.2023.02.013.YI Tuoyuan, HU Panhe, and LIU Zhen. ISAR images super-resolution method based on ameliorated CycleGAN[J]. Journal of Signal Processing, 2023, 39(2): 323–334. doi: 10.16798/j.issn.1003-0530.2023.02.013. [47] ZHOU Peng, MARTORELLA M, ZHANG Xi, et al. Circular scan ISAR mode super-resolution imaging of ships based on a combination of data extrapolation and compressed sensing[J]. IEEE Sensors Journal, 2019, 19(16): 6883–6894. doi: 10.1109/JSEN.2019.2913903. [48] GIUSTI E, CATALDO D, BACCI A, et al. ISAR image resolution enhancement: Compressive sensing versus state-of-the-art super-resolution techniques[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(4): 1983–1997. doi: 10.1109/taes.2018.2807283. [49] WANG Haobo, LI Kaiming, LU Xiaofei, et al. ISAR resolution enhancement method exploiting generative adversarial network[J]. Remote Sensing, 2022, 14(5): 1291. doi: 10.3390/rs14051291. [50] WANG Yong, JI Bingren, ZHAO Bin, et al. A novel super-resolution ISAR imaging method based on the EM-turbo technique[J]. Remote Sensing Letters, 2022, 13(8): 844–853. doi: 10.1080/2150704x.2022.2091962. [51] LEE S J and LEE S G. Super-resolution procedure for target responses in KOMPSAT-5 images[J]. Sensors, 2022, 22(19): 7189. doi: 10.3390/s22197189. [52] LIN Liupeng, SHEN Huanfeng, LI Jie, et al. FDFNet: A fusion network for generating high-resolution fully polSAR images[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4500905. doi: 10.1109/lgrs.2021.3127958. [53] LIN Liupeng, LI Jie, SHEN Huanfeng, et al. Low-resolution fully polarimetric SAR and high-resolution single-polarization SAR image fusion network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5216117. doi: 10.1109/TGRS.2021.3121166. [54] SUWA K and IWAMOTO M. A two-dimensional bandwidth extrapolation technique for polarimetric synthetic aperture radar images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(1): 45–54. doi: 10.1109/TGRS.2006.885406. [55] WEI Yangkai, LI Yinchuan, DING Zegang, et al. SAR parametric super-resolution image reconstruction methods based on ADMM and deep neural network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(12): 10197–10212. doi: 10.1109/TGRS.2021.3052793. [56] 李春茂, 吴顺君, 张林让. 基于边缘保持的自适应SAR图像超分辨重建算法[J]. 系统仿真学报, 2014, 26(2): 254–259. doi: 10.16182/j.cnki.joss.2014.02.020.LI Chunmao, WU Shunjun, and ZHANG Linrang. Adaptive edge-preserving based reconstruction algorithm for SAR images[J]. Journal of System Simulation, 2014, 26(2): 254–259. doi: 10.16182/j.cnki.joss.2014.02.020. [57] 李萌, 刘畅. 基于特征复用的膨胀-残差网络的SAR图像超分辨重建[J]. 雷达学报, 2020, 9(2): 363–372. doi: 10.12000/JR19110.LI Meng and LIU Chang. Super-resolution reconstruction of SAR images based on feature reuse dilated-residual convolutional neural networks[J]. Journal of Radars, 2020, 9(2): 363–372. doi: 10.12000/JR19110. [58] LI Yanshan, XU Fan, ZHOU Li, et al. Optical-guided residual learning network for synthetic aperture radar image super-resolution[J]. Journal of Applied Remote Sensing, 2022, 16(3): 036503. doi: 10.1117/1.Jrs.16.036503. [59] KANAKARAJ S, NAIR M S, and KALADY S. SAR image super resolution using importance sampling unscented kalman filter[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(2): 562–571. doi: 10.1109/jstars.2017.2779795. [60] WANG Zhou, BOVIK A C, SHEIKH H R, et al. Image quality assessment: From error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600–612. doi: 10.1109/TIP.2003.819861. [61] KANAKARAJ S, NAIR M S, and KALADY S. Adaptive importance sampling unscented kalman filter with kernel regression for SAR image super-resolution[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4004305. doi: 10.1109/lgrs.2020.3031600. [62] KANAKARAJ S, NAIR M S, and KALADY S. Adaptive importance sampling unscented kalman filter based SAR image super resolution[J]. Computers & Geosciences, 2019, 133: 104310. doi: 10.1016/j.cageo.2019.104310. [63] LIN Zhang, ZHANG Lei, MOU Xuanqin, et al. FSIM: A feature similarity index for image quality assessment[J]. IEEE Transactions on Image Processing, 2011, 20(8): 2378–2386. doi: 10.1109/TIP.2011.2109730. [64] SATTAR F, FLOREBY L, SALOMONSSON G, et al. Image enhancement based on a nonlinear multiscale method[J]. IEEE Transactions on Image Processing, 1997, 6(6): 888–895. doi: 10.1109/83.585239. [65] LEE J S, POTTIER E, 洪文, 李洋, 尹嫱, 等译. 极化雷达成像基础与应用[M]. 北京: 电子工业出版社, 2013: 1–312.LEE J S POTTIER E, HONG Wen, LI Yang, YIN Qiang, et al. translation. Polarimetric Radar Imaging From Basics to Applications[M]. Beijing: Publishing House of Electronics Industry, 2013: 1–312. [66] 吴永辉, 郁文贤, 计科峰, 等. 基于修正H-α方法的双极化SAR散射机理识别性能分析[J]. 电子学报, 2010, 38(3): 572–579.WU Yonghui, YU Wenxian, JI Kefeng, et al. Performance analysis of scattering mechanism identification of dual-polarization SAR using a modified H-α decomposition[J]. Acta Electronica Sinica, 2010, 38(3): 572–579. [67] 孙即祥. 现代模式识别[M]. 北京: 高等教育出版社, 2008: 186, 187.SUN Jixiang. Modern Pattern Recognition[M]. Beijing: Higher Education Press, 2008: 186, 187. [68] LIU Lu, HUANG Wei, and WANG Cheng. Texture image prior for SAR image super resolution based on total variation regularization using split Bregman iteration[J]. International Journal of Remote Sensing, 2017, 38(20): 5673–5687. doi: 10.1080/01431161.2017.1346325. [69] GOLDSTEIN T and OSHER S. The split bregman method for L1-regularized problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(2): 323–343. doi: 10.1137/080725891. [70] DONOHO D L. Sparse components of images and optimal atomic decompositions[J]. Constructive Approximation, 2001, 17(3): 353–382. doi: 10.1007/s003650010032. [71] DONG Chao, LOY C C, HE Kaiming, et al. Image super-resolution using deep convolutional networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(2): 295–307. doi: 10.1109/TPAMI.2015.2439281. [72] 陈思伟, 李永祯, 王雪松, 等. 极化SAR目标散射旋转域解译理论与应用[J]. 雷达学报, 2017, 6(5): 442–455. doi: 10.12000/JR17033.CHEN Siwei, LI Yongzhen, WANG Xuesong, et al. Polarimetric SAR target scattering interpretation in rotation domain: Theory and application[J]. Journal of Radars, 2017, 6(5): 442–455. doi: 10.12000/JR17033. [73] CEN Xi, SONG Xuan, LI Yachao, et al. A deep learning-based super-resolution model for bistatic SAR image[C]. 2021 International Conference on Electronics, Circuits and Information Engineering (ECIE), Zhengzhou, China, 2021: 228–233. doi: 10.1109/ECIE52353.2021.00056. [74] AO Dongyang, DUMITRU C O, SCHWARZ G, et al. Dialectical GAN for SAR image translation: From Sentinel-1 to TerraSAR-X[J]. Remote Sensing, 2018, 10(10): 1597. doi: 10.3390/rs10101597. [75] QIN Dan and GAO Xunzhang. Enhancing ISAR resolution by a generative adversarial network[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(1): 127–131. doi: 10.1109/LGRS.2020.2965743. [76] LIN Liupeng, LI Jie, YUAN Qiangqiang, et al. Polarimetric SAR image super-resolution via deep convolutional neural network[C]. 2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 2019: 3205–3208. doi: 10.1109/IGARSS.2019.8898160. [77] 林镠鹏, 李杰, 沈焕锋. 基于多尺度注意力机制的PolSAR深度学习超分辨率模型[J]. 遥感学报, 预初版. doi: 10.11834/jrs.20233002.LIN Liupeng, LI Jie, and SHEN Huanfeng. PolSAR image deep learning super-resolution model based on multi-scale attention mechanism[J]. National Remote Sensing Bulletin, in press. doi: 10.11834/jrs.20233002. [78] CHEN Yinbo, LIU Sifei, and WANG Xiaolong. Learning continuous image representation with local implicit image function[C]. 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, USA, 2021: 8624–8634. doi: 10.1109/CVPR46437.2021.00852. [79] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, USA, 2016: 770–778. doi: 10.1109/CVPR.2016.90. [80] ZHU Hongyu, XIE Chao, FEI Yeqi, et al. Attention mechanisms in CNN-based single image super-resolution: A brief review and a new perspective[J]. Electronics, 2021, 10(10): 1187. doi: 10.3390/electronics10101187. [81] GOODFELLOW I J, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial nets[C]. 27th International Conference on Neural Information Processing Systems, Montreal, Canada, 2014: 2672–2680. [82] LEDIG C, THEIS L, HUSZÁR F, et al. Photo-realistic single image super-resolution using a generative adversarial network[C]. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, USA, 2017: 105–114. doi: 10.1109/CVPR.2017.19. [83] WANG Xintao, YU Ke, WU Shixiang, et al. ESRGAN: Enhanced super-resolution generative adversarial networks[C]. Computer Vision – ECCV 2018 Workshops, Munich, Germany, 2019: 63–79. doi: 10.1007/978-3-030-11021-5_5. [84] ZHANG Lamei, ZOU Bin, HAO Huijun, et al. A novel super-resolution method of PolSAR images based on target decomposition and polarimetric spatial correlation[J]. International Journal of Remote Sensing, 2011, 32(17): 4893–4913. doi: 10.1080/01431161.2010.492251. [85] PASTINA D, LOMBARDO P, FARINA A, et al. Super-resolution of polarimetric SAR images of a ship[C]. IEEE 2001 International Geoscience and Remote Sensing Symposium, Sydney, Australia, 2001: 2343–2345. doi: 10.1109/IGARSS.2001.977996. [86] NOVAK L M and BURL M C. Optimal speckle reduction in polarimetric SAR imagery[C]. Twenty-Second Asilomar Conference on Signals, Systems and Computers, Pacific Grove, USA, 1988: 781–793. doi: 10.1109/ACSSC.1988.754657. [87] CHEN Jiong and YANG Jian. Super-resolution of polarimetric SAR images for ship detection[C]. 2007 International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications, Hangzhou, China, 2007: 1499–1502. doi: 10.1109/MAPE.2007.4393565. [88] STARK H and OSKOUI P. High-resolution image recovery from image-plane arrays, using convex projections[J]. Journal of the Optical Society of America A, 1989, 6(11): 1715–1726. doi: 10.1364/josaa.6.001715. [89] CAO Yue, XU Jiarui, LIN S, et al. GCNet: Non-local networks meet squeeze-excitation networks and beyond[C]. 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Korea (South), 2019: 1971–1980. doi: 10.1109/ICCVW.2019.00246. [90] VAN DER MAATEN L and HINTON G. Visualizing data using t-SNE[J]. Journal of Machine Learning Research, 2008, 9(86): 2579–2605. -





 下载:
下载:








 下载:
下载:
