A Privacy-preserving Data Alignment Framework for Vertical Federated Learning
-
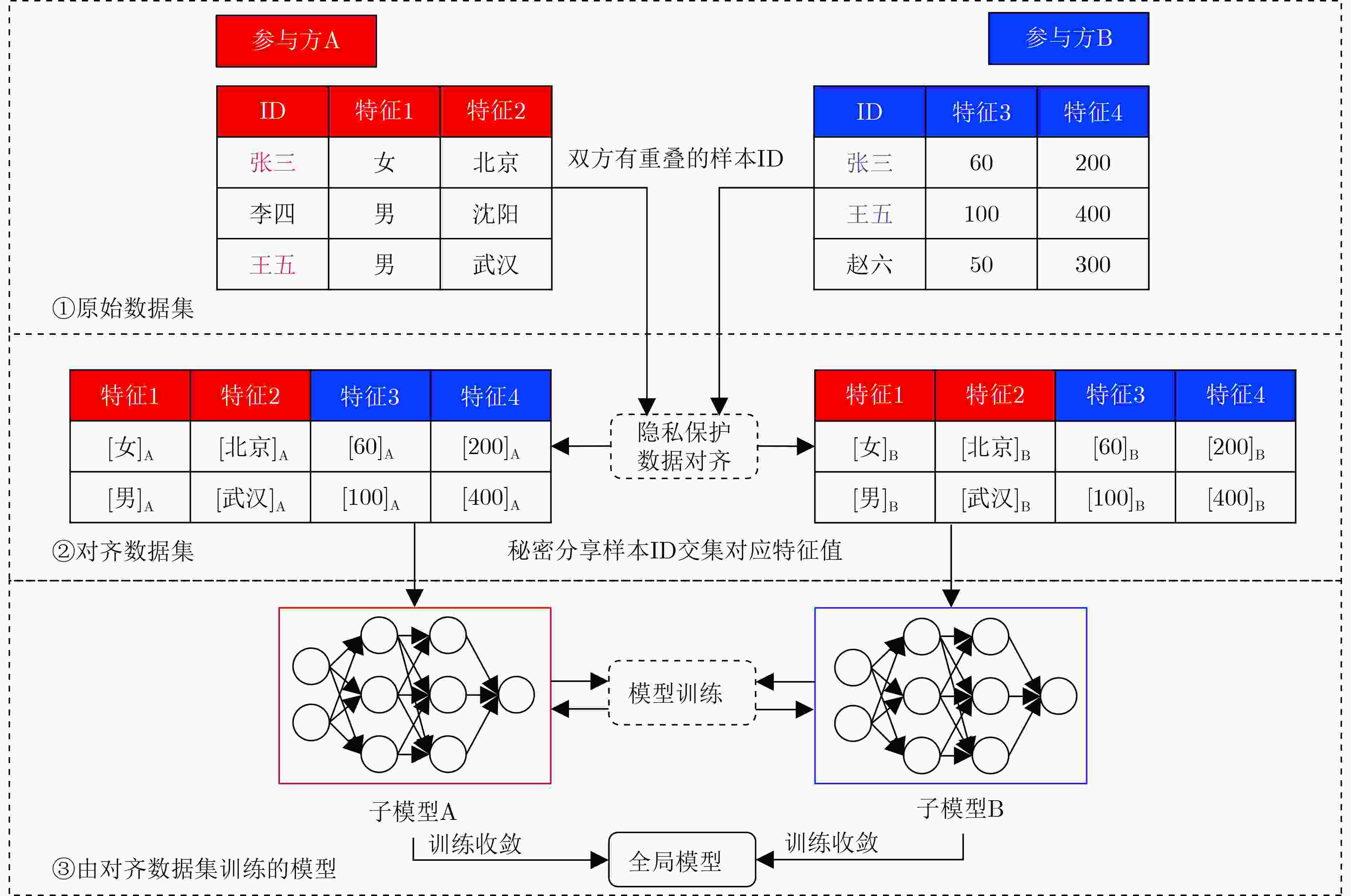
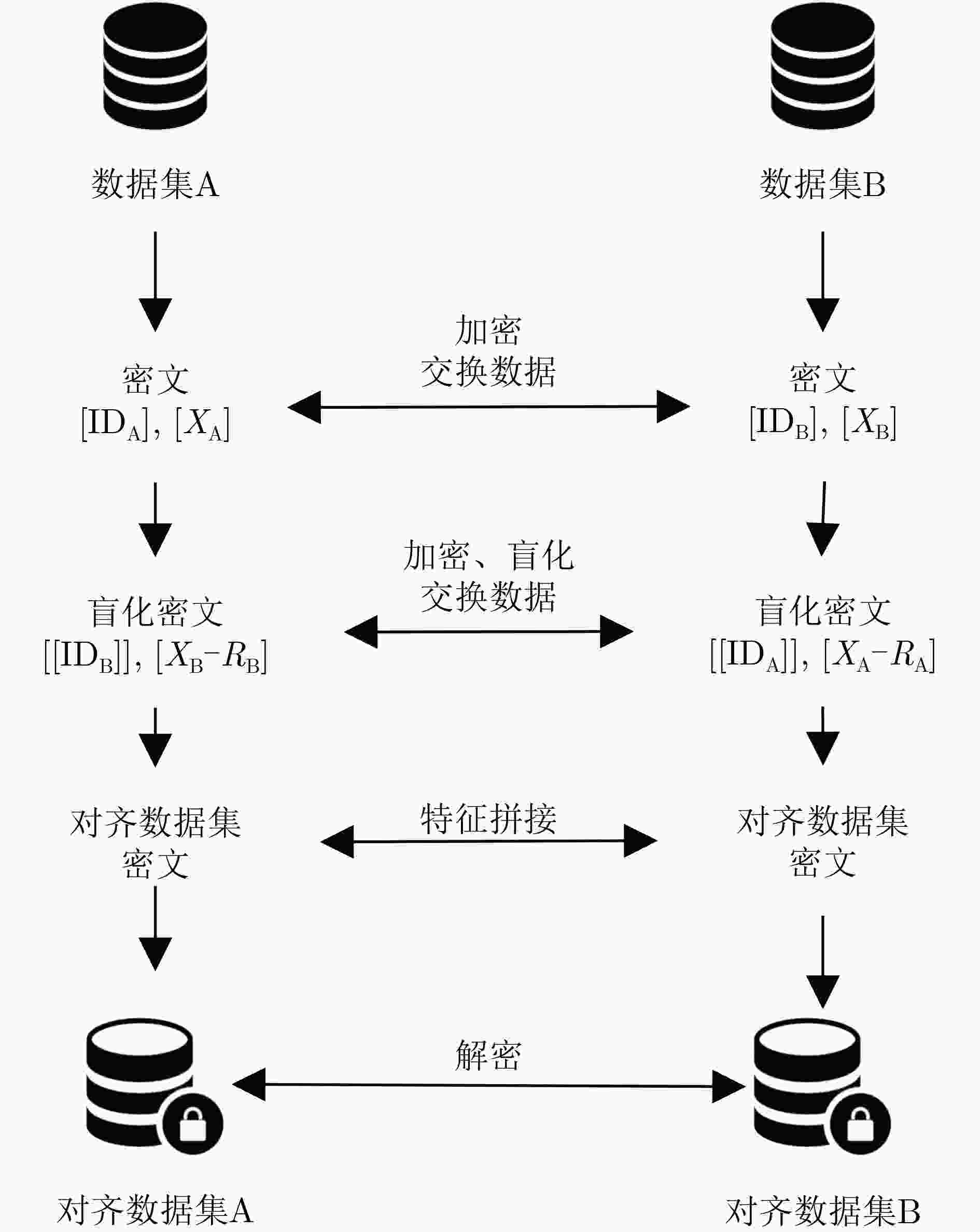
摘要: 纵向联邦学习中,各个客户端持有的数据集中包含有重叠的样本ID和不同维度的样本特征,需要进行数据对齐以适应模型训练。现有数据对齐技术一般将各方样本ID交集作为公开信息,如何在不泄露样本ID交集的前提下实现数据对齐成为亟需解决的问题。基于可交换加密和同态加密技术,该文构造了隐私保护的数据对齐框架ALIGN,包括数据加密、密文盲化、密文求交和特征拼接等步骤,使得相同的原始样本ID经过双重可交换加密可变换为相同的密文,并且对样本特征经同态加密后又进行了盲化处理。ALIGN框架能够对参与方样本ID的密文求交,将交集内样本ID对应的全部特征数据进行拼接并以秘密分享形式分配给参与方。相比现有数据对齐技术,该框架不仅能够保护样本ID交集的隐私性,同时能安全地删除样本ID交集外的样本信息。对ALIGN框架的安全性证明表明,除数据规模外,各客户端不能通过数据对齐获得关于对方数据的任何信息,保证了隐私保护策略的有效性。与现有工作相比,每增加10%的冗余数据,ALIGN框架利用所得数据对齐结果可将模型训练时间缩短约1.3秒,将模型训练准确度稳定在85%以上。仿真实验结果表明,通过ALIGN框架进行纵向联邦学习数据对齐,有利于提升后续模型训练的效率和模型准确度。Abstract: In vertical federated learning, the datasets of the clients have overlapping sample IDs and features of different dimensions, thus the data alignment is necessary for model training. As the intersection of the sample IDs is public in current data alignment technologies, how to align the data without any leakage of the intersection becomes a key issue. The proposed private-preserving data ALIGNment framework (ALIGN) is based on interchangeable encryption and homomorphic encryption technologies, mainly including data encryption, ciphertext blinding, private intersecting, and feature splicing. The sample IDs are encrypted twice based on an interchangeable encryption algorithm, where the same ciphertexts correspond to the same plaintexts, and the sample features are encrypted and then randomly blinded based on a homomorphic encryption algorithm. The intersection of the encrypted sample IDs is obtained, and the corresponding features are then spliced and secretly shared with the participants. Compared to the existing technologies, the privacy of the ID intersection is protected, and the samples corresponding to the IDs outside intersection can be removed safely in our framework. The security proof shows that each participant cannot obtain any knowledge of each other except for the data size, which guarantees the effectiveness of the private-preserving strategies. The simulation experiments demonstrate that the runtime is shortened about 1.3 seconds and the model accuracy keeps higher than 85% with every 10% reduction of the redundant data. The simulation experimental results show that using the ALIGN framework for vertical federated learning data alignment is beneficial for improving the efficiency and accuracy of subsequent model training.
-
表 1 本文符号汇总
符号 含义 $ {P_{\rm A}},{P_{\rm B}} $ 纵向联邦学习参与方 $ {n_{\rm A}} $ 参与方$ {P_{\rm A}} $的原始数据集包含的样本数量 $ {n_{\rm B}} $ 参与方$ {P_{\rm B}} $的原始数据集包含的样本数量 $ [n](n \in \mathbb{Z}) $ 集合$ \{ 1,2, \cdots ,n\} $ m 参与方$ {P_{\rm A}} $和$ {P_{\rm B}} $的样本ID交集大小 $\left\langle {\cdot } \right\rangle_{\rm A} $ 参与方$ {P_{\rm A}} $的秘密分享份额 $\left\langle {\cdot } \right\rangle_{\rm B} $ 参与方$ {P_{\rm B}} $的秘密分享份额 $ {[x]_k} $ 以密钥k加密明文x得到的密文 1 ALIGN框架任意参与方数据对齐算法
输入:数据集$ ({\text{ID}},X) $,可交换加密算法$ E( \cdot ) $及密钥k,同态加密算法$ H( \cdot ) $及公私钥对$ ({\text{pk,sk}}) $ 输出:数据对齐结果$ {\text{res}} $ Begin # ID加密和特征加密 $ P\;{\text{sends}}\;{\text{pk}}\;{\text{to}}\;P'\;{\text{and receives}}\;{\text{pk}}'\;{\text{from}}\;P' $ $ ({\text{ID}},X) $$ \leftarrow $$ ({E_k}({\text{ID}}),{H_{{\text{pk}}}}(X)) $ $ P\;{\text{sends}}\;({\text{ID}},X)\;{\text{to}}\;P'\;{\text{and receives}}\;({\text{I}}{{\text{D}}_1},{X_1})\;{\text{from}}\;P' $ # ID重加密和特征密文盲化 $ {\text{I}}{{\text{D}}_1} \leftarrow {E_k}({\text{I}}{{\text{D}}_1}) $ $ R = [] $ for i in $ {\text{range(|}}{X_1}{\text{|)}} $ $ {r_i} \leftarrow {\text{RandomGenerator}}(\cdot) $ # RandomGenerator(·)表示随机数生成器 $ R.{\text{append}}({r_i}) $ $ {X_1}[i] \leftarrow {X_1}[i] - {H_{{\text{pk}}}}({r_i}) $; end for $ {\text{dict}} \leftarrow \{ {\text{I}}{{\text{D}}_1}[i]:R[i] $for i in $ {\text{range(|I}}{{\text{D}}_{\text{1}}}{\text{|)\} }} $ $ \pi \leftarrow {\text{PermutationGenerator}}(\cdot) $ #PermutationGenerator(·)表示随机置换函数生成器,用于随机置换列表中元素的顺序 $ ({\text{I}}{{\text{D}}_1},{X_1}) \leftarrow \pi ({\text{I}}{{\text{D}}_1}),\pi ({X_1}) $ $ P\;{\text{sends}}\;({\text{I}}{{\text{D}}_1},{X_1})\;{\text{to}}\;P'\;{\text{and receives}}\;({\text{I}}{{\text{D}}_2},{X_2})\;{\text{from}}\;P' $ # ID密文求交和特征拼接 $ {\text{re}}{{\text{s}}_{\text{1}}}{\text{, re}}{{\text{s}}_2} = [],[] $; for i in $ {\text{range(|I}}{{\text{D}}_2}{\text{|)}} $ for $ {\text{id}} $ in $ {\text{I}}{{\text{D}}_1} $: if $ {\text{I}}{{\text{D}}_2}[i] = = {\text{id}} $: $ {\text{re}}{{\text{s}}_{\text{1}}}{\text{.append}}({X_2}[i]) $ $ {\text{re}}{{\text{s}}_2}{\text{.append}}({\text{dict[id}}]) $ end if end for end for # 解密生成秘密份额 $ {\text{result}} \leftarrow ({H^{{{ - 1}}}}_{{\text{sk}}}({\text{re}}{{\text{s}}_{\text{1}}}{\text{),re}}{{\text{s}}_{\text{2}}}) $ End 表 2 ALIGN框架运行时间
ID交集大小 运行时间(s) 50 2.30 100 4.49 150 6.69 200 8.82 250 11.07 -
[1] YANG Qiang, LIU Yang, CHEN Tianjian, et al. Federated machine learning: Concept and applications[J]. ACM Transactions on Intelligent Systems and Technology, 2019, 10(2): 12. doi: 10.1145/3298981. [2] 刘艺璇, 陈红, 刘宇涵, 等. 联邦学习中的隐私保护技术[J]. 软件学报, 2022, 33(3): 1057–1092. doi: 10.13328/j.cnki.jos.006446.LIU Yixuan, CHEN Hong, LIU Yuhan, et al. Privacy-preserving techniques in federated learning[J]. Journal of Software, 2022, 33(3): 1057–1092. doi: 10.13328/j.cnki.jos.006446. [3] LI Tian, SAHU A K, TALWALKAR A, et al. Federated learning: Challenges, methods, and future directions[J]. IEEE Signal Processing Magazine, 2020, 37(3): 50–60. doi: 10.1109/MSP.2020.2975749. [4] KAIROUZ P, MCMAHAN H B, AVENT B, et al. Advances and open problems in federated learning[J]. Foundations and Trends® in Machine Learning, 2021, 14(1/2): 1–210. doi: 10.1561/2200000083. [5] BELTRÁN E T M, PÉREZ M Q, SÁNCHEZ P M S, et al. Decentralized federated learning: Fundamentals, state of the art, frameworks, trends, and challenges[J]. IEEE Communications Surveys & Tutorials, 2023, 25(4): 2983–3013. doi: 10.1109/COMST.2023.3315746. [6] 陈晋音, 李荣昌, 黄国瀚, 等. 纵向联邦学习方法及其隐私和安全综述[J]. 网络与信息安全学报, 2023, 9(2): 1–20. doi: 10.11959/j.issn.2096−109x.2023017.CHEN Jinyin, LI Rongchang, HUANG Guohan, et al. Survey on vertical federated learning: Algorithm, privacy and security[J]. Chinese Journal of Network and Information Security, 2023, 9(2): 1–20. doi: 10.11959/j.issn.2096−109x.2023017. [7] LIU Yang, KANG Yan, ZOU Tianyuan, et al. Vertical federated learning: Concepts, advances and challenges[J]. arXiv: 2211.12814, 2023. [8] ROMANINI D, HALL A J, PAPADOPOULOS P, et al. Pyvertical: A vertical federated learning framework for multi-headed splitNN[J]. arXiv: 2104.00489, 2021. [9] LI Qun, THAPA C, ONG L, et al. Vertical federated learning: Taxonomies, threats, and prospects[J]. arXiv: 2302.01550, 2023. [10] WEI Kang, LI Jun, MA Chuan, et al. Vertical federated learning: Challenges, methodologies and experiments[J]. arXiv: 2202.04309, 2022. [11] FREEDMAN M J, NISSIM K, and PINKAS B. Efficient private matching and set intersection[C]. International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2004: 1–19. doi: 10.1007/978-3-540-24676-3_1. [12] PINKAS B, SCHNEIDER T, TKACHENKO O, et al. Efficient circuit-based PSI with linear communication[C]. The 38th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Darmstadt, Germany, 2019: 122–153. doi: 10.1007/978-3-030-17659-4_5. [13] PINKAS B, SCHNEIDER T, and ZOHNER M. Scalable private set intersection based on OT extension[J]. ACM Transactions on Privacy and Security, 2018, 21(2): 7. doi: 10.1145/3154794. [14] PINKAS B, ROSULEK M, TRIEU N, et al. PSI from PaXoS: Fast, malicious private set intersection[C]. The 39th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 2020: 739–767. doi: 10.1007/978-3-030-45724-2_25. [15] LU Linpeng and DING Ning. Multi-party private set intersection in vertical federated learning[C]. The 2020 IEEE 19th International Conference on Trust, Security and Privacy in Computing and Communications, Guangzhou, China, 2020: 707–714. doi: 10.1109/TrustCom50675.2020.00098. [16] HARDY S, HENECKA W, IVEY-LAW H, et al. Private federated learning on vertically partitioned data via entity resolution and additively homomorphic encryption[J]. arXiv: 1711.10677, 2017. [17] LIU Yang, ZHANG Xiong, and WAN Libin. Asymmetrical vertical federated learning[J]. arXiv: 2004.07427, 2020. [18] RINDAL P and SCHOPPMANN P. VOLE-PSI: Fast OPRF and circuit-psi from vector-ole[C]. The 40th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 2021: 901–930. doi: 10.1007/978-3-030-77886-6_31. [19] CHANDRAN N, GUPTA D, and SHAH A. Circuit-PSI with linear complexity via relaxed batch OPPRF[J]. Proceedings on Privacy Enhancing Technologies, 2022, 2022(1): 353–372. doi: 10.2478/POPETS-2022-0018. [20] RAGHURAMAN S and RINDAL P. Blazing fast PSI from improved OKVS and subfield vole[C]. 2022 ACM SIGSAC Conference on Computer and Communications Security, Los Angeles, USA, 2022: 2505–2517. doi: 10.1145/3548606.3560658. [21] LIU Yang, ZHANG Bingsheng, MA Yuxiang, et al. iPrivJoin: An ID-private data join framework for privacy-preserving machine learning[J]. IEEE Transactions on Information Forensics and Security, 2023, 18: 4300–4312. doi: 10.1109/TIFS.2023.3288455. [22] AGRAWAL R, EVFIMIEVSKI A, and SRIKANT R. Information sharing across private databases[C]. 2003 ACM SIGMOD International Conference on Management of Data, San Diego, USA, 2003: 86–97. doi: 10.1145/872757.872771. [23] AHIRWAL R R and AHKE M. Elliptic curve diffie-hellman key exchange algorithm for securing hypertext information on wide area network[J]. International Journal of Computer Science and Information Technologies, 2013, 4(2): 363–368. [24] PAILLIER P. Public-key cryptosystems based on composite degree residuosity classes[C]. International Conference on the Theory and Application of Cryptographic Techniques, Prague, Czech Republic, 1999: 223–238. doi: 10.1007/3-540-48910-X_16. [25] SHAMIR A. How to share a secret[J]. Communications of the ACM, 1979, 22(11): 612–613. doi: 10.1145/359168.359176. [26] BONAWITZ K A, EICHNER H, GRIESKAMP W, et al. Towards federated learning at scale: System design[C]. Machine Learning and Systems 2019, Stanford, USA, 2019. [27] SHAMIR A, RIVEST R L, and ADLEMAN L M. Mental poker[M]. KLARNER D A. The Mathematical Gardner. Boston: Springer, 1981: 37–43. doi: 10.1007/978-1-4684-6686-7_5. [28] POHLIG S and HELLMAN M. An improved algorithm for computing logarithms overGF(p)and its cryptographic significance (Corresp. )[J]. IEEE Transactions on information Theory, 1978, 24(1): 106–110. doi: 10.1109/TIT.1978.1055817. [29] DIFFIE W and HELLMAN M. New directions in cryptography[J]. IEEE Transactions on Information Theory, 1976, 22(6): 644–654. doi: 10.1109/TIT.1976.1055638. [30] LECUN Y. The MNIST database of handwritten digits[EB/OL]. http://yann.lecun.com/exdb/mnist/, 1998. [31] BARNES R. CrypTen[EB/OL].https://github.com/facebookresearch/CrypTen, 2020. -





 下载:
下载:



 下载:
下载:
