分组密码算法uBlock积分攻击的改进

王晨; 崔佳敏; 李木舟; 王美琴

doi:10.11999/JEIT231231

分组密码算法uBlock积分攻击的改进

doi: 10.11999/JEIT231231

王晨^{1, 3},
崔佳敏^{1, 3},
李木舟^2, ,,
王美琴^{1, 2, 3}

1.
山东大学网络空间安全学院(研究院) 青岛 266237
2.
泉城实验室济南 250100
3.
山东大学密码技术与信息安全教育部重点实验室济南 250100

基金项目: 国家重点研发计划(2018YFA0704702)，国家自然科学基金(62032014)，山东省自然科学基金重大基础研究项目(ZR202010220025)，青岛创新项目(QDBSH20230101008)

详细信息

作者简介:
王晨：女，博士生，研究方向为分组密码算法的安全性分析

崔佳敏：女，博士生，研究方向为对称密码算法的安全性分析

李木舟：男，博士，研究方向为对称密码算法的分析与设计

王美琴：女，教授，研究方向为对称密码算法的分析与设计

通讯作者:
李木舟　muzhouli@mail.sdu.edu.cn

中图分类号: TN918.4; TP309.7
计量
- 文章访问数: 294
- HTML全文浏览量: 160
- PDF下载量: 65
- 被引次数: 0
出版历程
- 收稿日期: 2023-11-07
- 修回日期: 2024-01-29
- 网络出版日期: 2024-03-09
- 刊出日期: 2024-05-30

Improved Integral Cryptanalysis on Block Cipher uBlock

WANG Chen^{1, 3},
CUI Jiamin^{1, 3},
LI Muzhou^{2
, ,},
WANG Meiqin^{1, 2, 3}

1.
School of Cyber Science and Technology, Shandong University, Qingdao 266237, China
2.
Quan Cheng Shandong Laboratory, Jinan 250100, China
3.
Key Laboratory of Cryptologic Technology and Information Security, Ministry of Education, Shandong University, Jinan 250100, China

Funds: The National Key Research and Development Program of China (2018YFA0704702), The National Natural Science Foundation of China (62032014), The Major Basic Research Project of Natural Science Foundation of Shandong Province, China (ZR202010220025), Qingdao Innovation Project (QDBSH20230101008)

摘要

摘要: 积分攻击是由Daemen等人(doi: 10.1007/BFb0052343)于1997年提出的一种密码分析方法，是继差分分析和线性分析之后最有效的密码分析方法之一。作为2018年全国密码算法设计竞赛分组算法的获胜算法，uBlock抵抗积分攻击的能力受到较多的关注。为了重新评估uBlock家族密码算法抵抗积分攻击的安全性，该文利用单项式传播技术，结合混合整数线性规划(MILP)工具搜索积分区分器，并利用部分和技术进行密钥恢复攻击。对于uBlock-128/128和uBlock-128/256，基于搜索到的9轮积分区分器分别进行了首个11轮和12轮攻击，数据复杂度为$ {2}^{127} $选择明文，时间复杂度分别为$ {2}^{127.06} $和$ {2}^{224} $次加密，存储复杂度分别为$ {2}^{44.58} $和 $ {2}^{138} $字节；对于uBlock-256/256，基于搜索到的10轮积分区分器进行了首个12轮攻击，数据复杂度为$ {2}^{253} $选择明文，时间复杂度为$ {2}^{253.06} $次加密，存储复杂度为$ {2}^{44.46} $字节。与之前uBlock的最优积分攻击结果相比，uBlock-128/128和uBlock-256/256的攻击轮数分别提高2轮，uBlock-128/256的攻击轮数提高3轮。本文的攻击说明，uBlock针对积分攻击依然有足够的安全冗余。
- 密码分析 /
- 分组密码 /
- uBlock /
- 积分攻击
Abstract: Integral attack is one of the most powerful cryptanalytic methods after differential and linear cryptanalysis, which was presented by Daemen et al. in 1997 (doi: 10.1007/BFb0052343). As the winning block cipher of China’s National Cipher Designing Competition in 2018, the security strength of uBlock against integral attack has received much attention. To better understand the integral property, this paper constructs the Mixed Integer Linear Programming (MILP) models for monomial prediction to search for the integral distinguishers and uses the partial sum techniques to perform key-recovery attacks. For uBlock-128/128 and uBlock-128/256, this paper gives the first 11 and 12-round attacks based on a 9-round integral distinguisher, respectively. The data complexity is $ {2}^{127} $ chosen plaintexts. The time complexities are $ {2}^{127.06} $ and $ {2}^{224} $ times encryptions, respectively. The memory complexities are $ {2}^{44.58} $ and $ {2}^{138} $ Byte, respectively. For uBlock-256/256, this paper gives the first 12-round attack based on a 10-round integral distinguisher. The data complexity is $ {2}^{253} $ chosen plaintexts. The time and memory complexities are $ {2}^{253.06} $ times encryptions and $ {2}^{44.46} $ Byte, respectively. The number of attacked rounds for uBlock-128/128 and uBlock-256/256 are improved by two rounds compared with the previous best ones. Besides, the number of attacked rounds for uBlock-128/256 is improved by three rounds. The results show that uBlock has enough security margin against integral attack.
- Cryptanalysis /
- Block cipher /
- uBlock /
- Integral attack

HTML全文

图 1 uBlock轮函数

下载: 全尺寸图片幻灯片

图 2 uBlock-128/128算法11轮密钥恢复

下载: 全尺寸图片幻灯片

表 1 uBlock积分分析结果比较

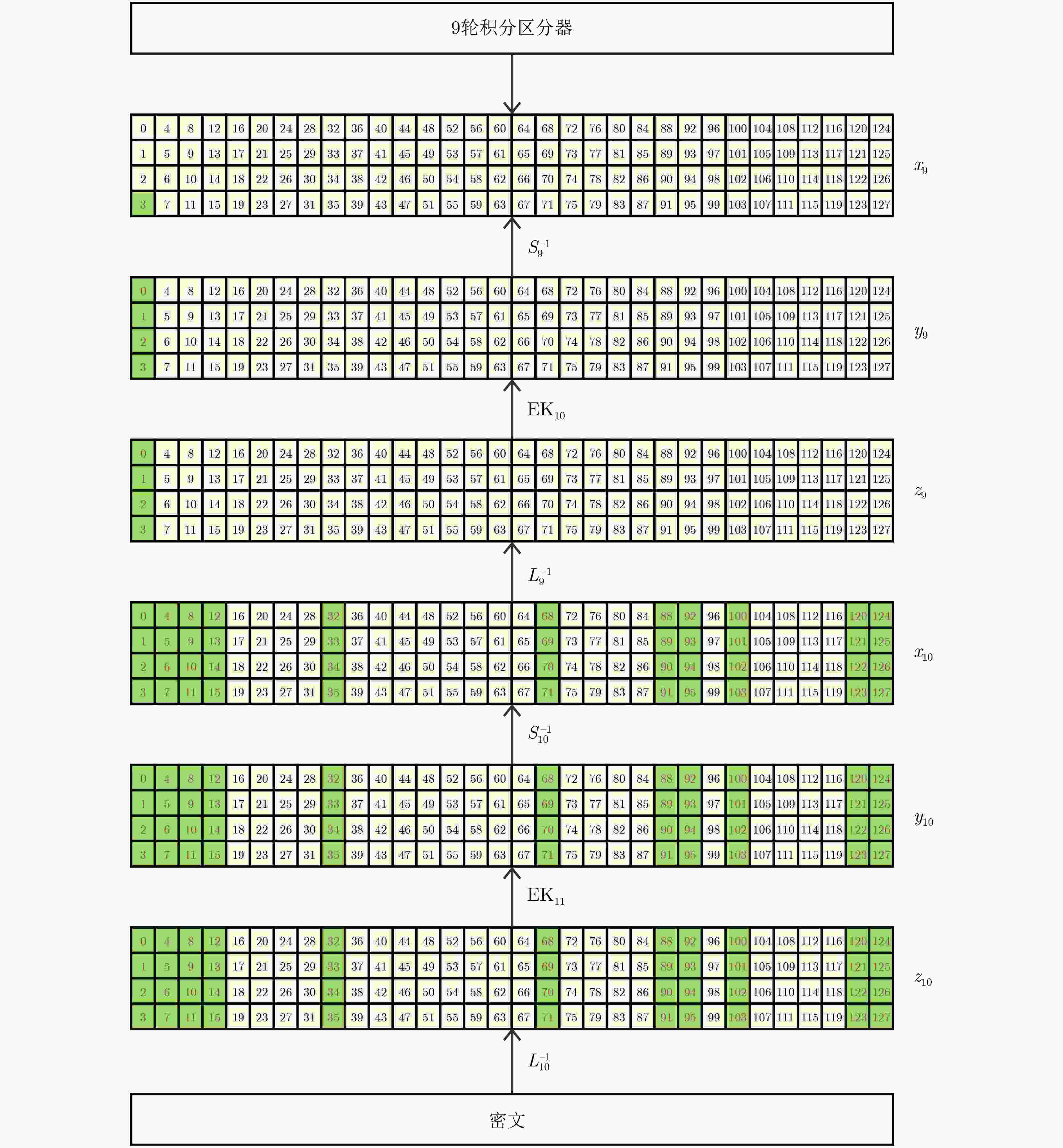
算法版本	攻击轮数	积分区分器	数据复杂度	时间复杂度	存储复杂度	参考文献
uBlock-128/128	9	$ \left({\mathcal{C}}^{4},{\mathcal{A}}^{124}\right)\stackrel{8\mathrm{R}}{\to }{\left({\mathcal{B}}^{1},{\mathcal{U}}^{2},{\mathcal{B}}^{1}\right)}^{32} $	$ {2}^{124} $	$ {2}^{125.47} $	$ {2}^{6.25} $	[24]
	10	$ \left({\mathcal{C}}^{4},{\mathcal{A}}^{124}\right)\stackrel{8\mathrm{R}}{\to }{\left({\mathcal{B}}^{1},{\mathcal{U}}^{1},{\mathcal{B}}^{2}\right)}^{32} $	$ {2}^{124} $	$ {2}^{124.07} $	$ {2}^{44.32} $	本文
	11	$ \left({\mathcal{A}}^{1},{\mathcal{C}}^{1},{\mathcal{A}}^{126}\right)\stackrel{9\mathrm{R}}{\to }{\left({\mathcal{U}}^{3},{\mathcal{B}}^{1}\right)}^{32} $	$ {2}^{127} $	$ {2}^{127.06} $	$ {2}^{44.58} $	本文
uBlock-128/256	9	$ \left({\mathcal{C}}^{4},{\mathcal{A}}^{124}\right)\stackrel{8\mathrm{R}}{\to }{\left({\mathcal{B}}^{1},{\mathcal{U}}^{2},{\mathcal{B}}^{1}\right)}^{32} $	$ {2}^{124} $	$ {2}^{125.47} $	$ {2}^{6.25} $	[24]
	11	$ \left({\mathcal{C}}^{4},{\mathcal{A}}^{124}\right)\stackrel{8\mathrm{R}}{\to }{\left({\mathcal{B}}^{1},{\mathcal{U}}^{1},{\mathcal{B}}^{2}\right)}^{32} $	$ {2}^{124} $	$ {2}^{179.19} $	$ {2}^{137.81} $	本文
	11	$ \left({\mathcal{A}}^{1},{\mathcal{C}}^{1},{\mathcal{A}}^{126}\right)\stackrel{9\mathrm{R}}{\to }{\left({\mathcal{U}}^{3},{\mathcal{B}}^{1}\right)}^{32} $	$ {2}^{127} $	$ {2}^{224} $	$ {2}^{46} $	本文
	12	$ \left({\mathcal{A}}^{1},{\mathcal{C}}^{1},{\mathcal{A}}^{126}\right)\stackrel{9\mathrm{R}}{\to }{\left({\mathcal{U}}^{3},{\mathcal{B}}^{1}\right)}^{32} $	$ {2}^{127} $	$ {2}^{224} $	$ {2}^{138} $	本文
uBlock-256/256	10	$ \left({\mathrm{C}}^{8},{\mathcal{A}}^{248}\right)\stackrel{9\mathrm{R}}{\to }{\left({\mathcal{B}}^{1},{\mathcal{U}}^{2},{\mathcal{B}}^{1}\right)}^{64} $	$ {2}^{248} $	$ {2}^{249.38} $	$ {2}^{7.25} $	[24]
	11	$ \left({\mathcal{C}}^{8},{\mathcal{A}}^{248}\right)\stackrel{9\mathrm{R}}{\to }{\left({\mathcal{B}}^{1},{\mathcal{U}}^{2},{\mathcal{B}}^{1}\right)}^{64} $	$ {2}^{248} $	$ {2}^{248.06} $	$ {2}^{44.32} $	本文
	12	$ \left({\mathcal{C}}^{3},{\mathcal{A}}^{253}\right)\stackrel{10\mathrm{R}}{\to }{\left({\mathcal{U}}^{3},{\mathcal{B}}^{1}\right)}^{64} $	$ {2}^{253} $	$ {2}^{253.06} $	$ {2}^{44.46} $	本文

下载: 导出CSV

表 2 4-bit S盒(S)

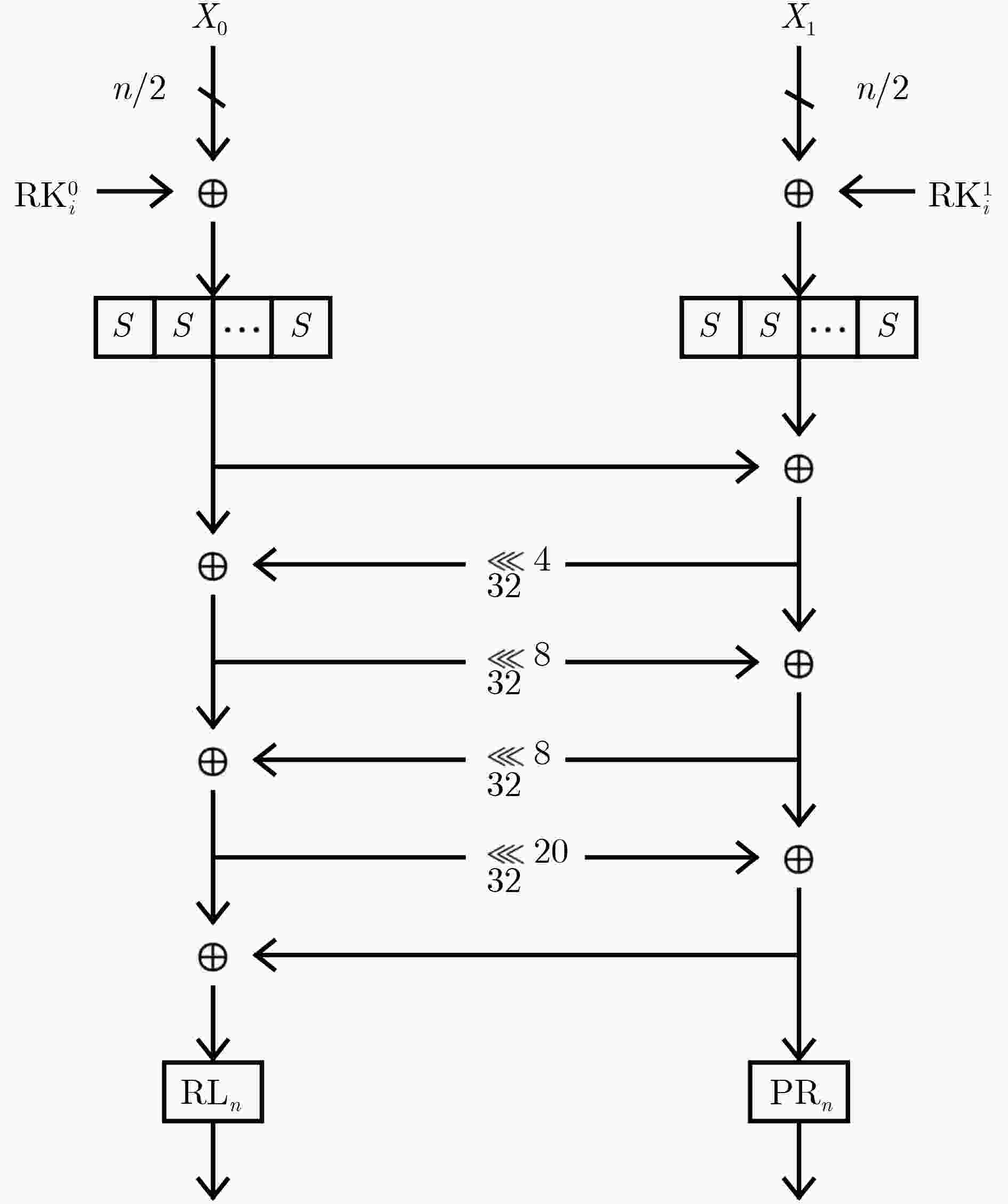
x	0x0	0x1	0x2	0x3	0x4	0x5	0x6	0x7	0x8	0x9	0xa	0xb	0xc	0xd	0xe	0xf
S(x)	0x7	0x4	0x9	0xc	0xb	0xa	0xd	0x8	0xf	0xe	0x1	0x6	0x0	0x3	0x2	0x5

下载: 导出CSV

表 3 $ \mathrm{P}{\mathrm{L}}_{{n}} $和$ \mathrm{P}{\mathrm{R}}_{{n}} $

类型	置换后
$ \mathrm{P}{\mathrm{L}}_{128} $	{1, 3, 4, 6, 0, 2, 7, 5}
$ \mathrm{P}{\mathrm{R}}_{128} $	{2, 7, 5, 0, 1, 6, 4, 3}
$ \mathrm{P}{\mathrm{L}}_{256} $	{2, 7, 8, 13, 3, 6, 9, 12, 1, 4, 15, 10, 14, 11, 5, 0}
$ \mathrm{P}{\mathrm{R}}_{256} $	{6, 11, 1, 12, 9, 4, 2, 15, 7, 0, 13, 10, 14, 3, 8, 5}

下载: 导出CSV

参考文献(30)

[1]	BIHAM E and SHAMIR A. Differential cryptanalysis of DES-like cryptosystems[C]. Conference on the Theory and Application of Cryptography. Santa Barbara, USA, 1990: 2–21. doi: 10.1007/3-540-38424-3_1.
[2]	BIHAM E and SHAMIR A. Differential cryptanalysis of DES-like cryptosystems[J]. Journal of Cryptology, 1991, 4(1): 3–72. doi: 10.1007/BF00630563.
[3]	MATSUI M. Linear cryptanalysis method for DES cipher[C]. Workshop on the Theory and Application of of Cryptographic Techniques, Lofthus, Norway, 1993, 765: 386–397. doi: 10.1007/3-540-48285-7_33.
[4]	DAEMEN J, KNUDSEN L, and RIJMEN V. The block cipher square[C]. The 4th International Workshop on Fast Software Encryption, Haifa, Israel, 1997: 149–165. doi: 10.1007/BFb0052343.
[5]	KNUDSEN L and WAGNER D. Integral cryptanalysis[C]. The 9th International Workshop on Fast Software Encryption, Leuven, Belgium, 2002: 112–127. doi: 10.1007/3-540-45661-9_9.
[6]	TODO Y. Structural evaluation by generalized integral property[C]. The 34th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Sofia, Bulgaria, 2015: 287–314. doi: 10.1007/978-3-662-46800-5_12.
[7]	TODO Y. Integral cryptanalysis on full MISTY1[C]. The 35th Annual Cryptology Conference, Santa Barbara, USA, 2015: 413–432. doi: 10.1007/978-3-662-47989-6_20.
[8]	TODO Y. Integral cryptanalysis on full MISTY1[J]. Journal of Cryptology, 2017, 30(3): 920–959. doi: 10.1007/s00145-016-9240-x.
[9]	TODO Y and MORII M. Bit-based division property and application to SIMON family[C]. The 23rd International Conference on Fast Software Encryption, Bochum, Germany, 2016: 357–377. doi: 10.1007/978-3-662-52993-5_18.
[10]	XIANG Zejun, ZHANG Wentao, BAO Zhenzhen, et al. Applying MILP method to searching integral distinguishers based on division property for 6 lightweight block ciphers[C]. The 22nd International Conference on the Theory and Application of Cryptology and Information Security, Hanoi, Vietnam, 2016: 648–678. doi: 10.1007/978-3-662-53887-6_24.
[11]	DERBEZ P and LAMBIN B. Fast MILP models for division property[J]. IACR Transactions on Symmetric Cryptology, 2022, 2022(2): 289–321. doi: 10.46586/tosc.v2022.i2.289-321.
[12]	ROHIT R and SARKAR S. Cryptanalysis of reduced round SPEEDY[C]. 13th International Conference on Cryptology in Africa, Fes, Morocco, 2022: 133–149. doi: 10.1007/978-3-031-17433-9_6.
[13]	SHIBA R, SAKAMOTO K, LIU Fukang, et al. Integral and impossible-differential attacks on the reduced-round Lesamnta-LW-BC[J]. IET Information Security, 2022, 16(2): 75–85. doi: 10.1049/ise2.12044.
[14]	SHIRAYA T, TAKEUCHI N, SAKAMOTO K, et al. MILP-based security evaluation for AEGIS/Tiaoxin-346/Rocca[J]. IET Information Security, 2023, 17(3): 458–467. doi: 10.1049/ise2.12109.
[15]	WANG Senpeng, HU Bin, GUAN Jie, et al. MILP-aided method of searching division property using three subsets and applications[C]. The 25th International Conference on the Theory and Application of Cryptology and Information Security, Kobe, Japan, 2019: 398–427. doi: 10.1007/978-3-030-34618-8_14.
[16]	HAO Yonglin, LEANDER G, MEIER W, et al. Modeling for three-subset division property without unknown subset[C]. The 39th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 2020: 466–495. doi: 10.1007/978-3-030-45721-1_17.
[17]	HAO Yonglin, LEANDER G, MEIER W, et al. Modeling for three-subset division property without unknown subset[J]. Journal of Cryptology, 2021, 34(3): 22. doi: 10.1007/s00145-021-09383-2.
[18]	HU Kai, SUN Siwei, WANG Meiqin, et al. An algebraic formulation of the division property: Revisiting degree evaluations, cube attacks, and key-independent sums[C]. The 26th International Conference on the Theory and Application of Cryptology and Information Security, Daejeon, South Korea, 2020: 446–476. doi: 10.1007/978-3-030-64837-4_15.
[19]	CUI Jiamin, HU Kai, WANG Qingju, et al. Integral attacks on pyjamask-96 and round-reduced pyjamask-128[C]. Cryptographers’ Track at the RSA Conference, Virtual Event, 2022: 223–246. doi: 10.1007/978-3-030-95312-6_10.
[20]	CUI Jiamin, HU Kai, WANG Meiqin, et al. On the field-based division property: Applications to MiMC, feistel MiMC and GMiMC[C]. The 28th International Conference on the Theory and Application of Cryptology and Information Security, Taipei, China, 2022: 241–270. doi: 10.1007/978-3-031-22969-5_9.
[21]	胡斌, 张贵显. $ {\mu }^{2} $算法的积分攻击和不可能差分攻击[J]. 电子与信息学报, 2022, 44(9): 3335–3342. doi: 10.11999/JEIT210638. HU Bin and ZHANG Guixian. Integral cryptanalysis and impossible differential cryptanalysis of the $ {\mu }^{2} $ algorithm[J]. Journal of Electronics & Information Technology, 2022, 44(9): 3335–3342. doi: 10.11999/JEIT210638.
[22]	吴文玲, 张蕾, 等. The Block Cipher uBlock [OL]. https://sfjs.cacrnet.org.cn/site/term/list_76_1.html. WU Wenling, ZHANG Lei, ZHENG Yafei, et al. The Block Cipher uBlock [OL]. https://sfjs.cacrnet.org.cn/site/term/list_76_1.html.
[23]	吴文玲, 张蕾, 郑雅菲, 等. 分组密码uBlock[J]. 密码学报, 2019, 6(6): 690–703. doi: 10.13868/j.cnki.jcr.000334. WU Wenling, ZHANG Lei, ZHENG Yafei, et al. The block cipher uBlock[J]. Journal of Cryptologic Research, 2019, 6(6): 690–703. doi: 10.13868/j.cnki.jcr.000334.
[24]	TIAN Wenqiang and HU Bin. Integral cryptanalysis on two block ciphers pyjamask and uBlock[J]. IET Information Security, 2020, 14(5): 572–579. doi: 10.1049/iet-ifs.2019.0624.
[25]	MAO Yongxia, WU Wenling, WANG Bolin, et al. Improved division property for ciphers with complex linear layers[C]. The 27th Australasian Conference on Information Security and Privacy, Wollongong, Australia, 2022: 106–124. doi: 10.1007/978-3-031-22301-3_6.
[26]	黄明, 张莎莎, 洪春雷, 等. 分组密码复杂线性层可分性传播的MILP刻画方法[J]. 软件学报, 2023: 1–13. doi: 10.13328/j.cnki.jos.006839. HUANG Ming, ZHANG Shasha, HONG Chunlei, et al. MILP modeling of division property propagation for block ciphers with complex linear layers[J]. Journal of Software, 2023: 1–13. doi: 10.13328/j.cnki.jos.006839.
[27]	https://www.sagemath.org.
[28]	SUN Siwei, HU Lei, WANG Peng, et al. Automatic security evaluation and (Related-key) differential characteristic search: Application to SIMON, PRESENT, LBlock, DES(L) and other bit-oriented block ciphers[C]. The 20th International Conference on the Theory and Application of Cryptology and Information Security, Kaoshiung, China, 2014: 158–178. doi: 10.1007/978-3-662-45611-8_9.
[29]	SUN Ling, WANG Wei, and WANG Meiqin. MILP-aided bit-based division property for primitives with non-bit-permutation linear layers[J]. IET Information Security, 2020, 14(1): 12–20. doi: 10.1049/iet-ifs.2018.5283.
[30]	FERGUSON N, KELSEY J, LUCKS S, et al. Improved cryptanalysis of rijndael[C]. The 7th International Workshop on Fast Software Encryption, New York, USA, 2000: 213–230. doi: 10.1007/3-540-44706-7_15.