1.   引言

非正交多址接入(Non-Orthogonal Multiple Access, NOMA)技术使无线通信突破正交资源限制，可以满足系统对更高的容量和频谱效率、更强的传输性能以及更低的时延。这些属性有助于为不同类型的服务提供更好的用户体验，符合第五代(Fifth Generation, 5G)无线通信系统中海量设备连接的需求^[1]。

近年来，对比传统的多用户通信系统主要依赖于正交多址 (Orthogonal Multiple Access, OMA)方案^[2]，即多个用户在某一域中相互正交。NOMA技术由于能够支持更多的并发通信链路而受到了广泛的研究关注。通常有两种类型的NOMA：功率域NOMA和码域NOMA。在功率域NOMA中，通过分配不同的功率等级^[2-4]来分隔在同一频率或时间资源上通信的多个用户，为不同的用户分配不同的码本或者序列。

稀疏码多址(Sparse Code Multiple Access, SCMA)^[5]是一种基于码域的NOMA技术，其特点是码本的稀疏设计。与SCMA性能强相关的两个主要的研究方向是优化码本(Codebook, CB)设计和多用户检测(MultiUser Detection, MUD)算法。研究者通常会针对某些特定无线信道的特点来设计和优化码本。针对码本的设计研究工作，文献[6]首次出现了利用m阶脉冲幅度调制(Pulse-Amplitude Modulation, PAM)技术设计码本。此后在文献[7]中，开发出基于星形正交振幅度调制(Star Quadrature Amplitude Modulation, Star-QAM)的瑞利信道和高斯信道的新型码本用以最小化误差概率。文献[8]提出一种基于交叉熵法的低复杂度码本设计算法来最大化稀疏码本之间的最小欧氏距离(Minimum Euclidean Distance, MED)。文献[9]通过设计一种增强型多维星座，获得了具有良好误码率性能的改进SCMA码本。在文献[10]中，黄金角调制方案被用于获得具有单次译码收敛性和优异误码率性能的码本。文献[11]提出一种新的极化调制方案来设计改进的SCMA码本。此外，受机器学习最新进展的影响与启发，文献[12]使用基于深度学习网络(Deep Neural Networks)的方法获得了改进的稀疏码本用以优化最小误码率(Bit Error Rate, BER)。

SCMA是未来6G系统中极具竞争力的关键技术之一，多用户检测是其中的重要问题[13]。得益于码本天然的稀疏性，研究多利用消息传递算法(Message Passing Algorithm, MPA)构建解码器检测和恢复多用户信号。相比MPA的迭代会造成复杂度高的问题，压缩感知(Compressed Sensing, CS)理论稀疏识别的特性在多用户检测中已被多次使用。压缩感知技术是一种通过对信号进行非均匀采样和稀疏表示来实现高效的信号重建和压缩的信号处理方法。它可以在比传统采样方法更低的采样率下获取信号的完整信息，从而实现对大数据的高效处理和传输。压缩感知技术的核心思想是将信号表示为一个稀疏向量，并通过非均匀采样获取信号的部分采样值，最后使用重建算法来恢复信号。通过利用稀疏表示的优势来提高信号重建的效率和精度。文献[14]提出一种基于CS的贪婪跟踪算法，计算阈值辅助自适应子空间跟踪以准确估计误差。文献[15]提出一种基于动态阈值和稳定性判断的MPA方案，通过简化因子图和减少迭代次数来降低计算复杂度。以上文献所提出的检测器都具有与原始MPA相似的误码率性能且有效降低了复杂度。但其系统框架依然属于传统的SCMA体系，码本和解码器的设计是仍是互相独立的。用户码本的设计未能结合数据和解码器的性质来提高性能。

在以上分析的基础上，本文研究了一种压缩感知辅助的低复杂度 SCMA系统优化设计方案。该系统使用离线训练自更新的码本，通过在发射端对发射信号进行稀疏化处理，在接收端利用压缩感知技术对多用户的稀疏信号进行高效的检测和重构，能够有效降低多用户检测的复杂度。仿真结果表明：本文提出的自更新码本设计方法设计的码本在高斯信道中的性能较传统的码本性能有明显提升，优化得到的压缩感知辅助的低复杂度 SCMA系统与传统SCMA系统相比拥有更低的复杂度，且在系统用户部分活跃时表现出较好的误码性能。

2.   SCMA系统

在SCMA系统中，为了提供大于1的过载因子，多个用户需要被叠加在相同的物理资源上。例如，对于过载率150% 的下行SCMA系统，假设J个独立用户的信息叠加在K个正交子载波，即资源元素(Resource Elements, RE)上进行传播。发射端根据用户码本，对用户 $j$ 的数据比特编码后映射为K维码字 ${\boldsymbol{x}}_{j}$，编码被定义为以下映射关系

其中M表示每个用户的码本中有M个码字，${\boldsymbol{B}}^{{\mathrm{log}}_{2}M}$表示维度为 ${\mathrm{log}}_{2}M$ 的二进制向量集合，${\boldsymbol{x}}_{j}=[{\boldsymbol{x}}_{1,j}, {\boldsymbol{x}}_{2,j},\cdots ,{\boldsymbol{x}}_{K,j}]^{\mathrm{T}}$为用户 $j$ 的SCMA码字向量，${b}_{j}$表示用户 $j$ 的二进制比特。

接收信号y进入信道到达接收端可表示为

其中 ${\boldsymbol{h}}_{j}={[{\boldsymbol{h}}_{1,j},{\boldsymbol{h}}_{2,j},\cdots ,{\boldsymbol{h}}_{K,j}]}^{\mathrm{T}}$为用户 $j$ 的信道向量，${\boldsymbol{n}}{\text{～}}\mathcal{C}\mathcal{N}(0,{\mathrm{\sigma }}^{2}\boldsymbol{I})$ 表示均值为0，方差为的 ${\mathrm{\sigma }}^{2}$ 分布的加性高斯白噪声矢量。

传统SCMA根据用户码本和因子矩阵，采用MPA不断迭代的方式从叠加信号中检测和恢复每个用户的信息。每一次的迭代经由信息传递和更新用户节点到资源节点的消息两个阶段。当信道状态是已知的或者噪声符合高斯分布N₀ 的理想情况下，原始MPA可以表示为

3.   自更新码本设计方法

SCMA性能增益强烈依赖于合理设计的稀疏码本，手工设计的码本质量限制了SCMA系统的性能。传统的SCMA系统在设计码本时未能利用到解码器特性。因此，本文为压缩感知辅助的低复杂度 SCMA系统设计了一种码本自更新(Self-Renewable, SR)方法。该方法采用类似反向传播神经网络(Back Propagation Neural Network, BPNN)构造思想。在稀疏向量重构训练过程中使用梯度下降法来更新初始码本。因自更新训练是离线完成的，生成的码本供在线推演使用。SR方法的自更新过程主要有3个步骤：线性无关码字矩阵的初始化、传播过程和码本自更新，下面将详细解释。

3.1   线性无关码字矩阵的初始化

在压缩感知辅助的低复杂度 SCMA系统中，为大多数用户定义了一个码本${{C}}^{L\times M}$，该码本的每一列称为一个码字。为满足信号需具备稀疏性的前提，本文引入线性无关码字矩阵 $\boldsymbol{A}\in {{C}}^{L\times (M/2)J}$，该矩阵只包含所有码本中线性无关的码字。例如，对于 150% 的码本，矩阵 $\boldsymbol{A}$ 包含 12 个码字，即所有码本的第1列和第2列。同时为满足稀疏重构的前提条件，将矩阵 $\boldsymbol{A}$ 中元素拆分为实部和虚部并进行列向拼接，矩阵 $\boldsymbol{A}$ 的行数将扩展两倍。其中，矩阵 $\boldsymbol{A}$ 的第 $j$ 部分对应用户 $j$ 采用码本的前 $\mathrm{M}/2$ 列，即

系统将拓展后的矩阵 ${\boldsymbol{A}}'$作为唯一可训练的参数，它可以是通过从独立且相同的复正态分布中随机采样来初始化的矩阵，即 ${\boldsymbol{A}}'{\text{～}}\mathcal{C}\mathcal{N}\left(0,{{\boldsymbol{I}}}^{L\times (\mathrm{M}/2)\times J}\right)$，当然也可以使用人工设计的拼接码本作为初始码本。

3.2   传播过程

如3.1节所描述的，经初始化处理后的码本作为唯一可训练参数。在系统用户全接入时，利用如下所示的因子图矩阵 $\boldsymbol{F}$ 将扩展后的码字映射到更高维度的稀疏码字。

每个用户j发送的一个符号 ${\boldsymbol{x}}_{j}\in {{C}}^{(M/2)J\times 1}$，转换为只包含{0, –1, 1} 3种元素的列向量${\boldsymbol{x}}_{j}$。${\boldsymbol{x}}_{j}$ 由 $M/2$ 个元素构成，其中仅有一个非零向量。J 个用户符号共同组成 $\boldsymbol{X}$, $\boldsymbol{X}$ 的稀疏度即为 J。本文自定义包含{1, 2, 3, 4}4种元素信号转换为列向量规则如表1所示。

表 1  自定义信号元素转换规则

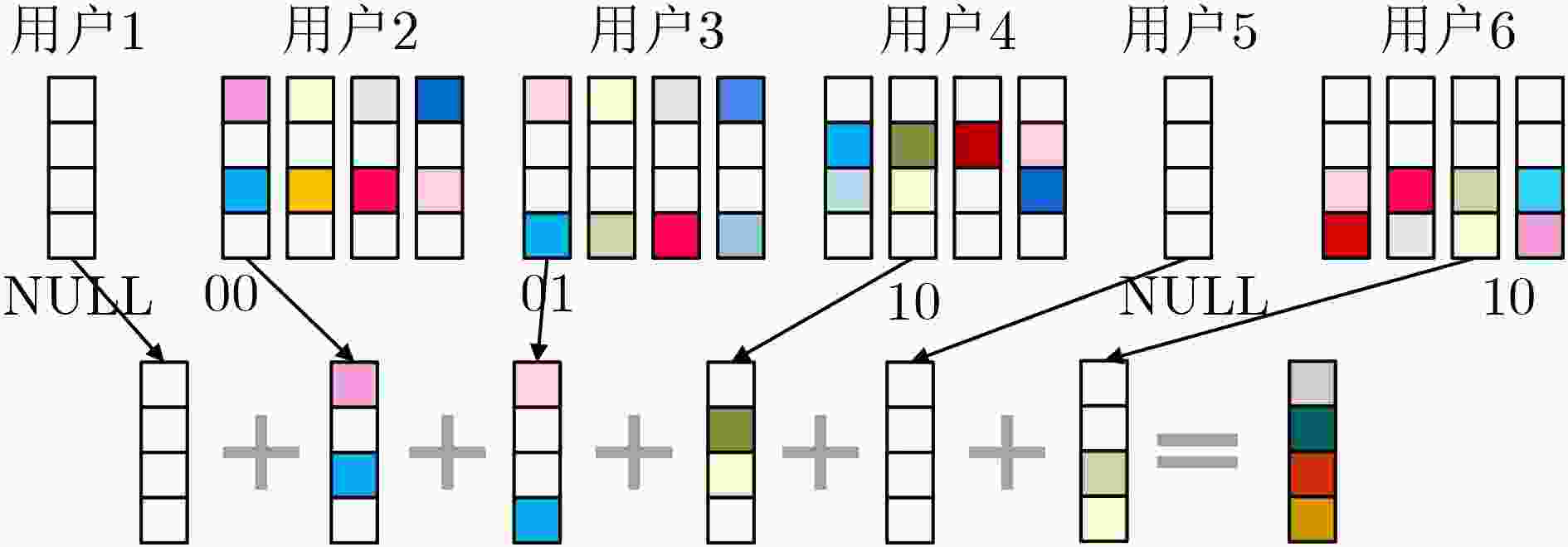
信号元素	列向量
1	${\left[1,\mathrm{ }0\right]}^{\mathrm{T}}$
2	${\left[0,\mathrm{ }1\right]}^{\mathrm{T}}$
3	${\left[0,\mathrm{ }-1\right]}^{\mathrm{T}}$
4	${\left[-1,\mathrm{ }0\right]}^{\mathrm{T}}$
NULL	${\left[0,\mathrm{ }0\right]}^{\mathrm{T}}$

下载: 导出CSV 

| 显示表格

例如，当6个用户全接入下发送信号：1, 2, 3, 4, 1, 2时，

当系统中只有部分用户为活跃状态时，$\boldsymbol{X}$ 的稀疏度小于 J，如图1所示。例如，用户1～6发送信号：NULL, 1, 1, 2, NULL, 3时，

图 1  部分活跃用户复用

下载: 全尺寸图片 幻灯片

将$\boldsymbol{X}$ 作为输入值经过信道的前向传播，定义接收端获取的接收信号为$\boldsymbol{Y}\in {{C}}^{K}$，将$\boldsymbol{Y}$送入解码器进行稀疏信号重构，得到相应用户符号概率 ${p}_{j}$。SR方法可将接收器解码过程看作一个分类问题，使用交叉熵损失函数(Cross entropy loss function)来寻找从所有用户的解码符号中获得的损失$L$，通过最小化损失 $L$ 来学习码本。计算$L$如

3.3   码本自更新

因为解码器的输出相对于其输入是可微分的，即从用户符号 ${\boldsymbol{x}}_{j}$ 到最终损失 $L$ 的所有运算都是可微分的。因此，可以求出最终损失$L$ 相对于 ${\boldsymbol{x}}_{j}$ 的梯度。使用具有学习率 $\eta$的基于梯度下降的优化器更新所有 J 个用户的可训练参数${\boldsymbol{x}}_{j}$如

其中t表示时刻，码本经过初始化处理之后，重复传播和自更新过程直到损失收敛。在自更新训练阶段中每次更新重构过程都遵循压缩感知原理，进行稀疏采样来获得发送的用户符号和记忆噪声。从而固定下最终更新的码本。图2演示了t时刻的码本更新过程。

图 2  码本更新过程

下载: 全尺寸图片 幻灯片

4.   压缩感知辅助的多用户检测算法

在众多CS稀疏信号重构算法中，由于贪婪算法具有较低的计算复杂度、可扩展性好、适用范围广、易于实现和理解等优势^[16]。本文选择应用最广的贪婪算法正交匹配追踪(Orthogonal Matching Pursuit, OMP)算法为基础对多用户检测算法进行设计和改进。提出了一种压缩感知辅助的多用户检测算法。该算法主要有两个步骤：构造稀疏信号重构问题和稀疏向量重构，下面将详细解释。

4.1   构造稀疏信号重构问题

引入的线性无关码字矩阵$\boldsymbol{A}$经过拆分和拓展处理得到矩阵 ${\boldsymbol{A}}{{{'}}}$，它的作用是从一个高维的信号空间中提取一个低维的表示，把高维信号映射到一个低维空间从而对信号进行采样和编码。接收信号$\boldsymbol{Y}$经过信道后表示为

根据上式可以看出压缩感知的稀疏重构问题就是在已知观测信号 $\boldsymbol{Y}$ 、观测矩阵${\boldsymbol{A}}'$、噪声矢量$n$下，恢复出原始信号。因为 $\boldsymbol{X}$ 是一个稀疏向量，故式(10)构成的欠定线性方程组具有无穷解或着无解。然而本文设计的矩阵 ${\boldsymbol{A}}'$ 仅包含所有码本中线性无关的码字，因此该欠定方程组可采用压缩感知的稀疏重构算法对稀疏信号进行唯一恢复。如图3稀疏信号重构模型所示，其中向量 $\boldsymbol{X}$ 被视为需重构的信号，矩阵 ${\boldsymbol{A}}'$ 被视为观测矩阵。至此使得系统的多用户检测问题转化为稀疏信号重构问题。

图 3  稀疏信号重构模型

下载: 全尺寸图片 幻灯片

4.2   稀疏向量重构

本节基于OMP算法在计算复杂度上的优势展开研究。处理后的信号仅包含{0,–1,1} 3种元素^[16]，在信道上传输后会受噪声影响产生较高的误码率，进而影响OMP算法对信号的重构能力。原始码本转换成的观测矩阵${\boldsymbol{A}}'$同样影响算法性能，在线使用经离线自更新训练的码本能提高重构能力。综合上述考虑，本文提出一种符号判决正交匹配追踪(Sign Decision Orthogonal Matching Pursuit, SD-OMP)算法，算法流程如算法1所示。该算法每次迭代时都基于符号对信号进行判决并更新残差，同时根据噪声的功率设置阈值，能有效解决对原始信号过估计的问题，提高稀疏向量的重构性能。

表 1  SD-OMP算法流程

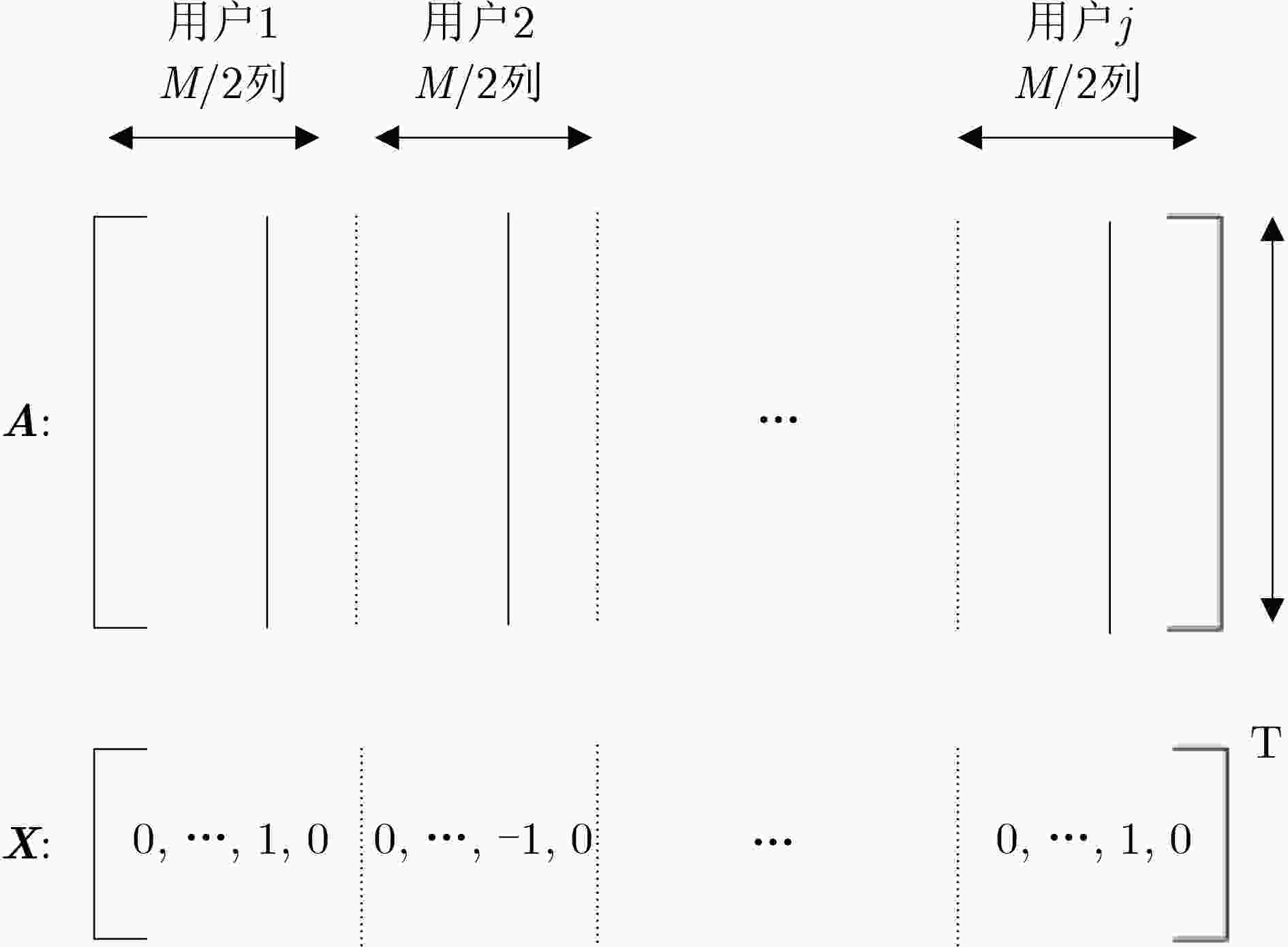
输入：观测信号 $\boldsymbol{y}$，观测矩阵 $\boldsymbol{A}$，稀疏度 $S$，门限值 ${V}_{\mathrm{t}\mathrm{h}}$
输出：估计的系数信号 $\widehat{\boldsymbol{x}}$
1.(初始化设置)：迭代索引$l=1$，初始化支撑集 　${\varOmega }\left(l-1\right)=\varphi$， 　初始残差$\boldsymbol{r}\left(l-1\right)=\boldsymbol{y}$;
2.$\rm{w}\rm{h}\rm{i}\rm{l}\rm{e}\;l\le S\;\rm{d}\rm{o}:$
3.(相关性计算)：${\varLambda }\left(l\right)=\mathrm{arg}\underset{i=\mathrm{1,2},\cdots ,K}{\mathrm{max}}{\left\|{\boldsymbol{A}}^{\mathrm{H}}\boldsymbol{r}(l-1)\right\|}_{2}$;
4.(更新支撑集)：${\varOmega }\left(l\right)={\varOmega }\left(l-1\right)\cup {\varLambda }\left(l\right)$;
5.(最小二乘估计)：$\widehat x = {({A_{\varOmega (l)}})^\dagger }{\boldsymbol{y}}$
6.(残差更新)：$\boldsymbol{r}\left(l\right)=\boldsymbol{y}-\boldsymbol{A}{\mathrm{sign}}\left({\widehat{\boldsymbol{x}}}^{\left(l\right)}\right)$;
7．${\rm{i}\rm{f}\left\|\boldsymbol{r}\left(l\right)\right\|}_{2} < {V}_{\mathrm{t}\mathrm{h}}$
8．$\rm{break}$;
9．$\rm{end}\;\rm{while}$
10.(输出估计的稀疏信号)：$\widehat{\boldsymbol{x}}={\mathrm{sign}}\left({\widehat{\boldsymbol{x}}}^{\left(L\right)}\right)$;

下载: 导出CSV 

| 显示表格

在进行步骤3相关性计算时，观测矩阵${\boldsymbol{A}}'$中的原子应当是归一化的，因在设计码本时已经进行了归一化处理，在训练和检测阶段可无需归一化。OMP 算法与凸优化相比计算速度更快，这是贪婪算法的一个优点。但 OMP 算法的性能受观测矩阵 ${\boldsymbol{A}}'$ 的相关性影响，其中的相关性表示矩阵${\boldsymbol{A}}'$中两列之间的相似性。例如式(11)两个矩阵

矩阵 ${\boldsymbol{A}}_{1}'$ 有很高的相关性，第2列与第1列很相似，矩阵${\boldsymbol{A}}_{2}'$ 相关性较小， 因为第2列与第1列、第3列相似度较低，相关性 $\mu$ 定义为

其中，$\mu \in (0, 1)$，如果 $\mu$ 值很高，OMP 算法通常会给出错误的重构结果。在本文中，矩阵$\boldsymbol{A}$与用户码本设计相关。因此，设计列相关性较小的用户码本对于SD-OMP算法的检测效果具有重要影响。

在步骤6中，残差更新的计算引入符号判决的设计原因是原始信号具有仅包含3个元素的特殊性。且由于该算法重构的信号越稀疏，重构性能越好。因此，在面对系统中用户随机接入时，$\boldsymbol{X}$ 的稀疏性直接影响到SD-OMP算法的检测性能。

在步骤7、步骤8中，根据噪声的功率 ${\sigma }^{2}$ 对残差${\Vert {\boldsymbol{r}}\left(l\right)\Vert }^{2}$进行设计。如果符号判决OMP算法能对稀疏信号精确估计，则残差仅由噪声组成，迭代过程应该终止。因此，为了防止所提算法对信号的过估计，可以利用噪声的能量来选择阈值。阈值可以计算为

且残差总是和观测矩阵已选择的列向量正交，意味着一个列向量不会被二次选择，结果能在有限的步骤内收敛。

4.3   计算复杂度分析

尽管SCMA码字的稀疏性，MPA的复杂性仍然非常高。这是因为MPA对资源节点上所有可能的信号进行遍历搜索会给带来指数级的复杂性。计算公式如下所示：

其中$i$为迭代次数，${d}_{{\mathrm{r}}}$和${d}_{{\mathrm{u}}}$分别表示资源节点和用户节点的度数。显然，MPA利用率越低其计算复杂度越低，应用时需要平衡性能和复杂度。

对于本文提出的压缩感知辅助的多用户检测算法，计算复杂度主要来自SD-OMP 算法部分。

其中$S$ 是当前迭代的稀疏度级别。可以观察，误差向量的稀疏度一般为 $S\ll K$。因此SD-OMP算法相对于MPA算法的复杂度是相对较低的，这一点在下一节仿真中得到了验证。

5.   仿真分析及性能对比

为验证压缩感知辅助的低复杂度 SCMA系统优化设计方案的有效性。在本节中，首先将自更新训练获得的SR码本和华为公司的SCMA码本^[17]、基于Star-QAM星座的码本^[9]应用在传统SCMA系统中进行仿真。其次固定SR码本，使用SD-OMP算法和MPA算法进行仿真对比验证压缩感知辅助的低复杂度SCMA系统设计具有较低的低复杂度。

在传统SCMA系统仿真实验中使用了广泛讨论的具有过载因子150%的SCMA系统，其参数设置如表2所示。

表 2  仿真参数设置

参数名称	参数值
资源元素数K	4
码字数 M	4
用户数 J	6
样本数	1280 bit
MPA迭代次数	3
自更新迭代次数	300

下载: 导出CSV 

| 显示表格

图4展示了在高斯信道下使用自更新训练获得的SR-CB码本、华为公司的SCMA码本和基于 Star-QAM 星座的码本，并使用 MPA解码器进行解码的误码率曲线。可以直观的看出，随着SNR的增加，自更新码本设计方法离线训练获得的SR码本性能比华为公司的SCMA码本和基于 Star-QAM 星座的码本性能优势更为明显。

图 4  传统SCMA系统各码本性能对比图

下载: 全尺寸图片 幻灯片

本文所述的多用户检测算法并非基于原始MPA算法的改进，为了使对比的各算法复杂度更加直观，使用计算复杂度下降率(Computational Complexity Reduction Rate, CCRR)来度量仿真复杂度，即

其中，${t}_{\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{r}}$表示提出的SD-OMP算法仿真时间，${t}_{\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{g}}$表示 MPA 仿真时间，则$0 < {\mathrm{C}\mathrm{C}\mathrm{R}\mathrm{R}}_{\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{r}} < 1$。

图5展示了过载因子150%的系统下使用SR码本验证SD-OMP算法与MPA算法在复杂度上的对比。实验统计了MPA算法分别迭代3次和6次的平均仿真时间，与SD-OMP算法的仿真时间计算得出CCRR曲线。此图可看出在仿真时， MPA算法随着SNR的增大，其仿真时间越来越长。并且为了达到更好的算法性能增加MPA算法的迭代次数时，与SD-OMP算法的CCRR进一步下降。即MPA算法的计算复杂度比SD-OMP算法的计算复杂度高。

图 5  多用户检测算法仿真CCRR对比图

下载: 全尺寸图片 幻灯片

图6展示了SD-OMP算法和MPA 算法在用户随机接入时的对比结果。仿真系统参数设置：系统过载率为 150%、正交资源块数为 4、总用户数为 6，MPA 迭代次数为 3。从图中可以看出，当系统中活跃用户较少时，SD-OMP算法相较于MPA 算法，具有更好的误码性能。例如，在活跃用户数为 2、空闲用户数为 4 时，SD-OMP算法的误码率表现最佳。然而，随着活跃用户数的增加，两种算法的误码性能逐渐变差，并且它们之间的性能差异也逐渐缩小。这是由于SD-OMP算法本身针对检测的信号稀疏度越小，重构的信号精确度越高的特点。在实际的SCMA系统中，接入用户数是通常是随机的，当系统中存在较少的活跃用户时，SD-OMP算法相对于MPA 算法具有更好的性能表现。

图 6  部分用户活跃时检测算法性能仿真曲线

下载: 全尺寸图片 幻灯片

6.   结论

本文提出了一种压缩感知辅助的低复杂度 SCMA系统优化设计方案。该方案首先设计了一种码本自更新方法离线训练生成SR码本，能够结合数据和解码器的性质来提高系统性能。其次通过在发射端对发射信号进行稀疏化处理，在接收端利用压缩感知技术对多用户的稀疏信号进行高效的检测和重构，有效降低多用户检测的复杂度。

仿真结果表明，基于本文提出的自更新码本设计方法得到的码本在高斯信道中的性能较传统的码本性能有明显提升，同时压缩感知辅助的低复杂度 SCMA系统优化设计方案与传统SCMA系统相比拥有较低的复杂度，且在系统用户部分活跃时误码性能表现较好。虽然本文研究的方案性能在降低复杂度方面表现较好，但压缩感知辅助的稀疏向量重构算法还有优化的空间，比如可在重构时使用马尔可夫链蒙特卡罗算法，平衡复杂度与误码率的同时进一步从测量信号中恢复原始信号，这将是本文后续研究的主要内容之一。