Extraction of Attributed Scattering Center Based on Physics Informed Machine Learning
-
摘要: 基于参数化散射中心模型进行参数估计是实现合成孔径雷达高级信息获取(SAR AIR)技术的基本思路之一,传统的属性散射中心(ASC)参数估计算法往往具有计算速度慢、算法复杂度高、对参数初值要求高等问题。对此,该文提出一个新的基于无监督学习的端到端框架用于从SAR图像反演ASC参数。首先,利用自编码式网络结构有效提取目标图像特征,缓解由于优化空间复杂非凸导致的直接求解困难,解决初值敏感问题;其次,通过嵌入ASC模型作为物理解码器以将编码器输出约束为正确的ASC参数;最后,通过端到端的模型架构进行学习和推理,达到降低算法复杂度及提高估计速度的目的。通过在仿真和实测数据上进行测试,实验结果表明在0.15 m分辨率测试集SAR图像上取得低于0.1 m的估计误差,反演单个散射中心平均耗时0.06 s,验证了该文所提方法的有效性、高效性与鲁棒性。
-
关键词:
- 属性散射中心模型 /
- 参数估计 /
- 基于物理知识的机器学习
Abstract: To estimate parameters of parameterized scattering center models is one of the basic methods for Synthetic Aperture Radar Advanced Information Retrieval (SAR AIR). Traditional Attributed Scattering Center (ASC) parameter estimation algorithms usually suffer from issues such as slow computation speed, high algorithm complexity, and high sensitivity to initial values of parameters. In this paper, a novel end-to-end framework for inverting ASC parameters from radar images based on unsupervised deep learning is proposed. Firstly, an autoencoder network structure is employed to effectively extract image features of targets, alleviating the difficulties solving directly caused by the complex non-convex optimization space and resolving the sensitivity to initial values. Secondly, the ASC model is embedded as a physical decoder to constrain the encoder output to correct ASC parameters. Finally, the end-to-end architecture are utlized to train and infer the model, achieving the purpose of reducing algorithm complexity and improving estimation speed. Through testing on simulated and measured data, experimental results indicate that the estimation error obtained on the SAR image test set with a resolution of 0.15 m is less than 0.1 m while the average processing time is 0.06 s for the inversion of one single scattering center, which demonstrate the effectiveness, efficiency, and robustness of the proposed approach. -
表 1 参数预测模块中的自定义激活函数
参数集矩阵列 对应参数 激活函数 1 $ x $ $ 4 \times \tanh () $ 2 $ y $ $4 \times \tanh ()$ 3 $ A $ $ 10 \times {\text{sigmoid}}() $ 4 $ \alpha $ $ {\text{sigmoid}}() $ 5 $ L $ $ 4 \times {\text{sigmoid}}() $ 1 内嵌物理的变分自编码器训练算法
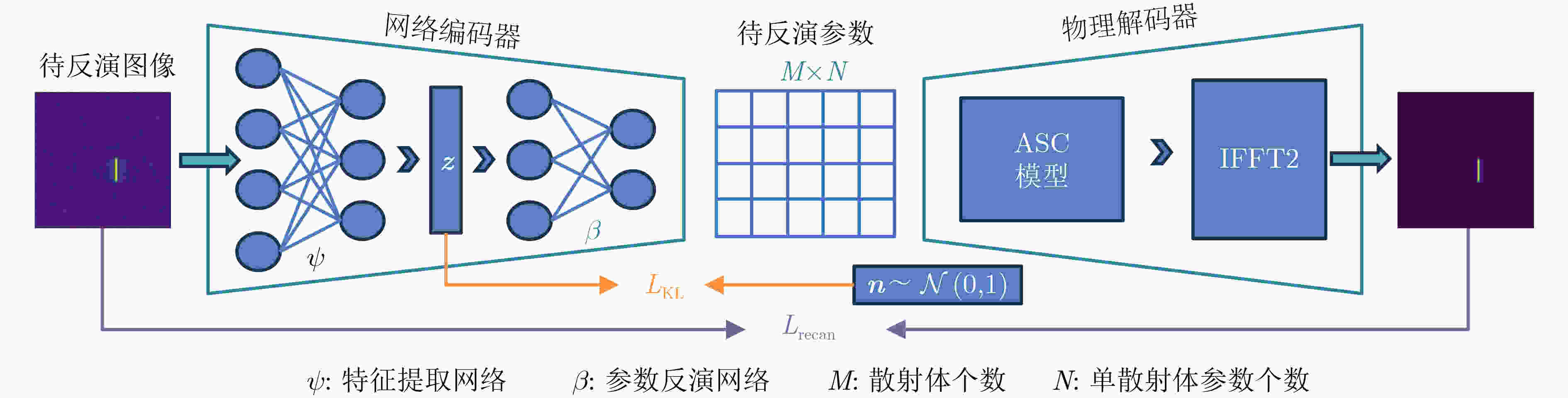
输入:观测数据$ D = \{ {{\boldsymbol{s}}^{{\text{(1)}}}},{{\boldsymbol{s}}^{{\text{(2)}}}}, \cdots ,{{\boldsymbol{s}}^{{\text{(}}d{\text{)}}}}\} $ 批处理大小$ n $,学习率$\alpha $,KL散度权重${\omega _{{\text{kld}}}}$,重建损失权重${\omega _{{\text{rec}}}}$ 隐变量维度$T$,散射体个数$M$,单散射体参数个数$N$,雷达系统参数sys 随机初始化:特征提取网络$\psi $,参数反演网络$\beta$ 重复: 在数据集中随机选择1个处理批次$ {\boldsymbol{S}} = \{ {{\boldsymbol{s}}^{{\text{(1)}}}},{{\boldsymbol{s}}^{{\text{(2)}}}}, \cdots ,{{\boldsymbol{s}}^{{\text{(n)}}}}\} $ 循环,对每个$ {{\boldsymbol{s}}^{(i)}} \in {\boldsymbol{S}}{\text{ }}(i = 1 \sim n) $: 从标准高斯分布$\mathcal{N}(0,1)$中生成噪声 $ {{\boldsymbol{n}}^{(i)}} = {[{n^{(1)}},{n^{(2)}}, \cdots ,{n^{(T)}}]^{\text{T}}} $ 隐变量服从分布的均值与标准差 ${{\boldsymbol{\mu }}^{(i)}} = {[{\mu ^{(1)}},{\mu ^{(2)}}, \cdots ,{\mu ^{(T)}}]^{\text{T}}},{{\boldsymbol{\sigma }}^{(i)}} = {[{\sigma ^{(1)}},{\sigma ^{(2)}}, \cdots ,{\sigma ^{(T)}}]^{\text{T}}} \leftarrow {{\mathrm{Extr}}} ({{\boldsymbol{s}}^{(i)}};\psi )$ 隐变量 ${{\boldsymbol{z}}^{(i)}} \leftarrow {{\boldsymbol{\mu }}^{(i)}} + {{\boldsymbol{\sigma }}^{(i)}} \odot {{\boldsymbol{n}}^{(i)}}$ 估计的ASC参数集 $ {{\boldsymbol{\varTheta }}^{(i)}} = {[{\varTheta ^{(1)}},{\varTheta ^{(2)}}, \cdots ,{\varTheta ^{(M \times N)}}]^{\text{T}}} \leftarrow {\text{Pred}}({{\boldsymbol{z}}^{(i)}};\beta ) $ 由估计参数重建图像 ${{\boldsymbol{\hat s}}^{(i)}} \leftarrow {{\mathrm{Imag}}} ({{\boldsymbol{\varTheta }}^{(i)}};{\text{sys}})$ 图像重建损失 $L_{{\text{recon}}}^{(i)} \leftarrow {\lambda _1} \times \displaystyle\sum\nolimits_{x = 1}^{{N_x}} {\displaystyle\sum\nolimits_{y = 1}^{{N_y}} {[{\boldsymbol{s}}_{{\mathrm{xy}}}^{(i)} - {\boldsymbol{\hat s}}_{{\mathrm{xy}}}^{(i)}]} } $ KL散度损失 $ L_{{\text{KL}}}^{(i)} \leftarrow - {\lambda _2} \times \dfrac{1}{2}\displaystyle\sum\nolimits_{l = 1}^T {[1 + \ln {{(\sigma _l^{(i)})}^2} - {{(\mu _l^{(i)})}^2} - {{(\sigma _l^{(i)})}^2}]} $ 结束循环 参数预测网络参数更新 $ \beta \leftarrow \beta - \alpha \dfrac{{\partial \left[ {{1 \mathord{\left/ {\vphantom {1 n}} \right. } n}\displaystyle\sum\nolimits_{i = 1}^n {L_{{\text{recon}}}^{(i)}} } \right]}}{{\partial \beta }} $ 特征提取网络参数更新 $ \psi \leftarrow \psi - \alpha \dfrac{{\partial \left[ {{1 \mathord{\left/ {\vphantom {1 n}} \right. } n}\displaystyle\sum\nolimits_{i = 1}^n {\left( {L_{{\text{recon}}}^{(i)} + L_{{\text{KL}}}^{(i)}} \right)} } \right]}}{{\partial \psi }} $ 直到 收敛 表 2 数据集参数的先验分布
参数 假设的先验分布 $ x $ [–4,4] 均匀分布 $ y $ [–4,4] 均匀分布 $ A $ [0,10] 均匀分布 $ \alpha $ {0,0.5,1} 离散均匀分布 $ L $ {0,(0,4]} 均匀分布 表 3 ASC参数估计结果
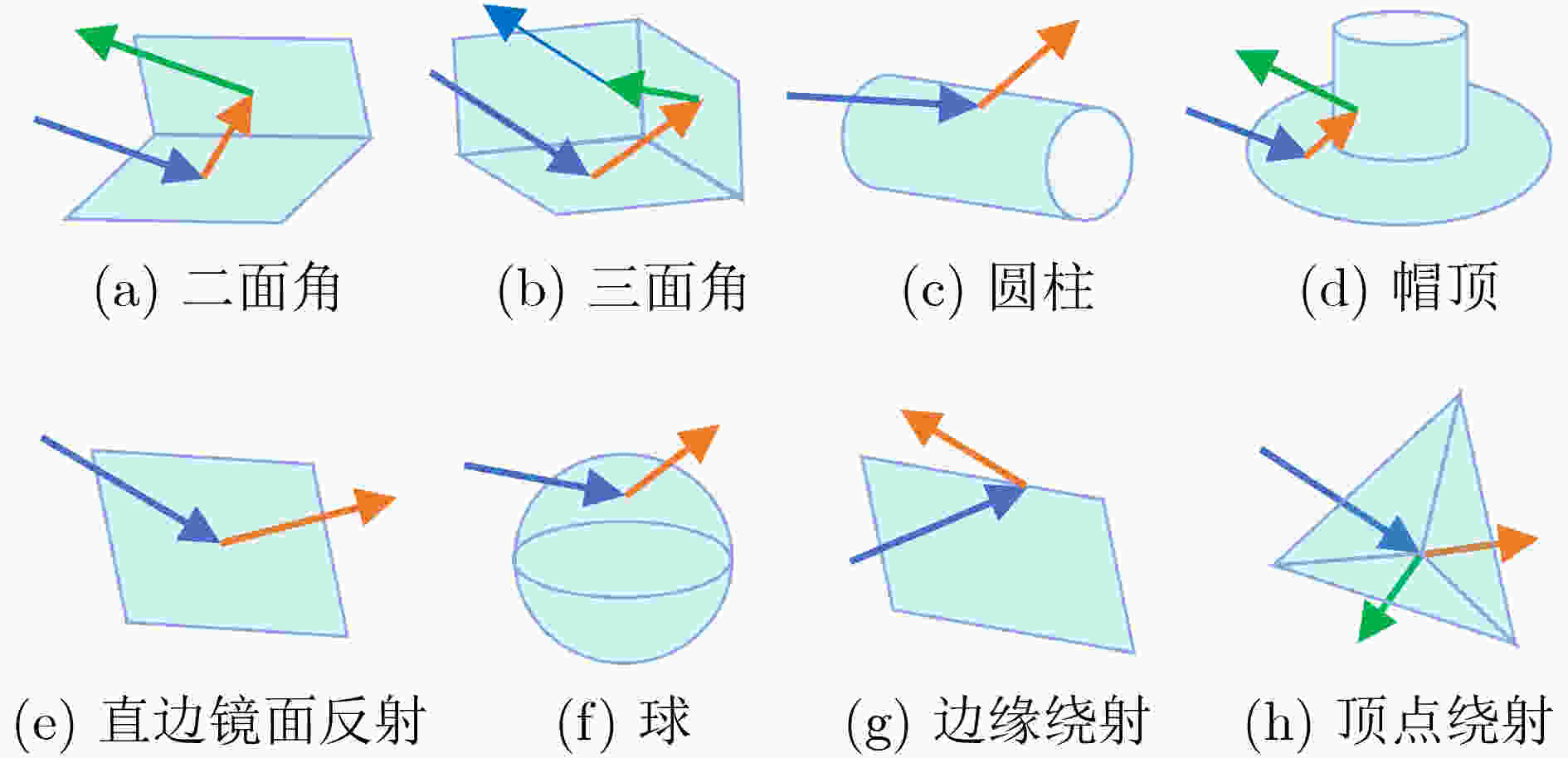
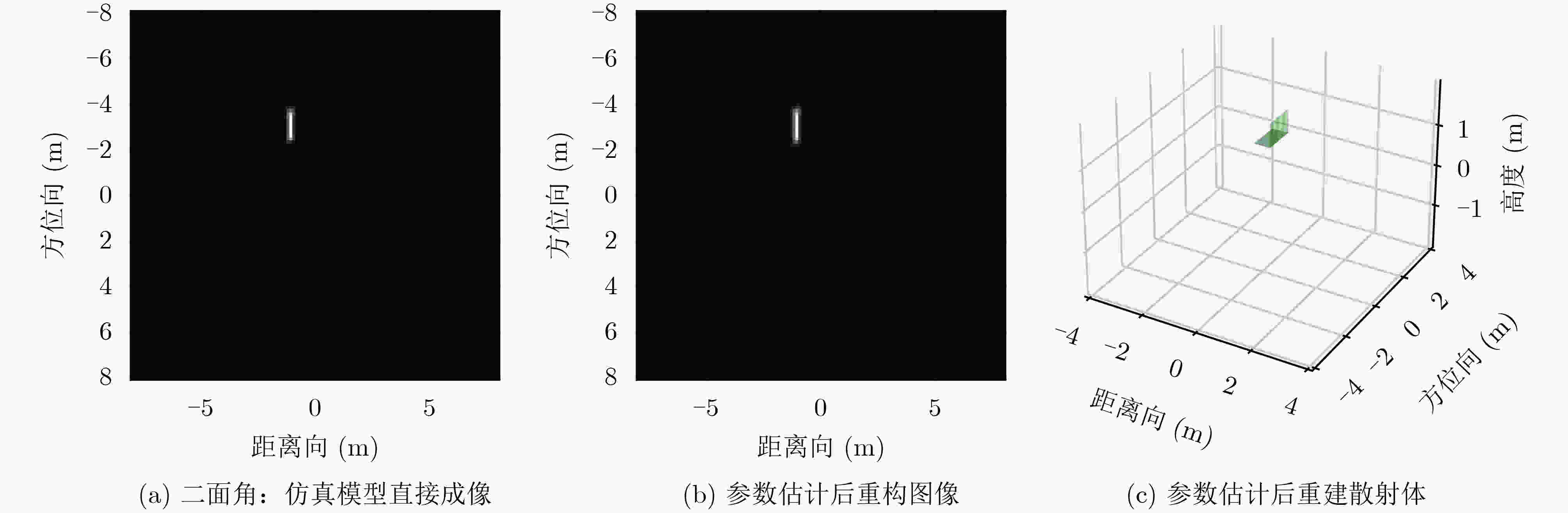
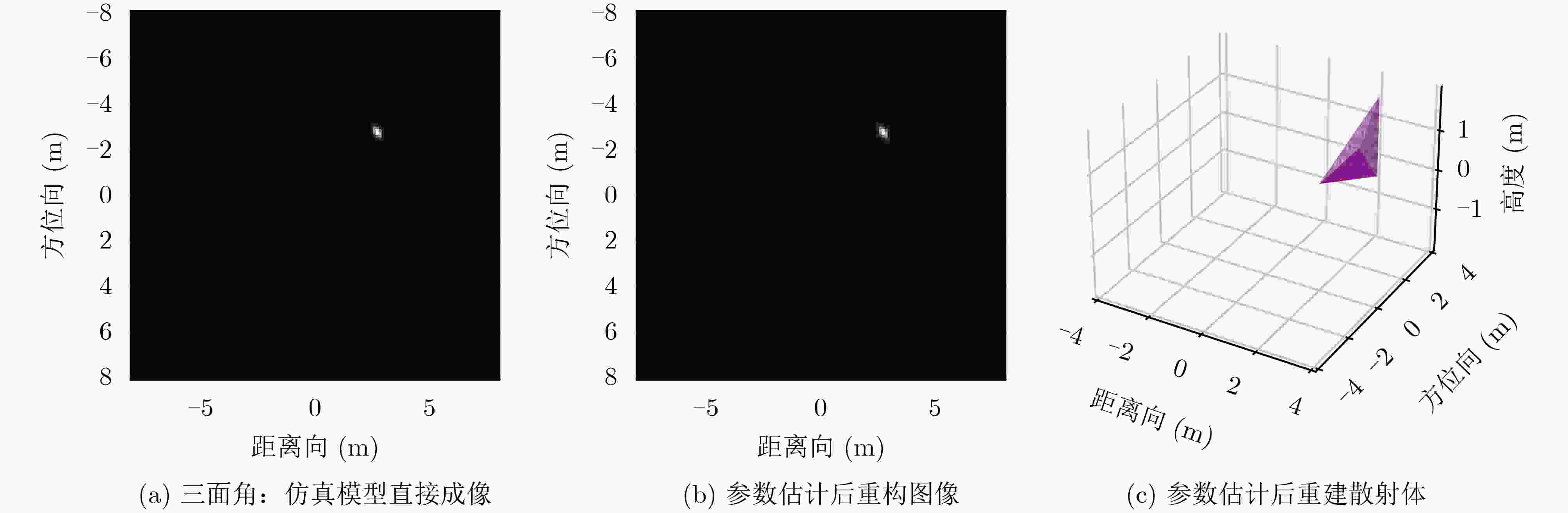
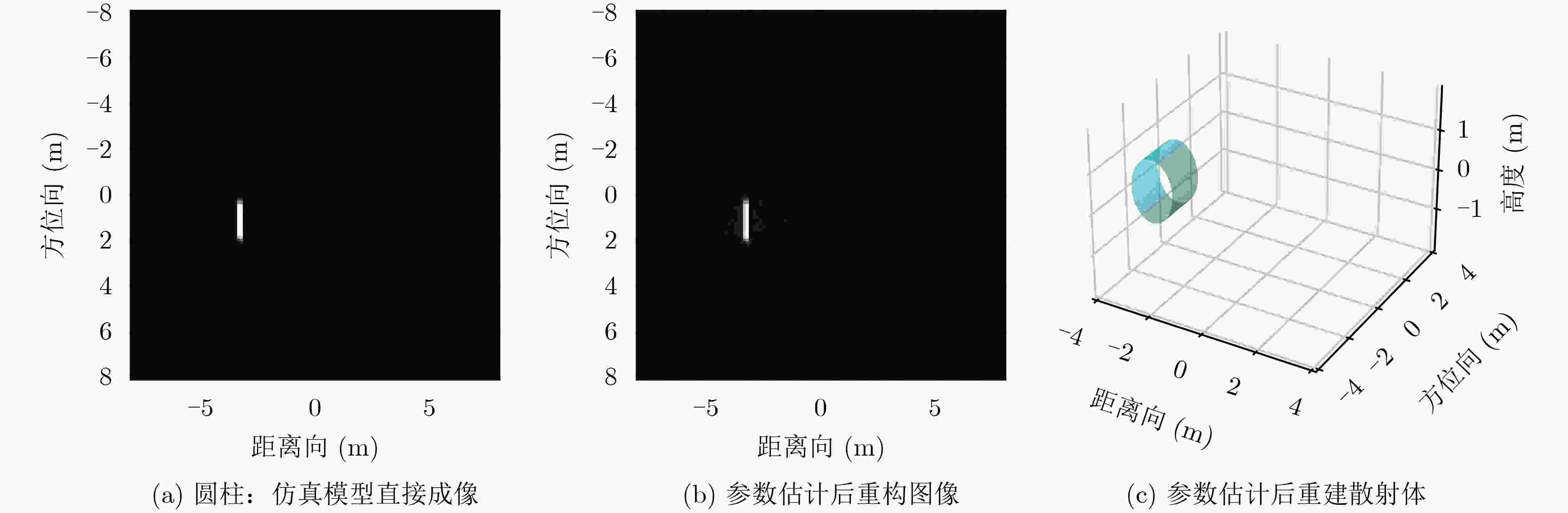
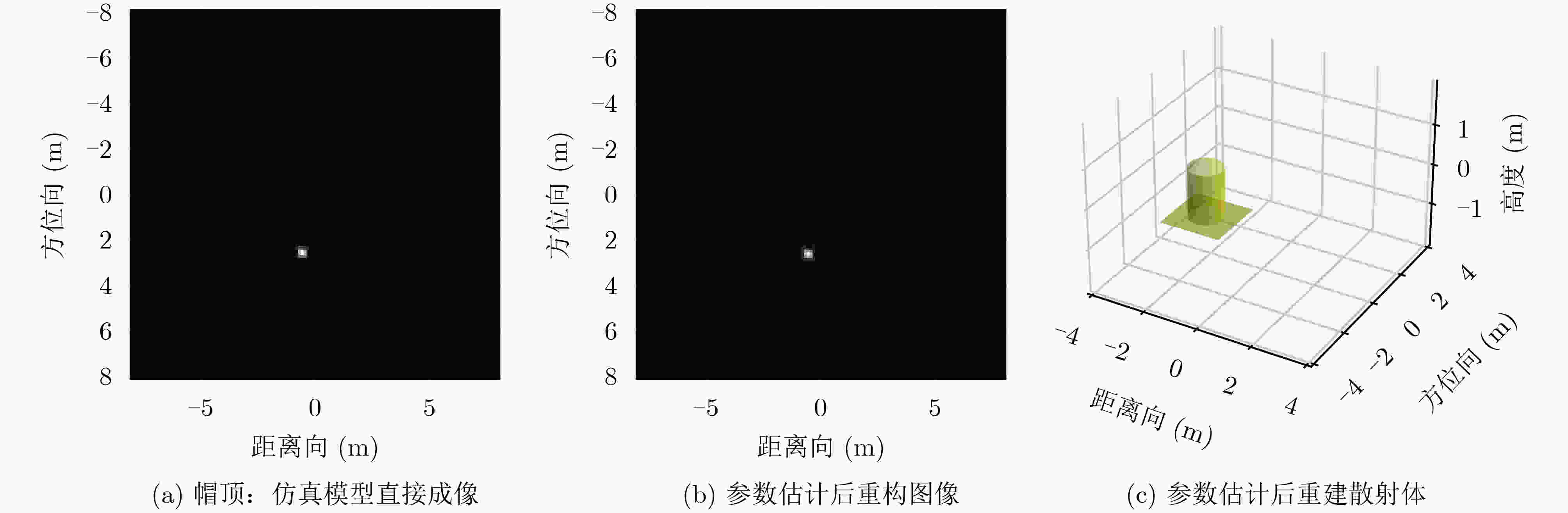
散射中心 $ x{\text{ (m)}} $ $ y{\text{ (m)}} $ $ A $ $ \alpha $ $ L{\text{ (m)}} $ 散射体结构 1 (图4) 真值 –1.1289 –3.0572 3.6384 1 1.3083 二面角 估计值 –1.1285 –3.0843 3.5226 1 1.2233 二面角 2 (图5) 真值 2.6069 –2.7878 2.2421 1 0 三面角 估计值 2.6110 –2.7970 2.2972 1 0 三面角 3 (图6) 真值 –3.2751 1.0433 3.6998 0.5 1.6510 圆柱 估计值 –3.2861 1.0202 3.7055 0.5 1.5857 圆柱 4 (图7) 真值 –0.6156 2.5096 9.7212 0.5 0 帽顶 估计值 –0.6186 2.4470 9.4620 0.5 0 帽顶 表 4 某多散射体目标ASC参数估计结果
散射中心 $ x{\text{ (m)}} $ $ y{\text{ (m)}} $ $ A $ $ \alpha $ $ L{\text{ (m)}} $ 散射体结构 01 1.3409 –1.6606 1.5001 1 0 三面角 02 1.7968 1.1601 3.1288 0.5 0 帽顶 03 1.5212 1.8534 1.5308 1 0 三面角 04 2.8507 –2.1188 4.1949 0.5 1.9380 圆柱 05 3.8858 0.9819 3.0929 0.5 1.5939 圆柱 06 2.8479 3.2429 4.0792 0.5 1.3463 圆柱 表 5 角反组实测图像ASC参数估计结果
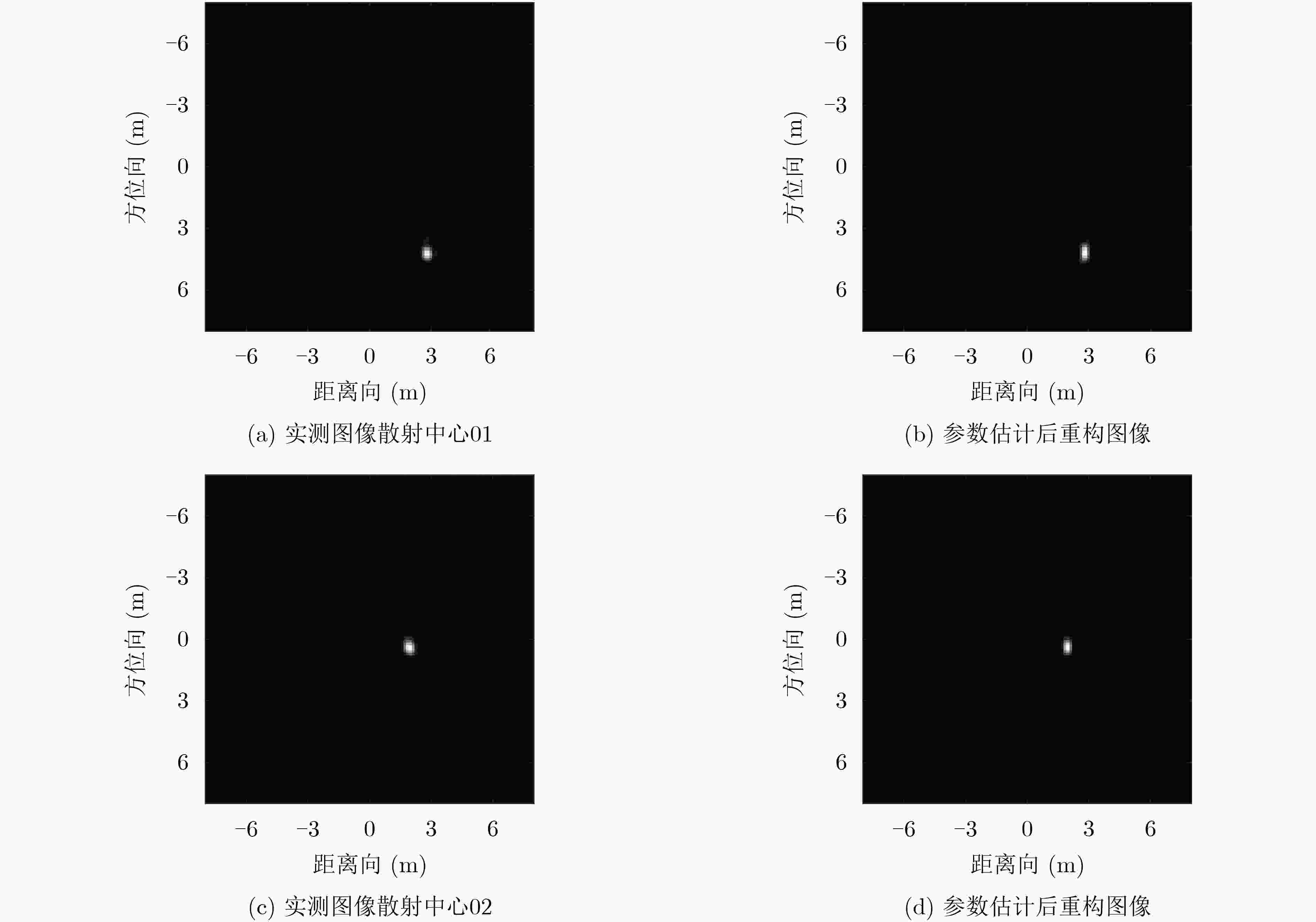
散射中心 $ x{\text{ (m)}} $ $ y{\text{ (m)}} $ $ A $ $ \alpha $ $ L{\text{ (m)}} $ 散射体结构 01 1.7070 –1.9574 5.3957 1 0 三面角 02 1.1773 –0.1327 2.4347 1 0 三面角 表 6 3种算法的计算耗时(s)
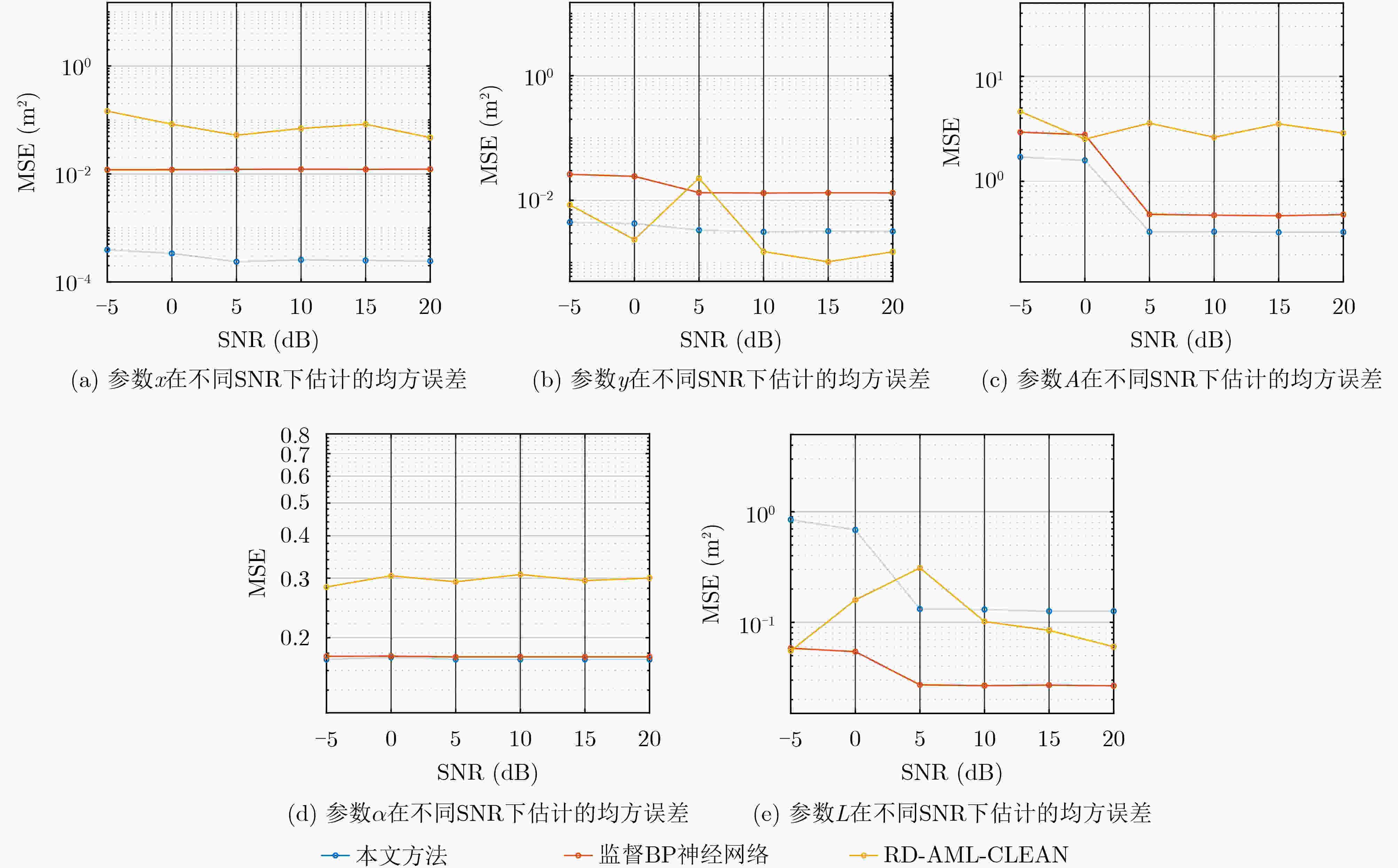
本文方法 监督BP神经网络 RD-AML-CLEAN 计算耗时 0.055 1 0.055 0 4.119 4 -
[1] 徐丰, 王海鹏, 金亚秋. 合成孔径雷达图像智能解译[M]. 北京: 科学出版社, 2020: 2–5.XU Feng, WANG Haipeng, and JIN Yaqiu. Intelligent Interpretation of Synthetic Aperture Radar Images[M]. Beijing: Science Press, 2020: 2–5. [2] CHEN Jiankun, PENG Lingxiao, QIU Xiaolan, et al. A 3D building reconstruction method for SAR images based on deep neural network[J]. Scientia Sinica Informationis, 2019, 49(12): 1606–1625. doi: 10.1360/SSI-2019-0100. [3] PENG Lingxiao, QIU Xiaolan, DING Chibiao, et al. Generating 3d point clouds from a single SAR image using 3D reconstruction network[C]. IGARSS 2019–2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 2019: 3685–3688. doi: 10.1109/IGARSS.2019.8900449. [4] 邢孟道, 谢意远, 高悦欣, 等. 电磁散射特征提取与成像识别算法综述[J]. 雷达学报, 2022, 11(6): 921–942. doi: 10.12000/JR22232.XING Mengdao, XIE Yiyuan, GAO Yuexin, et al. Electromagnetic scattering characteristic extraction and imaging recognition algorithm: A review[J]. Journal of Radars, 2022, 11(6): 921–942. doi: 10.12000/JR22232. [5] 计科峰. SAR图像目标特征提取与分类方法研究[D]. [博士论文], 中国人民解放军国防科技大学, 2003.JI Kefeng. Research on SAR image target feature extraction and classification methods[D]. [Ph. D. dissertation], National University of Defense Technology, 2003. [6] 段佳, 张磊, 盛佳恋, 等. 独立属性散射中心参数降耦合估计方法[J]. 电子与信息学报, 2012, 34(8): 1853–1859. doi: 10.3724/SP.J.1146.2011.01302.DUAN Jia, ZHANG Lei, SHENG Jialian, et al. Parameters decouple and estimation of independent attributed scattering centers[J]. Journal of Electronics & Information Technology, 2012, 34(8): 1853–1859. doi: 10.3724/SP.J.1146.2011.01302. [7] 石志广, 周剑雄, 赵宏钟, 等. 基于协同粒子群优化的GTD模型参数估计方法[J]. 电子学报, 2007, 35(6): 1102–1107. doi: 10.3321/j.issn:0372-2112.2007.06.020.SHI Zhiguang, ZHOU Jianxiong, ZHAO Hongzhong, et al. A GTD scattering center model parameter estimation method based on CPSO[J]. Acta Electronica Sinica, 2007, 35(6): 1102–1107. doi: 10.3321/j.issn:0372-2112.2007.06.020. [8] 李飞, 纠博, 刘宏伟, 等. 基于稀疏表示的SAR图像属性散射中心参数估计算法[J]. 电子与信息学报, 2014, 36(4): 931–937. doi: 10.3724/SP.J.1146.2013.00576.LI Fei, JIU Bo, LIU Hongwei, et al. Sparse representation based algorithm for estimation of attributed scattering center parameter on SAR imagery[J]. Journal of Electronics & Information Technology, 2014, 36(4): 931–937. doi: 10.3724/SP.J.1146.2013.00576. [9] YANG Dongwen, NI Wei, DU Lan, et al. Efficient attributed scatter center extraction based on image-domain sparse representation[J]. IEEE Transactions on Signal Processing, 2020, 68: 4368–4381. doi: 10.1109/tsp.2020.3011332. [10] XIE Yiyuan, XING Mengdao, GAO Yuexin, et al. Attributed scattering center extraction method for microwave photonic signals using DSM-PMM-regularized optimization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5230016. doi: 10.1109/TGRS.2022.3183855. [11] ZHANG Jinsong, XING Mengdao, and XIE Yiyuan. FEC: A feature fusion framework for SAR target recognition based on electromagnetic scattering features and deep CNN features[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(3): 2174–2187. doi: 10.1109/TGRS.2020.3003264. [12] FENG Sijia, JI Kefeng, WANG Fulai, et al. Electromagnetic scattering feature (ESF) module embedded network based on ASC model for robust and interpretable SAR ATR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5235415. doi: 10.1109/TGRS.2022.3208333. [13] FENG Sijia, JI Kefeng, ZHANG Linbin, et al. SAR target classification based on integration of ASC parts model and deep learning algorithm[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14: 10213–10225. doi: 10.1109/JSTARS.2021.3116979. [14] GERRY M J, POTTER L C, GUPTA I J, et al. A parametric model for synthetic aperture radar measurements[J]. IEEE Transactions on Antennas and Propagation, 1999, 47(7): 1179–1188. doi: 10.1109/8.785750. [15] POTTER L C and MOSES R L. Attributed scattering centers for SAR ATR[J]. IEEE Transactions on Image Processing, 1997, 6(1): 79–91. doi: 10.1109/83.552098. [16] KINGMA D P and WELLING M. Auto-encoding variational bayes[J]. arXiv: 1312.6114, 2013. doi: 10.48550/arXiv.1312.6114. [17] HORIE M, MORITA N, HISHINUMA T, et al. Isometric transformation invariant and equivariant graph convolutional networks[C]. The ICLR 2021, https://doi.org/10.48550/arXiv.2005.06316. [18] MENG Chuizheng, SEO S, CAO Defu, et al. When physics meets machine learning: A survey of physics-informed machine learning[J]. arXiv: 2203.16797, 2022. doi: 10.48550/arXiv.2203.16797. -





 下载:
下载:




 下载:
下载:
