基于深度学习的水声信道联合多分支合并与均衡算法

刘志勇; 金子皓; 杨洪娟; 刘彪; 唐新丰; 李博

doi:10.11999/JEIT231196

基于深度学习的水声信道联合多分支合并与均衡算法

doi: 10.11999/JEIT231196

刘志勇^{1, 3, 4},
金子皓¹,
杨洪娟^1, ,,
刘彪²,
唐新丰²,
李博¹

1.
哈尔滨工业大学(威海)信息科学与工程学院威海 264209
2.
北京宇航系统工程研究所北京 100076
3.
山东省海洋电子信息与智能无人系统重点实验室威海 264209
4.
海洋无人系统跨域协同与综合保障工业和信息化部重点实验室威海 264209

基金项目: 战略火箭创新基金(ZH2022007)，国家自然科学基金(61871148)，山东省重大科技创新工程(2020CXGC010705, 2021ZLGX05, 2022ZLGX04)

详细信息

作者简介:
刘志勇：男，副教授，研究方向为无线通信、水声通信

金子皓：男，硕士生，研究方向为水声通信、人工智能

杨洪娟：女，副教授，研究方向为无线通信、水声通信

刘彪：男，工程师，研究方向为水声通信、无线通信

唐新丰：男，工程师，研究方向为无线测控通信、数据链

李博：男，副教授，研究方向为无线通信、水声通信

通讯作者:
杨洪娟　hjyang@hit.edu.cn

中图分类号: TN929.3
计量
- 文章访问数: 64
- HTML全文浏览量: 31
- PDF下载量: 11
- 被引次数: 0
出版历程
- 收稿日期: 2023-10-31
- 修回日期: 2024-03-27
- 网络出版日期: 2024-05-07
- 刊出日期: 2024-05-10

Deep Learning-based Joint Multi-branch Merging and Equalization Algorithm for Underwater Acoustic Channel

LIU Zhiyong^{1, 3, 4},
JIN Zihao¹,
YANG Hongjuan^{1
, ,},
LIU Biao²,
TANG Xinfeng²,
LI Bo¹

1.
School of Information Science and Engineering, Harbin Institute of Technology (Weihai), Weihai 264209, China
2.
Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China
3.
Shandong Provincial Key Laboratory of Marine Electronic Information and Intelligent Unmanned Systems, Weihai 264209, China
4.
Key Laboratory of Cross-Domain Synergy and Comprehensive Support for Unmanned Marine Systems, Ministry of Industry and Information Technology, Weihai 264209, China

Funds: The Strategic Rocket Innovation Foundation (ZH2022007), The National Natural Science Foundation of China (61871148), The Major Scientific and Technological Innovation Project of Shandong Province of China (2020CXGC010705, 2021ZLGX05, 2022ZLGX04)

摘要

摘要: 为了更好地解决水声信道中的衰落及严重码间干扰问题，该文提出一种基于深度学习的联合多分支合并与均衡算法。该算法借助深度学习网络的非线性拟合能力，联合实现了多分支合并和均衡。在算法实现中，合并与均衡并非相互独立，而是基于深度学习网络的总输出计算出总误差，以总误差对网络参数实现联合调整，数据集则基于统计水声信道模型进行构建。仿真结果表明，相较于已有算法，所提算法能获得更快的收敛速度和更好的误码率性能，使得其能更好地适应水声信道。
- 水声通信 /
- 深度学习 /
- 水声信道 /
- 联合多分支合并与均衡
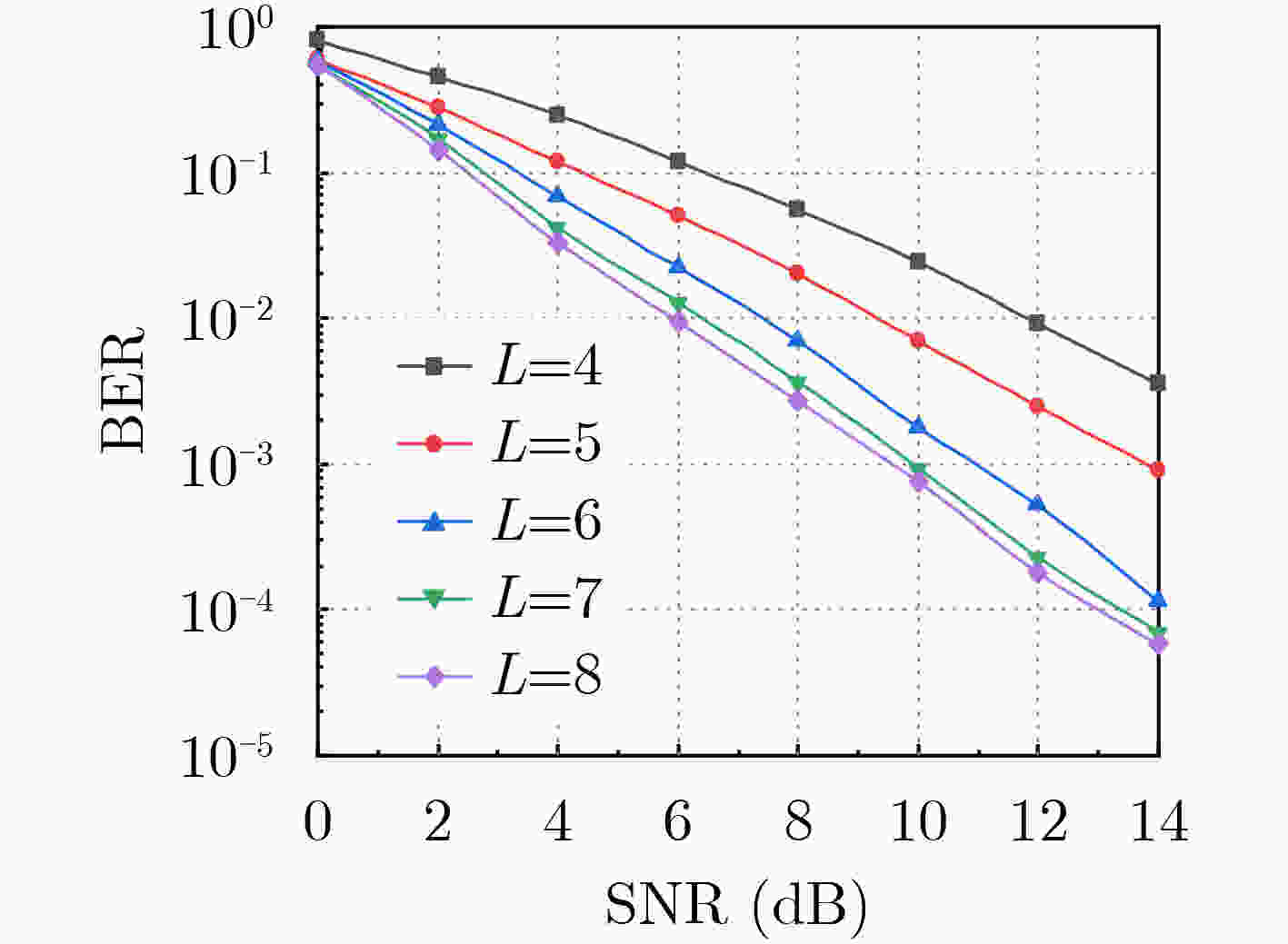
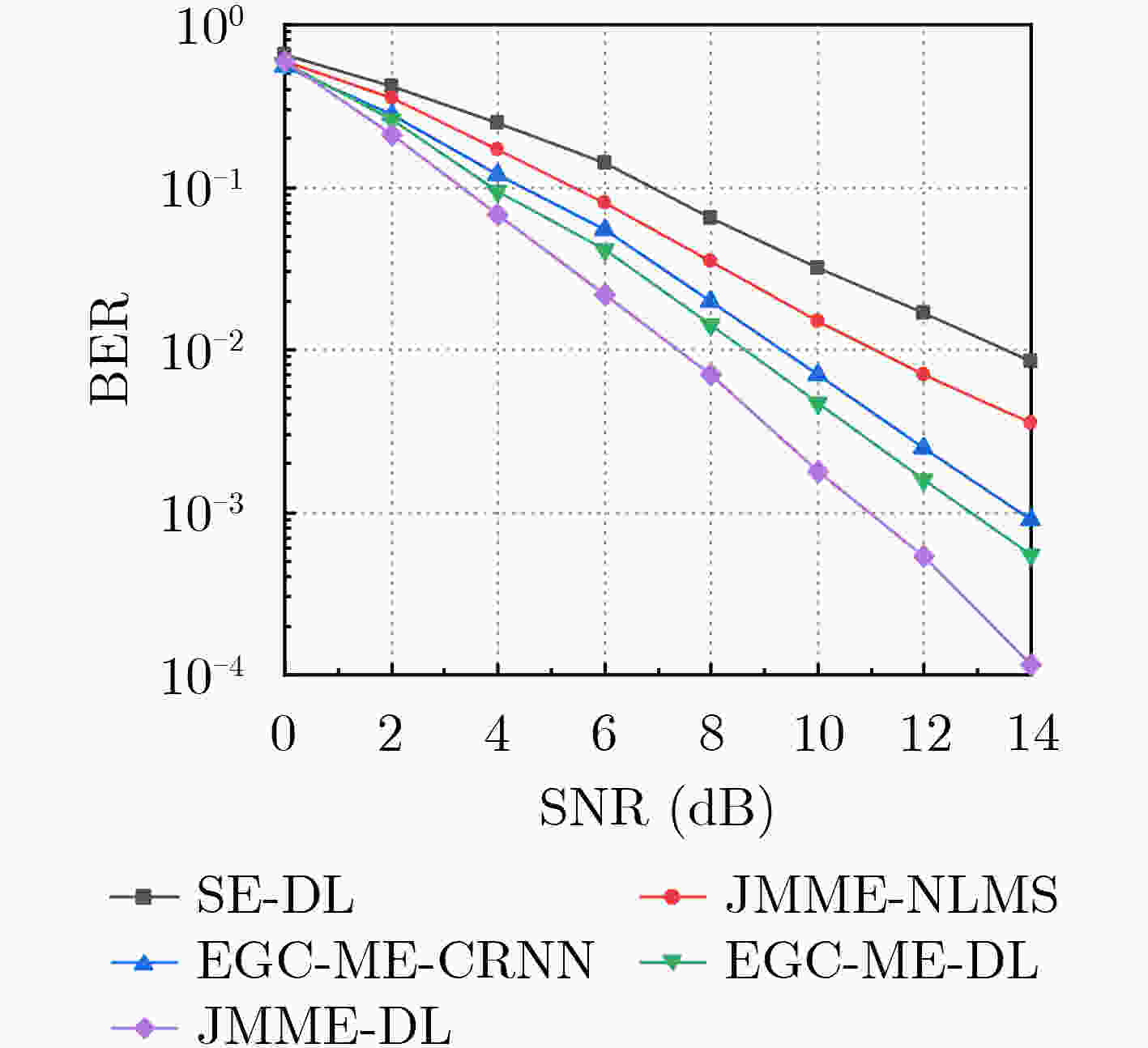
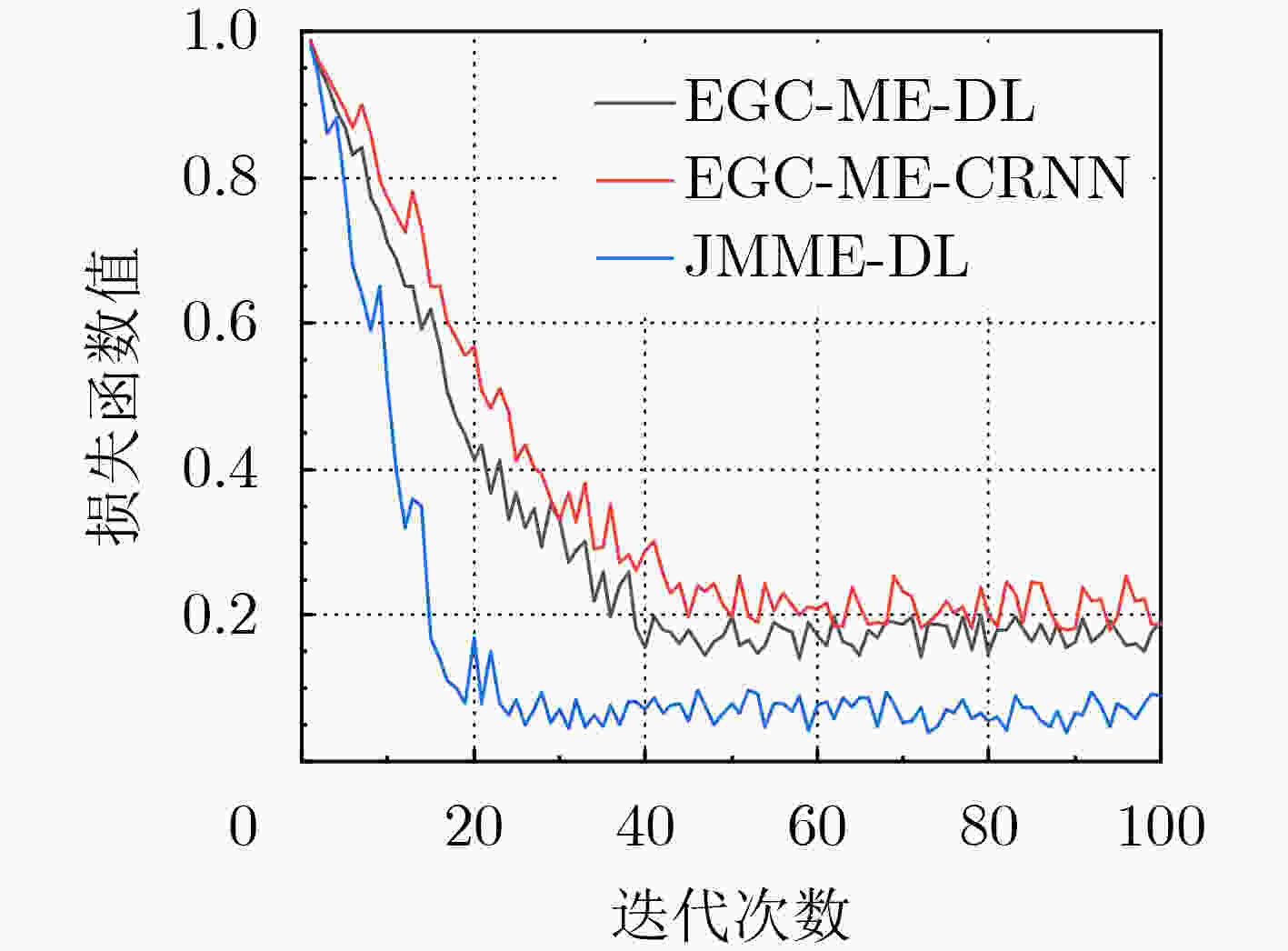
Abstract: To better solve the fading and severe inter-symbol interference problems in underwater acoustic channels, a Joint Multi-branch Merging and Equalization algorithm based on Deep Learning (JMME-DL) is proposed in this paper. The algorithm jointly implements multi-branch merging and equalization with the help of the nonlinear fitting ability of the deep learning network. The merging and equalization are not independent of each other, in the implementation of the algorithm, the total error is first calculated based on the total output of the deep learning network, and then the network parameters of each part are jointly adjusted with the total error, and the dataset is constructed based on the statistical underwater acoustic channel model. Simulation results show that the proposed algorithm achieves faster convergence speed and better BER performance compared to the existing algorithms, making it better adapted to underwater acoustic channels.
- Underwater acoustic communication /
- Deep learning /
- Underwater acoustic channel /
- Joint multi-branch merging and equalization

HTML全文

图 1 水声SIMO通信系统示意图

下载: 全尺寸图片幻灯片

图 2 JMME-DL算法结构示意图

下载: 全尺寸图片幻灯片

图 3 SIGMOID激活函数示意图

下载: 全尺寸图片幻灯片

图 4 发射机与各个水听器间的信道冲激响应

下载: 全尺寸图片幻灯片

图 5 网络层数对算法性能的影响对比图

下载: 全尺寸图片幻灯片

图 6 水声信道下算法误码率性能比较

下载: 全尺寸图片幻灯片

图 7 水声信道下算法收敛曲线

下载: 全尺寸图片幻灯片

1 JMME-DL算法

输入：训练集：$ \mathcal{D} = \left\{ {\left( {{r_i}(n),s(n)} \right)} \right\}_{i = 1}^N $中$ K $组数据；验证集：
$ V $；学习率：$ \alpha $；正则化系数：$ \lambda $；迭代次数：$ M $
初始化：$ {\boldsymbol{\theta}} ,{\boldsymbol{b}} $
repeat
for i = 1 2 ··· M do
(1) 从训练集$ \mathcal{D} $中选取$ K $组数据样本
(2) 前馈计算，直到最后一层并计算总输出
(3) 反向传播计算每一层的误差
// 计算每一层参数的导数
$ \dfrac{{\partial L}}{{\partial {{\boldsymbol{\theta}} }_{^{(i)}}^{^{(l)}}}} = {({{\boldsymbol{o}}}_i^{(l - 1)})^{\text{T}}}{{\boldsymbol{\delta}} }_i^l{\text{ }}(l = 1, \cdots ,L - 1) $
$ \dfrac{{\partial L}}{{\partial {{\boldsymbol{b}}}_{^{(i)}}^{^{(l)}}}} = {\text{sum}}\{ {{\boldsymbol{\delta}} }_i^l{\text{\} }}(l = 1, \cdots ,L - 1) $
// 更新参数
$ {{\boldsymbol{\theta}} }_{(i)}^{^{(l)}} = {{\boldsymbol{\theta }}}_{^{(i)}}^{^{(l)}} - \alpha {({{\boldsymbol{o}}}_i^{(l - 1)})^{\text{T}}}{{\boldsymbol{\delta}} }_i^l{\text{ }}(l = 1, \cdots ,L - 1) $
$ {{\boldsymbol{b}}}_{^{(i)}}^{^{(l)}} = {{\boldsymbol{b}}}_{^{(i)}}^{^{(l)}} - \alpha {{\boldsymbol{\delta}} }_i^l{\text{ }}(l = 1, \cdots ,L - 1) $
until训练的模型在验证集$ V $的错误率不再下降；
输出：$ {\boldsymbol{\theta}} ,{\boldsymbol{b}} $

下载: 导出CSV

表 1 水声信道仿真主要参数

仿真参数	数值
海水深度(m)	300
发射机深度(m)	100
水听器1深度(m) 水听器2深度(m)	120 125
水听器3深度(m)	130
发射机与水听器水平距离(m)	3000
水下传播系数	1.6
水下声速(m/s)	1500
载波频率(kHz)	10
带宽(kHz)	5

下载: 导出CSV

参考文献(12)

[1]	邵宗战. 现代水声通信技术发展探讨[J]. 科技创新与应用, 2022, 12(20): 152–155. doi: 10.19981/j.CN23-1581/G3.2022.20.036. SHAO Zongzhan. Discussion on the development of modern hydroacoustic communication technology[J]. Technology Innovation and Application, 2022, 12(20): 152–155. doi: 10.19981/j.CN23-1581/G3.2022.20.036.
[2]	XIE Lin, ZHAO Haili, TIAN Chengjun, et al. Comparison of several new improved variable-step LMS algorithms[C]. 2022 7th International Conference on Automation, Control and Robotics Engineering (CACRE), Xi’an, China, 2022: 229–233. doi: 10.1109/CACRE54574.2022.9834206.
[3]	GUO Xiaochen, ZHANG Youwen, and ZHENG Wei. Variable forgetting factor RLS algorithm for mobile single carrier SIMO underwater acoustic communication[C]. Proceedings of SPIE 12615, International Conference on Signal Processing and Communication Technology (SPCT 2022), Harbin, China, 2023: 1261519. doi: 10.1117/12.2674104.
[4]	CHENG Xing, LIU Dejun, WANG Chen, et al. Deep learning-based channel estimation and equalization scheme for FBMC/OQAM systems[J]. IEEE Wireless Communications Letters, 2019, 8(3): 881–884. doi: 10.1109/LWC.2019.2898437.
[5]	CHEN S, GIBSON G J, COWAN C F N, et al. Adaptive equalization of finite non-linear channels using multilayer perceptrons[J]. Signal Processing, 1990, 20(2): 107–119. doi: 10.1016/0165-1684(90)90122-F.
[6]	LAVANIA S, KUMAM B, MATEY P S, et al. Adaptive channel equalization using recurrent neural network under SUI channel model[C]. 2015 International Conference on Innovations in Information, Embedded and Communication Systems (ICIIECS), Coimbatore, India, 2015: 1–6. doi: 10.1109/ICIIECS.2015.7193035.
[7]	ZHANG Youwen, LI Junxuan, ZAKHAROV Y, et al. Deep learning based underwater acoustic OFDM communications[J]. Applied Acoustics, 2019, 154: 53–58. doi: 10.1016/j.apacoust.2019.04.023.
[8]	JARUWATANADILOK S. Underwater wireless optical communication channel modeling and performance evaluation using vector radiative transfer theory[J]. IEEE Press, 2008, 26(9): 1620–1627. doi: 10.1109/JSAC.2008.081202.
[9]	STOJANOVIC M, CATIPOVIC J, and PROAKIS J G. Adaptive multichannel combining and equalization for underwater acoustic communications[J]. The Journal of the Acoustical Society of America, 1993, 94(3): 1621–1631. doi: 10.1121/1.408135.
[10]	CHOI J W, RIEDL T J, KIM K, et al. Adaptive linear turbo equalization over doubly selective channels[J]. IEEE Journal of Oceanic Engineering, 2011, 36(4): 473–489. doi: 10.1109/JOE.2011.2158013.
[11]	LIU Zhiyong, WANG Yinghua, SONG Lizhong, et al. Joint adaptive combining and variable tap-length multiuser detector for underwater acoustic cooperative communication[J]. KSII Transactions on Internet and Information Systems, 2018, 12(1): 325–339. doi: 10.3837/tiis.2018.01.016.
[12]	QARABAQI P and STOJANOVIC M. Statistical characterization and computationally efficient modeling of a class of underwater acoustic communication channels[J]. IEEE Journal of Oceanic Engineering, 2013, 38(4): 701–717. doi: 10.1109/JOE.2013.2278787.