Survey on Optimised Design of Robust Chaotic Transmission Systems for Impulsive Noise under Power Line Communication Channels
-
摘要: 随着用户的剧增,现有的无线资源已经难以为继。因此,电力线通信(PLC)的重新启用引起了各大研究单位及工业界的关注。PLC由于信道环境复杂,现有处理方案复杂度及成本较高,因而导致其发展缓慢。其中针对脉冲噪声的研究工作最为广泛,如何在低成本情况下针对脉冲噪声实现数据传输的鲁棒性尤为重要。该文首先介绍PLC环境中几种主流噪声以及分类,而后描述具有低成本低复杂度的差分混沌键控(DCSK)及多元DCSK(MDCSK)调制技术。分别介绍与分析该系统在PLC中的特性,以及针对各种脉冲噪声种类存在的优势以及改进方式。其次该文将介绍一些相关编码调制新方案以便于提高带限环境下的传输质量。结果表明这些优化工作显著地改善了系统性能,针对PLC整体信道特性系统参数的调制及编码调制传输优化方案将成为未来工作的研究热点。Abstract: With the drastic increase in the number of users, the existing wireless resources have become unsustainable. Therefore, the reactivation of Power Line Communication (PLC) has attracted the attention of major research institutes and industries. The development of PLC has been slow due to the complexity of the channel environment and the complexity and high cost of existing processing solutions. The most extensive work has been done on impulse noise, and it is particularly important to achieve robustness of data transmission against impulse noise at low cost. Firstly, the mainstream noise in PLC environment and its classification are introduced in this paper, and then the Differential Chaos Shift Keying (DCSK) and M-ary DCSK (MDCSK) modulation techniques with low cost and low complexity are described. The characteristics of this system in PLCs are presented and analysed, as well as the advantages and improvements that exist for various types of impulse noise. Secondly, some relevant new coding and modulation schemes are introduced in order to improve the transmission quality in band-limited environments. The results show that these optimisations significantly improve the system performance. Subsequently, modulation and coded modulation transmission optimisation schemes for PLC overall channel characteristics system parameters will be a hot topic for future work.
-
1 PEXIT码型搜索算法
初始化: 设定 预先设定相关参数, 设定 J(σ) = I(Vi;LLR) 设定 SNR 程序: (1)计算作为输出外在MI的互信息; (2)根据VDMM的置换模式,在变量节点的输入端设置MI; (3)求得第j个VN→第i个CN的先验MI,并令其等于第j个VN→第i
个CN的外在MI;(4)求得第i个 CN → j个VN的先验 MI,并令其等于第j个
VN→第i个CN的外在MI;(5)求得后验概率对数似然比的计算公式 (6)对于 i = 0, 1, ···, n,重复执行迭代过程步骤 (3)—步骤(5),
直到后验概率对数似然比为1。表 1 不同抗击脉冲噪声方案的对比
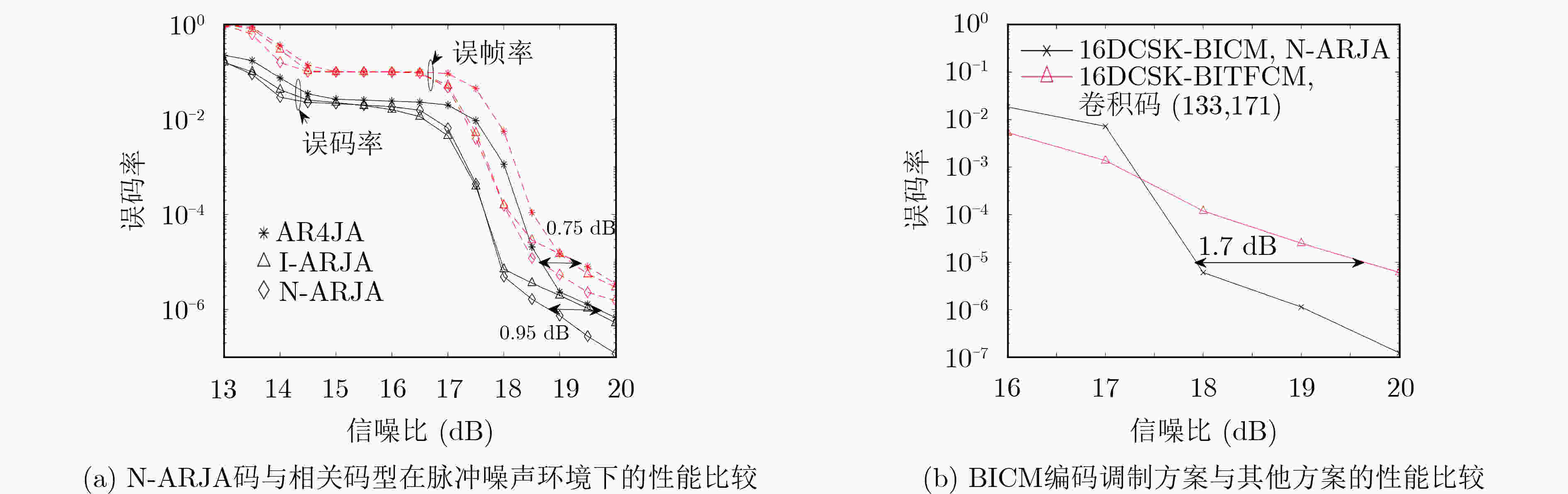
抗击噪声方案 基本原理 优点 缺点 RP-MDCSK 利用冗余信息进行平滑滤波抗噪 系统实现相对简单,硬件成本较低 引入冗余信息,降低系统的能量效率和频谱效率 JPCM-DCSK 指标调制分散能量进行抗噪 实现方案成熟,易于移植 计算复杂度高,降低系统的能量效率和频谱效率 DC-BICM-IR MyF滤波器、编码冗余信息、迭代接收抗噪 能够大幅度地提高系统的误码率性能 复杂度高,成本高,使用技术复杂 MDCSK-BICM 编码冗余信息,可变度匹配映射选择抗噪 硬件成本较低,低功耗 分析工具要求近似高斯 -
[1] IYIOLA A O, FAMILUA A D, SWART T G, et al. Modeling of burst impulse noise errors in an in-house M-QAM-based power line communications channel using the Fritchman–Markov model[J]. Sensors, 2023, 23(15): 6659. doi: 10.3390/s23156659. [2] DA SILVA COSTA L G, CANTARINO W M, CAMPONOGARA Â, et al. A notch filter-based coupling circuit for UNB and NB PLC systems[J]. Sensors, 2022, 22(24): 9722. doi: 10.3390/s22249722. [3] WANG Wenyuan and DOGANCAY K. Convergence issues in sequential partial-update LMS for cyclostationary white Gaussian input signals[J]. IEEE Signal Processing Letters, 2021, 28: 967–971. doi: 10.1109/LSP.2021.3074089. [4] AGRAWAL N and SHARMA P K. Capacity analysis of a NB-PLC system with background and impulsive noises[C]. 2017 International Conference on Computer, Communications and Electronics, Jaipur, India, 2017: 118–123. doi: 10.1109/COMPTELIX.2017.8003949. [5] CORTÉS J A, CAÑETE F J, and DÍEZ L. Channel estimation for OFDM-based indoor broadband power line communication systems[J]. Journal of Communications and Networks, 2023, 25(2): 151–166. doi: 10.23919/JCN.2022.000056. [6] SPAULDING A and MIDDLETON D. Optimum reception in an impulsive interference environment-Part I: Coherent detection[J]. IEEE Transactions on Communications, 1977, 25(9): 910–923. doi: 10.1109/TCOM.1977.1093943. [7] AGRAWAL N, SHARMA P K, and TSIFTSIS T A. Multihop DF relaying in NB-PLC system over Rayleigh fading and Bernoulli–Laplacian noise[J]. IEEE Systems Journal, 2019, 13(1): 357–364. doi: 10.1109/JSYST.2018.2870204. [8] MIDDLETON D. Non-Gaussian noise models in signal processing for telecommunications: New methods an results for class A and class B noise models[J]. IEEE Transactions on Information Theory, 1999, 45(4): 1129–1149. doi: 10.1109/18.761256. [9] KATAYAMA M, YAMAZATO T, and OKADA H. A mathematical model of noise in narrowband power line communication systems[J]. IEEE Journal on Selected areas in Communications, 2006, 24(7): 1267–1276. doi: 10.1109/JSAC.2006.874408. [10] LIN Jing, NASSAR M, and EVANS B L. Impulsive noise mitigation in powerline communications using sparse Bayesian learning[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(7): 1172–1183. doi: 10.1109/JSAC.2013.130702. [11] NIKITIN A V, SCUTTI D, NATARAJAN B, et al. Blind adaptive analog nonlinear filters for noise mitigation in powerline communication systems[C]. 2015 IEEE International Symposium on Power Line Communications and its Applications, Austin, USA, 2015: 1–6. doi: 10.1109/ISPLC.2015.7147580. [12] NASSAR M, GULATI K, MORTAZAVI Y, et al. Statistical modeling of asynchronous impulsive noise in powerline communication networks[C]. 2011 IEEE Global Telecommunications Conference, Houston, USA, 2011: 1–6. doi: 10.1109/GLOCOM.2011.6134477. [13] PIGHI R, FRANCESCHINI M, FERRARI G, et al. Fundamental performance limits of communications systems impaired by impulse noise[J]. IEEE Transactions on Communications, 2009, 57(1): 171–182. doi: 10.1109/TCOMM.2009.0901.060440. [14] HELSTROM C W. Detectability of signals in Laplace noise[J]. IEEE Transactions on Aerospace and Electronic Systems, 1989, 25(2): 190–196. doi: 10.1109/7.18680. [15] OMRI A, FERNANDEZ J H, and DI PIETRO R. Subcarrier-index modulation for OFDM-based PLC systems[C]. The 2023 IEEE Symposium on Computers and Communications, Gammarth, Tunisia, 2023: 649–655. doi: 10.1109/ISCC58397.2023.10217844. [16] OMRI A, FERNANDEZ J H, and DI PIETRO R. Extending device noise measurement capacity for OFDM-based PLC systems: Design, implementation, and on-field validation[J]. Computer Networks, 2023, 237: 110038. doi: 10.1016/j.comnet.2023.110038. [17] FERNANDEZ J H, LACASA L, OMRI A, et al. Ergodic capacity analysis of OFDM-based NB-PLC systems[C]. The 2022 24th International Conference on Advanced Communication Technology, PyeongChang, South Korea, 2022: 399–405. doi: 10.23919/ICACT53585.2022.9728888. [18] ALAM S, SELIM B, and KADDOUM G. Analysis and comparison of several mitigation techniques for Middleton class-A noise[C]. 2019 IEEE Latin-American Conference on Communications, Salvador, Brazil, 2019: 1–6. doi: 10.1109/LATINCOM48065.2019.8938020. [19] YANG Ping, GUAN Yongliang, LIU Xiaobei, et al. An improved hybrid turbo equalizer for single carrier transmission with impulsive noise and ISI[J]. IEEE Transactions on Vehicular Technology, 2017, 66(11): 9852–9861. doi: 10.1109/TVT.2017.2727322. [20] KADDOUM G and TADAYON N. Differential chaos shift keying: A robust modulation scheme for power-line communications[J]. IEEE Transactions on Circuits and Systems Ⅱ:Express Briefs, 2017, 64(1): 31–35. doi: 10.1109/TCSII.2016.2546901. [21] CAI Xiangming, XU Weikai, WANG Lin, et al. Joint energy and correlation detection assisted non-coherent OFDM-DCSK system for underwater acoustic communications[J]. IEEE Transactions on Communications, 2022, 70(6): 3742–3759. doi: 10.1109/TCOMM.2022.3169227. [22] ZHANG Haotian, ZHANG Lin, JIANG Yuan, et al. Reliable and secure deep learning-based OFDM-DCSK transceiver design without delivery of reference chaotic sequences[J]. IEEE Transactions on Vehicular Technology, 2022, 71(8): 8059–8074. doi: 10.1109/TVT.2022.3175968. [23] KADDOUM G, SOUJERI E, ARCILA C, et al. I-DCSK: An improved noncoherent communication system architecture[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2015, 62(9): 901–905. doi: 10.1109/TCSII.2015.2435831. [24] YANG Hua, JIANG Guoping, and DUAN Junyi. Phase-separated DCSK: A simple delay-component-free solution for chaotic communications[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2014, 61(12): 967–971. doi: 10.1109/TCSII.2014.2356914. [25] WANG Bingrui, CHEN Haoyu, XIE Zhaopeng, et al. Design of permutation index DCSK with noise reduction for short-range IoT communications[J]. IEEE Access, 2023, 10: 102332–102339. doi: 10.1109/ACCESS.2023.3317180. [26] TAO Yiwei, FANG Yi, CHEN Pingping, et al. Matrix reconstruction algorithm-assisted multi-carrier DCSK scheme: An effective solution for frequency-selective fading channel[J]. IEEE Wireless Communications Letters, 2023, 12(11): 1941–1945. doi: 10.1109/LWC.2023.3300353. [27] MIAO Meiyuan, BEN NAILA C, OKADA H, et al. Design and analysis of a multi-rate multiple-access differential chaos shift keying system[J]. IEICE Transactions on Communications, 2023, E106.B(10): 873–880. doi: 10.1587/transcom.2023EBP3005. [28] CAI Xiangming, XU Weikai, WANG Lin, et al. Design and performance analysis of a robust multi-carrier M-ary DCSK system: A noise suppression perspective[J]. IEEE Transactions on Communications, 2022, 70(3): 1623–1637. doi: 10.1109/TCOMM.2022.3144276. [29] TAO Yiwei, FANG Yi, MA Huan, et al. Multi-carrier DCSK with hybrid index modulation: A new perspective on frequency-index-aided chaotic communication[J]. IEEE Transactions on Communications, 2022, 70(6): 3760–3773. doi: 10.1109/TCOMM.2022.3169214. [30] ZHANG Mengxuan, CHENG Guixian, YANG Bohan, et al. Generalized carrier index differential chaos shift keying based SWIPT with conversion noise and path loss-effect[J]. Electronics, 2022, 11(15): 2406. doi: 10.3390/electronics11152406. [31] FANG Yi, ZHUO Junming, MA Huan, et al. Design and analysis of a new index-modulation-aided DCSK system with frequency-and-time resources[J]. IEEE Transactions on Vehicular Technology, 2023, 72(6): 7411–7425. doi: 10.1109/TVT.2023.3238379. [32] LIN Zixian, XU Weikai, SUN Haixin, et al. A hybrid DCSK scheme combining cyclic shift keying and code index modulation[J]. IEEE Communications Letters, 2023, 27(9): 2303–2307. doi: 10.1109/LCOMM.2023.3294514. [33] YAN Yufan, GUO Qin, CHEN Pingping, et al. Permutation index DCSK with spatial modulation for chaotic communications[C]. The 2022 IEEE 8th International Conference on Computer and Communications, Chengdu, China, 2022: 1546–1550. doi: 10.1109/ICCC56324.2022.10065663. [34] KANG Peng, ZHU Ziqiang, LIN Zhijian, et al. Design of chaotic-based PPM-PI-DCSK modulation for wireless communications[J]. IEEE Wireless Communications Letters, 2023, 12(10): 1662–1666. doi: 10.1109/LWC.2023.3283145. [35] LIU Zhaofeng, SO H C, LI Xiaopeng, et al. Robust and energy efficient sparse-Coded OFDM-DCSK system via matrix recovery[J]. IEEE Transactions on Communications, 2023, 71(8): 4839–4850. doi: 10.1109/TCOMM.2023.3279403. [36] YAO Wenjie, WANG Sheng, ZHANG Hao, et al. Design and analysis of a noise reduction PI-DCSK system for wireless underground power pipe gallery communications[C]. The 2023 4th Information Communication Technologies Conference, Nanjing, China, 2023: 44–48. doi: 10.1109/ICTC57116.2023.10154786. [37] ZHU Ziqiang, CHEN Pingping, LIN Zhijian, et al. DPI DCSK modulation with BCJR decoding[J]. International Journal of Bifurcation and Chaos, 2023, 33(4): 2350042. doi: 10.1142/S0218127423500426. [38] CHEN Haoyu, CHEN Pingping, FANG Yi, et al. Parallel differential chaotic shift keying with code index modulation for wireless communication[J]. IEEE Transactions on Communications, 2022, 70(8): 5113–5127. doi: 10.1109/TCOMM.2022.3187158. [39] MA Huan, FANG Yi, CHEN Pingping, et al. A novel differential chaos shift keying scheme with multidimensional index modulation[J]. IEEE Transactions on Wireless Communications, 2023, 22(1): 237–256. doi: 10.1109/TWC.2022.3192347. [40] FANG Yi, TAO Yiwei, MA Huan, et al. Design of a reconfigurable intelligent surface-assisted FM-DCSK-SWIPT scheme with non-linear energy harvesting model[J]. IEEE Transactions on Communications, 2023, 71(4): 1863–1877. doi: 10.1109/TCOMM.2023.3239647. [41] WANG Lin, CAI Guofa, and CHEN G R. Design and performance analysis of a new multiresolution M-ary differential chaos shift keying communication system[J]. IEEE Transactions on Wireless Communications, 2015, 14(9): 5197–5208. doi: 10.1109/TWC.2015.2434820. [42] CAI Guofa, FANG Yi, HAN Guojun, et al. A square-constellation-based M-ary DCSK communication system[J]. IEEE Access, 2016, 4: 6295–6303. doi: 10.1109/ACCESS.2016.2612224. [43] CAI Guofa, FANG Yi, and HAN Guojun. Design of an adaptive multiresolution M-ary DCSK system[J]. IEEE Communications Letters, 2017, 21(1): 60–63. doi: 10.1109/LCOMM.2016.2614682. [44] CAI Guofa, FANG Yi, HAN Guojun, et al. A new hierarchical M-ary DCSK communication system: Design and analysis[J]. IEEE Access, 2017, 5: 17414–17424. doi: 10.1109/ACCESS.2017.2740973. [45] 苗美媛, 宋丹, 徐位凯, 等. 非平稳信道下的鲁棒数据链优化设计综述——带限环境下的混沌传输系统[J]. 电子与信息学报, 2021, 43(1): 1–12. doi: 10.11999/JEIT200311.MIAO Meiyuan, SONG Dan, XU Weikai, et al. Survey of optimization design for robust data link over non-stationary channels-chaotic transmission systems over band-limited environments[J]. Journal of Electronics & Information Technology, 2021, 43(1): 1–12. doi: 10.11999/JEIT200311. [46] ZEHAVI E. 8-PSK trellis codes for a Rayleigh channel[J]. IEEE Transactions on Communications, 1992, 40(5): 873–884. doi: 10.1109/26.141453. [47] CAIRE G, TARICCO G, and BIGLIERI E. Bit-interleaved coded modulation[J]. IEEE Transactions on Information Theory, 1998, 44(3): 927–946. doi: 10.1109/18.669123. [48] DIVSALAR D and JONES C. Protograph based low error floor LDPC coded modulation[C]. 2005 IEEE Military Communications Conference, Atlantic City, USA, 2005: 378–385. doi: 10.1109/MILCOM.2005.1605713. [49] JIN Yi, JIANG Ming, and ZHAO Chunming. Optimized variable degree matched mapping for protograph LDPC coded modulation with 16QAM[C]. The 2010 6th International Symposium on Turbo Codes & Iterative Information Processing, Brest, France, 2010: 161–165. doi: 10.1109/ISTC.2010.5613828. [50] HE Yanchun, WANG Lin, ZHOU Chenglong, et al. A novel trellis-coded differential chaotic modulation system[C]. 2017 Wireless Telecommunications Symposium, Chicago, USA, 2017: 1–6. doi: 10.1109/WTS.2017.7943522. [51] CHEN Pingping, XIE Zhaopeng, FANG Yi, et al. Physical-layer network coding: An efficient technique for wireless communications[J]. IEEE Network, 2020, 34(2): 270–276. doi: 10.1109/MNET.001.1900289. [52] VINES R M, TRISSELL H J, GALE L J, et al. Noise on residential power distribution circuits[J]. IEEE Transactions on Electromagnetic Compatibility, 1984, EMC-26(4): 161–168. doi: 10.1109/TEMC.1984.304217. [53] CHAN M H L and DONALDSON R W. Amplitude, width, and interarrival distributions for noise impulses on intrabuilding power line communication networks[J]. IEEE Transactions on Electromagnetic Compatibility, 1989, 31(3): 320–323. doi: 10.1109/15.30920. [54] KATAYAMA M. Introduction to robust, reliable, and high-speed power-line communication systems[J]. IEICE Transactions on Fundamentals, 2001, E84-A(12): 2958–2965. [55] NIWA H, OONO O, KATAYAMA M, et al. A spread-spectrum system with dual processing gains designed for cyclic noise in power line communications[J]. IEICE Transactions on Fundamentals, 1997, E80-A(12): 2526–2533. [56] KADDOUM G and SHOKRANEH F. Analog network coding for multi-user multi-carrier differential chaos shift keying communication system[J]. IEEE Transactions on Wireless Communications, 2015, 14(3): 1492–1505. doi: 10.1109/TWC.2014.2367508. [57] KADDOUM G, RICHARDSON F D, ADOUNI S, et al. Multi-user multi-carrier differential chaos shift keying communication system[C]. The 2013 9th International Wireless Communications and Mobile Computing Conference, Sardinia, Italy, 2013: 1798–1802. doi: 10.1109/IWCMC.2013.6583829. [58] GALIAS Z and MAGGIO G M. Quadrature chaos-shift keying: Theory and performance analysis[J]. IEEE Transactions on Circuits and Systems I:Fundamental Theory and Applications, 2001, 48(12): 1510–1519. doi: 10.1109/TCSI.2001.972858. [59] YANG Hua, TANG W K S, CHEN Guanrong, et al. System design and performance analysis of orthogonal multi-level differential chaos shift keying modulation scheme[J]. IEEE Transactions on Circuits and Systems I:Regular Papers, 2016, 63(1): 146–156. doi: 10.1109/TCSI.2015.2510622. [60] GHOSH M. Analysis of the effect of impulse noise on multicarrier and single carrier QAM systems[J]. IEEE Transactions on Communications, 1996, 44(2): 145–147. doi: 10.1109/26.486604. [61] FAN Tingting, XU Weikai, WANG Lin, et al. A new APSK-based M-ary differential chaos shift keying modulation system[J]. IEEE Communications Letters, 2020, 24(12): 2701–2704. doi: 10.1109/LCOMM.2020.3019105. [62] THOMAS C, WEIDNER M, and DURRANI S. Digital amplitude-phase keying with M-ary alphabets[J]. IEEE Transactions on Communications, 1974, 22(2): 168–180. doi: 10.1109/TCOM.1974.1092165. [63] SHAMAI S and BAR-DAVID I. The capacity of average and peak-power-limited quadrature Gaussian channels[J]. IEEE Transactions on Information Theory, 1995, 41(4): 1060–1071. doi: 10.1109/18.391243. [64] 蔡相明, 徐位凯, 王琳. 差分混沌通信研究综述: 信号设计与性能优化[J]. 电子与信息学报, 2022, 44(10): 3683–3696. doi: 10.11999/JEIT220625.CAI Xiangming, XU Weikai, and WANG Lin. Survey of differential chaotic communications: Signal design and performance optimization[J]. Journal of Electronics & Information Technology, 2022, 44(10): 3683–3696. doi: 10.11999/JEIT220625. [65] KADDOUM G, SOUJERI E, and NIJSURE Y. Design of a short reference noncoherent chaos-based communication systems[J]. IEEE Transactions on Communications, 2016, 64(2): 680–689. doi: 10.1109/TCOMM.2015.2514089. [66] LUO Ronghua, YANG Hua, MENG Chao, et al. A novel SR-DCSK-based ambient backscatter communication system[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2022, 69(3): 1707–1711. doi: 10.1109/TCSII.2021.3109020. [67] HERCEG M, VRANJEŠ D, KADDOUM G, et al. Commutation code index DCSK modulation technique for high-data-rate communication systems[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2018, 65(12): 1954–1958. doi: 10.1109/TCSII.2018.2817930. [68] HERCEG M, KADDOUM G, VRANJEŠ D, et al. Permutation index DCSK modulation technique for secure multiuser high-data-rate communication systems[J]. IEEE Transactions on Vehicular Technology, 2018, 67(4): 2997–3011. doi: 10.1109/TVT.2017.2774108. [69] KADDOUM G, AHMED M F A, and NIJSURE Y. Code index modulation: A high data rate and energy efficient communication system[J]. IEEE Communications Letters, 2015, 19(2): 175–178. doi: 10.1109/LCOMM.2014.2385054. [70] KADDOUM G, NIJSURE Y, and TRAN H. Generalized code index modulation technique for high-data-rate communication systems[J]. IEEE Transactions on Vehicular Technology, 2016, 65(9): 7000–7009. doi: 10.1109/TVT.2015.2498040. [71] KADDOUM G and SOUJERI E. On the comparison between code-index modulation and spatial modulation techniques[C]. 2015 International Conference on Information and Communication Technology Research, Abu Dhabi, United Arab Emirates, 2015: 24–27. doi: 10.1109/ICTRC.2015.7156412. [72] XU Weikai, HUANG Tingting, and WANG Lin. Code-shifted differential chaos shift keying with code index modulation for high data rate transmission[J]. IEEE Transactions on Communications, 2017, 65(10): 4285–4294. doi: 10.1109/TCOMM.2017.2725261. [73] ZHENG Mingyang, HUANG Tingting, WANG Lin, et al. Performance analysis of M-ary DCSK system over narrow band power-line communications[C]. The 23rd Asia-Pacific Conference on Communications, Perth, Australia, 2017: 1–6. doi: 10.23919/APCC.2017.8304008. [74] CHENG LIN and FERREIRA H C. Time-diversity permutation coding scheme for narrow-band power-line channels[C]. 2012 IEEE International Symposium on Power Line Communications and Its Applications, Beijing, China, 2012: 120–125. doi: 10.1109/ISPLC.2012.6201335. [75] MIAO Meiyuan, WANG Lin, CHEN Guanrong, et al. Design and analysis of replica piecewise M-ary DCSK scheme for power line communications with asynchronous impulsive noise[J]. IEEE Transactions on Circuits and Systems I:Regular Papers, 2020, 67(12): 5443–5453. doi: 10.1109/TCSI.2020.3023749. [76] CAI Xiangming, XU Weikai, WANG Lin, et al. Design of joint position and constellation mapping assisted DCSK scheme subject to Laplacian impulsive noise[J]. IEEE Communications Letters, 2022, 26(2): 463–467. doi: 10.1109/LCOMM.2021.3128400. [77] MIAO Meiyuan, WANG Lin, KATZ M, et al. Hybrid modulation scheme combining PPM with differential chaos shift keying modulation[J]. IEEE Wireless Communications Letters, 2019, 8(2): 340–343. doi: 10.1109/LWC.2018.2871137. [78] ZHANG Yuyang, WANG Lin, CHEN Qiwang, et al. Optimization of constellation-based DC-BICM systems over power line channels[C]. The 2018 IEEE 29th Annual International Symposium on Personal, Indoor and Mobile Radio Communications, Bologna, Italy, 2018: 576–577. doi: 10.1109/PIMRC.2018.8580673. [79] 杨帆, 贾辉, 刘宝树, 等. α稳定脉冲噪声下宽带电力线通信系统性能分析[J]. 电子与信息学报, 2019, 41(6): 1374–1380. doi: 10.11999/JEIT180261.YANG Fan, JIA Hui, LIU Baoshu, et al. Performance analysis of broadband power-line communications systems under the alpha-stable impulsive noise[J]. Journal of Electronics & Information Technology, 2019, 41(6): 1374–1380. doi: 10.11999/JEIT180261. [80] 陶雄飞, 王跃东, 柳盼. 基于变量节点更新的LDPC码加权比特翻转译码算法[J]. 电子与信息学报, 2016, 38(3): 688–693. doi: 10.11999/JEIT150720.TAO Xiongfei, WANG Yuedong, and LIU Pan. Weighted bit-flipping decoding algorithm for LDPC codes based on updating of variable nodes[J]. Journal of Electronics & Information Technology, 2016, 38(3): 688–693. doi: 10.11999/JEIT150720. [81] CHEN Qiwang, WANG Lin, LYU Yibo, et al. Designing protograph-based LDPC Codes for iterative receivers on M-ary dcsk systems[J]. IEEE Transactions on Circuits and Systems Ⅱ:Express Briefs, 2018, 65(4): 466–470. doi: 10.1109/TCSII.2017.2741062. [82] MIAO Meiyuan, WANG Lin, and CHEN Guanrong. Performance and capacity analysis of MDCSK-BICM for impulsive noise in PLC[J]. IEEE Transactions on Power Delivery, 2022, 37(4): 3164–3175. doi: 10.1109/TPWRD.2021.3124561. [83] 洪少华, 王琳. 基于原模图LDPC码的分布式联合信源信道编码[J]. 电子与信息学报, 2017, 39(11): 2594–2599. doi: 10.11999/JEIT170113.HONG Shaohua and WANG Lin. Protograph LDPC based distributed joint source channel coding[J]. Journal of Electronics & Information Technology, 2017, 39(11): 2594–2599. doi: 10.11999/JEIT170113. -





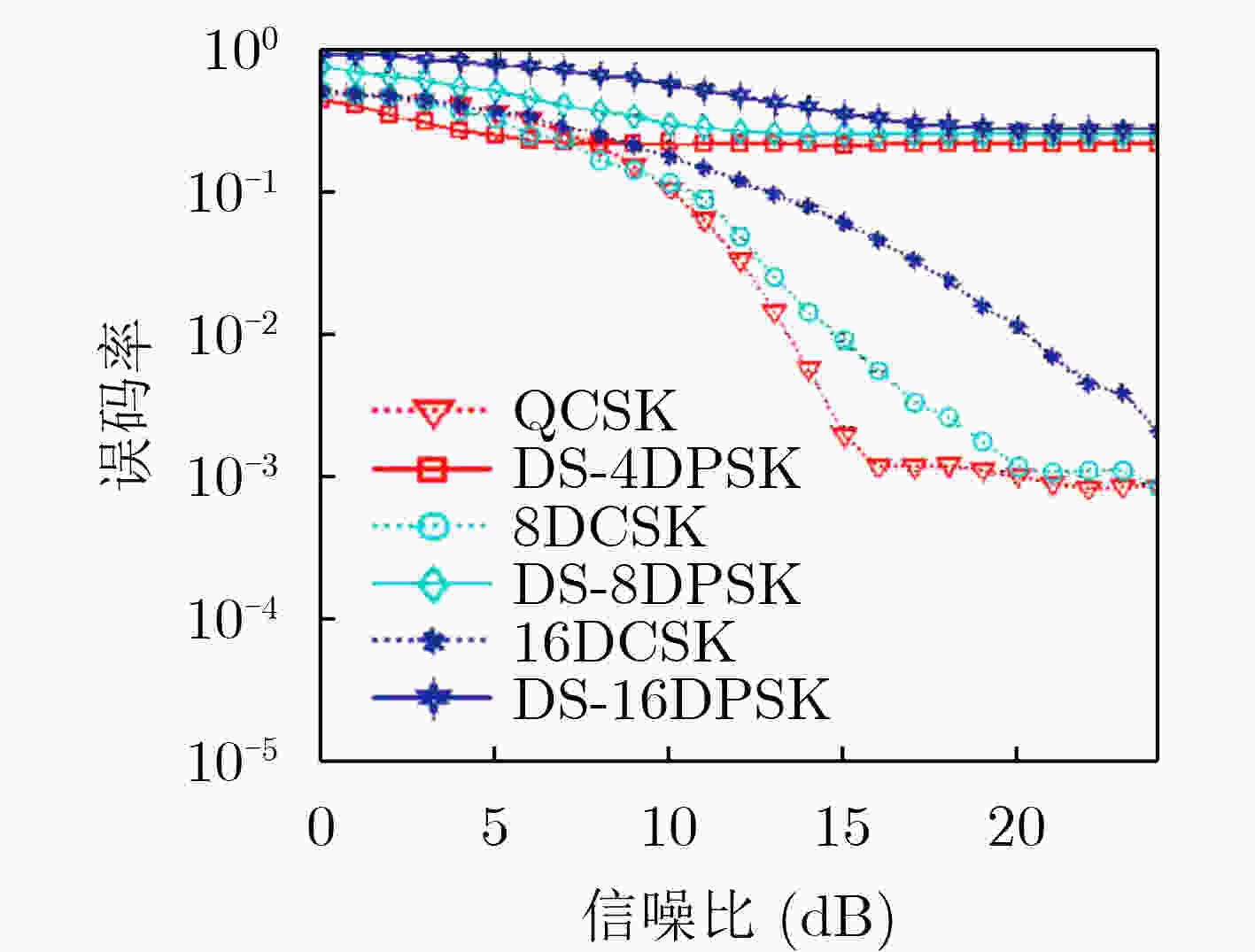
 下载:
下载:
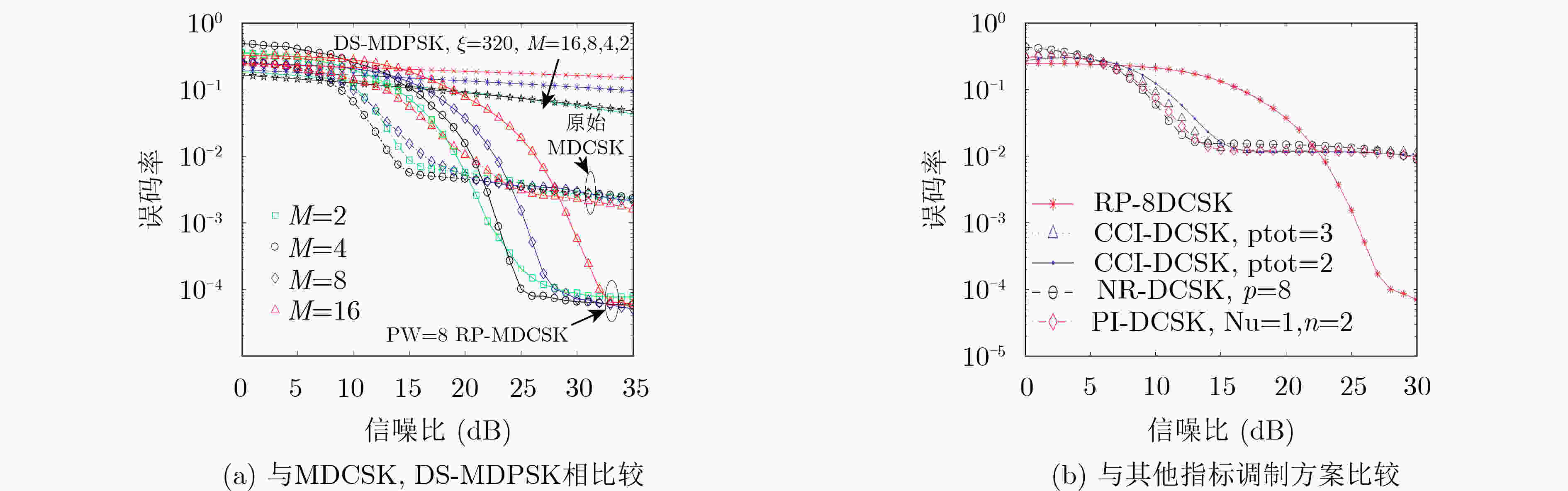
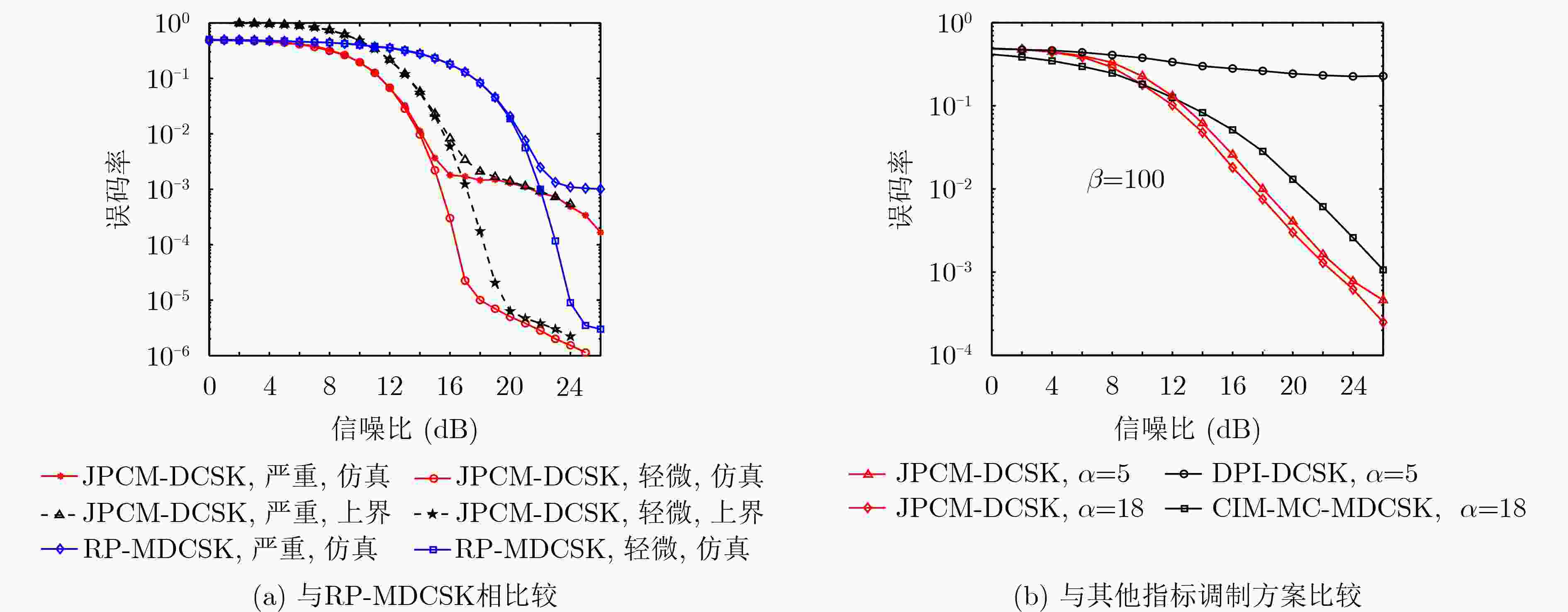
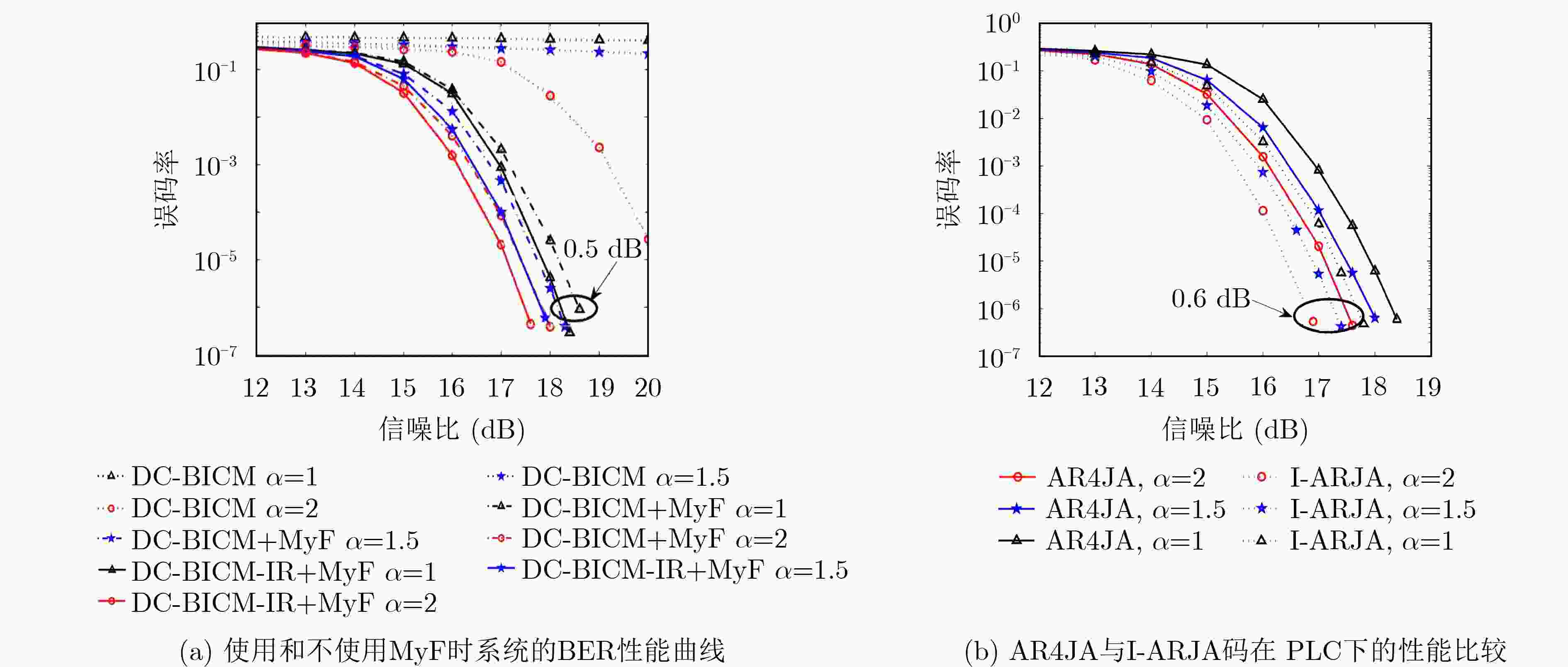


 下载:
下载:
