基于伪监督注意力短期记忆与多尺度去伪影网络的图像分块压缩感知

李俊辉; 侯兴松

doi:10.11999/JEIT231069

基于伪监督注意力短期记忆与多尺度去伪影网络的图像分块压缩感知

doi: 10.11999/JEIT231069

李俊辉,
侯兴松^,

西安交通大学信息与通信工程学院西安 710049

基金项目: 国家自然科学基金(62272376, 61872286)，陕西省重点研发项目(202DLGY04-05, S2021-YF-YBSF-0094)

详细信息

作者简介:
李俊辉：男，博士生，研究方向为图像压缩感知重建、图像压缩

侯兴松：男，教授，博士生导师，研究方向为图像压缩感知、图像压缩、计算机视觉

通讯作者:
侯兴松　houxs@mail.xjtu.edu.cn

中图分类号: TN911.73; TN751
计量
- 文章访问数: 223
- HTML全文浏览量: 76
- PDF下载量: 71
- 被引次数: 0
出版历程
- 收稿日期: 2023-10-07
- 修回日期: 2024-01-17
- 网络出版日期: 2024-01-20
- 刊出日期: 2024-02-10

Pseudo Supervised Attention Short-term Memory and Multi-Scale Deartifacting Network Based on Image Block Compressed Sensing

LI Junhui,
HOU Xingsong^,

School of Information and Communication Engineering, Xi’an Jiaotong University, Xi’an 710049, China

Funds: The National Natural Science Foundation of China (62272376, 61872286), Key R&D Program of Shaanxi Province, China (202DLGY04-05, S2021-YF-YBSF-0094)

摘要

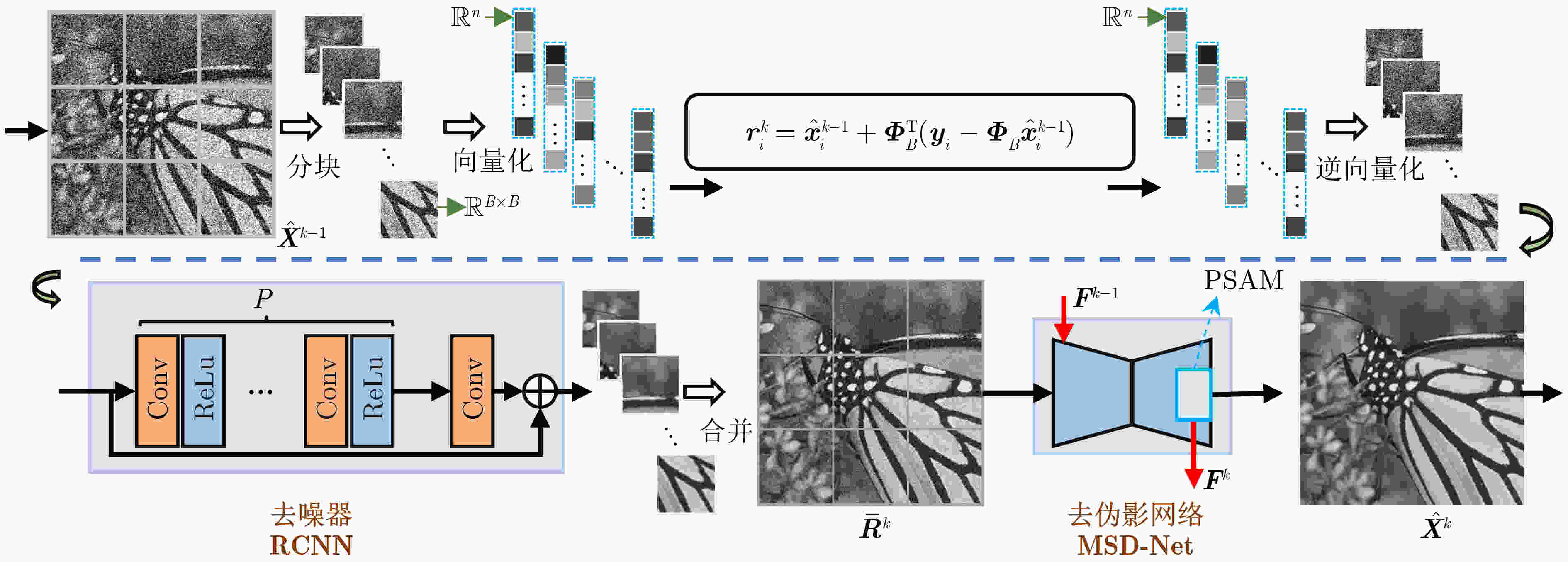
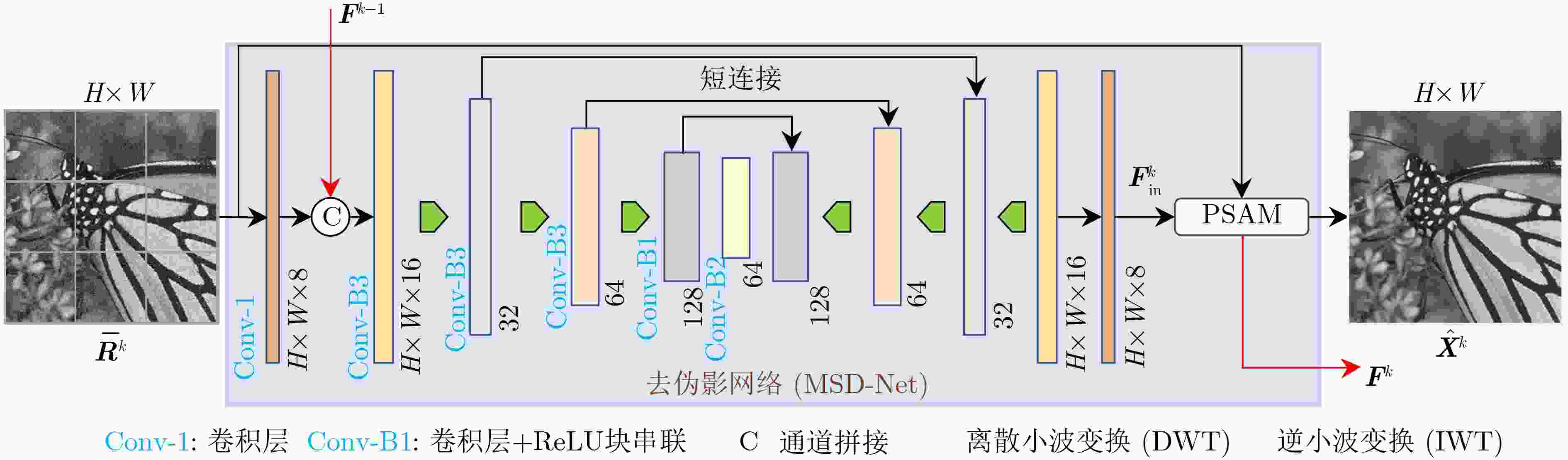
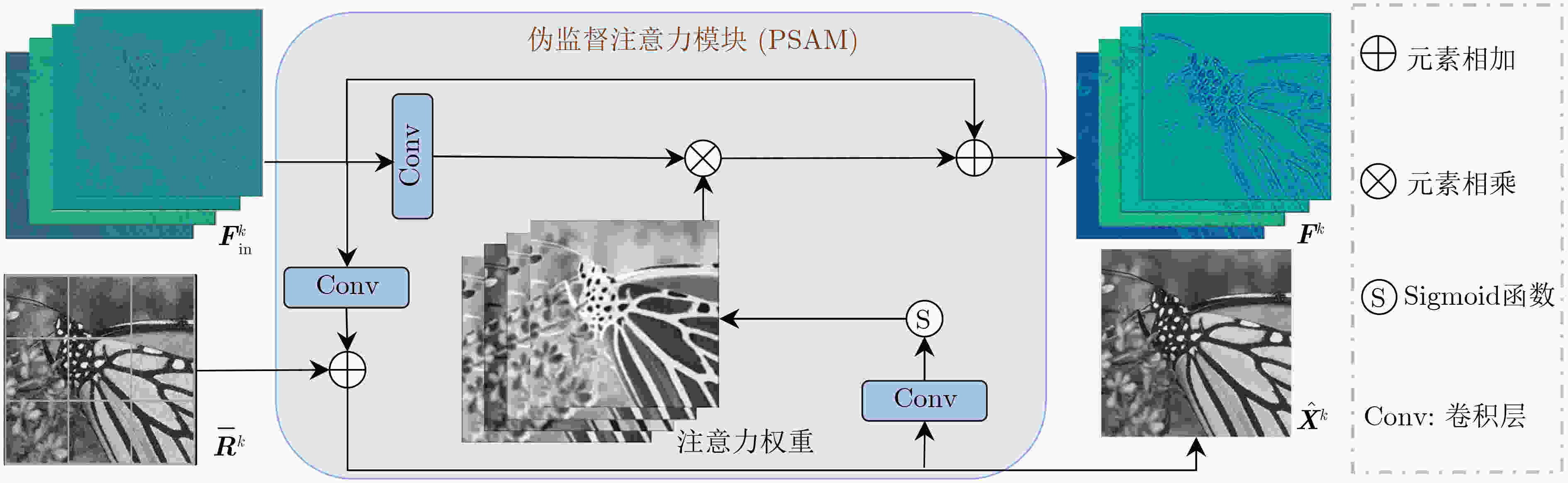
摘要: 基于深度展开网络的分块压缩感知(BCS)方法，在迭代去块伪影时通常会同时去除部分信号和保留部分块伪影，不利于信号恢复。为了改善重建性能，在学习去噪的迭代阈值(LDIT) 算法基础上，该文提出基于伪监督注意力短期记忆与多尺度去伪影网络(MSD-Net)的图像BCS迭代方法(PSASM-MD)。首先，在每步迭代中，利用残差网络并行地对每个图像子块单独去噪后再拼接。然后，对拼接后的图像采用含有伪监督注意力模块(PSAM)的MSD-Net进行特征提取，以更好地去除块伪影以提高重建性能。其中，PSAM被用于从含有块伪影的残差中抽取部分有用信号，并传递到下一步迭代实现短期记忆，以尽量避免去除有用信号。实验结果表明，该文方法相比现有先进的同类BCS方法在主观视觉感知和客观评价指标上均取得了更优的结果。
- 分块压缩感知 /
- 短期记忆 /
- 图像去伪影 /
- 深度展开网络
Abstract: Deep unfolding network based Block Compressed Sensing (BCS) methods typically remove some signal and retain certain block artifacts simultaneously during iterative deartifacting, which is unfavorable for signal recovery. To enhance reconstruction performance, based on Learned Denoising Iterative Thresholding (LDIT) algorithm. Pseudo Supervised Attention Short-term Memory and Multi-scale Deartifacting (PSASM-MD) based image BCS, is proposed in this paper. Initially, in each iteration, each image block is denoised separately in parallel using residual networks before being concatenated. Subsequently, in conjunction with the Pseudo-Supervised Attention Module (PSAM), Multi-Scale Deartifacting Network (MSD-Net) is used to perform feature extraction on the concatenated images, enabling more efficient removal of block artifacts and improving the reconstruction performance. In this case, PSAM is utilized to extract useful signal components from the residuals containing block artifacts, transfer the short-term memory to the subsequent iteration to minimize the removal of useful signals. Experimental results demonstrate that this approach outperforms existing state-of-the-art BCS methods both in subjective visual perception and objective evaluation metrics.
- Block Compressed Sensing (BCS) /
- Short-term memory /
- Image deartifacting /
- Deep unfolding network

HTML全文

图 1 PSASM-MD模型框架

下载: 全尺寸图片幻灯片

图 2 PSASM-MD中第k次迭代网络结构

下载: 全尺寸图片幻灯片

图 3 MSD-Net的网络结构

下载: 全尺寸图片幻灯片

图 4 PSAM的网络结构

下载: 全尺寸图片幻灯片

图 5 不同BCS算法在Set11中“Flinstones”和“Peppers”上的重建结果

下载: 全尺寸图片幻灯片

图 6 不同BCS算法在BSD68中的“test034” 和“test045”上的重建结果

下载: 全尺寸图片幻灯片

图 7 不同网络结构下中间迭代重建图的特征图以及最终的重建图

下载: 全尺寸图片幻灯片

图 8 不同迭代阶段的重建图像的残差图和PSAM提取的特征图以及最终重建图的残差图

下载: 全尺寸图片幻灯片

表 1 几种BCS算法在Set11上不同采样率下PSNR(dB)/SSIM的平均值

采样率$\gamma $(%)	ISTA-Net⁺	OPINE-Net⁺	AMP-Net	TransCS	TCS-Net	PSASM-MD
1	17.45/0.4131	20.15/0.5340	20.20/0.5580	-/-	21.09/0.5505	22.01/0.6077
4	21.56/0.6240	25.69/0.7920	25.26/0.7722	25.41/0.7883	25.46/0.7863	26.40/0.8001
10	26.49/0.8036	29.81/0.8884	29.40/0.8779	29.54/0.8877	29.04/0.8834	30.40/0.8906
25	32.44/0.9237	34.86/0.9509	34.63/0.9481	35.06/0.9548	33.94/0.9508	35.24/0.9519
50	38.07/0.9706	40.17/0.9797	40.34/0.9804	40.49/0.9815	-/-	40.90/0.9812

下载: 导出CSV

表 2 几种BCS算法在BSD68 上不同采样率下PSNR(dB)/SSIM的平均值

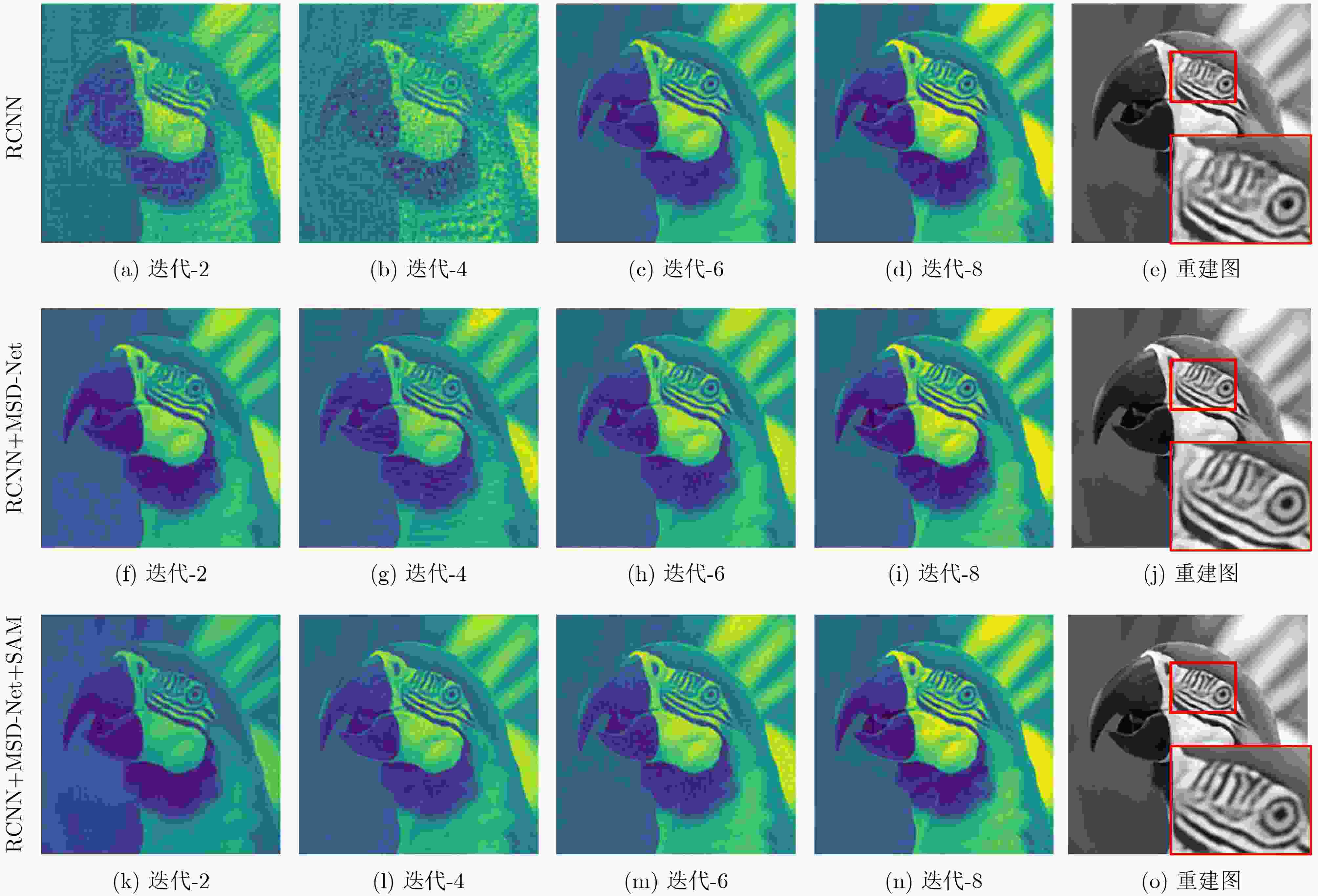
采样率$\gamma $(%)	ISTA-Net⁺	OPINE-Net⁺	AMP-Net	TransCS	TCS-Net	PSASM-MD
1	19.18/0.4201	22.11/0.5140	21.97/0.5086	-/-	22.26/0.5194	22.89/0.5530
4	22.34/0.5573	25.00/0.6825	25.40/0.6985	25.28/0.6881	25.07/0.6829	25.59/0.6847
10	25.30/0.7001	27.82/0.8045	27.41/0.8036	27.86/0.8086	27.42/0.8037	28.20/0.7993
25	29.31/0.8507	31.51/0.9061	31.56/0.9121	31.74/0.9121	30.94/0.9083	31.98/0.9069
50	34.01/0.9421	36.35/0.9660	36.64/0.9707	36.81/0.9699	-/-	37.19/0.9689

下载: 导出CSV

表 3 PSASM-MD不同网络结构下Set11上的平均PSNR(dB)/SSIM结果

采样率$\gamma $(%)	RCNN	RCNN+ DCNN^[14]	RCNN+ MSD-Net	RCNN+MSD-Net+PSAM
4	25.49/ 0.7676	26.06/0.7882	26.29/0.7962	26.40/0.7986
10	29.52/ 0.8773	29.98/0.8848	30.11/0.8873	30.38/0.8914

下载: 导出CSV

参考文献(25)

[1]	HOU Hao, SHAO Yuchen, GENG Yang, et al. PNCS: Pixel-level non-local method based compressed sensing undersampled MRI image reconstruction[J]. IEEE Access, 2023, 11: 42389–42402. doi: 10.1109/ACCESS.2023.3270900.
[2]	王洋, 杨孟宇, 赵首博. 基于自适应分块的高光谱图像压缩感知重构方法[J]. 电子与信息学报, 2023, 45(7): 2605–2613. doi: 10.11999/JEIT220738. WANG Yang, YANG Mengyu, and ZHAO Shoubo. Compressed sensing reconstruction of hyperspectral images based on adaptive blocking[J]. Journal of Electronics & Information Technology, 2023, 45(7): 2605–2613. doi: 10.11999/JEIT220738.
[3]	LIU Yang, YUAN Xin, SUO Jinli, et al. Rank minimization for snapshot compressive imaging[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2019, 41(12): 2990–3006. doi: 10.1109/TPAMI.2018.2873587.
[4]	TROPP J A and GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655–4666. doi: 10.1109/TIT.2007.909108.
[5]	BECK A and TEBOULLE M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(1): 183–202. doi: 10.1137/080716542.
[6]	METZLER C A, MOUSAVI A, and BARANIUK R. Learned D-AMP: Principled neural network based compressive image recovery[C]. The 31st International Conference on Neural Information Processing Systems, Long Beach, USA, 2017: 1770–1781. doi: 10.5555/3294771.3294940.
[7]	MOUSAVI A, PATEL A B, and BARANIUK R G. A deep learning approach to structured signal recovery[C]. The 53rd Annual Allerton Conference on Communication, Control, and Computing, Monticello, USA, 2015: 1336–1343. doi: 10.1109/ALLERTON.2015.7447163.
[8]	KULKARNI K, LOHIT S, TURAGA P, et al. ReconNet: Non-iterative reconstruction of images from compressively sensed measurements[C]. IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 449–458. doi: 10.1109/CVPR.2016.55.
[9]	GAN Hongping, SHEN Minghe, HUA Yi, et al. From patch to pixel: A transformer-based hierarchical framework for compressive image sensing[J]. IEEE Transactions on Computational Imaging, 2023, 9: 133–146. doi: 10.1109/TCI.2023.3244396.
[10]	LIU Ze, LIN Yutong, GAO Yue, et al. Swin transformer: Hierarchical vision transformer using shifted windows[C]. IEEE International Conference on Computer Vision, Montreal, Canada, 2021: 9992–10002. doi: 10.1109/ICCV48922.2021.00986.
[11]	ZHANG Jian, CHEN Bin, XIONG Ruiqin, et al. Physics-inspired compressive sensing: Beyond deep unrolling[J]. IEEE Signal Processing Magazine, 2023, 40(1): 58–72. doi: 10.1109/MSP.2022.3208394.
[12]	ZHANG Jian and GHANEM B. ISTA-Net: Interpretable optimization-inspired deep network for image compressive sensing[C]. IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, USA, 2018: 1828–1837. doi: 10.1109/CVPR.2018.00196.
[13]	ZHANG Jian, ZHAO Chen, and GAO Wen. Optimization-inspired compact deep compressive sensing[J]. IEEE Journal of Selected Topics in Signal Processing. 2020, 14(4): 765–774. doi: 10.1109/JSTSP.2020.2977507.
[14]	ZHANG Zhonghao, LIU Yipeng, LIU Jiani, et al. AMP-Net: Denoising-based deep unfolding for compressive image sensing[J]. IEEE Transactions on Image Processing, 2021, 30: 1487–1500. doi: 10.1109/TIP.2020.3044472.
[15]	CHEN Chang, XIONG Zhiwei, TIAN Xinmei, et al. Real-world image denoising with deep boosting[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 42(12): 3071–3087. doi: 10.1109/TPAMI.2019.2921548.
[16]	MA Jiayi, PENG Chengli, TIAN Xin, et al. DBDnet: A deep boosting strategy for image denoising[J]. IEEE Transactions on Multimedia, 2022, 24: 3157–3168. doi: 10.1109/TMM.2021.3094058.
[17]	SHEN Minghe, GAN Hongping, NING Chao, et al. TransCS: A transformer-based hybrid architecture for image compressed sensing[J]. IEEE Transactions on Image Processing, 2022, 31: 6991–7005. doi: 10.1109/TIP.2022.3217365.
[18]	CUI Wenxue, LIU Shaohui, JIANG Feng, et al. Image compressed sensing using non-local neural network[J]. IEEE Transactions on Multimedia, 2023, 25: 816–830. doi: 10.1109/TMM.2021.3132489.
[19]	ZHANG Kai, ZUO Wangmeng, CHEN Yunjin, et al. Beyond a Gaussian denoiser: Residual learning of deep CNN for image denoising[J]. IEEE Transactions on Image Processing, 2017, 26(7): 3142–3155. doi: 10.1109/TIP.2017.2662206.
[20]	RONNEBERGER O, FISCHER P, and BROX T. U-Net: Convolutional networks for biomedical image segmentation[C]. 18th International Conference, Munich, Germany, 2015: 234–241. doi: 10.1007/978-3-319-24574-4_28.
[21]	WANG Huake, LI Ziang, and HOU Xingsong. Versatile denoising-based approximate message passing for compressive sensing[J]. IEEE Transactions on Image Processing, 2023, 32: 2761–2775. doi: 10.1109/TIP.2023.3274967.
[22]	LIU Pengju, ZHANG Hongzhi, ZHANG Kai, et al. Multi-level wavelet-CNN for image restoration[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, USA, 2018: 886. doi: 10.1109/CVPRW.2018.00121.
[23]	MARTIN D, FOWLKES C, TAL D, et al. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics[C]. 8th IEEE International Conference on Computer Vision, Vancouver, Canada, 2001: 416–423. doi: 10.1109/ICCV.2001.937655.
[24]	WANG Zhou, BOVIK A C, SHEIKH H R, et al. Image quality assessment: From error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600–612. doi: 10.1109/TIP.2003.819861.
[25]	LOSHCHILOV I and HUTTER F. Decoupled weight decay regularization[C]. 7th International Conference on Learning Representations, New Orleans, USA, 2019.