A Robust Clutter Edge Detection Method Based on Model Order Selection Criterion
-
摘要: 在雷达目标自适应检测问题当中,辅助数据存在杂波边缘的情况将导致杂波协方差矩阵(CCM)的估计性能出现严重下降,极大地影响目标检测性能。为了解决这一问题,该文提出一种杂波边缘检测方法,能够对辅助数据中杂波边缘数量与位置进行自适应判别。首先,假定辅助数据中存在杂波边缘,采用模型阶数选择算法和最大似然估计方法完成杂波参数估计,其中杂波边缘位置由循环搜索方法得到。之后将杂波参数估计结果应用到检测算法中,通过广义似然比检验方法来判断杂波边缘是否存在。此外为了进一步提升算法在小样本条件下的稳健性,引入CCM的特殊结构作为先验知识,将算法推广至CCM为斜对称、谱对称以及中心对称3种结构的情况。仿真及实测数据均表明该文所提算法能够高效地识别雷达辅助数据中的杂波边缘数量和位置,先验知识的引入更能进一步改善算法在辅助数据量较小时的性能。Abstract: In the radar target adaptive detection problem, the presence of clutter edges in the auxiliary data will cause a serious decrease in the estimation performance of the Clutter Covariance Matrix (CCM), which greatly affects the target detection performance. In order to solve this problem, a clutter edge detection method is proposed, which can adaptively discriminate the number and position of clutter edges in auxiliary data. Firstly, assuming the presence of clutter edges in the auxiliary data, the model order selection algorithm and the maximum likelihood estimation method are used to complete the clutter parameter estimation, and the clutter edge position is obtained by the cyclic search method. Then, the clutter parameter estimation results are applied to the detection algorithm, and the existence of clutter edges is determined by the generalized likelihood ratio test method. In addition, in order to further improve the robustness of the algorithm under the condition of small samples, the special structure of CCM is introduced as a priori knowledge, and the algorithm is generalized to the situation where CCM is persymmetry, spectrum symmetry and central-symmetry. Both simulation and measured data show that the proposed algorithm can efficiently identify the number and location of clutter edges in radar auxiliary data, and the introduction of prior knowledge can further improve the performance of the algorithm when the amount of auxiliary data is small.
-
Key words:
- Adaptive radar detection /
- Clutter classification /
- Clutter edge /
- Knowledge-based
-
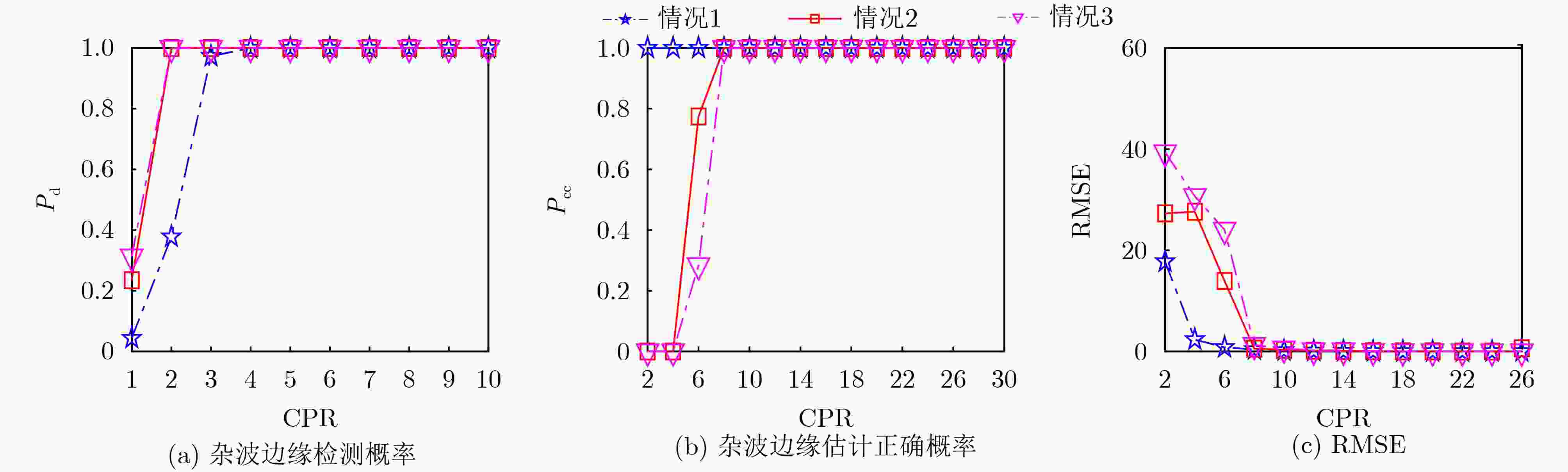
图 3 AIC准则下表1所示不同情况的$ {P_{\mathrm{d}}} $, $ {P_{{\mathrm{cc}}}} $以及RMSE随CPR的变化情况(协方差矩阵为中心对称结构)
1 杂波分类及参数估计流程
输入:$ {\boldsymbol{Z}} $, $ {{m}_{\max}} $, $ {L} $,收敛阈值$ \kappa $。 for $ m = 1,2,\cdots ,{m_{\max }} $ 初始化:$ {t} = 0 $, $ {L}_{j}^{(0)} = \dfrac{{{L} \times {j}}}{{m}},{j} = 1,2,\cdots ,{m} - 1 $ 重复迭代: $ {t} = {t} + 1 $ for $ j = 1,2,\cdots ,m - 1 $ 利用式(10)估计$ \hat {L}_{j}^{({t})} $。 end 利用式(2)计算当前对数似然函数$ {\left( {\ln {f_1}\left( {\boldsymbol{Z}} \right)} \right)^{\left( t \right)}} $, 直至满足收敛条件:
$ {\left\| {{{\left( {\ln {f_1}\left( {\boldsymbol{Z}} \right)} \right)}^{\left( t \right)}} - {{\left( {\ln {f_1}\left( {\boldsymbol{Z }}\right)} \right)}^{\left( {t - 1} \right)}}} \right\|_2} \le \kappa $。end 利用式(4)计算$ \hat {m} $。 利用式(12)判断环境是否均匀。 输出:$ \hat {m} $及$ {\hat {\boldsymbol{\varXi}} _{m}} $。 表 1 仿真参数设置
参数名称 情况1 情况2 情况3 杂波边缘数 1 2 3 杂波边缘位置$ {{\boldsymbol{\varXi}} _m} $ $ \left[ {60} \right] $ $ \left[ {60,90} \right] $ $ \left[ {30,60,90} \right] $ -
[1] KELLY E J. An adaptive detection algorithm[J]. IEEE Transactions on Aerospace and Electronic Systems, 1986, AES-22(2): 115–127. doi: 10.1109/TAES.1986.310745. [2] HAN Sudan, YAN Linjie, ZHANG Yuxuan, et al. Adaptive radar detection and classification algorithms for multiple coherent signals[J]. IEEE Transactions on Signal Processing, 2021, 69: 560–572. doi: 10.1109/TSP.2020.3047523. [3] SU Ningyuan, CHEN Xiaolong, GUAN Jian, et al. Maritime target detection based on radar graph data and graph convolutional network[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4019705. doi: 10.1109/LGRS.2021.3133473. [4] DE MAIO A. Rao test for adaptive detection in Gaussian interference with unknown covariance matrix[J]. IEEE Transactions on Signal Processing, 2007, 55(7): 3577–3584. doi: 10.1109/TSP.2007.894238. [5] CAO Jinkun and CHEN Gang. An adaptive radar detection for the target in clutter with unknown covariance based on the PPPT[C]. The 2nd International Conference on Intelligent Human-Machine Systems and Cybernetics, Nanjing, China, 2010: 294–297. doi: 10.1109/IHMSC.2010.173. [6] ASENDORF N and NADAKUDITI R R. The performance of a matched subspace detector that uses subspaces estimated from finite, noisy, training data[J]. IEEE Transactions on Signal Processing, 2013, 61(8): 1972–1985. doi: 10.1109/TSP.2013.2241058. [7] ORLANDO D and RICCI G. A Rao test with enhanced selectivity properties in homogeneous scenarios[J]. IEEE Transactions on Signal Processing, 2010, 58(10): 5385–5390. doi: 10.1109/TSP.2010.2053032. [8] LIU Jun, LIU Weijian, HAO Chengpeng, et al. Persymmetric subspace detectors with multiple observations in homogeneous environments[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(4): 3276–3284. doi: 10.1109/TAES.2020.2967244. [9] CANDAN Ç and PASCAL F. Covariance matrix estimation of texture correlated compound-gaussian vectors for adaptive radar detection[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(3): 3009–3020. doi: 10.1109/TAES.2022.3221385. [10] KRAUT S and SCHARF L L. The CFAR adaptive subspace detector is a scale-invariant GLRT[J]. IEEE Transactions on Signal Processing, 1999, 47(9): 2538–2541. doi: 10.1109/78.782198. [11] GRECO A S, BANDIERA F, DE MAIO A, et al. Adaptive radar detection of distributed targets in partially-homogeneous noise plus subspace interference[C]. 2006 IEEE International Conference on Acoustics Speech and Signal Processing Proceedings, Toulouse, France, 2006: III-III,doi: 10.1109/ICASSP.2006.1660640. [12] HAO Chengpeng, ORLANDO D, MA Xiaochuan, et al. Persymmetric Rao and Wald tests for partially homogeneous environment[J]. IEEE Signal Processing Letters, 2012, 19(9): 587–590. doi: 10.1109/LSP.2012.2207891. [13] HAN Sudan, ADDABBO P, ORLANDO D, et al. Radar clutter classification using expectation-maximization method[C]. 2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, Canada, 2021: 4585–4589. doi: 10.1109/ICASSP39728.2021.9413918. [14] ADDABBO P, BIONDI F, ORLANDO D, et al. Radar environment classificator with clustering capabilities[C]. The 29th European Signal Processing Conference (EUSIPCO), Dublin, Ireland, 2021: 1860–1864. doi: 10.23919/EUSIPCO54536.2021.9616164. [15] WATANABE S. A widely applicable Bayesian information criterion[J]. The Journal of Machine Learning Research, 2013, 14(1): 867–897. [16] STOICA P and SELEN Y. Model-order selection: A review of information criterion rules[J]. IEEE Signal Processing Magazine, 2004, 21(4): 36–47. doi: 10.1109/MSP.2004.1311138. [17] XU D, ADDABBO P, HAO C, et al. Adaptive strategies for clutter edge detection in Radar[J]. Signal Processing, 2021, 186: 108127. doi: 10.1016/j.sigpro.2021.108127. [18] WANG Tianqi, XU Da, HAO Chengpeng, et al. Clutter edges detection algorithms for structured clutter covariance matrices[J]. IEEE Signal Processing Letters, 2022, 29: 642–646. doi: 10.1109/LSP.2022.3149387. [19] REED I S, MALLETT J D, and BRENNAN L E. Rapid convergence rate in adaptive arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 1974, AES-10(6): 853–863. doi: 10.1109/TAES.1974.307893. [20] NITZBERG R. Application of maximum likelihood estimation of persymmetric covariance matrices to adaptive processing[J]. IEEE Transactions on Aerospace and Electronic Systems, 1980, AES-16(1): 124–127. doi: 10.1109/TAES.1980.308887. [21] XUE Jian, XU Shuwen, and LIU Jun. Persymmetric detection of radar targets in nonhomogeneous and Non-Gaussian Sea clutter[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5103709. doi: 10.1109/TGRS.2021.3086829. [22] DE MAIO A, ORLANDO D, HAO Chengpeng, et al. Adaptive detection of point-like targets in spectrally symmetric interference[J]. IEEE Transactions on Signal Processing, 2016, 64(12): 3207–3220. doi: 10.1109/TSP.2016.2539140. [23] HAO Chengpeng, ORLANDO D, FOGLIA G, et al. Knowledge-based adaptive detection: Joint exploitation of clutter and system symmetry properties[J]. IEEE Signal Processing Letters, 2016, 23(10): 1489–1493. doi: 10.1109/LSP.2016.2601931. [24] SCHUHMACHER D, VO B T, and VO B N. A consistent metric for performance evaluation of multi-object filters[J]. IEEE Transactions on Signal Processing, 2008, 56(8): 3447–3457. doi: 10.1109/TSP.2008.920469. [25] BILLINGSLEY J B, FARINA A, GINI F, et al. Statistical analyses of measured radar ground clutter data[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(2): 579–593. doi: 10.1109/7.766939. -






 下载:
下载:




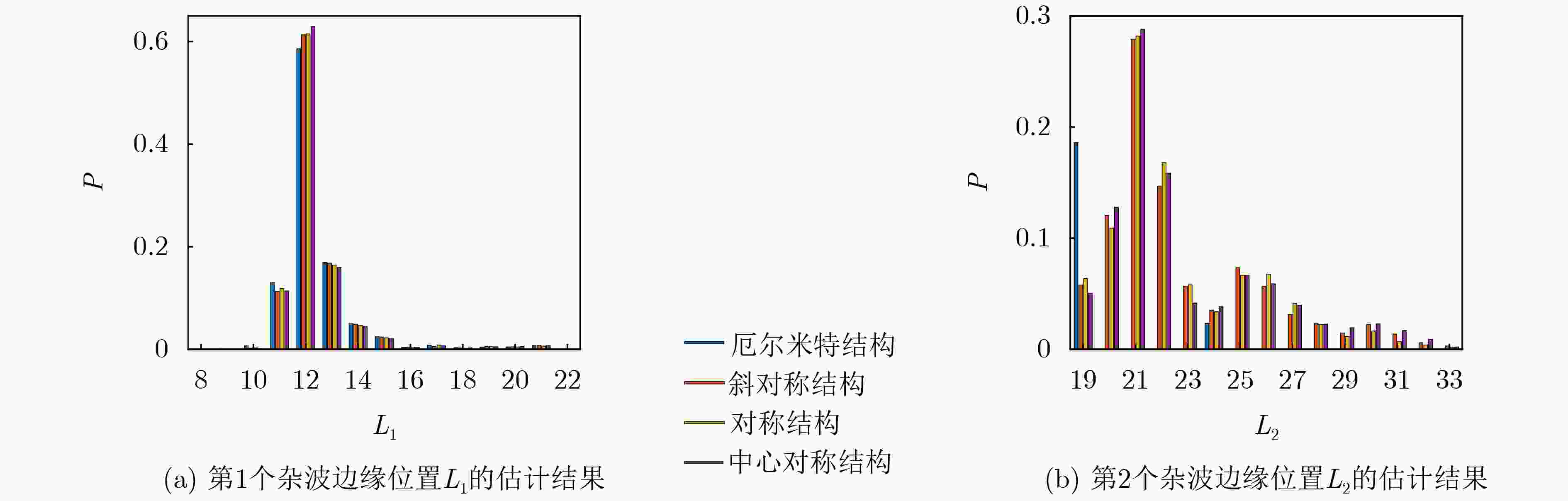


 下载:
下载:
