Survey of Satellite-ground Channel Models for Low Earth Orbit Satellites
-
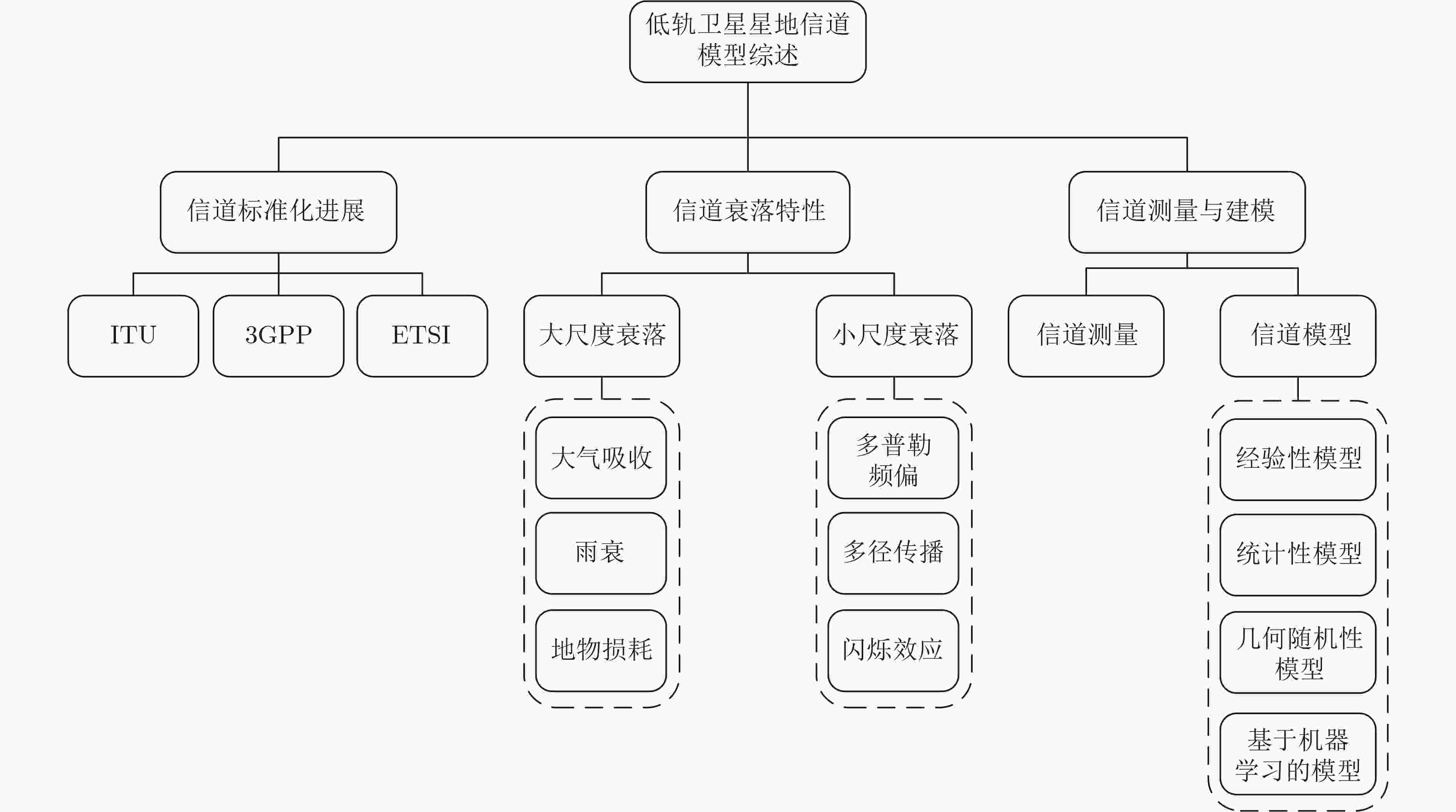
摘要: 低轨卫星(LEO)具备通信时延低、部署成本低、覆盖范围广的特点,已经成为了建设未来空天地一体化网络的重要组成部分。然而卫星通信中端到端传播距离长、经历衰落复杂、终端移动速度快,其信道特性与地面蜂窝网络信道具有很大差异。基于此,为了对低轨卫星星地信道特性以及信道模型有较为全面的认识,该文总结了目前国际标准组织对星地信道的标准化进展,讨论了星地信道在不同传播位置处的衰落特性,根据建模方法对已有的重要信道模型进行了划分与阐述,最后对未来的工作提出了展望。Abstract: Low Earth Orbit (LEO) satellite has the characteristics of low communication delay, low deployment cost and wide coverage, and has become an important part of the construction of the future space earth integrated network. However, satellite communication has large end-to-end propagation distance, complex fading and fast terminal movement speed, thus the channel characteristics are very different from the terrestrial cellular network. Based on this, in order to have a more comprehensive understanding of the characteristics and channel model of LEO satellite-ground channel, the current standardization progress of the satellite-ground channel by the international standards organization are summarized, the fading characteristics of the satellite ground channel at different propagation positions are discussed, the existing important channel models are classified and shown according to the modeling method, and finally the prospects for future work are proposed.
-
表 1 各标准特点与不足对比
标准组织 标准名称 标准特点 标准不足 ITU ITU-R P.618 大气吸收衰减、降雨和云雾衰减、闪烁效应等 仅支持城区,只考虑了遮蔽概率 ITU-R P.2108 地物损耗的计算 只支持城区和郊区,只考虑了地面段植被与建筑物的遮挡 ITU-R P.681 适用于陆地移动卫星(Land Mobile Satellite, LMS)的宽带和窄带信道模型,以及卫星到室内的信道模型 3GPP 3GPP TR 38.811 自由空间损耗、大气吸收损耗、降雨和云雾损耗、闪烁效应、多普勒频偏和变化率等,提出了TDL与CDL模型 基于5G蜂窝信道模型的改进,适用于低频段,没有考虑高移动性以及大气损耗 3GPP TR 38.821 规定了星地链路仿真参数配置、新空口(New Radio, NR)为支持NTN需要做出的调整等 ETSI DVB-S2 卫星广播技术帧结构、调制和信道编码方案、物理层组帧、基带信号成形等 仅对AWGN信道进行了优化 DVB-S2X 更完善的调制和信道编码方案、甚低信噪比通信方案等 表 2 3GPP TR 38.811标准中城区、郊区场景地物损耗参考值
仰角(º) S频段 Ka频段 城区 郊区 城区 郊区 10 34.3 19.52 44.3 29.5 20 30.9 18.17 39.9 24.6 30 29.0 18.42 37.5 21.9 40 27.7 18.28 35.8 20.0 50 26.8 18.63 34.6 18.7 60 26.2 17.68 33.8 17.8 70 25.8 16.50 33.3 17.2 80 25.5 16.30 33.0 16.9 90 25.5 16.30 32.9 16.8 表 3 国内外各组织信道测量对比
测量组织 频段 场景 测量卫星 ESA UHF/L/S/Ka 城区、郊区、乡村、移动列车等 MARECS、直升机模拟 NASA UHF/L/S 公路、乡村、丘陵等 ATS6, MARECS、直升机模拟 日本通信研究实验室 L 城区、公路、郊区、乡村 ETS-V 澳大利亚电信研究所 L 郊区、乡村 ETS-V CRC UHF/L 郊区、乡村 MARECS、热气球、直升机模拟 中国科学院 UHF 密集城区、郊区、草坪湖泊等空旷地区 LEO模拟器模拟 加利福尼亚大学 L 城区 Orbcomm, ridium NEXT 德国联邦国防军慕尼黑大学 Ka 密集城区、乡村、山地 无人机模拟 表 4 不同经验性模型的对比
表 5 不同统计性模型的对比
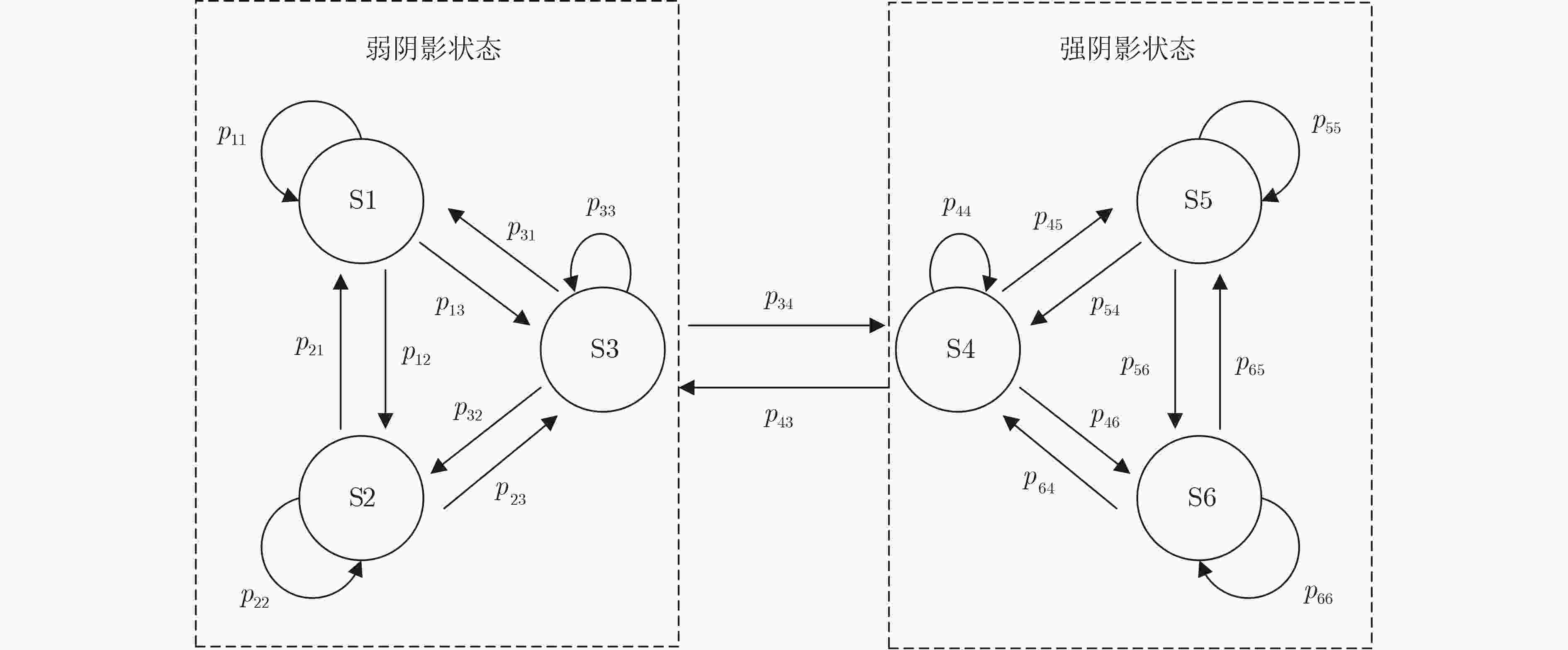
文献 频段 场景 状态数 模型构成 特点 [53,54] L 乡村 单状态 Rice/Lognormal 受遮挡的直射分量与不受遮挡的多径分量的组合 [55] L 城区/公路/郊区/乡村 单状态 Rice/Lognormal 直射分量与多径分量均受到同分布的阴影衰落 [56] L 乡村 单状态 Rice/Lognormal 直射分量与多径分量均受到阴影衰落,允许两个阴影衰落独立 [57] L 乡村 单状态 Rice/Nakagami 将阴影衰落改进为Nakagami分布 [58] L 城区/公路/郊区/乡村 单状态 Beckmann/
Lognormal将多径分量改进为Beckmann分布 [59] L/S/Ka 城区/公路 单状态 Rice/Rayleigh/
Lognormal可推导为其他经典模型 [60,61] L 乡村 单状态 Squared Rice/Nakagami 考虑了分集接收 [62] L 城区/公路 两状态 Rice/Rayleigh/
Lognormal信道分为“好状态”、“坏状态” [63] L 城区/郊区/乡村 两状态 Rice/Rayleigh/
Lognormal根据仰角判断信道状态 [64] L/S/Ka 城区/公路/郊区/乡村 3状态 Loo/Loo/Loo 以植被引起的轻微阴影作为第2状态 [65] L/S/Ka 城区/公路/郊区/乡村 3状态 Loo/RM/Loo 采用RM模型作为第2状态 [67] L 城区/公路/郊区/乡村 4状态 Rice/Rice/Rayleigh/Lognormal 将4种不同场景视为4种状态 [68] L 城区/公路/郊区/乡村 6状态 Rice/Rayleigh/
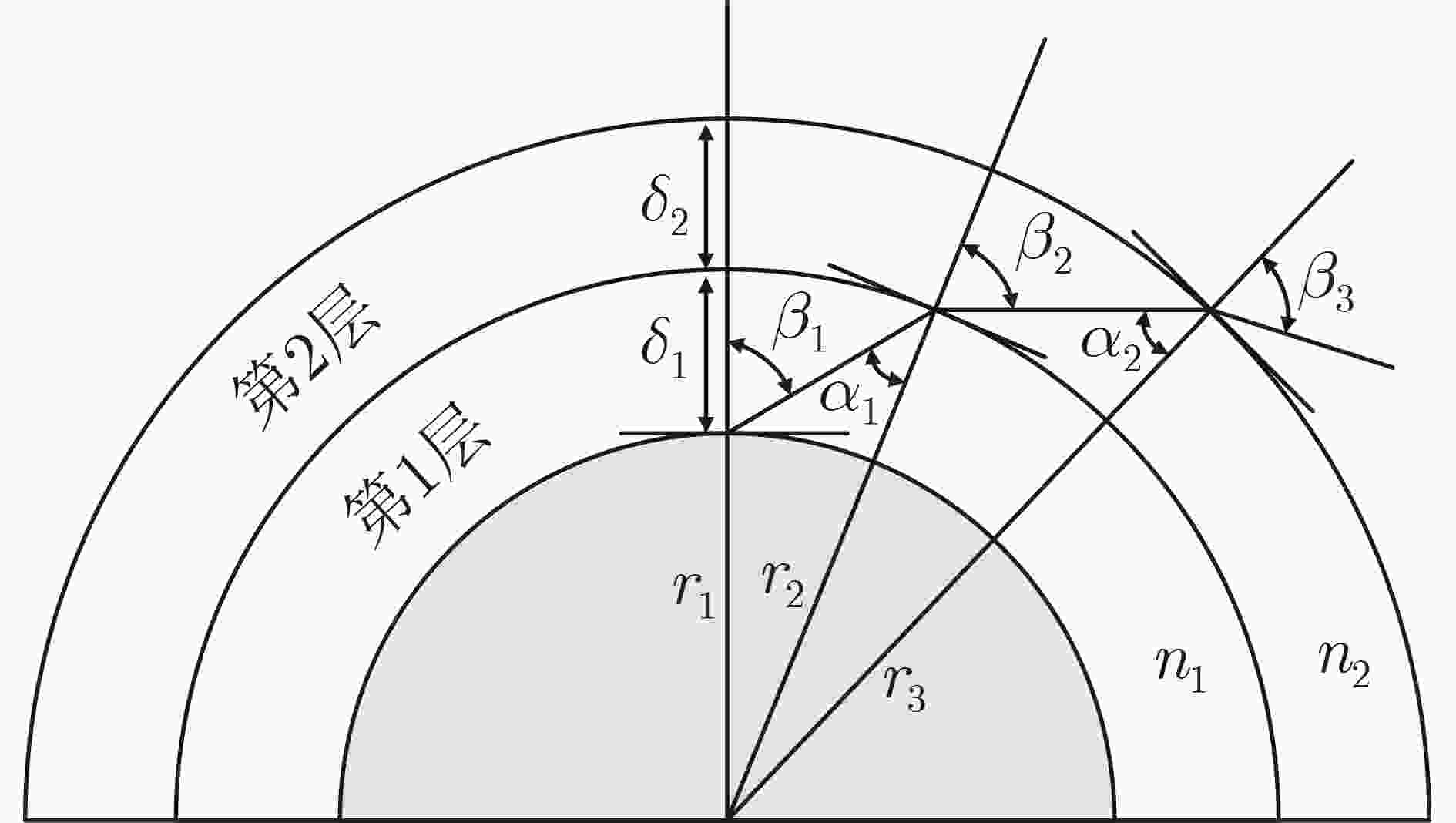
Lognormal将“好状态”与“坏状态”细分为6个子状态 [69] Ku 城区/公路 多状态 RJ-MCMC 无需认为假设状态数和每个状态的分布 [70] L/S 城区/公路/郊区/乡村 多状态 Rice/Nakagami 将卫星轨道分为“好区域”与“坏区域” 表 6 不同几何随机性模型的对比
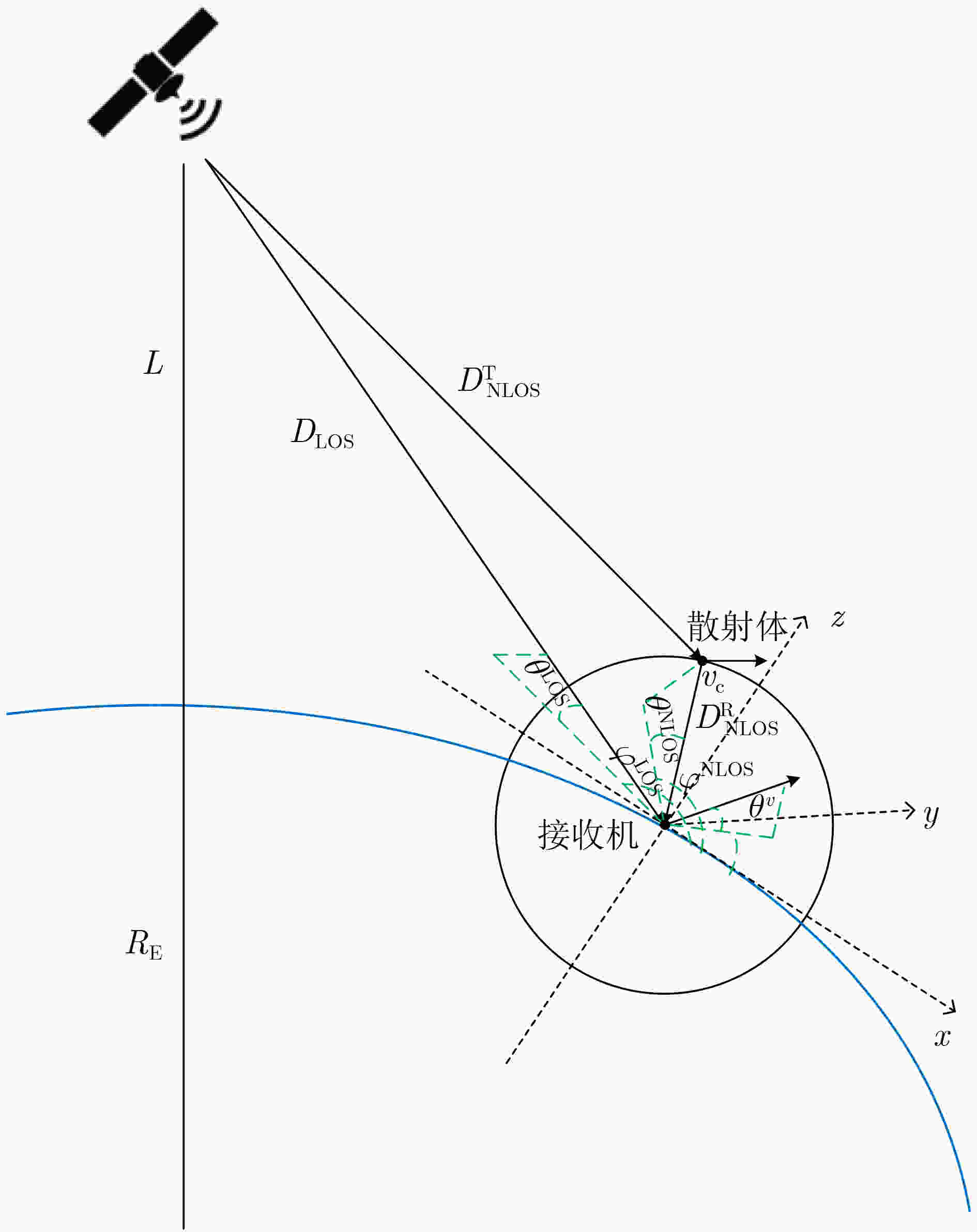
表 7 不同基于机器学习的模型对比
-
[1] IMT-2030(6G)推进组. 6G总体愿景与潜在关键技术白皮书[R]. 北京: IMT-2030 推进组, 2021.IMT-2030(6G) Promotion Group. 6G overall vision and potential key technology white paper[R]. Beijing: IMT-2030 Promotion Group, 2021. [2] 陈山枝. 关于低轨卫星通信的分析及我国的发展建议[J]. 电信科学, 2020, 36(6): 1–13. doi: 10.11959/j.issn.1000-0801.2020181.CHEN Shanzhi. Analysis of LEO satellite communication and suggestions for its development strategy in China[J]. Telecommunications Science, 2020, 36(6): 1–13. doi: 10.11959/j.issn.1000-0801.2020181. [3] 徐常志, 靳一, 李立, 等. 面向6G的星地融合无线传输技术[J]. 电子与信息学报, 2021, 43(1): 28–36. doi: 10.11999/JEIT200363.XU Changzhi, JIN Yi, LI Li, et al. Wireless transmission technology of satellite-terrestrial integration for 6G mobile communication[J]. Journal of Electronics & Information Technology, 2021, 43(1): 28–36. doi: 10.11999/JEIT200363. [4] NOSCHESE P, PORFILI S, and DI GIROLAMO S. ADS-B via iridium next satellites[C]. 2011 Tyrrhenian International Workshop on Digital Communications-Enhanced Surveillance of Aircraft and Vehicles, Capri, Italy, 2011: 213–218. [5] MCDOWELL J C. The low earth orbit satellite population and impacts of the SpaceX Starlink constellation[J]. The Astrophysical Journal Letters, 2020, 892(2): L36. doi: 10.3847/2041-8213/ab8016. [6] SU Mudan, SU Xing, ZHAO Qile, et al. BeiDou augmented navigation from low earth orbit satellites[J]. Sensors, 2019, 19(1): 198. doi: 10.3390/s19010198. [7] LIN Xingqin, ROMMER S, EULER S, et al. 5G from space: An overview of 3GPP non-terrestrial networks[J]. IEEE Communications Standards Magazine, 2021, 5(4): 147–153. doi: 10.1109/MCOMSTD.011.2100038. [8] BAEZA V M, LAGUNAS E, AL-HRAISHAWI H, et al. An overview of channel models for NGSO satellites[C]. 2022 IEEE 96th Vehicular Technology Conference (VTC2022-Fall), London, United Kingdom, 2022: 1–6. doi: 10.1109/VTC2022-Fall57202.2022.10012693. [9] ITU-R P. 618–2017 Propagation data and prediction methods required for the design of earth-space telecommunication systems[S]. 2017. [10] ITU-R. P. 2108-2021 Prediction of clutter loss: ITU-R Recommendation[S]. 2021. [11] HOSSEINIAN M, CHOI J P, CHANG S H, et al. Review of 5G NTN standards development and technical challenges for satellite integration with the 5G network[J]. IEEE Aerospace and Electronic Systems Magazine, 2021, 36(8): 22–31. doi: 10.1109/MAES.2021.3072690. [12] 3GPP TR 38.811-2020 Study on new radio (NR) to support non-terrestrial networks[S]. 2020. [13] 3GPP TR 38.901-2022 Study on channel model for frequencies from 0.5 to 100 GHz[S]. 2022. [14] 3GPP TR 38.821-2020 Solutions for NR to support non-terrestrial networks (NTN)[S]. 2020. [15] 3GPP TS 38.101-5-2023 NR; User Equipment (UE) radio transmission and reception; Part 5: Satellite access Radio Frequency (RF) and performance requirements[S]. 2023. [16] ITU-R P. 676-2022 Attenuation by atmospheric gases and related effects[S]. 2022. [17] 中华人民共和国工业和信息化部. YD/T 984-2020 卫星通信链路大气和降雨衰减计算方法[S]. 北京: 人民邮电出版社, 2020.Ministry of Industry and Information Technology. YD/T 984-2020 Methods for calculating attenuations by atmospheric gases and rain in the satellite communication link[S]. Beijing: Posts & Telecom Press, 2020. [18] PANAGOPOULOS A D, ARAPOGLOU P D M, and COTTIS P G. Satellite communications at Ku, Ka, and V bands: Propagation impairments and mitigation techniques[J]. IEEE Communications Surveys & Tutorials, 2004, 6(3): 2–14. doi: 10.1109/COMST.2004.5342290. [19] PANAGOPOULOS A D, ARAPOGLOU P D M, KANELLOPOULOS J D, et al. Long-term rain attenuation probability and site diversity gain prediction formulas[J]. IEEE Transactions on Antennas and Propagation, 2005, 53(7): 2307–2313. doi: 10.1109/TAP.2005.850762. [20] LIVIERATOS S, KATSAMBAS V, and KANELLOPOULOS J. A global method for the prediction of the slant path rain attenuation statistics[J]. Journal of Electromagnetic Waves and Applications, 2000, 14(5): 713–724. doi: 10.1163/156939300X01436. [21] KANELLOPOULOS S A, KOUROGIORGAS C I, PANAGOPOULOS A D, et al. Channel model for satellite communication links above 10GHz based on Weibull distribution[J]. IEEE Communications Letters, 2014, 18(4): 568–571. doi: 10.1109/LCOMM.2014.013114.131950. [22] KOUROGIORGAS C I and PANAGOPOULOS A D. Space-time stochastic rain fading channel for multiple LEO or MEO satellite slant paths[J]. IEEE Wireless Communications Letters, 2018, 7(3): 284–287. doi: 10.1109/LWC.2017.2772248. [23] CORNEJO A, LANDEROS-AYALA S, MATIAS J M, et al. Method of rain attenuation prediction based on long–short term memory network[J]. Neural Processing Letters, 2022, 54(4): 2959–2995. doi: 10.1007/s11063-022-10749-1. [24] DOMB M and LESHEM G. Rain Attenuation Prediction for 2.4-72GHz using LTSM, an artificial recurrent neural network technology[C]. 2021 International Conference on Electrical, Communication, and Computer Engineering (ICECCE), Kuala Lumpur, Malaysia, 2021: 1–6. doi: 10.1109/ICECCE52056.2021.9514095. [25] THIENNVIBOON P and WISUTIMATEEKORN S. Rain attenuation prediction modeling for Earth-space links using artificial neural networks[C]. 2019 16th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Pattaya, Thailand, 2019: 29–32. doi: 10.1109/ECTI-CON47248.2019.8955194. [26] HUANG Jiying, GONG Shuhong, and CAI Benxiao. The frequency scaling ratio factor of rain attenuation in Ka waveband along earth-space path in China[C]. 2011 Second International Conference on Mechanic Automation and Control Engineering, Inner Mongolia, China, 2011: 7831–7833. doi: 10.1109/MACE.2011.5988868. [27] 张蕊, 林乐科, 赵振维, 等. 5G共存分析中地物附加损耗模型研究[J]. 电波科学学报, 2017, 32(5): 578–583. doi: 10.13443/j.cjors.2017091802.ZHANG Rui, LIN Leke, ZHAO Zhenwei, et al. Research on clutter loss model in sharing studies of 5G[J]. Chinese Journal of Radio Science, 2017, 32(5): 578–583. doi: 10.13443/j.cjors.2017091802. [28] ISHIMOTO K, ICHITSUBO S, OMOTE H, et al. Elevation angle characteristics of clutter loss in urban areas for mobile communications[C]. 2019 International Symposium on Antennas and Propagation (ISAP), Xi'an, China, 2019: 1–4. [29] ITU-R P. 2040-2015 Effects of building materials and structures on radiowave propagation above about 100 MHz: Recommendation[S]. 2015. [30] MONTENEGRO-VILLACIEROS B, BISHOP J, and CHAREAU J M. Clutter loss measurements and simulations at 26 GHz and 40 GHz[C]. 2019 13th European Conference on Antennas and Propagation (EuCAP), Krakow, Poland, 2019: 1–5. [31] MONTENEGRO-VILLACIEROS B, CHAREAU J M, BISHOP J, et al. Clutter loss measurements in suburban environment at 26 GHz and 40 GHz[C]. 12th European Conference on Antennas and Propagation (EuCAP 2018), London, UK, 2018: 1–4. doi: 10.1049/cp.2018.0876. [32] ALI I, AL-DHAHIR N, and HERSHEY J E. Doppler characterization for LEO satellites[J]. IEEE Transactions on Communications, 1998, 46(3): 309–313. doi: 10.1109/26.662636. [33] GUIDOTTI A, VANELLI-CORALLI A, CAUS M, et al. Satellite-enabled LTE systems in LEO constellations[C]. 2017 IEEE International Conference on Communications Workshops (ICC Workshops), Paris, France, 2017: 876–881. doi: 10.1109/ICCW.2017.7962769. [34] LIN Xingqin, LIN Zhipeng, LÖWENMARK S E, et al. Doppler shift estimation in 5G new radio non-terrestrial networks[C]. 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 2021: 1–6. doi: 10.1109/GLOBECOM46510.2021.9685184. [35] KHAN T A and AFSHANG M. A stochastic geometry approach to Doppler characterization in a LEO satellite network[C]. ICC 2020–2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 2020: 1–6. doi: 10.1109/ICC40277.2020.9148880. [36] LIN Jiangnan, HOU Zhanwei, ZHOU Yiqing, et al. Map estimation based on Doppler characterization in broadband and mobile LEO satellite communications[C]. 2016 IEEE 83rd Vehicular Technology Conference (VTC Spring), Nanjing, China, 2016: 1–5. doi: 10.1109/VTCSpring.2016.7504336. [37] KIM S, PARK J, and LEE C. CNN-based Doppler shift estimation for low earth orbit satellites[C]. 2022 37th International Technical Conference on Circuits/Systems, Computers and Communications (ITC-CSCC), Phuket, Thailand, 2022: 1–3. doi: 10.1109/ITC-CSCC55581.2022.9894921. [38] VASYLYEV D, BÉNIGUEL Y, VOLKER W, et al. Modeling of ionospheric scintillation[J]. Journal of Space Weather and Space Climate, 2022, 12: 22. doi: 10.1051/swsc/2022016. [39] DING Sheng, LI Limin, and LIU Huijie. Multipath channel measurements and analysis at UHF band for LEO satellites[C]. 2010 International Conference on Communications and Mobile Computing, Shenzhen, China, 2010: 112–116. doi: 10.1109/CMC.2010.158. [40] ORABI M, KHALIFE J, and KASSAS Z M. Opportunistic navigation with Doppler measurements from Iridium Next and Orbcomm LEO satellites[C]. 2021 IEEE Aerospace Conference (50100), Big Sky, USA, 2021: 1–9. doi: 10.1109/AERO50100.2021.9438454. [41] ZHU Yazhou, HOFMANN C A, and KNOPP A. Ka-band LEO satellite internet of things channel characterization: Survey and measurement[C]. ICC 2022-IEEE International Conference on Communications, Seoul, Korea, 2022: 3076–3081. doi: 10.1109/ICC45855.2022.9838878. [42] MORAITIS N, MILAS V, and CON S TANTINOU P. On the empirical model comparison for the land mobile satellite channel[C]. 2007 IEEE 65th Vehicular Technology Conference-VTC2007-Spring, Dublin, Ireland, 2007: 1405–1409. doi: 10.1109/VETECS.2007.294. [43] BARTS R M and STUTZMAN W L. Modeling and simulation of mobile satellite propagation[J]. IEEE Transactions on Antennas and Propagation, 1992, 40(4): 375–382. doi: 10.1109/8.138838. [44] VOGEL W and GOLDHIRSH J. Tree attenuation at 869 MHz derived from remotely piloted aircraft measurements[J]. IEEE transactions on Antennas and Propagation, 1986, 34(12): 1460–1464. doi: 10.1109/TAP.1986.1143781. [45] GOLDHIRSH J and VOGEL W. Roadside tree attenuation measurements at UHF for land mobile satellite systems[J]. IEEE Transactions on Antennas and Propagation, 1987, 35(5): 589–596. doi: 10.1109/TAP.1987.1144137. [46] GOLDHIRSH J and VOGEL W J. Mobile satellite system fade statistics for shadowing and multipath from roadside trees at UHF and L-band[J]. IEEE Transactions on Antennas and Propagation, 1989, 37(4): 489–498. doi: 10.1109/8.24169. [47] GOLDHIRSH J and VOGEL W J. An overview of results derived from mobile-satellite propagation experiments[C]. The 2nd International Mobile Satellite Conference (IMSC 1990), Ottawa, Canada, 1990: 219–224. [48] VOGEL W J and GOLDHIRSH J. Mobile satellite system propagation measurements at L-band using MARECS-B2[J]. IEEE Transactions on Antennas and Propagation, 1990, 38(2): 259–264. doi: 10.1109/8.45129. [49] SFORZA M, BUONOMO S, and MARTINI A. ESA research activities in the field of channel modelling and simulation for land mobile satellite systems[J]. COST 227: Land Mobile Satellite Communications Systems, 1993(93): 044. [50] GOLDHIRSH J and VOGEL W J. An extended empirical roadside shadowing model for estimating fade distributions from UHF to K-band for mobile satellite communications[J]. Space Communications, 1995, 13(3): 225–237. [51] PARKS M A N, EVANS B G, and BUTT G. High elevation angle propagation results, applied to a statistical model and an enhanced empirical model[J]. Electronics Letters, 1993, 29(19): 1723–1725. doi: 10.1049/el:19931146. [52] AL-HOURANI A and GUVENC I. On modeling satellite-to-ground path-loss in urban environments[J]. IEEE Communications Letters, 2021, 25(3): 696–700. doi: 10.1109/LCOMM.2020.3037351. [53] LOO C. A statistical model for a land mobile satellite link[J]. IEEE Transactions on Vehicular Technology, 1985, 34(3): 122–127. doi: 10.1109/T-VT.1985.24048. [54] LOO C and SECORD N. Computer models for fading channels with applications to digital transmission[J]. IEEE Transactions on Vehicular Technology, 1991, 40(4): 700–707. doi: 10.1109/25.108380. [55] CORAZZA G E and VATALARO F. A statistical model for land mobile satellite channels and its application to nongeostationary orbit systems[J]. IEEE Transactions on Vehicular Technology, 1994, 43(3): 738–742. doi: 10.1109/25.312773. [56] HWANG S H, KIM K J, AHN J Y, et al. A channel model for nongeostationary orbiting satellite system[C]. 1997 IEEE 47th Vehicular Technology Conference. Technology in Motion, Phoenix, USA, 1997: 41–45. doi: 10.1109/VETEC.1997.596315. [57] ABDI A, LAU W C, ALOUINI M S, et al. A new simple model for land mobile satellite channels: First-and second-order statistics[J]. IEEE Transactions on Wireless Communications, 2003, 2(3): 519–528. doi: 10.1109/TWC.2003.811182. [58] XIE Yongjun and FANG Yuguang. A general statistical channel model for mobile satellite systems[J]. IEEE Transactions on Vehicular Technology, 2000, 49(3): 744–752. doi: 10.1109/25.845094. [59] 李兴, 吴诗其. 卫星移动通信信道LR2模型及系统性能分析[J]. 电波科学学报, 2003, 18(3): 305–310. doi: 10.3969/j.issn.1005-0388.2003.03.015.LI Xing and WU Shiqi. A LR2 model for mobile satellite channels and its system performance analysis[J]. Chinese Journal of Radio Science, 2003, 18(3): 305–310. doi: 10.3969/j.issn.1005-0388.2003.03.015. [60] ALFANO G and DE MAIO A. Sum of squared shadowed-rice random variables and its application to communication systems performance prediction[J]. IEEE Transactions on Wireless Communications, 2007, 6(10): 3540–3545. doi: 10.1109/TWC.2007.060202. [61] CLEMENTE M C and PARIS J F. Closed-form statistics for sum of squared Rician shadowed variates and its application[J]. Electronics Letters, 2014, 50(2): 120–121. doi: 10.1049/el.2013.0969. [62] LUTZ E, CYGAN D, DIPPOLD M, et al. The land mobile satellite communication channel-recording, statistics, and channel model[J]. IEEE Transactions on Vehicular Technology, 1991, 40(2): 375–386. doi: 10.1109/25.289418. [63] BISCHEL H, WERNER M, and LUTZ E. Elevation-dependent channel model and satellite diversity for NGSO S-PCNs[C]. Vehicular Technology Conference-VTC, Atlanta, USA, 1996: 1038–1042. doi: 10.1109/VETEC.1996.501469. [64] FONTÁN F P, GONZÁLEZ J P, FERREIRO M J S, et al. Complex envelope three-state Markov model based simulator for the narrow-band LMS channel[J]. International Journal of Satellite Communications, 1997, 15(1): 1–15. doi: 10.1002/(SICI)1099-1247(199701)15:1<1::AID-SAT563>3.0.CO;2-R. [65] 荣剑, 申东娅, 孙静. RM陆地移动卫星信道模型[J]. 云南大学学报: 自然科学版, 2006, 28(6): 487–491. doi: 10.3321/j.issn:0258-7971.2006.06.006.RONG Jian, SHEN Dongya, and SUN Jing. RM channel model for land mobile satellite[J]. Journal of Yunnan University: Natural Sciences Edition, 2006, 28(6): 487–491. doi: 10.3321/j.issn:0258-7971.2006.06.006. [66] CID E L, SANCHEZ G M, and ALEJOS A V. Wideband analysis of the satellite communication channel at Ku- and X-Bands[J]. IEEE Transactions on Vehicular Technology, 2016, 65(4): 2787–2790. doi: 10.1109/TVT.2015.2425037. [67] VUCETIC B and DU J. Channel modeling and simulation in satellite mobile communication systems[J]. IEEE Journal on Selected Areas in Communications, 1992, 10(8): 1209–1218. doi: 10.1109/49.166746. [68] SHEN Dongya, RONG Jian, YANG Yihuai, et al. The six-state Markov model for land mobile satellite channels[C]. 2005 IEEE International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications, Beijing, China, 2005: 1619–1622. doi: 10.1109/MAPE.2005.1618239. [69] ALASSEUR C, SCALISE S, HUSSON L, et al. A novel approach to model the land mobile satellite channel through reversible jump Markov chain Monte Carlo technique[J]. IEEE Transactions on Wireless Communications, 2008, 7(2): 532–542. doi: 10.1109/TWC.2008.05544. [70] LOPEZ-SALAMANCA J J, SEMAN L O, BEREJUCK M D, et al. Finite-state Markov chains channel model for CubeSats communication uplink[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(1): 142–154. doi: 10.1109/TAES.2019.2911769. [71] VOGEL W J and HONG U S. Measurement and modeling of land mobile satellite propagation at UHF and L-band[J]. IEEE Transactions on Antennas and Propagation, 1988, 36(5): 707–719. doi: 10.1109/8.192148. [72] SCHUBERT F M, FLEURY B H, PRIETO-CERDEIRA R, et al. A rural channel model for satellite navigation applications[C]. 2012 6th European Conference on Antennas and Propagation (EUCAP), Prague, Czech Republic, 2012: 2431–2435. doi: 10.1109/EuCAP.2012.6206522. [73] BAI Lu, WANG Chengxiang, GOUSSETIS G, et al. Channel modeling for satellite communication channels at Q-band in high latitude[J]. IEEE Access, 2019, 7: 137691–137703. doi: 10.1109/ACCESS.2019.2941975. [74] HU Lingling, ZHANG Zhizhong, DENG Bingguang, et al. Channel modeling for UAV-aided LEO satellite communication[C]. 2021 24th International Symposium on Wireless Personal Multimedia Communications (WPMC), Okayama, Japan, 2021: 1–6. doi: 10.1109/WPMC52694.2021.9700458. [75] JUNG D H, RYU J G, BYUN W J, et al. Performance analysis of satellite communication system under the shadowed-rician fading: A stochastic geometry approach[J]. IEEE Transactions on Communications, 2022, 70(4): 2707–2721. doi: 10.1109/TCOMM.2022.3142290. [76] PIACENTINI M and RINALDI F. Path loss prediction in urban environment using learning machines and dimensionality reduction techniques[J]. Computational Management Science, 2011, 8(4): 371–385. doi: 10.1007/s10287-010-0121-8. [77] UCCELLARI M, FACCHINI F, SOLA M, et al. On the use of support vector machines for the prediction of propagation losses in smart metering systems[C]. 2016 IEEE 26th International Workshop on Machine Learning for Signal Processing (MLSP), Vietri sul Mare, Italy, 2016: 1–6. doi: 10.1109/MLSP.2016.7738887. [78] OROZA C A, ZHANG Ziran, WATTEYNE T, et al. A machine-learning-based connectivity model for complex terrain large-scale low-power wireless deployments[J]. IEEE Transactions on Cognitive Communications and Networking, 2017, 3(4): 576–584. doi: 10.1109/TCCN.2017.2741468. [79] ATES H F, HASHIR S M, BAYKAS T, et al. Path loss exponent and shadowing factor prediction from satellite images using deep learning[J]. IEEE Access, 2019, 7: 101366–101375. doi: 10.1109/ACCESS.2019.2931072. [80] BAI Lu, XU Qian, WU Shangbin, et al. A novel atmosphere-informed data-driven predictive channel modeling for B5G/6G satellite-terrestrial wireless communication systems at Q-band[J]. IEEE Transactions on Vehicular Technology, 2020, 69(12): 14225–14237. doi: 10.1109/TVT.2020.3037212. [81] BAI Lu, XU Qian, HUANG Ziwei, et al. An atmospheric data-driven Q-band satellite channel model with feature selection[J]. IEEE Transactions on Antennas and Propagation, 2022, 70(6): 4002–4013. doi: 10.1109/TAP.2021.3137285. [82] ALON M M D and LESHEM G. Satellite to ground station, attenuation prediction for 2.4–72 GHz using LTSM, an artificial recurrent neural network technology[J]. Electronics, 2022, 11(4): 541. doi: 10.3390/electronics 11040541. [83] AL HOMSSI B, CHAN C C, WANG Ke, et al. Deep learning forecasting and statistical modeling for Q/V-band LEO satellite channels[J]. IEEE Transactions on Machine Learning in Communications and Networking, 2023, 1: 78–89. doi: 10.1109/TMLCN.2023.3286793. [84] KUMAR R and ARNON S. Deep learning based scintillation prediction for satellite link using measured data[C]. 2022 45th International Conference on Telecommunications and Signal Processing (TSP), Prague, Czech Republic, 2022: 246–249. doi: 10.1109/TSP55681.2022.9851250. -





 下载:
下载:
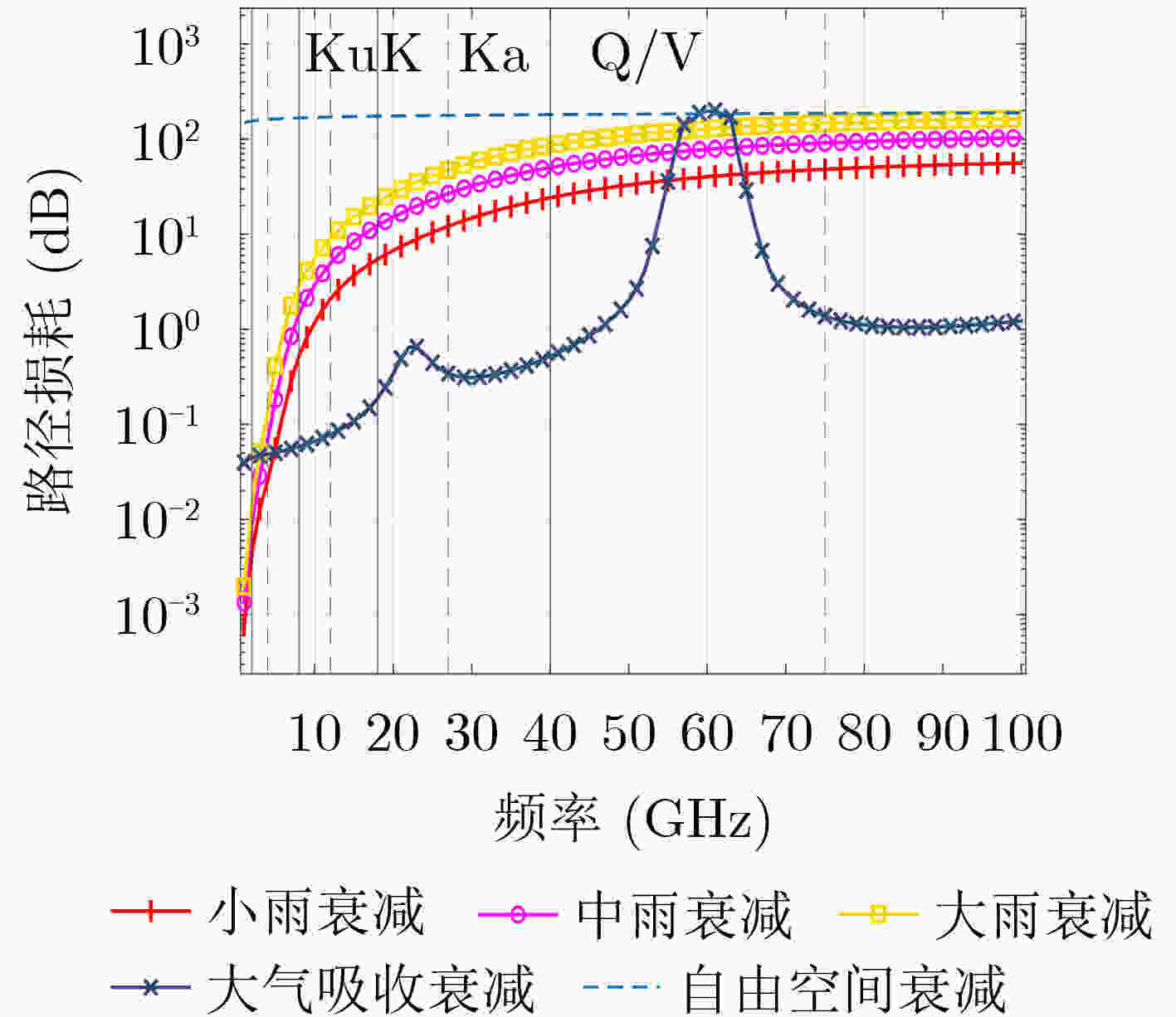
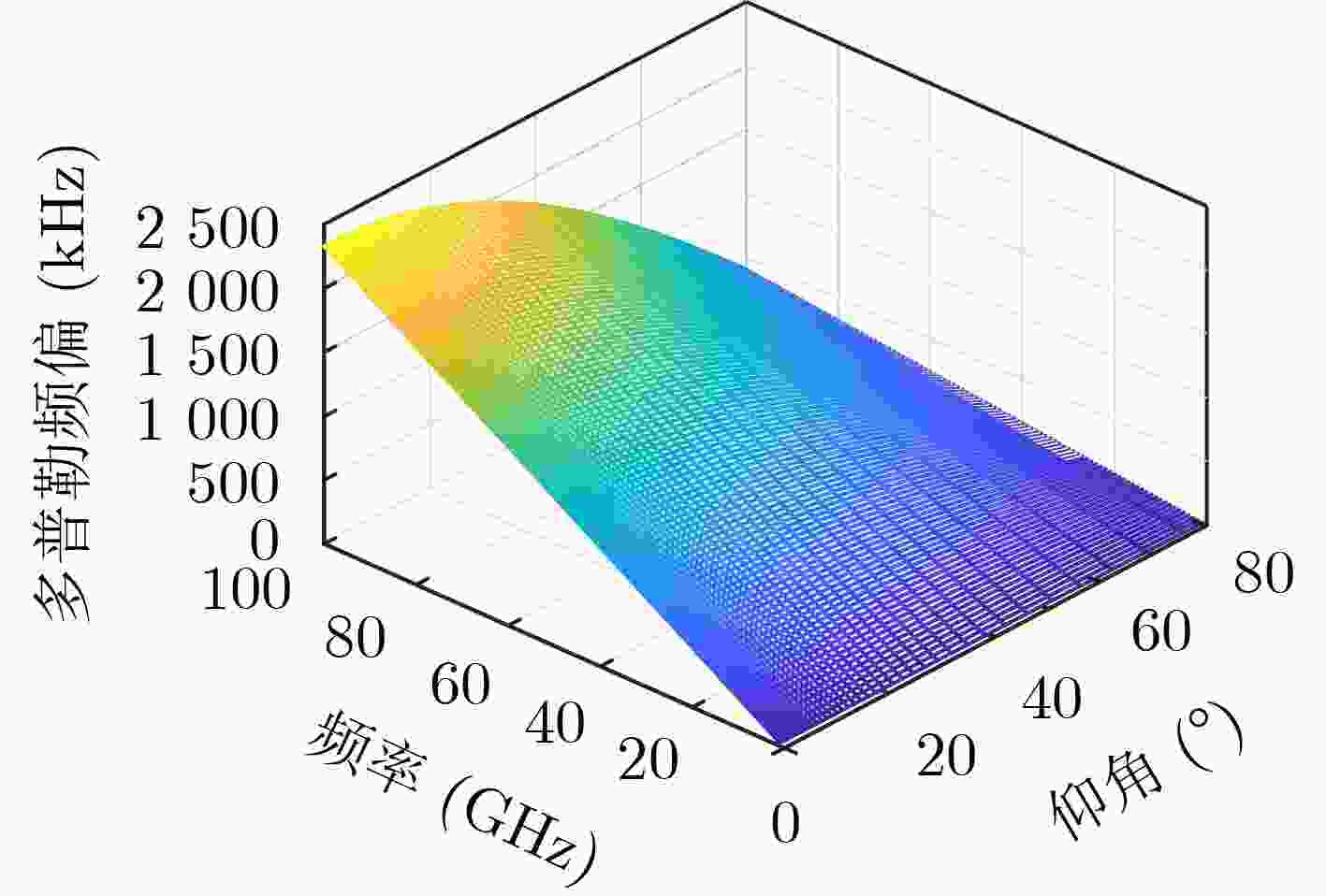


 下载:
下载:
