Multi-Agent Deep Reinforcement Learning with Clustering and Information Sharing for Traffic Light Cooperative Control
-
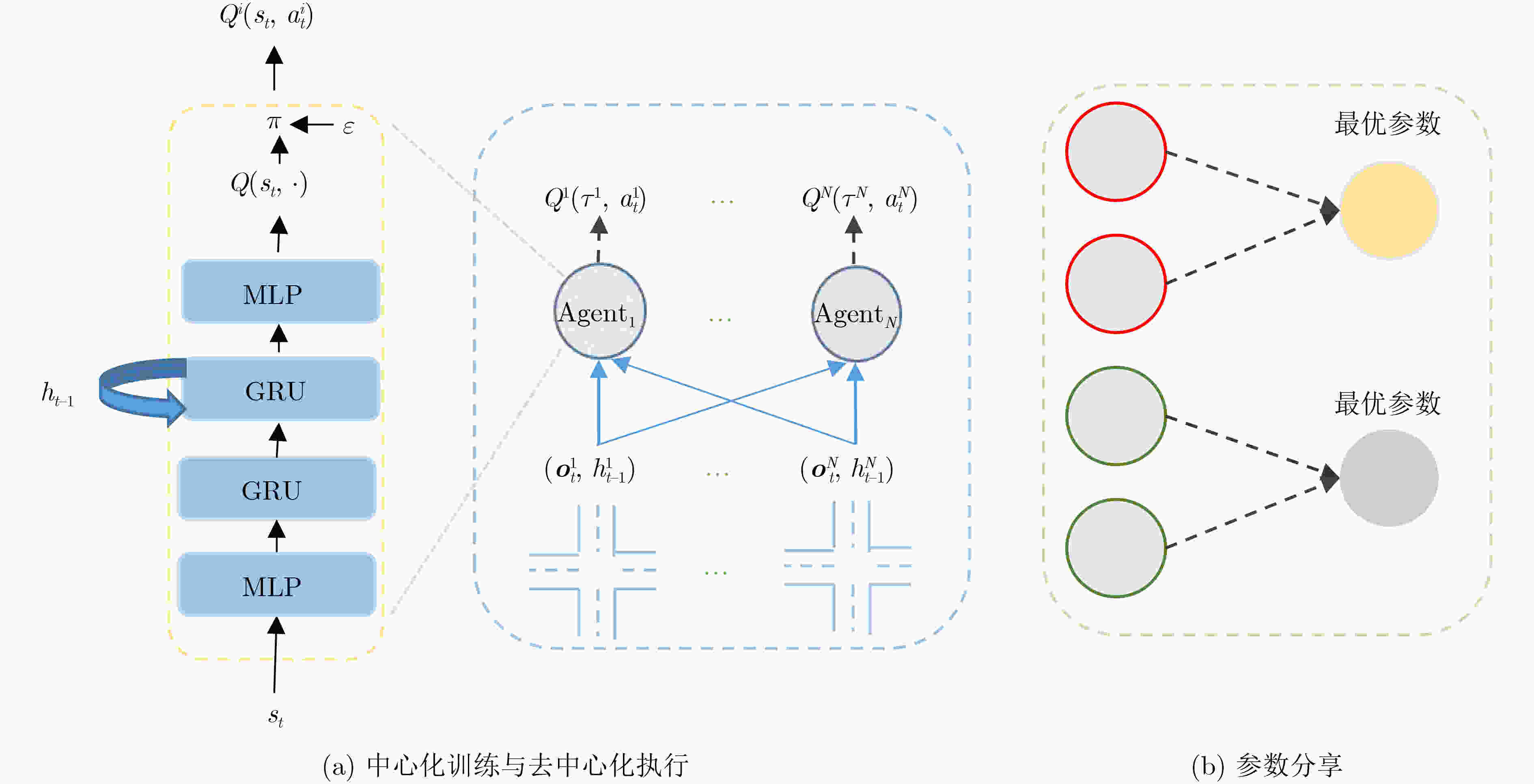
摘要: 该文提出一种适用于多路口交通灯实时控制的多智能体深度循环Q-网络(MADRQN),目的是提高多个路口的联合控制效果。该方法将交通灯控制建模成马尔可夫决策过程,将每个路口的控制器作为智能体,根据位置和观测信息对智能体聚类,然后在聚类内部进行信息共享和中心化训练,并在每个训练过程结束时将评价值最高的值函数网络参数分享给其它智能体。在城市交通仿真软件(SUMO)下的仿真实验结果表明,所提方法能够减少通信的数据量,使得智能体之间的信息共享和中心化训练更加可行和高效,车辆平均等待时长少于当前最优的基于多智能体深度强化学习的交通灯控制方法,能够有效地缓解交通拥堵。Abstract: In order to improve the joint control effect of multi-crossing, Multi-Agent Deep Recurrent Q-Network (MADRQN) for real-time control of multi-intersection traffic signals is proposed in this paper. Firstly, the traffic light control is modeled as a Markov decision process, wherein one controller at each crossing is considered as an agent. Secondly, agents are clustered according to their position and observation. Then, information sharing and centralized training are conducted within each cluster. Also the value function network parameters of agents with the highest critic value are shared with other agent at the end of every training process. The simulated experimental results under Simulation of Urban MObility (SUMO) show that the proposed method can reduce the amount of communication data, make information sharing of agents and centralized training more feasible and efficient. The average delay of vehicles is reduced obviously compared with the state-of-the-art traffic light control methods based on multi-agent deep reinforcement learning. The proposed method can effectively alleviate traffic congestion.
-
算法1 MADRQN算法伪代码 初始化:MDRQN网络及目标网络,经验回放池D,训练轮数${N_{\rm e}}$=100,每轮训练步数T=300,智能体数量N=15,智能体位置向量
${{\boldsymbol{p}}^{{i}}},i = 1,2, \cdots ,{N}$,聚类数量${N_{\rm c}}$(未定,初始化为0),聚类内智能体数量${N_{{\mathrm{A}}}}$(未定,初始化为0),聚类间隔步数C=1000,聚类迭代次数
K=2 500,节点移动系数$ {\varepsilon _{{\mathrm{b}}}} = 0.1 $和$ {\varepsilon _{{\mathrm{n}}}} = 0.1 $,边的最大年龄${\mathrm{AM}} = 30$,误差衰减系数$\beta = 0.9$,参数移动系数$ {c_1} = 0.9 $和$ {c_2} = 0.3 $奖励
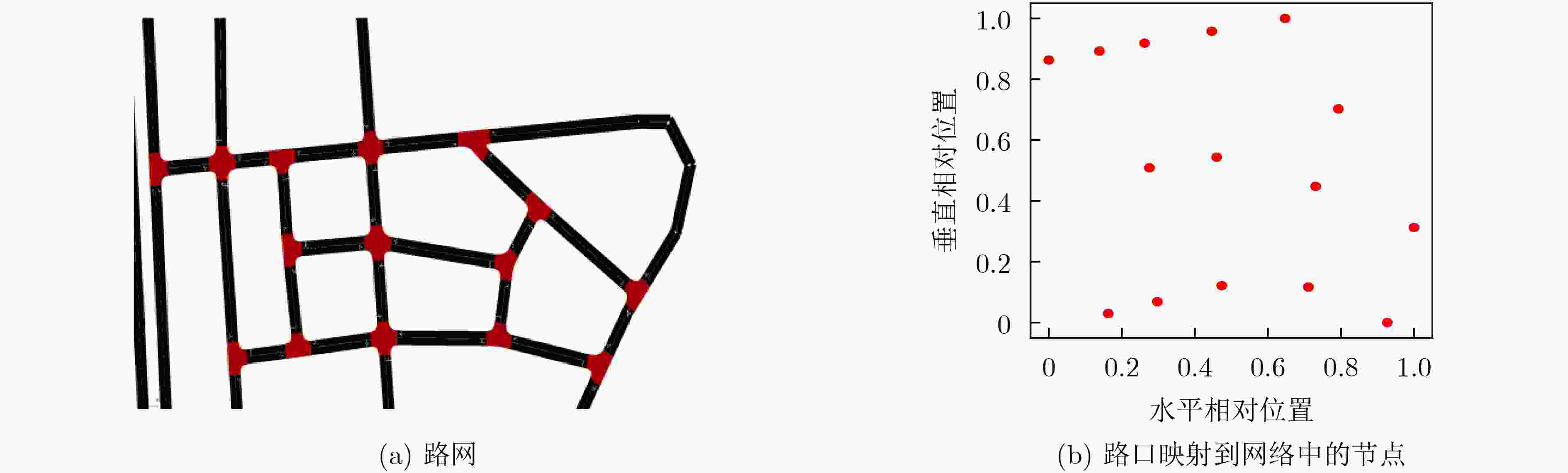
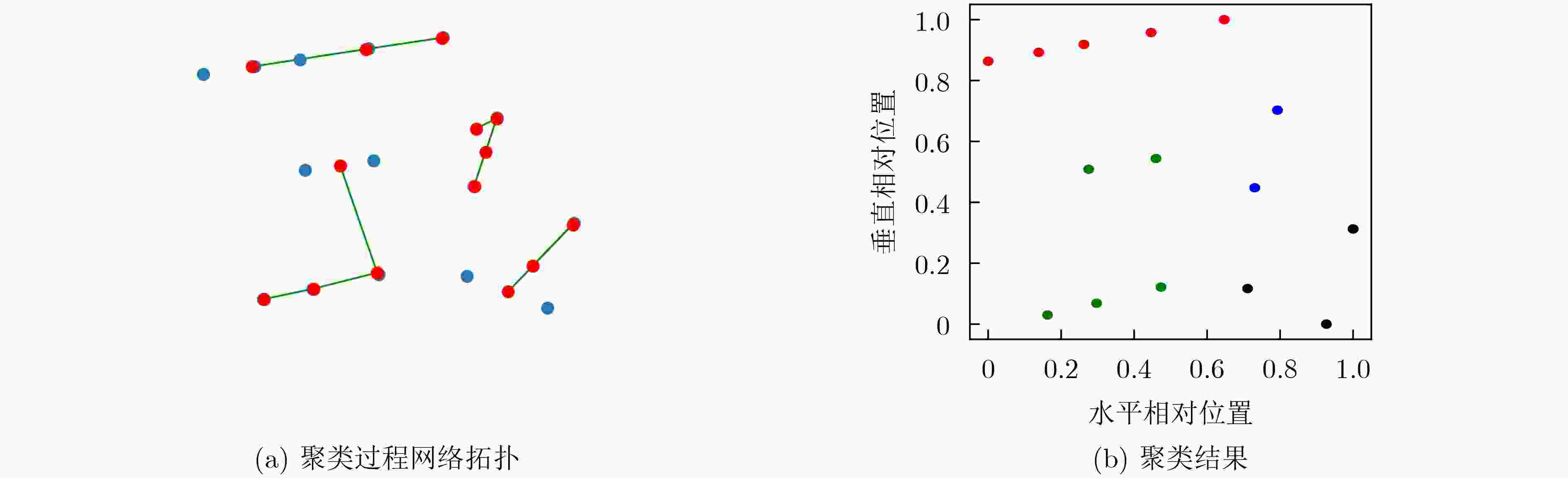
折扣因子$ \gamma = 0.9 $,学习率$ \alpha = 5{\mathrm{e}} - 4 $(1) for ep=1 to ${N_{{\mathrm{e}}}}$ do (2) 获取时间步t=0的路口观测${\boldsymbol{o}}_{{0}}^{{i}},i = 1,2, \cdots ,{N}$ (3) 初始化立即奖励$r_0^i = 0$,动作$a_0^i = - 1$,动作选择的贪婪参数$ \varepsilon={\left(1-\dfrac{\mathrm{e}\mathrm{p}}{{M}}\right)}^{2} $ (4) while t<T do # 以下是每隔C个时间步对智能体聚类 (5) if t%C=0 Then (6) 从全部智能体的混合特征集合$\{ ({{\boldsymbol{p}}^{{i}}},{\boldsymbol{o}}_{{\tau }}^{{i}})\} $中随机选择两个特征向量${{\boldsymbol{v}}_{{a}}}$和${{\boldsymbol{v}}_{{b}}}$,分别将其映射为GNG网络的初始节点a和b (7) for k=0 to K do (8) 从集合$\{ ({{\boldsymbol{p}}^{{i}}},{\boldsymbol{o}}_{{\tau }}^{{i}})\} $中选择一个新的特征向量$ {\boldsymbol{x}} $,计算$ {\boldsymbol{x}} $与网络节点对应向量的距离$||{{{{\boldsymbol{v}}}}_{{j}}} - {{{\boldsymbol{x}}}}|{|^2},j = 1,2, \cdots ,{N_{k}}$,${N_{k}}$表示网络
当前节点数量。然后找到距离最近和次近节点${s_1}$和${s_2}$,对应特征向量为${{\boldsymbol{v}}_{{{{s}}_{{1}}}}}$和${{\boldsymbol{v}}_{{{{s}}_{{2}}}}}$(9) 朝着x的方向,分别移动节点${s_1}$和${s_1}$的邻居节点${S_{{N_{{s_1}}}}}$ $ {s_1} \leftarrow {s_1} + {\varepsilon _{{\mathrm{b}}}} \cdot ||{\boldsymbol{x}} - {{\boldsymbol{v}}_{{{{s}}_{{1}}}}}||_2^2 $ $ {S_{{{N}_{{{s}_{1}}}}}} \leftarrow {S_{{{N}_{{{s}_{1}}}}}} + {\varepsilon _{{n}}} \cdot ||{\boldsymbol{x}} - {{\boldsymbol{v}}_{{{{N}}_{{{s1}}}}}}||_2^2 $ (10) 若${s_1}$与${s_2}$没有边,则连接${s_1}$和${s_2}$,将所有包含${s_1}$的边的年龄加1 (11) 遍历网络全部的边,将年龄大于${\mathrm{AM}}$的边删除,再删除孤立的节点 (12) 找出累计误差$\sum\nolimits_{k = 0}^K {\left\|{{\boldsymbol{x}}_{{k}}} - {{\boldsymbol{v}}_{{{{s}}_{{j}}}}}\right\|_2^2} $最大的节点q和次最大的节点p,在二者的中点插入新的节点r,分别连接r与q、r与p,删除
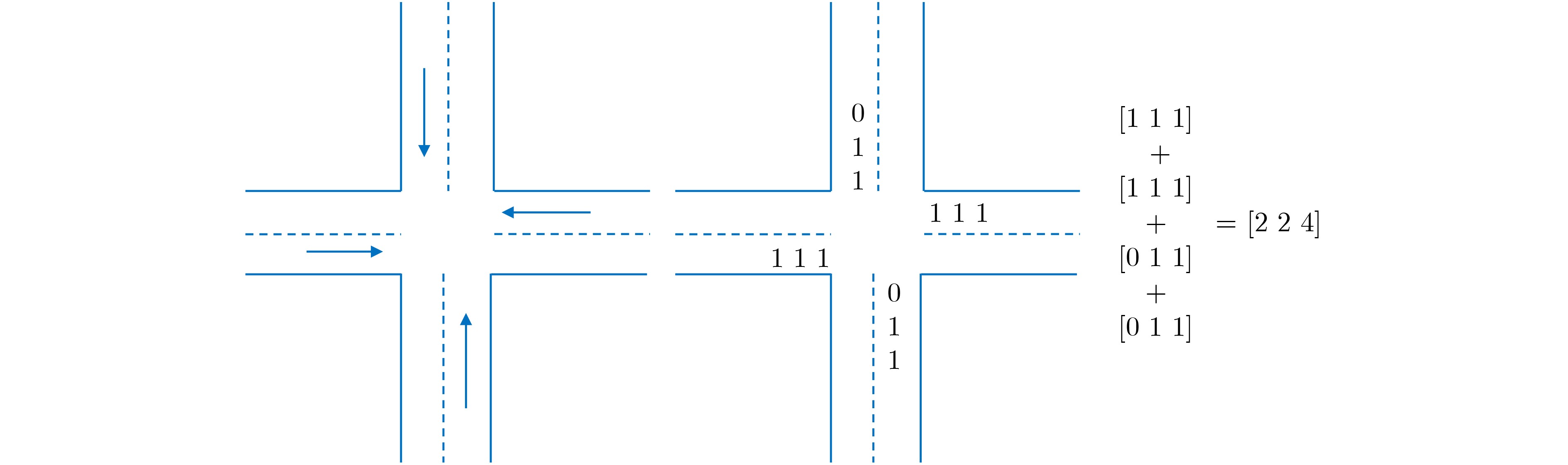
p与q的连接(13) 将节点p与q的误差乘以衰减系数$\beta $,将q的误差作为r的误差14 end for # 以下与环境交互,收集经验数据 (14) for ${i_{{\mathrm{c}}}} = 1$ to $ {{N}}_{\mathrm{c}} $ do #不同的聚类 (15) for $ {{i}}_{\mathrm{{\mathrm{a}}}}=1 $ to $ {{N}}_{\mathrm{A}} $ do #聚类内不同的智能体 (16) 获取观测${\boldsymbol{o}}_t^{{i_{\mathrm{a}}}}$,根据策略执行动作$a_t^{{i_{\mathrm{a}}}}$,接收奖励$r_t^{{i_{\mathrm{a}}}}$,获取新观测${{o}}_{{{t + 1}}}^{{{{i}}_{\rm{a}}}}$ (17) 将数据$ \left({\boldsymbol{o}}_{{t}}^{{1}}, \cdots ,{\boldsymbol{o}}_{{t}}^{{{{N}}_{\rm{A}}}},a_t^1, \cdots ,a_t^{{N_{\mathrm{A}}}},r_t^1, \cdots ,r_t^{{N_{\mathrm{A}}}},{\boldsymbol{o}}_{{{t + 1}}}^{{1}}, \cdots ,{\boldsymbol{o}}_{{{t + 1}}}^{{{{N}}_{\rm{A}}}}\right) $存入经验池D (18) end while # 以下为训练部分 (19) for ${i_{\mathrm{c}}} = 1$ to $ {{N}}_{{{\mathrm{c}}}} $ do #不同的聚类 (20) for $ {{i}}_{\rm{a}}=1 $ to $ {{N}}_{\rm{A}} $ do #聚类内不同的智能体 (21) for batch in由D构造的DataLoader do (22) 共享观测${s_t} = \left\{ {\boldsymbol{o}}_{{t}}^{{1}},{\boldsymbol{o}}_{{t}}^{2}, \cdots ,{\boldsymbol{o}}_{{t}}^{{{{N}}_{\rm{A}}}}\right\} ,{s_{t + 1}} = \left\{ {\boldsymbol{o}}_{{{t + 1}}}^{{1}},{\boldsymbol{o}}_{{{t + 1}}}^{{2}}, \cdots ,{\boldsymbol{o}}_{{{t + 1}}}^{{{{N}}_{\rm{A}}}}\right\} $动作、奖励分别为$a_t^{{i_{\mathrm{a}}}}$和$r_t^{{i_{\mathrm{a}}}}$ (23) 根据式(4)—式(6),计算损失和更新智能体的网络参数 (24) end for (25) end for (26) 根据式(8)—式(10)将网络参数向聚类内最优和个体历史最优移动 (27) end for (28) 清空经验池D (29) end for 表 1 实验及算法参数设置
参数 数值(范围) 观测范围 各路口进车道400 m 智能体数量N 15 车辆长度 5 ${\text{m}}$ 最小车辆间距 1~2 ${\text{m}}$ 最大速度 40~50 ${\text{km/h}}$ 车辆加速度 0.5~1 m/s2 车辆减速度 –5~–3.5 m/s2 训练轮数M 100 每轮最大步数T 5 400 学习率$\alpha $ 5e–4 折扣因子$\gamma $ 0.9 贪婪参数$ \varepsilon $ 初始为1递减至0.001 回放池大小$|D|$ 5 000 -
[1] PANDIT K, GHOSAL D, ZHANG H M, et al. Adaptive traffic signal control with vehicular ad hoc networks[J]. IEEE Transactions on Vehicular Technology, 2013, 62(4): 1459–1471. doi: 10.1109/TVT.2013.2241460. [2] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 770–778. doi: 10.1109/CVPR.2016.90. [3] 邵明莉, 曹鹗, 胡铭, 等. 面向优先车辆感知的交通灯优化控制方法[J]. 软件学报, 2021, 32(8): 2425–2438. doi: 10.13328/j.cnki.jos.006191.SHAO Mingli, CAO E, HU Ming, et al. Traffic light optimization control method for priority vehicle awareness[J]. Journal of Software, 2021, 32(8): 2425–2438. doi: 10.13328/j.cnki.jos.006191. [4] HADDAD T A, HEDJAZI D, and AOUAG S. A new deep reinforcement learning-based adaptive traffic light control approach for isolated intersection[C]. The 5th International Symposium on Informatics and its Applications, M'sila, Algeria, 2022: 1–6. doi: 10.1109/ISIA55826.2022.9993598. [5] GENDERS W and RAZAVI S. Using a deep reinforcement learning agent for traffic signal control[J]. arXiv preprint arXiv: 1611.01142, 2016. [6] TIGGA A, HOTA L, PATEL S, et al. A deep Q-learning-based adaptive traffic light control system for urban safety[C]. The 4th International Conference on Advances in Computing, Communication Control and Networking, Greater Noida, India, 2022: 2430–2435. doi: 10.1109/ICAC3N56670.2022.10074123. [7] 邹翔宇, 黄崇文, 徐勇军, 等. 基于深度学习的通信系统中安全能效的控制[J]. 电子与信息学报, 2022, 44(7): 2245–2252. doi: 10.11999/JEIT211611.ZOU Xiangyu, HUANG Chongwen, XU Yongjun, et al. Secure energy efficiency in communication systems based on deep learning[J]. Journal of Electronics & Information Technology, 2022, 44(7): 2245–2252. doi: 10.11999/JEIT 211611. [8] 唐伦, 李质萱, 蒲昊, 等. 基于多智能体深度强化学习的无人机动态预部署策略[J]. 电子与信息学报, 2023, 45(6): 2007–2015. doi: 10.11999/JEIT220513.TANG Lun, LI Zhixuan, PU Hao, et al. A dynamic pre-deployment strategy of UAVs based on multi-agent deep reinforcement learning[J]. Journal of Electronics & Information Technology, 2023, 45(6): 2007–2015. doi: 10.11999/JEIT220513. [9] KANG Leilei, HUANG Hao, LU Weike, et al. A dueling deep Q-network method for low-carbon traffic signal control[J]. Applied Soft Computing, 2023, 141: 110304. doi: 10.1016/j.asoc.2023.110304. [10] TUNC I and SOYLEMEZ M T. Fuzzy logic and deep Q learning based control for traffic lights[J]. Alexandria Engineering Journal, 2023, 67: 343–359. doi: 10.1016/j.aej.2022.12.028. [11] BÁLINT K, TAMÁS T, and TAMÁS B. Deep reinforcement learning based approach for traffic signal control[J]. Transportation Research Procedia, 2022, 62: 278–285. doi: 10.1016/j.trpro.2022.02.035. [12] RASHID T, SAMVELYAN M, DE WITT C S, et al. QMIX: Monotonic value function factorisation for deep multi-agent reinforcement Learning[C]. The 35th International Conference on Machine Learning, Stockholm, Sweden, 2018: 6846–6859. [13] SON K, KIM D, KANG W J, et al. QTRAN: Learning to factorize with transformation for cooperative multi-agent reinforcement learning[C]. The 36th International Conference on Machine Learning, Long Beach, USA, 2019: 5887–5896. [14] LOWE R, WU Y I, TAMAR A, et al. Multi-agent actor-critic for mixed cooperative-competitive environments[C]. The 31st International Conference on Neural Information Processing Systems, Long Beach, USA, 2017: 6382–6393. [15] FOERSTER J, FARQUHAR G, AFOURAS T, et al. Counterfactual multi-agent policy gradients[C]. The 32nd AAAI Conference on Artificial Intelligence, New Orleans, USA, 2018. doi: 10.1609/aaai.v32i1.11794. [16] SU Haoran, ZHONG Y D, DEY B, et al. EMVLight: A decentralized reinforcement learning framework for efficient passage of emergency vehicles[C]. The 36th AAAI Conference on Artificial Intelligence, 2021: 4593–4601. doi: 10.48550/arXiv.2109.05429. [17] YANG Shantian, YANG Bo, ZENG Zheng, et al. Causal inference multi-agent reinforcement learning for traffic signal control[J]. Information Fusion, 2023, 94: 243–256. doi: 10.1016/j.inffus.2023.02.009. [18] WANG Zixin, ZHU Hanyu, HE Mingcheng, et al. GAN and multi-agent DRL based decentralized traffic light signal control[J]. IEEE Transactions on Vehicular Technology, 2022, 71(2): 1333–1348. doi: 10.1109/TVT.2021.3134329. [19] 丛珊. 基于多智能体强化学习的交通信号灯协同控制算法的研究[D]. [硕士论文], 南京信息工程大学, 2022. doi: 10.27248/d.cnki.gnjqc.2022.000386.CONG Shan. Multi-agent deep reinforcement learning based traffic light cooperative control[D]. [Master dissertation], Nanjing University of Information Science & Technology, 2022. doi: 10.27248/d.cnki.gnjqc.2022.000386. [20] ZHU Ruijie, LI Lulu, WU Shuning, et al. Multi-agent broad reinforcement learning for intelligent traffic light control[J]. Information Sciences, 2023, 619: 509–525. doi: 10.1016/j.ins.2022.11.062. [21] FRITZKE B. A growing neural gas network learns topologies[C]. The 7th International Conference on Neural Information Processing Systems, Denver, USA, 1994: 625–632. -





 下载:
下载:
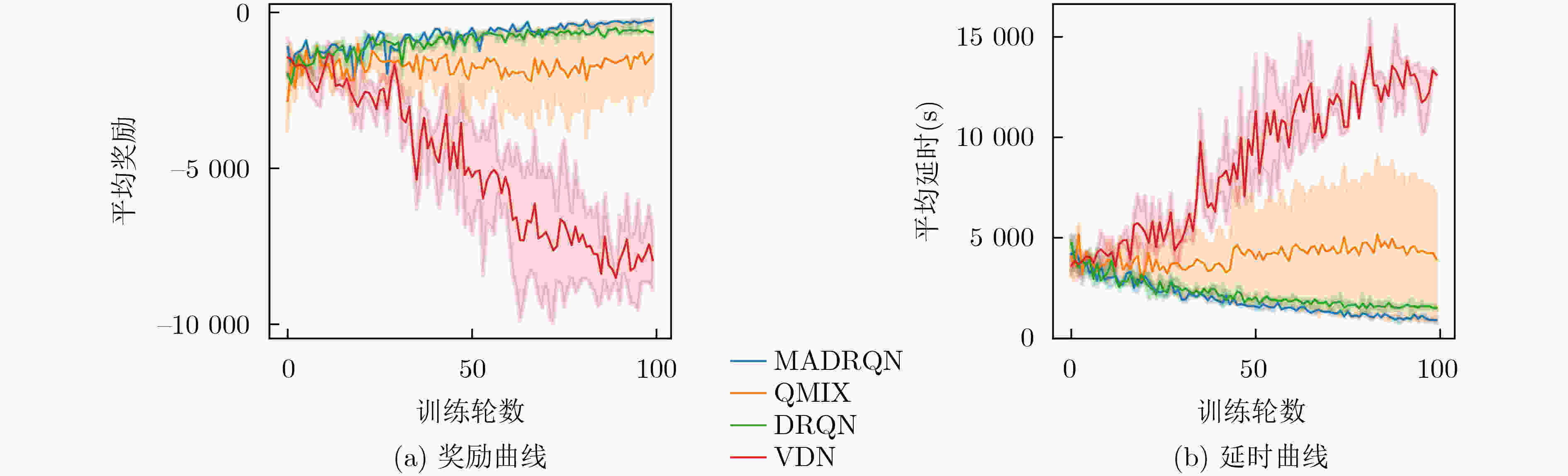
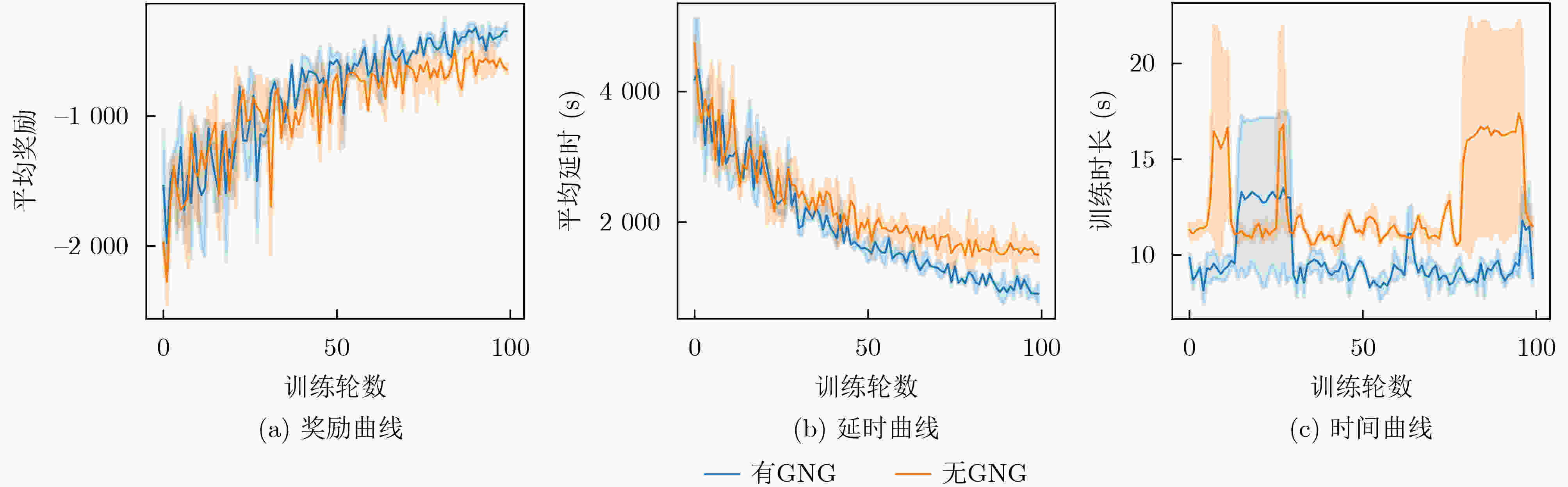
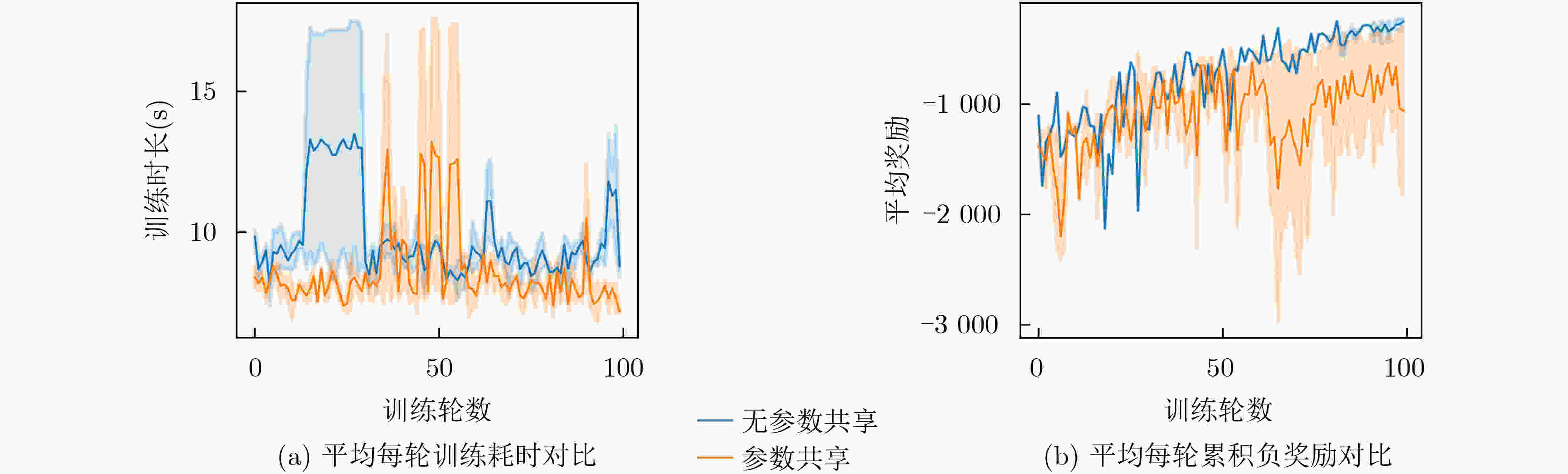


 下载:
下载:
