Automatic Generation of General Electromagnetic Countermeasures under an Unknown Game Paradigm
-
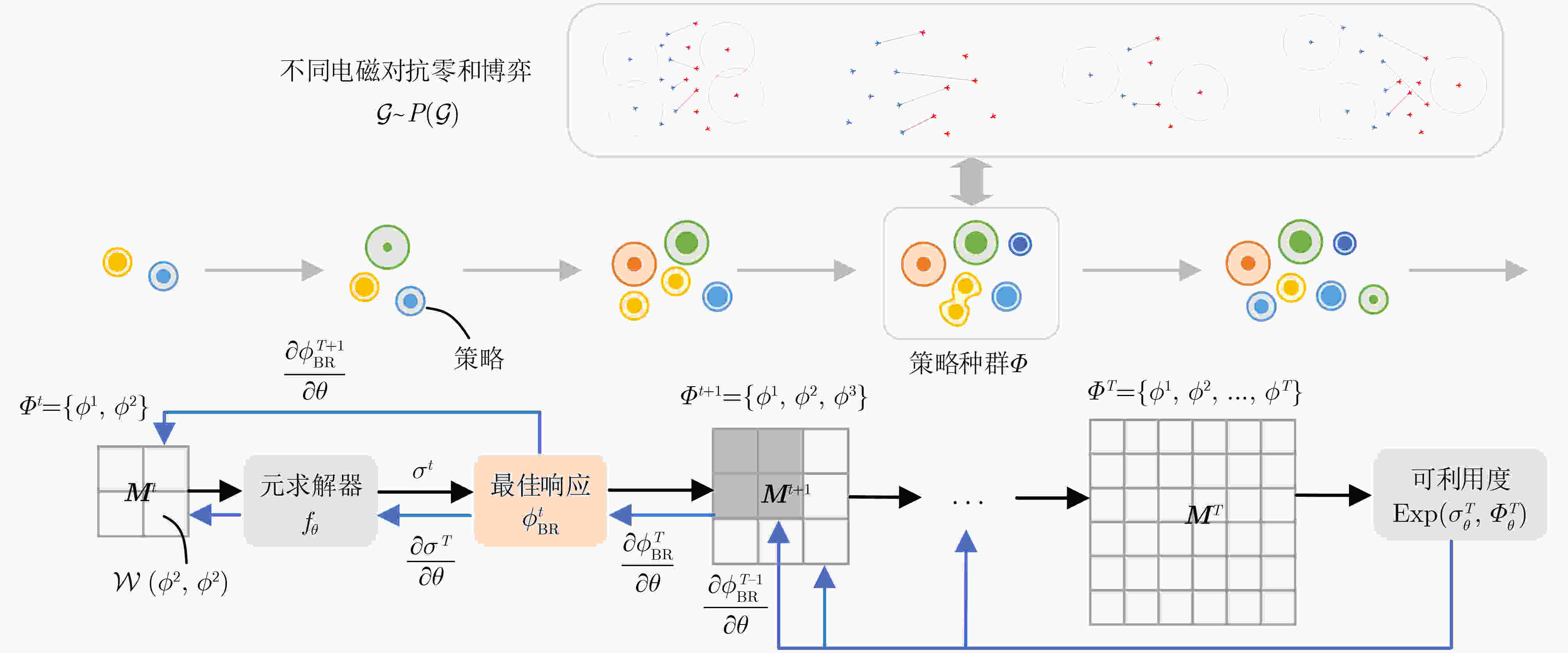
摘要: 电磁空间对抗通常被建模为零和博弈,但是当作战环境变化时零和博弈双方需要适应新的未知任务,人工设定的博弈规则不再适用。为了避免人为设计显式博弈策略,该文提出一种基于种群的多智能体电磁对抗方法(PMAEC),以实现在未知博弈范式下的通用电磁对抗策略自动生成。首先,基于模拟电磁博弈对抗环境的多智能体对抗平台(MaCA),采用元博弈框架建立电磁对抗策略种群优化问题模型,并将其分解为内部和外部优化目标。其次,结合元学习技术,通过自动课程学习(ACL)优化元求解器模型。最后,通过迭代更新最佳响应策略,扩充并强化策略种群以适应不同难度的博弈挑战。在MaCA平台上的仿真结果表明,所提的PMAEC方法能使元博弈收敛到更低的可利用度,并且训练得到的电磁对抗策略种群可以泛化到更复杂的零和博弈,实现模型从简单场景训练扩展至复杂电磁对抗环境的大规模博弈,增强电磁对抗策略的泛化能力。Abstract: The electromagnetic space confrontation in electronic warfare is generally modeled as a zero-sum game. However, as the battlefield environment evolves, both sides of the game must adapt to new and unknown tasks, rendering manually designed game rules ineffective. A novel method called Population-based Multi-Agent Electromagnetic Countermeasure (PMAEC) is proposed to overcome the limitations of explicit game strategies. This approach enables the automatic generation of general electromagnetic countermeasure policies in unknown game paradigms. First, a meta-game framework is used to model the optimization problem of the electromagnetic countermeasure policy-population, which is decomposed into internal and external optimization based on electromagnetic game environments of the Multi-agent Combat Arena(MaCA) platform. Second, the meta-solver model is optimized by combining Auto-Curriculum Learning(ACL) with Meta-Learning technology. The PMAEC method involves iterative updates of the best response policy, expanding and strengthening the policy population to overcome the challenges leveraged by various difficult games. Simulation results of the MaCA platform demonstrate that the proposed method successfully bestows the meta-game with lower exploitability. Further, the trained population of electromagnetic countermeasure policies can be generalized to more complex zero-sum games. This approach extends the model from training based on simple scenarios to large-scale games in complex electromagnetic countermeasure environments, consequently enhancing the generalization capability of the strategies.
-
算法1 基于种群的多智能体电磁对抗算法(PMAEC) (1) 给定博弈分布 $ p(\mathcal{G}) $,学习率 $ \eta $和 $ \mu $,时间窗 $ T $,初始化策略池
${\varPhi ^0}$和元求解器参数 $ \theta $(2) for每次训练迭代 (3) 从 $ p(\mathcal{G}) $中采样 $ K $个博弈 (4) for每个博弈 (5) for时间窗内每个时刻 (6) 计算 $ t - 1 $时刻的元策略 ${\sigma ^{t - 1} } = {f_\theta }({ {\boldsymbol{M} }^{t - 1} })$ (7) 初始化最佳响应策略 $ {\phi ^0} $ (8) 根据式(23)计算最佳响应 $\phi _{{\rm{BR}}}^t$ (9) 将 $\phi _{{\rm{BR}}}^t$添加至种群 ${\varPhi ^t} = {\varPhi ^{t - 1} } \cup \phi _{{\rm{BR}}}^t$ (10) end for (11) 计算 $ T $时刻的元策略 ${\sigma^T} = {f_\theta }({ {\boldsymbol{M} }^T})$ (12) 根据式(1)计算可利用度 ${\rm{Exp} }\left( {\sigma _\theta ^T,\varPhi _\theta ^T} \right)$ (13) end for (14) 根据式(10)、式(24) 、式(25)计算元梯度 ${\nabla _\theta }\mathcal{J}_{{\rm{out}}}^k(\theta )$ (15) 根据式(27)更新元求解器参数 $ \theta $ (16) end for (17) 储存当前元求解器模型 $ {f_\theta } $ 表 1 PMAEC算法参数列表
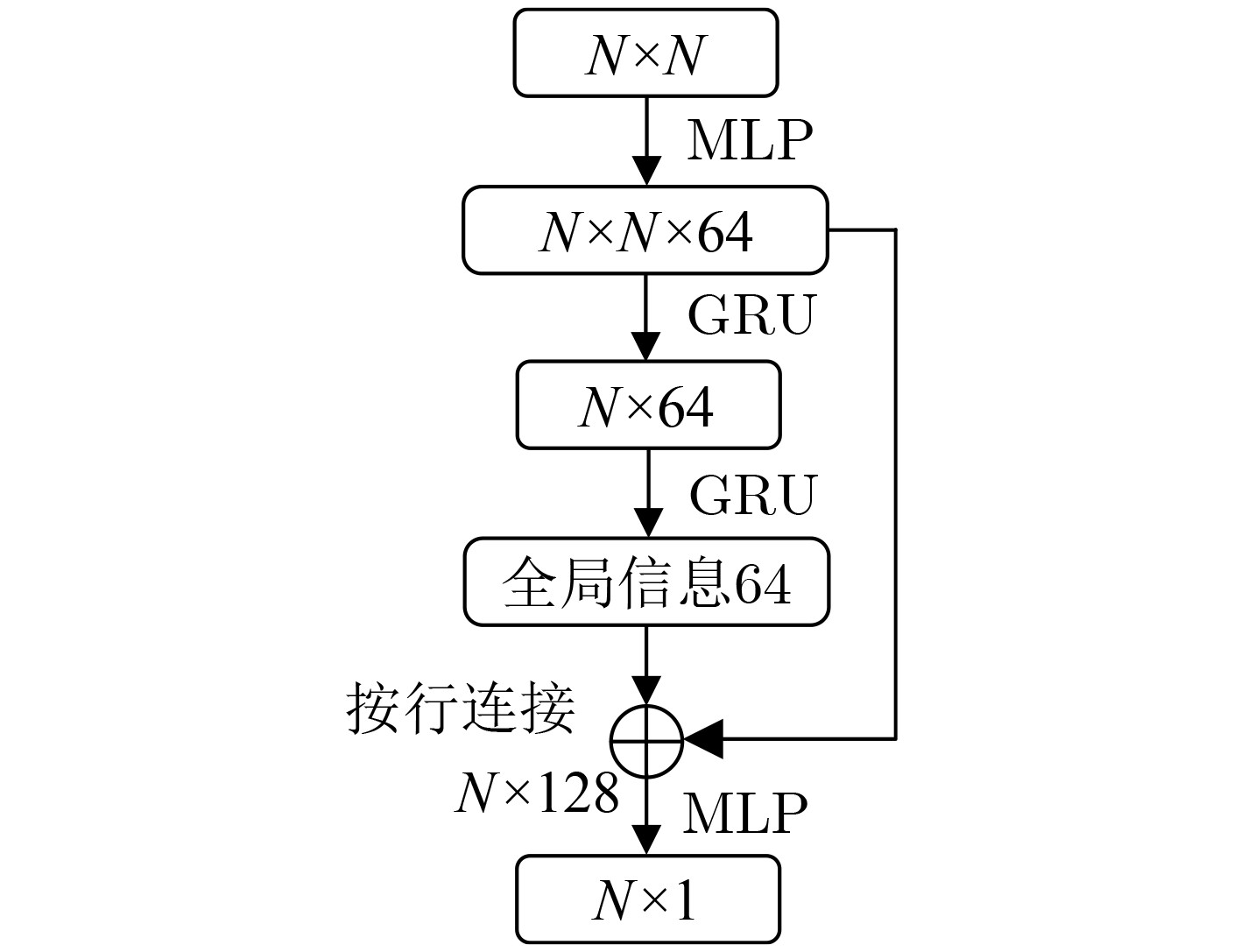
参数名称 数值 外部学习率 $ \mu $ 0.01 元训练迭代次数 100 元批尺寸 5 模型类型 GRU 窗口大小 [1, 3, 5] 内部学习率 $ \eta $ 25.0 内部梯度迭代次数 5 可利用度学习率 10.0 内部可利用度迭代次数 20 表 2 可利用度均值和标准差对比
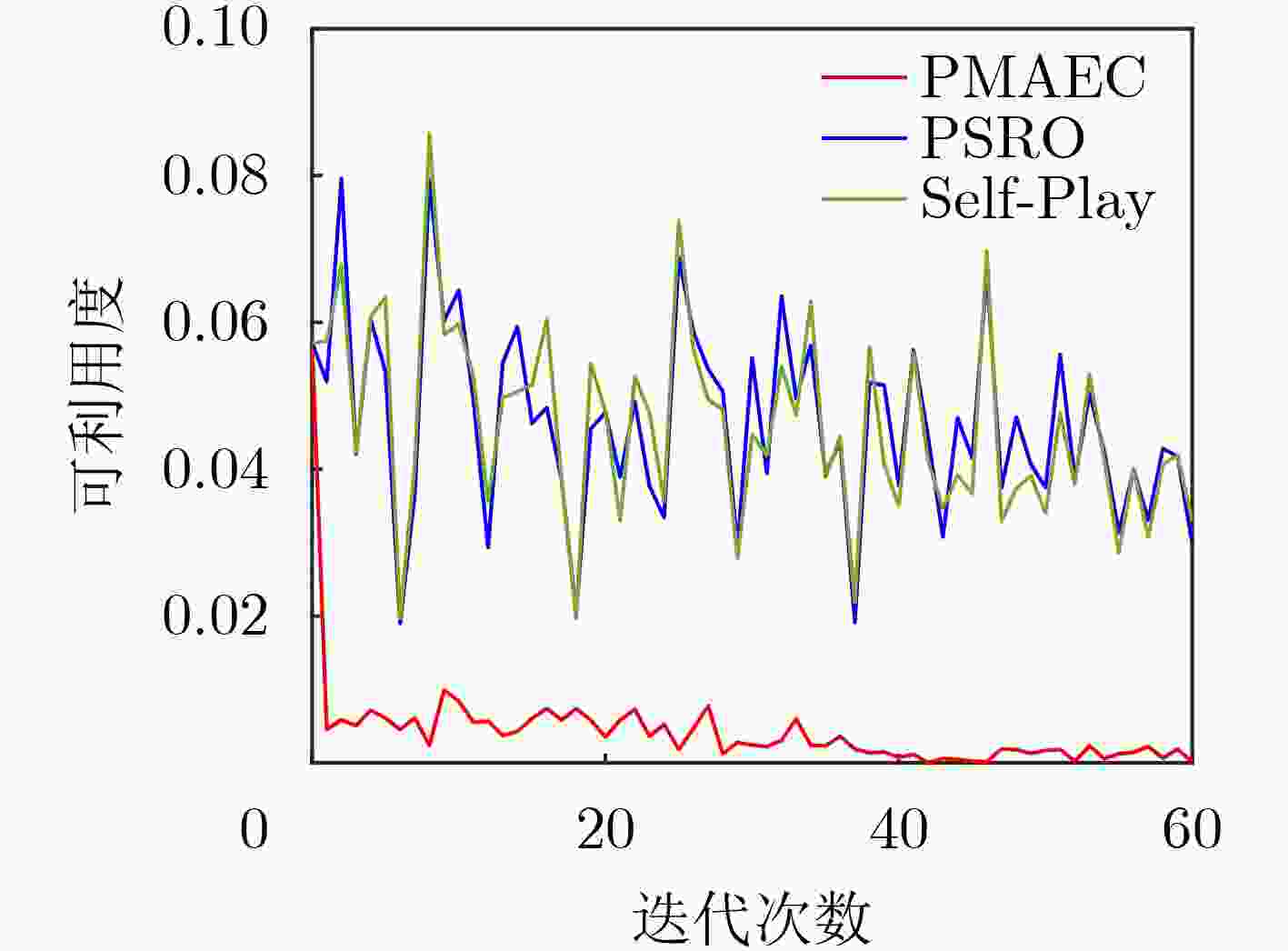
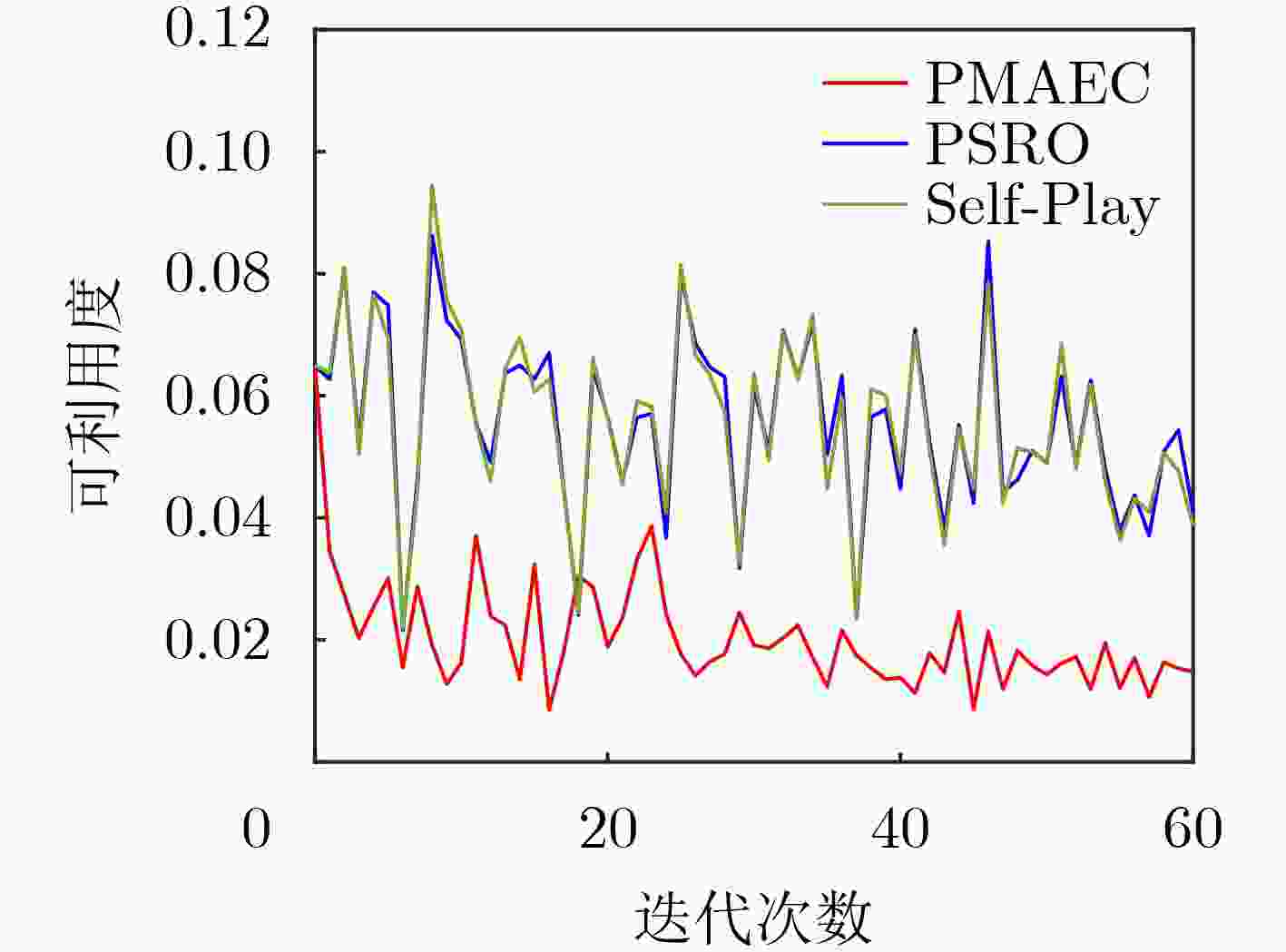
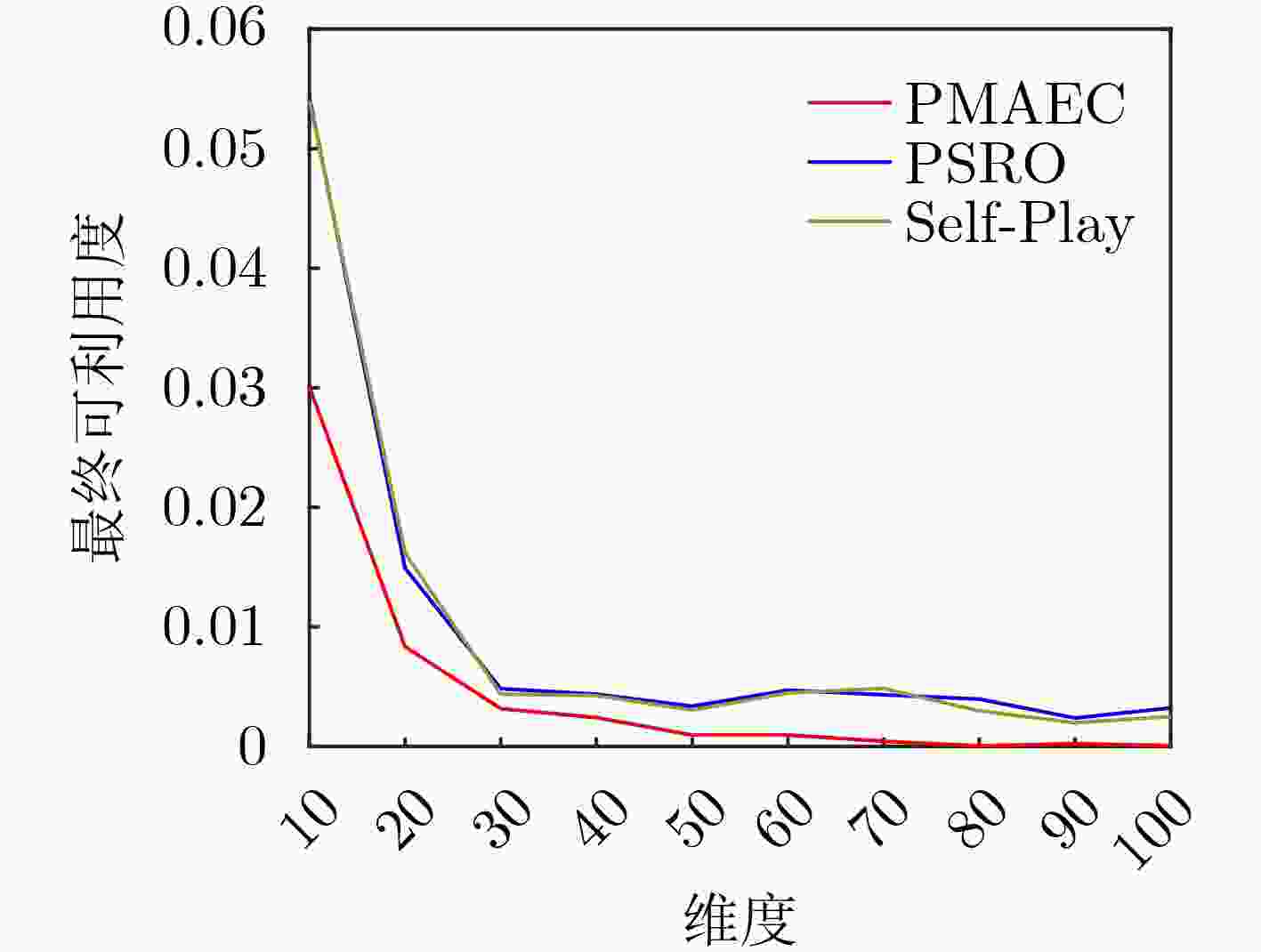
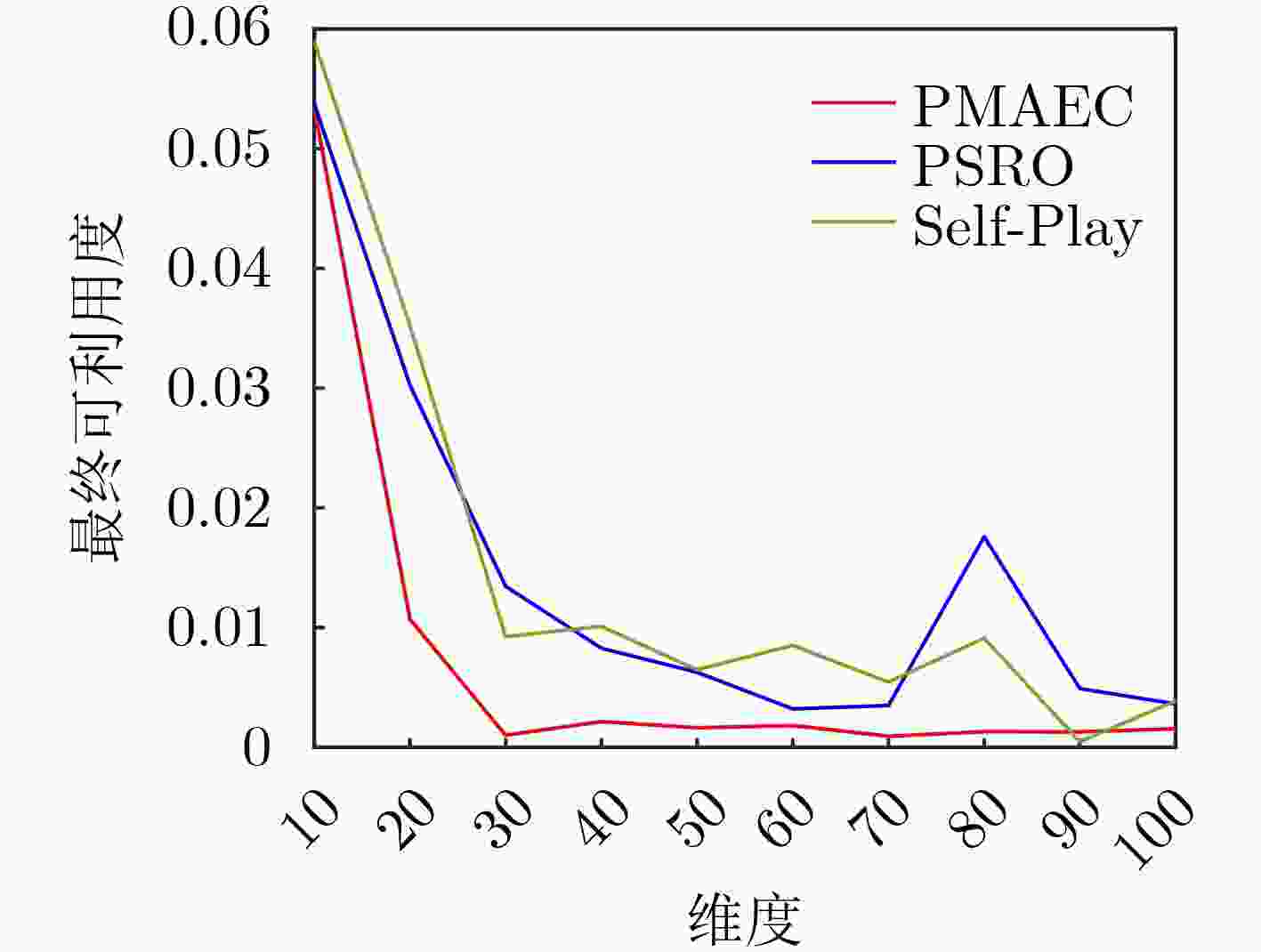
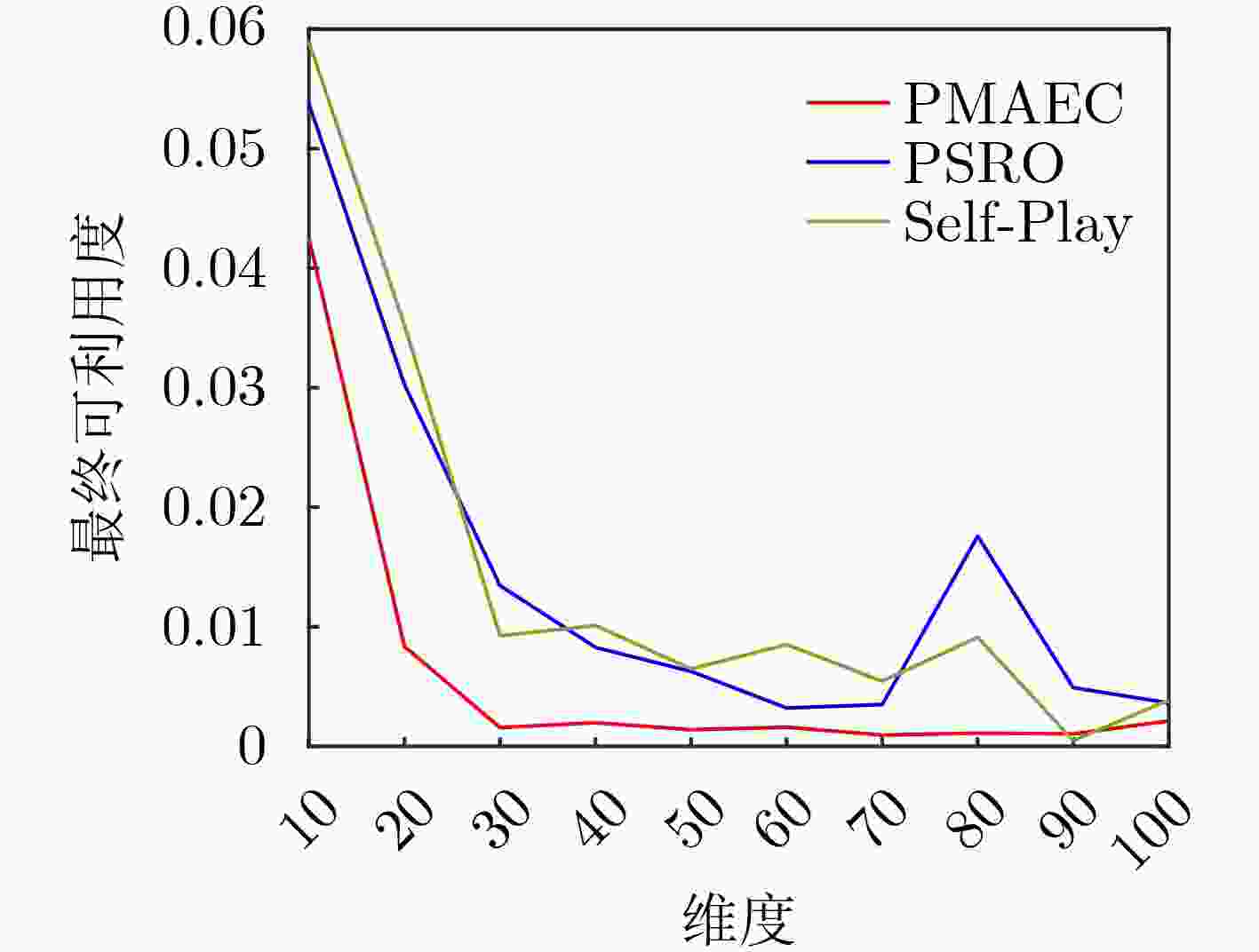
算法 异构地图 同构地图 均值 标准差 均值 标准差 PMAEC 0.0017 0.0064 0.0186 0.0079 PSRO 0.0464 0.013 0.056 0.015 Self-Play 0.0465 0.0133 0.0558 0.0151 -
[1] QUAN Siji, QIAN Weiping, GUQ J, et al. Radar-communication integration: An overview[C]. The 7th IEEE/International Conference on Advanced Infocomm Technology, Fuzhou, China, 2014: 98–103. [2] 李光久, 李昕. 博弈论简明教程[M]. 镇江: 江苏大学出版社, 2013.LI Guangjiu and LI Xin. A Brief Tutorial on Game Theory[M]. Zhenjiang: Jiangsu University Press, 2013. [3] MUKHERJEE A and SWINDLEHURST A L. Jamming games in the MIMO wiretap channel with an active eavesdropper[J]. IEEE Transactions on Signal Processing, 2013, 61(1): 82–91. doi: 10.1109/TSP.2012.2222386 [4] NGUYEN D N and KRUNZ M. Power minimization in MIMO cognitive networks using beamforming games[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(5): 916–925. doi: 10.1109/JSAC.2013.130510 [5] DELIGIANNIS A, PANOUI A, LAMBOTHARAN S, et al. Game-theoretic power allocation and the Nash equilibrium analysis for a multistatic MIMO radar network[J]. IEEE Transactions on Signal Processing, 2017, 65(24): 6397–6408. doi: 10.1109/TSP.2017.2755591 [6] LIU Pengfei, WANG Lei, SHAN Zhao, et al. A dynamic game strategy for radar screening pulse width allocation against jamming using reinforcement learning[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(5): 6059–6072. [7] LI Kang, JIU Bo, PU Wenqiang, et al. Neural fictitious self-play for radar antijamming dynamic game with imperfect information[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(6): 5533–5547. doi: 10.1109/TAES.2022.3175186 [8] ZHAO Chenyu, WANG Qing, LIU Xiaofeng, et al. Reinforcement learning based a non-zero-sum game for secure transmission against smart jamming[J]. Digital Signal Processing, 2021, 112: 103002. doi: 10.1016/j.dsp.2021.103002 [9] LI Wen, CHEN Jin, LIU Xin, et al. Intelligent dynamic spectrum anti-jamming communications: a deep reinforcement learning perspective[J]. IEEE Wireless Communications, 2022, 29(5): 60–67. doi: 10.1109/MWC.103.2100365 [10] LECUN Y, BENGIO Y, and HINTON G. Deep learning[J]. Nature, 2015, 521(7553): 436–444. doi: 10.1038/nature14539 [11] ANDREW A M. Reinforcement learning: An introduction by Richard S. Sutton and Andrew G. Barto, Adaptive computation and machine learning series, MIT Press (Bradford book), Cambridge, Mass., 1998, xviii + 322 pp, ISBN 0-262-19398-1, (hardback, £31.95)[J].Robotica, 1999, 17(2): 229–235. [12] WANG Haozhi, WANG Qing, and CHEN Qi. Opponent’s dynamic prediction model-based power control scheme in secure transmission and smart jamming game[J]. IEEE Internet of Things Journal, To be published. [13] KRISHNAMURTHY V, ANGLEY D, EVANS R, et al. Identifying cognitive radars-inverse reinforcement learning using revealed preferences[J]. IEEE Transactions on Signal Processing, 2020, 68: 4529–4542. doi: 10.1109/TSP.2020.3013516 [14] PATTANAYAK K, KRISHNAMURTHY V, and BERRY C. How can a cognitive radar mask its cognition?[C]. 2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 2022: 5897–5901. [15] LAURENT G J, MATIGNON L, LE FORT-PIAT N, et al. The world of independent learners is not Markovian[J]. International Journal of Knowledge-based and Intelligent Engineering Systems, 2011, 15(1): 55–64. doi: 10.3233/KES-2010-0206 [16] LEIBO J Z, HUGHES E, LANCTOT M, et al. Autocurricula and the emergence of innovation from social interaction: A manifesto for multi-agent intelligence research[EB/OL].https://arxiv.org/abs/1903.00742, 2019. [17] PORTELAS R, COLAS C, WENG Lilian, et al. Automatic curriculum learning for deep RL: A short survey[C]. Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, Yokohama, Japan, 2020: 4819–4825. [18] LANCTOT M, ZAMBALDI V, GRUSLYS A, et al. A unified game-theoretic approach to multiagent reinforcement learning[C]. Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, USA, 2017: 4193–4206. [19] BAKER B, KANITSCHEIDER I, MARKOV T, et al. Emergent tool use from multi-agent autocurricula[C]. 8th International Conference on Learning Representations, Addis Ababa, Ethiopia, 2020. [20] SILVER D, SCHRITTWIESER J, SIMONYAN K, et al. Mastering the game of go without human knowledge[J]. Nature, 2017, 550(7676): 354–359. doi: 10.1038/nature24270 [21] JADERBERG M, CZARNECKI W M, DUNNING I, et al. Human-level performance in 3D multiplayer games with population-based reinforcement learning[J]. Science, 2019, 364(6443): 859–865. doi: 10.1126/science.aau6249 [22] XU Zhongwen, VAN HASSELT H, and SILVER D. Meta-gradient reinforcement learning[C]. Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, Canada, 2018: 2402–2413. [23] XU Zhongwen, VAN HASSELT H P, HESSEL M, et al. Meta-gradient reinforcement learning with an objective discovered online[C]. Proceedings of the 34th International Conference on Neural Information Processing Systems, Vancouver, Canada, 2020: 1279. [24] FINN C, ABBEEL P, and LEVINE S. Model-agnostic meta-learning for fast adaptation of deep networks[C]. Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 2017: 1126–1135. [25] FENG Xidong, SLUMBERS O, WAN Ziyu, et al. Neural auto-curricula in two-player zero-sum games[C/OL]. Proceedings of the 34th International Conference on Neural Information Processing Systems, 2021, 3504–3517. [26] HOLLAND J H. Genetic algorithms[J]. Scientific American, 1992, 267(1): 66–72. doi: 10.1038/scientificamerican0792-66 [27] SEHGAL A, LA Hung, LOUIS S, et al. Deep reinforcement learning using genetic algorithm for parameter optimization[C]. 2019 Third IEEE International Conference on Robotic Computing (IRC), Naples, Italy, 2019: 596–601. [28] LIU Haoqiang, ZONG Zefang, LI Yong, et al. NeuroCrossover: An intelligent genetic locus selection scheme for genetic algorithm using reinforcement learning[J]. Applied Soft Computing, 2023, 146: 110680. doi: 10.1016/j.asoc.2023.110680 [29] SONG Yanjie, WEI Luona, YANG Qing, et al. RL-GA: A reinforcement learning-based genetic algorithm for electromagnetic detection satellite scheduling problem[J]. Swarm and Evolutionary Computation, 2023, 77: 101236. doi: 10.1016/j.swevo.2023.101236 [30] CETC-TFAI. MaCA[EB/OL].https://github.com/CETC-TFAI/MaCA, 2023. [31] MULLER P, OMIDSHAFIEI S, ROWLAND M, et al. A generalized training approach for multiagent learning[C]. 8th International Conference on Learning Representations, Addis Ababa, Ethiopia, 2020: 1–35. [32] TUYLS K, PEROLAT J, LANCTOT M, et al. A generalised method for empirical game theoretic analysis[C]. 17th International Conference on Autonomous Agents and MultiAgent Systems, Stockholm, Sweden, 2018: 77–85. [33] OH J, HESSEL M, CZARNECKI W M, et al. Discovering reinforcement learning algorithms[C]. Proceedings of the 34th International Conference on Neural Information Processing Systems, Vancouver, Canada, 2020: 1060–1070. [34] BALDUZZI D, GARNELO M, BACHRACH Y, et al. Open-ended learning in symmetric zero-sum games[C]. Proceedings of the 36th International Conference on Machine Learning, Long Beach, USA, 2019: 434–443. [35] 罗俊仁, 张万鹏, 袁唯淋, 等. 面向多智能体博弈对抗的对手建模框架[J]. 系统仿真学报, 2022, 34(9): 1941–1955. doi: 10.16182/j.issn1004731x.joss.21-0363LUO Junren, ZHANG Wanpeng, YUAN Weilin, et al. Research on opponent modeling framework for multi-agent game confrontation[J]. Journal of System Simulation, 2022, 34(9): 1941–1955. doi: 10.16182/j.issn1004731x.joss.21-0363 [36] CHUNG J, GULCEHRE C, CHO K, et al. Empirical evaluation of gated recurrent neural networks on sequence modeling[EB/OL].https://arxiv.org/abs/1412.3555, 2014. [37] BERGER U. Brown's original fictitious play[J]. Journal of Economic Theory, 2007, 135(1): 572–578. doi: 10.1016/j.jet.2005.12.010 [38] LONG J, SHELHAMER E, and DARRELL T. Fully convolutional networks for semantic segmentation[C]. Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, USA, 2015: 3431–3440. -





 下载:
下载:
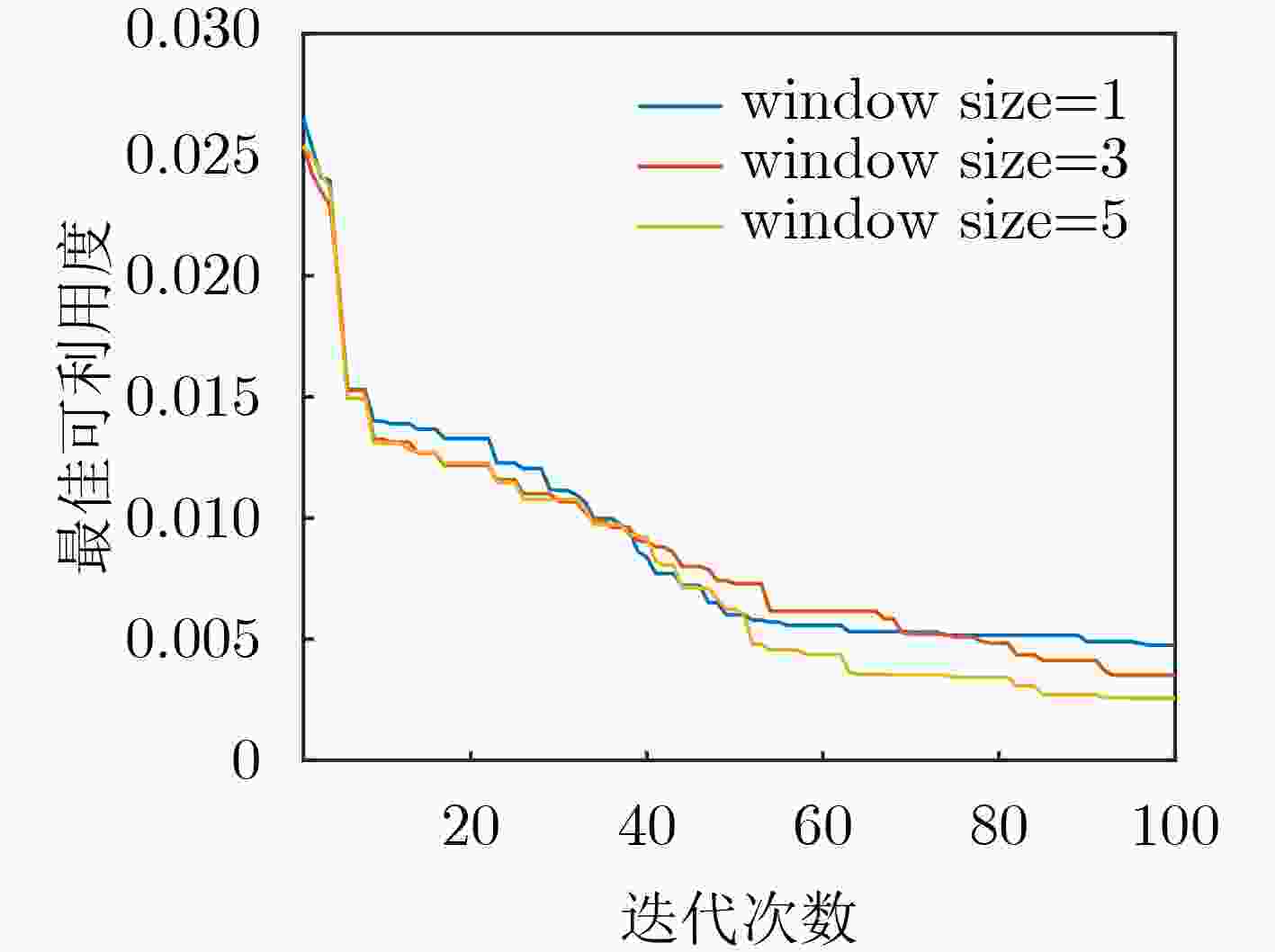
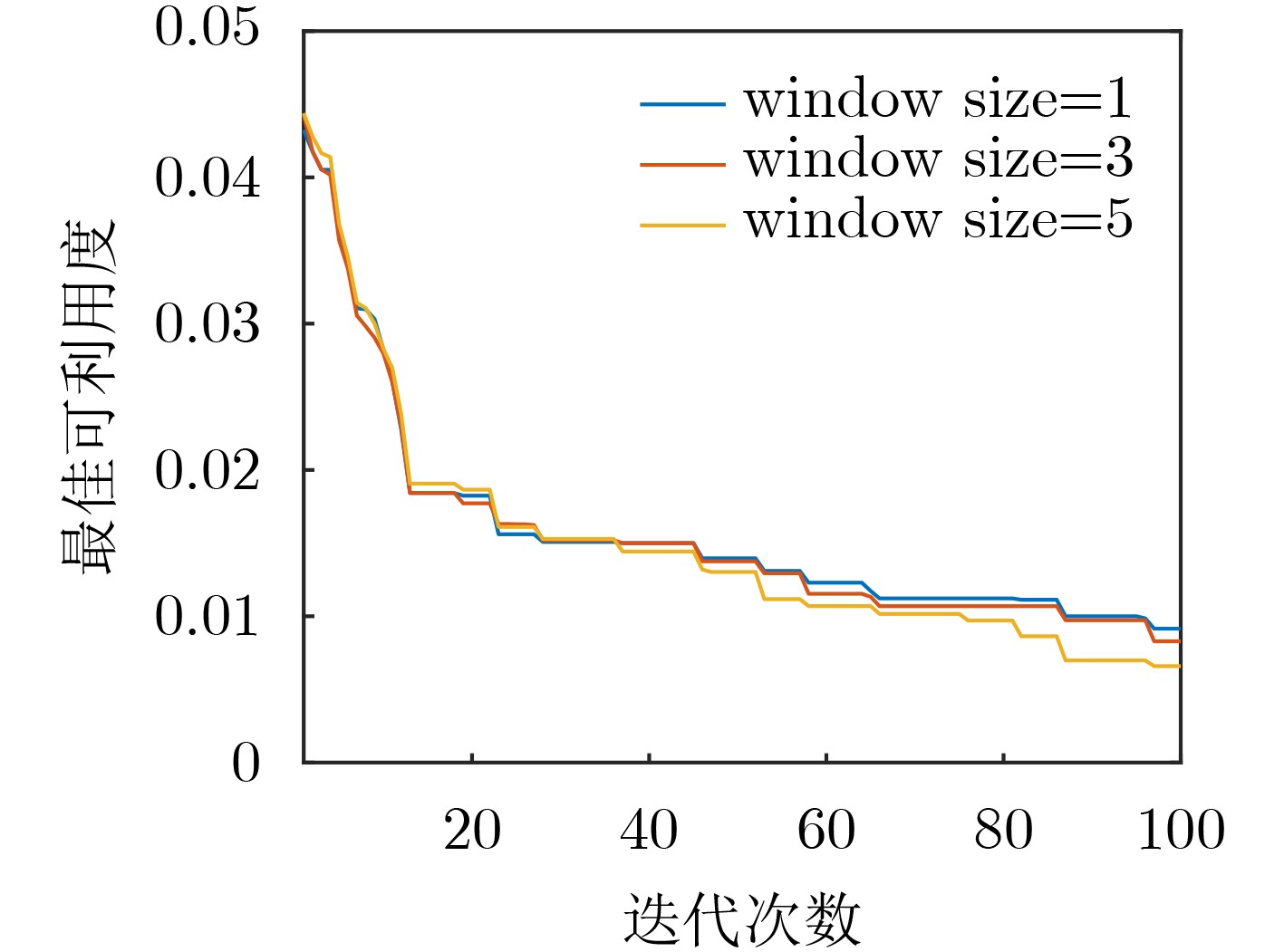
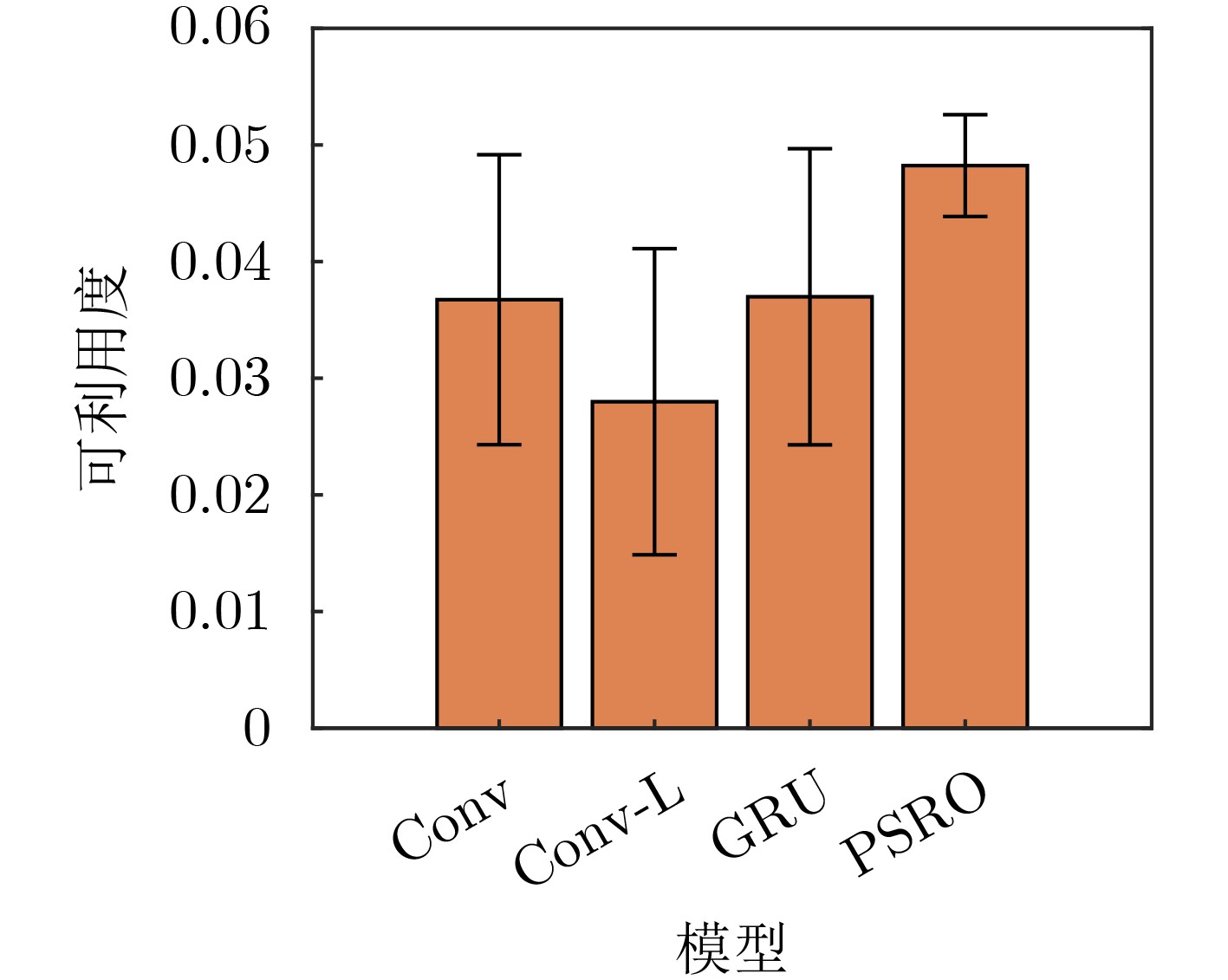
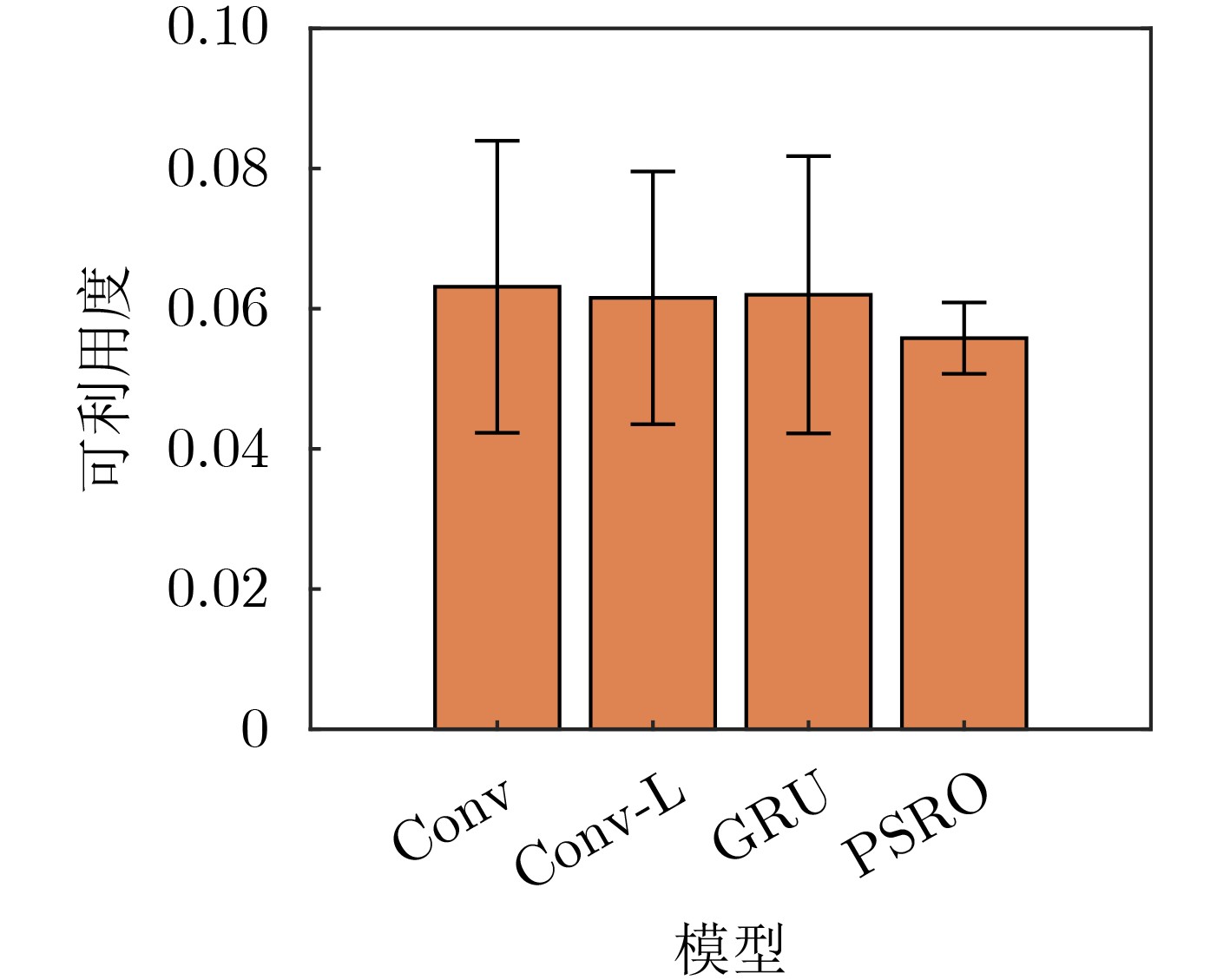


 下载:
下载:
