A Time Transfer Tracking Loop Based on Adaptive Kalman Filter in Complex Conditions
-
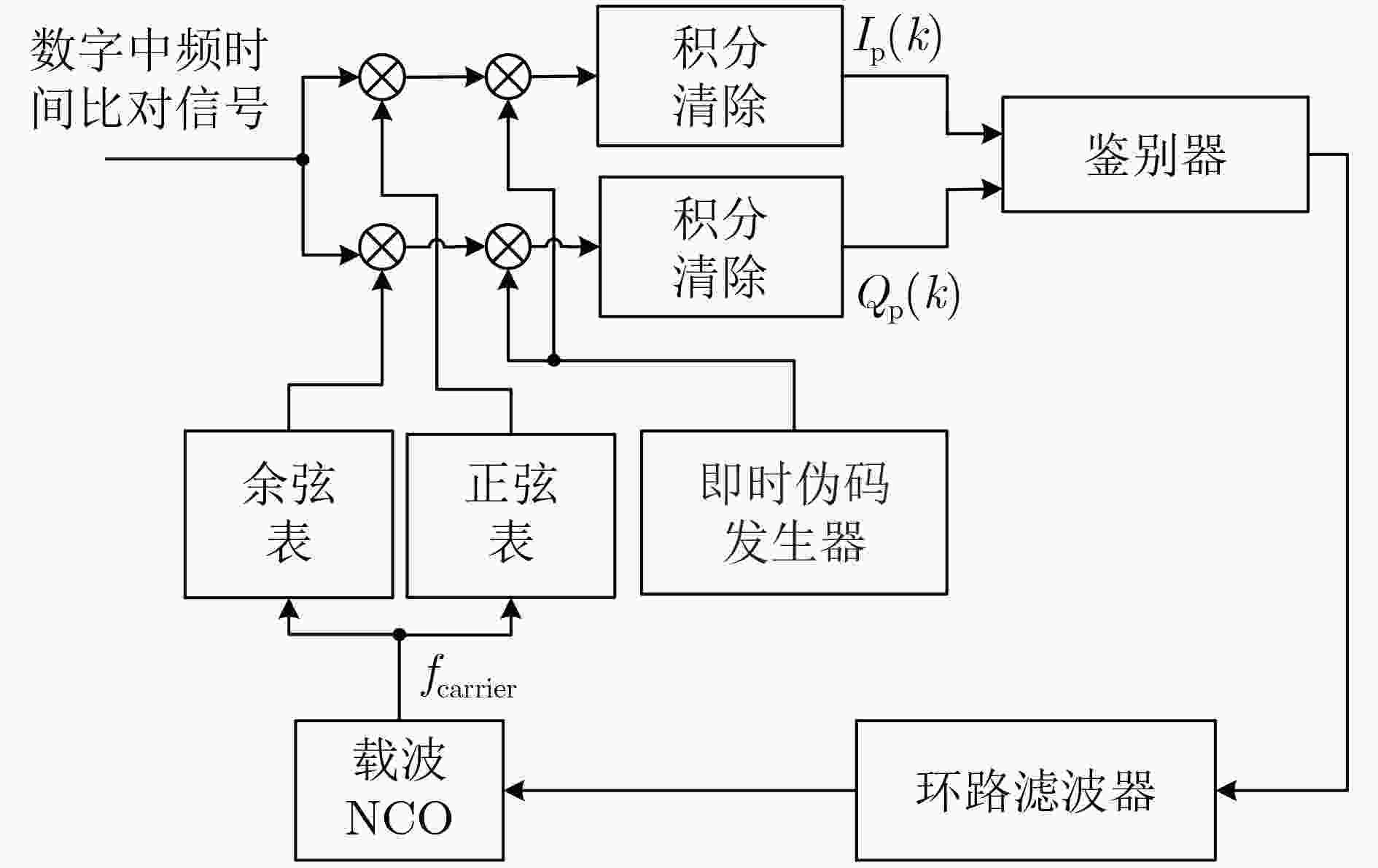
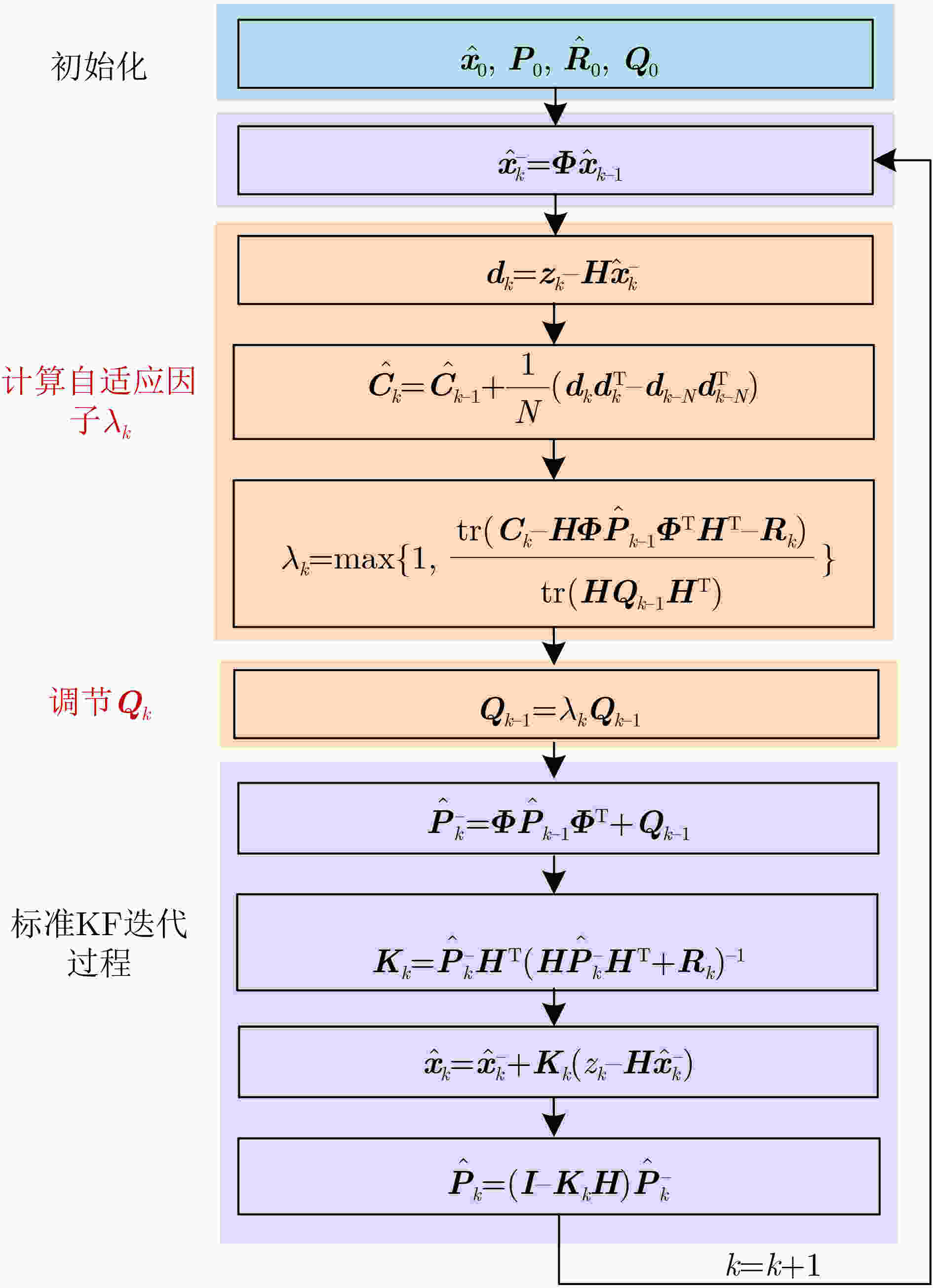
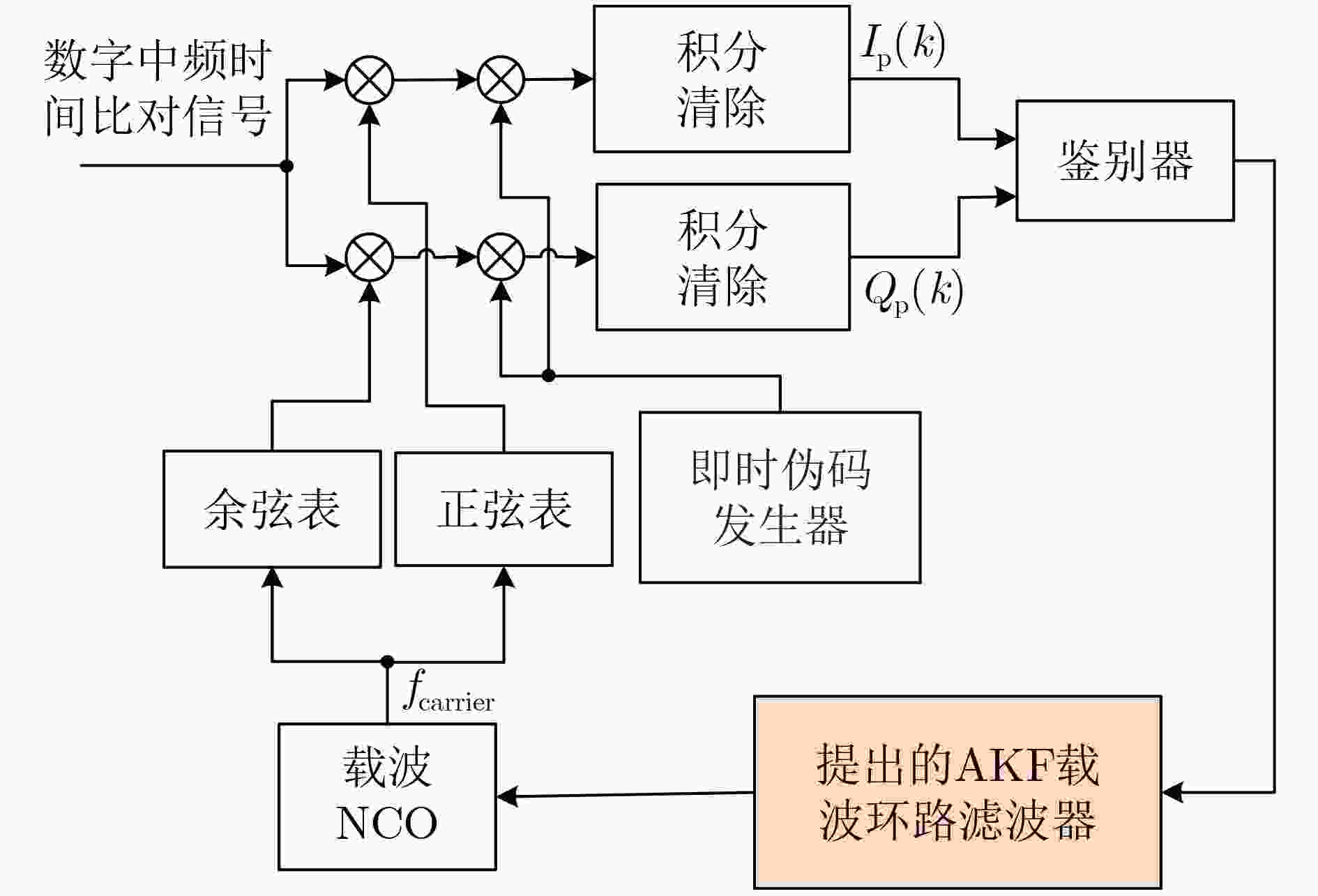
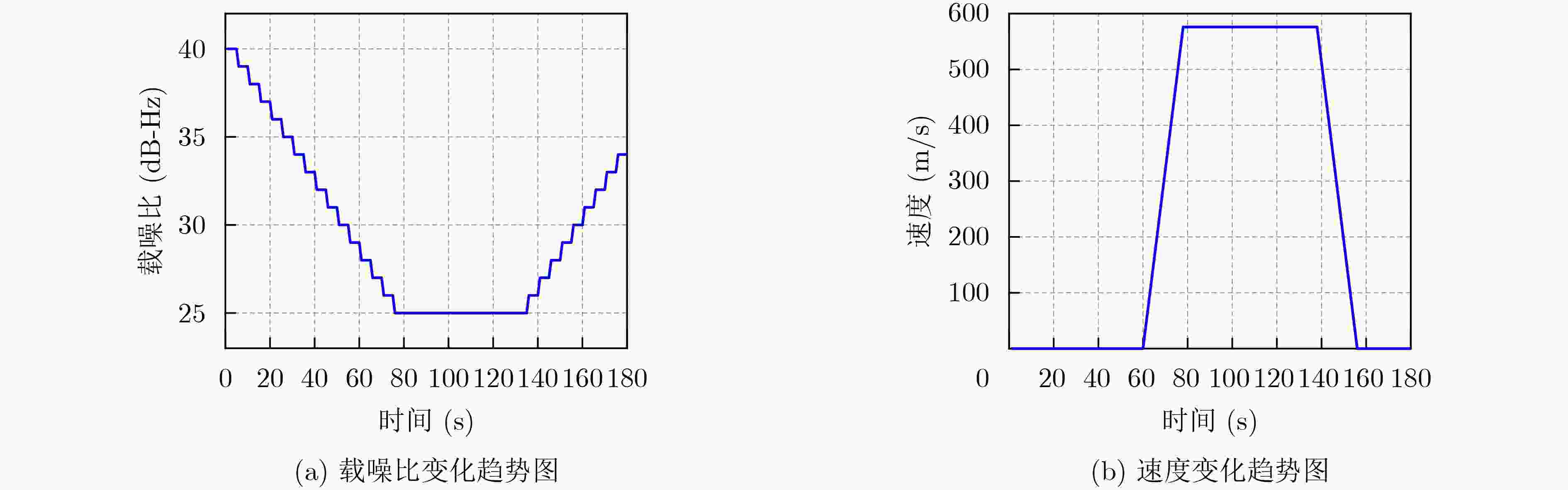
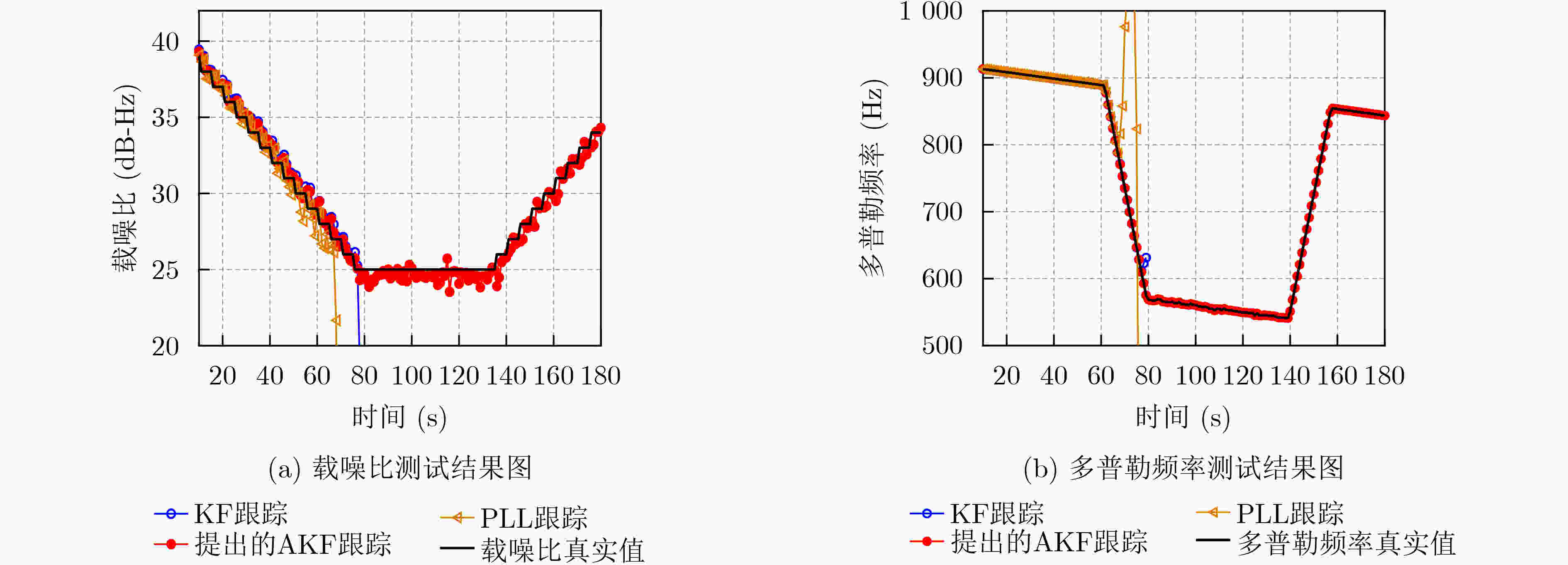
摘要: 在雷达、车载等动态协同组网系统中,高精度时间同步是该系统正常工作的基本条件。但是在动态组网系统或者低截获场景下,时间比对信号强度弱,并处于动态场景,此时时间同步系统鲁棒性差、同步精度低。因此,需要提高时间同步系统在复杂的动态组网系统下的时间同步精度。调制解调器是双向时间比对系统的核心设备,而跟踪环路是其中关键部分。复杂场景下跟踪环路很容易失锁,为了提高跟踪环路鲁棒性,该文提出一种基于自适应卡尔曼滤波(AKF)的跟踪算法。该算法引入自适应因子来调节系统噪声协方差矩阵,从而应对外部变化的输入信号。试验结果显示,与传统锁相环跟踪环路(PLL)和标准卡尔曼滤波跟踪环相比,在弱信号和动态信号同时存在时该算法跟踪鲁棒性和自适应性更好,并且算法复杂度不高。该算法对于提高动态协同组网系统的时间同步精度具有重要意义。
-
关键词:
- 双向时间同步 /
- 时间比对信号跟踪环路 /
- 复杂动态和弱信号场景 /
- 自适应卡尔曼滤波算法
Abstract: In dynamic collaborative networking systems such as radar and vehicular network systems, high precision time synchronization is a basic condition for the normal operation of these systems. However, in dynamic network systems and low interception scenarios, the time transfer signal is weak and dynamic simultaneously, and thus the time synchronization system has poor robustness and synchronization accuracy. Accordingly, it is necessary to improve the time synchronization accuracy in complex dynamic networking systems. The time transfer modem is the core device of the two-way time transfer system, and the tracking loop is a key part of it. The tracking loop can easily lose lock in complex conditions. To improve the robustness of the tracking loop, an Adaptive Kalman Filter (AKF) tracking algorithm is proposed. This tracking loop employs the adaptive factor to adjust the system noise covariance matrices to adapt to the variable input signal. The test results show that, compared with the traditional Phase Lock Loop (PLL) tracking method and the standard KF tracking loop, the proposed tracking loop shows better robustness and adaptability under weak signal and dynamic conditions. Moreover, the computational complexity of the proposed algorithm is not high. This algorithm is of great significance for improving the time synchronization accuracy of complex dynamic collaborative networking systems. -
表 1 迭代1次所需的计算量
算法计算量 乘法数 加法数 标准KF计算量 102 81 AKF自适应因子的计算量 43 28 AKF增加的计算量 42% 34% -
[1] 杨俊, 单庆晓. 卫星授时原理与应用[M]. 北京: 国防工业出版社, 2013: 1–16.YANG Jun and SHAN Qingxiao. Satellite Timing Principle and Application[M]. Beijing: National Defense Industry Press, 2013: 1–16. [2] CRESPI F V, SANDENBERGH S, O’HAGAN D, et al. Dynamic two-way time transfer between moving platforms for netted radar applications[C]. 2023 24th International Radar Symposium (IRS), Berlin, Germany, 2023. doi: 10.23919/IRS57608.2023.10172403. [3] 蒋伊琳, 尹子茹, 宋宇. 基于卷积神经网络的低截获概率雷达信号检测算法[J]. 电子与信息学报, 2022, 44(2): 718–725. doi: 10.11999/JEIT210132JIANG Yilin, YIN Ziru, and SONG Yu. Low probability of intercept radar signal detection algorithm based on convolutional neural networks[J]. Journal of Electronics & Information Technology, 2022, 44(2): 718–725. doi: 10.11999/JEIT210132 [4] 景月娟. 动态站的卫星双向时间传递关键技术研究[D]. [博士论文], 中国科学院大学, 2016.JING Yuejuan. Study on key technologies of two-way satellite time transfer based on mobile station[D]. [Ph. D. dissertation], University of Chinese Academy of Sciences, 2016. [5] WANG Wei, YANG Xuhai, LI Weichao, et al. Research on the influence of the residual effects of TWSTFT on the triangular closure difference[J]. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 5503512. doi: 10.1109/TIM.2022.3219488 [6] HUANG Y J, FUJIEDA M, TAKIGUCHI H, et al. Stability improvement of an operational two-way satellite time and frequency transfer system[J]. Metrologia, 2016, 53(2): 881–890. doi: 10.1088/0026-1394/53/2/881 [7] WON J H, DÖTTERBÖCK D, and EISSFELLER B. Performance comparison of different forms of Kalman filter approaches for a vector-based GNSS signal tracking loop[J]. Navigation, 2010, 57(3): 185–199. doi: 10.1002/j.2161-4296.2010.tb01777.x [8] FAN Yunsheng, QIAO Shuanghu, WANG Guofeng, et al. A modified adaptive Kalman filtering method for maneuvering target tracking of unmanned surface vehicles[J]. Ocean Engineering, 2022, 266: 112890. doi: 10.1016/j.oceaneng.2022.112890 [9] FARIÑA B, TOLEDO J, and ACOSTA L. Augmented Kalman filter design in a localization system using onboard sensors with intrinsic delays[J]. IEEE Sensors Journal, 2023, 23(11): 12105–12113. doi: 10.1109/JSEN.2023.3269126 [10] LIU Shede, ZHANG Tao, ZHANG Jiayu, et al. A new coupled method of SINS/DVL integrated navigation based on improved dual adaptive factors[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 8504211. doi: 10.1109/TIM.2021.3106118 [11] TANG Xinghua, FALCO G, FALLETTI E, et al. Theoretical analysis and tuning criteria of the Kalman filter-based tracking loop[J]. GPS Solutions, 2015, 19(3): 489–503. doi: 10.1007/s10291-014-0408-2 [12] KAZEMI P L, O'DRISCOLL C, and LACHAPELLE G. Digital phase locked loop with frequency rate feedback[C]. The 22nd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2009), Savannah, USA, 2009: 201–208. [13] YIN Zhonggang, LI Guoyin, ZHANG Yanqing, et al. Symmetric-strong-tracking-extended-Kalman-filter-based sensorless control of induction motor drives for modeling error reduction[J]. IEEE Transactions on Industrial Informatics, 2019, 15(2): 650–662. doi: 10.1109/TII.2018.2810850 [14] MENG Yang, GAO Shesheng, ZHONG Yongmin, et al. Covariance matching based adaptive unscented Kalman filter for direct filtering in INS/GNSS integration[J]. Acta Astronautica, 2016, 120: 171–181. doi: 10.1016/j.actaastro.2015.12.014 [15] GAO Wei, LI Jingchun, ZHOU Guangtao, et al. Adaptive Kalman filtering with recursive noise estimator for integrated SINS/DVL systems[J]. The Journal of Navigation, 2015, 68(1): 142–161. doi: 10.1017/S0373463314000484 [16] LO K, LU Qiang, and KWON W H. Comments on “optimal solution of the two-stage Kalman estimator”[J]. IEEE Transactions on Automatic Control, 2002, 47(1): 198–199. doi: 10.1109/9.981745 -






 下载:
下载:



 下载:
下载:
