Proximal Policy Optimization Algorithm for UAV-assisted MEC Vehicle Task Offloading and Power Control
-
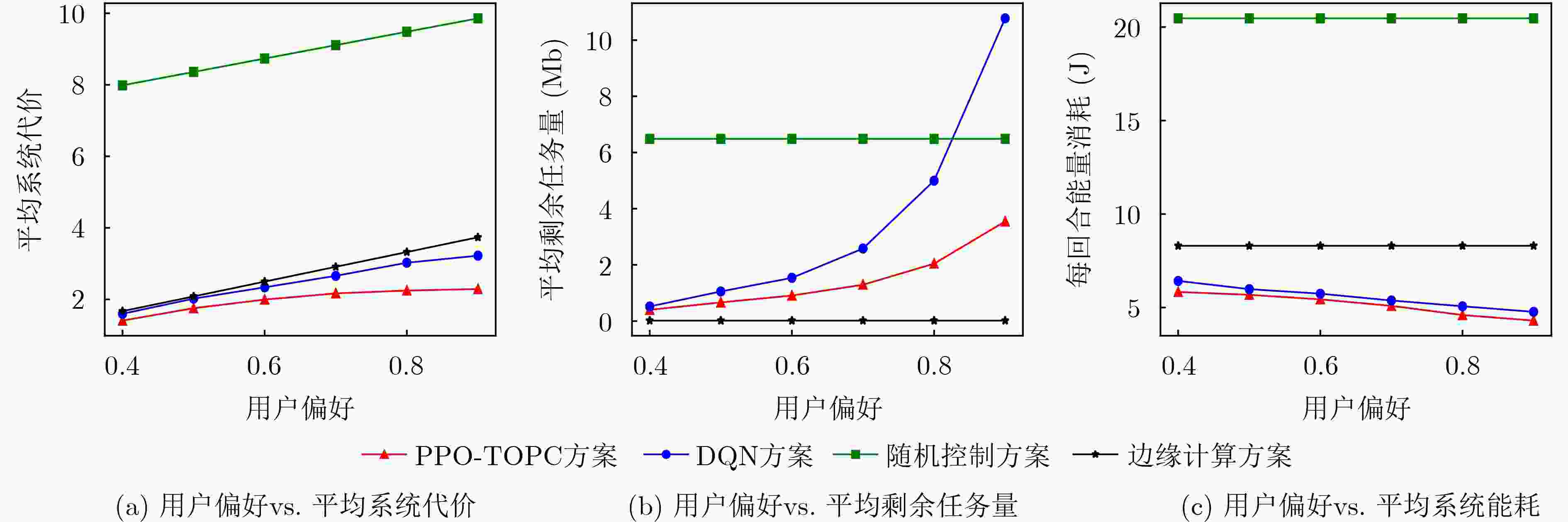
摘要: 无人机(UAVs)辅助移动边缘计算(MEC)架构是灵活处理车载计算密集、时延敏感型任务的有效模式。但是,如何在处理任务时延与能耗之间达到最佳均衡,一直是此类车联网应用中长期存在的挑战性问题。为了解决该问题,该文基于无人机辅助移动边缘计算架构,考虑无线信道时变特性及车辆高移动性等动态变化特征,构建出基于非正交多址(NOMA)的车载任务卸载与功率控制优化问题模型,然后将该问题建模成马尔可夫决策过程,并提出一种基于近端策略优化(PPO)的分布式深度强化学习算法,使得车辆只需根据自身获取局部信息,自主决策任务卸载量及相关发射功率,从而达到时延与能耗的最佳均衡性能。仿真结果表明,与现有方法相比较,本文所提任务卸载与功率控制近端策略优化方案不仅能够显著获得更优的时延与能耗性能,所提方案平均系统代价性能提升至少13%以上,而且提供一种性能均衡优化方法,能够通过调节用户偏好权重因子,达到系统时延与能耗水平之间的最佳均衡。Abstract: The architecture of Mobile Edge Computing (MEC), assisted by Unmanned Aerial Vehicles (UAVs), is an efficient model for flexible management of mobile computing-intensive and delay-sensitive tasks. Nevertheless, achieving an optimal balance between task latency and energy consumption during task processing has been a challenging issue in vehicular communication applications. To tackle this problem, this paper introduces a model for optimizing task offloading and power control in vehicle networks based on UAV-assisted mobile edge computing architecture, using a Non-Orthogonal Multiple Access (NOMA) approach. The proposed model takes into account dynamic factors like vehicle high mobility and wireless channel time-variations. The problem is modeled as a Markov decision process. A distributed deep reinforcement learning algorithm based on Proximal Policy Optimization (PPO) is proposed, enabling each vehicle to make autonomous decisions on task offloading and related transmission power based on its own perceptual local information. This achieves the optimal balance between task latency and energy consumption. Simulation results reveal that the proposed proximal policy optimization algorithm for task offloading and power control scheme not only improves the performance of task latency and energy consumption compared to existing methods, The average system cost performance improvement is at least 13% or more. but also offers a performance-balanced optimization method. This method achieves optimal balance between the system task latency and energy consumption level by adjusting user preference weight factors.
-
表 1 缩略语表
符号 符号含义 $ \sigma _{\mathrm{R}}^2 $ 加性高斯白噪声方差 $ {{\boldsymbol{n}}}{(}t{)} $ 加性高斯白噪声矢量 $ h_i^{\mathrm{p}}(t) $ 车辆i在t时刻的大尺度衰落 $ {{\boldsymbol{h}}}_i^{\mathrm{s}}(t) $ 车辆i在t时刻的小尺度衰落矢量 $ {h_{\mathrm{r}}} $ 单位距离信道功率增益 $ {{{\boldsymbol{P}}}_{{\text{BS}}}} $ 基站位置 $ {{{\boldsymbol{P}}}_{{\mathrm{UAV}}}}(t) $ t时刻无人机位置 $ {{{\boldsymbol{P}}}_i}(t) $ 第i辆车在t时刻的位置 $ d_i^{\mathrm{o}}(t) $ 第i辆车在t时刻与基站或无人机之间传输速率 $ d_i^{\mathrm{l}}(t) $ 第i辆车在t时刻的本地计算量 $ E_i^{\mathrm{l}}(t) $ 第i辆车在t时刻的本地能耗 $ E_i^{\mathrm{o}}(t) $ 第i辆车在t时刻为任务卸载而使用的传输功率所消耗的能量 $ {q_n}(\theta ) $ 重要性采样比率 $ \lambda $ 折扣系数 $ L(\theta) $ 网络损失函数 $ \hat A_n^{{\text{GAE}}(\gamma ,\phi )} $ 广义估计函数 1 PPO-TOPC算法流程
输入:车辆观测到的局部信息 输出:车辆为任务计算的所使用的CPU频率占比、输出功率 1.随机初始化神经网络模型参数; 2.for iteration = 1,2,…M do 3. 初始化仿真环境参数、训练模型网络参数; 4. for i = 1,2,···,N do 5. 车辆观测局部信息${{\boldsymbol{s}}_i}$; 6. 将${{\boldsymbol{s}}_i}$输入到当前网络,得到决策动作${{\boldsymbol{a}}_i}$; 7. 将${{\boldsymbol{a}}_i}$作为参数输入至环境中得到下一状态${{\boldsymbol{s}}_{i + 1}}$和当前动作
奖励${r_i}$;8. 车辆在本地缓存$\left\{ {{{\boldsymbol{a}}_i},{{\boldsymbol{s}}_i},{r_i}} \right\}$; 9. end for 10. 利用缓存数据和式(28)、式(33)计算估计函数和评价网络损
失函数值并更新评价网络;11. for step = 1,2,···,K do 12. 利用缓存数据和式(31)计算重要性权重 13. 根据公式(30)更新当前网络; 14. end for 15. 使用当前网络权重来更新目标网络; 16.end 表 2 主要仿真参数
参数 数值 $ \gamma $ 0.9 $ \alpha $ 1e–4 $ p_{\max }^{\mathrm{o}} $ (W) 1 $ p_{\max }^{\mathrm{l}} $ (W) 1 $ {v_{{\mathrm{vh}}}} $ (m/s) 15 $ {v_{{\mathrm{uav}}}} $ (m/s) 10 $ {Z_{{\mathrm{UAV}}}} $ (m) 50 $ {C_{{\mathrm{BS}}}} $(m) 300 $ h $(m) 10 $ L $(cycle/bit) 500 -
[1] ALAM M Z and JAMALIPOUR A. Multi-agent DRL-based Hungarian algorithm (MADRLHA) for task offloading in multi-access edge computing internet of vehicles (IoVS)[J]. IEEE Transactions on Wireless Communications, 2022, 21(9): 7641–7652. doi: 10.1109/TWC.2022.3160099. [2] DU Shougang, CHEN Xin, JIAO Libo, et al. Energy efficient task offloading for UAV-assisted mobile edge computing[C]. Proceedings of 2021 China Automation Congress (CAC), Kunming, China, 2021: 6567–6571. doi: 10.1109/CAC53003.2021.9728502. [3] LIU Haoqiang, ZHAO Hongbo, GENG Liwei, et al. A distributed dependency-aware offloading scheme for vehicular edge computing based on policy gradient[C]. Proceedings of the 8th IEEE International Conference on Cyber Security and Cloud Computing (CSCloud)/2021 7th IEEE International Conference on Edge Computing and Scalable Cloud (EdgeCom), Washington, USA, 2021: 176–181. doi: 10.1109/CSCloud-EdgeCom52276.2021.00040. [4] 李斌, 刘文帅, 费泽松. 面向空天地异构网络的边缘计算部分任务卸载策略[J]. 电子与信息学报, 2022, 44(9): 3091–3098. doi: 10.11999/JEIT220272.LI bin, LIU Wenshuai, and FEI Zesong. Partial computation offloading for mobile edge computing in space-air-ground integrated network[J]. Journal of Electronics & Information Technology, 2022, 44(9): 3091–3098. doi: 10.11999/JEIT220272. [5] CUI Yaping, DU Lijuan, WANG Honggang, et al. Reinforcement learning for joint optimization of communication and computation in vehicular networks[J]. IEEE Transactions on Vehicular Technology, 2021, 70(12): 13062–13072. doi: 10.1109/TVT.2021.3125109. [6] NIE Yiwen, ZHAO Junhui, GAO Feifei, et al. Semi-distributed resource management in UAV-aided MEC systems: A multi-agent federated reinforcement learning approach[J]. IEEE Transactions on Vehicular Technology, 2021, 70(12): 13162–13173. doi: 10.1109/TVT.2021.3118446. [7] LIU Zongkai, DAI Penglin, XING Huanlai, et al. A distributed algorithm for task offloading in vehicular networks with hybrid fog/cloud computing[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2022, 52(7): 4388–4401. doi: 10.1109/TSMC.2021.3097005. [8] HAN Xu, TIAN Daxin, SHENG Zhengguo, et al. Reliability-aware joint optimization for cooperative vehicular communication and computing[J]. IEEE Transactions on Intelligent Transportation Systems, 2021, 22(8): 5437–5446. doi: 10.1109/TITS.2020.3038558. [9] DONG Peiran, NING Zhaolong, MA Rong, et al. NOMA-based energy-efficient task scheduling in vehicular edge computing networks: A self-imitation learning-based approach[J]. China Communications, 2020, 17(11): 1–11. doi: 10.23919/JCC.2020.11.001. [10] ZHANG Fenghui, WANG M M, BAO Xuecai, et al. Centralized resource allocation and distributed power control for NOMA-integrated NR V2X[J]. IEEE Internet of Things Journal, 2021, 8(22): 16522–16534. doi: 10.1109/JIOT.2021.3075250. [11] 李斌, 刘文帅, 谢万城, 等. 智能反射面赋能无人机边缘网络计算卸载方案[J]. 通信学报, 2022, 43(10): 223–233. doi: 10.11959/j.issn.1000-436x.2022196.LI Bin, LIU Wenshuai, XIE Wancheng, et al. Computation offloading scheme for RIS-empowered UAV edge network[J]. Journal on Communications, 2022, 43(10): 223–233. doi: 10.11959/j.issn.1000-436x.2022196. [12] BUDHIRAJA I, KUMAR N, TYAGI S, et al. Energy consumption minimization scheme for NOMA-based mobile edge computation networks underlaying UAV[J]. IEEE Systems Journal, 2021, 15(4): 5724–5733. doi: 10.1109/JSYST.2021.3076782. [13] WANG Ningyuan, LI Feng, CHEN Dong, et al. NOMA-based energy-efficiency optimization for UAV enabled space-air-ground integrated relay networks[J]. IEEE Transactions on Vehicular Technology, 2022, 71(4): 4129–4141. doi: 10.1109/TVT.2022.3151369. [14] KATWE M, SINGH K, SHARMA P K, et al. Dynamic user clustering and optimal power allocation in UAV-assisted full-duplex hybrid NOMA system[J]. IEEE Transactions on Wireless Communications, 2022, 21(4): 2573–2590. doi: 10.1109/TWC.2021.3113640. [15] GAN Xueqing, JIANG Yuke, WANG Yufan, et al. Sum rate maximization for UAV assisted NOMA backscatter communication system[C]. Proceedings of the 6th World Conference on Computing and Communication Technologies (WCCCT), Chengdu, China, 2023: 19–23. doi: 10.1109/WCCCT56755.2023.10052259. [16] ASHRAF M I, LIU Chenfeng, BENNIS M, et al. Dynamic resource allocation for optimized latency and reliability in vehicular networks[J]. IEEE Access, 2018, 6: 63843–63858. doi: 10.1109/ACCESS.2018.2876548. [17] KHOUEIRY B W and SOLEYMANI M R. An efficient NOMA V2X communication scheme in the Internet of vehicles[C]. Proceedings of the IEEE 85th Vehicular Technology Conference (VTC Spring), Sydney, Australia, 2017: 1–7. doi: 10.1109/VTCSpring.2017.8108427. [18] CHEN Yingyang, WANG Li, AI Yutong, et al. Performance analysis of NOMA-SM in vehicle-to-vehicle massive MIMO channels[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(12): 2653–2666. doi: 10.1109/JSAC.2017.2726006. [19] ZHANG Di, LIU Yuanwei, DAI Linglong, et al. Performance analysis of FD-NOMA-based decentralized V2X systems[J]. IEEE Transactions on Communications, 2019, 67(7): 5024–5036. doi: 10.1109/TCOMM.2019.2904499. [20] TANG S J W, NG K Y, KHOO B H, et al. Real-time lane detection and rear-end collision warning system on a mobile computing platform[C]. Proceedings of the IEEE 39th Annual Computer Software and Applications Conference, Taichung, China, 2015: 563–568. doi: 10.1109/COMPSAC.2015.171. [21] ZHAN Wenhan, LUO Chunbo, WANG Jin, et al. Deep-reinforcement-learning-based offloading scheduling for vehicular edge computing[J]. IEEE Internet of Things Journal, 2020, 7(6): 5449–5465. doi: 10.1109/JIOT.2020.2978830. [22] ZHONG Ruikang, LIU Xiao, LIU Yuanwei, et al. Multi-agent reinforcement learning in NOMA-aided UAV networks for cellular offloading[J]. IEEE Transactions on Wireless Communications, 2022, 21(3): 1498–1512. doi: 10.1109/TWC.2021.3104633. [23] NGO H Q, LARSSON E G, and MARZETTA T L. Energy and spectral efficiency of very large multiuser MIMO systems[J]. IEEE Transactions on Communications, 2013, 61(4): 1436–1449. doi: 10.1109/TCOMM.2013.020413.110848. [24] ZHU Hongbiao, WU Qiong, WU Xiaojun, et al. Decentralized power allocation for MIMO-NOMA vehicular edge computing based on deep reinforcement learning[J]. IEEE Internet of Things Journal, 2022, 9(14): 12770–12782. doi: 10.1109/JIOT.2021.3138434. [25] LIU Yuan, XIONG Ke, NI Qiang, et al. UAV-assisted wireless powered cooperative mobile edge computing: Joint offloading, CPU control, and trajectory optimization[J]. IEEE Internet of Things Journal, 2020, 7(4): 2777–2790. doi: 10.1109/JIOT.2019.2958975. [26] TSE D and VISWANATH P. Fundamentals of Wireless Communication[M]. Cambridge: Cambridge University Press, 2005. [27] SCHULMAN J, MORITZ P, LEVINE S, et al. High-dimensional continuous control using generalized advantage estimation[J]. arXiv: 1506.02438, 2015. doi: 10.48550/arXiv.1506.02438. -





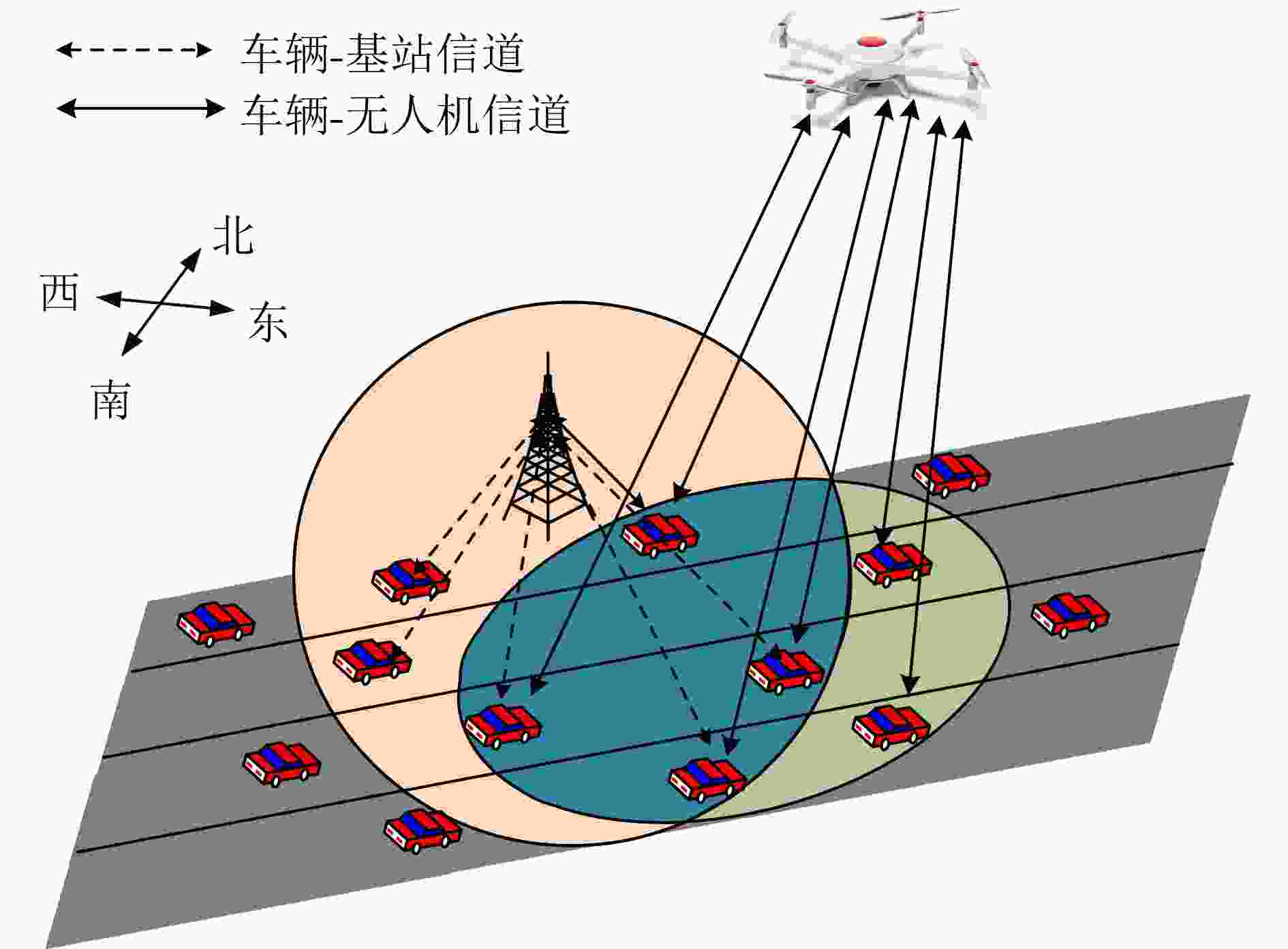
 下载:
下载:
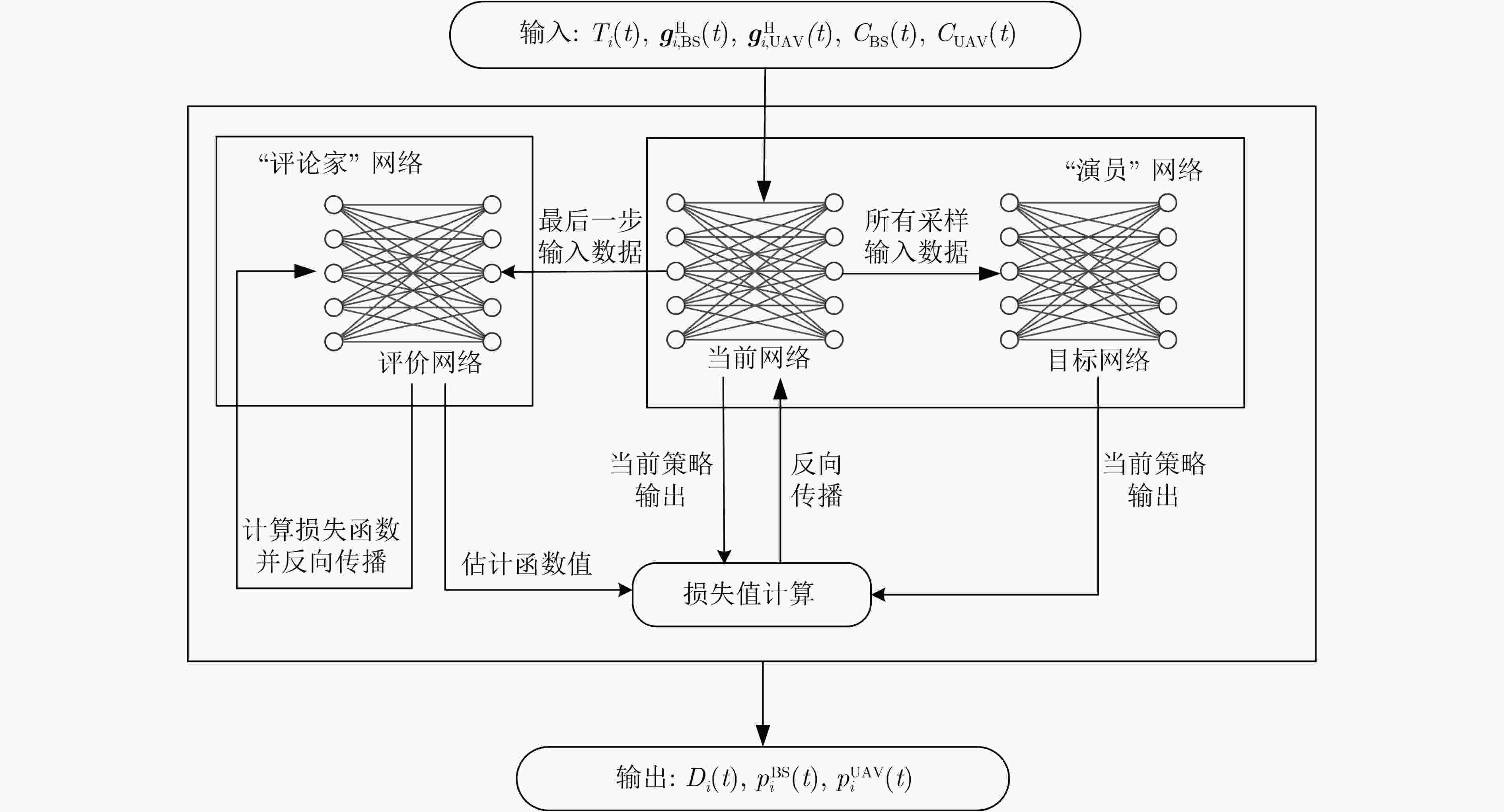
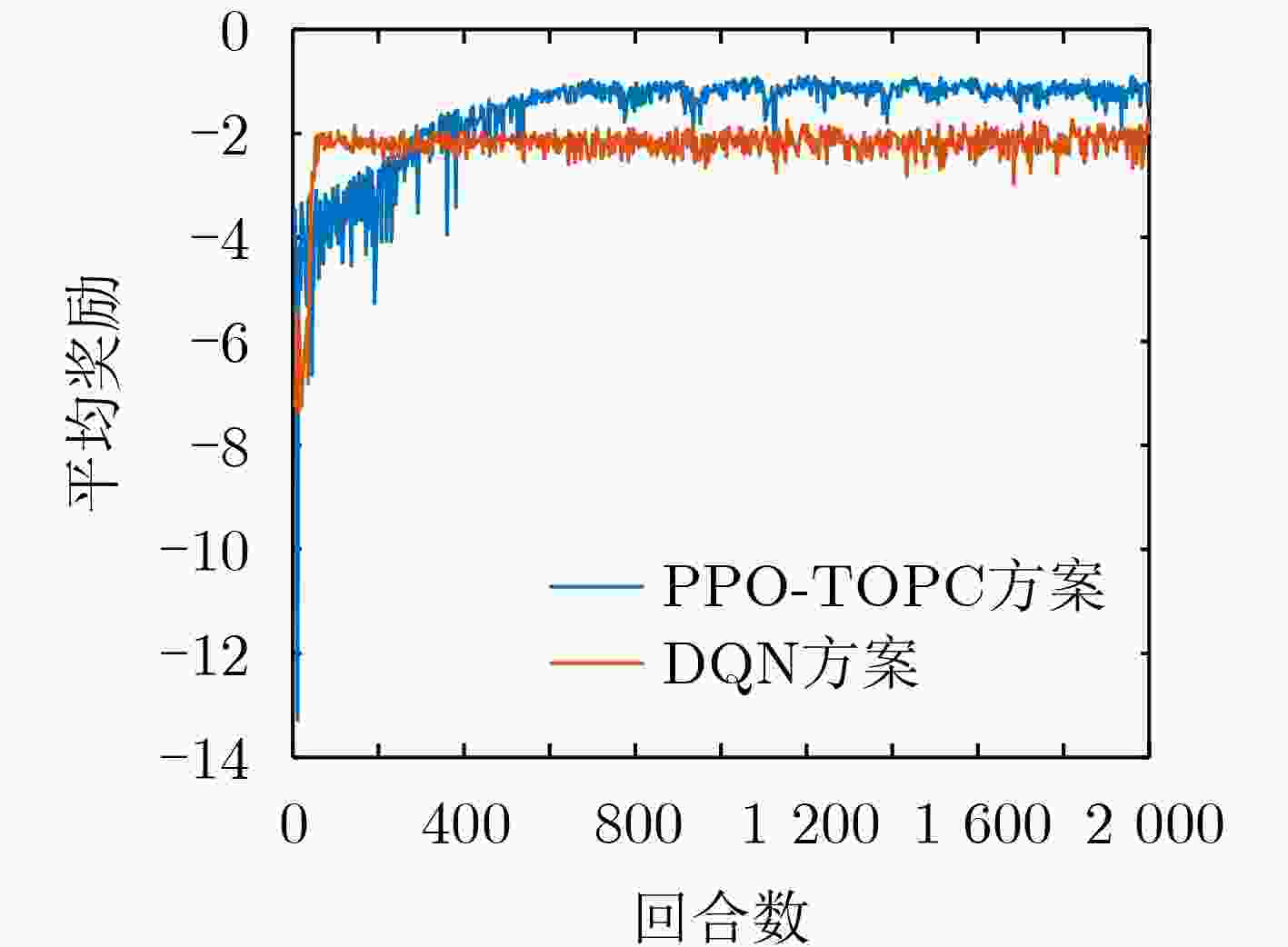
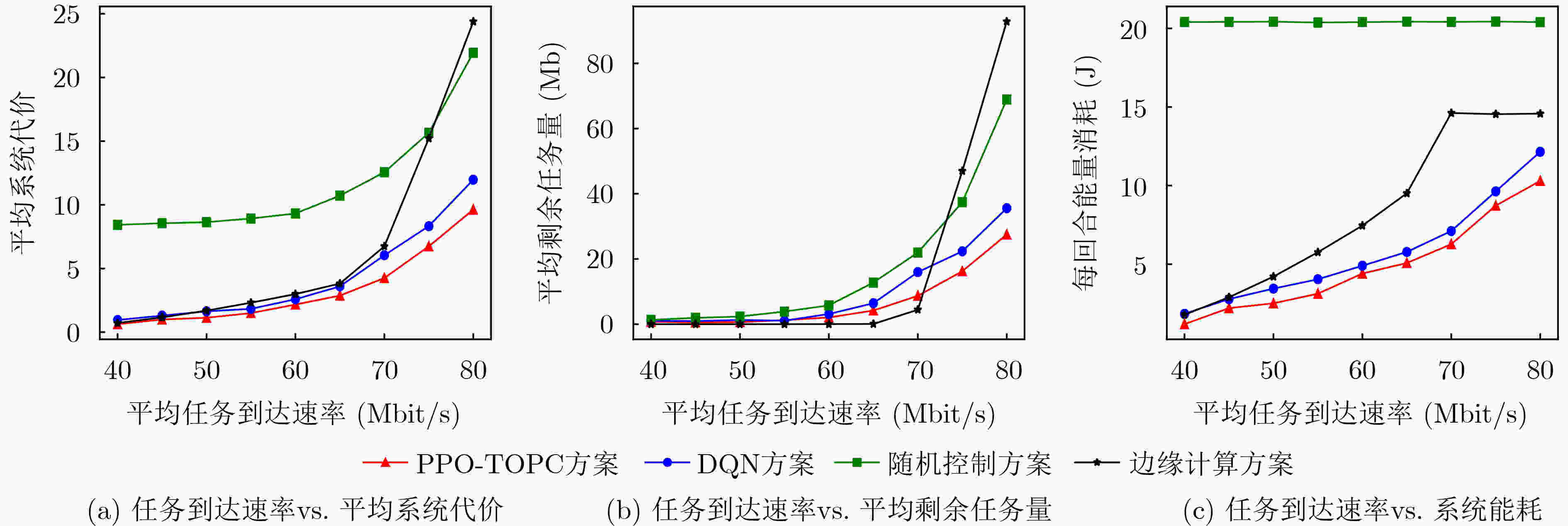



 下载:
下载:
