A Vector Analysis Method for Coupling Effects Between Energy Selective Structures and Antennas
-
摘要: 为了深入分析能量选择防护结构(ESS)等周期结构作为天线罩时与天线产生的耦合效应，提高分析效率，该文提出一种基于坡印廷矢量法的耦合效应分析方法。该文从收发互易的角度，将天线当作发射器而非常规方法中的接收器对天线的电磁特性进行分析。从接收的角度理解，天线是一种从自由空间中捕获能量的装置，而能量分布可以通过坡印廷能流密度曲线来描述。同样地，能量选择防护结构对电磁波的扰动也可以通过能流密度曲线来描述。因此，天线、防护结构以及二者的耦合效应均可通过能流密度曲线进行研究和分析。结果表明，该文所提方法与常规分析方法具有良好的一致性。相比于常规分析方法，该文方法可同时对天线与防护结构的耦合效应进行可视化分析与量化评估，指导防护结构的尺寸、形状设计以及最佳安装位置，显著提高设计效率。Abstract: In order to analyze the coupling effect between periodic structures such as Energy Selection Structures (ESS) and antennas when ESS are used as radomes, and improve analysis efficiency, an analysis method based on Poynting vector methods is proposed in this paper. In the perspective of reciprocity between transmission and reception, the electromagnetic characteristics of antennas are analyzed as transmitters rather than receivers in conventional methods. From the perspective of reception, an antenna is regarded as a device that captures energy from free space. Therefore, the energy distribution can be described by the Poynting energy flow density curve. Similarly, the disturbance of electromagnetic waves caused by ESS can also be described by Poynting streamlines. Therefore, antennas, protective structures, and their coupling effects can be studied and analyzed through Poynting streamlines. The results indicate that the proposed method poses a good consistency with conventional analysis methods. Compared to conventional analysis methods, the proposed method in this paper can simultaneously visualize and quantitatively evaluate the coupling effect between antennas and ESS. The results can be used for the design of the size, shape, and optimal installation position of ESS, thus significantly improving design efficiency.
-
1. 引言
电磁空间被视为继海、陆、空、天之后的第5维空间，发展电磁防护技术、维护电磁空间安全具有重要学术和工程价值。能量选择防护结构(简称防护结构，Energy Selective Structure, ESS)是一种传输特性随入射波电场强度自适应变化的电磁结构，在前门电磁防护方面有重要应用价值。对于低能量的工作信号，防护结构处于透波状态，电磁波可以无损地传播；而对于高能量的攻击信号，ESS能自适应切换到防护状态，屏蔽强电磁脉冲。
ESS的概念和定义由国防科技大学刘培国教授团队[1]在2009年首次提出，经过持续研究和探索，积累了一系列理论和实物成果[2–7]。该团队的杨成[2]在其博士论文中对ESS进行了系统研究，首次通过强电磁辐照实验验证了ESS的非线性响应，推动了能量选择防护研究的快速发展。此后，该团队的易波[3]提出了基于3维电磁结构的能量选择ESS，刘晨曦[4]探索了双层能量选择ESS的设计潜力，虎宁等人[5–7]提出了基于等效电路模型的ESS设计方法和ESS响应阈值调控方法，推动了ESS的工程化应用。王轲[8]从应用需求出发，提出了多款带通能量选择ESS，并设计制作了第1款应用于北斗导航设备的电磁防护罩。近年来，ESS受到国内外学者的广泛关注，多个不同学术机构的研究人员[9–15]提出了一系列新思路、新方法，进一步丰富和拓展了ESS功能和应用场景。
ESS的一个典型应用场景是作为天线罩安装于天线前端，然而天线和ESS都是经过特殊设计的电磁结构，各自与自由空间处于良好的阻抗匹配状态。当ESS应用于天线前端，尤其是应用于天线近场区域时，会与天线产生耦合，影响天线的电磁性能，因此需要对二者的耦合效应进行深入分析，现有文献未对此问题进行专门研究。常规分析方法是将天线当作发射器，通过电磁场分布来研究二者的耦合效应，而天线近场区域的场分量非常复杂，难以得到清晰直观的结论。从收发互易的角度，将天线当作接收器而非发射器进行分析时，上述问题可以得到简化。从接收的角度理解，天线是一种从自由空间中捕获能量的装置，而能量分布可以通过坡印廷能流密度曲线来描述。同样地，ESS对电磁波的扰动也可以通过能流密度曲线来描述。因此，天线、ESS以及二者的耦合效应都可以通过能流密度曲线进行研究和分析。在以前的研究中，相关学者[16–18]使用坡印廷能流密度曲线分析了天线增益、方向性以及天线阵列单元之间的耦合等问题，与常规分析方法相比，本文所提方法提供了一个新的分析视角，从坡印廷能流密度曲线的角度理解ESS和天线之间的耦合作用。本方法同时提供了可视化分析效果和量化分析结果，而常规分析方法则无法同时实现上述效果。此外，采用本方法得到天线的能流密度曲线分布之后，即可对ESS放置的位置进行预判，从而降低仿真设计的盲目性，显著提高设计效率。
本文对ESS与天线的耦合效应分析方法进行了研究，实现了ESS与天线耦合效应的可视化分析与量化评估。本文的内容安排如下：第2节以偶极子天线为例介绍了坡印廷矢量法的基本原理；第3节以一款矩形喇叭天线以及一款单频ESS为例，具体分析了ESS与喇叭天线的耦合效应，验证了坡印廷矢量法的有效性，第4节对本文内容进行了总结。
2. 方法原理
2.1 天线的能流密度分布特性
从接收的角度观察天线时，天线可以理解为一个接收空间电磁能量的装置，而电磁能量的多少可以用能流密度曲线来表示。显然，天线对能流密度曲线的作用可以分为两个方面。首先，天线本身是一个金属体，它具有一定的电磁散射特性，会对原本均匀分布的能流密度曲线产生扰动，使能流密度曲线的方向发生变化。其次，天线作为一个接收器，能吸收入射电磁波的一部分能量，对应的这部分能流密度曲线终止于天线的负载。被吸收的能流密度曲线的多少表征了天线获得空间电磁能量的能力，所以天线的吸收口径可以通过终止于天线负载的能流密度曲线的边界来计算，用Sp来表示。具体地，Sp可以通过式(1)得到
Sp=∑σ(i)ΔxΔy (1) 其中， Δx和 Δy是能流密度曲线的空间间隔，该间隔可以通过仿真软件进行设置，根据天线吸收口径的大小设置合适的值即可，本文中设置为 Δx= Δy = 0.01 λ，σ (i)的定义为
σ(i)=1, σ(i)∈Sloadσ(i)=0, 其他} (2) 其中，Sload是负载所在的闭合曲面。本文中，首先使用商用软件CST 2021 MWS工作室计算天线周围的坡印廷矢量分布，然后利用Python 编程生成坡印廷能流密度曲线，最后在Matlab中使用Boundary函数将终止于天线负载区域的能流密度曲线进行标记，所有能流密度曲线的包络即为天线的有效面积。能流密度曲线的间隔 Δx和 Δy按照二分法取步进，当 Δx和 Δy变化引起天线有效面积的变化小于0.5%时，认为其达到精度需要。图1给出了在平面波入射下，长度为0.5 λ的对称振子天线在完全匹配状态时的能流密度曲线分布及在远场区域中计算的吸收口径。其中，红色的线代表被天线吸收的能流密度曲线，其边界代表对称振子天线的吸收口径(图1中黄色区域)，而蓝色的线代表未被对称振子吸收的能流密度曲线。根据IEEE的标准定义，天线的有效接收面积为接收天线终端的最大功率与入射波的功率通量密度之比[19]
Ae=Gλ24π (3) 其中，G是天线的增益，λ为波长。该振子天线的增益为2.12 dBi，通过式(3)得到的有效接收面积为0.126λ2；而通过能流密度曲线定义的吸收口径为0.123λ2，二者的相对误差为2.3%，计算结果基本一致，表明通过能流密度曲线定义的吸收口径同样可以表征天线的电磁特性。
与Ae不同的是，通过能流密度曲线定义的吸收口径Sp不仅仅是一个标量信息，Sp的形状描述了天线吸收能量的空间分布，增加了对天线理解的维度。除了在天线的远场区域计算Sp之外，还可以在天线近场区域计算Sp。图2给出了对称振子天线在几个典型位置的吸收口径，结果显示，对称振子天线的吸收口径是一个椭圆。随着吸收口径所在平面的位置从近场区(0.05λ)增加到远场区(3λ)，椭圆的长轴与短轴的方向发生了偏转。吸收口径形状变化的同时，大小也发生了变化。图3给出了对称振子天线不同位置吸收口径的大小变化，随着距离增加，Sp首先增大，并在大约0.2λ处达到峰值，此后随距离增大而降低并在天线的远场区(0.5λ)逐渐趋于稳定，大小与通过式(1)定义的有效接收面积一致。
在天线与ESS的优化过程中，可以充分利用天线的吸收口径提供的信息。当需要在某一位置加载ESS时，只需要根据天线的吸收口径的形状和大小确定ESS的尺寸和大小即可。考虑到阵列的边缘效应，ESS的尺寸应该略大于天线的吸收口径，避免边缘处能流曲线的不均匀性带来的影响。此外，ESS对天线产生的影响还可以通过天线吸收口径的变化进行量化评估。当ESS加载于天线前端，使得天线吸收口径变大时，表明面ESS对天线产生了有利的影响，反之，天线吸收口径减小时，则证明产生了不利影响。同时，天线吸收口径形状的变化还提供了天线吸收入射波能量的空间变化，这是常规的分析方法无法提供的。
图4给出了对称振子天线沿y方向放置，入射波从z方向入射时对称振子附近的能流密度曲线分布。可以看出，天线对入射波的能流密度曲线产生了明显的扰动。在xoz平面，能流密度曲线在天线的远场区域是均匀分布的。随着距离靠近天线，能流密度曲线向外张开，在天线附近变得更加稀疏。部分能流密度曲线延伸到对称振子的下方，然后改变方向被天线吸收。在yoz平面，能流密度曲线的变化比xoz平面平缓，在靠近天线时，能流密度曲线向天线中心聚拢，分布更加密集。可以看出，在yoz平面有更多的能流密度曲线被天线吸收。
在得到天线的能流密度曲线分布之后，可以对ESS放置的位置进行预判。在能流密度曲线分布均匀的区域，天线对电磁波扰动的程度小，电磁场分布较均匀，适合加载ESS；反之能流密度曲线变化较快、分布不均匀的区域则表示此处天线对电磁能量的扰动强烈，电磁场处于快速变化的状态，场分量复杂，不适合加载ESS。以对称振子天线为例，在天线周围(小于0.1λ)，能流密度曲线变化剧烈，且具有多个不同的方向，该区域显然是不适合放置ESS的，而在距离天线较远的位置，如0.4λ处，虽然该区域仍然属于天线的近场，但能流密度曲线分布已经比较均匀，与均匀平面波的能流密度曲线分布相当，因此在该区域中加载ESS对天线性能的影响较小。对于不同的天线，其能流密度曲线分布也不相同，需要根据情况具体分析。注意到只需要进行一次全波仿真，就能判断适合ESS加载的大致区域，因此该方法是相对高效的。
2.2 ESS的能流密度分布特性
ESS虽然不吸收电磁波，但同样会对周围的电磁能量产生扰动，当ESS加载于天线前端时，其对能流密度曲线的扰动会对天线吸收能量的效果产生影响。在前文的研究中，ESS被视为无限大的周期阵列，通过周期边界条件下的传输系数评估其电磁性能。而本节将从坡印廷矢量的角度对ESS的电磁特性进行分析。以文献[7]中设计的ESS为研究对象，对ESS的能流密度曲线分布特性进行探究。ESS的基本信息如图5所示，选取ESS阵列包括12×9个单元，尺寸为1.92 λ×1.12 λ。在透波状态下，该结构在中心频率6 GHz处的插入损耗小于0.5 dB，电磁波几乎可以无损耗地透过；在防护状态，ESS具有超过30 dB的防护效能，电磁波被屏蔽。其他详细信息及其工作原理已在文献中详细阐述，本节不做赘述。
ESS放置在z = 0切面处，使用平面波对其进行激励，能流密度曲线分布如图6所示。可以看出，当能流密度曲线接近ESS阵列时，发生了明显的偏折，能流密度曲线首先向ESS的中心聚集，穿过ESS后向两侧扩展，随着远离ESS阵列，再次向中心区域聚集，最后保持不变。除了靠近ESS阵列边缘的少量能流密度曲线外，大部分能流密度曲线经过ESS阵列之后变得更加集中，这表明虽然ESS没有吸收任何能量，但使穿过ESS的能流密度曲线更加密集，从而更容易被后端的天线吸收。需要说明的是，不同ESS的能流密度曲线分布是不同的，与ESS的谐振方式、阵列的尺寸等因素有关。对于给定的ESS阵列，应当选取ESS能流密度曲线分布均匀、能流密度变化小的区域加载天线，从而降低其对天线的影响。
2.3 ESS与天线耦合效应分析流程总结
上文使用能流密度曲线重新定义了天线吸收口径，并分别讨论了天线和ESS的能流密度曲线分布特性。上述过程获得的信息可以用于二者耦合效应的分析并指导ESS设计，主要作用包括：
(1)天线吸收口径的形状给出了ESS最优尺寸和位置的参考。当ESS作为天线罩时，最先产生的一个问题就天线罩的大小和形状如何确定。如果天线罩过小，无法覆盖天线的吸收口径，那么入射波不经过天线罩也可被天线吸收，这种情况下无法发挥天线罩预期的作用。反之，如果天线罩的尺寸过大，就会增加额外的成本，造成了不必要的浪费。此外，通过对ESS和天线的能流密度曲线特性分析，可以得到ESS对天线能流密度曲线分布扰动最小、吸收口径变化最小的位置，即为ESS的最优加载位置。
(2)天线和ESS的能流密度曲线分布可以对ESS与天线的耦合效应进行可视化的分析和量化评估。天线和ESS的电磁特性可以用其周围的能流密度曲线分布来分析，当ESS加载于天线前端时，二者的耦合效应必然会反映在能流密度曲线分布的变化上。通过能流密度曲线的分布，就可以对二者的耦合效应进行可视化的分析。耦合效应的大小可以通过吸收口径变化的大小进行量化评估。同时，吸收口径的形状还可以反映天线吸收电磁波能量的空间分布。最后，给出坡印廷矢量法分析天线和ESS的一般流程，如图7所示。首先使用坡印廷矢量法对天线和ESS分别进行分析，得到天线的吸收口径、能流密度曲线分布以及ESS的能流密度曲线分布。然后通过天线的吸收口径确定ESS的参考尺寸，并根据二者的能流密度曲线分布选择ESS放置的初始位置。初始位置的选择应当使天线和ESS都处于彼此能流密度曲线分布较为均匀的区域。接下来对二者的耦合效应进行分析，使用吸收口径的变化进行量化比较，得到ESS对天线吸收口径影响最小的位置作为ESS加载的最优位置。最后通过常规分析方法进行仿真验证，比较天线的增益、驻波等指标是否满足要求。
3. ESS与喇叭天线耦合效应分析实例
3.1 喇叭天线的能流密度分布特性
本节使用坡印廷矢量法对矩形喇叭天线进行分析，具体尺寸如图8所示。在阻抗匹配状态下，使用垂直于喇叭口面的平面波进行激励，获得喇叭天线在中心频点的能流密度分布。
图9(a)和图9(b)显示了喇叭天线在E面和H面的能流密度分布。可以看出，在天线的影响下，入射波的能流密度曲线出现了较为明显的变化。根据距喇叭口面的位置，可以将能流密度曲线分为3个区域，即Area I,Area II和Area III。在Area I中。能流密度曲线在3个区域中的分布特点、变化大小不同，反射处对应区域中电磁能量的分布特性也不同。
图9(c)显示了在z = 9λ 处获得的喇叭天线的吸收口径，结果显示，矩形喇叭天线的吸收口径并不是和喇叭口面一样的矩形，而是一个纺锤形。具体而言，喇叭口面两侧的大部分区域的能流密度曲线都被天线负载吸收，而中间部分未被吸收。这与图9(a)和图9(b)中能流密度曲线的分布一致。通过坡印廷矢量获得的矩形喇叭天线的吸收口径为0.752 λ2；通过式(3)计算的有效接收面积值为0.760 λ2，相对误差仅为1.1%，两者具有良好的一致性，误差主要来源于全波仿真的计算误差以及后处理过程中边界提取的误差。
3.2 ESS最优加载位置
为了分析ESS和矩形喇叭天线之间的耦合效应，将ESS和矩形喇叭天线进行联合仿真，计算ESS放置在矩形喇叭天线不同位置时矩形喇叭天线能流密度曲线分布以及吸收口径的变化，使用Zd表示ESS与喇叭天线口面之间的距离。图10计算了Zd = 0.1λ时矩形喇叭天线的能流密度曲线分布和吸收口径。在E面，能流密度曲线在靠近矩形喇叭天线中心的位置出现了两个旋涡，导致该处的能流密度曲线不能被矩形喇叭天线吸收。实际上，旋涡处的能流密度曲线穿过了E面，进入了其他平面。由于ESS的存在，在喇叭口面边缘处，更多的能流密度曲线进入了矩形喇叭天线的负载。这部分能流密度曲线首先被ESS所捕获，沿ESS流动到靠近矩形喇叭天线中间的区域后脱离ESS，进入矩形喇叭天线负载，这表明ESS与矩形喇叭天线深度耦合，起到了引导能量流动的作用。在H面，能流密度曲线向矩形喇叭天线两侧弯曲，最终未被矩形喇叭天线吸收。
与无ESS相比，矩形喇叭天线的能流密度分布在加载ESS以后产生了显著变化，表明ESS和矩形喇叭天线之间存在强烈的耦合，ESS作为矩形喇叭天线的一部分参与了矩形喇叭天线接收电磁波的过程。图10(c)显示了矩形喇叭天线吸收口径的变化，矩形喇叭天线的吸收口径在x方向扩张的同时分裂成了两个不连续的部分，这表明加载ESS以后，矩形喇叭天线中心区域不再吸收电磁能量，与前文基于能流密度曲线分析的结果一致。值得指出的是，不加ESS时，计算得到的吸收口径是0.85λ2，加载ESS后的吸收口径为0.72λ2。从数值上比较，加载ESS以后吸收口径的变化并不显著，但是从吸收口径的形状比较，二者存在明显差别。
为了更加深入地分析ESS和矩形喇叭天线之间耦合的原因，对矩形喇叭天线有无ESS时附近的电场和磁场分布进行了计算。图11显示了有无ESS时矩形喇叭天线附近的电场分布，加载ESS以后，矩形喇叭天线的电场分布变化较小，表明二者之间没有产生强烈的电场耦合。图12显示了有无ESS时矩形喇叭天线附近的磁场分布，结果显示，加载ESS以后，矩形喇叭天线附近的磁场分布发生了明显变化，在ESS上激发了强烈的磁谐振，从而引起了电磁能量的扰动。
通过对电场和磁场分布的分析进一步验证了基于坡印廷矢量法的分析结果，证明了该方法的可行性。对比场分析和坡印廷量法分析的结果可以看出，场分析只提供了一个定性的分析结果，通过该结果可以判断天线和ESS是否出现耦合，但不能判断耦合效应是有利还是不利，也不能评估耦合的强弱程度。对比之下，基于坡印廷矢量法的分析结果能提供清晰的物理图景和量化比较，体现了坡印廷矢量分析方法的优越性。
为了更加详细地探究ESS在不同位置对矩形喇叭天线吸收口径的影响，对其位置进行参数扫描，结果如图13所示。当ESS距离矩形喇叭天线很近时(Zd < 0.2 λ, Area III)，喇叭天线的吸收口径有一定程度的减小，原因在于ESS与天线存在强耦合，产生了不利影响。随着ESS逐渐远离天线(Zd >0.2 λ, Area II)，吸收口径出现了波动，这是因为在近场区域，天线的场分布不均匀，随着距离的变化ESS对天线的吸收口径产生了不同影响，这也为ESS与天线的优化提供了空间。最后，当ESS的距离继续增加，到达天线的远场后(Zd > 4.5 λ, Area I)，吸收口径不再发生变化，这表明ESS对天线的影响达到了稳定状态。根据计算结果，当ESS距离矩形喇叭天线 时，喇叭天线具有最大吸收口径，可以作为ESS最优加载位置。总体而言，加载ESS以后天线的吸收口径增大，对天线产生了有利影响。
3.3 验证分析
前文中将天线当作接收器，利用能流密度分布分析了矩形喇叭天线和ESS之间的耦合效应，并利用吸收口径进行了量化评估。为了验证坡印廷矢量法的分析结果，将天线重新当作发射器，使用波端口进行激励，计算天线的增益、方向图、S参数等信息，使用常规分析方法评估加载ESS后天线性能的变化。
图14比较了ESS位于几个典型位置时矩形喇叭天线方向图的变化，当ESS距离较远时(9λ)，主瓣方向上的增益在E面和H面都有一定的增加，而当距离天线较近时(0.14λ)，增益有轻微的降低，这与坡印廷矢量法分析的结论一致。在副瓣方向上，当ESS距离较远时，副瓣上升，当距离较近时(0.14λ)，副瓣降低，情况与主瓣相反，这是由于ESS只覆盖了主瓣方向，主瓣方向上的能量增强了，必然导致副瓣的能量减少，反之亦然。在背瓣方向上，ESS在不同位置时天线的背瓣都有不同程度的增大，这是因为ESS本身的透波率并不是100%，必然引起部分反射，导致背瓣升高。总体而言，副瓣和背瓣的变化不大。
图15比较了ESS在不同位置时矩形喇叭天线的S参数，当ESS位于天线远场时，S参数基本没有变化，这表明ESS对天线的匹配状态影响较小；当ESS距离较近时，S参数有比较明显的变化，在部分频段的表现甚至优于无ESS时的结果，这表明ESS和矩形喇叭天线之间的耦合作用使得天线的阻抗匹配状态更佳。
最后，计算了ESS在不同位置时矩形喇叭天线的增益变化，并将其和吸收口径进行了对比。如图16所示，当从接收的角度得到天线的吸收口径增大时，从发射的角度得到的天线的增益也增大，二者具有良好的一致性，证明了坡印廷矢量法分析的可靠性。显然，只有在ESS处于Area III时，矩形喇叭天线增益降低，在其他位置，矩形喇叭天线的增益都有不同程度的增加。根据仿真结果，最大增益出现在ESS距离天线1.7λ处，矩形喇叭天线的吸收口径从0.72λ2增加到0.93λ2。对应地，矩形喇叭天线的增益从9.88 dBi增加到10.85 dBi。
4. 结论
本文提出一种ESS与天线耦合效应矢量分析方法，首先以振子天线为例对该方法的原理与分析流程进行了详细说明。该方法从接收的角度对天线进行研究，使用有效口径与能流密度曲线评估天线的电磁性能，可对ESS与天线的耦合效应进行可视化分析与量化评估，指导ESS的尺寸、形状以及最优位置设计。其次，将所提方法应用于ESS与喇叭天线之的耦合效应分析，验证了所提方法的有效性。首先详细分析了ESS与喇叭天线之间的耦合机理，确定了ESS加载的最优位置，其次将所提方法与常规方法的分析结果进行了比较，二者吻合良好。虽然本文提出的设计方法是以一款平面的ESS与喇叭天线为例进行分析的，但对于其他不同类型的ESS与天线也具有借鉴意义，为ESS与天线耦合效应分析提供了新的分析工具。虽然本文只对偶极子天线和喇叭天线进行了分析，但分析过程和方法对大部分天线都是适用的，其应用场景是较为丰富的。
-
[1] 刘培国, 刘晨曦, 谭剑锋, 等. 强电磁防护技术研究进展[J]. 中国舰船研究, 2015, 10(2): 2–6. doi: 10.3969/j.issn.1673-3185.2015.02.002LIU Peiguo, LIU Chenxi, TAN Jianfeng, et al. Analysis of the research development on HPM/EMP protection[J]. Chinese Journal of Ship Research, 2015, 10(2): 2–6. doi: 10.3969/j.issn.1673-3185.2015.02.002 [2] 杨成. 能量选择表面仿真、测试与防护应用研究[D]. [博士论文], 国防科学技术大学, 2016.YANG Cheng. Simulation, mesurement and protection application of energy selective surface[D]. [Ph. D. dissertation], National University of Defense Technology, 2016. [3] 易波. 新型电磁结构在隐身和电磁防护中的应用研究[D]. [博士论文], 国防科学技术大学, 2017.YI Bo. Research on stealth and electromagnetic protection technology based on new-type electromagnetic structure[D]. [Ph. D. dissertation], National University of Defense Technology, 2017. [4] 刘晨曦. 能量选择表面设计与仿真[D]. [硕士论文], 国防科学技术大学, 2015.LIU Chenxi. Design and simulation of energy selective surface[D]. [Master dissertation], National University of Defense Technology, 2015. [5] 虎宁, 查淞, 刘晨曦, 等. 一种双频能量选择表面的设计[J]. 微波学报, 2022, 38(6): 1–5. doi: 10.14183/j.cnki.1005-6122.202206001HU Ning, ZHA Song, LIU Chenxi, et al. Design of a dual-band energy selective surface[J]. Journal of Microwaves, 2022, 38(6): 1–5. doi: 10.14183/j.cnki.1005-6122.202206001 [6] HU Ning, ZHA Song, TIAN Tao, et al. Design and analysis of multiband energy selective surface based on semiconductors[J]. IEEE Transactions on Electromagnetic Compatibility, 2022, 64(4): 1076–1085. doi: 10.1109/TEMC.2022.3166156 [7] HU Ning, ZHAO Yuting, ZHANG Jihong, et al. High performance energy selective surface based on equivalent circuit design approach[J]. IEEE Transactions on Antennas and Propagation, 2022, 70(6): 4526–4538. doi: 10.1109/TAP.2021.3137293 [8] 王轲. 能量选择结构设计与导航防护应用研究[D]. [硕士论文], 国防科技大学, 2017.WANG Ke. Research on energy selective structure design and navigation protection application[D]. [Master dissertation], National University of Defense Technology, 2017. [9] WAKATSUCHI H, LONG Jiang, and SIEVENPIPER D F. Waveform selective surfaces[J]. Advanced Functional Materials, 2019, 29(11): 1806386. doi: 10.1002/adfm.201806386 [10] ZHOU Lin and SHEN Zhongxiang. 3-D absorptive energy-selective structures[J]. IEEE Transactions on Antennas and Propagation, 2021, 69(9): 5664–5672. doi: 10.1109/TAP.2021.3061097 [11] ZHOU Lin and SHEN Zhongxiang. Diffusive energy-selective surface with low backscattering[J]. IEEE Transactions on Antennas and Propagation, 2022, 70(1): 430–439. doi: 10.1109/TAP.2021.3098603 [12] LUO Zhangjie, WANG Qiang, ZHANG Xinge, et al. Intensity-dependent metasurface with digitally reconfigurable distribution of nonlinearity[J]. Advanced Optical Materials, 2019, 7(19): 1900792. doi: 10.1002/adom.201900792 [13] CHEN Zhenzhen, CHEN Xing, and XU Guanghui. A spatial power limiter using a nonlinear frequency selective surface[J]. International Journal of RF and Microwave Computer Aided Engineering, 2018, 28(4): e21205. doi: 10.1002/mmce.21205 [14] DENG Feng, XI XiuJuan, LI Jing, et al. A Method of designing a field-controlled active frequency selective surface[J]. IEEE Antennas and Wireless Propagation Letters, 2015, 14: 630–633. doi: 10.1109/lawp.2014.2375376 [15] QIN Dongmei, MA Runbo, SU Jinrong, et al. Ultra-wideband strong field protection device based on metasurface[J]. IEEE Transactions on Electromagnetic Compatibility, 2020, 62(6): 2842–2848. doi: 10.1109/TEMC.2020.3020840 [16] DIAO Junming and WARNICK K F, et al. Practical superdirectivity with resonant screened apertures motivated by a poynting streamlines analysis[J]. IEEE Transactions on Antennas and Propagation, 2018, 66(1): 432–437. doi: 10.1109/tap.2017.2772929 [17] DIAO Junming, LIU Lu, and WARNICK K F. Understanding the Element-gain paradox for receiving arrays using poynting streamlines[C]. 2018 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, Boston, USA, 2018: 1457–1458. [18] LIU Lu, DIAO Junming, and WARNICK K F. Array antenna gain enhancement with the poynting streamline method[J]. IEEE Antennas and Wireless Propagation Letters, 2020, 19(1): 143–147. doi: 10.1109/LAWP.2019.2956219 [19] IEEE. IEEE Std 145-2013 IEEE standard for definitions of terms for antennas[S]. IEEE, 2014: 1–50. -
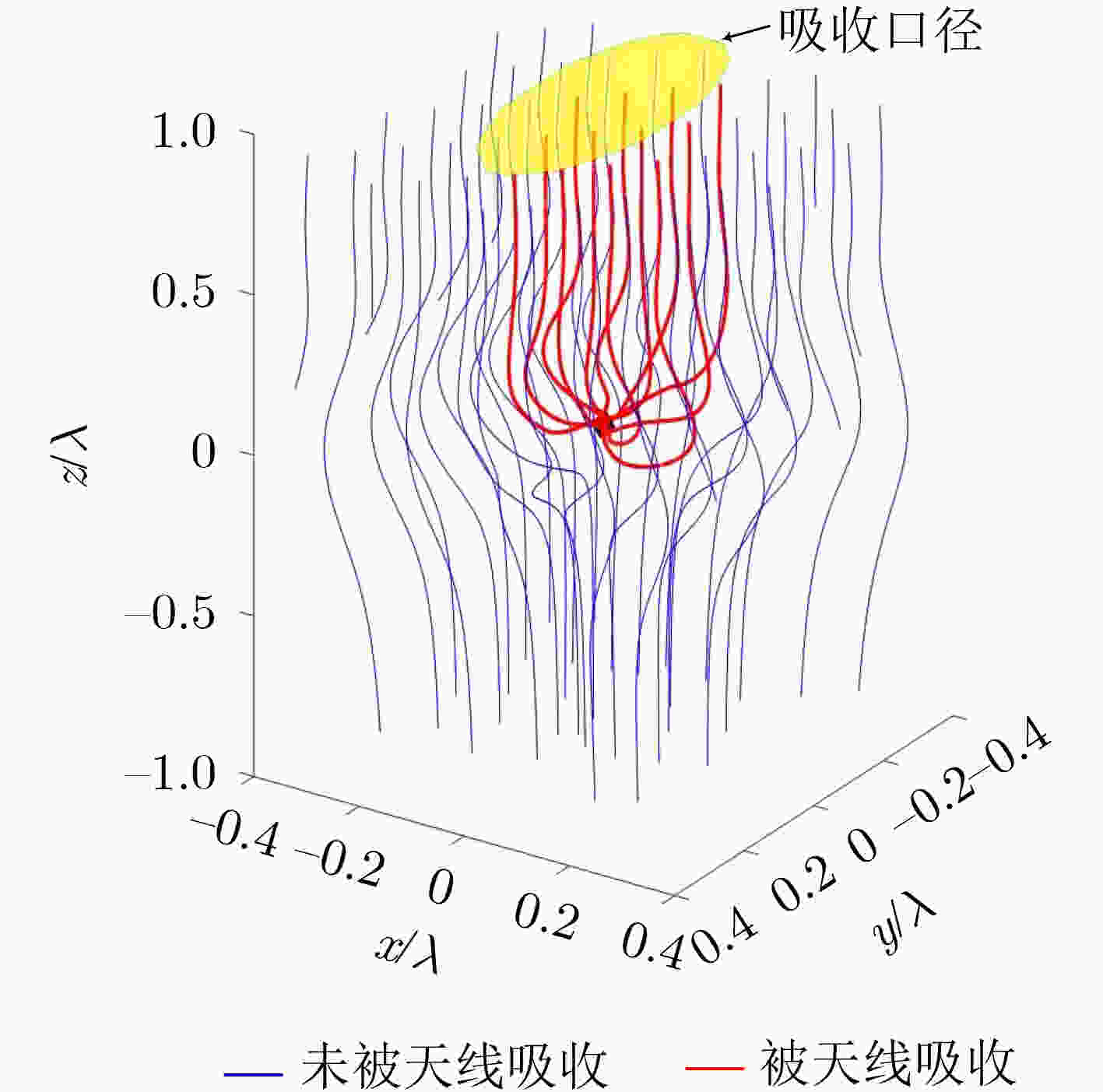
下载:
下载:
计量
- 文章访问数: 399
- HTML全文浏览量: 294
- PDF下载量: 41
- 被引次数: 0
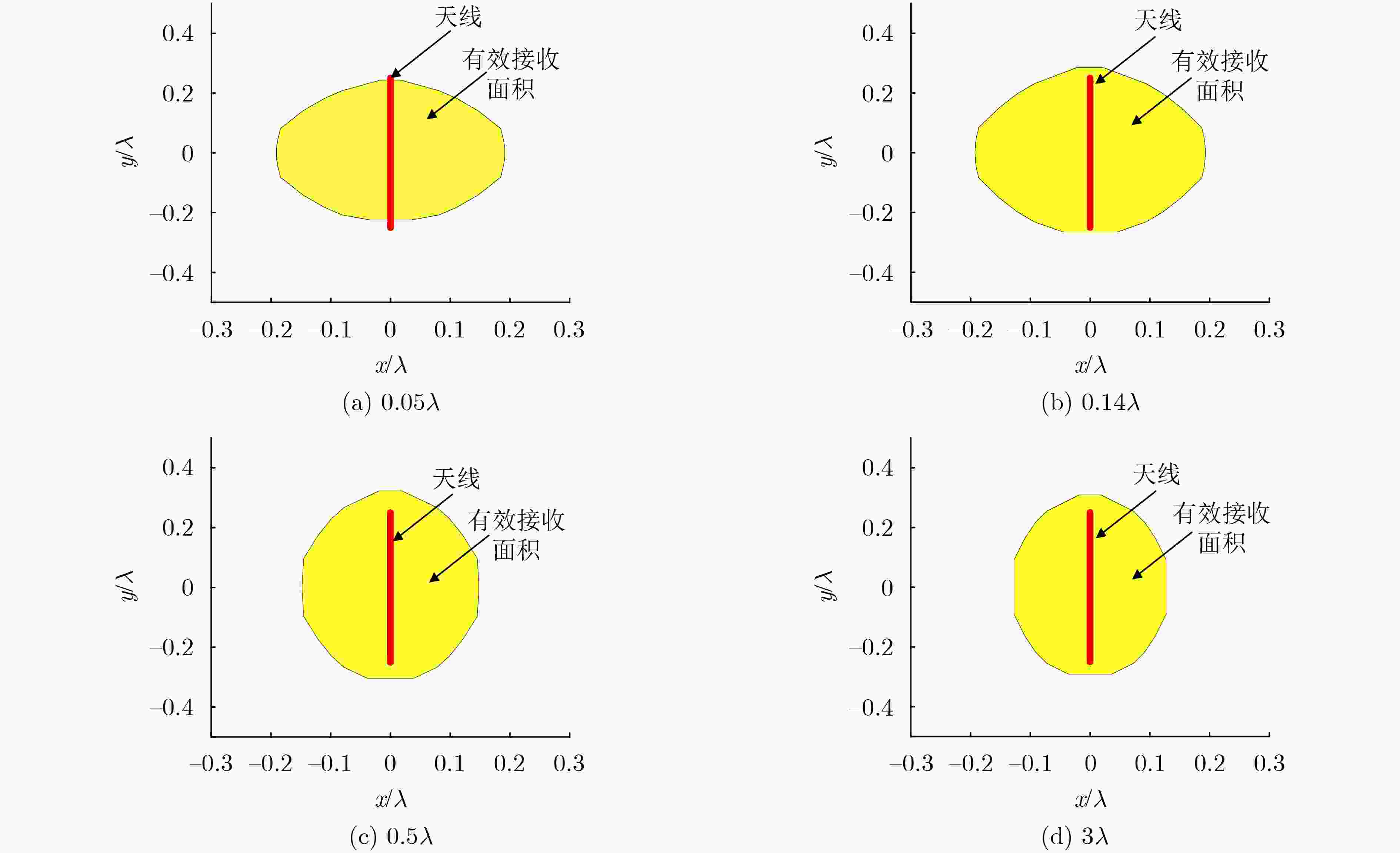
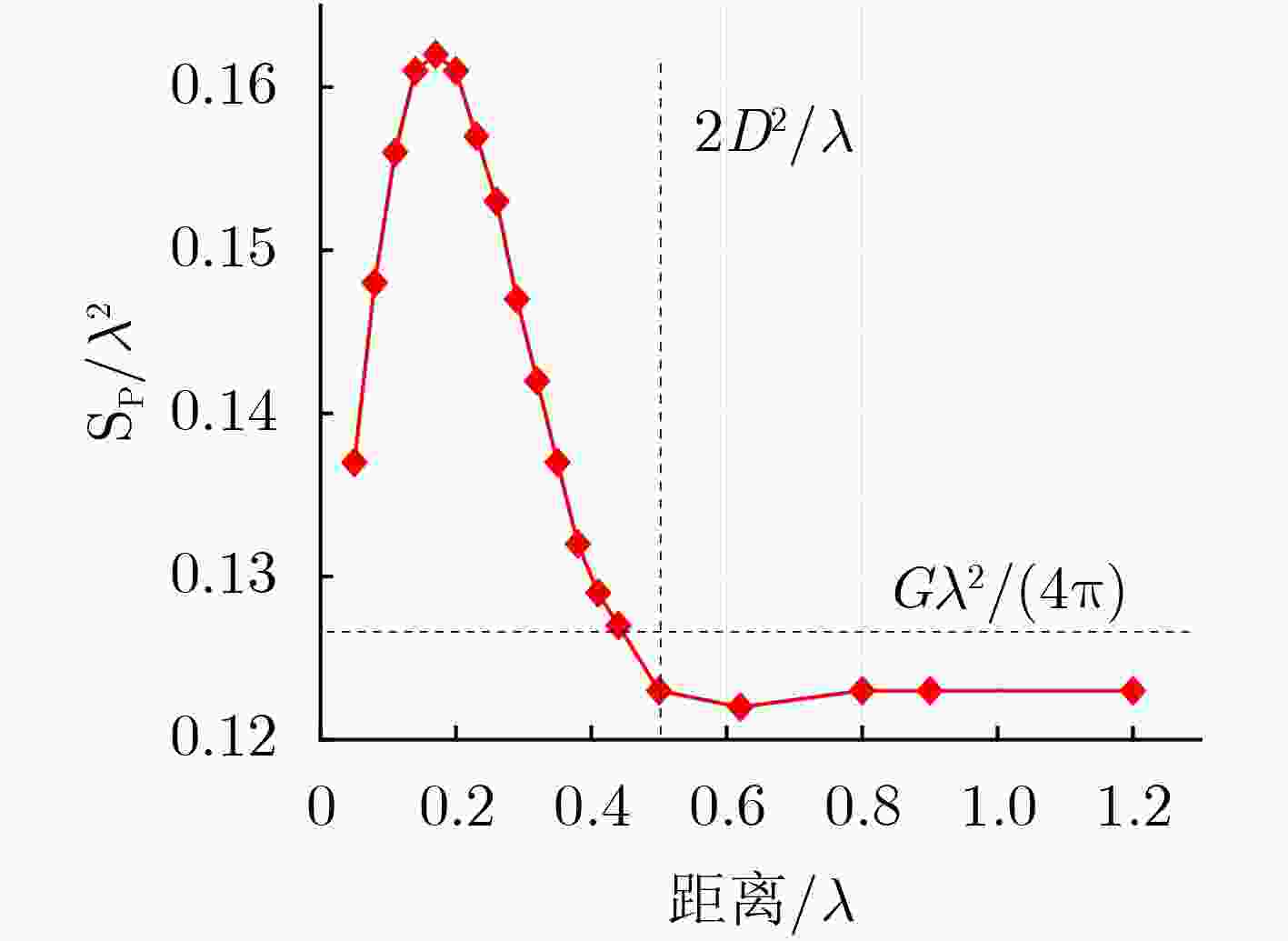
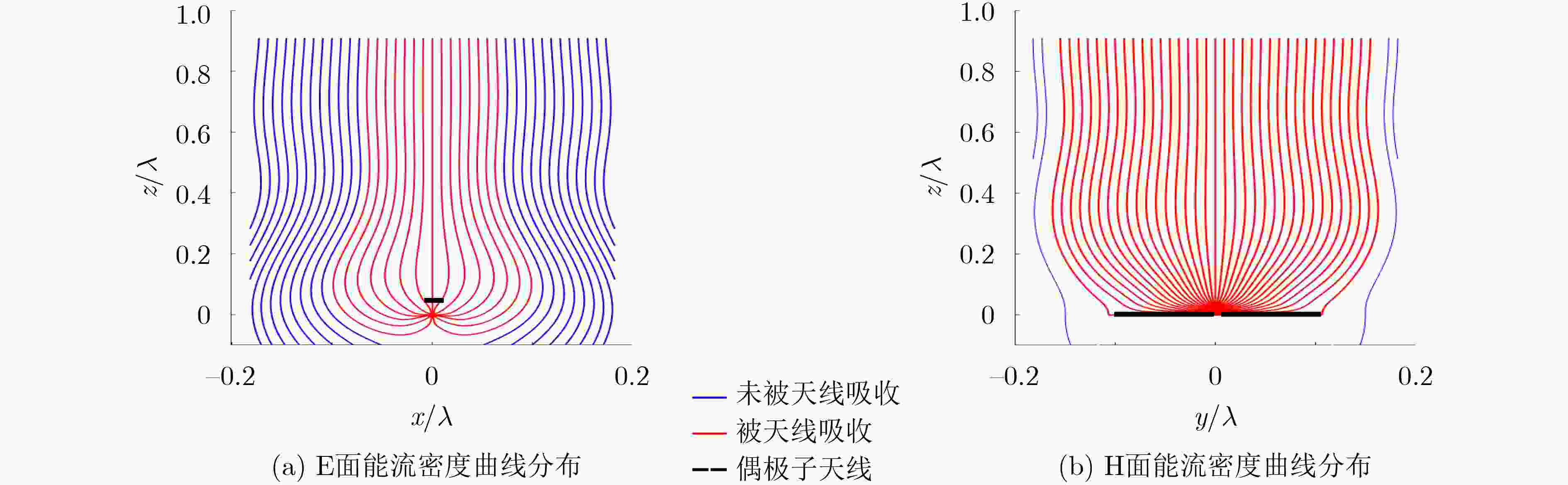
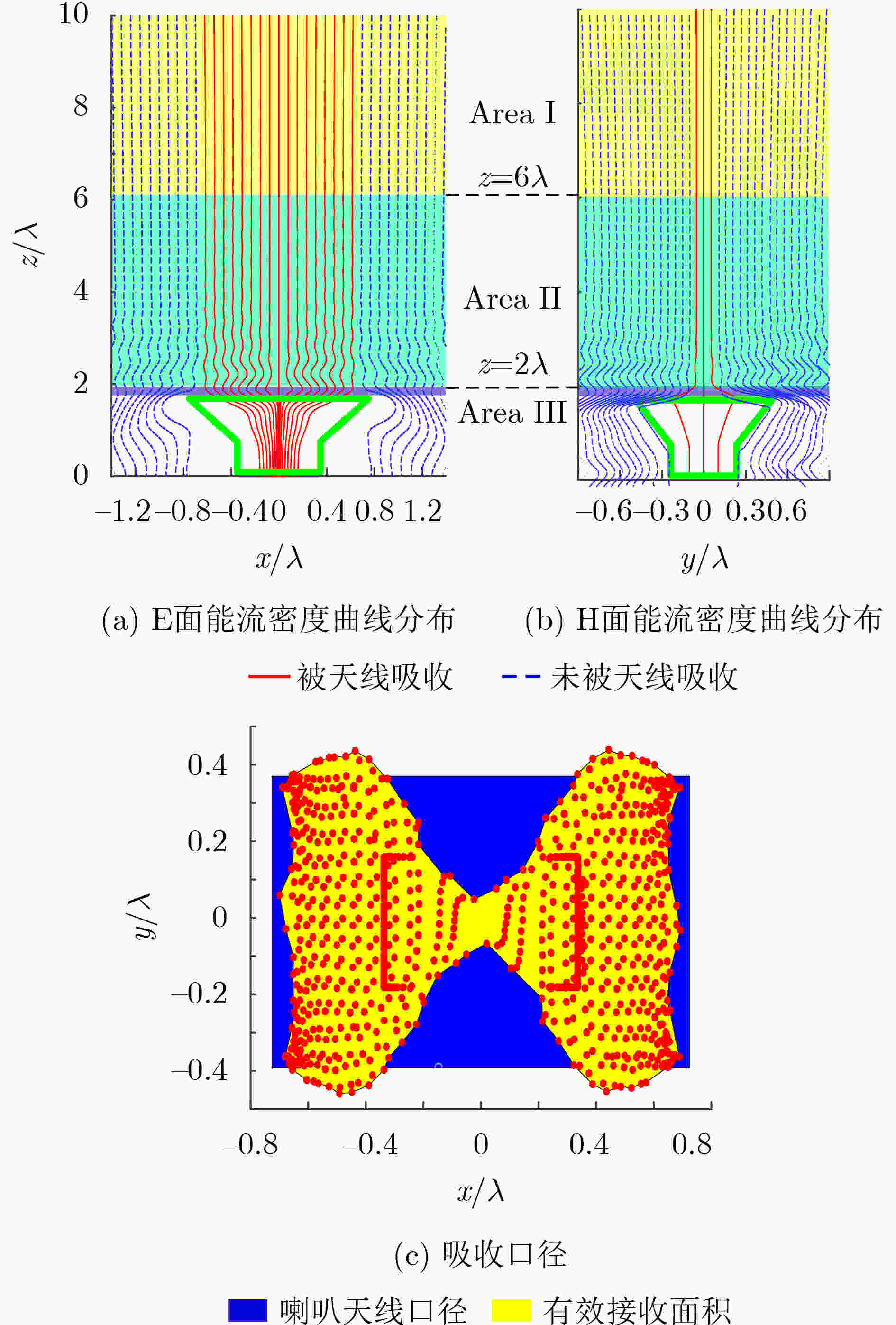
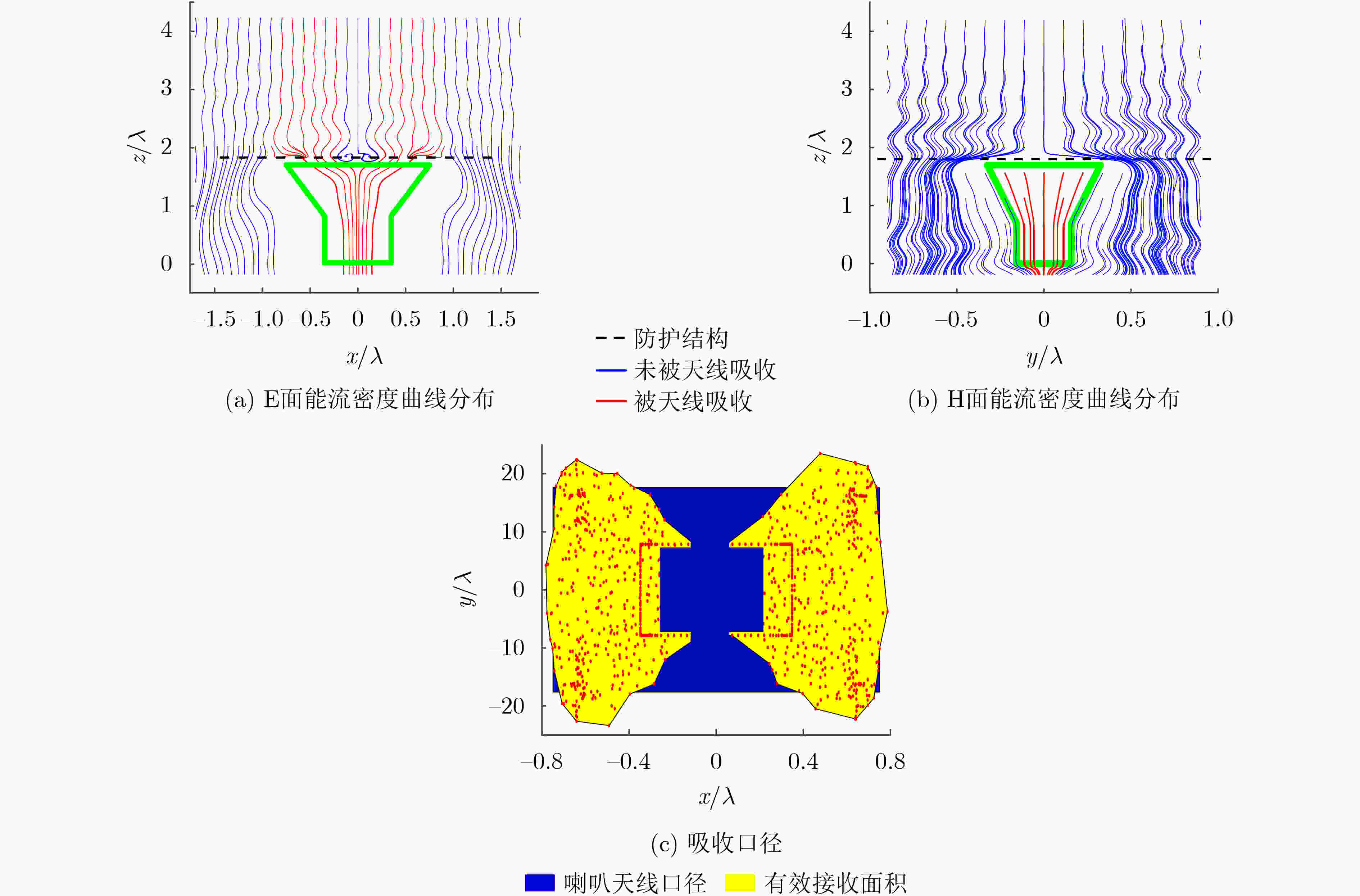
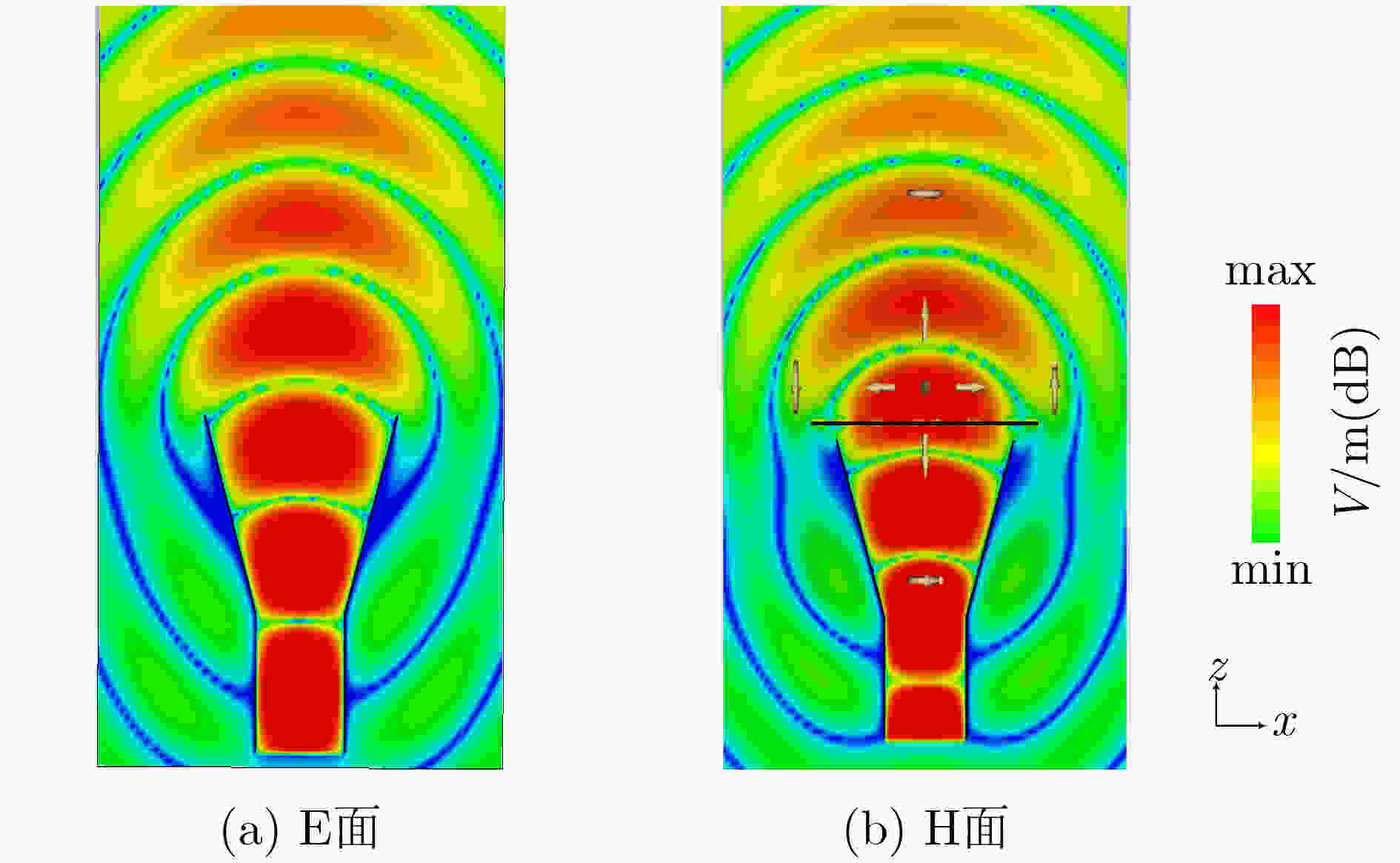
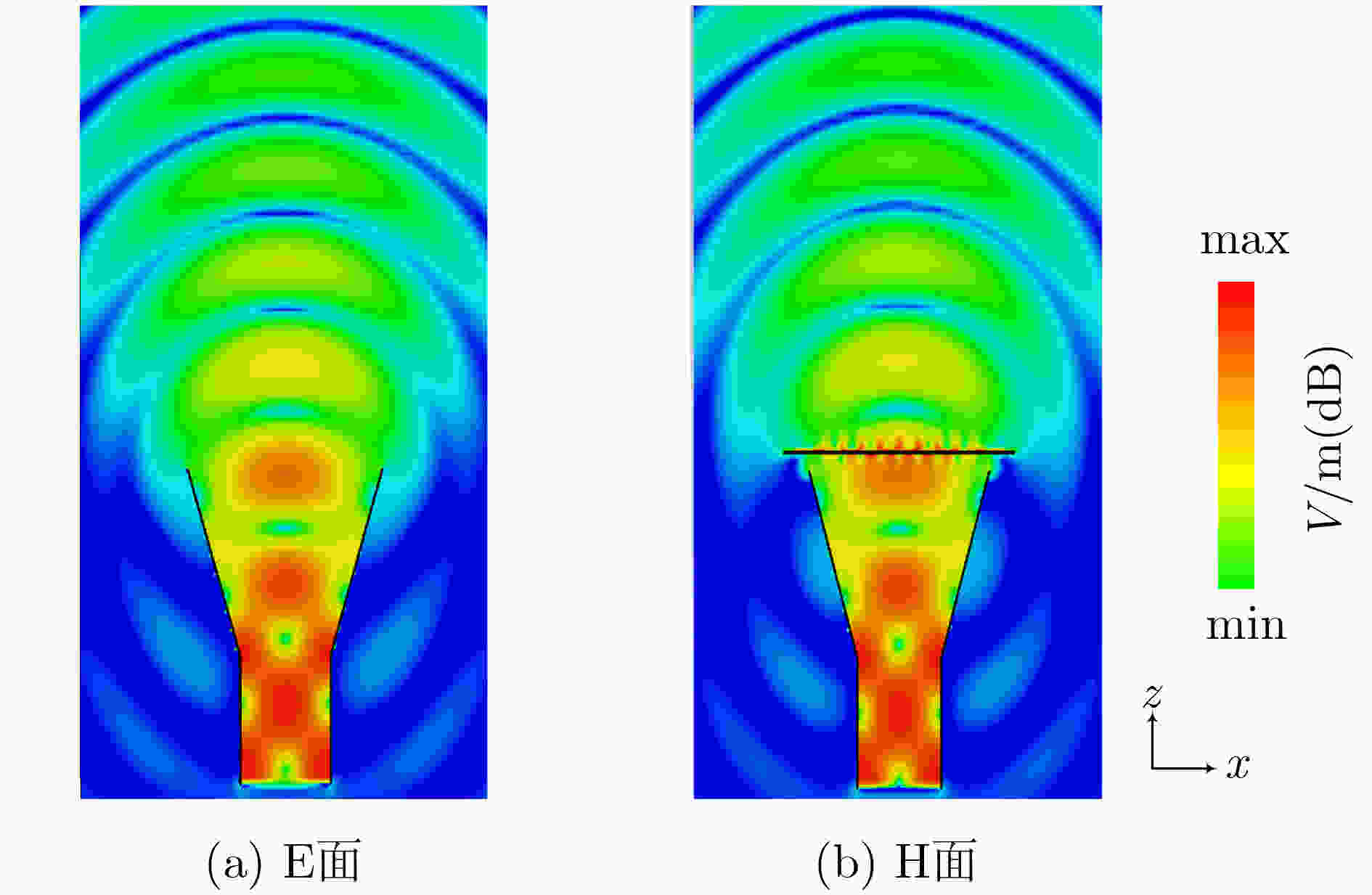
下载:
