Weak Targets Detection and Estimation Based on Joint Use of Doppler and Micro-Doppler
-
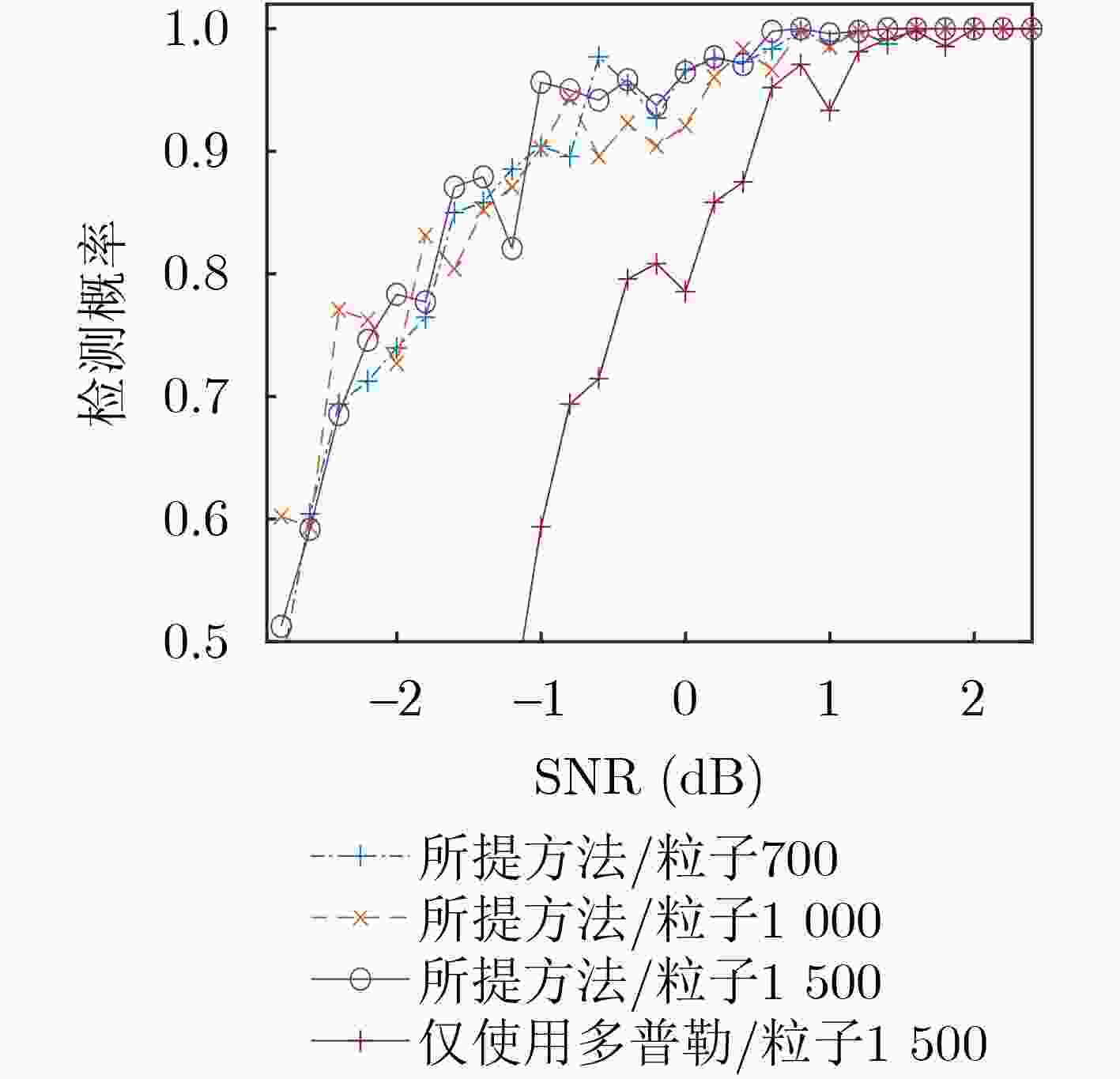
摘要: 近年来,无人机(UAVs)等低慢小目标对现有低空空域管理带来了巨大挑战。这类目标由于其飞行高度低、飞行速度慢及雷达散射截面(RCS)面积小,导致其回波信噪比(SNR)低,传统基于目标多普勒信息的检测估计方法检测概率低,参数估计不准确。对于无人机类低慢小目标的检测估计,除了可以利用目标径向运动产生的多普勒信息外,还可以利用目标微动部件产生的微多普勒信息,通过有效聚集因微动而分散在多个多普勒单元格内的能量,可望实现目标信噪比的提升。该文针对旋翼类低慢小目标,充分挖掘目标回波中蕴含的多普勒信息和微多普勒信息,在随机集框架下对旋翼无人机目标的多普勒和微多普勒信息进行联合建模,提出一种基于(CBMeMBer)滤波器的多普勒和微多普勒联合检测估计方法,利用贝叶斯估计实现了目标多普勒信息和微多普勒信息的有效积累和融合利用,可以提高雷达低慢小目标的检测估计性能。仿真试验表明,该方法可实现对旋翼无人机目标的稳定检测与状态估计,相比于仅利用目标多普勒信息的传统检测方法,检测灵敏度提高了2 dB。
-
关键词:
- 信号检测 /
- 微多普勒 /
- 参数估计 /
- CBMeMBer滤波器
Abstract: In recent years, low-altitude slow and small targets, such as Unmanned Aerial Vehicles (UAVs), have posed a great challenge to the management of existing low-altitude airspace. These targets have low echo Signal Noise Ratio (SNR) due to their low flight altitude, slow flight speed and small Radar Cross Section (RCS), which result in low detection probability and inaccurate parameter estimation by traditional detection and estimation methods based on Doppler information of target. In addition to the Doppler information generated by the radial motion of the target, the micro-Doppler information generated by the micro-motion parts of the target can also be used for the detection and estimation of low-altitude slow and small targets like UAVs, which is expected to improve the SNR of the target by aggregating the energy dispersed in multiple Doppler cells due to the micro-motion. In this paper, a joint Doppler and micro-Doppler detection and estimation method based on the Cardinality Balanced Multi-target Multi-Bernoulli (CBMeMBer) filter is proposed, which makes full usage of the Doppler and micro-Doppler information contained in the echoes of UAV targets. By jointly modelling the Doppler and micro-Doppler information of UAV targets under the framework of Random Finite Sets (RFS), effective integration and fusion of Doppler and micro-Doppler information can be achieved. This leads to a better detection and estimation performance of low-altitude slow and small targets. Simulation experiments show that the method can achieve stable detection and state estimation of UAV targets, and the detection sensitivity is improved by 2 dB compared with the traditional detection method that only uses target Doppler information. -
算法1 无人机目标CBMeMBer滤波器 输入:当前时刻测量 ${{\boldsymbol{Y}}_k} = {\{ {y_{1,k}}, \cdots ,{y_{m,k}}\} _{{N_r} \times {N_v}}}$、上一时刻滤波状态 $ r_{k - 1}^{(i)},\{ w_{k - 1}^{(i,j)},{\boldsymbol{x}}_{k - 1}^{(i,j)}\} _{j = 1}^{L_{k - 1}^{(i)}},\quad i \in [1,{M_{k - 1}}] $ 输出:本时刻滤波状态 $ r_k^{(i)},\{ w_k^{(i,j)},{\boldsymbol{x}}_k^{(i,j)}\} _{j = 1}^{L_k^{(i)}},\quad i \in [1,{M_k}] $ (1) 根据建议分布采样新生粒子状态 ${\boldsymbol{x}}_{\varGamma ,k}^{(i,j)}{\text{~}}b_k^{(i)}( \cdot |{{\boldsymbol{Y}}_k}),j = 1,2, \cdots ,L_{\varGamma ,k}^{(i)}$ (2) 计算新生粒子权重 $w_{\varGamma ,k}^{(i,j)} = \dfrac{{{p_{\varGamma ,k}}({\boldsymbol{x}}_{\varGamma ,k}^{(i,j)})}}{{b_k^{(i)}({\boldsymbol{x}}_{\varGamma ,k}^{(i,j)}|{{\boldsymbol{Y}}_k})}}$
(3) 新生粒子权重归一化 $\tilde w_{\varGamma ,k}^{(i,j)} = \dfrac{{w_{\varGamma ,k}^{(i,j)}}}{{\displaystyle\sum\limits_{j = 1}^{L_{\varGamma ,k}^{(i)}} {w_{\varGamma ,k}^{(i,j)}} }}$(4) 根据建议分布采样预测粒子状态 ${\boldsymbol{x} }_{P,k|k - 1}^{(i,j)}{\text{~} }q_k^{(i)}( \cdot |{\boldsymbol{x} }_{k - 1}^{(i,j)},{ {\boldsymbol{Y} }_k}),j = 1,2, \cdots ,L_{k - 1}^{(i)}$ 一般设 $ q_k^{(i)}( \cdot |{\boldsymbol{x}}_{k - 1}^{(i,j)},{{\boldsymbol{Y}}_k}) = {f_{k|k - 1}}( \cdot |{\boldsymbol{x}}_{k - 1}^{(i,j)}) $, ${f_{k|k - 1}}( \cdot |{\boldsymbol{x}}_{k - 1}^{(i,j)})$由式(15)给出 (5) 根据式(16)为 ${\boldsymbol{x}}_{P,k|k - 1}^{(i,j)}$添加噪声 (6) 更新预测粒子权重 $w_{P,k|k - 1}^{(i,j)} = \dfrac{{w_{k - 1}^{(i,j)}{f_{k|k - 1}}({\boldsymbol{x}}_{P,k|k - 1}^{(i,j)}|{\boldsymbol{x}}_{k - 1}^{(i,j)}){p_{S,k}}({\boldsymbol{x}}_{k - 1}^{(i,j)})}}{{q_k^{(i)}({\boldsymbol{x}}_{P,k|k - 1}^{(i,j)}|{\boldsymbol{x}}_{k - 1}^{(i,j)},{{\boldsymbol{Y}}_k})}}$
(7) 预测粒子权重归一化 $\tilde w_{P,k|k - 1}^{(i,j)} = \dfrac{{w_{P,k|k - 1}^{(i,j)}}}{{\displaystyle\sum\limits_{j = 1}^{L_{k - 1}^{(i)}} {w_{P,k|k - 1}^{(i,j)}} }}$(8) 根据上一时刻滤波状态计算本时刻单个伯努利项存在概率 $r_{P,k|k - 1}^{(i)} = r_{k - 1}^{(i)}\displaystyle\sum\limits_{j = 1}^{L_{k - 1}^{(i)}} {w_{k - 1}^{(i,j)}} {p_{S,k}}({\boldsymbol{x}}_{k - 1}^{(i,j)})$ (9) 根据新生模型计算新生多伯努利密度存在概率 $r_{\varGamma ,k}^{(i)}$ (10) 将新生粒子合并到预测粒子中 $\{ w_{k|k - 1}^{(i,j)},{\boldsymbol{x} }_{k|k - 1}^{(i,j)}\} _{j = 1}^{L_{k - 1}^{(i)} } = \{ w_{\varGamma ,k|k - 1}^{(i,j)},{\boldsymbol{x} }_{\varGamma ,k|k - 1}^{(i,j)}\} \cup \{ w_{P,k|k - 1}^{(i,j)},{\boldsymbol{x} }_{P,k|k - 1}^{(i,j)}\}$ (11) 使用式(22)计算后验粒子权重 $\hat w_k^{(i,j)} = w_{k|k - 1}^{(i,j)}{g_{{y_k}}}({\boldsymbol{x}}_{k|k - 1}^{(i,j)})$
(12) 计算粒子权重总和 $\varrho _k^{(i)} = \displaystyle\sum\limits_{j = 1}^{L_{k|k - 1}^{(i)}} {\hat w_k^{(i,j)}} $
(13) 计算后验多伯努利密度存在概率 $r_k^{(i)} = \dfrac{{r_{k|k - 1}^{(i)}\varrho _k^{(i)}}}{{1 - r_{k|k - 1}^{(i)} + r_{k|k - 1}^{(i)}\varrho _k^{(i)}}}$(14) 后验粒子权重归一化 $w_k^{(i,j)} = \dfrac{{\hat w_k^{(i,j)}}}{{\varrho _k^{(i)}}}$ (15) 后验粒子状态为上一时刻预测状态 ${\boldsymbol{x}}_k^{(i,j)} = {\boldsymbol{x}}_{k|k - 1}^{(i,j)}$ (16) 根据粒子权重分布对 $\{ w_{k - 1}^{(i,j)},{\boldsymbol{x}}_{k - 1}^{(i,j)}\} _{j = 1}^{L_{k - 1}^{(i)}}$重采样,然后将权重设置为相同值并归一化 表 1 仿真雷达参数
参数 值 帧间隔 ε=1 s 最大不模糊距离 200 m 最大不模糊速度 20 m/s 帧分辨率 Nr×Nv=256×512 距离测量误差 $\zeta_r=3 \;{\rm{m}}$ 速度测量误差 $\zeta_v=5 \;{\rm{m/s}}$ 强度测量误差 $\zeta_{\rm{s}}=0.3 $ 雷达系统增益 ks=1×1019 表 2 仿真目标参数
参数 值 初始距离 r0=20 010 m 运动速度 v=1 m/s 旋转角速度 $\omega $=0.06π rad/s 初始旋转相位 θ0=0 桨叶个数 B=2 测量强度 ρ=1 表 3 两种算法运行 100 次平均每帧使用时间
算法 最大粒子数 时间(s) 仅使用多普勒特征 1 500 0.068 本文算法 700 0.066 本文算法 1 000 0.101 本文算法 1 500 0.143 -
[1] CHEN V C. Analysis of radar micro-Doppler with time-frequency transform[C]. The Tenth IEEE Workshop on Statistical Signal and Array Processing (Cat. No. 00TH8496), Pocono Manor, USA, 2000: 463–466. [2] CHEN V C, LI F, HO S S, et al. Micro-Doppler effect in radar: Phenomenon, model, and simulation study[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(1): 2–21. doi: 10.1109/TAES.2006.1603402 [3] CHEN V C. The Micro-Doppler Effect in Radar[M]. 2nd ed. Norwood: Artech House, 2019. [4] 秦晓雨, 邓彬, 董俊, 等. 太赫兹雷达直升机旋翼目标微动特性研究[J]. 太赫兹科学与电子信息学报, 2023, 21(3): 317–324. doi: 10.11805/TKYDA2022058QIN Xiaoyu, DENG Bin, DONG Jun, et al. Micro-motion characteristics of helicopter blades based on THz radar[J]. Journal of Terahertz Science and Electronic Information Technology, 2023, 21(3): 317–324. doi: 10.11805/TKYDA2022058 [5] 冯维婷, 梁青. 闪烁现象下基于微动补偿的旋转叶片参数估计方法[J]. 信号处理, 2022, 38(12): 2617–2627. doi: 10.16798/j.issn.1003-0530.2022.12.016FENG Weiting and LIANG Qing. A method for parameters estimation of rotating blades based on micro-motion compensation under flashing[J]. Journal of Signal Processing, 2022, 38(12): 2617–2627. doi: 10.16798/j.issn.1003-0530.2022.12.016 [6] 陈小龙, 陈唯实, 饶云华, 等. 飞鸟与无人机目标雷达探测与识别技术进展与展望[J]. 雷达学报, 2020, 9(5): 803–827. doi: 10.12000/JR20068CHEN Xiaolong, CHEN Weishi, RAO Yunhua, et al. Progress and prospects of radar target detection and recognition technology for flying birds and unmanned aerial vehicles[J]. Journal of Radars, 2020, 9(5): 803–827. doi: 10.12000/JR20068 [7] CHEN Shiqian, DONG Xingjian, XING Guanpei, et al. Separation of overlapped non-stationary signals by ridge path regrouping and intrinsic chirp component decomposition[J]. IEEE Sensors Journal, 2017, 17(18): 5994–6005. doi: 10.1109/JSEN.2017.2737467 [8] BRUNI V, TARTAGLIONE M, and VITULANO D. A pde-based analysis of the spectrogram image for instantaneous frequency estimation[J]. Mathematics, 2021, 9(3): 247. doi: 10.3390/math9030247 [9] HU Yue, TU Xiaotong, LI Fucai, et al. Adaptive instantaneous frequency ridge extraction based on target tracking for frequency-modulated signals[J]. ISA Transactions, 2022, 128: 665–674. doi: 10.1016/j.isatra.2021.10.011 [10] LI Yifan, YANG Yaocheng, FENG Ke, et al. Automated and adaptive ridge extraction for rotating machinery fault detection[J]. IEEE/ASME Transactions on Mechatronics, 2023: 1–11. [11] 赵彤璐, 廖桂生, 杨志伟. 基于短时迭代自适应-逆Radon变换的微多普勒提取方法[J]. 电子学报, 2016, 44(3): 505–513. doi: 10.3969/j.issn.0372-2112.2016.03.002ZHAO Tonglu, LIAO Guisheng, and YANG Zhiwei. Micro-Doppler extraction based on short-time iterative adaptive approach and inverse radon transform[J].Acta Electronica Sinica, 2016, 44(3): 505–513. doi: 10.3969/j.issn.0372-2112.2016.03.002 [12] HOUGH P V C. Method and means for recognizing complex patterns[P]. USA Patent, 3069654A, 1962-12-18. [13] DING Yipeng, LIU Runjin, SHE Yanlong, et al. Micro-Doppler trajectory estimation of human movers by Viterbi–Hough joint algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5113111. doi: 10.1109/TGRS.2022.3171208 [14] MAHLER R P S. Statistical Multisource-Multitarget Information Fusion[M]. Boston: Artech House, 2007. [15] VO B T. Random finite sets in multi-object filtering[D]. [Ph. D. dissertation], The University of Western Australia, 2008. [16] VO B T, SEE C M, MA N, et al. Multi-sensor joint detection and tracking with the Bernoulli filter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1385–1402. doi: 10.1109/TAES.2012.6178069 [17] VO B T, VO B N, and CANTONI A. The cardinality balanced multi-target multi-Bernoulli filter and its implementations[J]. IEEE Transactions on Signal Processing, 2009, 57(2): 409–423. doi: 10.1109/TSP.2008.2007924 [18] VO B N, VO B T, and PHUNG D. Labeled random finite sets and the Bayes multi-target tracking filter[J]. IEEE Transactions on Signal Processing, 2014, 62(24): 6554–6567. doi: 10.1109/TSP.2014.2364014 [19] VO B N, SINGH S, and DOUCET A. Sequential Monte Carlo methods for multitarget filtering with random finite sets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1224–1245. doi: 10.1109/TAES.2005.1561884 [20] VO B N and MA W K. The Gaussian mixture probability hypothesis density filter[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4091–4104. doi: 10.1109/TSP.2006.881190 [21] SHIM C, VO B T, VO B N, et al. Linear complexity Gibbs sampling for generalized labeled multi-Bernoulli filtering[J]. IEEE Transactions on Signal Processing, 2023, 71: 1981–1994. doi: 10.1109/TSP.2023.3277220 [22] 蔡飞. 雷达弱小目标检测与跟踪技术研究[D]. [博士论文], 国防科学技术大学, 2015.CAI Fei. Research on detection and tracking technologies for dim targets in radar[D]. [Ph. D. dissertation], National University of Defense Technology, 2015. [23] VO B N, VO B T, PHAM N T, et al. Joint detection and estimation of multiple objects from image observations[J]. IEEE Transactions on Signal Processing, 2010, 58(10): 5129–5141. doi: 10.1109/TSP.2010.2050482 -





 下载:
下载:




 下载:
下载:
