一种低复杂度的正交时频空系统接收机设计

廖勇; 李雪

doi:10.11999/JEIT230625

一种低复杂度的正交时频空系统接收机设计

doi: 10.11999/JEIT230625

廖勇^,,
李雪

重庆大学微电子与通信工程学院重庆 400044

基金项目: 重庆市自然科学基金(CSTB2023NSCQ-MSX0025)

详细信息

作者简介:
廖勇：男，副研究员，研究方向为高速移动通信系统及其关键技术

李雪：女，硕士生，研究方向为高速移动通信中的信道估计

通讯作者:
廖勇　liaoy@cqu.edu.cn

中图分类号: TN929.5
计量
- 文章访问数: 278
- HTML全文浏览量: 92
- PDF下载量: 20
- 被引次数: 0
出版历程
- 收稿日期: 2023-06-25
- 修回日期: 2023-09-12
- 网络出版日期: 2023-09-15

Low Complexity Receiver Design for Orthogonal Time Frequency Space Systems

LIAO Yong^,,
LI Xue

School of Microelectronics and Communication Engineering, Chongqing University, Chongqing 400044, China

Funds: Chongqing Natural Science Foundation (CSTB2023NSCQ-MSX0025)

摘要

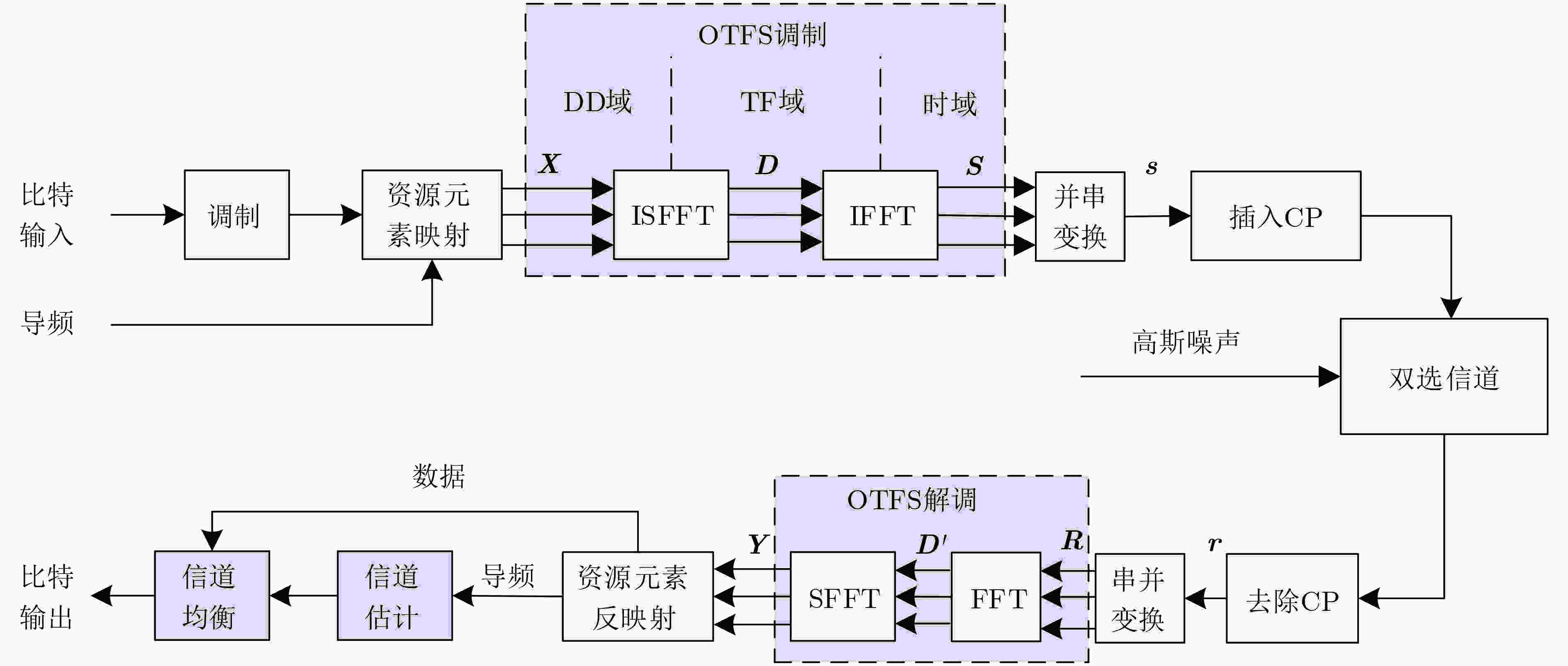
摘要: 正交时频空(OTFS)调制可以将时间和频率选择性信道转换为时延-多普勒(DD)域的非选择性信道，这为高速移动场景建立可靠的无线通信提供了解决方案。然而，在车联网等复杂的多散射场景下，信道存在严重的多普勒间干扰(IDI)，这给OTFS接收机信号的准确解调带来了极大的挑战。针对上述问题，该文提出一种联合稀疏贝叶斯学习(SBL)和阻尼最小二乘最小残差(d-LSMR)的OTFS接收机设计。首先，根据OTFS时域和DD域的关系，采用基扩展模型(BEM)将信道估计问题转换为基系数恢复问题，精准估计包括多普勒采样点在内的DD域信道。然后，提出一种高效的转换算法将基系数转换为信道等效矩阵。其次，将信道估计中估计得到的噪声，用于d-LSMR均衡器中进行信道均衡，并利用DD域信道矩阵的稀疏性实现快速收敛。系统仿真结果表明，与目前代表性的OTFS接收机相比，该文所提方案实现了更好的误码率性能，同时降低了计算复杂度。
- OTFS /
- 信道估计 /
- 信道均衡 /
- 高速移动 /
- 稀疏贝叶斯学习 /
- BEM
Abstract: Orthogonal Time Frequency Space (OTFS) can convert the doubly-selective channels into non-selective channels in the Delay-Doppler (DD) domain, which provides a solution for establishing reliable wireless communication in high-mobility scenarios. However, serious Inter-Doppler Interference (IDI) exists in complex multi-scattering scenarios such as internet of vehicles, which brings great challenges to the accurate demodulation of OTFS receiver signals. To solve these problems, a kind of joint Sparse Bayesian Learning (SBL) and damped Least Square Minimum Residual (d-LSMR) OTFS receiver is proposed. Firstly, based on the relationship between OTFS time domain and DD domain, the channel estimation problem is transformed into a Basis Expansion Model (BEM) to accurately estimate DD domain channels including Doppler sampling points. Then, an efficient conversion algorithm is proposed to convert the basis coefficients into channel equivalent matrix. Additionally, the noise estimated in channel estimation is used in d-LSMR equalizer, and the sparse channel matrix in DD domain is adopted to achieve fast convergence. System simulation results show that compared with the current representative OTFS receiver, the proposed scheme achieves better bit error rate performance and reduces the computational complexity.
- Orthogonal Time Frequency Space(OTFS) /
- Channel estimation /
- Channel equalization /
- High-mobility scenarios /
- Sparse Bayesian learning /
- Basis Expansion Model (BEM)

HTML全文

图 1 OTFS传输系统

下载: 全尺寸图片幻灯片

图 2 SBL算法的收敛过程

下载: 全尺寸图片幻灯片

图 3 d-LSMR算法的收敛过程

下载: 全尺寸图片幻灯片

图 4 调制方式为QPSK时接收机BER性能

下载: 全尺寸图片幻灯片

图 5 调制方式为16QAM时接收机BER性能

下载: 全尺寸图片幻灯片

算法1　基于SBL学习的基系数估计
输入：$ {\boldsymbol{y}} $,${\boldsymbol{\varPhi } }$
输出：$ {\boldsymbol{\tilde c}} $, $ \beta $
(1) 初始化：${\bar {\boldsymbol{\alpha} } ^{(0)} } = {{\text{0}}}$, $\beta = 1$
(2) while $\|\|{\bar {\boldsymbol{\alpha} } ^{(i)} } - {\bar {\boldsymbol{\alpha} } ^{(i - 1)} }\|\| < {\varepsilon _{\boldsymbol{\alpha}} }$
(3) 　for $j = 1,2, \cdots ,{{QL} }$
(4) 　　超参数更新：${\bar \alpha ^{\left( i \right)} }\left( j \right) = \varSigma _{jj}^{(i - 1)} + {\left( { {\boldsymbol{\mu} } _{\boldsymbol{c}}^{\left( {i - 1} \right)}\left( j \right)} \right)^2}$
(5) 　end
(6) 　噪声更新：${\beta ^{(i)} } = \frac{ {\|\|{\boldsymbol{y} } - {\boldsymbol{\varPhi \mu } }_c^{(i)}\|\|_2^2} }{ { {N_{\boldsymbol{p}}} - {\boldsymbol{\varSigma } }_{\boldsymbol{c}}^{(i)}(j)(1 - {\alpha ^{(i)} }(j)\varSigma _{jj}^{(i)})} }$
(7) 　后验更新：通过式(7)和式(8)，更新后验参数${\boldsymbol{\varSigma}} _{\boldsymbol{c}}^{\left( i \right)}$和${\boldsymbol{\mu}} _{\boldsymbol{c}}^{\left( i \right)}$
(8) 　$i = i + 1$
(9) end

下载: 导出CSV

算法2　基于d-LSMR的基系数均衡
输入：$ {\boldsymbol{y}} $,$ {\boldsymbol{\tilde c}} $, ${\sigma ^2}$
输出：$ {\boldsymbol{\tilde x}} $
(1) for $q = 1,2, \cdots ,Q$
(2) 　　${\boldsymbol{H = H} }{ + }\left( { {\text{circ} }\left( {\left( { {{\boldsymbol{\varXi}} _q} \odot {c_q}\left( 0 \right)} \right), \cdots \left( { {{\boldsymbol{\varXi}} _q} \odot {c_q}\left( {L - 1} \right)} \right)} \right)} \right)$
(3) end
(4) 初始化：$ {{\eta }_1}{{\boldsymbol{\nu }}_1} = {\boldsymbol{y}} $, $ {{\xi }_1}{{\boldsymbol{\omega }}_1} = {{\boldsymbol{H}}^{\text{H}}}{{\boldsymbol{\nu }}_1} $, $i = 0$ (d-LSMR均衡)
(5) while $i < M$ or ${\varepsilon _i}$收敛
(6) 　　$ {{\eta }_{i + 1}}{{\boldsymbol{\nu }}_{i + 1}} = {\boldsymbol{H}}{{\boldsymbol{\omega }}_i} - {{\xi }_i}{{\boldsymbol{\nu }}_i} $
(7) 　　$ {{\xi }_{i + 1}}{{\boldsymbol{\omega }}_{i + 1}} = {{\boldsymbol{H}}^{\text{H}}}{{\boldsymbol{\nu }}_{i + 1}} - {{\eta }_{i + 1}}{{\boldsymbol{\omega }}_i} $
(8) 　　根据式(22)QR分解得到$ {{\boldsymbol{\bar R}}_{m + 1}} $
(9) 　　求解(21)得到${{\boldsymbol{z}}_i}$，并计算残量
(10) 　 $i = i + 1$
(11) end
(12) $\tilde{{\boldsymbol{x}}}={\boldsymbol{\mathcal{W}}}{\text{} }_{i-1}{{\boldsymbol{z}}}_{i-1}$

下载: 导出CSV

表 1 信道估计/均衡算法复杂度对比

	算法	时间复杂度
信道估计	BEM-LS	$ O\left( {{M^2}{N^2}\left( {QL} \right)} \right) $
	BEM-LMMSE	$ O\left( {{M^2}{N^2}\left( {QL} \right)} \right) $
	BEM-SBL	$ O\left( {{I_S}{M^2}{N^2}\left( {QL} \right)} \right) $
信道均衡	ZF	$ O\left( {{M^3}{N^3}} \right) $
	LMMSE	$ O\left( {{M^3}{N^3}} \right) $
	d-LMSR	$ O\left( {2{M^2}{N^2} + I_K^3} \right) $

下载: 导出CSV

表 2 仿真系统参数

参数名称	参数值
子载波个数($M$)	32
符号个数($N$)	16
载波频率	5.9 GHz
调制方式	QPSK/16QAM
用户移动速度	121.5～607.5 km/h
子载波间隔	15 kHz
信道模型	EVA^[20]
CP长度	7

下载: 导出CSV

参考文献(20)

[1]	YUAN Weijie, LI Shuangyang, WEI Zhiqiang, et al. New delay Doppler communication paradigm in 6G era: A survey of orthogonal time frequency space (OTFS)[J]. China Communications, 2023, 20(6): 1–25. doi: 10.23919/JCC.fa.2022-0578.202306.
[2]	邢旺, 唐晓刚, 周一青, 等. 面向OTFS的时延-多普勒域信道估计方法综述[J]. 通信学报, 2022, 43(12): 188–201. doi: 10.11959/j.issn.1000-436x.2022224. XING Wang, TANG Xiaogang, ZHOU Yiqing, et al. Survey of channel estimation method in delay-Doppler domain for OTFS[J]. Journal on Communications, 2022, 43(12): 188–201. doi: 10.11959/j.issn.1000-436x.2022224.
[3]	WEI Zhiqiang, YUAN Weijie, LI Shuangyang, et al. Orthogonal time-frequency space modulation: A promising next-generation waveform[J]. IEEE Wireless Communications, 2021, 28(4): 136–144. doi: 10.1109/MWC.001.2000408.
[4]	LIAO Yong and LI Xue. Joint multi-domain channel estimation based on sparse Bayesian learning for OTFS system[J]. China Communications, 2023, 20(1): 14–23. doi: 10.23919/JCC.2023.01.002.
[5]	WU Yiyan and ZOU W Y. Orthogonal frequency division multiplexing: A multi-carrier modulation scheme[J]. IEEE Transactions on Consumer Electronics, 1995, 41(3): 392–399. doi: 10.1109/30.468055.
[6]	蒋占军, 刘庆达, 张鈜, 等. 高速移动通信系统中OTFS分数多普勒信道估计加窗研究[J]. 电子与信息学报, 2022, 44(2): 646–653. doi: 10.11999/JEIT210561. JIANG Zhanjun, LIU Qingda, ZHANG Hong, et al. Study on OTFS fractional Doppler channel estimation and windowing in high-speed mobile communication systems[J]. Journal of Electronics &Information Technology, 2022, 44(2): 646–653. doi: 10.11999/JEIT210561.
[7]	WEI Zhiqiang, YUAN Weijie, LI Shuangyang, et al. Transmitter and receiver window designs for orthogonal time-frequency space modulation[J]. IEEE Transactions on Communications, 2021, 69(4): 2207–2223. doi: 10.1109/TCOMM.2021.3051386.
[8]	WEI Zhiqiang, YUAN Weijie, LI Shuangyang, et al. Performance analysis and window design for channel estimation of OTFS modulation[C]. 2021 IEEE International Conference on Communications, Montreal, Canada, IEEE, 2021: 1–7.
[9]	RAMACHANDRAN M K and CHOCKALINGAM A. MIMO-OTFS in high-Doppler fading channels: Signal detection and channel estimation[C]. 2018 IEEE Global Communications Conference, Abu Dhabi, United Arab Emirates, IEEE, 2018: 206–212.
[10]	RAVITEJA P, PHAN K T, and HONG Yi. Embedded pilot-aided channel estimation for OTFS in delay–Doppler channels[J]. IEEE Transactions on Vehicular Technology, 2019, 68(5): 4906–4917. doi: 10.1109/TVT.2019.2906357.
[11]	QU Huiyang, LIU Guanghui, ZHANG Lei, et al. Low-dimensional subspace estimation of continuous-Doppler-spread channel in OTFS systems[J]. IEEE Transactions on Communications, 2021, 69(7): 4717–4731. doi: 10.1109/TCOMM.2021.3072744.
[12]	SURABHI G D and CHOCKALINGAM A. Low-complexity linear equalization for OTFS modulation[J]. IEEE Communications Letters, 2020, 24(2): 330–334. doi: 10.1109/LCOMM.2019.2956709.
[13]	THAJ T and VITERBO E. Low complexity iterative rake decision feedback equalizer for zero-padded OTFS systems[J]. IEEE Transactions on Vehicular Technology, 2020, 69(12): 15606–15622. doi: 10.1109/TVT.2020.3044276.
[14]	ZEMEN T, BERNADO L, CZINK N, et al. Iterative time-variant channel estimation for 802.11p using generalized discrete prolate spheroidal sequences[J]. IEEE Transactions on Vehicular Technology, 2012, 61(3): 1222–1233. doi: 10.1109/TVT.2012.2185526.
[15]	游康勇, 杨立山, 刘玥良, 等. 基于稀疏贝叶斯学习的网格自适应多源定位[J]. 电子与信息学报, 2018, 40(9): 2150–2157. doi: 10.11999/JEIT171238. YOU Kangyong, YANG Lishan, LIU Yueliang, et al. Adaptive grid multiple sources localization based on sparse Bayesian learning[J]. Journal of Electronics &Information Technology, 2018, 40(9): 2150–2157. doi: 10.11999/JEIT171238.
[16]	FONG D C L and SAUNDERS M. LSMR: An iterative algorithm for sparse least-squares problems[J]. SIAM Journal on Scientific Computing, 2011, 33(5): 2950–2971. doi: 10.1137/10079687X.
[17]	HONG Linyi and ZHANG Naimin. On the preconditioned MINRES method for solving singular linear systems[J]. Computational and Applied Mathematics, 2022, 41(7): 304. doi: 10.1007/s40314-022-02007-w.
[18]	DANAEI K, MORADZADEH A, NOROUZI G H, et al. 3D inversion of gravity data with unstructured mesh and least-squares QR-factorization (LSQR)[J]. Journal of Applied Geophysics, 2022, 206: 104781. doi: 10.1016/j.jappgeo.2022.104781.
[19]	GOLUB G and KAHAN W. Calculating the singular values and pseudo-inverse of a matrix[J]. Journal of the Society for Industrial and Applied Mathematics Series B Numerical Analysis, 1965, 2(2): 205–224. doi: 10.1137/0702016.
[20]	3GPP TS 36.101 (V17.0. 0) Technical specification group radio access network; Evolved universal terrestrial radio access (E-UTRA); User equipment (UE) radio transmission and reception[S]. 2020.